Stability and Distributed Optimization for AC Microgrid Considering Line Losses and Time Delay
Abstract
:1. Introduction
2. Related Works and Problem Formulations
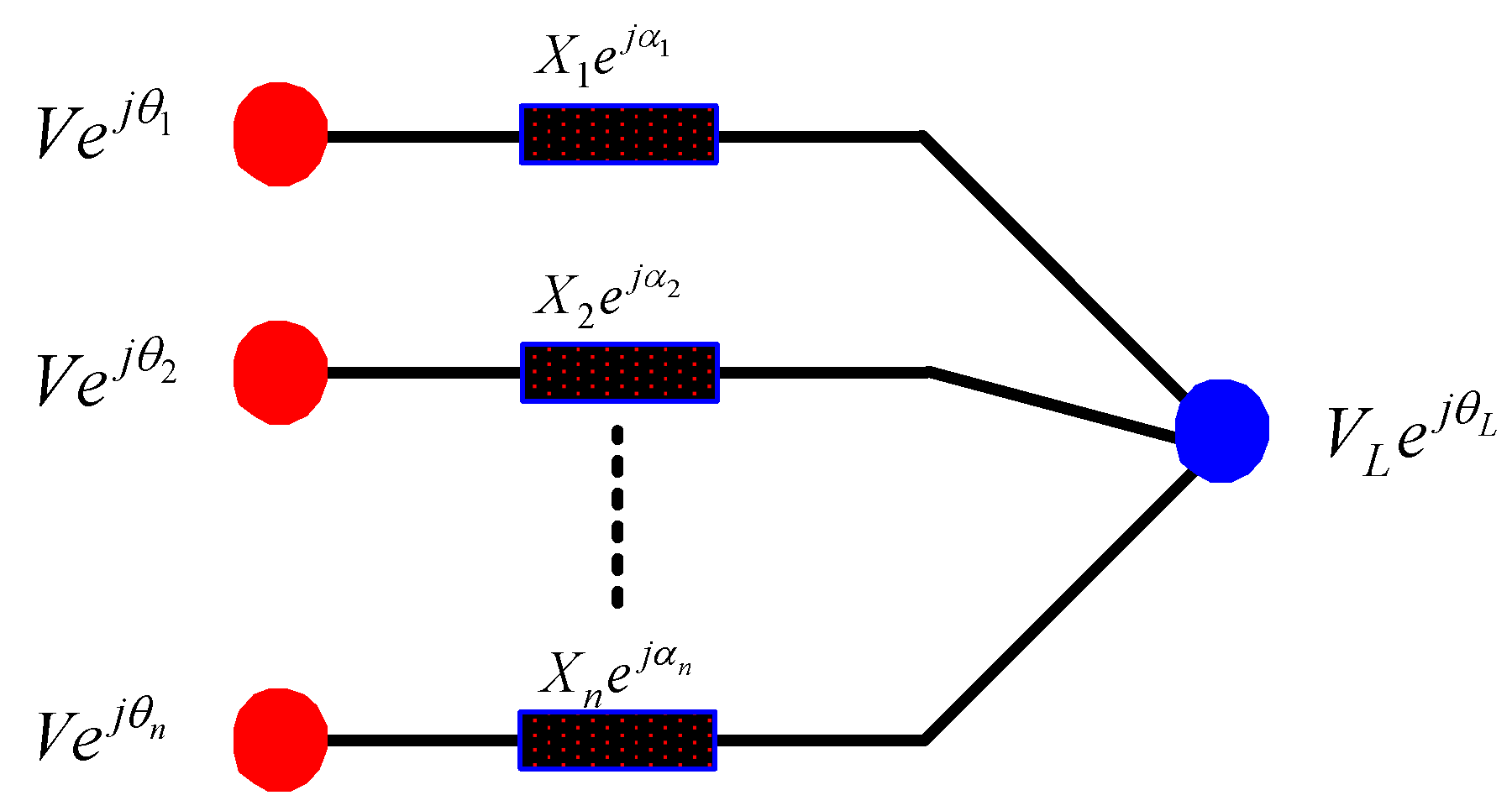
2.1. The Economic Dispatch Problem Considering Line Losses
2.2. The Existing Distributed Optimal Dispatch Approaches
2.3. Motivations of This Paper
3. The Proposed Distributed Cooperative Control Method for Optimal Dispatch Considering Line Losses
3.1. The Optimality Conditions of the ED Problem Considering Line Losses
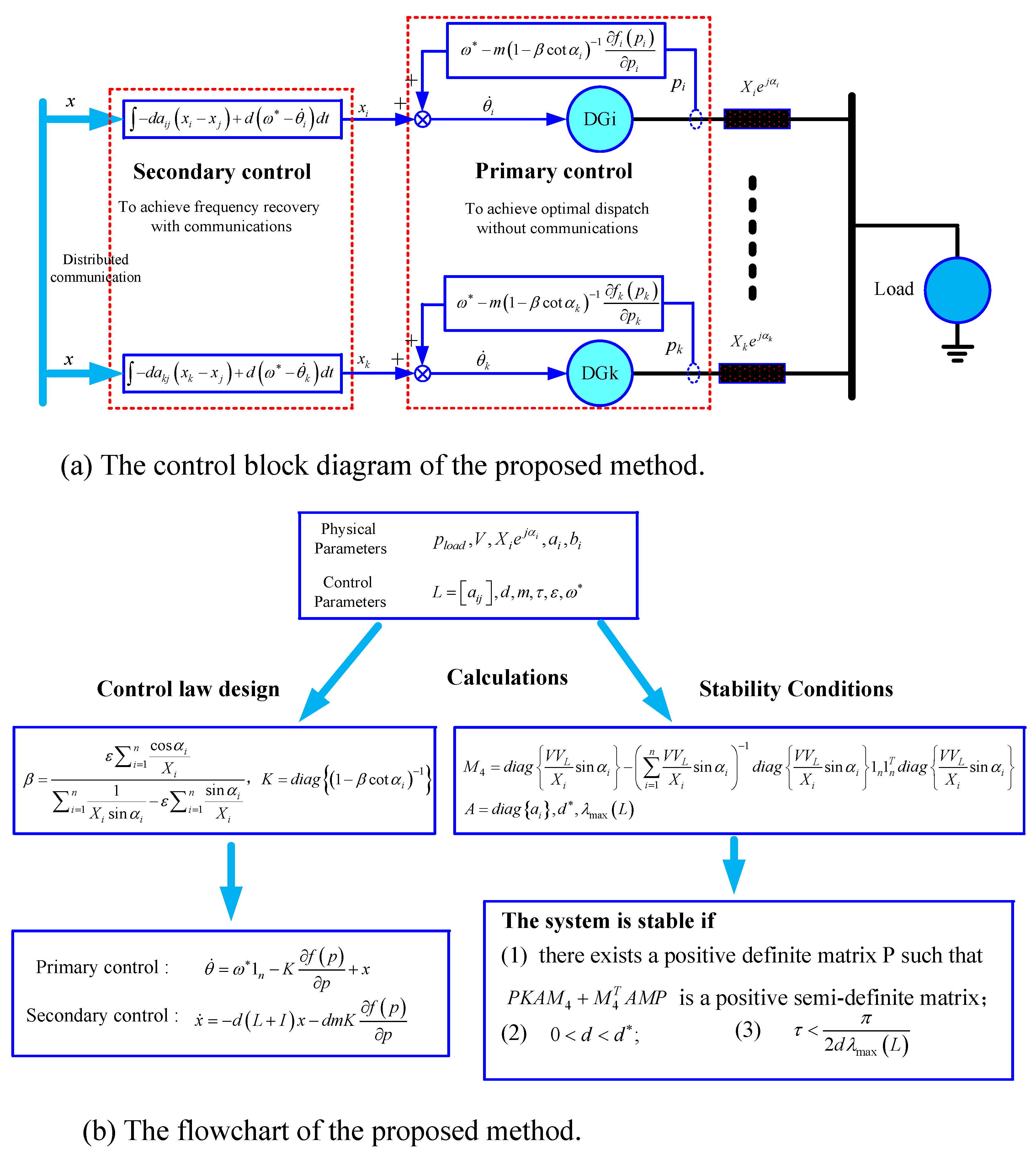
3.2. The Proposed Distributed Cooperative Control Method
3.3. Comparative Analysis
4. Stability Analysis of the System under the Proposed Method
4.1. Stability Analysis of the System without Communications
4.2. Stability Analysis of the System without Communication Delay
4.3. Stability Analysis of the System with Communication Delay
5. Simulations
5.1. Stability Test of the System under the Proposed Method
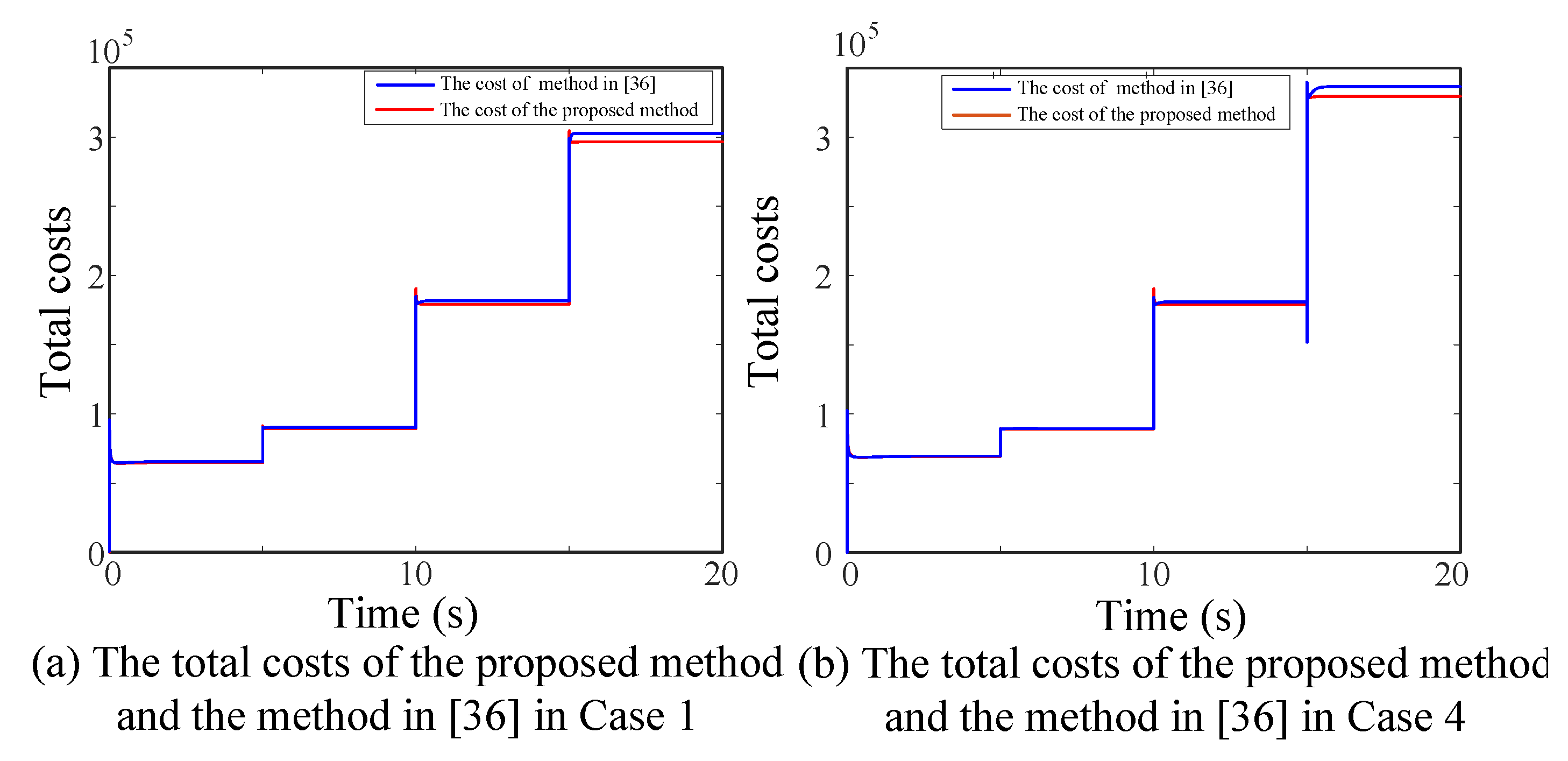
5.2. Compared with the Existing Method in [36]
5.3. Discussions about the Performance of the Proposed Method under Parameter Uncertainties
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, H.; Li, L.; Wang, L.; Su, M.; Zhao, Y.; Guerrero, J.M. A novel decentralized economic operation in islanded AC microgrids. Energies 2017, 10, 804. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Su, M.; Sun, Y.; Li, L.; Han, H.; Zhang, X.; Zheng, M. Optimal criterion and global/sub-optimal control schemes of decentralized economical dispatch for AC microgrid. Int. J. Electr. Power Energy Syst. 2019, 104, 38–42. [Google Scholar] [CrossRef]
- Low, S.H.; Lapsley, D.E. Optimization flow control. I. Basic algorithm and convergence. IEEE/ACM Trans. Netw. 1999, 7, 861–874. [Google Scholar] [CrossRef] [Green Version]
- Lavaei, J.; Low, S.H. Zero duality gap in optimal power flow problem. IEEE Trans. Power Syst. 2011, 27, 92–107. [Google Scholar] [CrossRef] [Green Version]
- Halilbašić, L.; Pinson, P.; Chatzivasileiadis, S. Convex relaxations and approximations of chance-constrained AC-OPF problems. IEEE Trans. Power Syst. 2018, 34, 1459–1470. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Cui, B.; Wang, Z.; Gu, C. SDP-based optimal power flow with steady-state voltage stability constraints. IEEE Trans. Smart Grid 2018, 10, 4637–4647. [Google Scholar] [CrossRef]
- Sojoudi, S.; Fattahi, S.; Lavaei, J. Convexification of generalized network flow problem. Math. Program. 2019, 173, 353–391. [Google Scholar] [CrossRef]
- Cui, B.; Sun, X.A. A new voltage stability-constrained optimal power-flow model: Sufficient condition, SOCP representation, and relaxation. IEEE Trans. Power Syst. 2018, 33, 5092–5102. [Google Scholar] [CrossRef] [Green Version]
- Bakirtzis, A.G.; Biskas, P.N.; Zoumas, C.E.; Petridis, V. Optimal power flow by enhanced genetic algorithm. IEEE Trans. Power Syst. 2002, 17, 229–236. [Google Scholar] [CrossRef]
- Gaing, Z.L. Particle swarm optimization to solving the economic dispatch considering the generator constraints. IEEE Trans. Power Syst. 2003, 18, 1187–1195. [Google Scholar] [CrossRef]
- Bilal, M.; Shahzad, M.; Arif, M.; Ullah, B.; Hisham, S.B.; Ali, S.S.A. Annual cost and loss minimization in a radial distribution network by capacitor allocation using pso. Appl. Sci. 2021, 11, 11840. [Google Scholar] [CrossRef]
- Shahzad, M.; Shafiullah, Q.; Akram, W.; Arif, M.; Ullah, B. Reactive power support in radial distribution network using mine blast algorithm. Elektron. Elektrotechnika 2021, 27, 33–40. [Google Scholar] [CrossRef]
- Shahzad, M.; Akram, W.; Arif, M.; Khan, U.; Ullah, B. Optimal siting and sizing of distributed generators by strawberry plant propagation algorithm. Energies 2021, 14, 1744. [Google Scholar] [CrossRef]
- Pan, X.; Chen, M.; Zhao, T.; Low, S.H. DeepOPF: A feasibility-optimized deep neural network approach for AC optimal power flow problems. arXiv 2022, arXiv:2007.01002. [Google Scholar] [CrossRef]
- Shahzad, M.; Ahmad, I.; Gawlik, W.; Palensky, P. Active power loss minimization in radial distribution networks with analytical method of simultaneous optimal DG sizing. In Proceedings of the 2016 IEEE International Conference on Industrial Technology (ICIT), Taipei, Taiwan, 14–17 March 2016; pp. 470–475. [Google Scholar]
- Ihsan, M.; Shahzad, M.; Ullah, N. Analytical method for optimal reactive power support in power network. In Proceedings of the 2019 2nd International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 30–31 January 2019; pp. 1–6. [Google Scholar]
- Shahzad, M.; Qadir, A.; Ullah, N.; Mahmood, Z.; Saad, N.M.; Ali, S.S.A. Optimization of on-grid hybrid renewable energy system: A case study on Azad Jammu and Kashmir. Sustainability 2022, 14, 5757. [Google Scholar] [CrossRef]
- Ishraque, M.; Shezan, S.A.; Rana, M.; Muyeen, S.; Rahman, A.; Paul, L.C.; Islam, M. Optimal sizing and assessment of a renewable rich standalone hybrid microgrid considering conventional dispatch methodologies. Sustainability 2021, 13, 12734. [Google Scholar] [CrossRef]
- Rana, M.M.; Rahman, A.; Uddin, M.; Sarkar, M.R.; Shezan, S.A.; Ishraque, M.F.; Rafin, S.S.H.; Atef, M. A comparative analysis of peak load shaving strategies for isolated microgrid using actual data. Energies 2022, 15, 330. [Google Scholar] [CrossRef]
- Arfeen, Z.A.; Sheikh, U.U.; Azam, M.K.; Hassan, R.; Faisal Shehzad, H.M.; Ashraf, S.; Abdullah, M.P.; Aziz, L. A comprehensive review of modern trends in optimization techniques applied to hybrid microgrid systems. Concurr. Comput. Pract. Exp. 2021, 33, e6165. [Google Scholar] [CrossRef]
- Han, H.; Wang, H.; Sun, Y.; Yang, J.; Liu, Z. Distributed control scheme on cost optimisation under communication delays for DC microgrids. IET Gener. Transm. Distrib. 2017, 11, 4193–4201. [Google Scholar] [CrossRef]
- Shezan, S.; Delwar, M.H.; Anowar, M.T.; Islam, M.; Kabir, M.; Reduanul, M.; Hasan, M. Technological analysis of a solar-wind-battery-diesel hybrid energy system with fuzzy logic controller. Int. J. Res. Eng. Sci. (IJRES) 2016, 4, 46–57. [Google Scholar]
- Nutkani, I.U.; Loh, P.C.; Wang, P.; Blaabjerg, F. Decentralized economic dispatch scheme with online power reserve for microgrids. IEEE Trans. Smart Grid 2015, 8, 139–148. [Google Scholar] [CrossRef]
- Nutkani, I.U.; Chiang Loh, P.; Blaabjerg, F. Cost-based droop scheme with lower generation costs for microgrids. IET Power Electron. 2014, 7, 1171–1180. [Google Scholar] [CrossRef]
- Cingoz, F.; Elrayyah, A.; Sozer, Y. Plug-and-play nonlinear droop construction scheme to optimize islanded microgrid operations. IEEE Trans. Power Electron. 2016, 32, 2743–2756. [Google Scholar] [CrossRef]
- Nutkani, I.U.; Loh, P.C.; Wang, P.; Blaabjerg, F. Linear decentralized power sharing schemes for economic operation of AC microgrids. IEEE Trans. Ind. Electron. 2015, 63, 225–234. [Google Scholar] [CrossRef]
- Elrayyah, A.; Cingoz, F.; Sozer, Y. Construction of nonlinear droop relations to optimize islanded microgrid operation. IEEE Trans. Ind. Appl. 2015, 51, 3404–3413. [Google Scholar] [CrossRef]
- Chen, F.; Chen, M.; Li, Q.; Meng, K.; Zheng, Y.; Guerrero, J.M.; Abbott, D. Cost-based droop schemes for economic dispatch in islanded microgrids. IEEE Trans. Smart Grid 2016, 8, 63–74. [Google Scholar] [CrossRef] [Green Version]
- Guo, F.; Wen, C.; Mao, J.; Song, Y.D. Distributed economic dispatch for smart grids with random wind power. IEEE Trans. Smart Grid 2015, 7, 1572–1583. [Google Scholar] [CrossRef]
- Tang, Z.; Hill, D.J.; Liu, T. A novel consensus-based economic dispatch for microgrids. IEEE Trans. Smart Grid 2018, 9, 3920–3922. [Google Scholar] [CrossRef]
- Li, Q.; Gao, D.W.; Zhang, H.; Wu, Z.; Wang, F.Y. Consensus-based distributed economic dispatch control method in power systems. IEEE Trans. Smart Grid 2017, 10, 941–954. [Google Scholar] [CrossRef]
- Binetti, G.; Davoudi, A.; Lewis, F.L.; Naso, D.; Turchiano, B. Distributed consensus-based economic dispatch with transmission losses. IEEE Trans. Power Syst. 2014, 29, 1711–1720. [Google Scholar] [CrossRef]
- Liu, T.; Tan, X.; Sun, B.; Wu, Y.; Tsang, D.H. Energy management of cooperative microgrids: A distributed optimization approach. Int. J. Electr. Power Energy Syst. 2018, 96, 335–346. [Google Scholar] [CrossRef]
- Li, Z.; Zang, C.; Zeng, P.; Yu, H.; Li, S. Fully distributed hierarchical control of parallel grid-supporting inverters in islanded AC microgrids. IEEE Trans. Ind. Inform. 2017, 14, 679–690. [Google Scholar] [CrossRef]
- Molzahn, D.K.; Dörfler, F.; Sandberg, H.; Low, S.H.; Chakrabarti, S.; Baldick, R.; Lavaei, J. A survey of distributed optimization and control algorithms for electric power systems. IEEE Trans. Smart Grid 2017, 8, 2941–2962. [Google Scholar] [CrossRef]
- Xu, Y.; Dong, Z.; Li, Z.; Liu, Y.; Ding, Z. Distributed optimization for integrated frequency regulation and economic dispatch in microgrids. IEEE Trans. Smart Grid 2021, 12, 4595–4606. [Google Scholar] [CrossRef]
- Yang, J.; Feng, W.; Hou, X.; Xia, Q.; Zhang, X.; Wang, P. A distributed cooperative control algorithm for optimal power flow and voltage regulation in DC power system. IEEE Trans. Power Deliv. 2019, 35, 892–903. [Google Scholar] [CrossRef]
- Zhao, T.; Ding, Z. Distributed finite-time optimal resource management for microgrids based on multi-agent framework. IEEE Trans. Ind. Electron. 2017, 65, 6571–6580. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Sun, H. Distributed finite-time convergence control of an islanded low-voltage AC microgrid. IEEE Trans. Power Syst. 2017, 33, 2339–2348. [Google Scholar] [CrossRef]
- Li, Z.; Cheng, Z.; Liang, J.; Si, J.; Dong, L.; Li, S. Distributed event-triggered secondary control for economic dispatch and frequency restoration control of droop-controlled AC microgrids. IEEE Trans. Sustain. Energy 2019, 11, 1938–1950. [Google Scholar] [CrossRef]
- Shezan, S.; Lai, C.Y. Optimization of hybrid wind-diesel-battery energy system for remote areas of Malaysia. In Proceedings of the 2017 Australasian Universities Power Engineering Conference (AUPEC), Melbourne, VIC, Australia, 19–22 November 2017; pp. 1–6. [Google Scholar]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Su, M.; Sun, Y.; Yuan, W.; Han, H.; Feng, J. Existence and stability of equilibrium of DC microgrid with constant power loads. IEEE Trans. Power Syst. 2018, 33, 6999–7010. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Su, M.; Sun, Y.; Zhang, X.; Liang, X.; Zheng, M. A comprehensive study on the existence and stability of equilibria of DC-distribution networks with constant power loads. IEEE Trans. Autom. Control 2021, 67, 1988–1995. [Google Scholar] [CrossRef]
- Su, M.; Liu, Z.; Sun, Y.; Han, H.; Hou, X. Stability analysis and stabilization methods of DC microgrid with multiple parallel-connected DC–DC converters loaded by CPLs. IEEE Trans. Smart Grid 2016, 9, 132–142. [Google Scholar] [CrossRef]
- Simpson-Porco, J.W.; Dörfler, F.; Bullo, F. Synchronization and power sharing for droop-controlled inverters in islanded microgrids. Automatica 2013, 49, 2603–2611. [Google Scholar] [CrossRef] [Green Version]
- Stykel, T. Stability and inertia theorems for generalized Lyapunov equations. Linear Algebra Its Appl. 2002, 355, 297–314. [Google Scholar] [CrossRef] [Green Version]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Patience Hall: Hoboken, NJ, USA, 2002; Volume 115. [Google Scholar]





| The Costs of Case 1/ Case 4 under the Proposed Method | The Costs of Case 1/Case 4 under the Method in [36] | |
|---|---|---|
| = 2 kW | 64,719.2/69,474.5 | 64,796.8/69,637.7 |
| = 2.5 kW | 89,269.8/89,269.8 | 89,540.0/89,540.0 |
| = 4 kW | 179,104.4/179,104.4 | 181,067.6/181,067.6 |
| = 5.5 kW | 296,492.8/329,715.1 | 302,075.7/336,635.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, S.; Wang, L.; Li, T.; Cheng, Z.; Hu, X.; Liu, Z.; Huang, J. Stability and Distributed Optimization for AC Microgrid Considering Line Losses and Time Delay. Electronics 2023, 12, 1698. https://doi.org/10.3390/electronics12071698
Zeng S, Wang L, Li T, Cheng Z, Hu X, Liu Z, Huang J. Stability and Distributed Optimization for AC Microgrid Considering Line Losses and Time Delay. Electronics. 2023; 12(7):1698. https://doi.org/10.3390/electronics12071698
Chicago/Turabian StyleZeng, Siming, Lei Wang, Tiecheng Li, Ziwei Cheng, Xuekai Hu, Zhangjie Liu, and Jungao Huang. 2023. "Stability and Distributed Optimization for AC Microgrid Considering Line Losses and Time Delay" Electronics 12, no. 7: 1698. https://doi.org/10.3390/electronics12071698






