Distributed Economic Control Method for Energy Storage Unit with Random Time Delay
Abstract
:1. Introduction
2. Preliminaries
2.1. Algebraic Graph Theory
2.2. Economic Dispatch
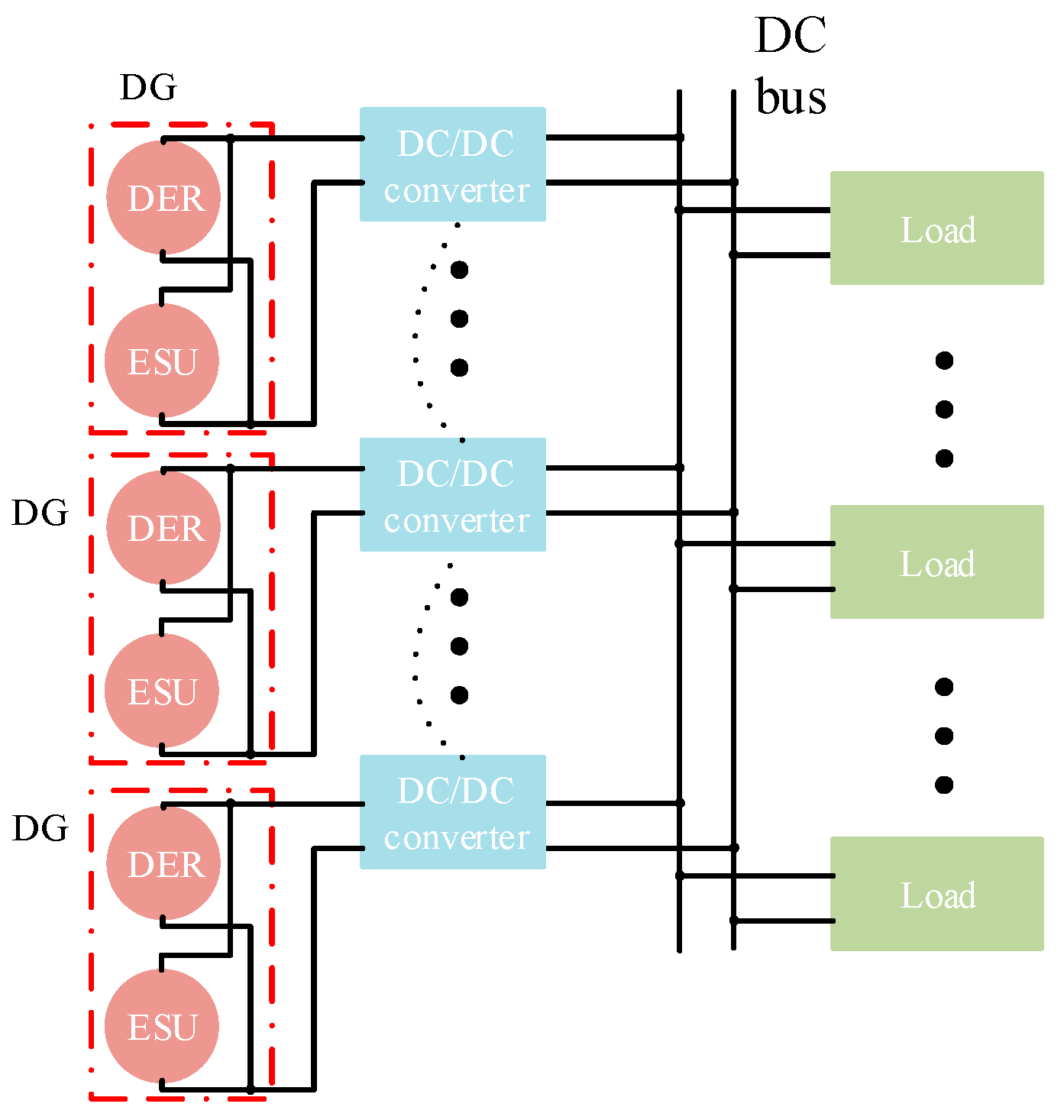
2.3. Control Structure
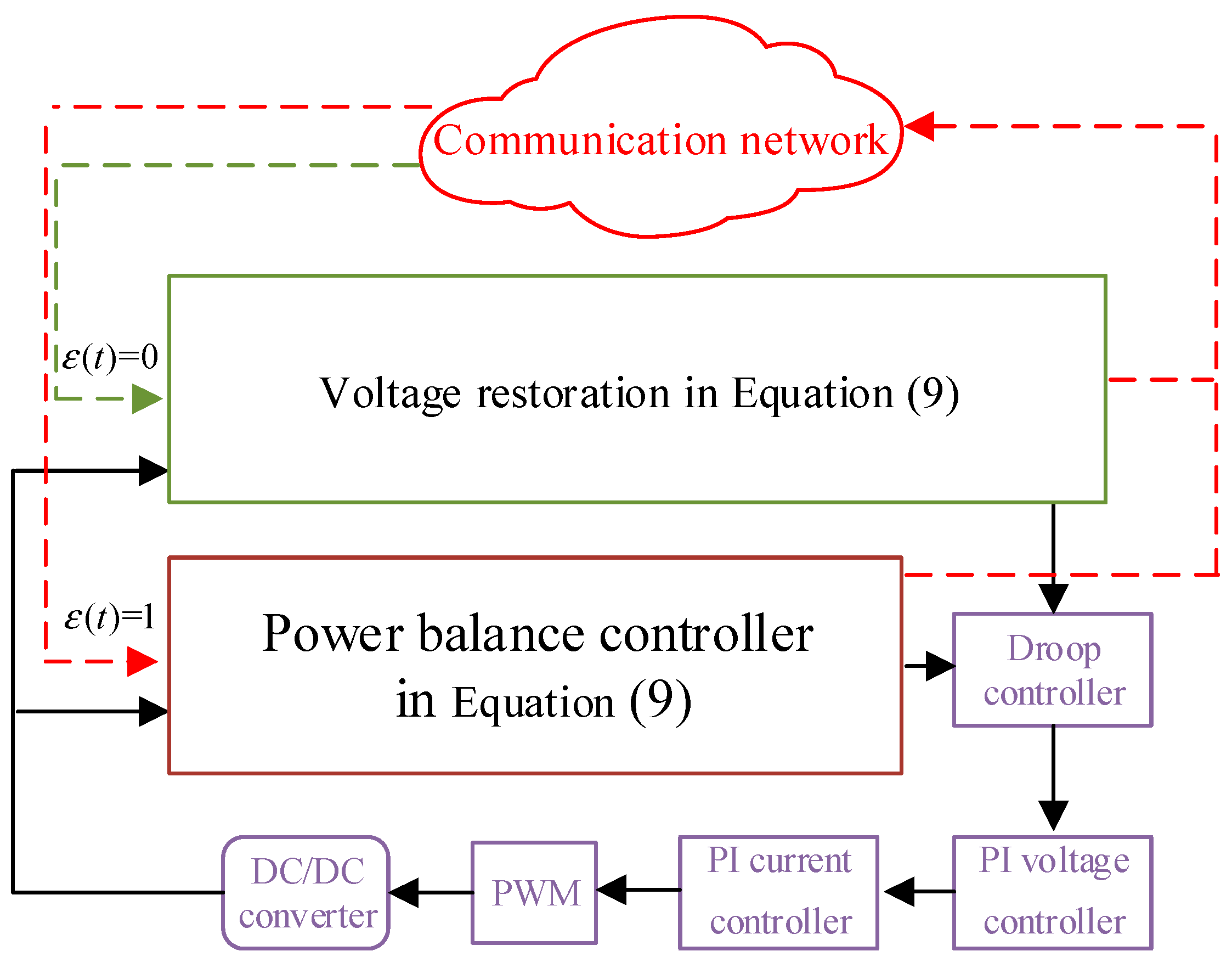
3. Proposed Control Scheme
3.1. Distributed Cooperative Control for Economic Operation
3.1.1. Voltage Restoration
3.1.2. Power Balance
3.2. Distributed Cooperative Control for Economic Dispatch with Random Delay Effect
3.3. Stability Analysis
3.3.1. Voltage Restoration
3.3.2. Economic Power Sharing
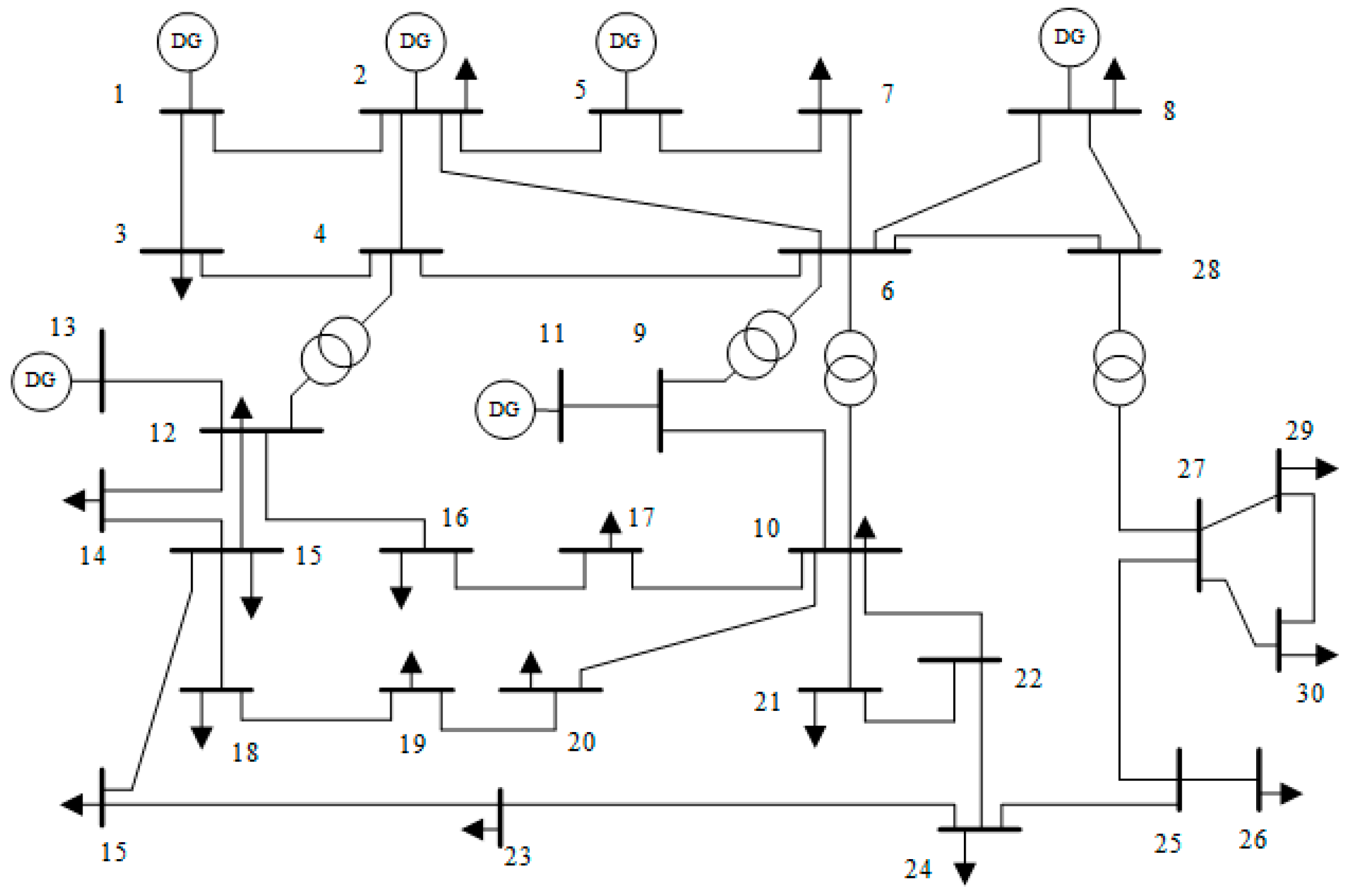
4. Simulation
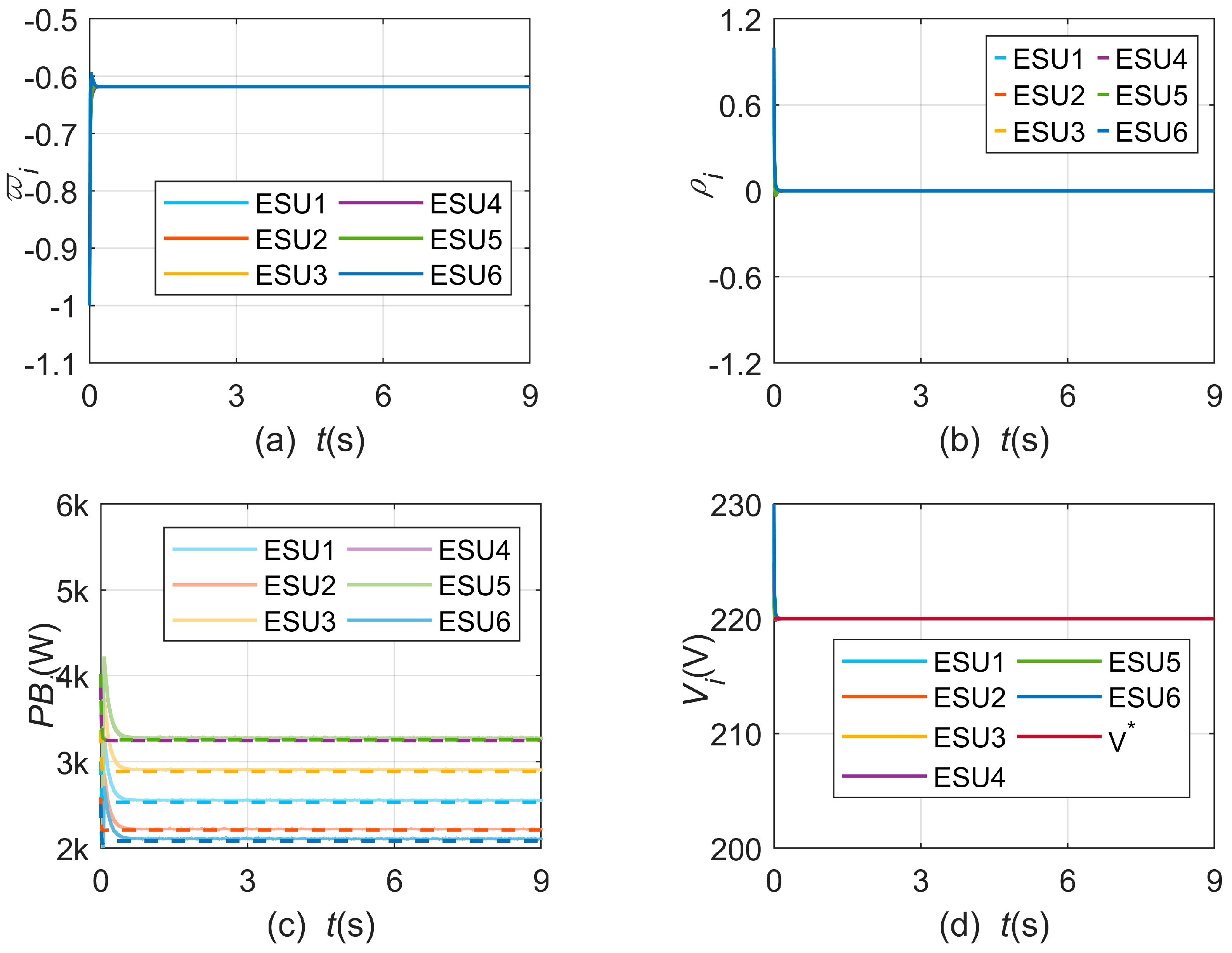
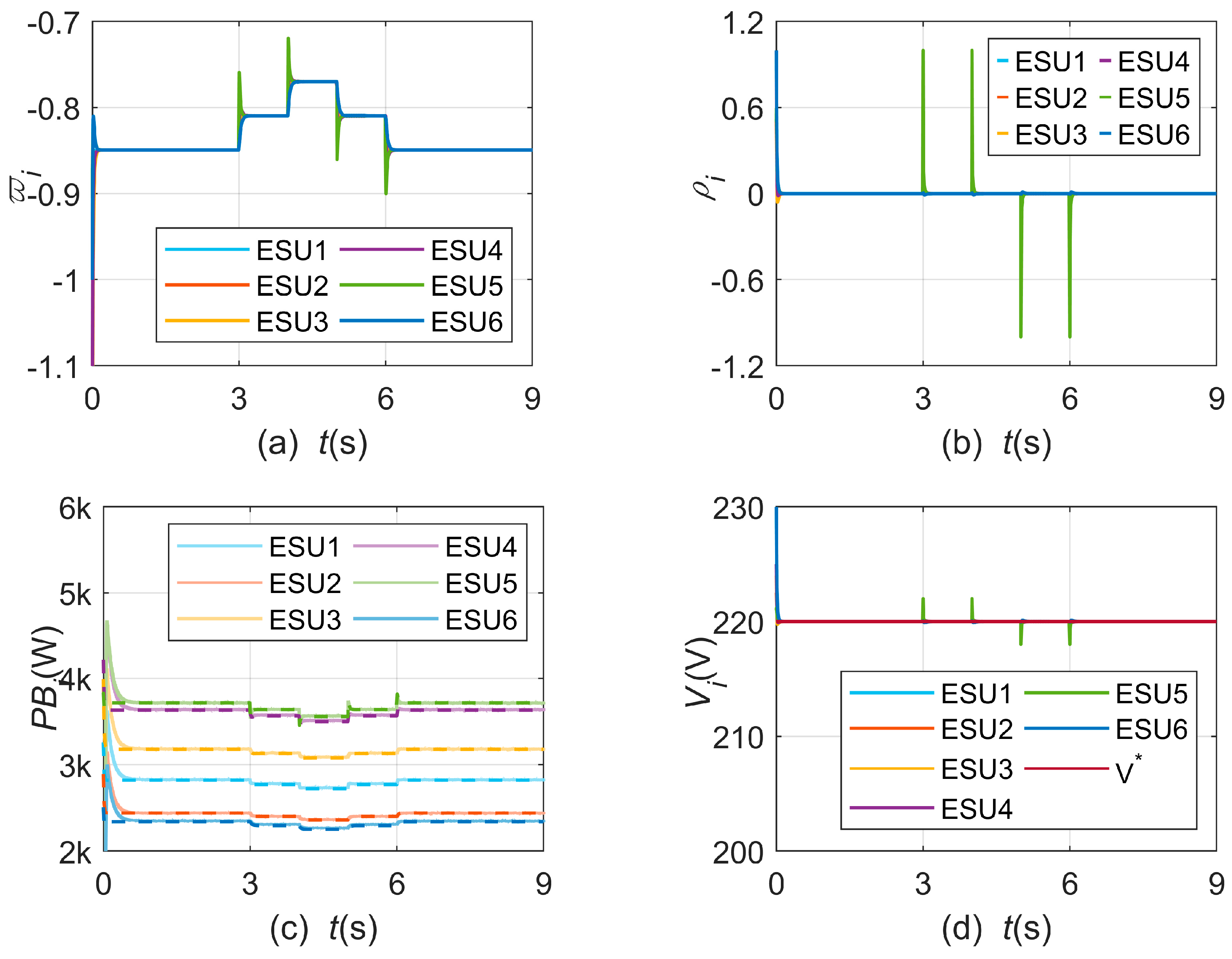
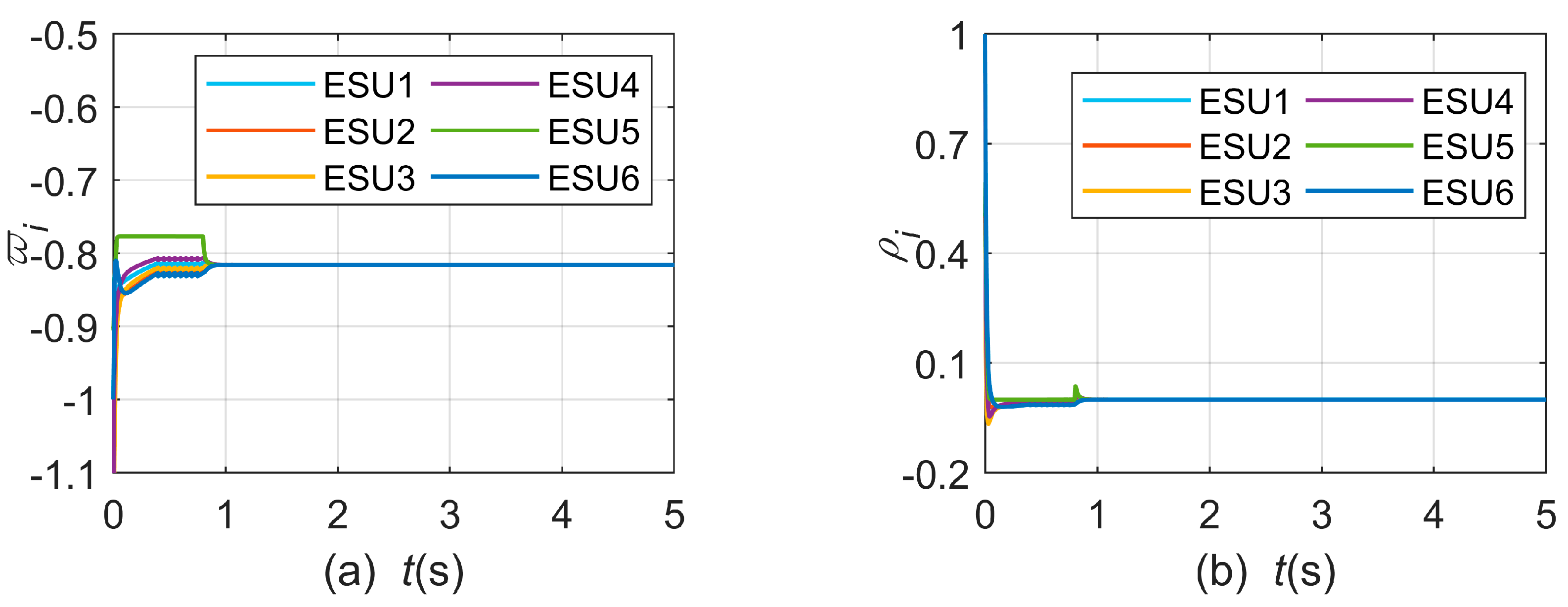
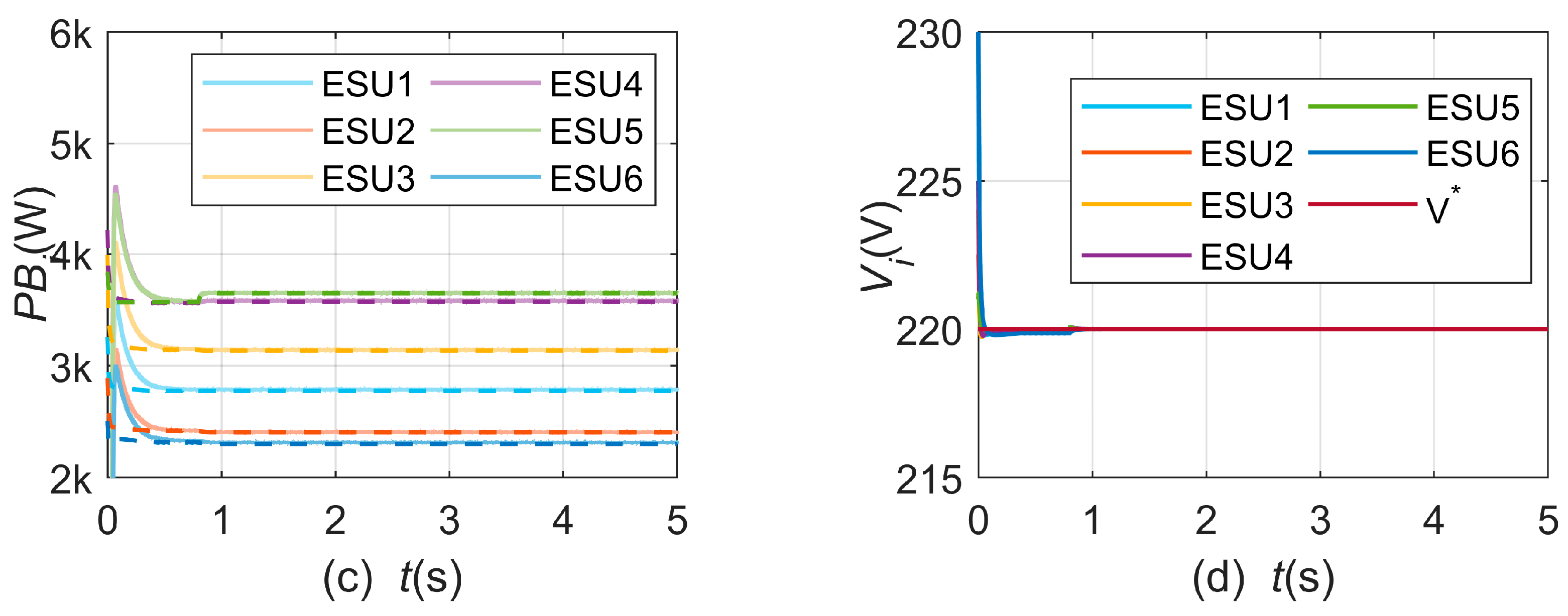
4.1. Case 1: Normal Operation
4.2. Case 2: Load Variation
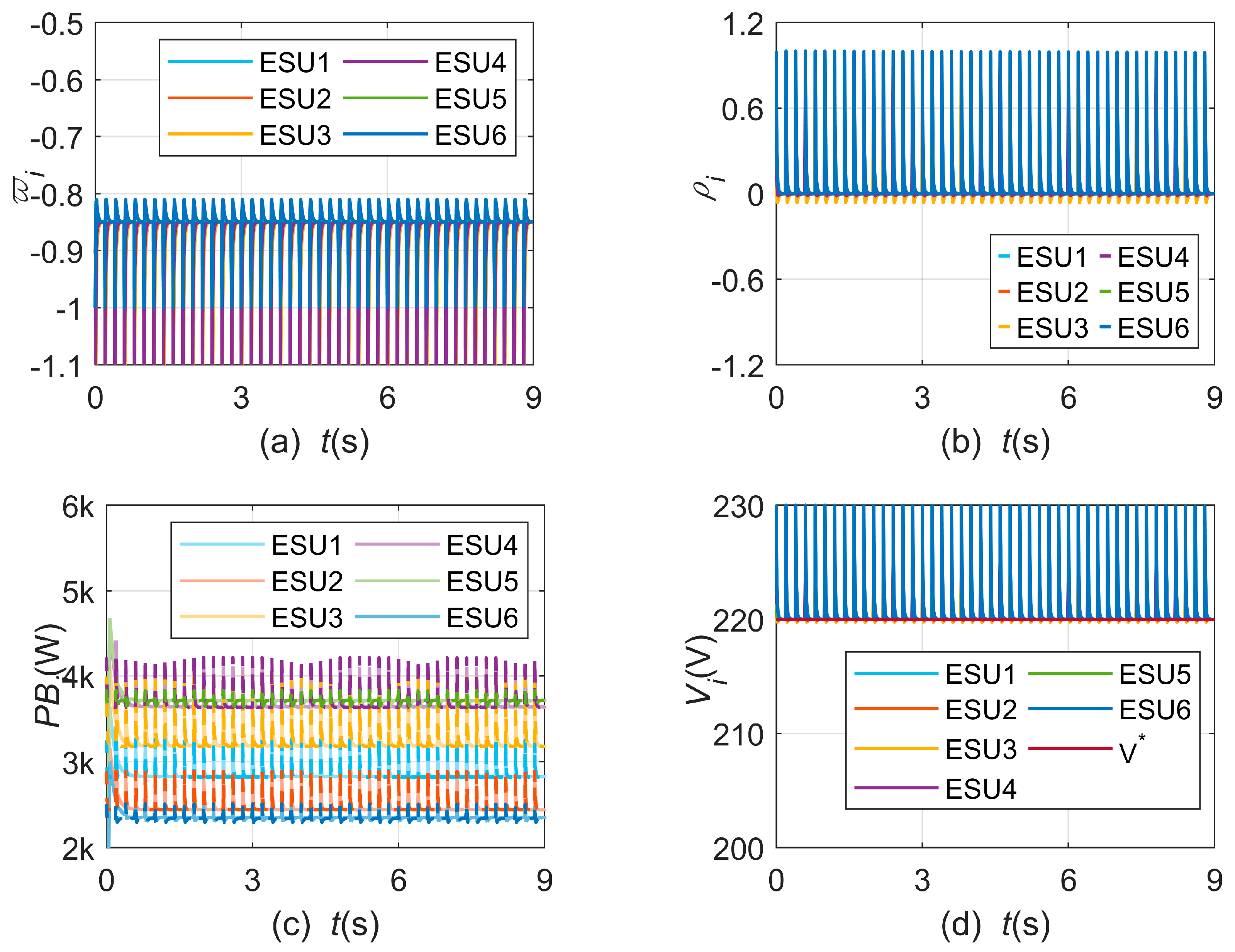
4.3. Case 3: Communication Failure
4.4. Case 4: Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lai, J.; Lu, X.; Yu, X.; Monti, A. Stochastic Distributed Secondary Control for AC Microgrids via Event-Triggered Communication. IEEE Trans. Smart Grid 2019, 11, 2746–2759. [Google Scholar] [CrossRef]
- Lai, J.; Lu, X.; Yu, X.; Yao, W.; Wen, J.; Cheng, S. Distributed Multi-DER Cooperative Control for Master-Slave-Organized Microgrid Networks with Limited Communication Bandwidth. IEEE Trans. Ind. Inform. 2018, 15, 3443–3456. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Schenato, L.; Garone, E. A distributed optimal power management system for microgrids with plug&play capabilities. Adv. Control. Appl. 2021, 3, 65. [Google Scholar]
- Liu, G.; Ferrari, M.F.; Ollis, T.B.; Tomsovic, K. An MILP-Based Distributed Energy Management for Coordination of Networked Microgrids. Energies 2022, 15, 6971. [Google Scholar] [CrossRef]
- Alagoz, B.B.; Kaygusuz, A.; Karabiber, A. A user-mode distributed energy management architecture for smart grid applications. Energy 2012, 44, 167–177. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Liang, H.; Man, Y.; Li, F.; Li, W. Collaborative optimization of dynamic grid dispatch with wind power. Int. J. Electr. Power Energy Syst. 2021, 133, 107196. [Google Scholar] [CrossRef]
- Sakthivel, V.P.; Suman, M.; Sathya, P.D. Combined economic and emission power dispatch problems through multi-objective squirrel search algorithm. Appl. Soft Comput. 2021, 100, 106950. [Google Scholar] [CrossRef]
- Xu, J.; Wang, B.; Sun, Y.; Xu, Q.; Liu, J.; Cao, H.; Jiang, H.; Lei, R.; Shen, M. A day-ahead economic dispatch method considering extreme scenarios based on wind power uncertainty. CSEE J. Power Energy Syst. 2019, 5, 224–233. [Google Scholar] [CrossRef]
- Tang, C.; Xu, J.; Tan, Y.; Sun, Y.; Zhang, B. Lagrangian Relaxation with Incremental Proximal Method for Economic Dispatch with Large Numbers of Wind Power Scenarios. IEEE Trans. Power Syst. 2019, 34, 2685–2695. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, C.; Tong, L. Pricing Multi-Interval Dispatch Under Uncertainty Part I: Dispatch-Following Incentives. IEEE Trans. Power Syst. 2021, 36, 3865–3877. [Google Scholar] [CrossRef]
- Baros, S.; Chen, Y.C.; Dhople, S.V. Examining the Economic Optimality of Automatic Generation Control. IEEE Trans. Power Syst. 2021, 36, 4611–4620. [Google Scholar] [CrossRef]
- Liu, Q.; Le, X.; Li, K. A Distributed Optimization Algorithm Based on Multiagent Network for Economic Dispatch with Region Partitioning. IEEE Trans. Cybern. 2021, 51, 2466–2475. [Google Scholar] [CrossRef] [PubMed]
- Selladurai, R.; Chelladurai, C.; Jayakumar, M. Optimal dispatch of generators based on network constrained to enhance power deliverable using the heuristic approach. Environ. Sci. Pollut. Res. 2022, 22, 1. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Xing, J.; Jiang, Z.; Li, J. Decentralized economic dispatch of an isolated distributed generator network. Int. J. Electr. Power Energy Syst. 2019, 105, 297–304. [Google Scholar] [CrossRef]
- Psarros, G.N.; Dratsas, P.A.; Papathanassiou, S.A. A comparison between central- and self-dispatch storage management principles in island systems. Appl. Energy 2021, 298, 117181. [Google Scholar] [CrossRef]
- Hou, H.; Chen, Y.; Liu, P.; Xie, C.; Huang, L.; Zhang, R.; Zhang, Q. Multisource Energy Storage System Optimal Dispatch Among Electricity Hydrogen and Heat Networks from the Energy Storage Operator Prospect. IEEE Trans. Ind. Appl. 2022, 58, 2825–2835. [Google Scholar] [CrossRef]
- Chen, G.; Zhao, Z. Delay Effects on Consensus-Based Distributed Economic Dispatch Algorithm in Microgrid. IEEE Trans. Power Syst. 2018, 33, 602–612. [Google Scholar] [CrossRef]
- Zhang, Y.; He, Y.; Long, F.; Zhang, C.-K. Mixed-Delay-Based Augmented Functional for Sampled-Data Synchronization of Delayed Neural Networks with Communication Delay. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Qian, Y.; Wang, P. Leader-following consensus of delayed multi-agent systems with aperiodically intermittent communications. Neurocomputing 2021, 466, 49–57. [Google Scholar] [CrossRef]
- Pang, N.; Luo, Y.; Zhu, Y. A novel model for linear dynamic system with random delays. Automatica 2019, 99, 346–351. [Google Scholar] [CrossRef]
- Yu, M.; Song, C.; Feng, S.; Tan, W. A consensus approach for economic dispatch problem in a microgrid with random delay effects. Int. J. Electr. Power Energy Syst. 2020, 118, 105794. [Google Scholar] [CrossRef]
- Yu, C.; Zhou, H.; Lu, X.; Lai, J. Frequency Synchronization and Power Optimization for Microgrids With Battery Energy Storage Systems. IEEE Trans. Control. Syst. Technol. 2021, 29, 2247–2254. [Google Scholar] [CrossRef]
- Lai, J.; Lu, X.; Monti, A.; De Doncker, R.W. Event-Driven Distributed Active and Reactive Power Dispatch for CCVSI-Based Distributed Generators in AC Microgrids. IEEE Trans. Ind. Appl. 2020, 56, 3125–3136. [Google Scholar] [CrossRef]
| Parameter | Symbol | Value |
|---|---|---|
| Nominal voltage | V* | 220 V |
| DG power | PG,i | {12, 10, 11, 11, 12, 11} kW |
| Local load | PL,i | {6, 7.5, 8, 8.5, 9.5, 6} kW |
| Total demand | PL | 46 kW |
| Droop coefficient | Di | {10, 5, 4, 5, 2, 8} |
| Charging coefficient | αi | −0.038 |
| Charging coefficient | βi | 0.118 |
| Time delay | τ | [0, 0.16] s |
| Voltage restoration delay bound | τVmax | 0.22 s |
| Economic control delay bound | τBmax | 0.18 s |
| Maximum allowable delay bound | τmax | 0.18 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Gong, Q.; Chen, J.; Fang, L. Distributed Economic Control Method for Energy Storage Unit with Random Time Delay. Electronics 2023, 12, 1770. https://doi.org/10.3390/electronics12081770
Chen S, Gong Q, Chen J, Fang L. Distributed Economic Control Method for Energy Storage Unit with Random Time Delay. Electronics. 2023; 12(8):1770. https://doi.org/10.3390/electronics12081770
Chicago/Turabian StyleChen, Shi, Qingwu Gong, Jing Chen, and Li Fang. 2023. "Distributed Economic Control Method for Energy Storage Unit with Random Time Delay" Electronics 12, no. 8: 1770. https://doi.org/10.3390/electronics12081770





