Design and Evaluation of Dynamic Topology for Mega Constellation Networks
Abstract
:1. Introduction
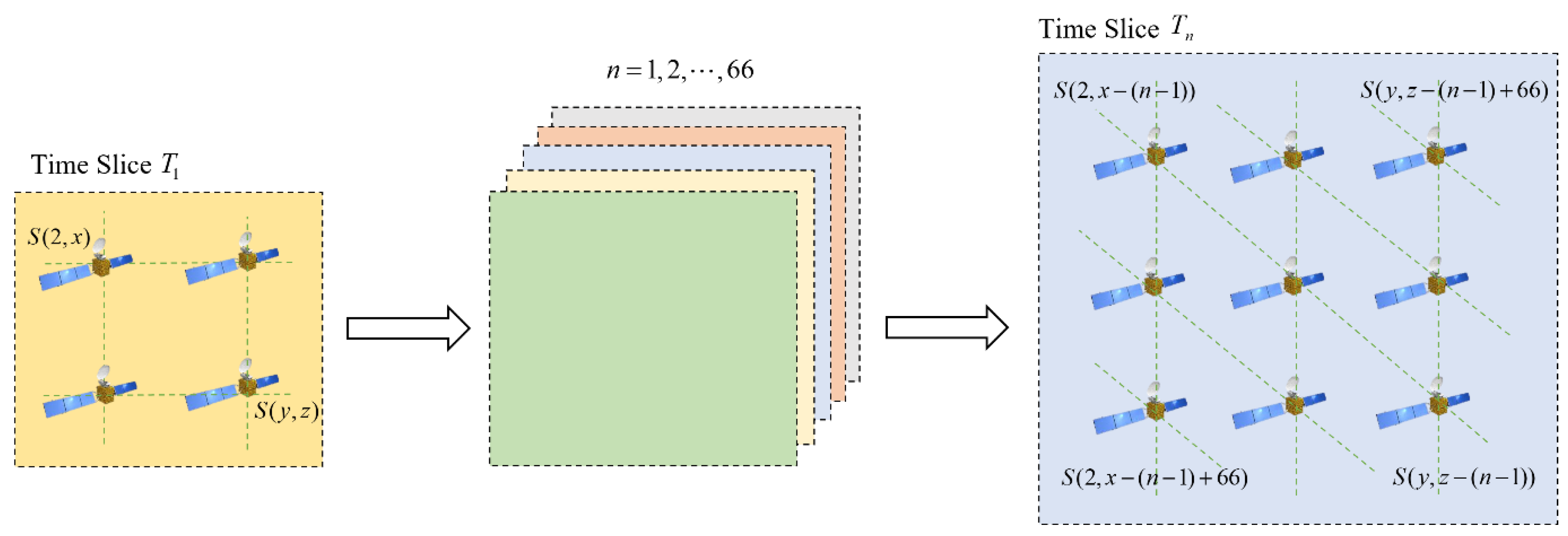
- Based on the complexity of the number of satellites and the periodic and predictable nature of their movements within mega constellations, a virtual topology is constructed using equidistant time slicing to enable dynamic simulation and management of the topology;
- After introducing dynamic links, two different combinations were adopted for the three fixed links, and based on the dynamic link selection algorithm, connection thresholds were set for each satellite to obtain the corresponding dynamic topology during each time slice;
- A joint simulation platform established a call model based on global population density to perform network performance simulations and compare the designed static topology, two dynamic topologies, and a benchmark topology. The evaluation was focused on the performance of different topology networks in three aspects: average call distance, number of hops for packet forwarding, and total time delay.
2. Related Works
2.1. Static Satellite Network Topology
2.2. Dynamic Satellite Network Topology
- 1.
- Based on the shortest distance strategy.
- 2.
- Based on the maximum visible time strategy.
3. Problem Analysis
3.1. Time Slice Division Principle
3.2. Combination of Three Fixed Links
- The connection method of intra-OP ISLs plus one AOPL enables the links within each orbit to connect with the preceding and following neighboring satellites at any given time, allowing for hop-by-hop transmission in either direction along the orbit. In the network topology, the AOPLs on the right side provide data transmission from west to east, while the AOPLs on the left provide the opposite direction [21].
- The connection method of one intra-OP ISL plus two AOPLs ensures that the links between the two orbits are always connected to the nearest adjacent satellite nodes at any given time, allowing for hop-by-hop data transmission in the east–west direction. As the adjacent satellite nodes on the same orbit are relatively stationary, permanent links of equal length exist for both forward and backward directions [22].
3.3. Dynamic Link Selection Algorithm
| Algorithm 1 Pseudocode for the dynamic link selection |
| Input: Connectivity threshold C_M←4 for each satellite, initial satellite // specify the connection degree at the initial time Output: Set of satellite link results for each time slice LISL_SET 1: ISL_SET ←, TempMap ←, entry ← 2: for t ← 1 to 2 // first calculate connectivity in the first two time slices of 3: SNN ← selectNonNer // take the set of satellites in non-adjacent orbits to 4: for i ← 1 to 66, j ← 1 to 24, SNN ← 5: d ←// calculate the ISL distance between and 6: TempMap.add // the address key is satellite and the value is 7: end 8: SortByDistance(TempMap) // sorted by call distance from smallest to largest 9: For entry IN TempMap // define entry as address key 10: IF C (T, entry) > C_M Then 11: S(T).remove(entry) 12: Else 13: LISL_SET.add((T,S1),entry) // t time slice and entry.key satellite establish link 14: C(T,S1) ←4; C(T,entry) ←4 15: Next entry 16: Next T 17: For K ← 3 to 66 // dynamic links for the remaining time slices of are inferred from the dynamic link pattern 18: ISL_SET ← DLSRGenerater(S1,LISL_SET,K) 19: Next K 20: For P←3 to 23 // all dynamic links based on combined dynamic link selection strategy and track change pattern 21: ISL_SET ← DLSRAndCATS(ISL_SET,C,S,P) 22: Next P |
4. Modeling System Approach
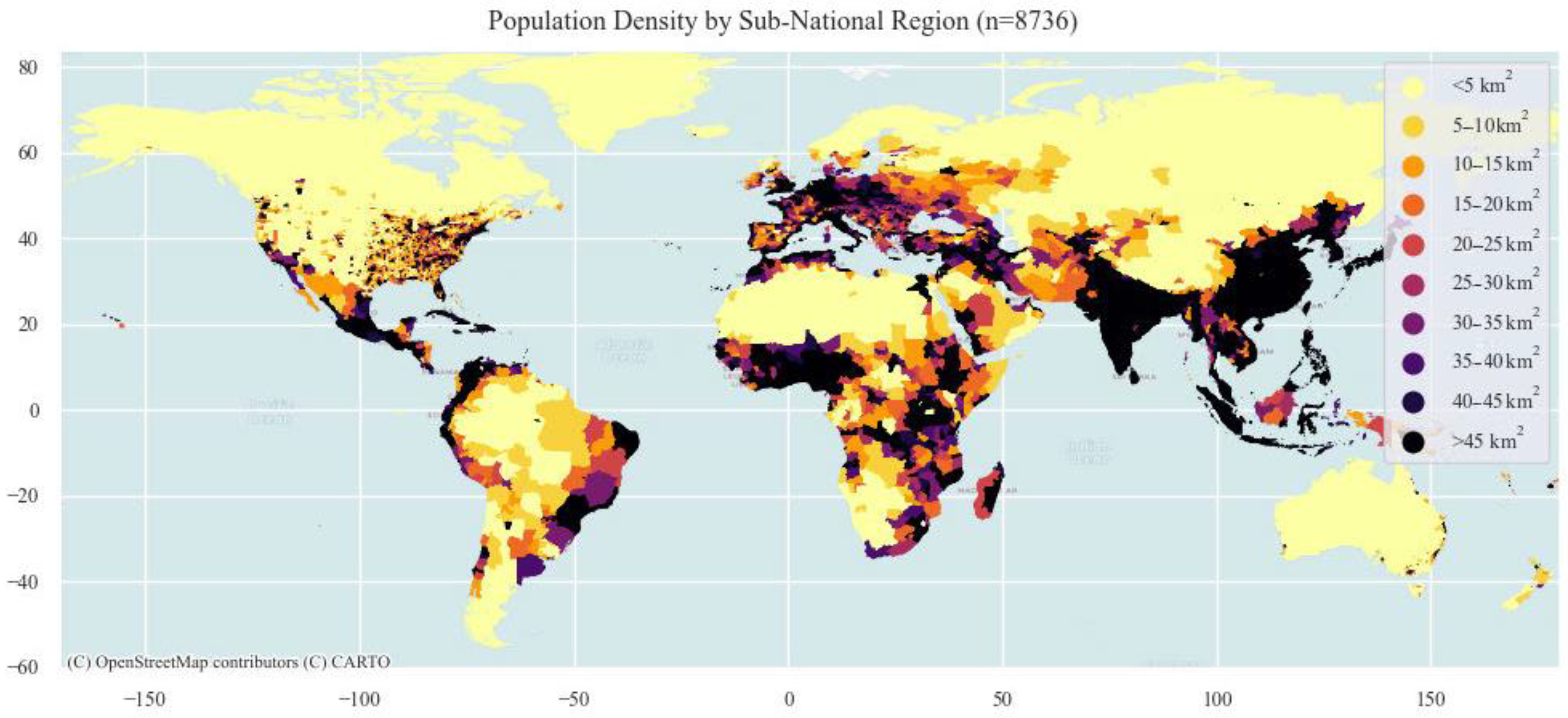
4.1. Call Model Based on Global Population Density
4.2. General Framework of the Simulation
- The ground stations A to B send service requests sequentially in the calling order, and the corresponding satellite with the longest service time within the visual range is selected by combining the Time strategy, in which the satellite node connected to ground station A is called source satellite C and the satellite node connected to ground station B is called target satellite D;
- ISLs are constructed according to different connection strategies, resulting in different topologies for the entire mega constellation network;
- After setting the time slice size, the link connections of satellites in each time slice are recorded in the matrix K of ISLs, and the shortest path P from C to D in the LEO satellite network is obtained by Dijkstra’s algorithm, with a static network topology table generated in different time slices;
- Analyze the resource allocation of the remaining channels of all satellites in the shortest path P. If the remaining channels are not zero, access to the current call is allowed while the total number of channels in the path is subtracted by one. If there are no remaining free channels, the call is blocked directly at the current moment, and the result is recorded as a call failure;
- Continue to access new call requests and repeat the above process until there are no new ones.
4.3. Simulation Parameter Settings
- The distribution of calls in the continuous time from sending to receiving shows a negative exponential distribution.
- The time of arrival of calls at the receiving end obeys an independent Poisson distribution with the parameter .
- The density of call service requests is adjusted by changing the value of the parameter .
5. Performance Evaluation
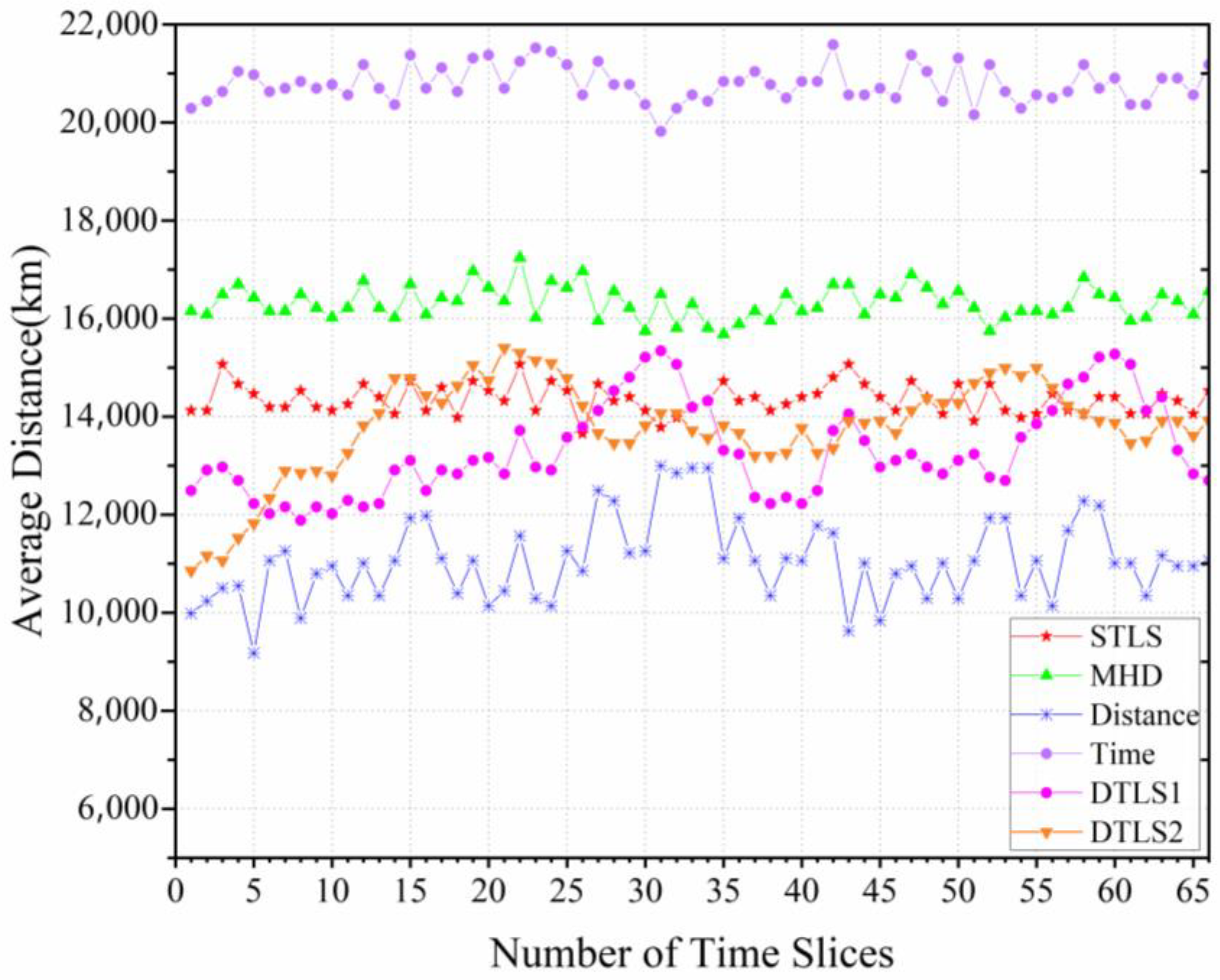
5.1. Average Call Distance of Transmitted Packets
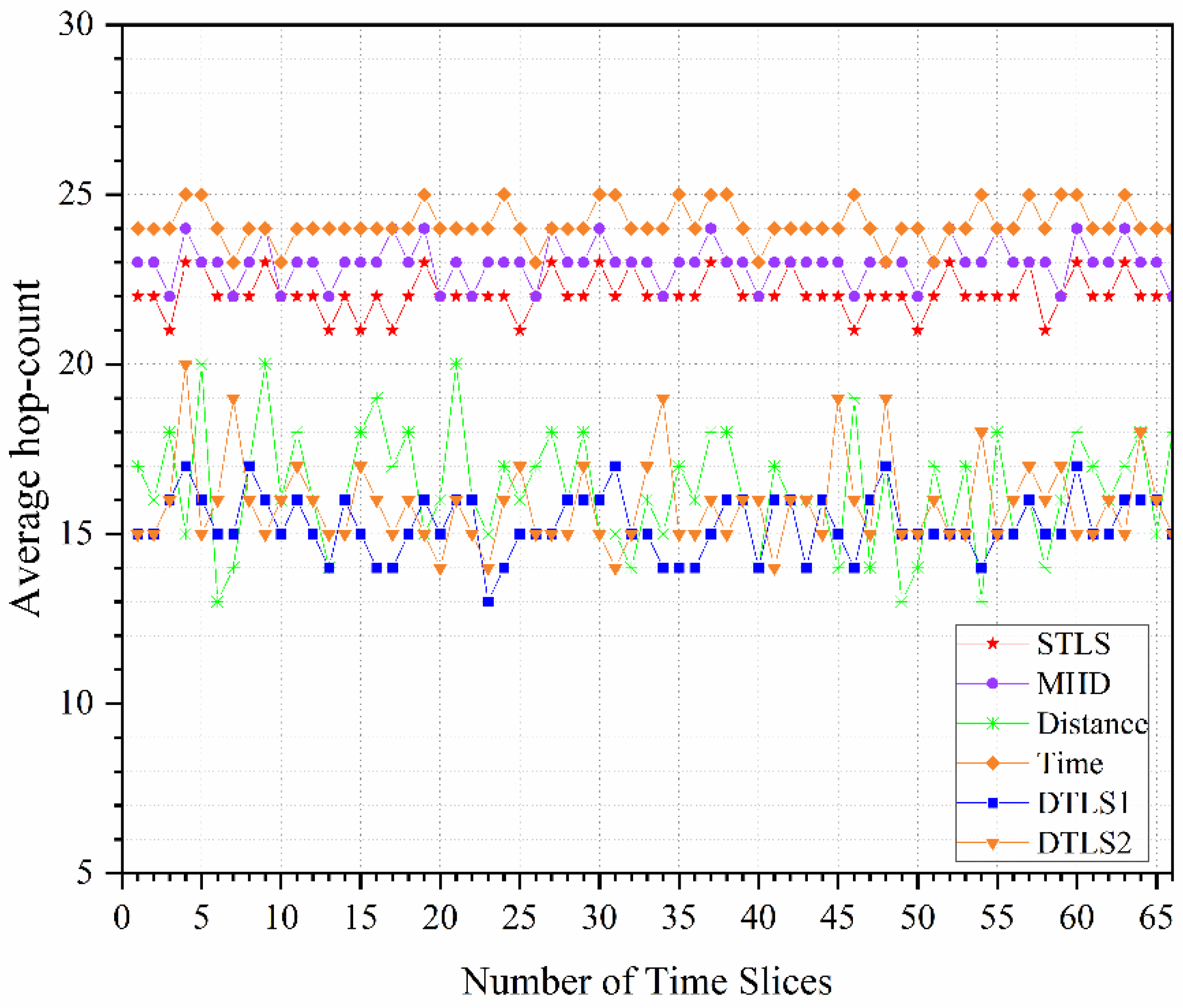
5.2. Number of Hops for Packet Forwarding
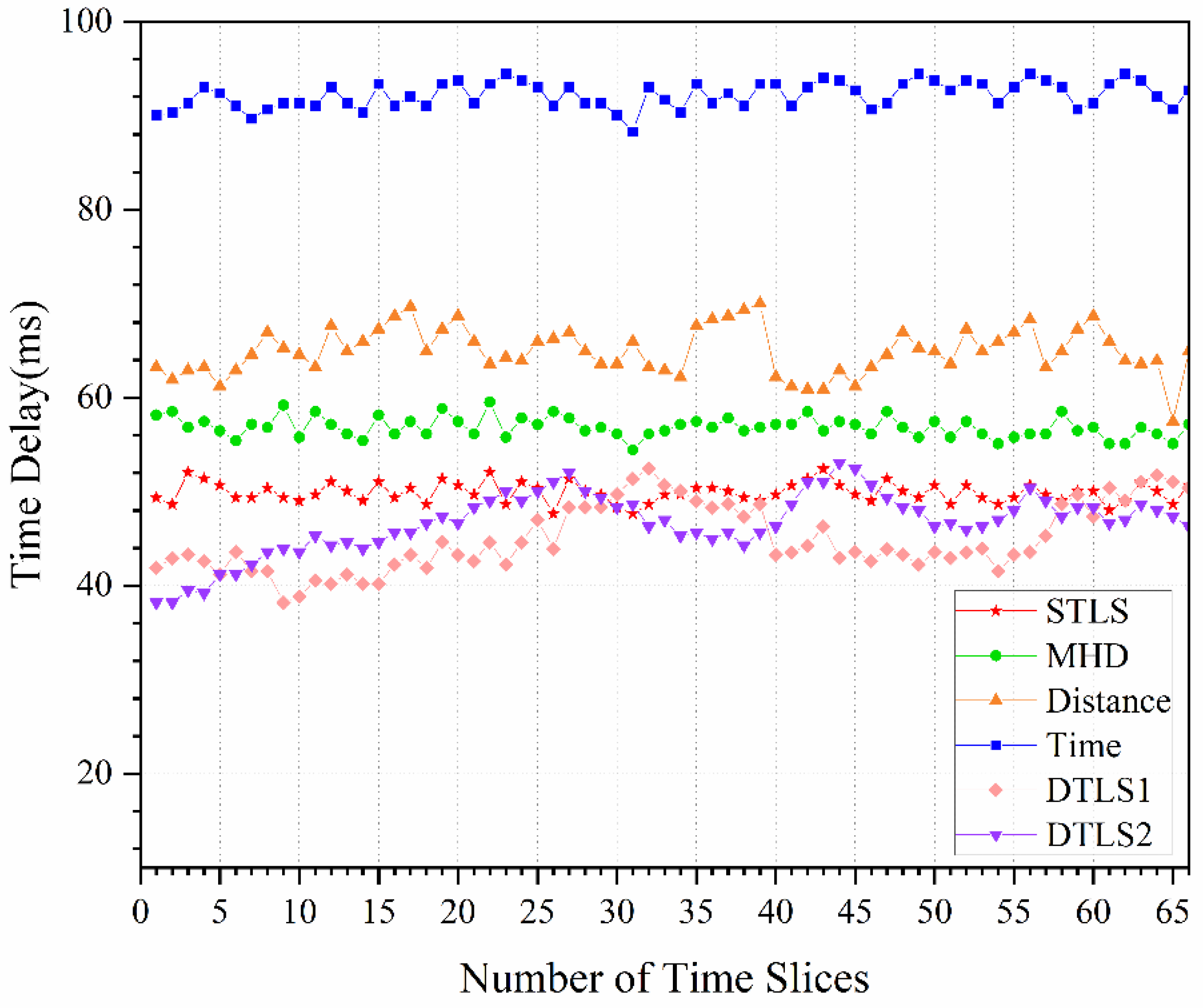
5.3. Total Time Delay
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LEO | Low earth orbit |
| ISLs | Inter-satellite links |
| STLS | Static topology of satellites |
| DTLS | Dynamic topology of satellites |
| LPCR | Low-complexity probability routing algorithm |
| MHD | Manhattan network |
| NOPL | Non-adjacent orbital plane link |
| OP | Orbital plane |
| AOPL | Adjacent OP ISL |
References
- Kodheli, O.; Lagunas, E.; Maturo, N.; Sharma, S.K.; Shankar, B.; Montoya, J.F.M.; Duncan, J.C.M.; Spano, D.; Chatzinotas, S.; Kisseleff, S.; et al. Satellite Communications in the New Space Era: A Survey and Future Challenges. IEEE Commun. Surv. Tutor. 2021, 23, 70–109. [Google Scholar] [CrossRef]
- Wei, L.; Shuai, J.; Liu, Y.; Wang, Y.; Zhang, L. Service Customized Space-Air-Ground Integrated Network for Immersive Media: Architecture, Key Technologies, and Prospects. China Commun. 2022, 19, 1–13. [Google Scholar] [CrossRef]
- Lee, Y.; Choi, J.P. Connectivity Analysis of Mega-Constellation Satellite Networks With Optical Intersatellite Links. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 4213–4226. [Google Scholar] [CrossRef]
- Lin, Z.; An, K.; Niu, H.; Hu, Y.; Chatzinotas, S.; Zheng, G.; Wang, J. SLNR-Based Secure Energy Efficient Beamforming in Multibeam Satellite Systems. IEEE Trans. Aerosp. Electron. Syst. 2022, 1–4. [Google Scholar] [CrossRef]
- Guo, K.; Dong, C.; An, K. NOMA-Based Cognitive Satellite Terrestrial Relay Network: Secrecy Performance Under Channel Estimation Errors and Hardware Impairments. IEEE Internet Things J. 2022, 9, 17334–17347. [Google Scholar] [CrossRef]
- Chen, Q.; Giambene, G.; Yang, L.; Fan, C.; Chen, X. Analysis of Inter-Satellite Link Paths for LEO Mega-Constellation Networks. IEEE Trans. Veh. Technol. 2021, 70, 2743–2755. [Google Scholar] [CrossRef]
- Roth, M.; Brandt, H.; Bischl, H. Implementation of a Geographical Routing Scheme for Low Earth Orbiting Satellite Constellations Using Intersatellite Links. Int. J. Satell. Commun. Netw. 2021, 39, 92–107. [Google Scholar] [CrossRef]
- Sundaram, K.; Vellupillai, S. Designing a Novel Star Topology Using Operad Linear Differential Theory. Wirel. Pers. Commun. 2021, 120, 565–585. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, Y.; Zhang, Y.; He, X.; Liu, Y.; Zhang, J. Intersatellite Laser Link Planning for Reliable Topology Design in Optical Satellite Networks: A Networking Perspective. IEEE Trans. Netw. Serv. Manage. 2022, 19, 2612–2624. [Google Scholar] [CrossRef]
- Roth, M.M.H.; Brandt, H.; Bischl, H. Distributed SDN-Based Load-Balanced Routing for Low Earth Orbit Satellite Constellation Networks. In Proceedings of the 17th Signal Processing for Space Communications Workshop (ASMS/SPSC), Graz, Austria, 6 September 2022; pp. 1–8. [Google Scholar]
- Noakes, M.D.; Cain, J.B.; Nieto, J.W. An Adaptive Link Assignment Algorithm for Dynamically Changing Topologies. IEEE Trans. Commun. 1993, 41, 694–706. [Google Scholar] [CrossRef]
- Xiaogang, Q.; Jiulong, M.; Dan, W.; Lifang, L.; Shaolin, H. A Survey of Routing Techniques for Satellite Networks. J. Commun. Inf. Netw. 2016, 1, 66–85. [Google Scholar]
- Alhussein, O.; Do, P.T.; Ye, Q.; Li, J.; Shi, W.; Zhuang, W.; Shen, X.; Li, X.; Rao, J. A Virtual Network Customization Framework for Multicast Services in NFV-Enabled Core Networks. IEEE J. Sel. Areas Commun. 2020, 38, 1025–1039. [Google Scholar] [CrossRef]
- Dai, C.-Q.; Zhang, M.; Li, C.; Zhao, J.; Chen, Q. QoE-Aware Intelligent Satellite Constellation Design in Satellite Internet of Things. IEEE Internet Things J. 2021, 8, 4855–4867. [Google Scholar] [CrossRef]
- Marbel, R.; Yozevitch, R.; Grinshpoun, T.; Ben-Moshe, B. Dynamic Network Formation for FSO Satellite Communication. Appl. Sci. 2022, 12, 738. [Google Scholar] [CrossRef]
- Cao, X.; Li, Y.; Xiong, X.; Wang, J. Dynamic Routings in Satellite Networks: An Overview. Sensors 2022, 22, 4552. [Google Scholar] [CrossRef]
- Lin, Z.; Lin, M.; Champagne, B.; Zhu, W.-P.; Al-Dhahir, N. Secrecy-Energy Efficient Hybrid Beamforming for Satellite-Terrestrial Integrated Networks. IEEE Trans. Commun. 2021, 69, 6345–6360. [Google Scholar] [CrossRef]
- Chaudhry, A.U.; Yanikomeroglu, H. Laser Intersatellite Links in a Starlink Constellation: A Classification and Analysis. IEEE Veh. Technol. Mag. 2021, 16, 48–56. [Google Scholar] [CrossRef]
- Amanor, D.N.; Edmonson, W.W.; Afghah, F. Intersatellite Communication System Based on Visible Light. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2888–2899. [Google Scholar] [CrossRef]
- Lan, T.; Li, H.; Wu, Q.; Lai, Z.; Liu, J. Exploiting Path Diversity to Increase System Performance in Mega-Constellations. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, 29 March 2021; pp. 1–7. [Google Scholar]
- Chengzhuo, W.; Suyang, L.; Xiye, G.; Jun, Y. Dynamic Optimization of Laser Inter-Satellite Link Network Topology Based on Genetic Algorithm. In Proceedings of the 2019 14th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Changsha, China, 1–3 November 2019; pp. 1331–1342. [Google Scholar]
- Lin, Z.; Lin, M.; de Cola, T.; Wang, J.-B.; Zhu, W.-P.; Cheng, J. Supporting IoT With Rate-Splitting Multiple Access in Satellite and Aerial-Integrated Networks. IEEE Internet Things J. 2021, 8, 11123–11134. [Google Scholar] [CrossRef]
- Lin, Z.; Niu, H.; An, K.; Wang, Y.; Zheng, G.; Chatzinotas, S.; Hu, Y. Refracting RIS-Aided Hybrid Satellite-Terrestrial Relay Networks: Joint Beamforming Design and Optimization. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3717–3724. [Google Scholar] [CrossRef]
- Zhu, Q.; Tao, H.; Cao, Y.; Li, X. Laser Inter-Satellite Link Visibility and Topology Optimization for Mega Constellation. Electronics 2022, 11, 2232. [Google Scholar] [CrossRef]
- WorldPop Hub. Population Density/Unconstrained Individual Countries 2000–2020 (1 km Resolution). Available online: https://hub.worldpop.org/geodata/listing?id=76 (accessed on 20 December 2022).



| Topology Type | Advantages | Disadvantages |
|---|---|---|
| Star topology [8] | Simple structure, easy to improve | Inability to achieve full coverage and heavy burden on central nodes |
| Ring topology | Stable communications in the coverage area | Low communication efficiency and poor scalability |
| Tree topology | Small diameter and efficient routing | Root nodes are heavily burdened and prone to congestion |
| Mesh topology [9] | High reliability, high redundancy, low latency, many links | High cost, difficult to control and inefficient |
| Satellite Parameters | Value |
|---|---|
| Models | walker1584 |
| Track height | 550 km |
| Number of track planes | 66 |
| Number of satellites in orbit | 24 |
| Track inclination | 53° |
| Operating cycle | 95.7 min |
| Timepiece size | 87 s |
| Number of channels per satellite | 300 |
| Minimum elevation angle of the ground station to access the satellite | 40° |
| Type | Network Topology | Description |
|---|---|---|
| Baseline topology | MHD | Manhattan Network defines the mesh connection method |
| Distance | Dynamic allocation strategy based on shortest distance | |
| Time | Dynamic allocation strategy based on maximum visibility time | |
| The optimized topology designed in this paper | STLS | 2 intra-OP links plus 2 AOPLs |
| DTLS1 | 2 intra-OP links plus 1 AOPL plus 1 dynamic link | |
| DLTS2 | 1 intra-OP link plus 2 AOPLs plus 1 dynamic link |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Q.; Wang, X.; Yang, H.; Cao, Y. Design and Evaluation of Dynamic Topology for Mega Constellation Networks. Electronics 2023, 12, 1784. https://doi.org/10.3390/electronics12081784
Zhu Q, Wang X, Yang H, Cao Y. Design and Evaluation of Dynamic Topology for Mega Constellation Networks. Electronics. 2023; 12(8):1784. https://doi.org/10.3390/electronics12081784
Chicago/Turabian StyleZhu, Qinyu, Xinmin Wang, Haitao Yang, and Yanhua Cao. 2023. "Design and Evaluation of Dynamic Topology for Mega Constellation Networks" Electronics 12, no. 8: 1784. https://doi.org/10.3390/electronics12081784
APA StyleZhu, Q., Wang, X., Yang, H., & Cao, Y. (2023). Design and Evaluation of Dynamic Topology for Mega Constellation Networks. Electronics, 12(8), 1784. https://doi.org/10.3390/electronics12081784






