A Novel Variable On-Time Control Scheme for Boundary Conduction Mode SEPIC PFC Converter
Abstract
:1. Introduction
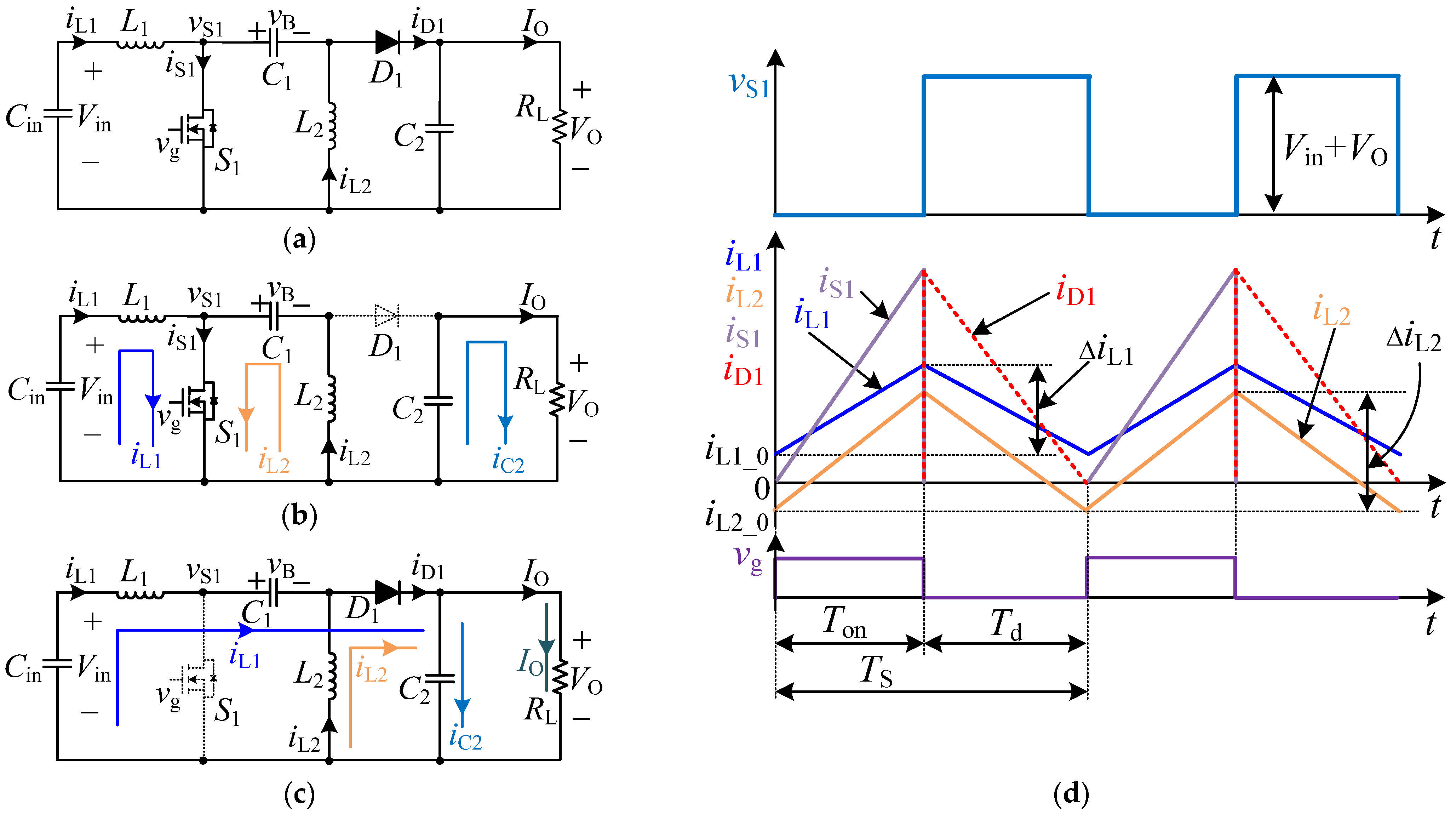
2. Boundary Conduction Mode SEPIC Power Factor Correction Converter with Constant-On-Time Control
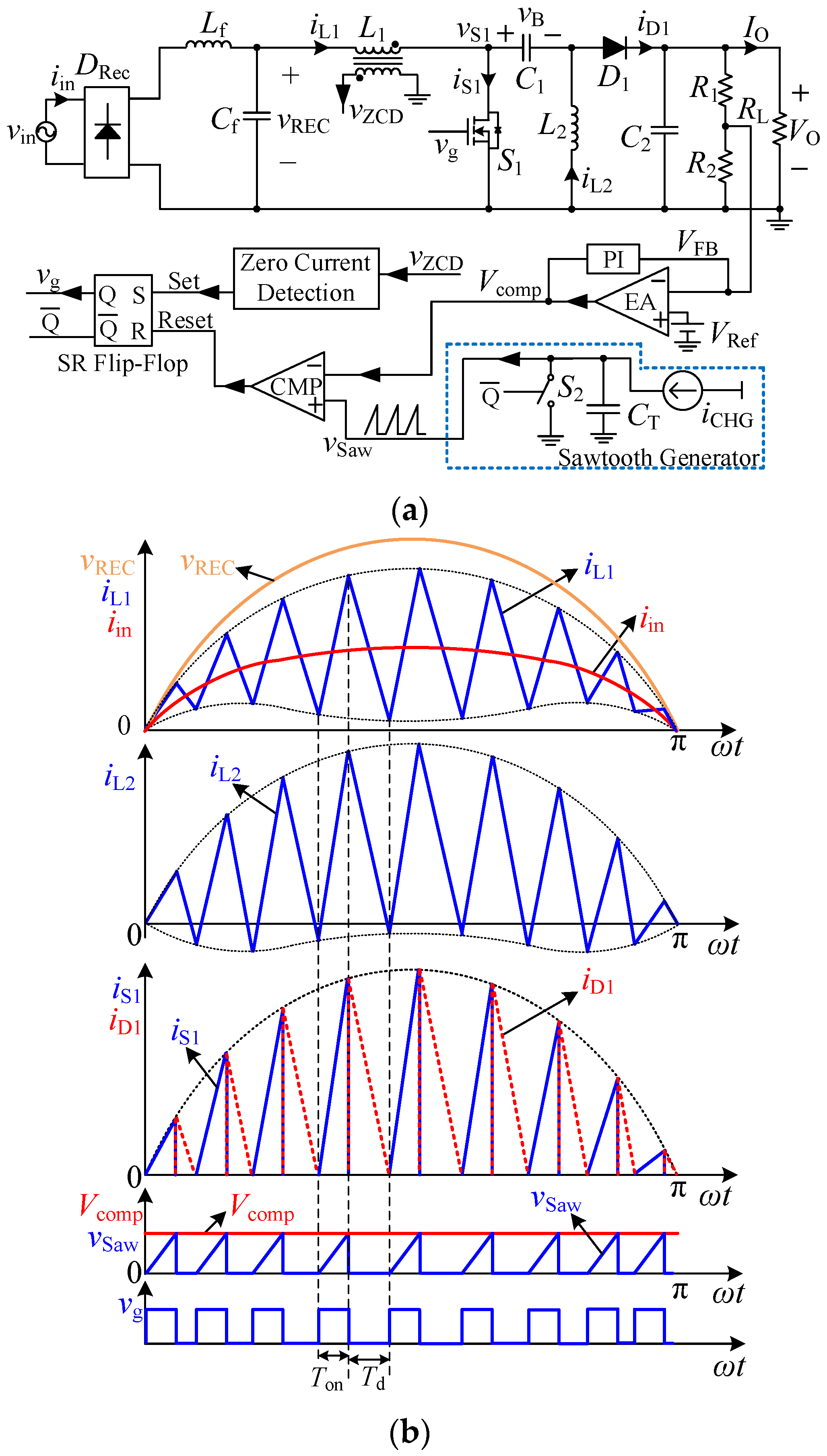
3. Variable-On-Time Control Scheme
4. Performance Comparison
4.1. Comparison of Input Current and Power Factor
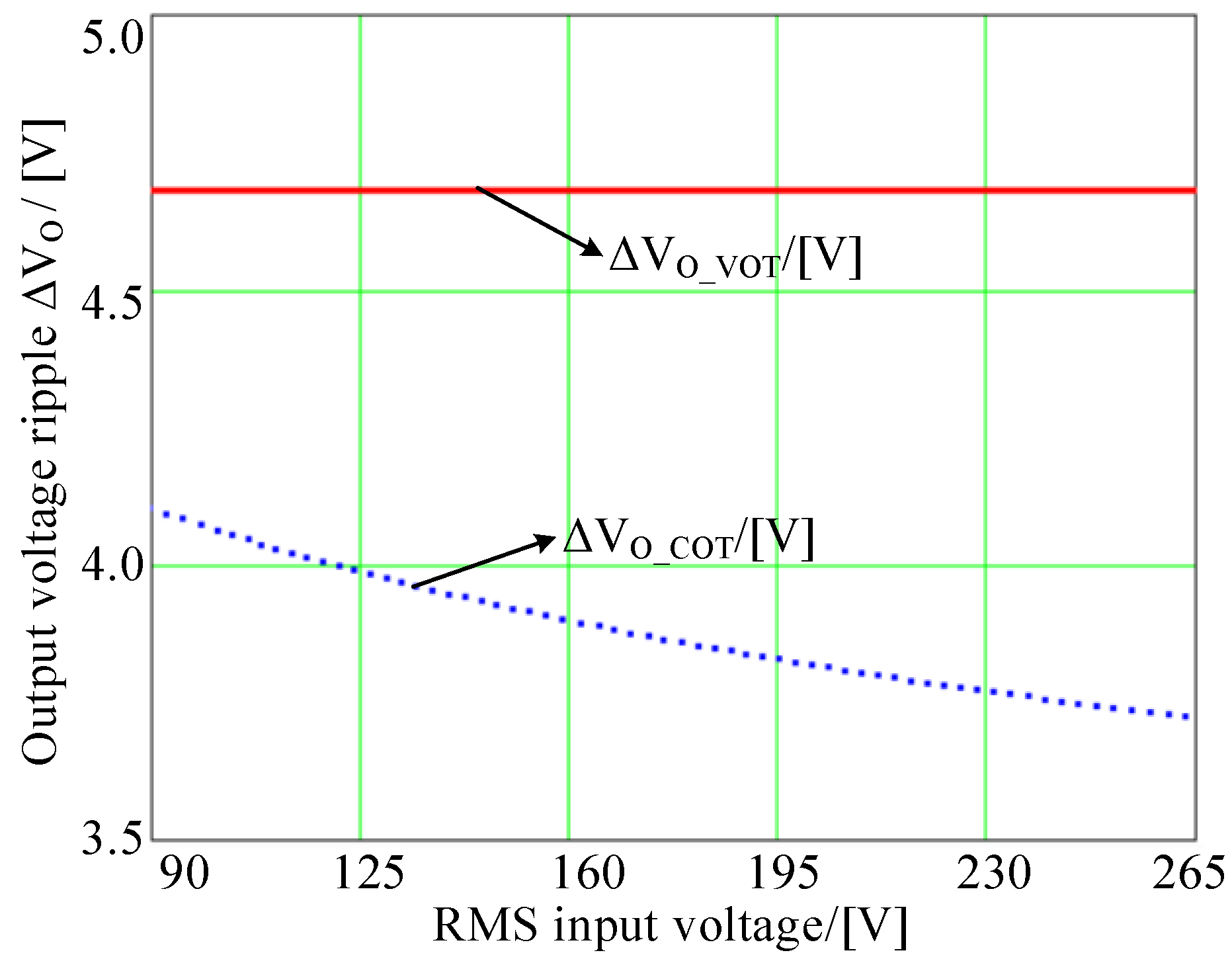
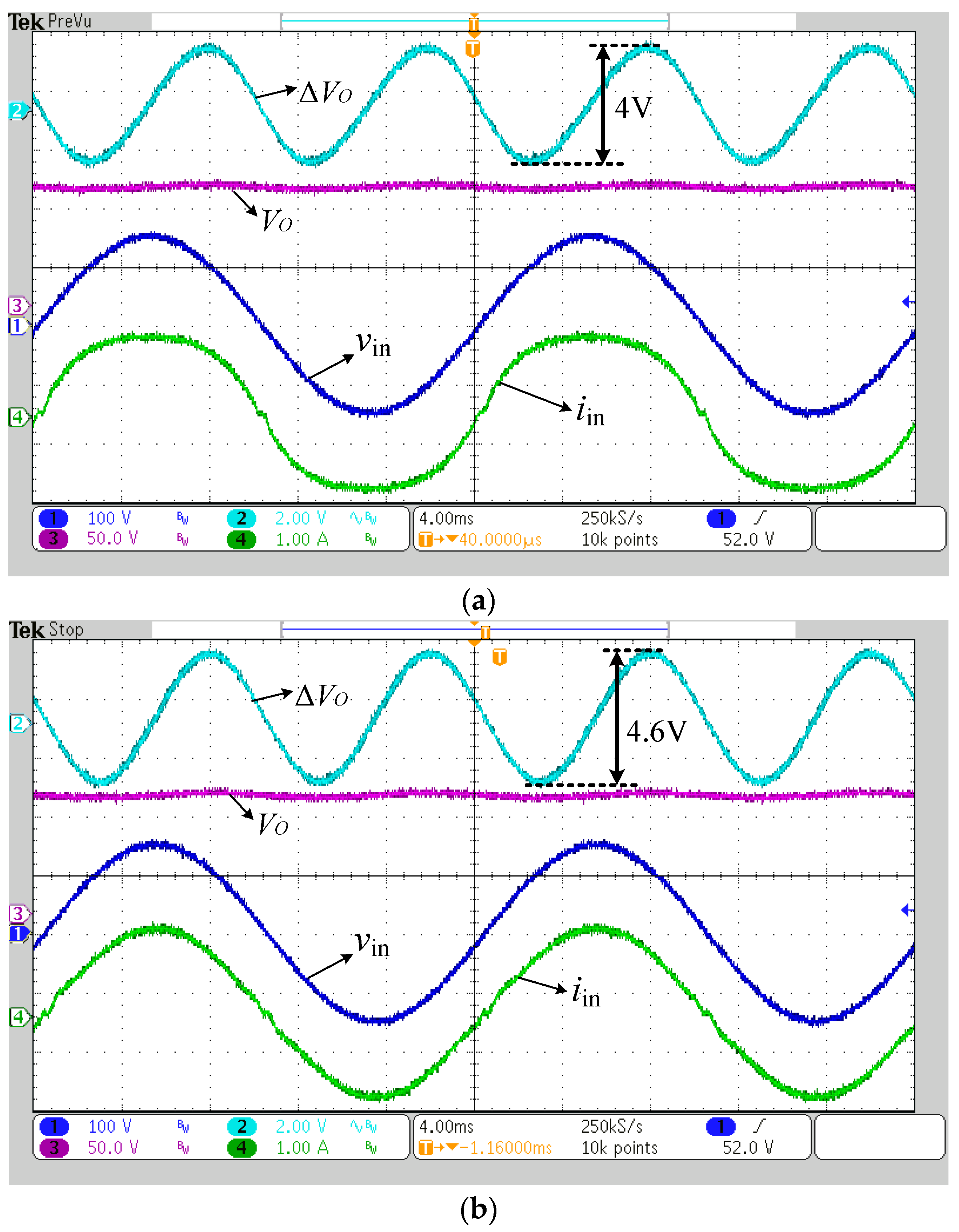
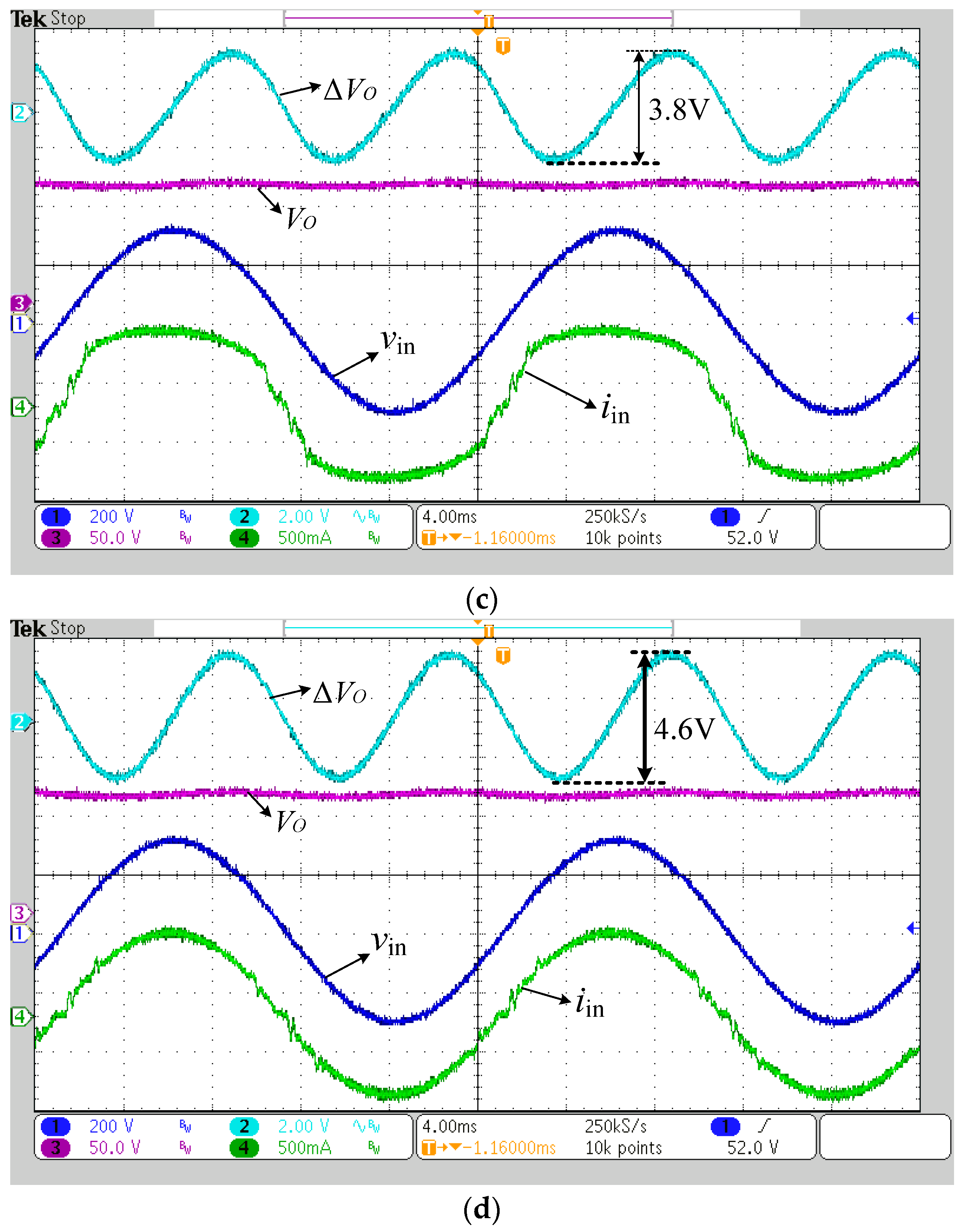
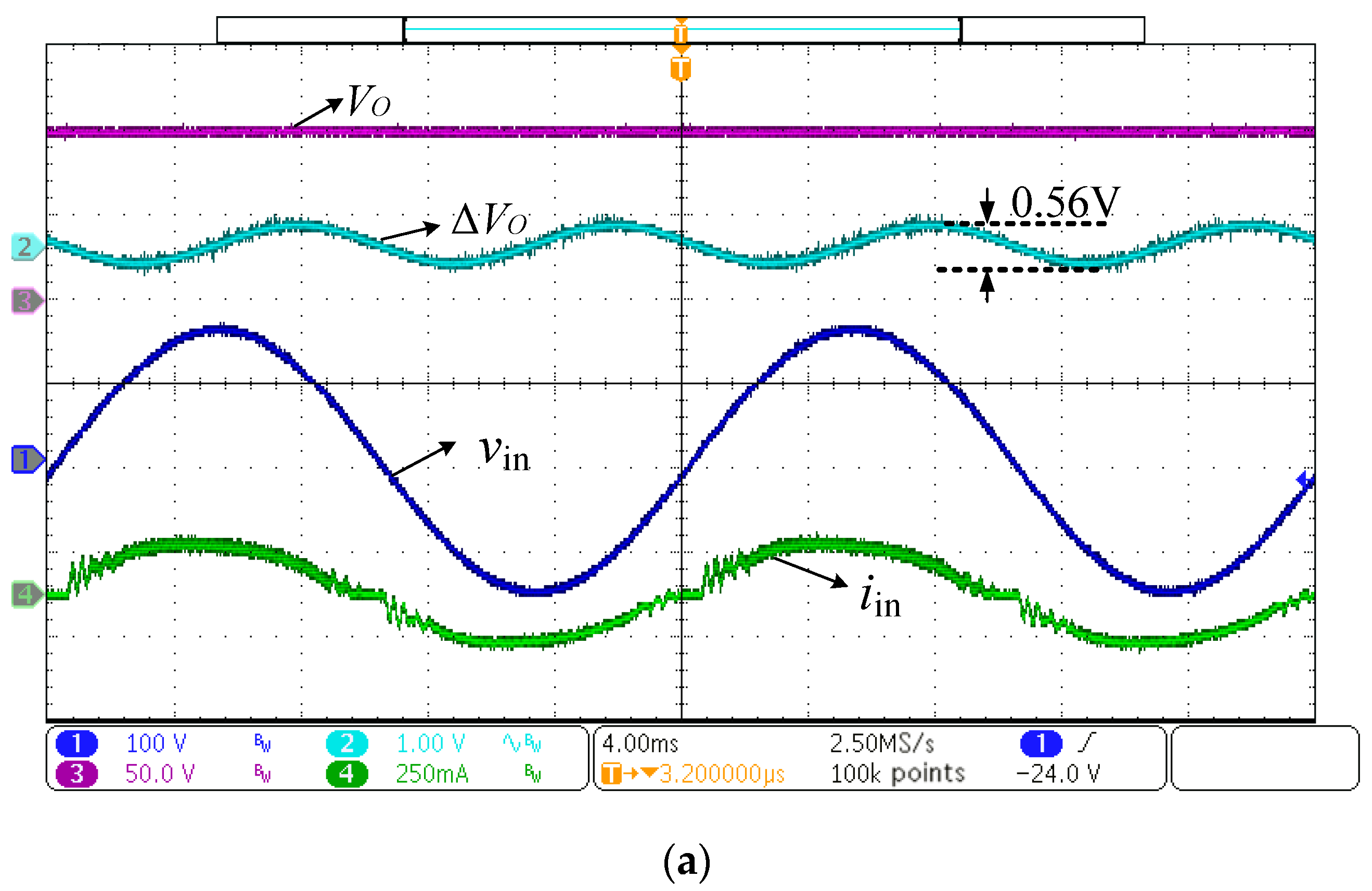
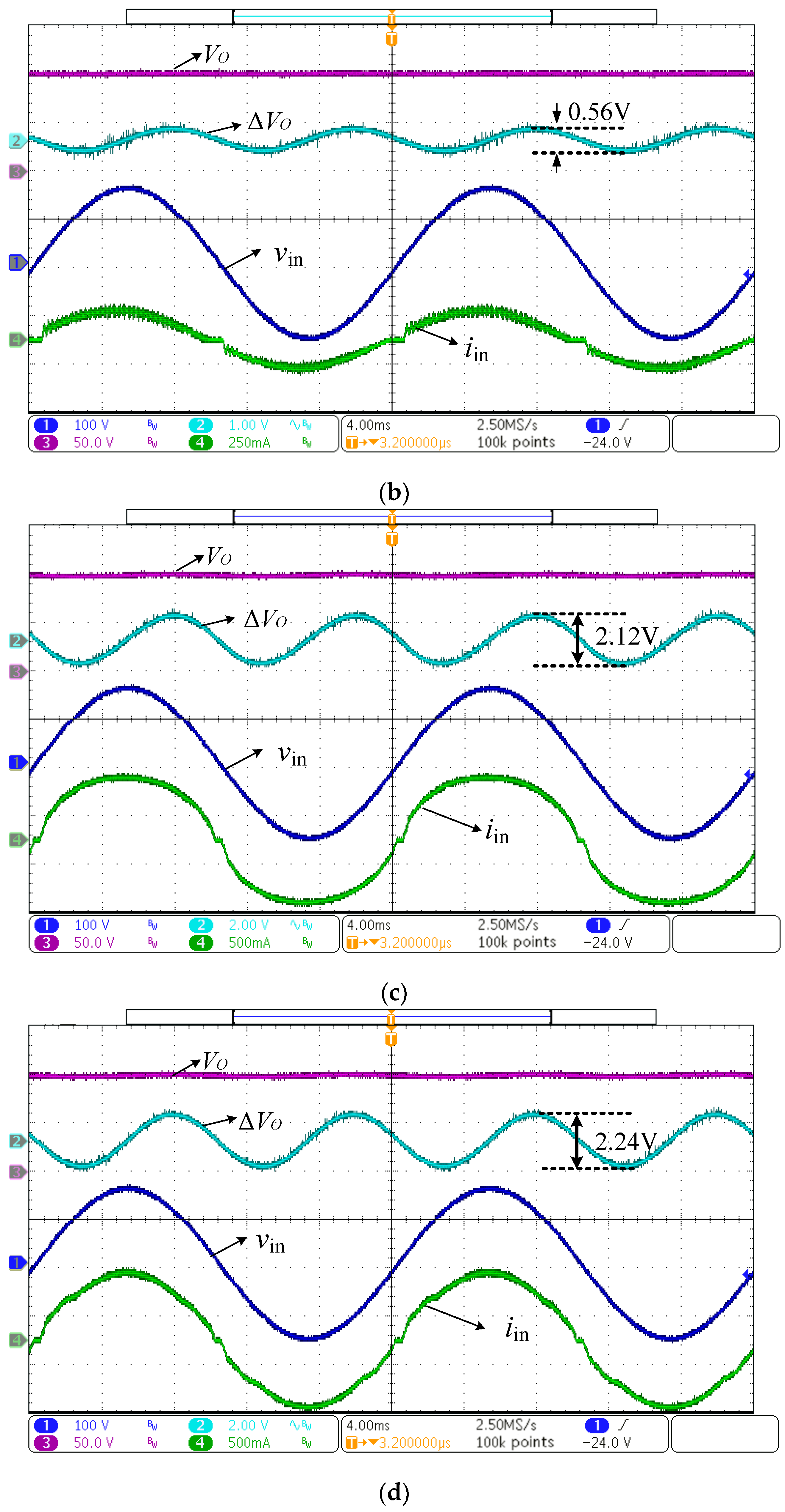
4.2. Comparison of Output Voltage Ripple
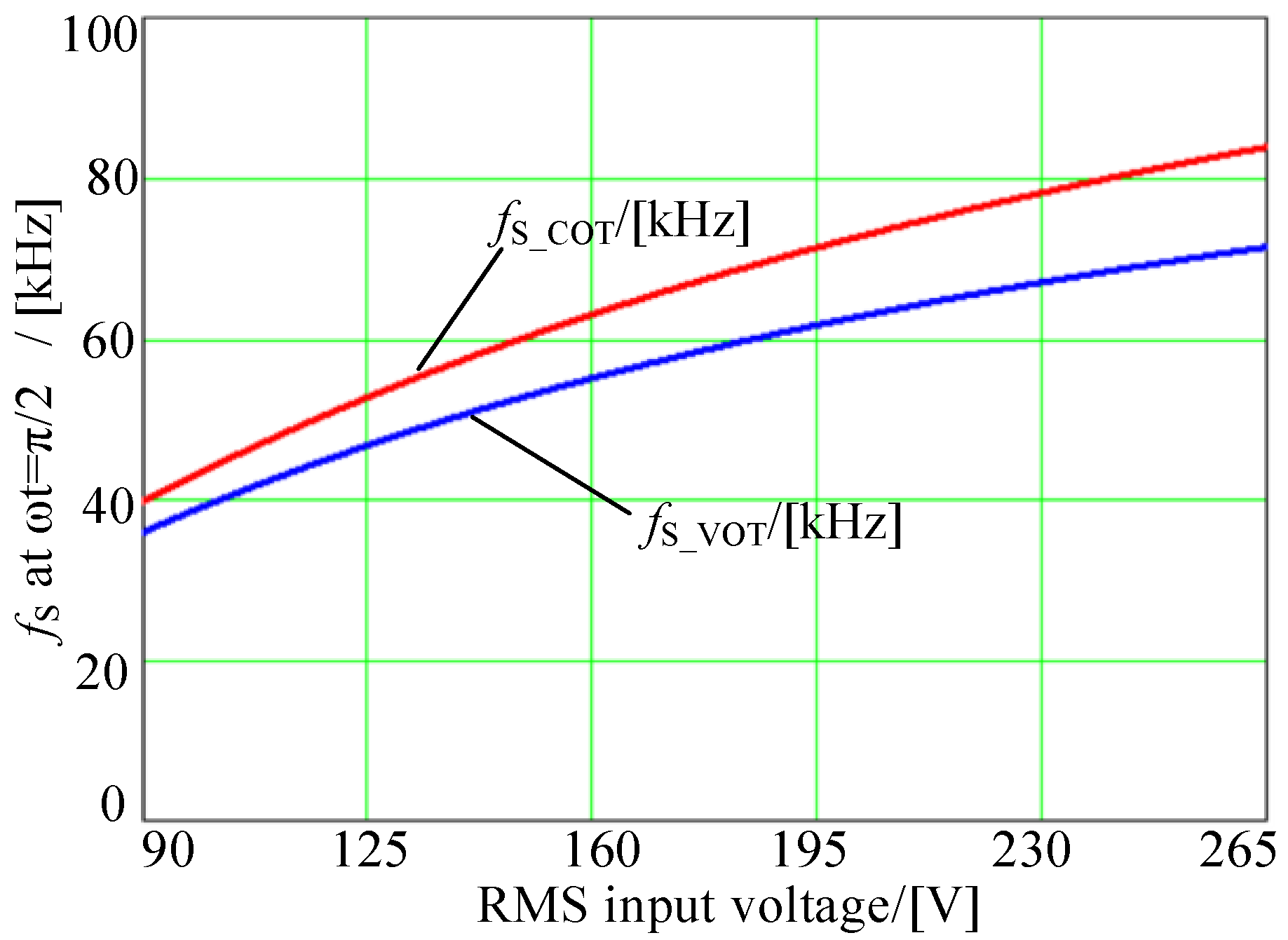
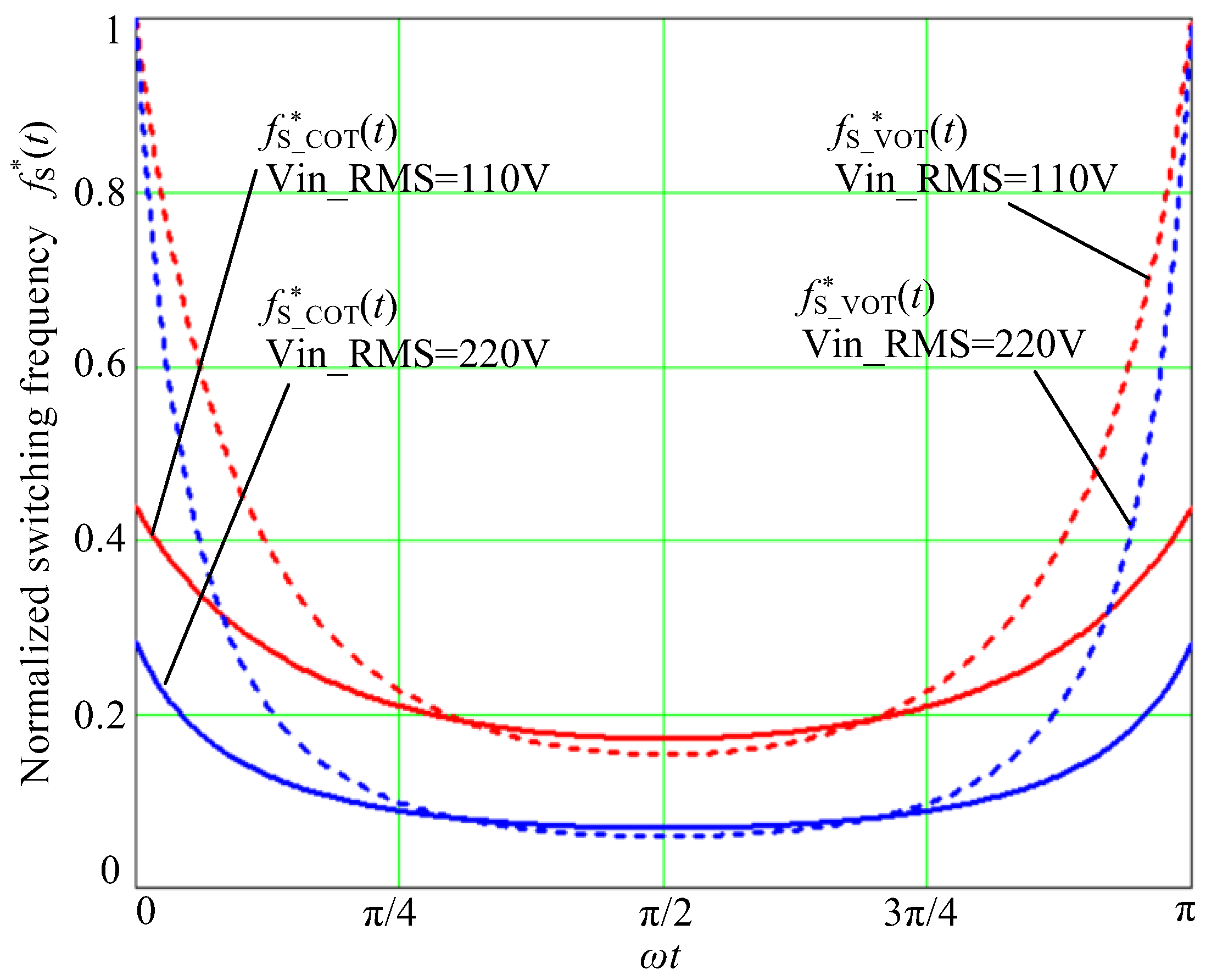
4.3. Comparison of Switching Frequency
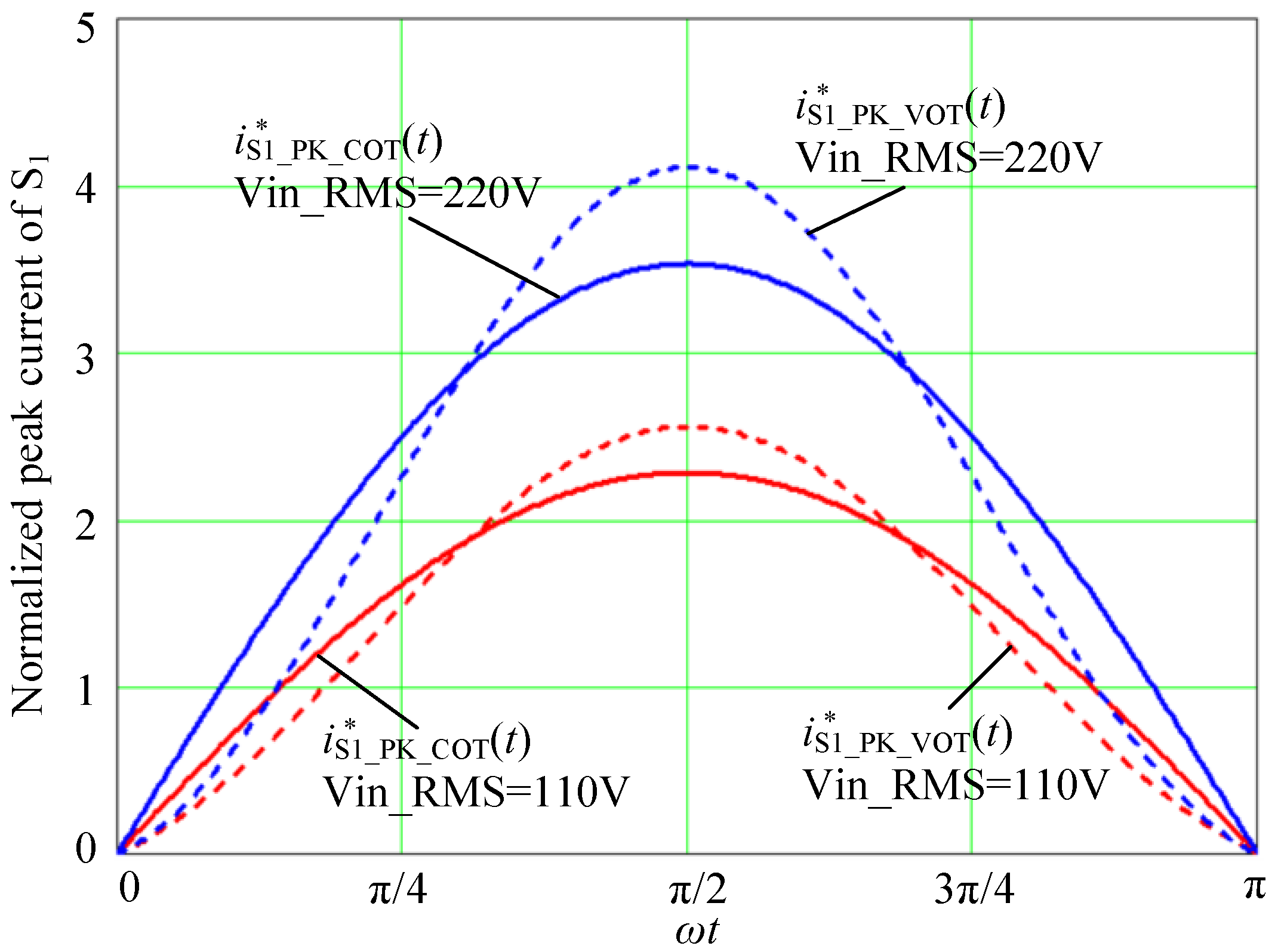
4.4. Comparison of Peak Current of Main Switch
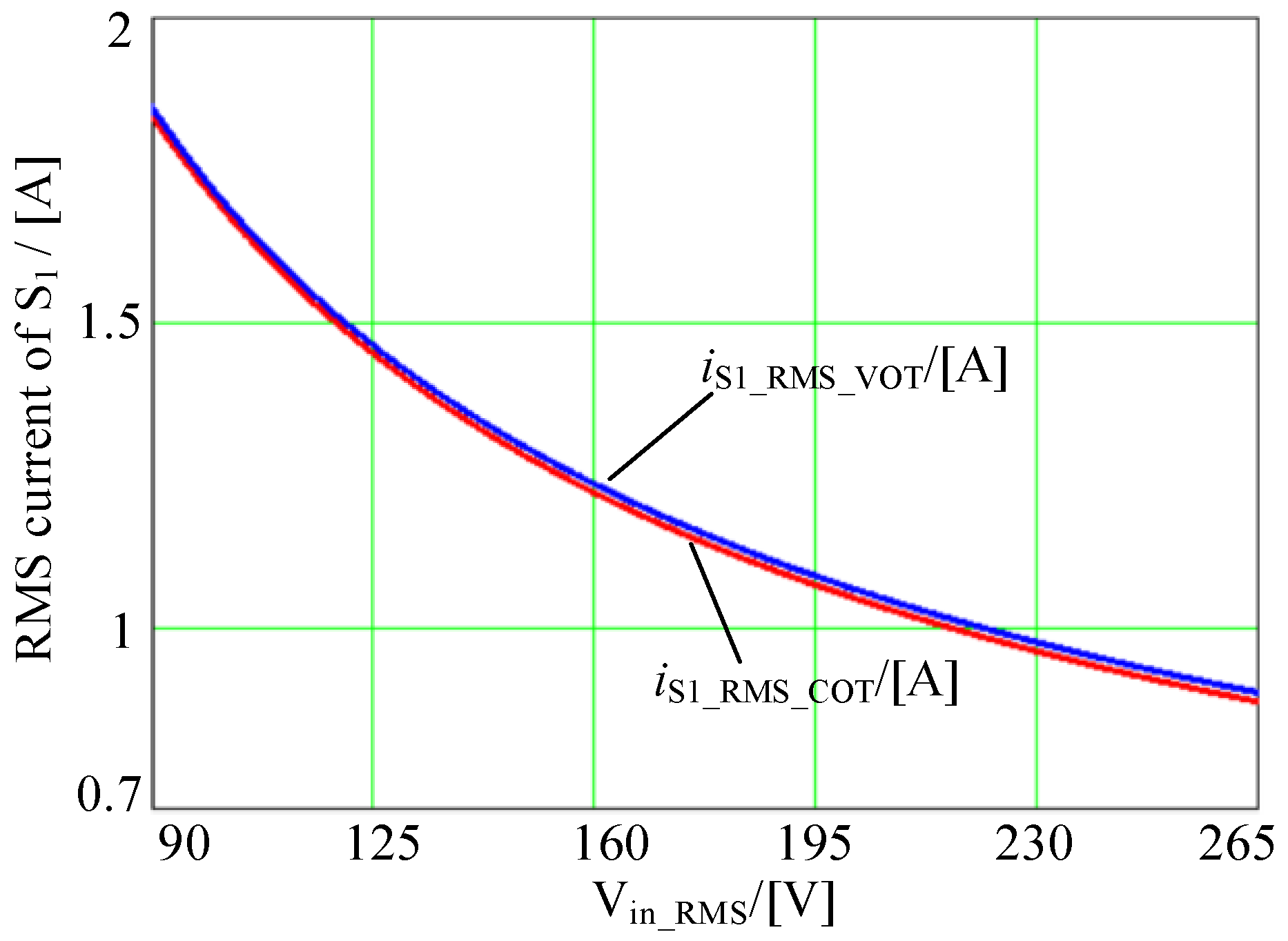
4.5. Comparison of RMS Current of Main Switch
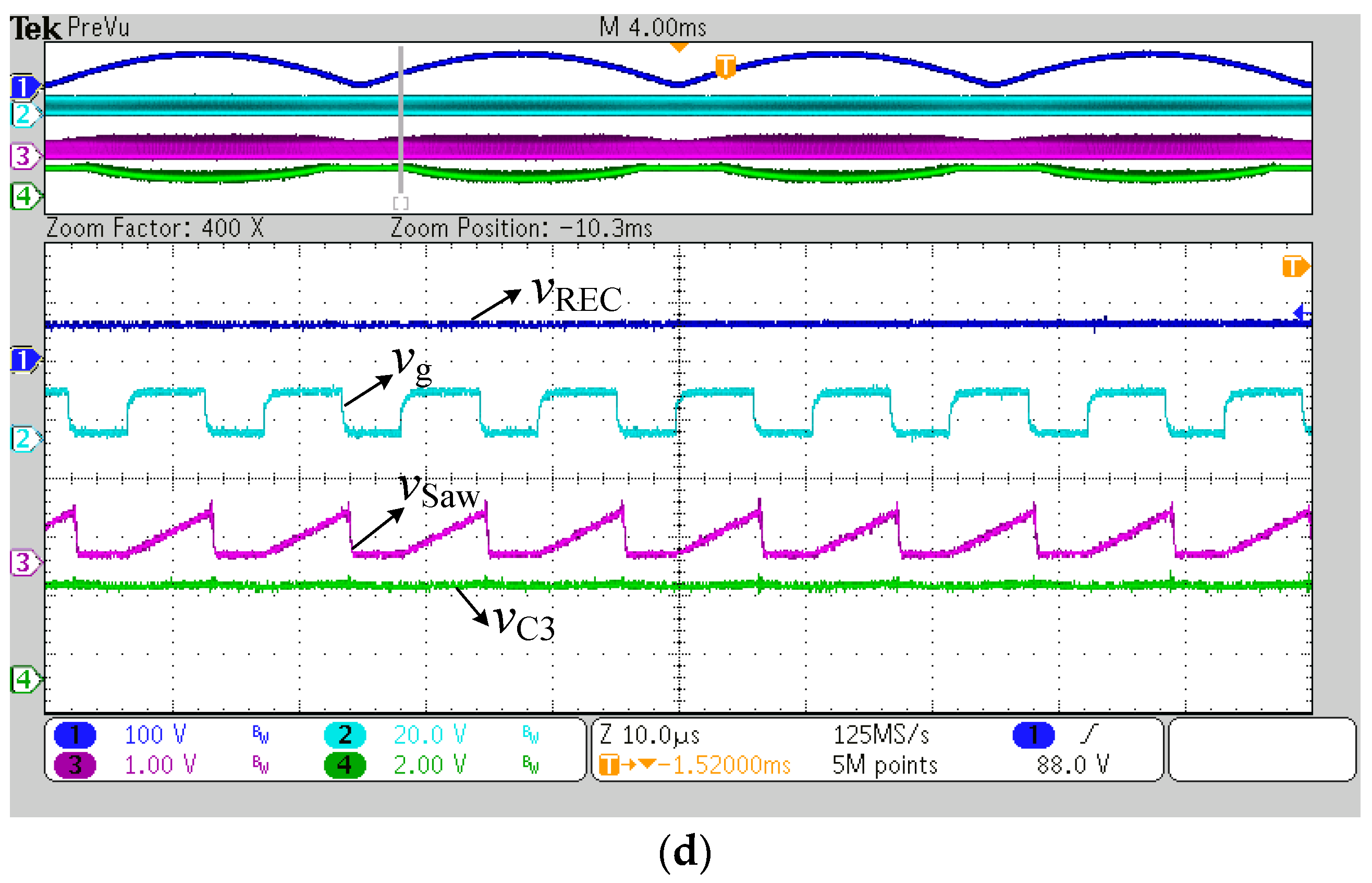
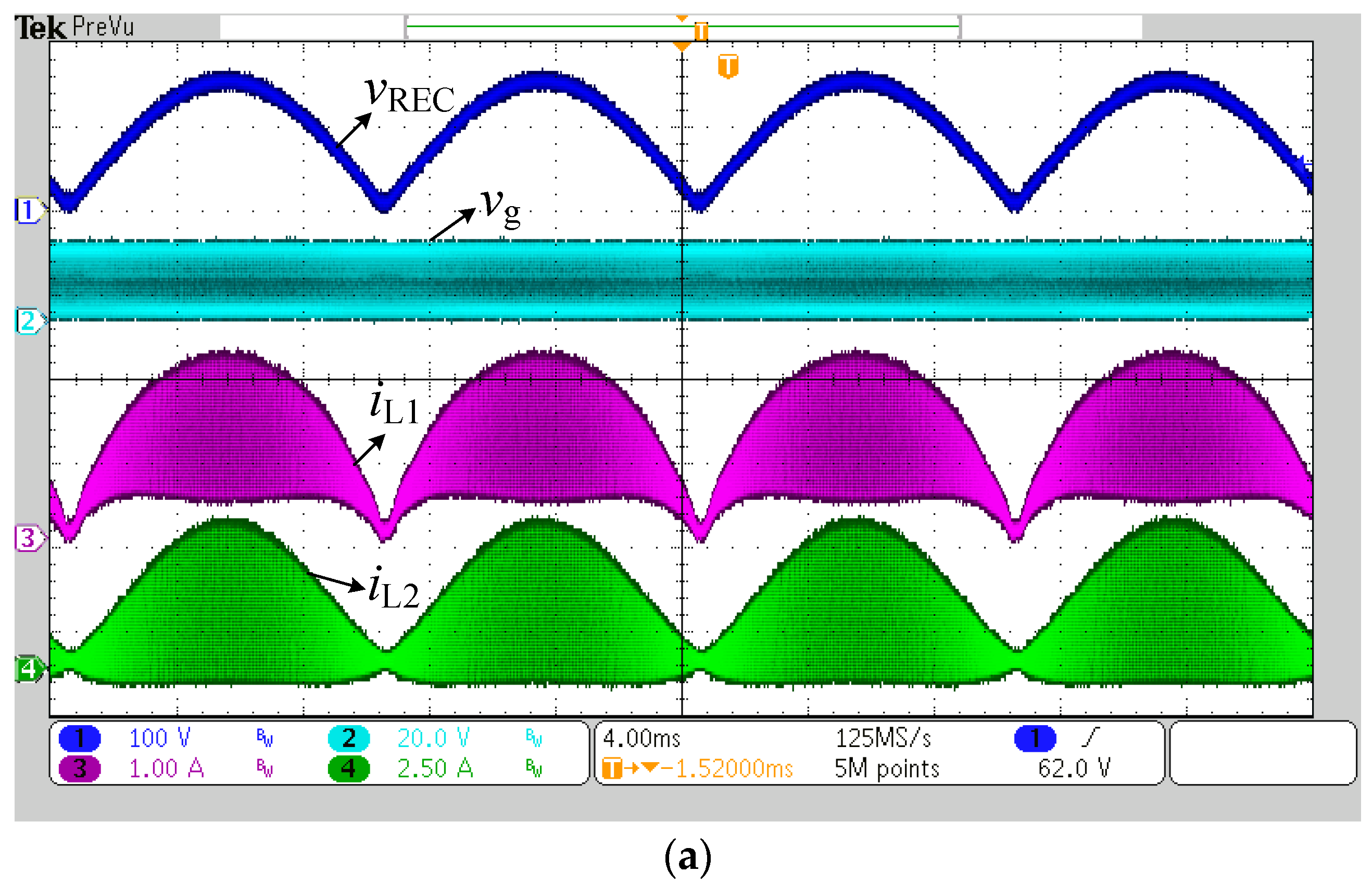
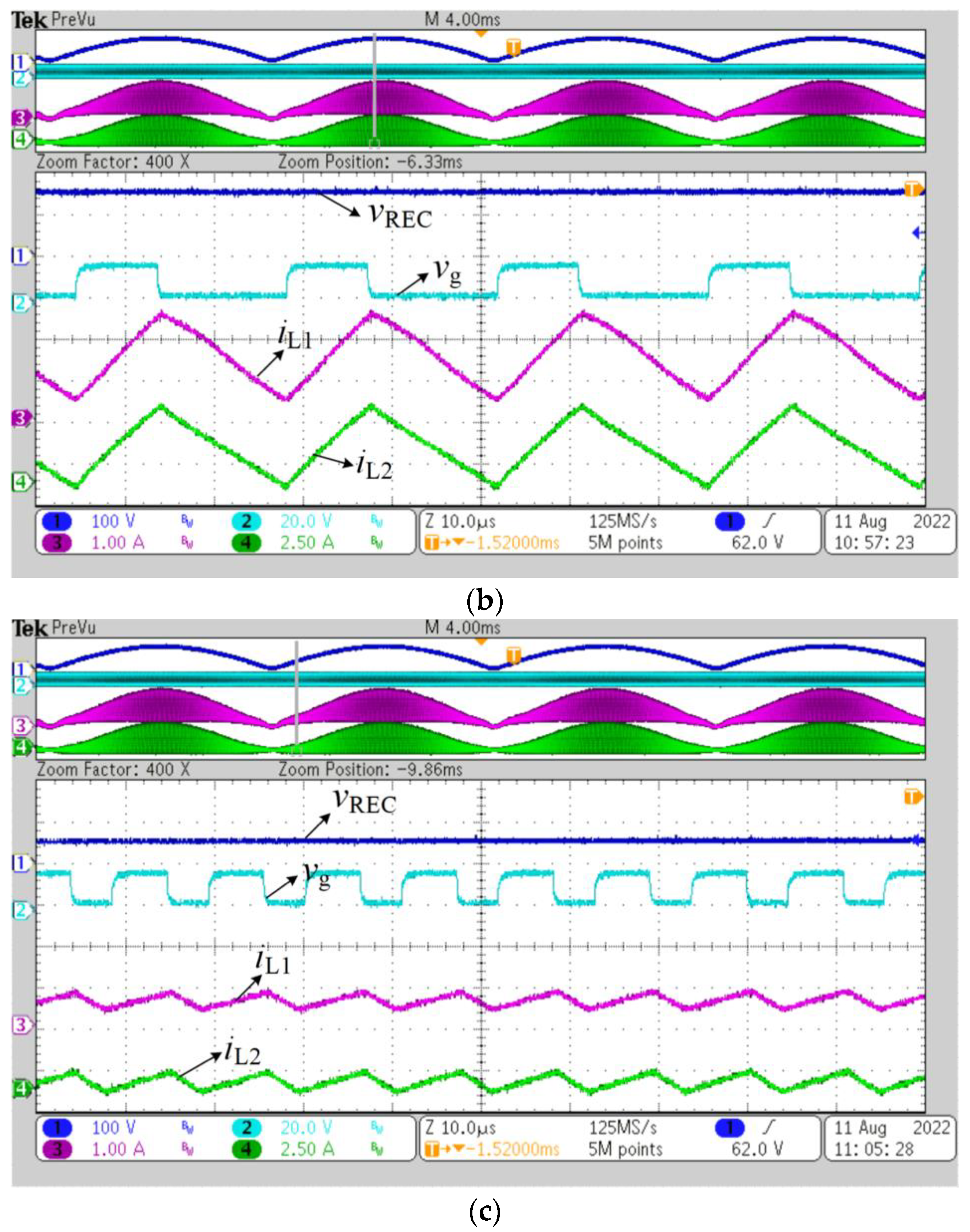
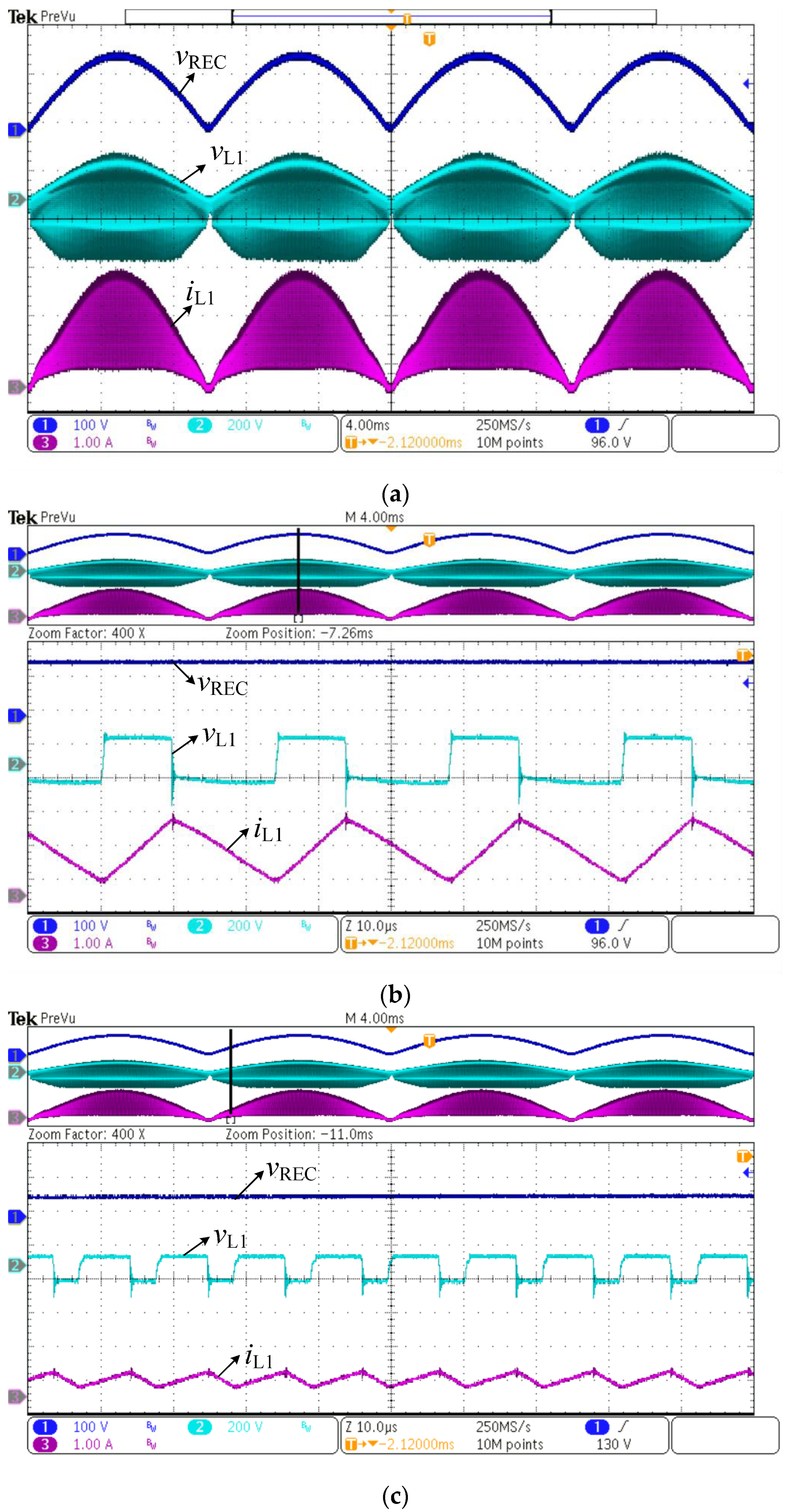
5. Analysis of Simulation and Experimental Results
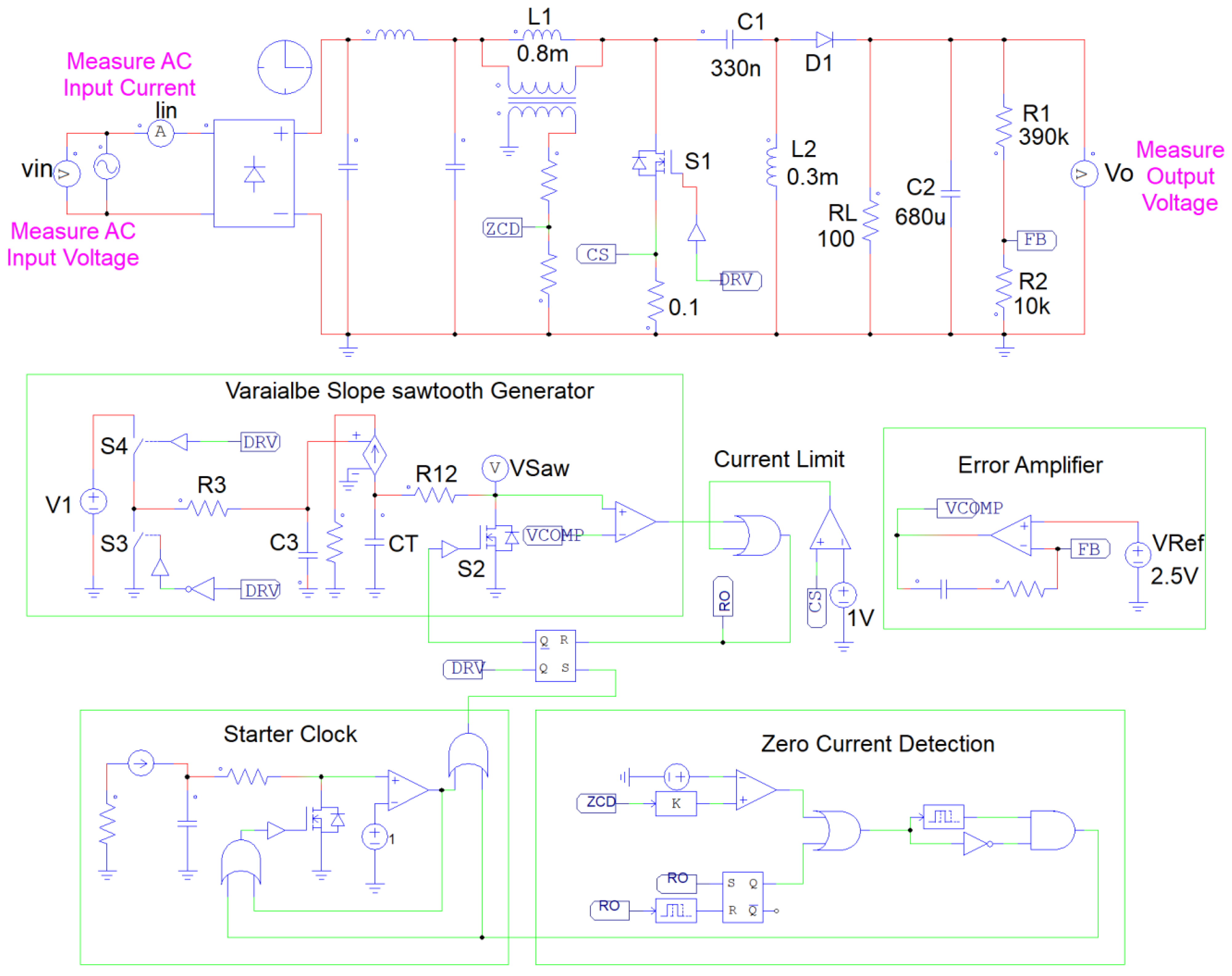
5.1. Analysis of Simulation Results
| Key Parameters | VOT and COT |
|---|---|
| AC Input Voltage Range Vin_RMS | 90–265 V |
| Output Voltage VO | 100 V |
| Line Frequency fL | 50 Hz |
| Rated Output Current IO | 1 A |
| Output Filter Capacitor CO | 680 μF |
| Middle capacitor C1 | 1 μF |
| Inductor L1 | 800 μH |
| Inductor L2 | 300 μH |
| Main switch S1 | FCPF190N60 |
| Freewheeling diode D1 | RHRP1560 |
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Alternating Current |
| BCM | Boundary Conduction Mode |
| CCM | Continuous Conduction Mode |
| COT | Constant On-Time |
| DC | Direct Current |
| DCM | Discontinuous Conduction Mode |
| PFC | Power Factor Correction |
| PF | Power Factor |
| RMS | Root Mean Square |
| SEPIC | Single Ended Primary Inductor Converter |
| THD | Total Harmonic Distortion |
| VOT | Variable On-Time |
| VCCS | Voltage-Controlled Current Source |
Notation
| C | Capacitance |
| D(t) | The duty cycle of the main power switch S1 |
| fL | Line frequency of AC input power source |
| fS_COT | Switching frequency of COT control |
| fS_VOT | Switching frequency of VOT control |
| f*S_COT | Normalized switching frequency of COT control |
| f*S_VOT | Normalized switching frequency of VOT control |
| g1 | Control ratio of voltage-controlled current source iCHG |
| iCHG | Charge current for capacitor CT |
| iD1 | Current flowing through diode D1 |
| iD1_AVG_COT | Average current flowing through diode D1 with COT control |
| iD1_PK_COT | Peak current flowing through diode D1 with COT control |
| Input current | |
| iin | The amplitude of second-order harmonic current of D1 with COT control |
| iin_COT | Input current with COT control |
| Iin_RMS_COT | RMS value of input current with COT control |
| iin_VOT | Input current with VOT control |
| i*in_COT | Normalized input current with COT control |
| i*in_VOT | Normalized input current with VOT control |
| iL1 | Current flowing through inductor L1 |
| iL1_0 | Initial value of iL1 when the main switch S1 starts to turn on |
| iL1_avg | The average value of the current flowing through L1 |
| iL2 | Current flowing through inductor L2 |
| iL2_0 | Initial value of iL2 when the main switch S1 starts to turn on |
| IO | Output current of SEPIC PFC converter |
| iS1 | Current flowing through S1 |
| iS1_PK_COT | Peak current of S1 with COT control |
| iS1_PK_VOT | Peak current of S1 with VOT control |
| i*S1_PK_COT | Normalized peak current of S1 with COT control |
| i*S1_PK_VOT | Normalized peak current of S1 with VOT control |
| IS1_RMS_COT | RMS current of S1 with COT control |
| IS1_RMS_VOT | RMS current of S1 with VOT control |
| L | Inductance |
| PFCOT | Power factor with COT control |
| PFVOT | Power factor with VOT control |
| Pin_COT | Input power with COT control |
| R | Resistance |
| Td | Time of diode D1 forward bias |
| Td_COT | Time of diode D1 forward bias with COT control |
| Ton | Turn-on time of main power switch S1 |
| Ton_COT | Turn-on time of S1 with COT control |
| Ton_VOT | Turn-on time of S1 with VOT control |
| TS | Switching period |
| TS_COT | Switching period with COT control |
| V1 | Voltage source V1 in variable slope sawtooth generator shown in Figure 4 |
| vB | Voltage of the middle capacitor C1 |
| Vcomp | Output voltage of error amplifier |
| vC3 | The voltage of C3 |
| vg | Driving signal of S1 |
| vin | Input voltage |
| VM | Amplitude of AC input power source |
| VO | Output voltage |
| vREC | Rectified AC input voltage |
| vSaw | The voltage of sawtooth generator at the positive input terminal of comparator |
| ΔiL1 | Inductor current ripple of L1 |
| ΔiL1_COT | Inductor current ripple of L1 with COT control |
| ΔiL2 | Inductor current ripple of L2 |
| ΔVO | Output voltage ripple |
| ΔVO_COT | Output voltage ripple with COT control |
| ΔVO_VOT | Output voltage ripple with VOT control |
| ω | Angular frequency of AC input power source |
References
- Garcia, O.; Cobos, J.A.; Prieto, R.; Alou, P.; Uceda, J. Single phase power factor correction: A survey. IEEE Trans. Power Electron. 2003, 18, 749–755. [Google Scholar] [CrossRef] [Green Version]
- Singh, B.; Singh, B.N.; Chandra, A.; Al-Haddad, K.; Pandey, A.; Kothari, D.P. A review of single-phase improved power quality AC-DC converters. IEEE Trans. Ind. Electron. 2003, 50, 962–981. [Google Scholar] [CrossRef] [Green Version]
- Costa, P.J.S.; Font, C.H.I.; Lazzarin, T.B. A family of single-phase voltage-doubler high-power-factor SEPIC rectifiers operating in DCM. IEEE Trans. Power Electron. 2017, 32, 4279–4290. [Google Scholar] [CrossRef]
- Limits for Harmonic Current Emissions (Equipment Input Current ≤16 A per Phase); International Electrotechnical Commission Standard 61000-3-2; Electromagnetic Compatibility (EMC): Luxembourg, 2009.
- IEEE Recommended Practices and Requirements for Harmonics Control in Electric Power Systems; IEEE Standard 519; IEEE: Piscataway, NJ, USA, 2014.
- Wu, X.; Yang, J.; Zhang, J.; Qian, Z. Variable on-time (VOT)-controlled critical conduction mode buck PFC converter for high-input AC/DC HB-LED lighting applications. IEEE Trans. Power Electron. 2012, 27, 4530–4539. [Google Scholar] [CrossRef]
- Liu, X.; Wan, Y.; He, M.; Zhou, Q.; Meng, X. Buck-type single-switch integrated PFC converter with low total harmonic distortion. IEEE Trans. Ind. Electron. 2021, 68, 6859–6870. [Google Scholar] [CrossRef]
- Yao, K.; Ruan, X.; Mao, X.; Ye, Z. Variable-duty-cycle control to achieve high input power factor for DCM boost PFC converter. IEEE Trans. Ind. Electron. 2011, 58, 1856–1865. [Google Scholar] [CrossRef]
- Chen, Y.L.; Chen, Y.M. Line current distortion compensation for DCM/CRM Boost PFC converters. IEEE Trans. Power Electron. 2016, 31, 2026–2038. [Google Scholar] [CrossRef]
- Frivaldsky, M.; Pipiska, M.; Spanik, P. Evaluation of the perspective power transistor structures on efficiency performance of PFC circuit. Electronics 2021, 10, 1571. [Google Scholar] [CrossRef]
- Chen, J.; Maksimovic, D.; Erickson, R.W. Analysis and design of a low-stress buck-boost converter in universal-input PFC applications. IEEE Trans. Power Electron. 2006, 21, 320–329. [Google Scholar] [CrossRef]
- Bist, V.; Singh, B. An adjustable-speed PFC bridgeless Buck–Boost converter-fed BLDC motor drive. IEEE Trans. Ind. Electron. 2014, 61, 2665–2677. [Google Scholar] [CrossRef]
- Brkovic, M.; Cuk, S. Automatic current shaper with fast output regulation and soft-switching. In Proceedings of the Intelec 93: 15th International Telecommunications Energy Conference, Paris, France, 27–30 September 1993; pp. 379–386. [Google Scholar]
- Pandey, R.; Singh, B. A power-factor-corrected LLC resonant converter for electric vehicle charger using Cuk converter. IEEE Trans. Ind. Appl. 2019, 55, 6278–6286. [Google Scholar] [CrossRef]
- Elkhateb, A.; Rahim, N.A.; Selvaraj, J.; Uddin, M.N. Fuzzy-logic-controller-based SEPIC converter for maximum power point tracking. IEEE Trans. Ind. Appl. 2014, 50, 2349–2358. [Google Scholar] [CrossRef]
- Durgadevi, S.; Umamaheswari, M.G. Analysis and design of single phase power factor correction with DC–DC SEPIC Converter for fast dynamic response using genetic algorithm optimised PI controller. IET Circ. Devices Syst. 2018, 12, 164–174. [Google Scholar] [CrossRef]
- Munuswamy, R.; Govindarajan, U.; Anbukumar, K. Performance comparison and stability analysis of ACM and ENLC controlled SEPIC PFC converter. IET Power Electron. 2020, 13, 991–1001. [Google Scholar] [CrossRef]
- Kanaan, H.Y.; Al-Haddad, K.; Sauriole, G.; Chaffai, R. Practical design of a SEPIC power factor corrector with DC-voltage regulation. In Proceedings of the 2006 IEEE International Symposium on Industrial Electronics, Montreal, QC, Canada, 9–13 July 2006; pp. 964–969. [Google Scholar]
- Burgardt, I.; Agostini, E.; Font, C.H.I.; Nascimento, C.B. Dimmable flicker-free power LEDs lighting system based on a SEPIC rectifier using a regenerative snubber. IET Power Electron. 2016, 9, 891–899. [Google Scholar] [CrossRef]
- Tian, G.; Qi, W.; Yan, Y.; Jiang, Y. High power factor LED power supply based on SEPIC converter. Electron. Lett. 2014, 50, 1866–1868. [Google Scholar] [CrossRef]
- Shi, C.; Wang, H.; Dusmez, S.; Khaligh, A. A SiC-Based high-efficiency isolated onboard PEV charger with ultrawide DC-link voltage range. IEEE Trans. Ind. Appl. 2017, 53, 501–511. [Google Scholar] [CrossRef]
- Gopalarathnam, T.; Toliyat, H.A. A new topology for unipolar brushless DC motor drive with high power factor. IEEE Trans. Power Electron. 2003, 18, 1397–1404. [Google Scholar] [CrossRef]
- Singh, B.; Singh, S. Single-phase power factor controller topologies for permanent magnet brushless DC motor drives. IET Power Electron. 2010, 3, 147–175. [Google Scholar] [CrossRef]
- Chiu, H.; Lo, Y.; Chen, J.; Cheng, S.; Lin, C.; Mou, S. A High-Efficiency Dimmable LED Driver for Low-Power Lighting Applications. IEEE Trans. Ind. Electron. 2010, 57, 735–743. [Google Scholar] [CrossRef]
- Pandey, R.; Singh, B. PFC-SEPIC converter-fed half-bridge LLC resonant converter for e-bike charging applications. IET Electr. Syst. Transp. 2020, 10, 225–233. [Google Scholar] [CrossRef]
- Kwon, J.M.; Choi, W.Y.; Lee, J.J.; Kim, E.H.; Kwon, B.H. Continuous-conduction-mode SEPIC converter with low reverse-recovery loss for power factor correction. IEE Proc. Electr. Power Appl. 2006, 153, 673–681. [Google Scholar] [CrossRef] [Green Version]
- Ye, Z.; Greenfeld, F.; Liang, Z. Offline SEPIC converter to drive the high brightness white LED for lighting applications. In Proceedings of the 2008 34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 3 April 2008; pp. 1994–2000. [Google Scholar]
- Shi, C.; Khaligh, A.; Wang, H. Interleaved SEPIC power factor preregulator using coupled inductors in discontinuous conduction mode with wide output voltage. IEEE Trans. Ind. Appl. 2016, 52, 3461–3471. [Google Scholar] [CrossRef]
- Bianchin, C.G.; Gules, R.; Badin, A.A.; Romaneli, E.F.R. High-Power-Factor rectifier using the modified SEPIC converter operating in discontinuous conduction mode. IEEE Trans. Power Electron. 2015, 30, 4349–4364. [Google Scholar] [CrossRef]
- Jassim, B.M.H. SEPIC AC-DC converter for aircraft application. In Proceedings of the MELECON 2014—2014 17th IEEE Mediterranean Electrotechnical Conference, Beirut, Lebanon, 13–16 April 2014; pp. 12–16. [Google Scholar]
- Ye, Z.; Greenfeld, F.; Liang, Z. Design consideration of a high power factor SEPIC converter for high brightness white LED lighting applications. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 2657–2663. [Google Scholar]
- Simonetti, D.S.L.; Sebastian, J.; Uceda, J. The discontinuous conduction mode Sepic and Cuk power factor preregulators: Analysis and design. IEEE Trans. Ind. Electron. 1997, 44, 630–637. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Chang, C. Analysis and design of SEPIC converter in boundary conduction mode for universal-line power factor correction applications. In Proceedings of the 2001 IEEE 32nd Annual Power Electronics Specialists Conference, Vancouver, BC, Canada, 17–21 June 2001; pp. 742–747. [Google Scholar]
- Yan, T.; Xu, J.; Zhang, F.; Sha, J.; Dong, Z. Variable-on-time-controlled critical-conduction-mode Flyback PFC converter. IEEE Trans. Ind. Electron. 2014, 61, 6091–6099. [Google Scholar] [CrossRef]
- Memon, A.H.; Yao, K.; Chen, Q.; Guo, J.; Hu, W. Variable-On-Time control to achieve high input power factor for a CRM-integrated Buck–Flyback PFC converter. IEEE Trans. Power Electron. 2017, 32, 5312–5322. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y.; Mo, Q.; Chen, M.; Qian, Z. An improved control strategy based on multiplier for CRM Flyback PFC to reduce line current peak distortion. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 901–905. [Google Scholar]
- Shen, X.; Yan, T.; Li, Q.; Wang, Y.; Chen, W. Variable on-time controlled boundary conduction mode single-ended primary inductor converter power factor correction converter. Electron. Lett. 2018, 54, 97–99. [Google Scholar] [CrossRef]
- Falin, J. Designing DC/DC Converters Based on SEPIC Topology. Available online: https://www.ti.com/lit/an/slyt309/slyt309.pdf (accessed on 9 February 2023).
- Zhang, D. AN-1484 Designing a SEPIC Converter. Available online: https://www.ti.com/lit/an/snva168e/snva168e.pdf (accessed on 9 February 2023).
- Zhang, R.; Liu, S.; Li, B.; Zhao, N.; Wang, G.; Xu, D. Totem-Pole bridgeless Boost PFC converter based on GaN HEMT for air conditioning applications. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; pp. 1–9. [Google Scholar]
- Wei, Y.; Luo, Q.; Wang, J.; Sun, P. Analysis and design of the DCM operation boost PFC converter with magnetic control. IET Power Electron. 2019, 12, 3697–3706. [Google Scholar] [CrossRef]
- Schonberger, J. Modeling a PFC Controller Using PLECS. Available online: https://www.plexim.com/sites/default/files/plecs_pfc.pdf (accessed on 9 February 2023).
- Sahin, M.E.; Okumus, H.I. Comparison of different controllers and stability analysis for photovoltaic powered Buck-Boost DC-DC converter. Electr. Power Compon. Syst. 2018, 46, 149–161. [Google Scholar] [CrossRef]
- Sahin, M.E.; Okumus, H.I.; Aydemir, M.T. Implementation of an electrolysis system with DC/DC synchronous buck converter. Int. J. Hydrogen Energy 2014, 39, 6802–6812. [Google Scholar] [CrossRef]

















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, X.; Chen, W.; Li, Q.; Wang, Y. A Novel Variable On-Time Control Scheme for Boundary Conduction Mode SEPIC PFC Converter. Electronics 2023, 12, 1807. https://doi.org/10.3390/electronics12081807
Shen X, Chen W, Li Q, Wang Y. A Novel Variable On-Time Control Scheme for Boundary Conduction Mode SEPIC PFC Converter. Electronics. 2023; 12(8):1807. https://doi.org/10.3390/electronics12081807
Chicago/Turabian StyleShen, Xia, Weirong Chen, Qi Li, and Yingmin Wang. 2023. "A Novel Variable On-Time Control Scheme for Boundary Conduction Mode SEPIC PFC Converter" Electronics 12, no. 8: 1807. https://doi.org/10.3390/electronics12081807
APA StyleShen, X., Chen, W., Li, Q., & Wang, Y. (2023). A Novel Variable On-Time Control Scheme for Boundary Conduction Mode SEPIC PFC Converter. Electronics, 12(8), 1807. https://doi.org/10.3390/electronics12081807








