Abstract
As a common fault of transformer winding, inter-turn short circuits cause severe consequences, such as excessive current and serious deformation of winding. Aiming to solve the problem of inter-turn short circuit at the end-winding and middle-winding of high frequency transformers (HFT), this paper considers the electromagnetic vibration characteristics of inter-turn short circuits (interleaved winding and continuous winding) at different positions, and the HFT is established by the multi-physical field coupling principle. Coupling equations for the inter-turn short circuit, as well as electromagnetic force and sound pressure level, are established to characterize the vibration noise mechanism of inter-turn short circuits. Furthermore, the HFT equivalent model is simulated in 3D finite element method (FEM) to emulate the real transformer operation and investigate the impact of interleaved winding and continuous winding under inter-turn short circuit faults. The short-circuit current and axial flux leakage, as well as the harmonic response of vibration acceleration and sound pressure level distribution, are obtained when inter-turn short circuits occur at different positions. Finally, the results show that the electromagnetic effect of the inter-turn short circuit in end-winding is worse than it is in middle-winding. Advantages in resisting impulse current make interleaved winding superior to continuous winding in terms of vibration and noise.
1. Introduction
As electrical equipment, transformers provide a better power supply mode for rapid economic development. Many problems still need to be solved for transformers, however, such as inter-turn short circuits [1,2,3]. An inter-turn short circuit is caused by direct contact between two or more adjacent coils due to the damage of the insulation layer [4,5,6]. The damage to the insulation layer is mainly caused by excessive stress in the transformer manufacturing process and insulation aging after long-term operation [7,8,9]. The probability of transformer damage obviously increases obviously after a short circuit, and transformer damage accidents caused by short circuit account for about 50% of the total accidents [10,11,12].
To maintain the stable operation of transformer, many researchers study transformer faults under inter-turn short circuits. In [13], the spectral density estimation method is used to optimize the transfer function, which enhances the anti-disturbance ability of the transfer function. Errors caused by different external conditions such as oil quality and oil temperature are then overcome. In [14], the influence of different physical fault levels on the corresponding changes in equivalent circuit parameters is studied, and the relationship diagram between various winding axial displacement levels and the changes in transformer equivalent circuit parameters are introduced. The research results promote the accurate qualitative and quantitative analysis of transformer FRA characteristics. In [15,16], the characteristic curve of the repetitive pulse method is used to diagnose inter-turn short circuit faults. In [17,18], a fault location method of transformer inter-turn short circuits based on traveling wave analysis is proposed. In [19], the transformer correlation coefficient of frequency response function is analyzed, and a monitoring system for inter-turn short circuits in transformers is established. In [20], the relationship between winding deformation and leakage inductance parameters is utilized to realize on-line monitoring of transformer winding vibration and deformation. In [21], the fault phase of inter-turn short circuits based on the variation characteristics of transformer magnetic fields is identified. In [22], the corresponding relationship between transformer short-circuit current and vibration signal is established, and transformer inter-turn short circuit faults are identified using frequency spectrum analysis of vibration signals. In [23], to address the problem of inter-turn short circuits in the transformer’s low-voltage side winding, the short circuit winding is considered as equivalent to two different windings; the influence of inter-turn short circuit on the winding voltage is studied. In [24,25], the static mechanical characteristics of winding inter-turn insulation pad are studied, and the relationship between the material properties and dynamic characteristics of the pad are described. In [26], the characteristics of winding vibration under different pre-tightening force and temperature are studied, giving a more comprehensive understanding of winding vibration. In [27], to obtain the vibration signal of the iron core and winding, theoretical analysis is used to conduct no-load and load experiments on the transformer. Eventually, the state of the iron core and the winding with the time domain of the signal are expressed. In [28], the vibration model of winding is built, and the vibration mechanical characteristics of winding after electromagnetic and mechanical coupling are analyzed. In [29], vibration acceleration sensors are placed on the surface of the transformer oil tank, insulating oil, and winding. The frequency spectrum characteristics between vibration signals of different structures in the transformer are compared and analyzed. All the above studies are based on extracting and analyzing the external parameters of transformer inter-turn short circuit faults to monitor and locate the fault. There are few studies examining the relationship between the changes in electromagnetic parameters and vibration.
In this paper, a 10 kVA, 5 kHz nanocrystalline HFT is studied to reveal the inter-turn short circuit effect in the high frequency band. Based on the multi-physics coupling principle, a 3D model of the transformer is established by FEM. Then, the electromagnetic characteristics of the primary middle-winding and end-winding in the inter-turn short circuit of the interleaved winding and continuous winding are studied. The distribution characteristics of short-circuit current and axial magnetic leakage of the fault transformer are obtained. In addition, harmonic response analysis of the vibration acceleration is conducted to obtain the main frequency band of the acceleration. Finally, the propagation characteristics in the sound field are characterized by sound pressure level.
2. Electromagnetic Vibration Noise Mechanism of High Frequency Transformer under Inter-Turn Short Circuits
2.1. Equivalent Electromagnetic Coupling Model under Inter-Turn Short Circuit
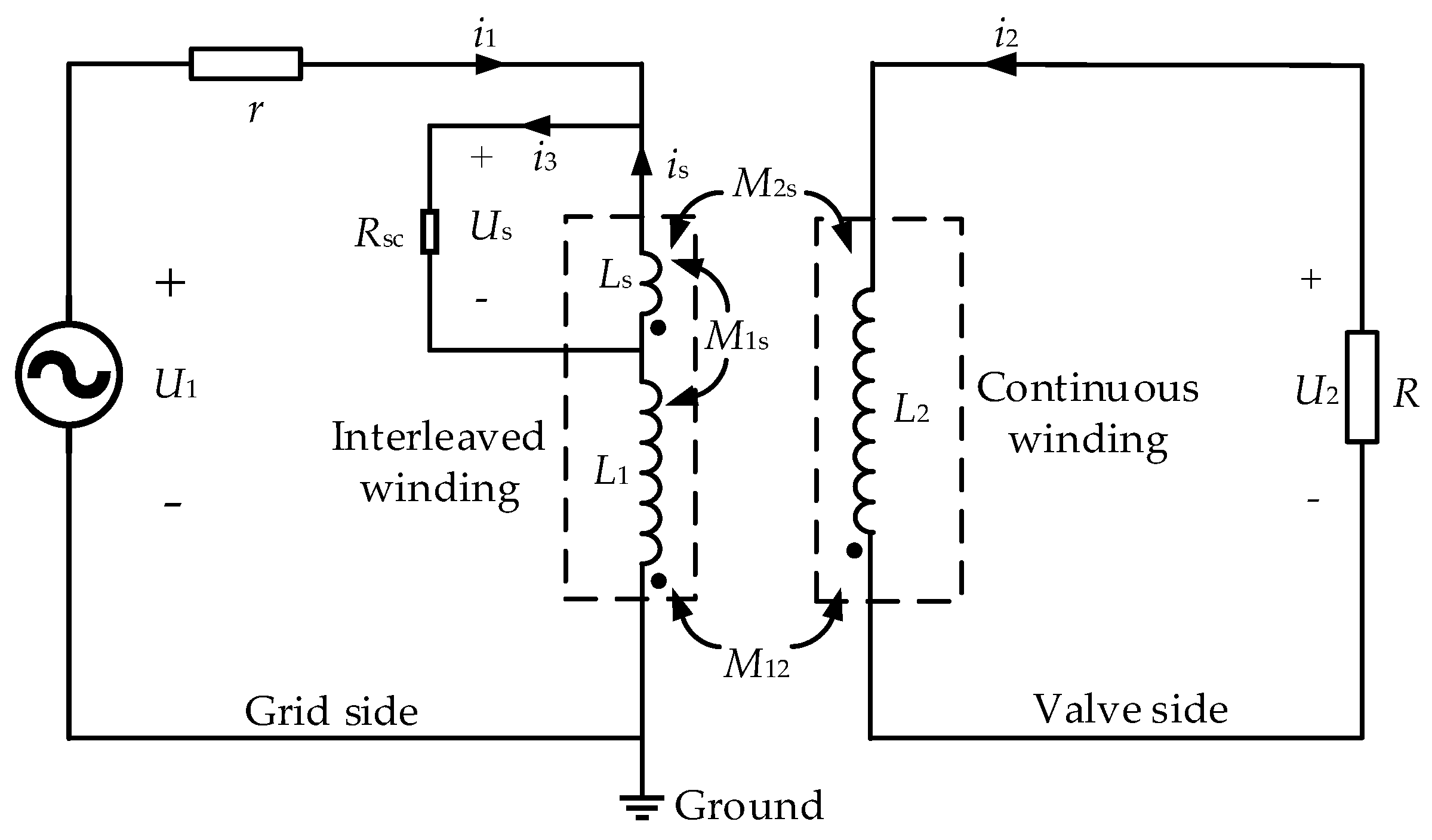
The inter-turn short circuit fault position of HFT is set in the primary winding. Three types of winding exist when the inter-turn short circuit occurs in the primary winding: the primary winding without a short circuit, the short circuit winding, and the secondary winding; all the above windings are coupled with each other. The schematic diagram is shown in Figure 1. Us is almost 0 when the short circuit occurs. The excitation winding is mainly the unshort-circuited part of the primary side, and the weak coupling between the secondary winding and the short circuit winding is ignored. The electromagnetic relationship of inter-turn short circuit in primary winding can be expressed as:
where U1, U2, i1 and i2, are the port voltage and port current, respectively. Us and is are the voltage and current of short circuit winding. M12, M1s, and M2s are the mutual inductance among windings. L1, Ls, and L2 are the self-inductance of windings. r is the internal resistance of power supply. Rsc is a short circuit resistance connected in series on the short-circuit line to characterize different degrees of inter-turn short circuit. Rsc is set to 0.01 Ω to indicate serious inter-turn short circuit.
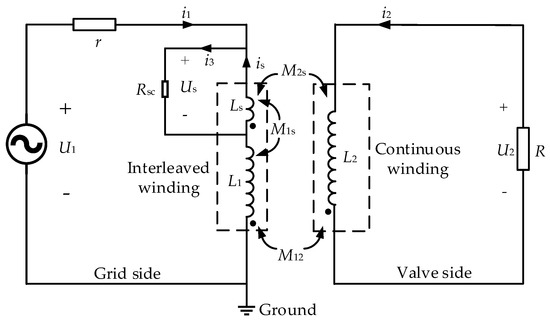
Figure 1.
Schematic diagram of inter-turn short circuit.
In addition, the inter-turn geometric capacitance and the inter-cake geometric capacitance of the high-frequency transformer wire cake belong to distributed capacitance, while the capacitance on the winding equivalent circuit is lumped capacitance, so the distributed capacitance needs to be equivalent to lumped capacitance, that is, longitudinal capacitance. The interleaved winding functions through interleaved transposition; an advantage of this behavior is that the longitudinal capacitance of the winding can be improved by increasing the voltage between turns. Finally, the impulse voltage distribution of the winding can meet the high insulation strength requirements. Therefore, capacitance coupling needs to be considered.
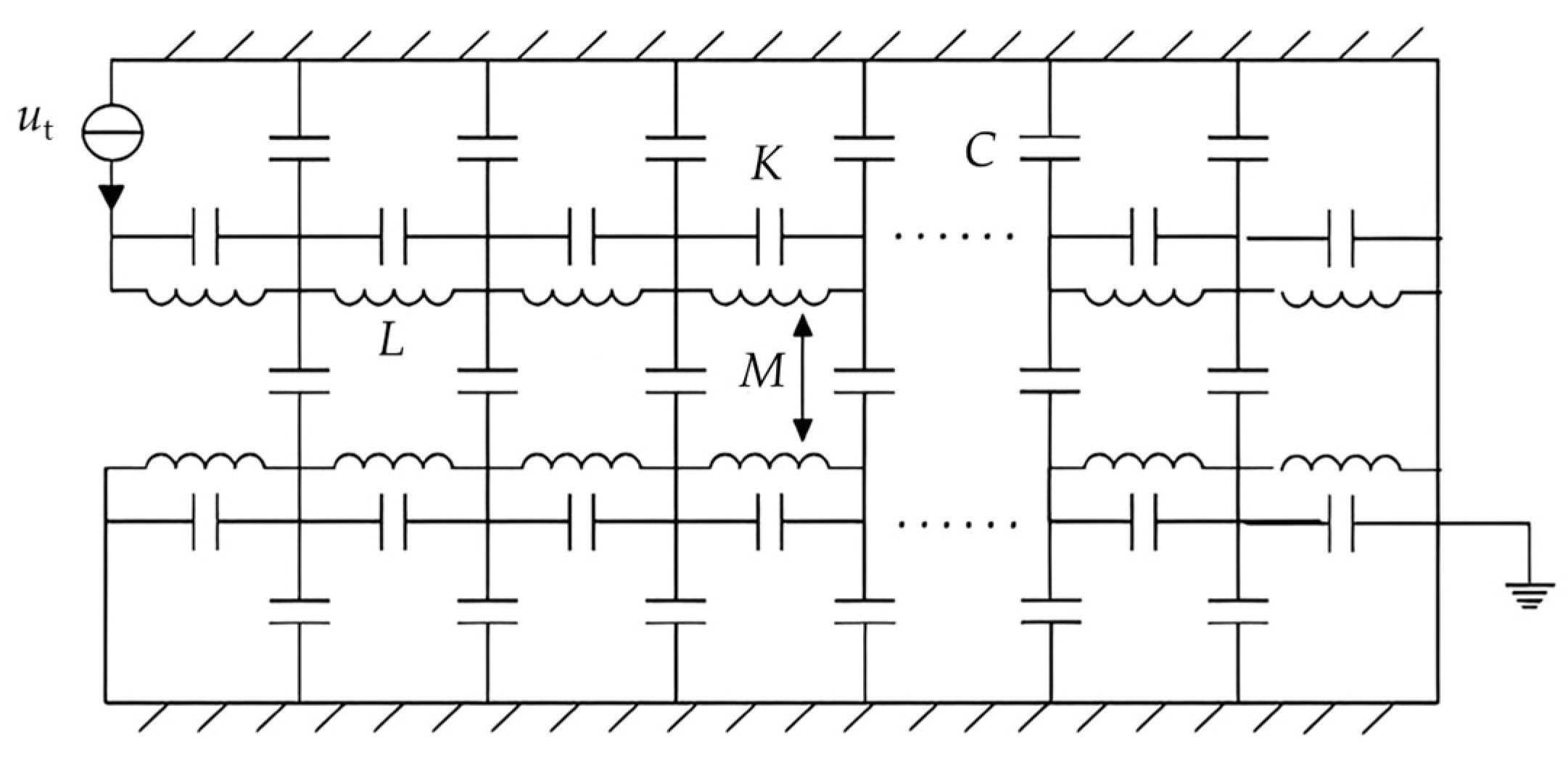
Under the high frequency inter-turn short circuit condition, the HFT is equivalent to the distributed parameter circuit model of series capacitance, parallel capacitance, self-inductance and mutual inductance. The schematic diagram of HFT interleaved winding capacitance coupling is shown in Figure 2, where L is the self-inductance, M is the mutual inductance, C is the winding capacitance to ground, K is the winding series capacitance, and ut is the short-circuit impulse wave voltage.
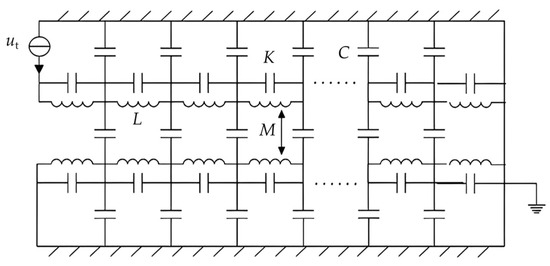
Figure 2.
Equivalent circuit of HFT winding.
Based on the equivalent circuit model, the second-order differential equation is established as:
where Cq is the cutset capacitance matrix and Γq is the cutset inductance matrix. The differential equation is solved to obtain the time-domain distribution of voltage between nodes and ground. The interleaved winding forms a voltage difference between the wires through interleaved transposition, causing an inter-turn capacitance between the windings. An advantage of the interleaved winding is how the longitudinal capacitance of the winding can be improved by increasing the voltage between turns. Finally, the impulse voltage distribution of the winding can meet the high insulation strength requirements.
2.2. Stress Calculation of Transformer Iron Core and Winding
Inter-turn short circuits cause forced vibration of transformer windings. By coupling the transient analysis results of electromagnetic field to the stress field above, the transient value of winding electromagnetic force on time domain can be obtained. The strain of iron core and winding material are transformed into excitation force using the principle of elasticity. The electromagnetic force of transformer winding is calculated using the virtual displacement method:
where Fr is the electromagnetic force acting in the r direction and Wm is the magnetic field energy storage of the winding leakage magnetic field. i and LD are the winding current and inductance, respective; they are calculated based on the electromagnetic coupling principle.
Considering that the nanocrystalline iron core is isotropic, the volume force density f0 of the iron core under magnetic field force is:
where J is the current density. B is the magnetic induction intensity; H is the magnetic field intensity. μ’ is the medium permeability. τ is the volume density of the medium. The first term is the Lorentz force density component of the element. The second term is Maxwell force density component. The third term is the magnetostrictive force density term.
2.3. Analysis of Acoustic Field
When an inter-turn short circuit occurs, the short-circuit current is very large. The magnetization of the core enters the saturation region, which results in increased transformer and electromagnetic noise, i.e., the vibration noise from the core and the winding that are caused by magnetic leakage.
Sound pressure is a physical quantity used to measure the strength of sound. Sound pressure can be expressed by instantaneous sound pressure and root mean square sound pressure. The sound pressure transformation of a sound field medium on a unit area of an instantaneous relative static pressure at a certain point is the instantaneous sound pressure, and the root mean square value of the instantaneous sound pressure in a certain time period is the root mean square sound pressure.
Taking the vibration of transformer core winding as the boundary condition, the noise distribution of transformer is obtained. The noise intensity is expressed by sound pressure, and the noise level is expressed by sound pressure level Lp.
where Lp is the sound pressure level in dB. p is sound pressure in Pa. p0 is the reference sound pressure, and the standard sound pressure value of air is 2 × 10−5 Pa. When the sound field is calculated in time domain, the signal of the sound pressure in the air domain can be obtained, and the calculated value of the noise sound pressure level around the transformer under the condition of inter-turn short circuit can be obtained through a certain quantitative relationship.
3. Modeling of High Frequency Transformer
To analyze the physical and operating characteristics of HFT under inter-turn short circuits, a model of the 10 kVA HFT is established, and the corresponding inter-turn short external circuit is built. The HFT models under normal and short circuits conditions are shown in Figure 3. The HFT is a shell-type single-phase step-down transformer. The outer winding is a primary winding with 40 turns; its rated voltage is 500 V, and it has 40 winding turns. The inter-winding is a low voltage winding with a rated voltage of 250 V and 20 turns.
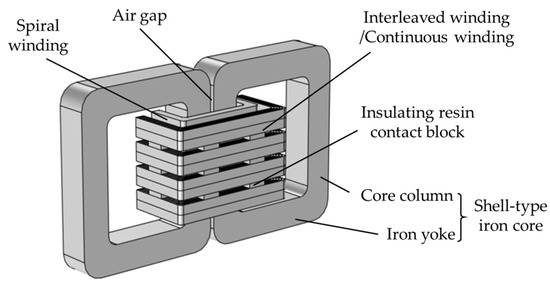
Figure 3.
Schematic diagram of nanocrystalline HFT model.
The thickness of the nanocrystalline iron core and the air gap between windings is smaller than that of windings; this is required to effectively save time in simulation calculation to meet the precision calculation requirements. The free tetrahedron mesh is adopted for the air gap between windings and nanocrystalline iron core when the iron core, windings, and air domain are meshed; this improves the accuracy of the simulation results. The model contains a mesh of 77,551 vertices and 402,470 elements. When calculating the multi-physics field, the transient solution is carried out. A fully coupled solver is adopted, the maximum number of iterations is set to 25, the solver step is set to 2 × 10−6 s, and the total solution time is 2 × 10−4 s.
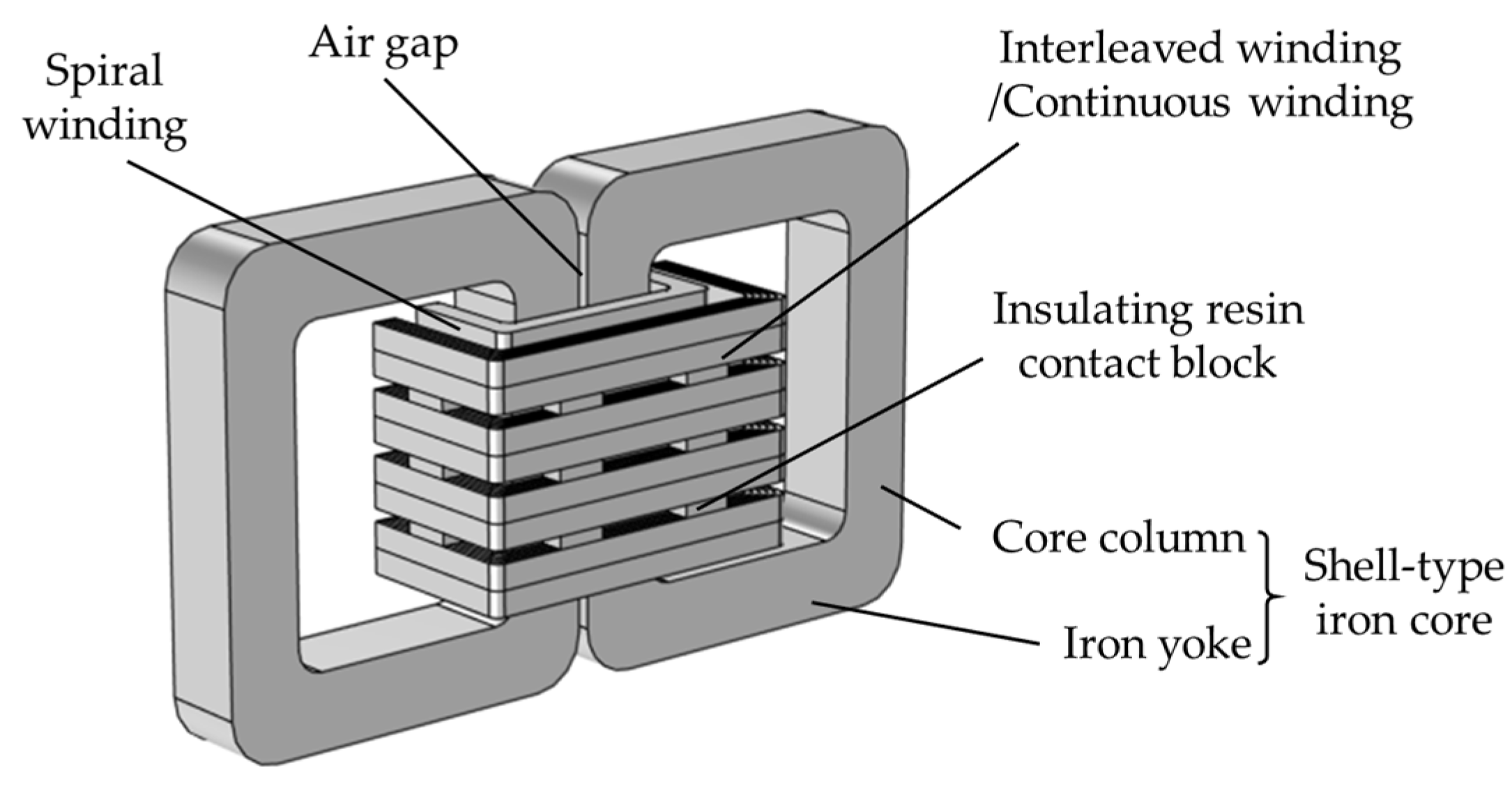
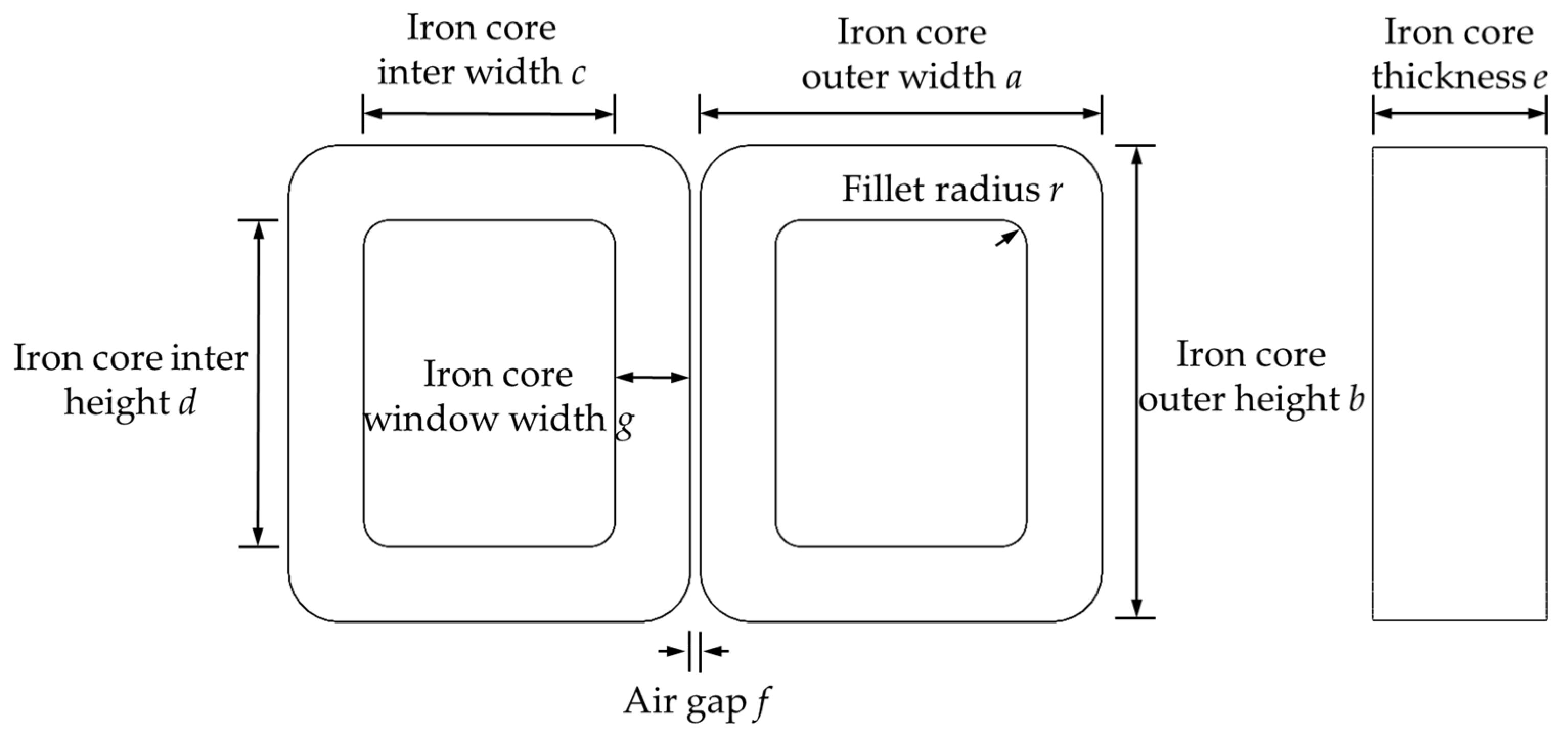
The iron core of HFT adopts a shell structure, which has the advantages of high mechanical strength and convenient transportation. The schematic diagram of the HFT iron core is shown in Figure 4. The iron core is formed by stacking nanocrystalline alloy sheets, which have the advantages of high magnetic permeability and low loss. Its lamination thickness and lamination coefficient are 18 μm and 0.8, respectively. The structure parameters of the shell-type nanocrystalline iron core are shown in Table 1.
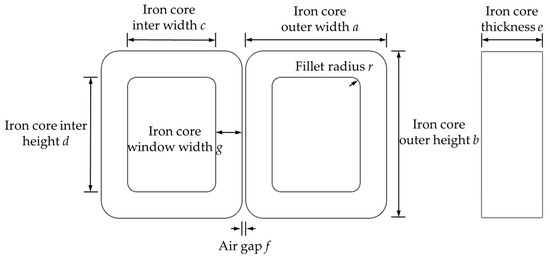
Figure 4.
Schematic diagram of shell-type iron core model, where, “a”, “b”, “c”, “d” and “e” are the outer width, outer height, inter width, inter height and thickness of iron core, respectively. “f” and “r” are the air gap and fillet radius, respectively.

Table 1.
Structure parameters of shell-type nanocrystalline iron core.
Due to the high supply voltage and winding current frequency of HFT, the winding is greatly affected by the skin effect, and most of the current exists on the surface near the wire. The skin depth can be calculated as follows:
where f (=5000 Hz) is the power supply frequency, μ (=4π × 10−7 H/m) and σ (=6 × 107 S/m) are the permeability and conductivity of copper, respectively. Ka is the AC resistance coefficient of the winding.
When the conductor works in a high-frequency environment, the ratio between alternative current resistance should be consistent with direct current, that is, K = 1. According to the calculation results, it can be obtained that the skin depth is 0.92 mm. Under normal circumstances, the thickness of the conductor is generally selected to be within two times of the skin depth. The length and width of the primary winding are set to 5 mm and 1 mm, respectively, in this paper, and the cross-sectional area of selected conductor is 5 mm2. QZ-2 thick insulated polyester enameled flat copper wire can meet these requirements for a conductor. Specific parameters are shown in Table 2.

Table 2.
Wire specific parameters.
Interleaved winding and continuous winding are commonly used winding types; they both have the advantages of high mechanical strength and good heat dissipation performance. Both are established under the same copper consumption and resistance.
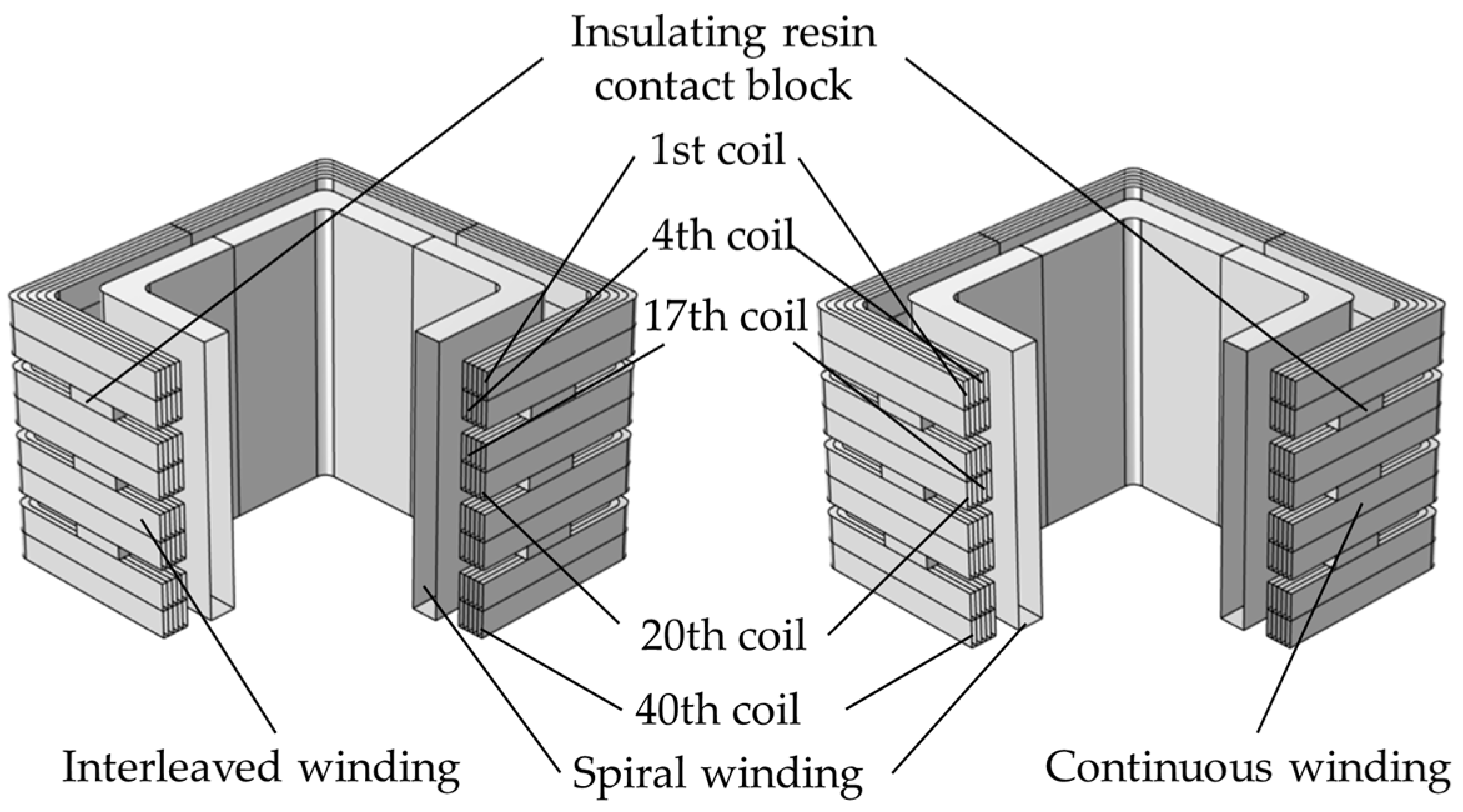
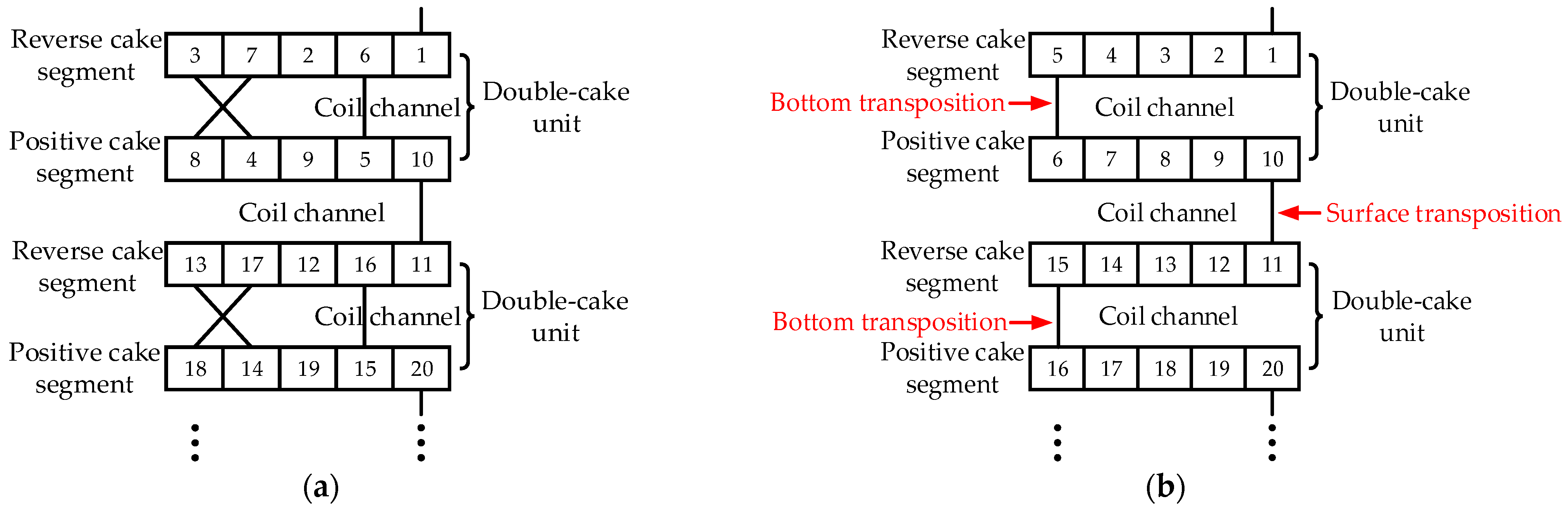
Continuous winding refers to concentric winding that consists of multiple wire cakes strung along the axis of windings. The odd-numbered wire cakes are arranged successively from the outside to the inside to become a reverse cake, while the even-numbered wire cakes are arranged successively from the inside to the outside to become a positive cake. The interleaved winding is not connected in series directly between two adjacent turns; instead, is a special wire cake connected in series after several turns are spaced. The structures above are shown in Figure 5. The double-cake unit of interleaved winding is a special form of continuous winding; it is formed by a reverse cake segment and a positive cake segment in pairs, with a shape very similar to that of continuous winding. The grid side windings of the two are shown in Figure 6. The common spiral winding structure is used on the valve side. To simplify the modeling process, the valve side winding is equivalent to a whole, that is, a square ring with uniform multi-turns.
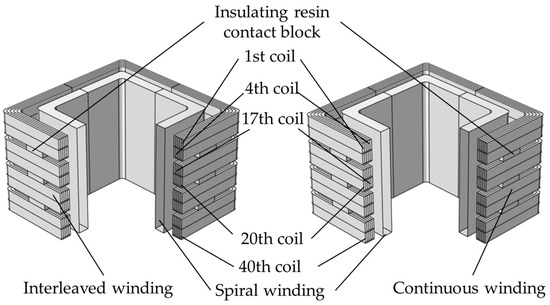
Figure 5.
Schematic diagram of interleaved and continuous winding models.
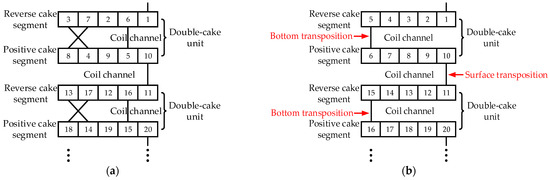
Figure 6.
Outspread diagram of primary winding (a) Interleaved winding; (b) Continuous winding.
As shown in Figure 6, there are 40 turns in the primary winding. Each coil is modeled; the end inter-turn short circuit is for the 1st–4th coils and the middle inter-turn short circuit is for 17th–20th coils. Because the winding modes of 21–40 turns coil and 1–20 turns coil are the same, they are not shown one by one.
4. Analysis of Vibration and Noise Characteristics under Inter-Turn Short Circuits
4.1. Analysis of Short-Circuit Current and Axial Magnetic Flux Leakage
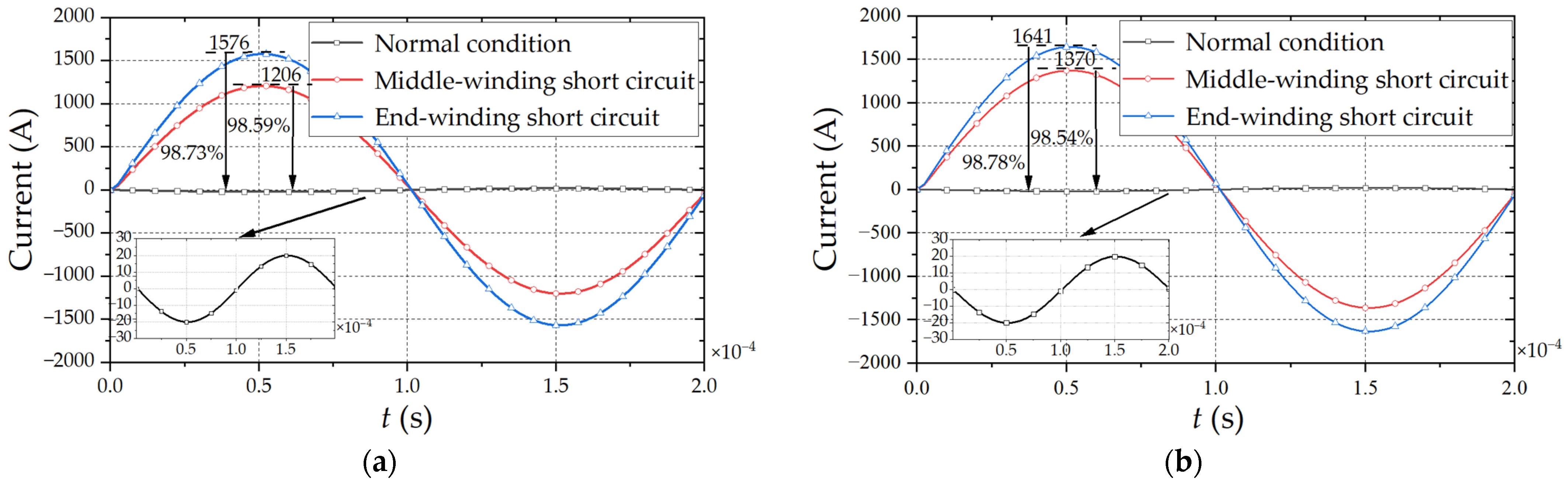
When HFT operates at rated load, 10% inter-turn short circuit turns (4 turns) fault is set at the primary middle-winding and end-winding. The winding current phases are opposite under the rated load and the short circuit fault because the short-circuit winding can be regarded as the secondary side when local windings are short circuited. When the current passing through the windings is working normally, increases on the primary side cause increases in the flux linkage. Therefore, the back EMF increases. According to Lenz’s law, short-circuit turns generate back EMF to hinder external changes. At the same time, reverse current is generated. The same is true when the current of the primary coil decreases. The simulation results of the winding current of the primary winding are shown in Figure 7.
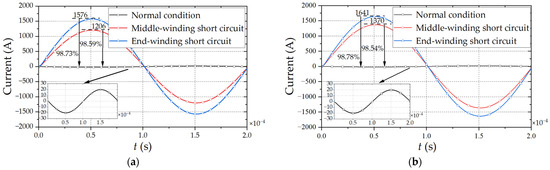
Figure 7.
Rated and short-circuit current of primary winding (a) Interleaved winding; (b) Continuous winding.
It can be seen from Figure 7 that the amplitude of the primary interleaved winding current is 20 A when HFT operates at rated load, which is the same as the rated load current of the continuous winding. At the same time, the amplitude of the primary interleaved winding is 1206 A and 1576 A when the inter-turn short circuit fault occurs at the end-winding and middle-winding. The short-circuit currents are 60.3 times and 78.8 times of the rated load current, respectively, and about 12% and 4% lower than the fault current of the continuous winding, respectively.
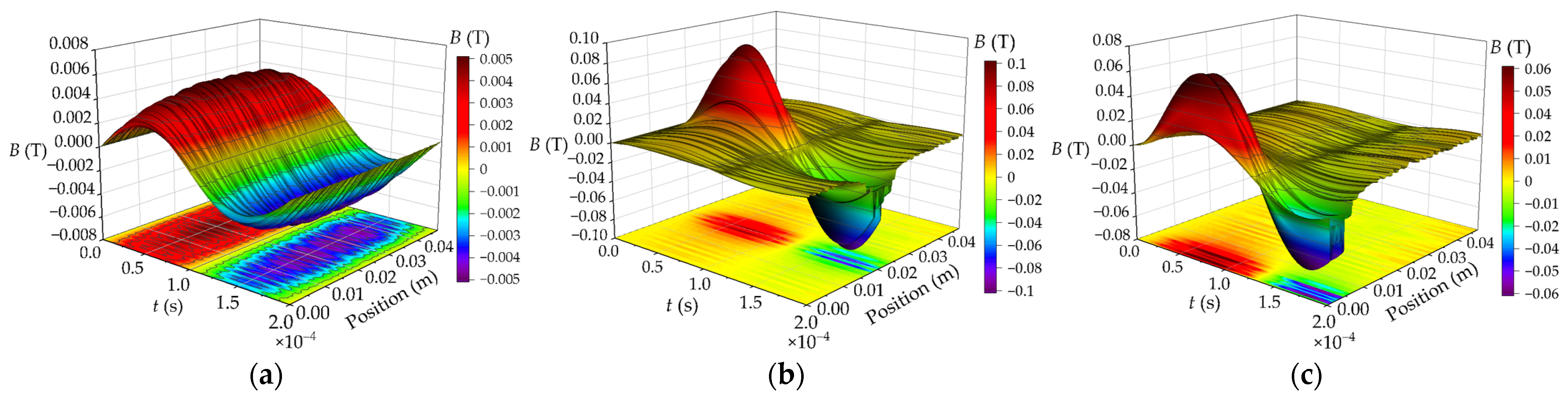
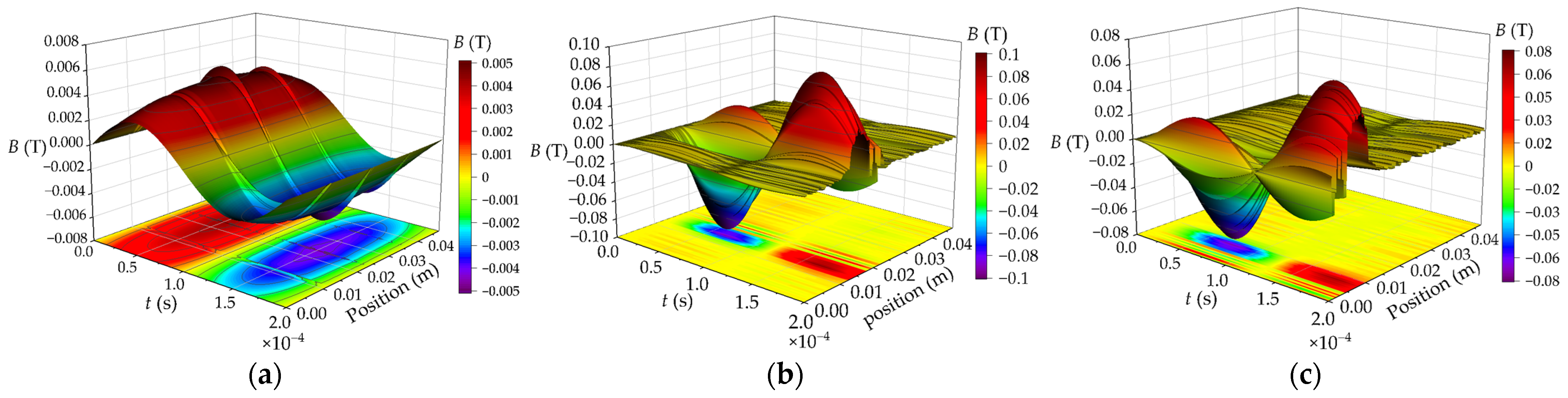
In order to analyze the leakage magnetic field distribution of the winding where the short-circuit turns are located, a path is set on the primary winding that moves from top to bottom, and the magnetic field intensity curve of this path is drawn. The axial magnetic flux leakage distribution of interleaved winding and continuous winding is shown in Figure 8 and Figure 9. The leakage magnetic field near inter-turn short circuit of interleaved winding of HFT increases sharply, and the maximum magnetic flux leakage is 0.09 T and 0.06 T, respectively, which is 12–18 times that of normal operation and slightly less than that of continuous winding. The axial magnetic flux leakage of short circuit winding gradually decreases from the fault point to both sides along the axial direction, and the magnetic flux leakage of winding far away from short circuit turns is obviously reduced.
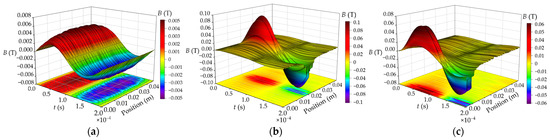
Figure 8.
Comparison of axial magnetic flux leakage distribution of interleaved winding (a) Normal condition; (b) Middle-winding short circuit; (c) End-winding short circuit.
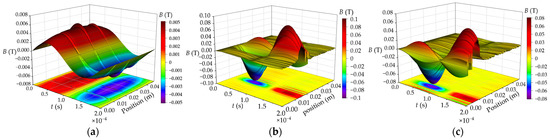
Figure 9.
Comparison of axial magnetic flux leakage distribution of continuous winding (a) Normal condition; (b) Middle-winding short circuit; (c) End-winding short circuit.
4.2. Analysis of Winding Vibration Acceleration Harmonic Response and Stress Distribution
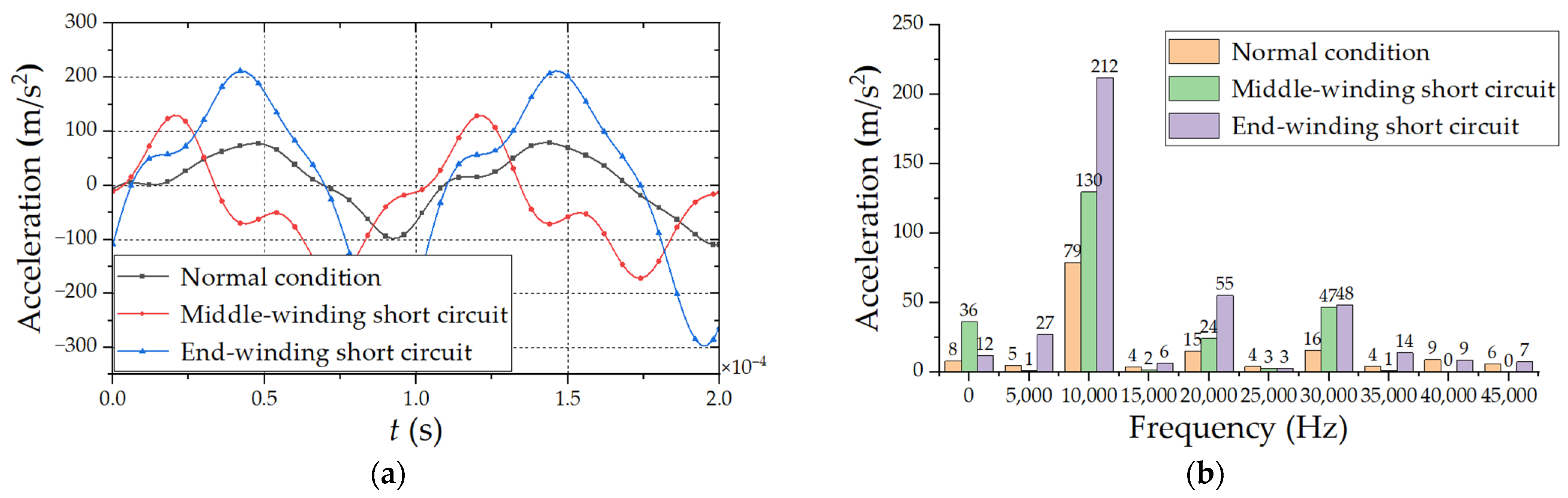
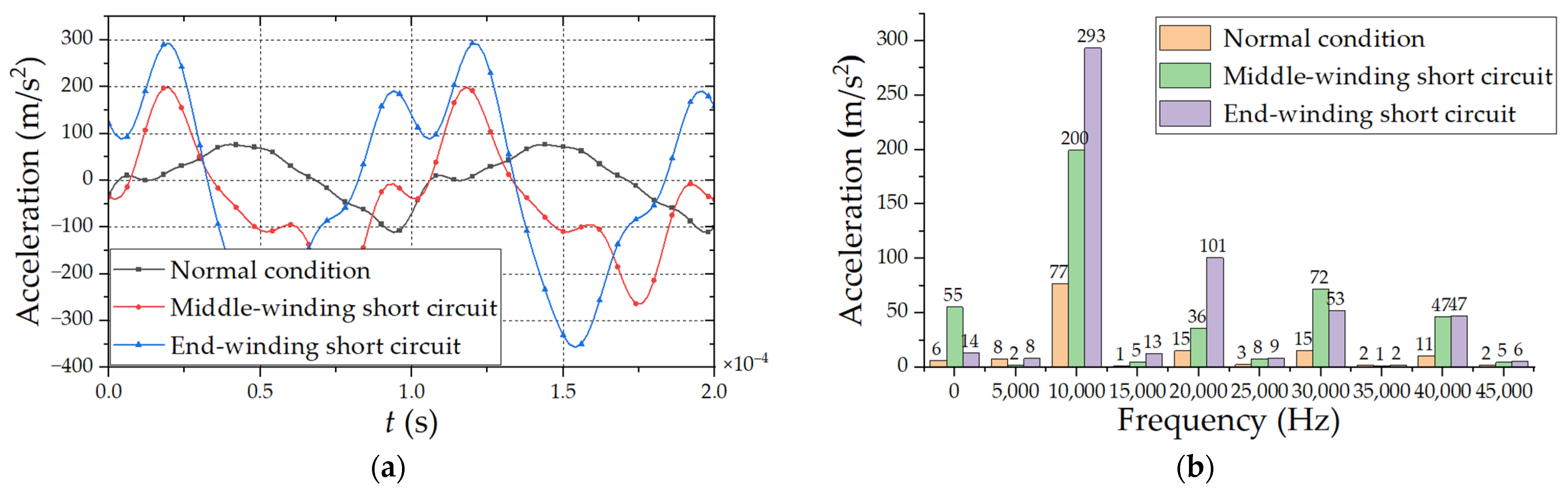
The vibration acceleration of inter-turn short circuit faults in different positions of HFT is simulated, and the schematic diagram of vibration acceleration in time domain is obtained. The vibration acceleration results are decomposed by Fourier transform, and the harmonic response distribution of winding vibration acceleration is obtained, as shown in Figure 10 and Figure 11. The time domain acceleration period under different working conditions is 0.0001 s. The frequency band is mainly 0–45,000 Hz, and the second harmonic component is the largest. The acceleration amplitude of interleaved winding is similar to that of continuous winding under normal working conditions, but the maximum value under fault conditions is obviously smaller than that of continuous winding.
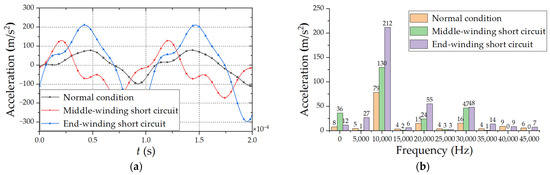
Figure 10.
Comparison of vibration acceleration under different interleaved winding fault positions (a) Time domain waveform diagram; (b) Harmonic response analysis.
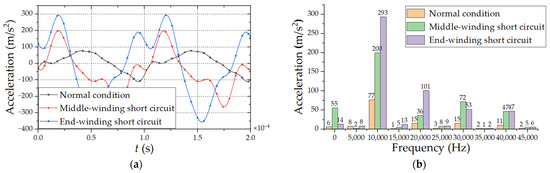
Figure 11.
Comparison of vibration acceleration under different continuous winding fault positions (a) Time domain waveform diagram. (b) Harmonic response analysis.
Due to the surge of current and the increase of local magnetic flux leakage when the inter-turn short circuit occurs in winding, there is obvious vibration from the fault-winding under the action of electromagnetic force, and the acceleration of the windings on both sides decreases gradually. The acceleration amplitude of the inter-turn short circuit in the middle-winding is slightly less than it is in the end-winding.
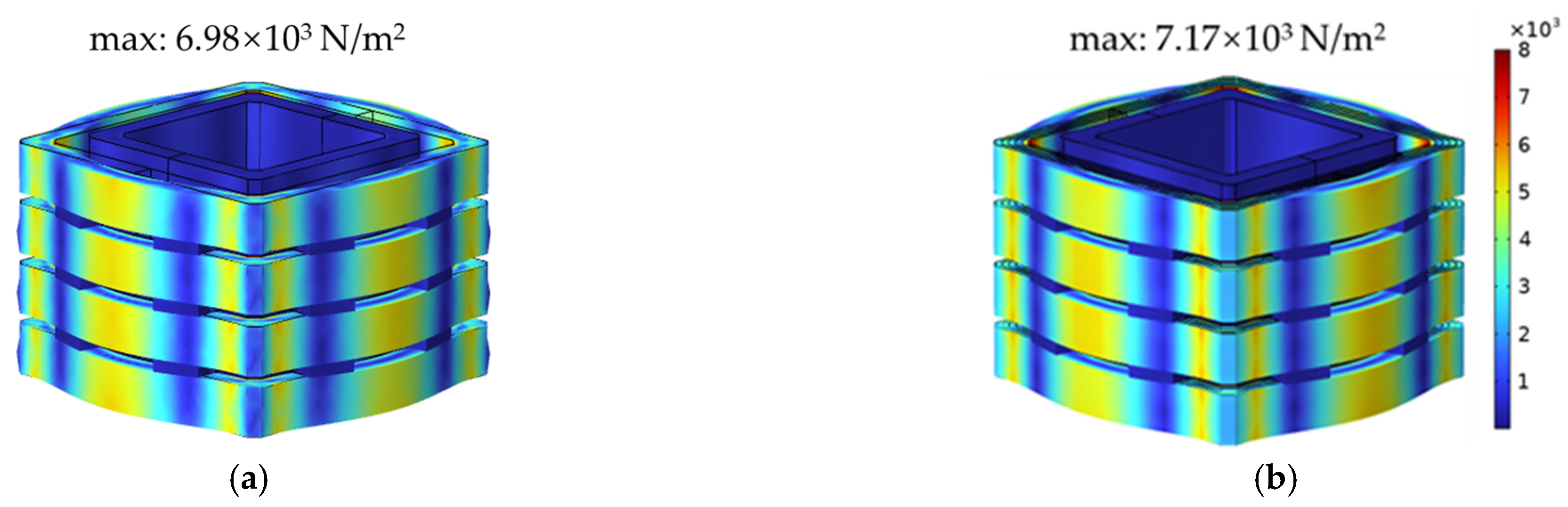
The inter-turn short circuit stress distributions at different positions of transformer winding are shown in Figure 12, Figure 13 and Figure 14. Among them, since the interleaved winding has the advantage of uniform current and voltage distribution, the stress of the interleaved winding is smaller than that of the continuous winding under normal working conditions. Since the leakage flux directions of wire cakes differ at each position, the wire cakes bear tensile or compressive forces in different directions, and the short circuit winding vibrates violently. The winding force corresponds to the vibration acceleration, and the main frequency of vibration is 10,000 Hz.
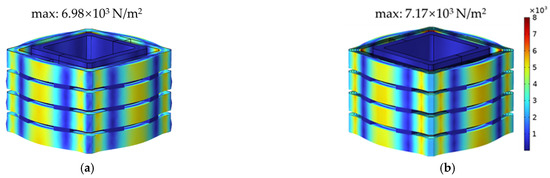
Figure 12.
Stress distribution under normal condition (a) Interleaved winding; (b) Continuous winding.

Figure 13.
Stress distribution under middle-winding short circuit (a) Interleaved winding; (b) Continuous winding.

Figure 14.
Stress distribution under end-winding short circuit (a) Interleaved winding; (b) Continuous winding.
It can be seen that three different stress and deformation distribution patterns exist before and after short circuit. The stress points become more and more disordered under the influence of an inter-turn short circuit. For the HFT with interleaved winding, the maximum stress on iron core increases from 6.98 × 103 N/m2 to 2.55 × 105 N/m2 and 3.07 × 105 N/m2, respectively, which is determined by the current flowing through windings. The concentration distribution of Lorentz force in the windings continues to increase. The HFT with continuous winding is distributed in a similar way.
4.3. Acoustic Field Distribution
The calculated result of the stress field is taken as the excitation of the sound field, and the sound pressure level distributions are shown in Figure 15, Figure 16 and Figure 17. It can be seen from the sound pressure level distribution diagram in the longitudinal section of HFT that the normal working conditions and fault conditions of the two windings show the same law, and the maximum sound pressure level appears in the HFT body and gradually decreases into the air. Meanwhile, the sound pressure level distribution of interleaved winding is slightly smaller than that of continuous winding, meaning that the distribution of sound pressure level before and after short circuit is completely different. The sound pressure level becomes more widely distributed under the influence of the inter-turn short circuit. For the HFT with interleaved winding, the maximum sound pressure level on the transformer increases from 93.5 dB to 112 dB and 122 dB respectively, which depends on the vibration intensity on the transformer core and windings. Similarly, the HFT with continuous winding also has the distribution patterns mentioned above.

Figure 15.
Sound pressure level distribution diagram under normal condition (a) Interleaved winding; (b) Continuous winding.

Figure 16.
Sound pressure level distribution diagram under middle-winding short circuit (a) Interleaved winding; (b) Continuous winding.

Figure 17.
Sound pressure level distribution diagram under end-winding short circuit (a) Interleaved winding; (b) Continuous winding.
5. Conclusions
In this paper, a multi-physical field model of a 10 kVA HFT under an inter-turn short circuit condition is established. The electromagnetic vibration noise of the transformer under normal conditions and fault conditions is simulated and analyzed, and the distribution laws of winding current, magnetic flux leakage, vibration acceleration and sound pressure level are obtained. This paper offers several significant conclusions.
Short-circuit current and magnetic flux leakage have little difference when inter-turn short circuit occurs at different positions, and the electromagnetic effect caused by end-winding short circuit is worse. At the same time, strengthening the insulation level at the primary end-winding of HFT is more beneficial to the short circuit impact resistance.
The analysis results from winding stress distribution and vibration acceleration harmonic response show that the magnetic flux leakage of end-winding inter-turn short circuit is higher than the middle-winding inter-turn short circuit. The frequency spectrum distribution of winding acceleration is complicated, but the vibration frequency spectrum is mainly concentrated in the frequency band of 0–45,000 Hz. Among them, the second harmonic vibration is the most severe.
The distribution of sound pressure level in the longitudinal section of HFT gradually decreases from the transformer body to the air. The sound pressure level of interleaved winding and continuous winding are 93.5 dB and 98.6 dB, respectively, under normal working conditions. The distribution law of inter-turn short circuit is basically the same, but the sound pressure level of the former is slightly smaller than that of the latter.
Author Contributions
Conceptualization, W.Z. and H.D.; methodology, W.Z. and H.D.; software, H.D. and C.D.; validation, H.D., W.Z. and C.D.; formal analysis, H.D.; investigation, W.Z.; resources, C.D.; data curation, H.D. and C.D.; writing—original draft preparation, H.D. and C.D.; writing—review and editing, W.Z. and M.L.; visualization, W.Z. and M.L.; supervision, W.Z. and M.L.; project administration, W.Z. and M.L.; funding acquisition, W.Z. and M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Project of National Key Research and Development Program of China, grant number 2022YFB2404100.
Data Availability Statement
The original data supporting the conclusion of this paper can be directly provided by authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xiao, H.; He, X.; Li, C. Probability Density Forecasting of Wind Power Based on Transformer Network with Expectile Regression and Kernel Density Estimation. Electronics 2023, 12, 1187. [Google Scholar] [CrossRef]
- Yang, P.; Wang, T.; Yang, H.; Meng, C.; Zhang, H.; Cheng, L. The Performance of Electronic Current Transformer Fault Diagnosis Model: Using an Improved Whale Optimization Algorithm and RBF Neural Network. Electronics 2023, 12, 1066. [Google Scholar] [CrossRef]
- Cervero, D.; Fotopoulou, M.; Muñoz-Cruzado, J.; Rakopoulos, D.; Stergiopoulos, F.; Nikolopoulos, N.; Voutetakis, S.; Sanz, J.F. Solid State Transformers: A Critical Review of Projects with Relevant Prototypes and Demonstrators. Electronics 2023, 12, 931. [Google Scholar] [CrossRef]
- Li, X.; Lu, K.; Zhao, Y.; Chen, D.; Yi, P.; Hua, W. Incorporating harmonic-analysis-based loss minimization into MPTC for efficiency improvement of FCFMPM motor. IEEE Trans. Ind. Electron. 2022, 70, 6540–6550. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, Q.; Mei, L.; Shen, S.; Ye, Z.; Li, D.; Yang, W.; Zhou, X. Dense Multiscale Feature Learning Transformer Embedding Cross-Shaped Attention for Road Damage Detection. Electronics 2023, 12, 898. [Google Scholar] [CrossRef]
- Lu, W.; Shi, C.; Fu, H.; Xu, Y. A Power Transformer Fault Diagnosis Method Based on Improved Sand Cat Swarm Optimization Algorithm and Bidirectional Gated Recurrent Unit. Electronics 2023, 12, 672. [Google Scholar] [CrossRef]
- Li, X.; Xue, Z.; Yan, X.; Zhang, L.; Ma, W.; Hua, W. Low-complexity multivector-based model predictive torque control for PMSM with voltage preselection. IEEE Trans. Power Electron. 2021, 36, 11726–11738. [Google Scholar] [CrossRef]
- Liu, H.; Chen, J.; Li, J.; Shao, L.; Ren, L.; Zhu, L. Transformer Fault Warning Based on Spectral Clustering and Decision Tree. Electronics 2023, 12, 265. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Li, J.; Yang, M.; Wan, J.; Xiao, X. Research on the Electromagnetic Characteristics of an Integrated Multi-Winding Inductive Filtering Converter Transformer and Its Filter System. Electronics 2023, 12, 227. [Google Scholar] [CrossRef]
- Huang, Y.-C.; Wu, W.-B.; Kuo, C.-C. Application of Fault Overlay Method and CNN in Infrared Image of Detecting Inter-Turn Short-Circuit in Dry-Type Transformer. Electronics 2023, 12, 181. [Google Scholar] [CrossRef]
- Jeong, D.-K.; Yun, H.-J.; Park, S.-H.; Kim, M.-H.; Ryu, M.-H.; Baek, J.-W.; Kim, H.-S. 13.2 kV Class 3-Phase Solid State Transformer System Based on EtherCAT Communication. Electronics 2022, 11, 3092. [Google Scholar] [CrossRef]
- Himanshu; Singh, H.; Kumar, P.S.; Ali, M.U.; Lee, H.Y.; Khan, M.A.; Park, G.S.; Kim, H.-J. High Frequency Transformer’s Parasitic Capacitance Minimization for Photovoltaic (PV) High-Frequency Link-Based Medium Voltage (MV) Inverter. Electronics 2018, 7, 142. [Google Scholar] [CrossRef]
- Coffeen, L.; Britton, J.; Rickmann, J. A New Technique to Detect Winding Displacements in Power Transformers Using Frequency Response Anaiysis. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003. [Google Scholar]
- Hashemnia, N.; Abu-Siada, A.; Islam, S. Improved Power Transformer Winding Fault Detection Using FRA Diagnostics-Part 1: Axial Displacement Simulation. IEEE Trans. Dielectr Electr Insul. 2015, 22, 556–563. [Google Scholar] [CrossRef]
- Li, Y.; Liu, N.; Liang, Y. Oil-Immersed Transformer Load Capacity Evaluation Model Based on Temperature Rise Characteristics. Chin. J. Electr. Eng. 2018, 38, 6737–6746. [Google Scholar]
- Li, Z.; Peng, M.; Huang, Q. Application of Traveling Wave Reflection Method in Fault Location of Transformer Winding Inter-Turn Short Circuit. Power Syst. Prot. Control 2016, 44, 84–89. [Google Scholar]
- Xu, Y.M.; Guo, R.; Zhang, H. Calculation of Short-Circuit Electric Power of Power Transformer Windings. J. Electr. Mach. Control 2014, 18, 36–42. [Google Scholar]
- Zhao, Z.; Li, G.; Li, J. Analysis of Short-Circuit Resistance of Large Power Transformers Based on Finite Element Method. High Volt. Technol. 2014, 40, 3214–3220. [Google Scholar]
- Xu, Y.; Gong, Y.P.; Liu, Y. Block Frequency Analysis Method for Transformer Winding Frequency Response Data. Autom. Power Syst. 2014, 38, 91–97. [Google Scholar]
- Chen, M.; Wang, M.; Zheng, J. On-Line Detection Method for Short-Circuit Reactance of Distribution Transformers Considering Asymmetric Load. High Volt. Technol. 2015, 41, 881–886. [Google Scholar]
- Zhao, Z.; Li, G.; Li, J.; Zhang, S.; Liu, Y.; Gao, F. Analyzing the Short-Cinuit Withstanding Ability of Large Power Transformer Based the Fem Method. High Volt. Eng. 2014, 40, 3214–3220. [Google Scholar]
- Bagheri, M.; Phung, B.T. Frequency Response and Vibration Analysis in Transformer Winding Turn-To-Turn Fault Recognition. In Proceedings of the 2016 International Conference on Smart Green Technology in Electrical and Information Systems (ICSGTEIS), Denpasar, Indonesia, 6–8 October 2016; pp. 10–15. [Google Scholar]
- Xu, Y.; Gong, Y.; Liu, Y.; Ma, W.; Zhao, Q.; Wang, W. Transformer Winding Frequency Response Data Analysis with Block Frequency Point Method. Autom. Electr. Power Syst. 2014, 38, 91–97. [Google Scholar]
- Watts, G.B. A Mathematical Treatment of The Dynamic Behaviour of A Power-Transformer Winding Under Axial Short-Circuit Forces. Proc. Inst. Electr. Eng. 2010, 110, 551–560. [Google Scholar] [CrossRef]
- McNutt, W.J.; Johnson, W.M.; Nelson, R.A.; Ayers, R.E. Power Transformen Short-Circuit Strength-Requirements, Design, and Demonstration. IEEE Trans. Power App. Syst. 1970, 89, 1955–1969. [Google Scholar] [CrossRef]
- Swihart, D.O.; Wright, D.V. Dynamic Stiffness and Damping of Transformer Pressboard During Axial Short Circuit Vibration. IEEE Trans. Power App. Syst. 1976, 95, 721–730. [Google Scholar] [CrossRef]
- Berler, Z.; Golubev, A.; Rusov, V.; Tsvetkov, V.; Patterson, C. Vibro-Acoustic Method of Transformer Clamping Pressure Monitoring. In Proceedings of the Conference Record of the 2000 IEEE International Symposium on Electrical Insulation (Cat. No.00CH37075), Anaheim, CA, USA, 5 April 2000; pp. 263–266. [Google Scholar]
- Madin, A.B.; Whitaker, J.D. The Dynamic Behaviour of A Transformer Winding Under Axial Short-Circuit Forces. Proc. Inst. Electr. Eng. 1963, 110, 535–550. [Google Scholar] [CrossRef]
- Beltle, M.; Tenbohlen, S. Usability of Vibration Measurement for Power Transformer Diagnosis and Monitoring. In Proceedings of the 2012 IEEE International Conference on Condition Monitoring and Diagnosis, Bali, Indonesia, 23–27 September 2012; pp. 281–284. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).