Mismatch-Shaping Switching Scheme for Split-Array Capacitive DACs

Abstract

Capacitive DACs (C-DACs) are widely used as stand-alone DACs or in an ADC as auxiliary DACs. An important performance metric of a C-DAC is its energy consumption and the linearity between the digital input and the analog output. In multi-bit C-DACs, the mismatch between the capacitors can degrade linearity, which can be important in high-resolution applications. In this work, we analyze the power consumption and linearity performance of a class of C-DACs called split-array C-DACs. We show that the simple element rotation technique, which is widely used to suppress the mismatch error of DACs, cannot be used with the power-efficient three-level switching scheme to effectively suppress the mismatch error. Then, we propose a switching scheme which can be used with the power efficient three-level switching and can suppress the in-band mismatch error effectively.

1. Introduction

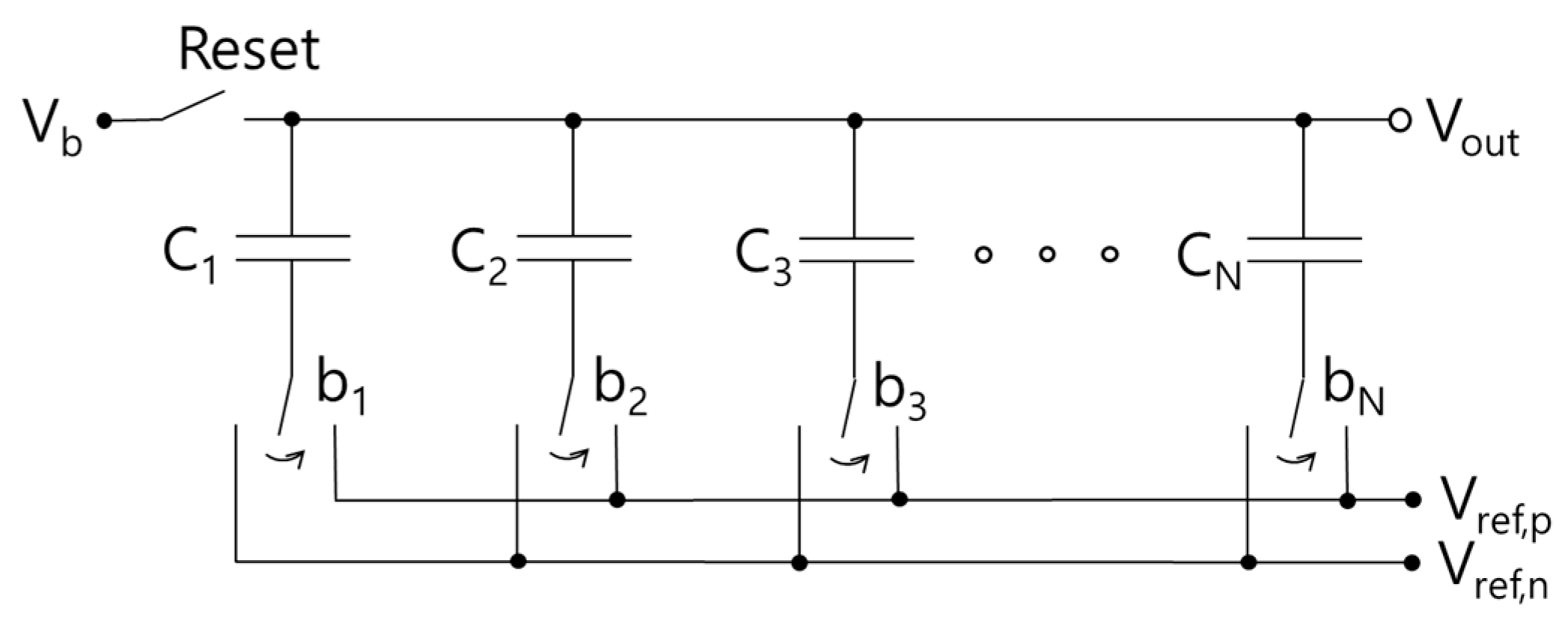
The capacitive digital-to-analog converter (C-DAC) is a popular type of DAC, which produces output voltage through charge redistribution between capacitors. C-DACs are especially widely used as auxiliary DACs in analog-to-digital converters (ADCs) such as delta-sigma ADCs, SAR ADCs, or pipelined ADCs, which require DACs to produce feedback signal which should be compared with the input signal [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. An important characteristic of a C-DAC is the dynamic power consumption associated with the switching of the C-DAC. The switching energy of a C-DAC is dependent on the particular procedure in which capacitors are charged and discharged to produce the desired output requested by the digital code.

The power consumption is especially important for C-DACs employed in SAR ADCs, which require relatively high-resolution C-DACs. Furthermore, the bit-by-bit sequential nature of the switching makes the power efficiency sensitive to the details of the switching procedure. Therefore, there has been extensive research about low-power switching schemes for C-DACs used in SAR ADCs. In the conventional C-DAC reported in [1], high power consumption occurs when a trial capacitor switching is reversed and a new trial switching is carried out with the next capacitor. The split-capacitor array scheme of [2] uses two sub-arrays of capacitors, of which one sub-array is dedicated to raise the output voltage, while the other is used to lower the output voltage. It improves the power efficiency, because it does not need the switching reversal to occur in the conventional C-DAC. When the split-capacitor array scheme is used with a C-DAC with differential output, the common-mode output level can be constant, which is an advantage in many applications [3]. In the monotonic switching scheme of [4], two single-ended outputs of the differential output of the C-DAC monotonically go down, eliminating the need for switching reversal. It can achieve a very good power efficiency; however, the variation of the common-mode output can be a disadvantage. In the V_CM-based scheme of [5], three voltage levels—V_ref, V_CM, and 0—are used to minimize the switching energy. However, the accuracy of V_CM level limits the linearity of the C-DAC.

In many C-DACs, the digital input bits to the C-DAC can be applied simultaneously [5,6]. This can improve the power efficiency of the C-DAC, which obviates the need for a complex switching scheme. In those applications, one of the most simple and versatile C-DAC schemes is the split-array C-DAC. With the split-array C-DAC, two switching schemes are used concurrently. They are “two-level switching” and “three-level switching” schemes. In the more conventional two-level switching, every capacitor pair—one from each sub-array—is either up- or down-switched. In the three-level switching, capacitors in one of the sub-arrays are not switched at all, while selected capacitors in the other sub-array are switched.

For a multi-bit C-DAC, another concern is the nonlinear error resulting from mismatches between the capacitors forming the capacitor arrays. When an array of identical elements is used in a DAC, and all the digital input bits are available simultaneously, an effective way to reduce the mismatch error is to use the element rotation technique which is also known as data-weighted averaging (DWA) [15,16]. By shuffling the capacitor array in a systematic way, it shapes the mismatch error in such a way that its low spectral component is suppressed. Therefore, when the element rotation is applied with the oversampling technique, the in-band (i.e., low-frequency) mismatch error is reduced and we can improve the signal-to-distortion ratio (SDR).

In this work, we investigate the power consumption and mismatch error of the split-capacitor C-DAC, where the digital input bits are available simultaneously. We show that for a low-power operation of the C-DAC, a switching scheme called “three-level switching” should be used. We also show that in a C-DAC using the three-level switching scheme, simple application of the element rotation to each array can produce harmonic distortion components in the in-band. Then, we propose to combine the element rotation with the switching of two sub-arrays after each conversion and show that the proposed scheme can move the in-band harmonic distortion components to a high-frequency region where they do not degrade the SDR.

The remainder of this work is organized as follows. In Section 2.1, we start by explaining the operation of a simple C-DAC. In Section 2.2, we discuss the capacitor mismatch error and the element rotation to shape it. In Section 2.3, the split-array C-DAC is described including its power consumption and its mismatch error. In Section 3, we present the proposed switching scheme and its benefits. In Section 4, we discuss the results and, in Section 5, we conclude.

2. C-DAC Theory

2.1. Basic C-DAC Operation

Figure 1 shows the schematic diagram of a basic C-DAC. C_k (k = 1,2,…, N) is a capacitor array, $V_{ref,p}$ and $V_{ref,n}$ are positive and negative reference voltage, respectively. $V_{ref,p}-V_{ref,n}$ represents the output swing range. The top plates of the capacitors are connected to V_out and the bottom plates are connected to $V_{ref,p}$ or $V_{ref,n}$ depending on the binary control signal b_k. During the “reset” phase, the V_out is connected to V_b and the bottom plates are connected to $V_{ref,n}$ (b_k = 0). During the output phase, the reset switch is turned off and the bottom plates of some capacitors are switched to $V_{ref,p}$ according to b_k. Now, the DAC output can be expressed as follows.

$$V_{out}=V_b+\frac{{\sum }_{k=1}^N{b}_k{C}_k}{\sum _{k=1}^N{C}_k}(V_{ref,p}-V_{ref.n})$$

(1)

(Note that in SAR ADC applications, V_b can be an external input signal V_in and the capacitor array also functions as a sampling capacitor of the input signal.)

The relative size of the capacitors in the array is chosen according to the signaling scheme, which is also related to the format of the control signal b_k. The two most widely used schemes are binary coding and thermometer coding. In the binary coding scheme, binary-weighted capacitor arrays are used, where $C_k=2^{N-k+1}{C}_u$. Here, C_u is the unit capacitance. In the thermometer coding scheme, nominal values of all capacitors are identical ($C_k=C_u)$ and the output voltage is simply determined by the number of control bits having a value of “1”. For a given dynamic range requirement of the C-DAC, the thermometer coding has the disadvantage of a larger number of control bits ($N=2^{N_{bit}})$ compared to N = N_bit of binary coding. However, it has the advantage of smaller differential nonlinearity (DNL) than the binary coding, because for an output change corresponding to one least significant bit (LSB), only a single unit capacitor is switched in the thermometer coding. In contrast, in a binary coding scheme, it is possible that all capacitors undergo switching when the control bits are changed from (0111…11) to (100…00). Furthermore, the thermometer coding scheme can be easily used with element rotation, which will be explained shortly. In the remainder of this work, we focus on C-DACs with nominally identical capacitors with thermometer coded control bits.

2.2. Component Mismatch and the Element Rotation

As mentioned above, when using the thermometer coding scheme for the C-DAC of Figure 1, ideally, all the capacitors should be identical. In this case, the C-DAC output is simply determined by the number of bits of b_k with a value of “1”. When the number of bits having a value of “1” is M, we can select any M capacitors out of N. Obviously, the simplest choice would be to choose C_k from $1\le k\le M$. However, actual fabricated capacitors have mismatches resulting in slightly different capacitance values. Due to the mismatch, the above simple method to choose capacitors results in nonlinear error in the C-DAC output, because a particular mismatch error is associated with each digital input code. Figure 2 shows the MATLAB behavioral simulation results. N = 16 (i.e., 4 bits) and the capacitance distribution was assumed to follow normal distribution with 1% standard deviation. We use this mismatch distribution throughout the rest of this work. Figure 2a shows the sinusoidal output of the C-DAC and Figure 2b shows the output error from the capacitor mismatch. We can observe that the output error is coupled to the output voltage itself. Figure 3a shows the power spectrum of the error signal from the simulation for Figure 2. We can observe strong harmonic distortion at multiples of the input frequency (f_sig/f_s = 131/8192).

To alleviate the nonlinear distortion from the mismatch, various mismatch-shaping techniques have been investigated, and the element rotation has been found to be one of the simplest and most effective methods [15,16]. In the element rotation, capacitor array elements are used in sequence in successive operations of the C-DAC. For example, if C₁ to C₃ were used in the n-th conversion and four capacitors were used for the (n + 1)-th conversion, C₄ to C₇ are selected. It is known that, if element rotation is used, the error power is not concentrated at the harmonics of the input signal and the error spectrum undergoes 1st order shaping, of which the mismatch transfer function (MTF) is $\left(1-z^{-1}\right).$ Therefore, the low-frequency component of the error signal is greatly suppressed. If the element rotation technique is used with the oversampling technique, the total in-band error power can be greatly reduced. Figure 3b shows the power spectrum of the error signal when the element rotation was employed. We can observe the absence of strong harmonic components observed in Figure 3a and the suppression of the low-frequency components by the mismatch shaping clearly. In Figure 3b, the red curve represents the predicted 1st order MTF. We observe good agreement between the MTF and the behavioral simulation results.

2.3. Split-Array C-DAC

Equation (1) shows that the output voltage of the C-DAC of Figure 1 changes only in one direction from V_b. This is because the bottom plates of every capacitor are connected to V_ref,n during the reset phase. However, in many applications, it is preferred that the output change in both directions from V_b. That kind of behavior can be obtained by using the so-called split-array C-DAC, of which the schematic is shown in Figure 4 [2]. Here, a C-DAC consists of two arrays of capacitors: C_p,k and C_n,k. During the reset phase, the bottom plates of C_p,k and C_n,k are connected to V_ref,n and V_ref,p, respectively. During the output phase, C_p,k and C_n,k are used to raise and lower V_out, respectively.

There are two methods to switch the capacitors of the C-DAC of Figure 4. In the first method, both the C_n,k array and C_p,k array are switched to produce the output. For example, if M out of N capacitors of the C_p,k array are used to raise V_out, then (N − M) capacitors of the C_n,k array are used to lower V_out. Then, the output voltage can be expressed by

$$V_{out}=V_b+\frac{\left(2M-N\right)}{2N}\left(V_{ref,p}-V_{ref,n}\right).$$

(2)

Note that if M < N/2, V_out < V_b, and if M > N/2, V_out > V_b. We can combine C_p,k and C_n,k with the same k to define capacitor pairs. Then, we can say that the whole C-DAC structure of Figure 4 consists of a new array of N such capacitor pairs, and we can say that, in this switching scheme, each element of the array is switched to either “+1” or “−1”. Therefore, we call this switching scheme “two-level switching”. Note that in the two-level switching scheme, N out of 2N capacitors are always switched.

In the second switching method, the number of switched capacitors is smaller. If the desired output is higher than V_b (V_out > V_b), no element of the C_n,k array switches and only the C_p,k array capacitors switch. If M_1p out of N elements of the C_p,k array switch and none of the C_n,k array switches, then V_out can be expressed by

$$V_{out}=V_b+\frac{M_{1p}}{2N}\left(V_{ref,p}-V_{ref,n}\right)$$

(3)

Comparing Equations (2) and (3), we observe that if M_1p = 2M − N, the second switching method would produce the same V_out as the first switching method. If V_out < V_b, by switching M_1n capacitors of the C_n,k array, we can obtain the following output.

$$V_{out}=V_b-\frac{M_{1n}}{2N}\left(V_{ref,p}-V_{ref,n}\right)$$

(4)

Let us form an array of capacitor pairs as described above. In this switching scheme, the pairs can be classified into three groups: the pairs which switch up (“+1”), those which switch down (“−1”), and those which do not switch (“0”). For example, when V_out > V_b, there are M_1p elements switching up, (N − M_1p) elements not switching, and zero elements switching down. When V_out < V_b, there are M_1n elements switching down, (N − M_1n) elements not switching, and zero elements switching up. Therefore, we call this switching scheme “three-level switching” [13,17].

The three-level switching scheme has an advantage of low switching energy when compared to the two-level scheme because the number of capacitors being switched is smaller. The energy consumption per conversion using three-level and two-level schemes is given as the following.

$$\begin{array}{cc}{E}_{3level}& =C_u{\left(V_{ref,p}-V_{ref,n}\right)}^2\frac{M_{1p\left(n\right)}(N-M_{1p\left(n\right)})}{2N}\hfill \\ & =\left\{\begin{array}{cc}{C}_u{\left(V_{ref,p}-V_{ref,n}\right)}^2\frac{(2M-N)(N-M)}{N},& 2M\ge N\\ C_u{\left(V_{ref,p}-V_{ref,n}\right)}^2\frac{(N-2M)M}{N},& 2M<N\end{array}\right.\hfill \end{array}$$

(5)

and

$$E_{2level}={4C}_u{\left(V_{ref,p}-V_{ref,n}\right)}^2\frac{M(N-M)}{N},$$

(6)

respectively.

Figure 5 shows the switching energy of the C-DAC as functions of the digital input code. If a uniform distribution of the output code is assumed, then the average switching energy of the three-level and two-level schemes for a large N is given as

$$E_{3level,avg}\cong \frac{1}{12}N{C}_u{\left(V_{ref,p}-V_{ref,n}\right)}^2,$$

(7)

and

$$E_{2level,avg}\cong \frac{2}{3}N{C}_u{\left(V_{ref,p}-V_{ref,n}\right)}^2,$$

(8)

respectively. Comparing Equations (7) and (8), we predict that the power consumption of the three-level switching is only 1/8 of that of two-level switching.

2.4. Mismatch Shaping with Split-Array C-DAC

In terms of the power consumption, the three-level switching of the C-DAC of Figure 4 is superior to the two-level switching. However, the three-level switching scheme has an issue associated with the application of element rotation to suppress the mismatch error. The source of the problem is that the C-DAC of Figure 4 has two sub-arrays: C_p,k and C_n,k, which are used to raise and lower the output voltage, respectively. If we apply the element rotation to these sub-arrays separately, it only shuffles the mismatches between elements of the same sub-arrays and cannot deal with the mismatches between two sub-arrays. The effect of the mismatch between the sub-arrays is different depending on whether the three-level switching or the two-level switching is used. In the two-level switching, the two sub-arrays actually undergo the same element rotation, and there is actually one unified element rotation. In the three-level switching, the element rotations for two sub-arrays are separate from each other. To concentrate on the mismatch between the two sub-arrays, we investigate the case where there is no mismatch within sub-arrays and there is mismatch between sub-arrays only. Then, C_p,k and C_n,k can be represented by $C_{p,k}=C_u+\mathsf{\Delta }C/2$ and $C_{n,k}=C_u-\mathsf{\Delta }C/2$ (1 ≤ k ≤ N), where $\mathsf{\Delta }C$ is the mismatch between the sub-arrays. As C_p,k and C_n,k are constant with regard to k, the element rotations have no effect, and if the two-level switching scheme is used the output is given as

$$\begin{array}{cc}{V}_{out}& =V_b+\frac{M\left(C_u+\mathsf{\Delta }C\right)-\left(N-M\right)\left(C_u-\mathsf{\Delta }C\right)}{N\left(C_u+\mathsf{\Delta }C\right)+N\left(C_u-\mathsf{\Delta }C\right)}\left(V_{ref,p}-V_{ref,n}\right)\hfill \\ & =V_b+\frac{\left(2M-N\right)}{2N}\left(V_{ref,p}-V_{ref,n}\right)+V_{os},\hfill \end{array}$$

(9)

where

$$V_{os}=\frac{\mathsf{\Delta }C}{2C_u}\left(V_{ref,p}-V_{ref,n}\right).$$

(10)

In Equations (9) and (10), we observe that the mismatch between C_p,k and C_n,k results in a constant output offset voltage, which does not depend on the input. When the three-level switching is used with the same C-DAC, the output is given as

$$V_{out}=\left\{\begin{array}{cc}{V}_b+\frac{\left(2M-N\right)\left(1+\mathsf{\Delta }C/C_u\right)}{2N}\left(V_{ref,p}-V_{ref,n}\right),& M\ge N/2\\ V_b+\frac{\left(2M-N\right)\left(1-\mathsf{\Delta }C/C_u\right)}{2N}\left(V_{ref,p}-V_{ref,n}\right),& M<N/2\end{array}\right.$$

(11)

In Equation (11), the input–output characteristic of the C-DAC has different slopes for M > N/2 and M < N/2. This leads to serious nonlinear distortion of the output.

Figure 6 shows the power spectra of the error signals from MATLAB behavioral simulations of the split-array C-DAC employing the element rotation (N = 16). The capacitor mismatch distribution used for the simulations for Figure 3 was used in the simulations (i.e., normal distribution with 1% standard deviation). Figure 6a shows the spectrum when the two-level switching was used. We can observe the mismatch error-shaping from element rotation. We also observe a relatively large dc offset component as predicted by Equation (10). Figure 6b shows the spectrum from simulations with the three-level switching. Here, we observe the signature of a strong mismatch error shaping. However, we also observe strong distortion components at the harmonic frequencies of the input signal.

3. Proposed Switching Scheme

In Section 2, we found that three-level switching of C-DACs of Figure 4 has the advantage of low power consumption while it suffers from nonlinear distortion from the mismatch between the sub-arrays which cannot be suppressed by conventional element rotation. In this work, we propose a switching scheme which is mainly based on the three-level switching but switches the role of the positive and negative sub-arrays in each operation of the DAC.

Figure 7 shows the schematic diagram of a C-DAC employing the proposed switching scheme. b_n,k and b_p,k are the thermometer coded input. “E-R” represents element rotation. CK_oe indicates whether the current conversion is an odd- or even-numbered one. CK_oe can be simply produced by dividing the master operation clock by 2. When CK_oe = 0 (i.e., even-numbered conversion), b_n,k and b_p,k are connected to b′_n,k and b’_p,k, respectively. When CK_oe = 1 (i.e., odd-numbered conversion), b_n,k is connected to b′_p,k and b_p,k is connected to b′_n,k. The inverters in the “cross-paths” are used to change the role of “down capacitors” and “up capacitors”. Four element rotation processors are used: the positive and negative sub-arrays have two processors each to process the element rotation for direct and cross-connections separately.

Figure 8 shows the spectrum of the error signal obtained from behavioral simulations of the split-array C-DAC using the proposed switching scheme. The same capacitor mismatch distribution as that for Figure 6 was used in the simulations. In Figure 8, we observe that the harmonics of the output signal frequency of f_sig resulting from the mismatch between positive and negative sub-arrays have been moved from $2m\times f_{sig}$ to $f_s/2-2m\times f_{sig}$, where m is an integer. The shift of the harmonic distortion frequency is from the mixing of the switching frequency between the sub-arrays (${=f}_s/2$) with the input signal. If we assume there is no mismatch within each sub-array and focus on the mismatch between two sub-arrays, δ, the DAC output sequence can be represented as

$$V_{out}\left(k\right)=V_{in}\left(k\right)\left(1+{\left(-1\right)}^k\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(V_{in}\left(k\right)\right)\cdot \delta \right)$$

(12)

where (−1)^k represents the switching between the sub-arrays. In Equation (12), the second term in the parenthesis represents the error signal. Let us suppose a sinusoidal input of $V_{in}\left(k\right)=\sin \left(2\pi {(f}_{sig}/f_s)k\right)$, where f_sig and f_s are the sampling frequency of the DAC and the signal frequency, respectively, is applied. Then, the error signal can be represented as

$$V_{err}\left(k\right)=\delta \sin \left(\frac{{2\pi f}_{sig}}{f_s}k\right)\cos \left(\pi k\right)\sum _{l=0}{a}_l\sin \left(\frac{2\pi \left(2l+1\right)f_{sig}}{f_s}k\right),$$

(13)

where the summation represents the Fourier expansion of sign[V_in(k)]. Now, it can be easily shown that V_err(k) contains frequency components at $f=\left(f_s/2\pm 2l\cdot f_{sig}\right)$.

As the harmonics are present near the Nyquist frequency, they can be removed by low-pass filtering easily with other out-of-band mismatch error signals. In Figure 8, we also observe that the mismatch error-shaping function is different from that in Figure 3b or Figure 6. As the positive and the negative sub-arrays change the role after each operation, there are two clock delays before a sub-array is used for the same role, and as a result, the MTF is changed from $\left(1-z^{-1}\right)$ to $\left(1-z^{-2}\right)$, which is shown in Figure 8 as a red curve. A disadvantage of the new transfer function is the increase in the mismatch error at low frequencies. The MTF at low frequencies can be approximated by

$$\begin{array}{c}\left(1-z^{-2}\right)\\ =1-e^{-2j\omega }\\ \cong 2j\omega ,\end{array}$$

(14)

where ω is the normalized angular frequency. Therefore, the in-band mismatch error power is expected to increase by factor of 4 (6 dB) compared to that from simple element rotation without exchanging the role of positive and negative arrays.

Figure 9 compares the in-band mismatch error power from various switching schemes. MATLAB behavioral simulations were repeated while varying the input frequency. When no mismatch error shaping is applied, the total in-band distortion is very high (>−67 dB). When the simple element rotation is applied to each sub-array independently, the two-level switching produces very low distortion error, which is around −90 dB at low signal frequencies. When the three-level switching is used with the simple element rotation, it suffers from mismatch between the positive and negative sub-arrays and produces large distortion of about −70 dB. Finally, we observe that the distortion from the three-level switching is drastically suppressed by using the scheme proposed in this work, where the role of the positive and negative sub-arrays is switched per cycle. We can also observe that the in-band distortion from the proposed scheme is still larger by about 3 dB than those from the two-level switching with element rotation, which is actually smaller than predicted from the change in the mismatch transfer function described above.

4. Discussion

From the results of Section 3, we conclude that in order to obtain a high SDR, both the three-level switching scheme and the two-level switching scheme require the element rotation. When a three-level switching is used, additional switching of positive and negative sub-arrays in successive operations is needed to move the harmonic distortion resulting from the mismatch between the sub-arrays from base band to frequencies around the Nyquist frequency. When the proposed scheme is combined with oversampling, the high frequency error component can be removed by low-pass filtering.

As already observed in Section 3 in relation to Figure 9, the total in-band distortion from the proposed scheme is still larger than that from the two-level switching with simple element rotation by about 3 dB. The distortion power from the mismatch is proportional to the relative variance of the unit capacitance (${\mathsf{\sigma }}_{\mathrm{C}}^2$), which, in turn, is inversely proportional to the unit capacitance. Therefore, for the proposed scheme to produce the same in-band distortion power as the two-level switching with element rotation, the unit capacitance used by the proposed three-level switching should be two times larger than that used by two-level switching, which implies two times larger switching power consumption. In Figure 5, we observed that, with identical unit capacitance, the three-level switching consumes eight times less power than two-level switching. Now, with three-level switching requiring two times more unit capacitance, it is predicted that the C-DAC switching power saving factor of the proposed scheme will be reduced from eight to four.

The proposed scheme requires more complex digital control logic, which leads to an increase in the power consumption and chip area. The two-level switching scheme requires a single element rotation processor, whereas the proposed three-level switching requires four element rotation processors as shown in Figure 7. (We also need additional switches and multiplexers, however, the power consumption increase from these should be insignificant compared to that from the additional element rotation processor.) A common element rotation processor consists of a digital log₂N-bit accumulator and an N-input, log₂N-stage shifter. Therefore, the power consumption and area overhead from the additional logic reduce the benefit of using the proposed three-level switching. However, as the CMOS technology scales down, it is expected that the overhead from the additional logic will continue to shrink.

The proposed scheme can be applied to C-DACs with differential output as shown in Figure 10. In this structure, the C_pp,k sub-array switches with the C_pn,k sub-array, and C_np,k switches with C_nn,k to push the mismatch errors between the sub-arrays to the high-frequency area. It is noted that the differential C-DAC of Figure 10 uses the same control signal as the single-ended output C-DAC of Figure 7. Therefore, the digital logic power does not increase from that of the single-ended one, while the capacitor switching power saving from using the proposed scheme is increased by a factor of two. Therefore, the benefit of the proposed switching scheme should be larger when applied to a differential output C-DAC.

5. Conclusions

In this work, we analyzed the power consumption and the linearity performance of split-array C-DACs. The power consumption of a split-array C-DAC can be reduced by using a three-level switching scheme, where only a part of positive or negative sub-array is switched while the other sub-array does not experience switching. However, the C-DACs using three-level switching can suffer from larger nonlinear distortion resulting from mismatches between capacitors in the array than those using conventional two-level switching. When two-level switching is used, the mismatch error can be effectively shaped out of the signal band to a high-frequency range by using element rotation. However, when three-level switching is used, the mismatch between positive and negative sub-arrays cannot be taken care of by using simple element rotation, which is applied separately to the positive and negative sub-arrays. In this work, we proposed a three-level switching, in which element rotation is combined with the switching of two sub-arrays. In the proposed scheme, the nonlinear distortion from mismatches within sub-arrays is shaped out of the signal band while that from mismatch between the sub-arrays is shifted to a high-frequency area around one half of the sampling frequency. Therefore, by using the proposed scheme, we can exploit the power efficiency of a three-level switching while minimizing the added nonlinear distortion from element mismatch.