Slow-Scale Nonlinear Control of a H-Bridge Photovoltaic Inverter
Abstract
:1. Introduction
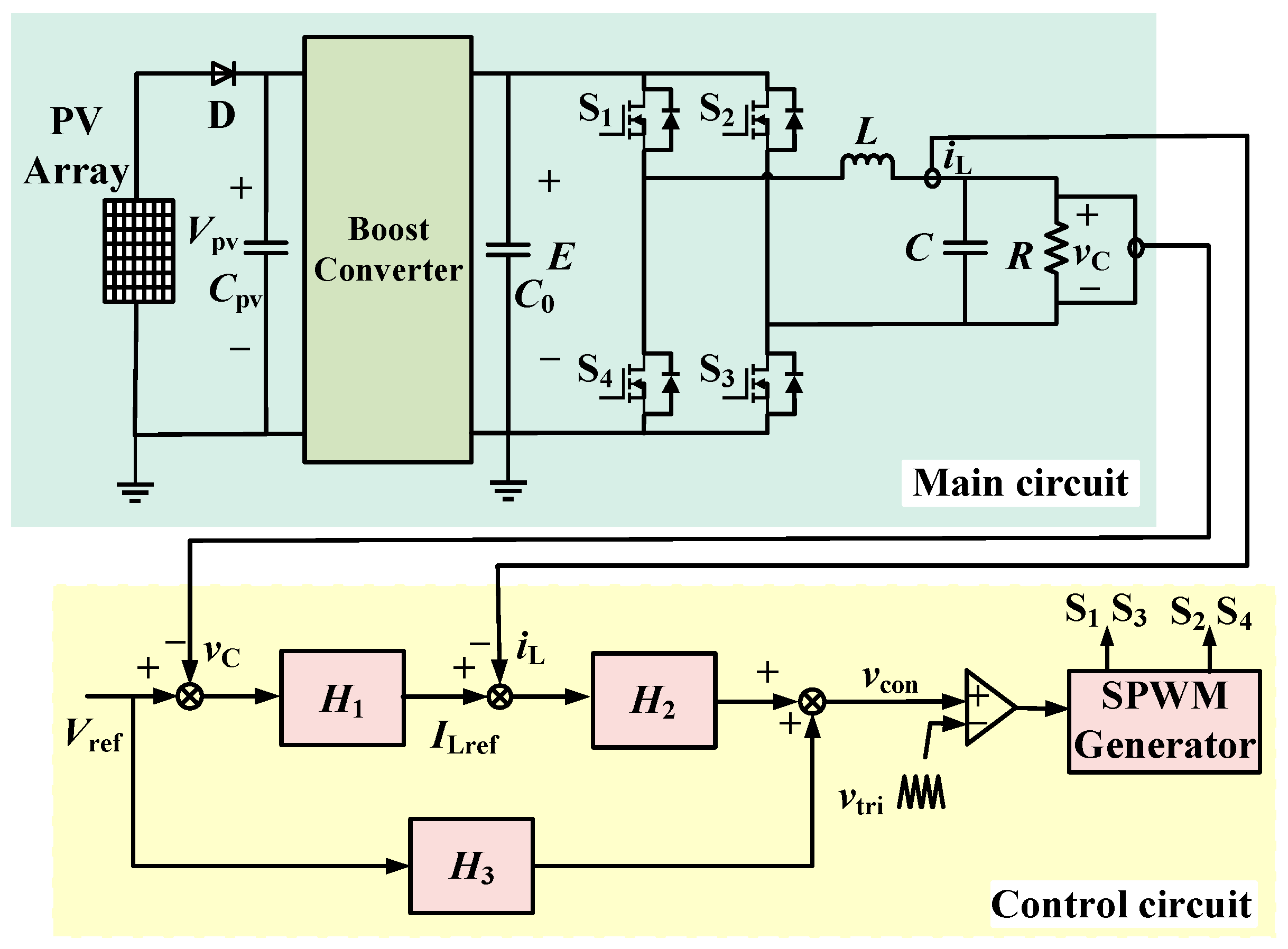
2. System Description
2.1. Circuit Operation Principle
2.2. State Equations
3. Simulation Results and Slow-Scale Nonlinear Behavior Analysis
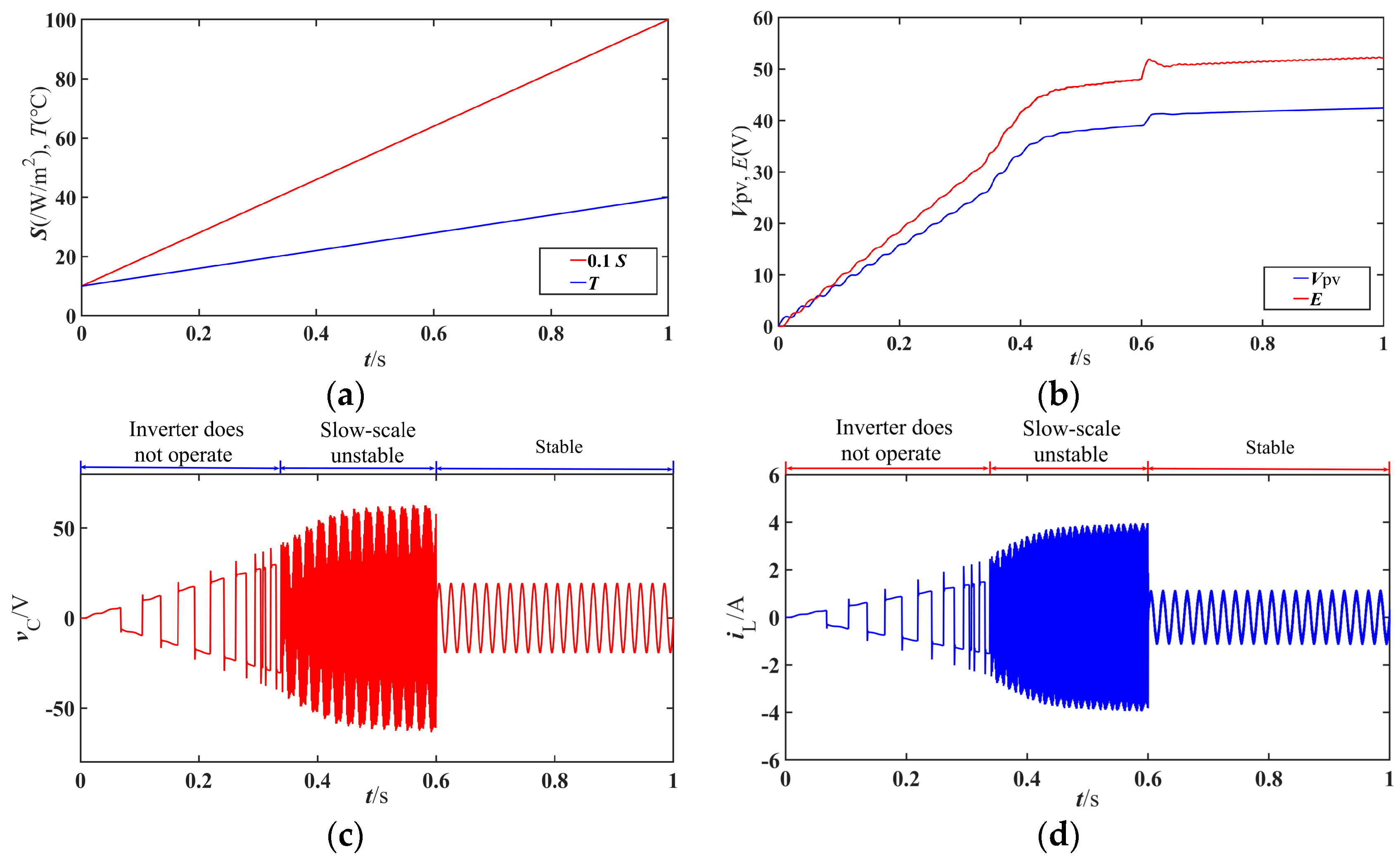
3.1. Simulation Results
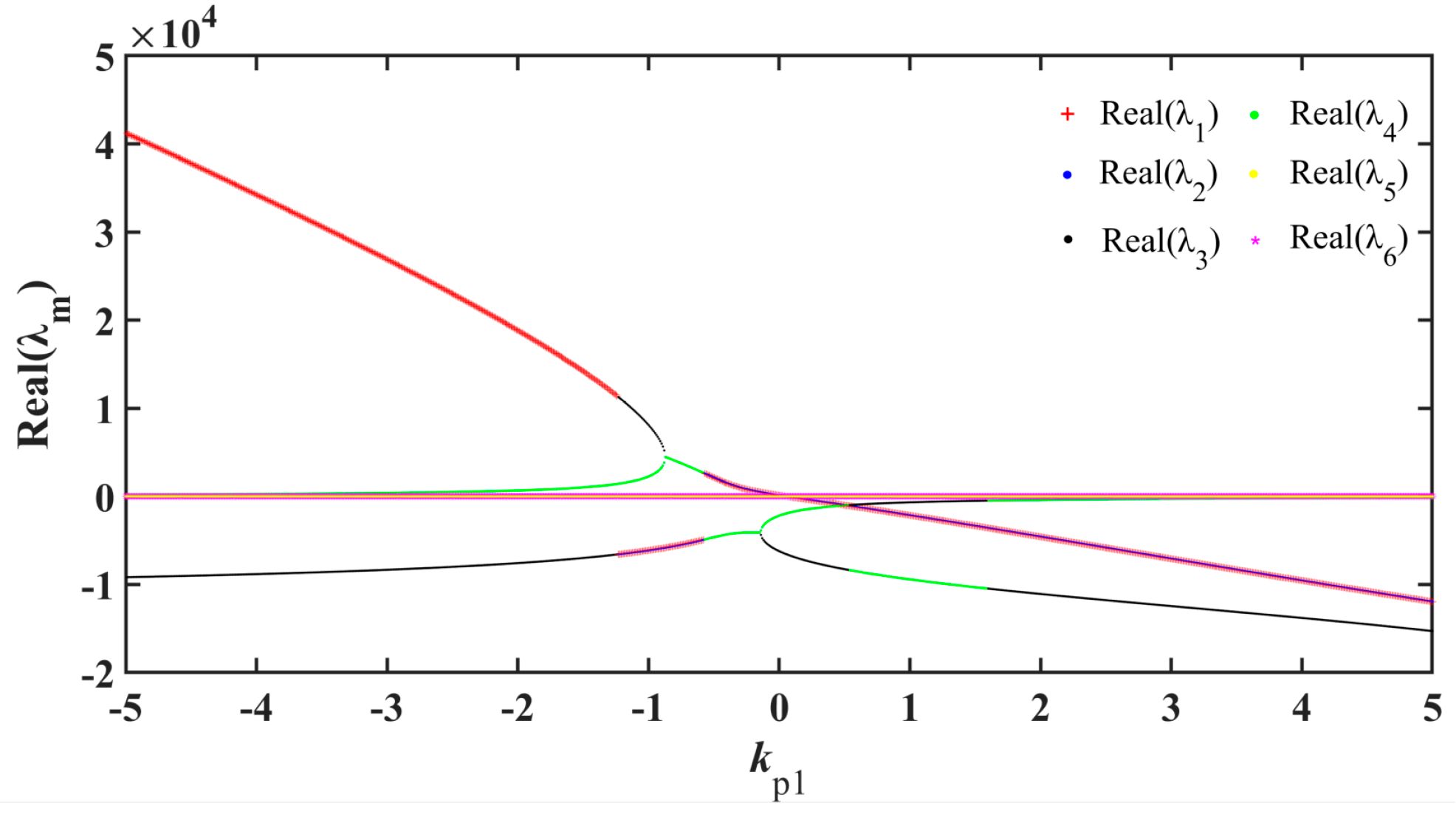
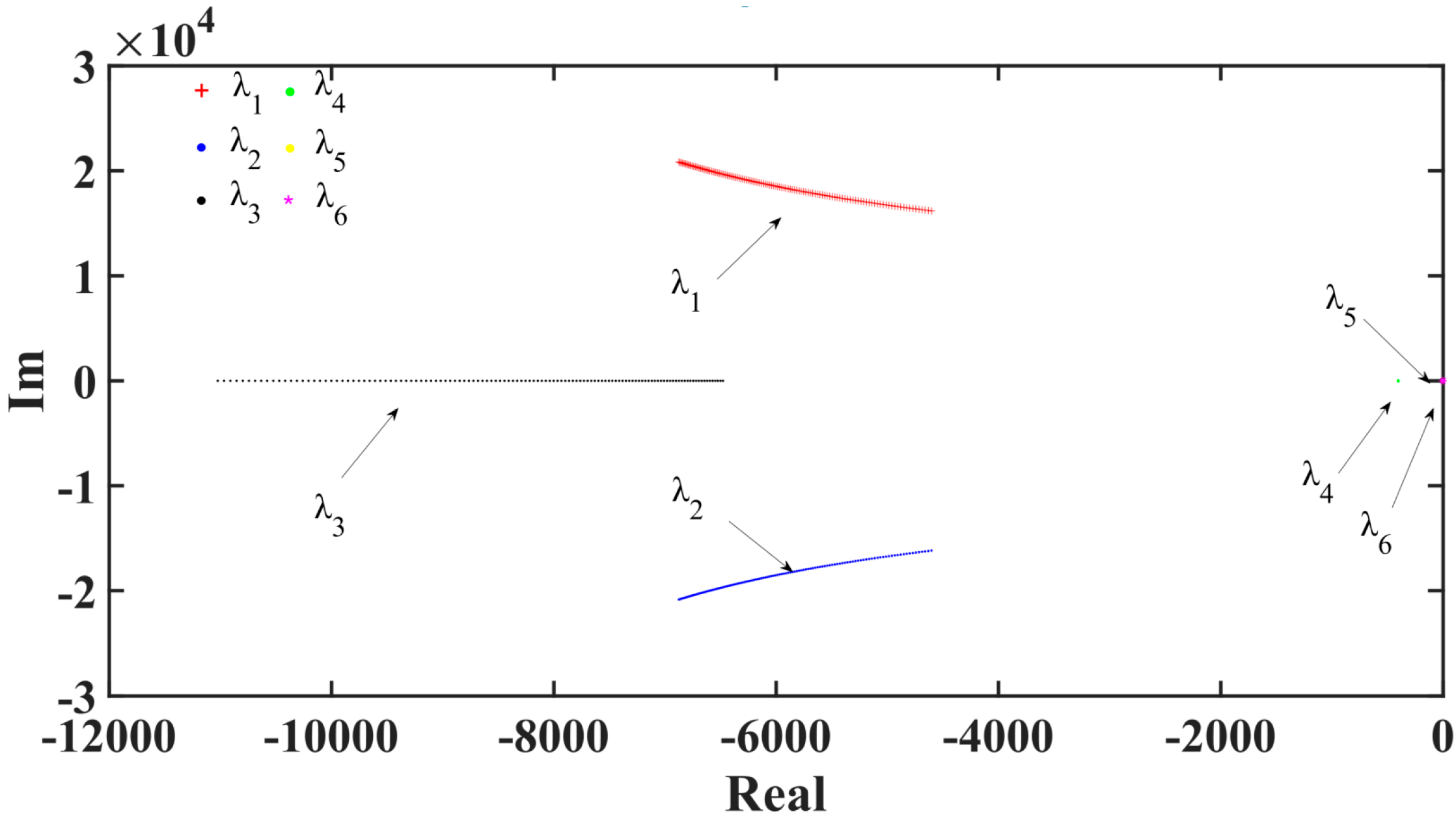
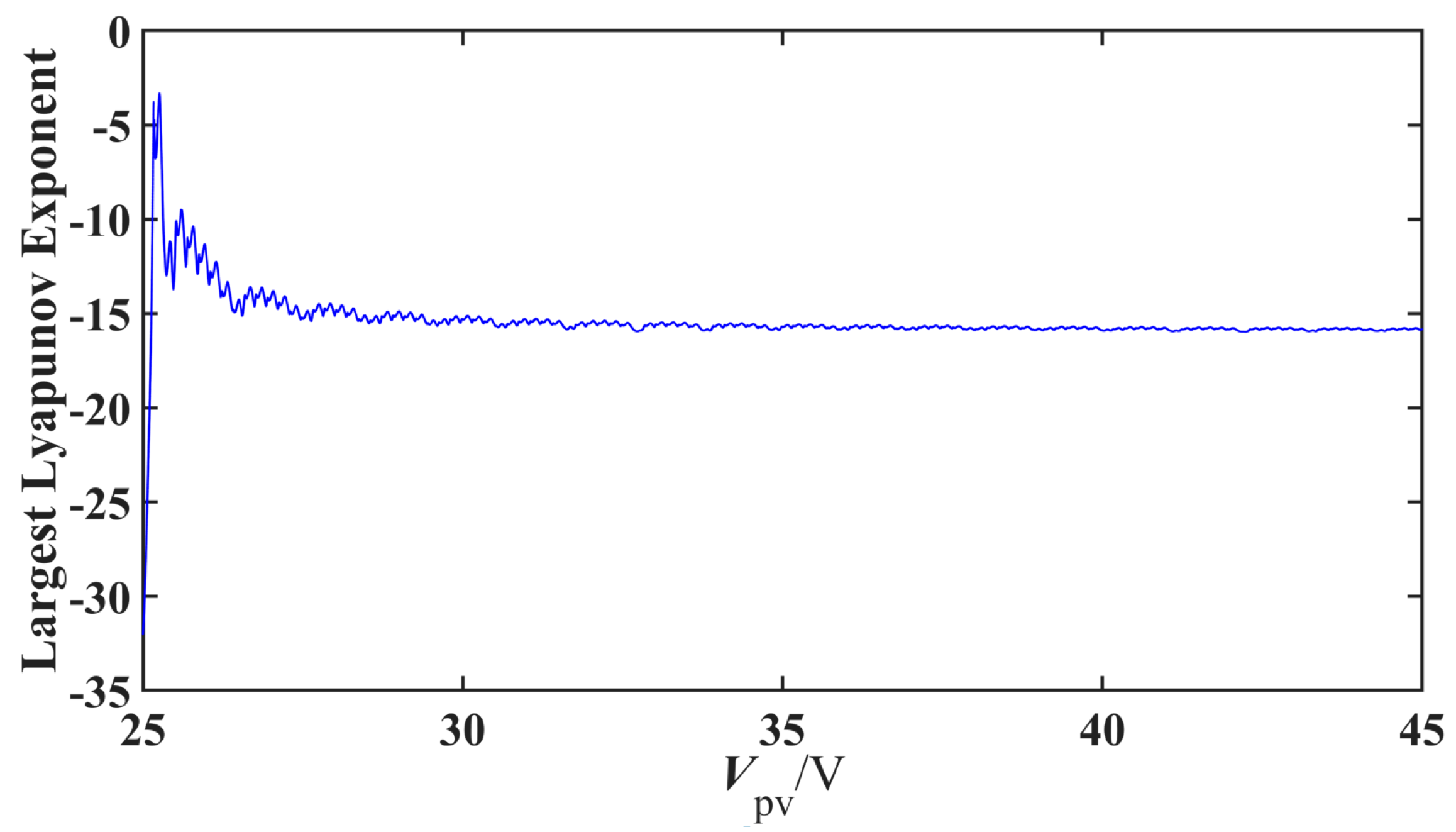
3.2. Analysis of the Slow-Scale Nonlinear Behavior
4. Control of Slow-Scale Nonlinear Behavior
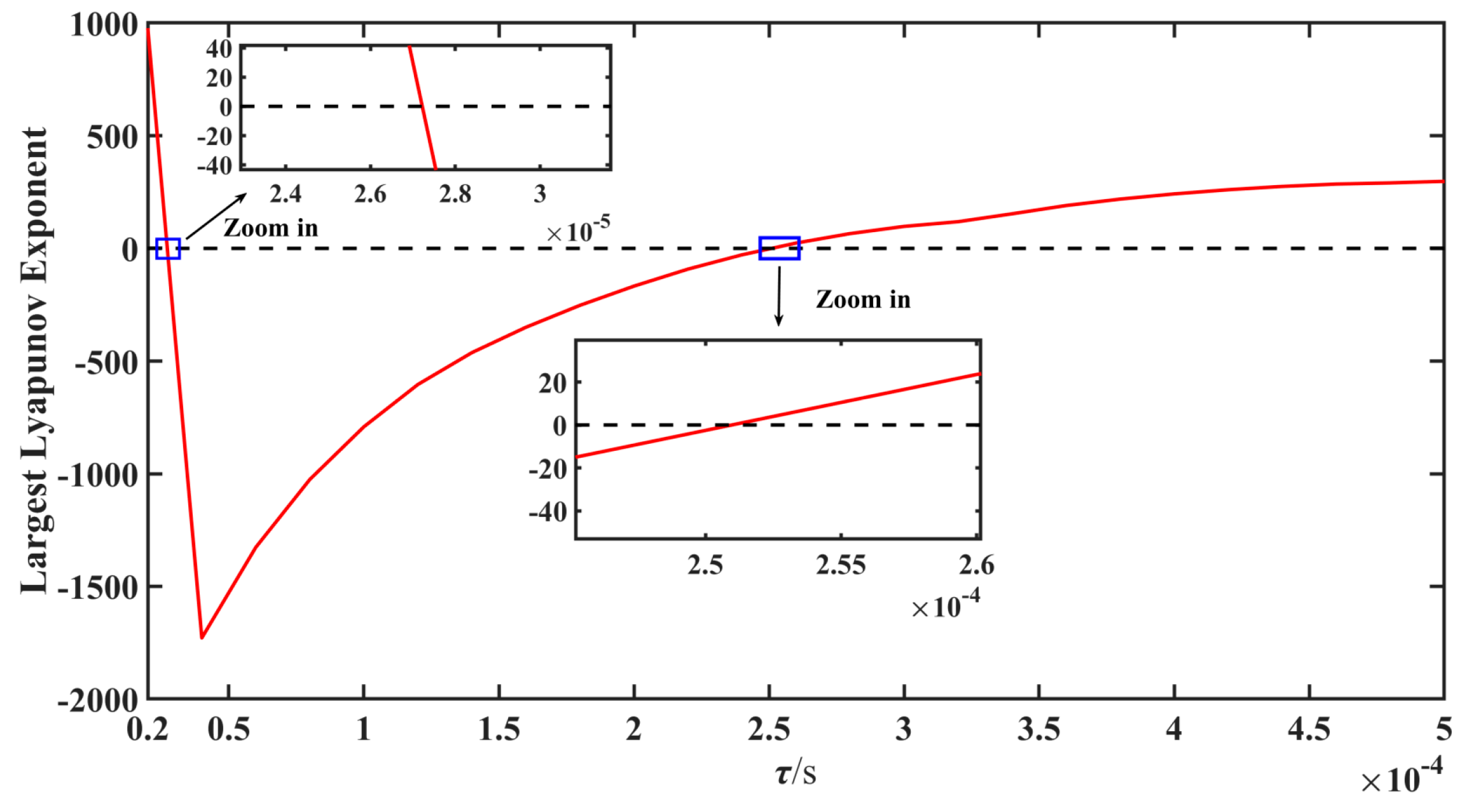
4.1. A Slow-Scale Nonlinear Control Based on TDFC
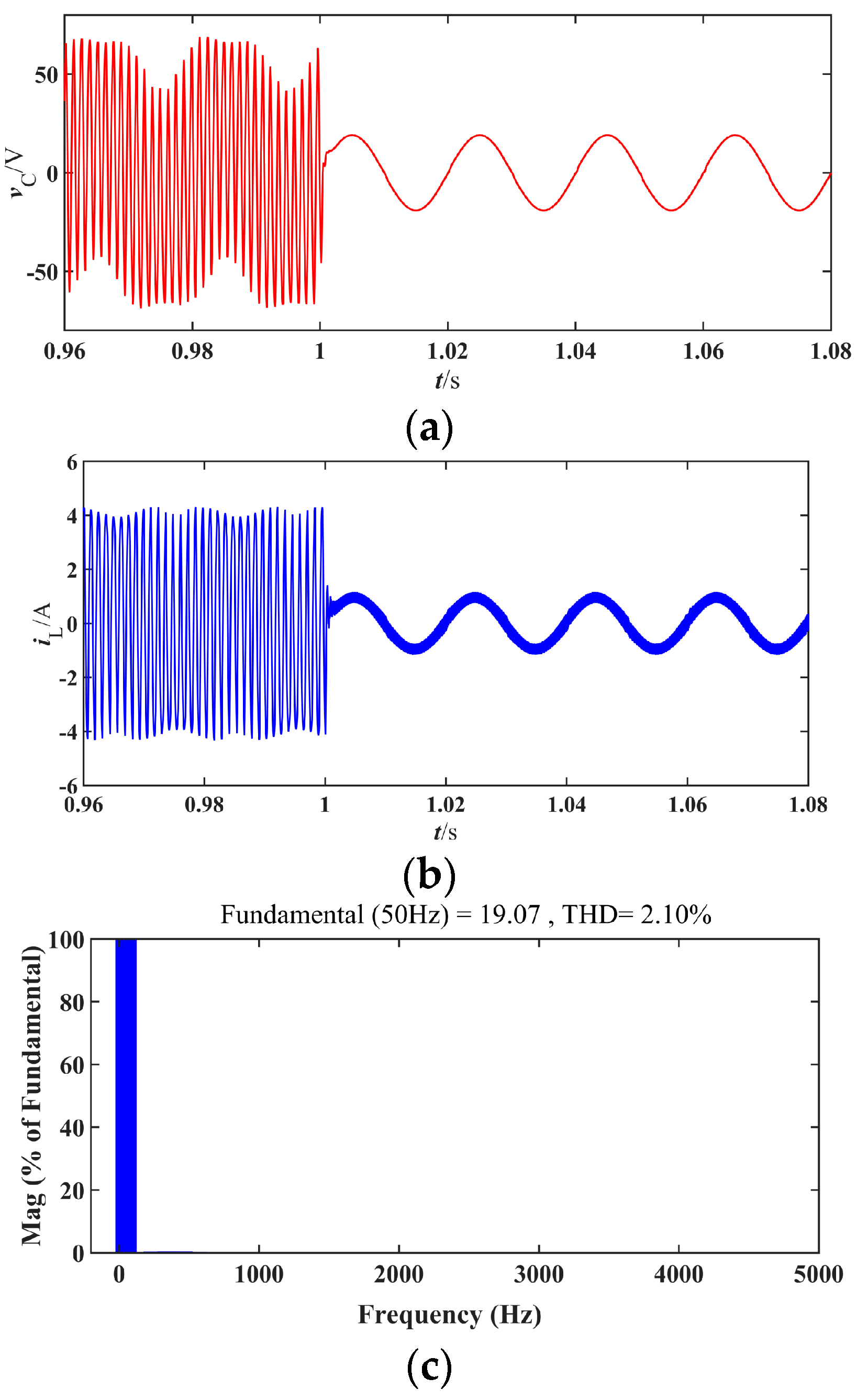
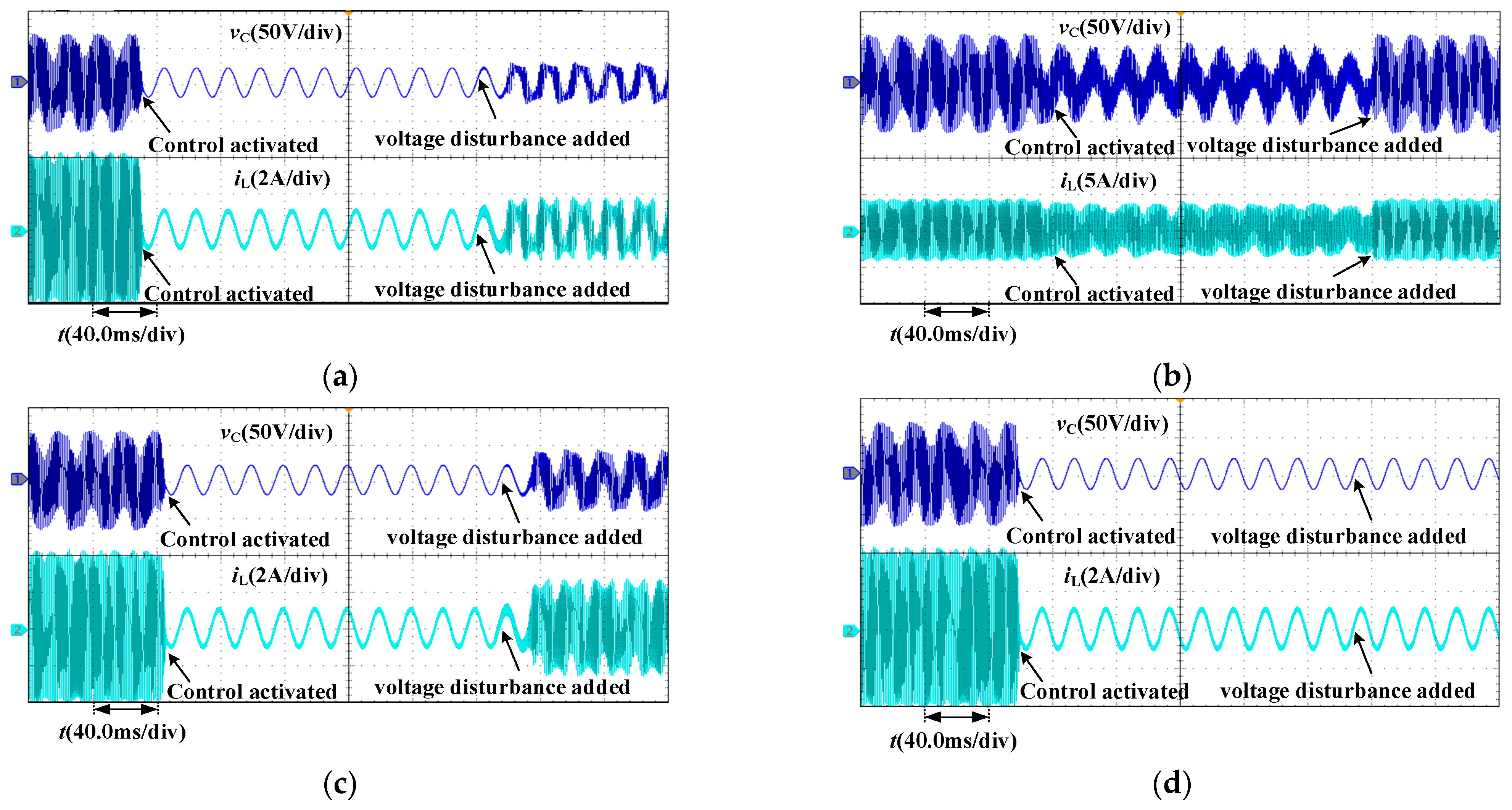
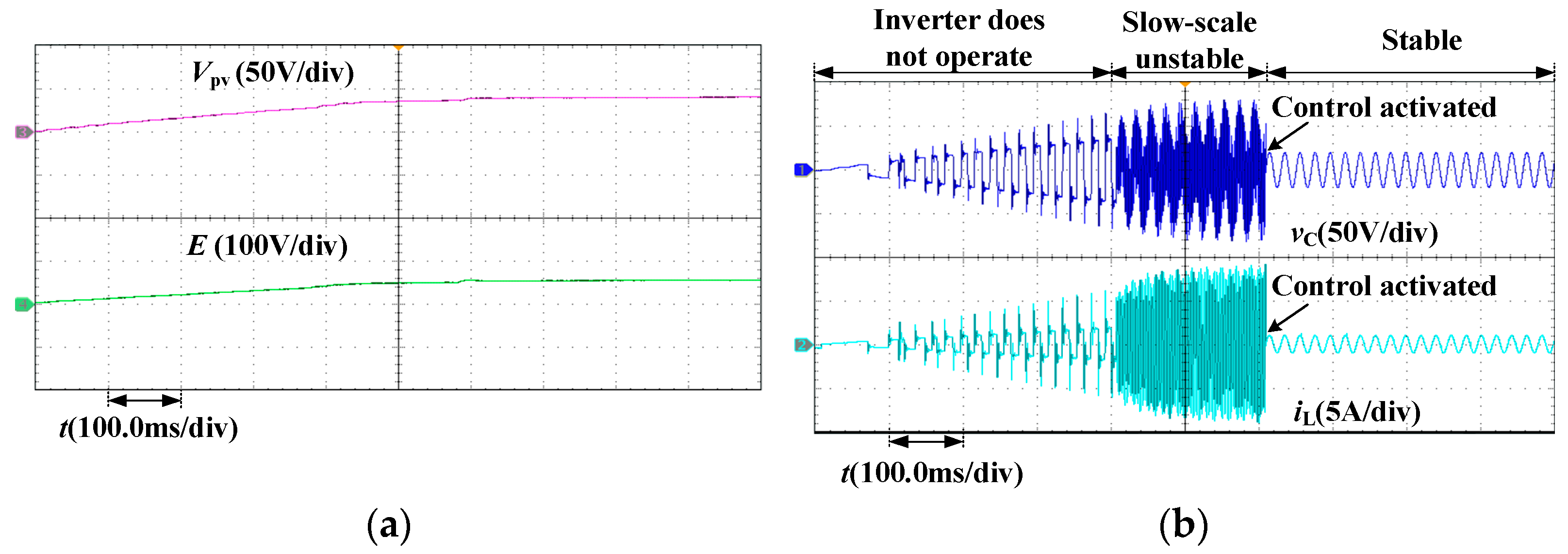
4.2. Validation of Simulation Results
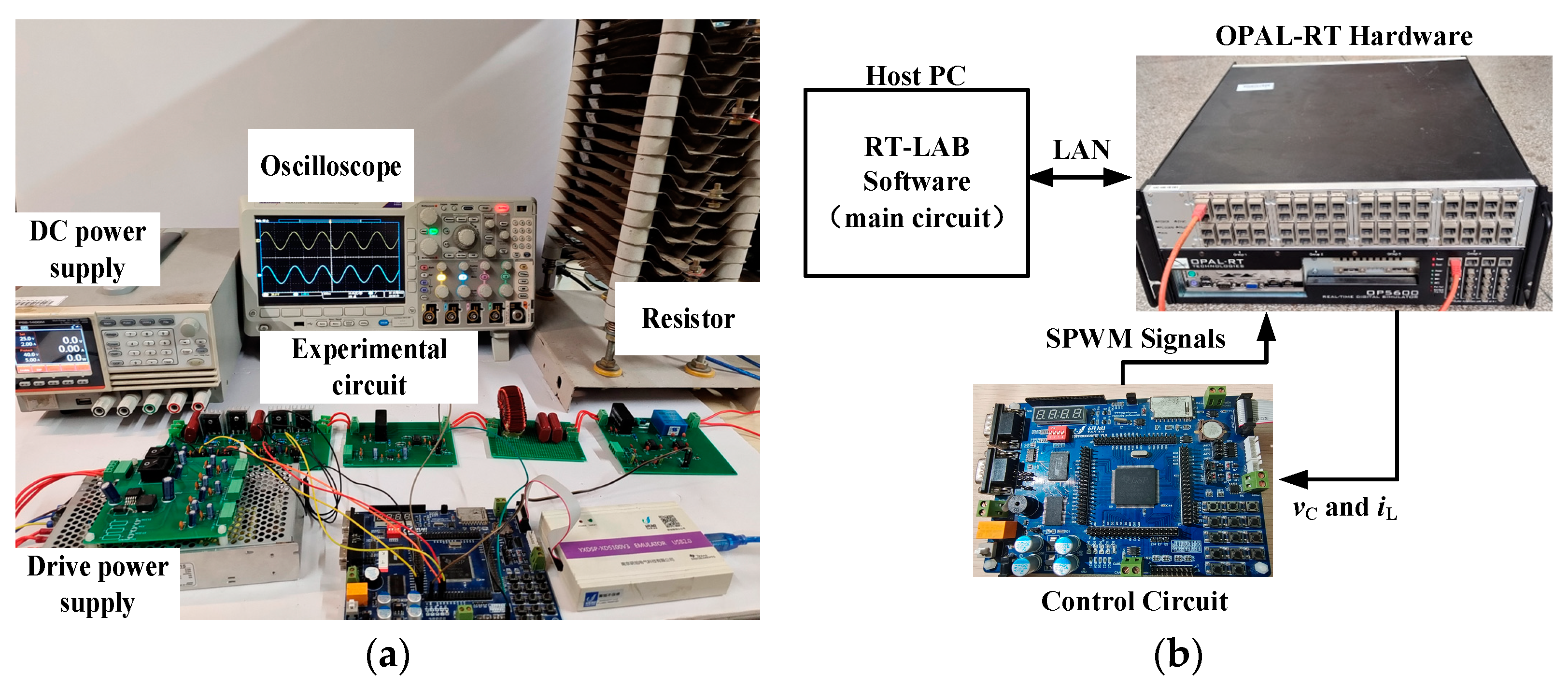
5. Validation of Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, H.; Wang, X.; Fan, T.; Wang, J.; Lin, Z.; Shen, Y.; Su, J.; Zhang, P. DC Series Arc Fault Detection Method in Photovoltaic System Based on Multiple Frequency Selections for Common-Mode Conductive Voltage. IEEE Trans. Power Electron. 2022, 37, 15538–15553. [Google Scholar] [CrossRef]
- Kumaresan, A.; Tafti, H.D.; Kandasamy, N.K.; Glen; Farivar, G.; Pou, J.; Subbaiyan, T. Flexible Power Point Tracking for Solar Photovoltaic Systems Using Secant Method. IEEE Trans. Power Electron. 2021, 36, 9419–9429. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, D. Review of Soft-Switching Topologies for Single-Phase Photovoltaic Inverters. IEEE Trans. Power Electron. 2022, 37, 1926–1944. [Google Scholar] [CrossRef]
- Yang, L.; Yang, L.; Ma, X. Slow-Scale and Fast-Scale Instabilities in Parallel-Connected Single-Phase H-Bridge Inverters: A Design-Oriented Study. Int. J. Bifurc. Chaos 2020, 30, 2050005. [Google Scholar] [CrossRef]
- Asahara, H.; Kousaka, T. Bifurcation Analysis in a PWM Current-Controlled H-Bridge inverter. Int. J. Bifurc. Chaos 2011, 21, 985–996. [Google Scholar] [CrossRef]
- Avrutin, V.; Mosekilde, E.; Zhanybai; Zhusubaliyev, T.; Gardini, L. Onset of chaos in a single-phase power electronic inverter. Chaos 2015, 25, 043114. [Google Scholar] [CrossRef]
- Avrutin, V.; Zhusubaliyev, Z.T.; Mosekilde, E. Cascades of alternating pitchfork and flip bifurcations in H-bridge inverters. Phys. D 2017, 345, 27–39. [Google Scholar] [CrossRef]
- Zhang, H.; Dong, S.; Yi, C.; Guan, W. Fast-scale non-linear distortion analysis of peak-current-controlled buck–boost inverters. Int. J. Electron. 2017, 105, 274–288. [Google Scholar] [CrossRef]
- Liu, W.; Wang, F.; Ma, X. Slow-Scale Instability in Voltage-Mode Controlled H-Bridge Inverter with Memristive Load. Int. J. Bifurc. Chaos 2016, 26, 1650200. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Mandal, K.; Parui, S. A Filippov method based analytical perspective on stability analysis of a DC-AC H-bridge inverter with nonlinear rectifier load. Int. J. Circuit Theory Appl. 2022, 50, 1686–1708. [Google Scholar] [CrossRef]
- Cao, H.; Wang, F. Slow-Scale Bifurcation in Three-Level T-Type Inverter With Passive Memristive Load. IEEE Trans. Ind. Electron. 2022, 69, 7963–7973. [Google Scholar] [CrossRef]
- Yang, F.; Yang, L.; Ma, X. Fast-Scale Bifurcation Analysis in One-Cycle Controlled H-Bridge Inverter. Int. J. Bifurc. Chaos 2016, 26, 1650199. [Google Scholar] [CrossRef]
- Zhang, H.; Wan, X.; Li, W.; Ding, H.; Yi, C. Observer-Pattern Modeling and Slow-Scale Bifurcation Analysis of Two-Stage Boost Inverters. Int. J. Bifurc. Chaos 2017, 27, 1750096. [Google Scholar] [CrossRef]
- Kavitha, A.; Uma, G. Control of chaos in SEPIC DC-DC converter. Int. J. Control Autom. Syst. 2010, 8, 1320–1329. [Google Scholar] [CrossRef]
- Bao, B.C.; Xu, J.P.; Liu, Z. Mode shift and stability control of a current mode controlled buck-boost converter operating in discontinuous conduction mode with ramp compensation. Chin. Phys. B 2009, 18, 4742–4747. [Google Scholar]
- Cao, L.; Pan, Y.N.; Liang, H.J.; Huang, T.W. Observer-Based Dynamic Event-Triggered Control for Multiagent Systems with Time-Varying Delay. IEEE Trans. Cybern. 2023, 53, 3376–3387. [Google Scholar] [CrossRef] [PubMed]
- Zhao, G.T.; Cao, L.; Li, X.M.; Zhou, Q. Observer-based dynamic event-triggered control for nonstrict-feedback stochastic nonlinear multiagent systems. Appl. Math. Comput. 2022, 430, 127289. [Google Scholar] [CrossRef]
- Zhang, L.L.; Che, W.W.; Chen, B.; Lin, C. Adaptive Fuzzy Output-Feedback Consensus Tracking Control of Nonlinear Multiagent Systems in Prescribed Performance. IEEE Trans. Cybern. 2023, 53, 1932–1943. [Google Scholar] [CrossRef]
- Roopaei, M.; Sahraei, B.R.; Lin, T.C. Adaptive sliding mode control in a novel class of chaotic systems. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 4158–4170. [Google Scholar] [CrossRef]
- Ma, W.; Wang, L.; Zhang, R.; Li, J.; Dong, Z.; Zhang, Y.; Hu, M.; Liu, S. Hopf Bifurcation and Its Control in the One-Cycle Controlled Cuk Converter. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 1411–1415. [Google Scholar] [CrossRef]
- Ma, W.; Wang, M.; Li, C. Control of bifurcation in the one-cycle controlled Cuk converter. Nonlinear Dyn. 2012, 67, 2573–2583. [Google Scholar] [CrossRef]
- Fu, C.-B.; Tian, A.-H.; Yu, K.-N.; Lin, Y.-H.; Yau, H.-T. Analyses and Control of Chaotic Behavior in DC-DC Converters. Math. Probl. Eng. 2018, 2018, 7439137. [Google Scholar] [CrossRef]
- Morcillo, J.; Burbano, D.; Angulo, F. Adaptive Ramp Technique for Controlling Chaos and Subharmonic Oscillations in DC–DC Power Converters. IEEE Trans. Power Electron. 2016, 31, 5330–5343. [Google Scholar] [CrossRef]
- Pyragas, K. Continuous control of chaos by self-controlling feedback. Phys. Lett. A 1992, 170, 421–428. [Google Scholar] [CrossRef]
- Telles Ribeiro, J.G.; Pereira, M.; Cunha, A., Jr.; Lovisolo, L. Controlling chaos for energy harvesting via digital extended time-delay feedback. Eur. Phys. J. Spec. Top. 2022, 231, 1485–1490. [Google Scholar] [CrossRef]
- Park, M.J.; Lee, S.H.; Kaviarasan, B.; Kwon, O.M. Secure Communication in Complex Dynamical Networks via Time-Delayed Feedback Control. IEEE Trans. Syst. Man. Cybern. Syst. 2022, 53, 1116–1125. [Google Scholar] [CrossRef]
- Hong, G.; Zhongmin, D.; Yanlin, Z.; Hongbo, Y.; Xinjie, Z.; Lingzi, M.; Qi, L. Time-delayed feedback control of nonlinear dynamics in a giant magnetostrictive actuator. Nonlinear Dyn. 2022, 108, 1371–1394. [Google Scholar] [CrossRef]





| Circuit Parameters | Values |
|---|---|
| PV array output voltage under the standard condition Vpv | 42 V |
| Duty cycle of the Boost converter d | 0.2 |
| DC side input voltage E | 1.25 Vpv |
| Inductance L | 4 mH |
| Capacitance C | 10 uF |
| Resistance R | 20 Ω |
| Switching period Ts | 5 × 10−5 s |
| Given reference voltage frequency f | 50 Hz |
| Given reference voltage amplitude Vrefm | 20 V |
| Outer loop integral control coefficient kiv | 2000 A/(V∗s) |
| Inner loop proportional control coefficient kpc | 0.5 V/A |
| Inner loop integral control coefficient kic | 1000 V/(A∗s) |
| Given voltage feedforward control coefficient kp | 1 |
| Maximum value of vtri (VH) | 1 |
| Minimum value of vtri (VL) | −1 |
| kpv | λ1,2 | λ3 | λ4 | State |
|---|---|---|---|---|
| 0.3 | −1939 ± 14852i | −2098 | −5524 | Stable |
| 0.22 | −1188 ± 13256i | −2086 | −7038 | Stable |
| 0.18 | −716 ± 12488i | −2081 | −7987 | Stable |
| 0.1262 | 0 ± 11531i | −2075 | −9425 | Hopf bifurcation |
| 0.10 | 368 ± 11105i | −2072 | −10,164 | Unstable |
| 0.05 | 1078 ± 10360i | −2068 | −11,589 | Unstable |
| 0.005 | 1704 ± 9755i | −2064 | −12,844 | Unstable |
| 0.001 | 1759 ± 9703i | −2064 | −12,954 | Unstable |
| Device or Equipment | Manufacturer Model | Device or Equipment | Manufacturer Model |
|---|---|---|---|
| Diode | RHRP860 | Power MOSFET | IRFP360 |
| Driver chip | HCPL-3120 | Current sensor | CSM025AY |
| Voltage sensor | CHV-25P | Operational amplifier | TL071CP |
| Digital signal processor | TMSF28335 | OPAL-RT hardware | OP5600 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Z.; Gong, R.; Lu, Y. Slow-Scale Nonlinear Control of a H-Bridge Photovoltaic Inverter. Electronics 2023, 12, 2000. https://doi.org/10.3390/electronics12092000
Yin Z, Gong R, Lu Y. Slow-Scale Nonlinear Control of a H-Bridge Photovoltaic Inverter. Electronics. 2023; 12(9):2000. https://doi.org/10.3390/electronics12092000
Chicago/Turabian StyleYin, Zhihong, Renxi Gong, and Yimin Lu. 2023. "Slow-Scale Nonlinear Control of a H-Bridge Photovoltaic Inverter" Electronics 12, no. 9: 2000. https://doi.org/10.3390/electronics12092000
APA StyleYin, Z., Gong, R., & Lu, Y. (2023). Slow-Scale Nonlinear Control of a H-Bridge Photovoltaic Inverter. Electronics, 12(9), 2000. https://doi.org/10.3390/electronics12092000






