A Field Programmable Gate Array Placement Methodology for Netlist-Level Circuits with GPU Acceleration
Abstract
:1. Introduction
2. Related Work
3. Approach
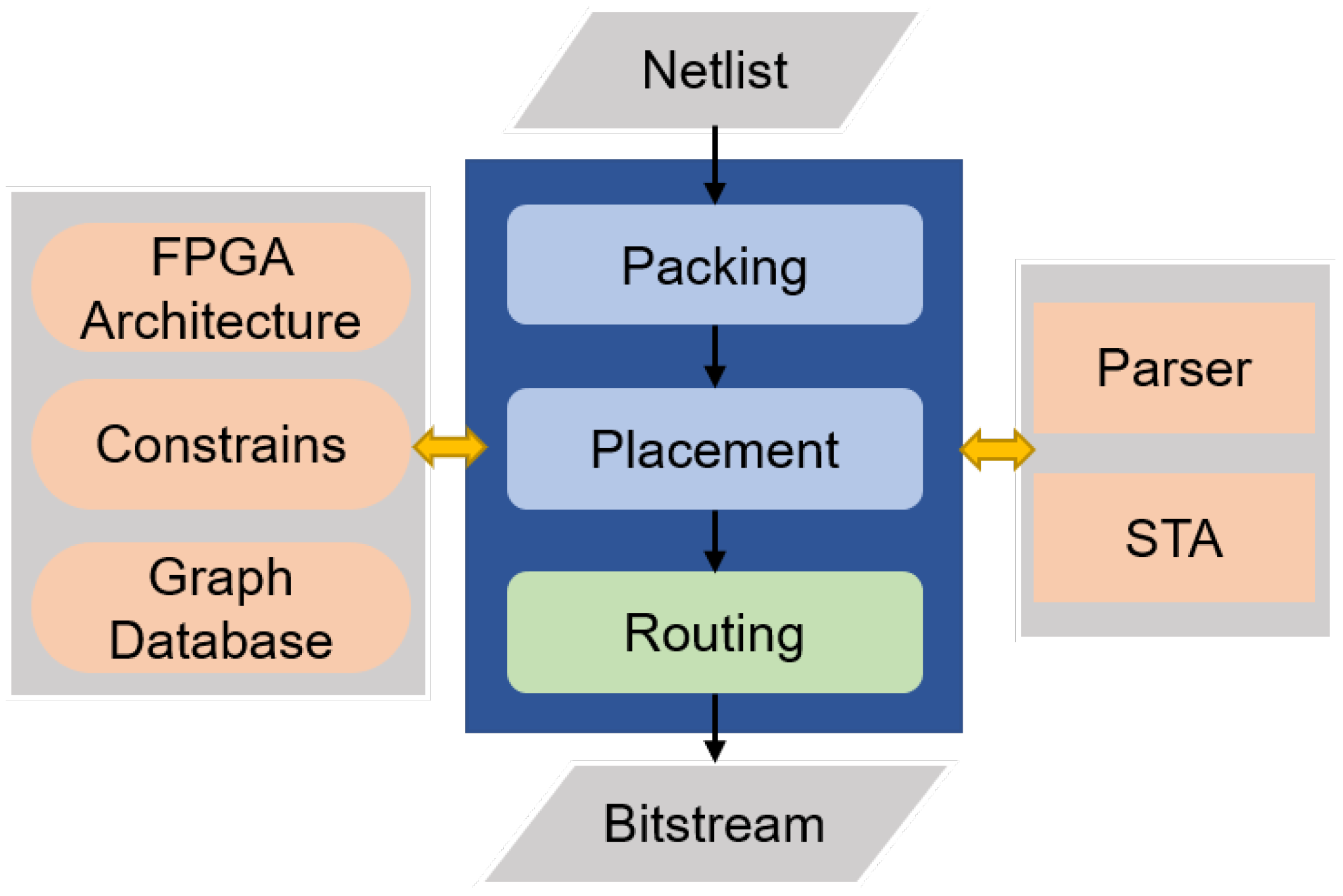
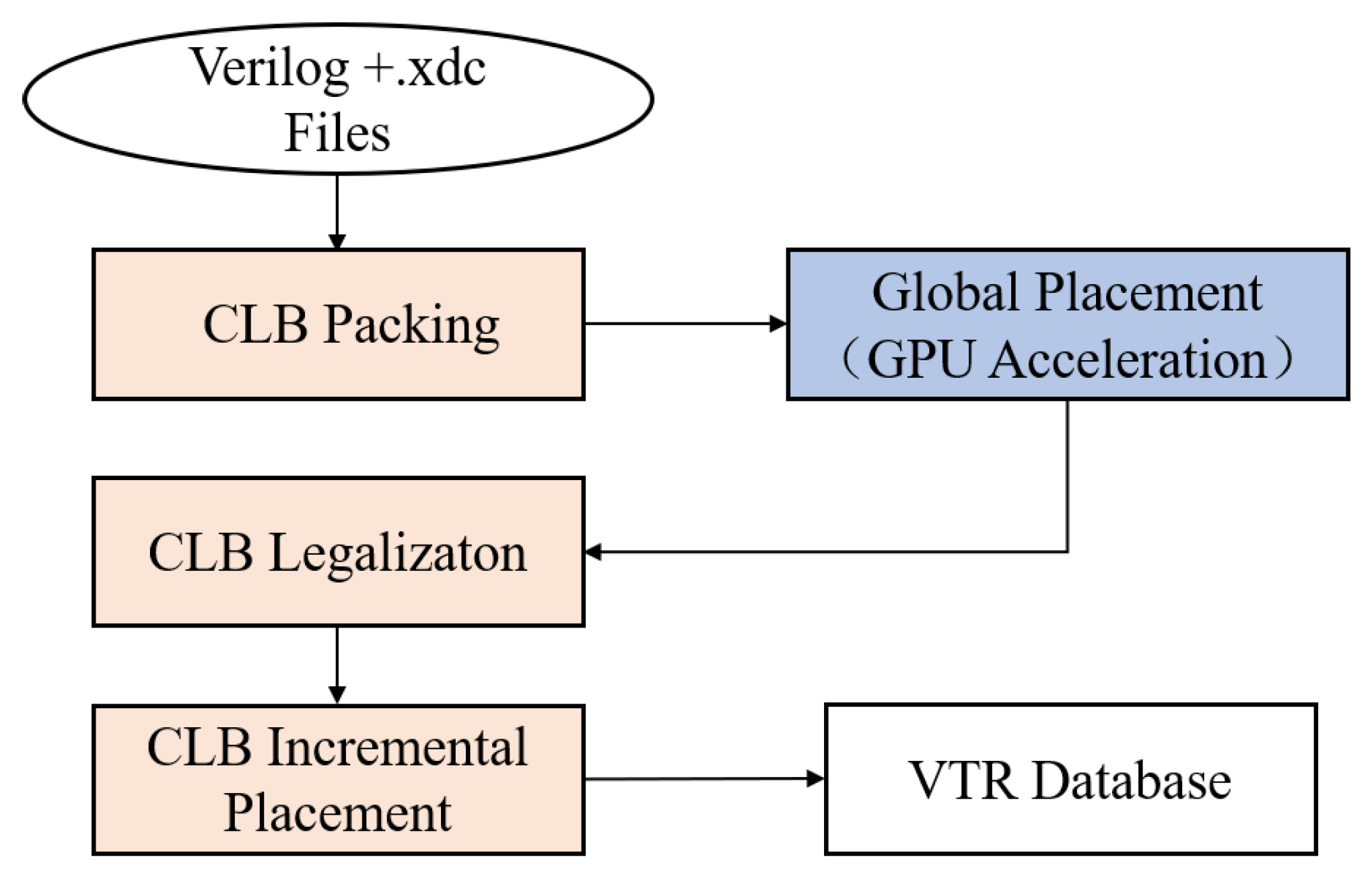
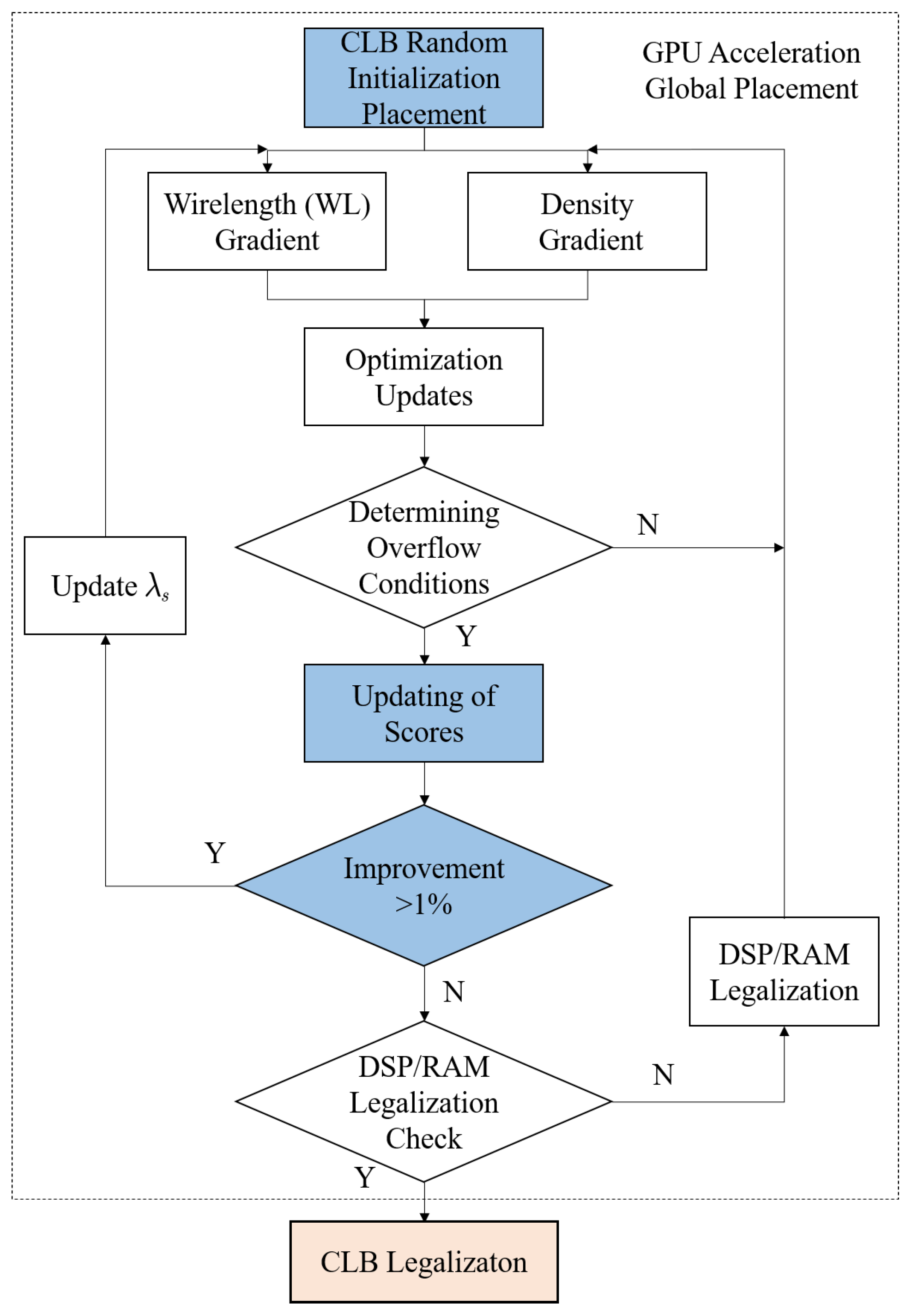
3.1. Proposed Methodology
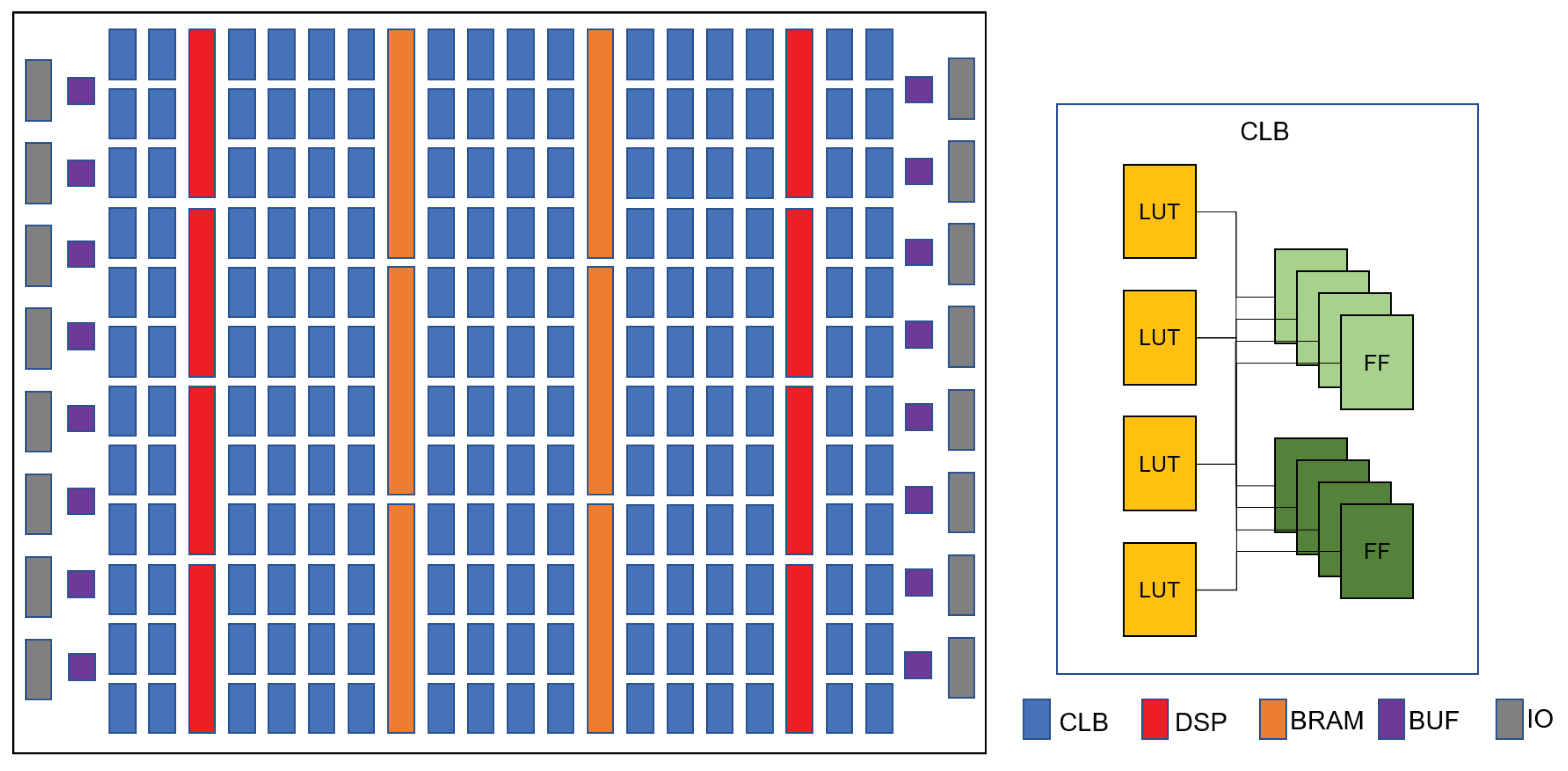
3.2. Parser Design
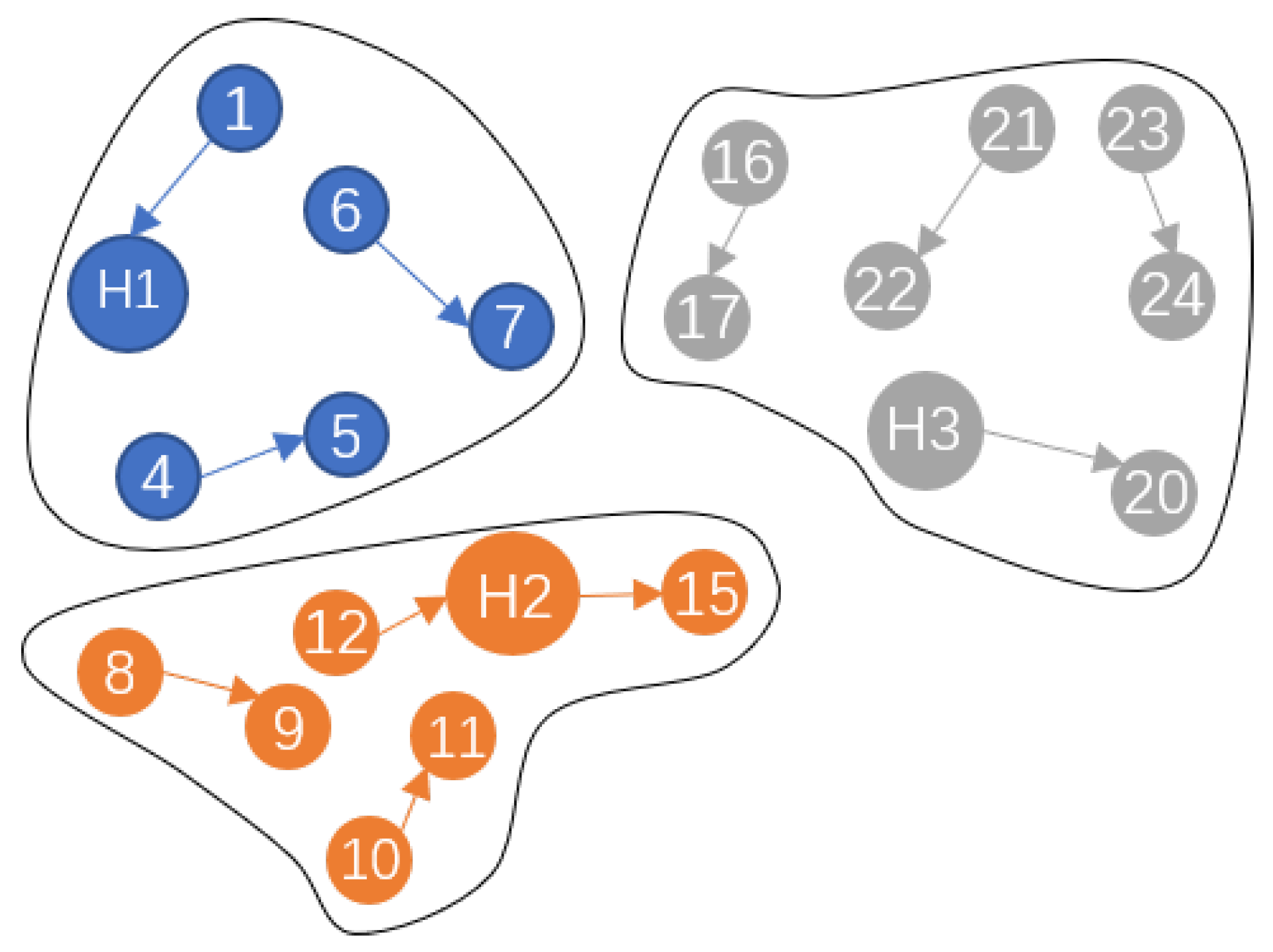
3.3. CLB Packing Design
| Algorithm 1 Weighted Edmonds’ Blossom Algorithm for CLB Packing |
Require: CLB division regions are planned. |
Ensure: LUTs and FFs relation graph built. |
1: while ture do |
2: Initialize data structure. |
3: |
4: for do |
5: HCS merging process. |
6: Edmonds’ blossom matching process. |
7: end for |
8: if meet constraints then |
9: return |
10: end if |
11: end while |
3.4. Improvements to the GPU Acceleration Framework
3.5. Incremental Optimization
| Algorithm 2 CLB Legalization |
Input: , FPGA source, . |
Output: CLB Legalization Location: . |
1: Instance unit weights sorted to form initial to-be-legalized array . |
2: for do |
3: () |
4: if , , Legalization rule determination then |
5: () |
6: else |
7: Incremental adjustment of the calculated value of the coordinates. |
8: end if |
9: end for |
| Algorithm 3 CLB Incremental Placement |
Input: CLB Optimized Location. |
Output: CLB Legalization Location: . |
while Number of iterations N && HPWL local optimal solution && Timing result satisfied do |
2: AP_run( ) |
Collect statistical HPWL and timing results. |
4: N- - |
end while |
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Przybył, A. FPGA-Based Optimization of Industrial Numerical Machine Tool Servo Drives. Electronics 2023, 12, 3585. [Google Scholar] [CrossRef]
- Li, D.; Feng, X.; Shen, C.; Chen, Q.; Yang, L.; Qiu, S.; Jin, X.; Liu, M. Vector-Based Dedicated Processor Architecture for Efficient Tracking in VSLAM Systems. IEEE Embed. Syst. Lett. 2023, 15, 182–185. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, M.; Liu, Z.; Du, X.; Xie, S.; Ma, H.; Ding, G.; Ren, W.; Zhou, F.; Sun, W.; et al. Progress in a novel architecture for high performance processing. Jpn. J. Appl. Phys. 2018, 57, 04FA03. [Google Scholar] [CrossRef]
- Hikawa, H. Place-and-Route Analysis of FPGA Implementation of Nested Hardware Self-Organizing Map Architecture. Electronics 2023, 12, 4523. [Google Scholar] [CrossRef]
- Li, R.; Wu, J.; Liu, M.; Chen, Z.; Zhou, S.; Feng, S. HcveAcc: A high-performance and energy-efficient accelerator for tracking task in VSLAM system. In Proceedings of the 2020 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 9–13 March 2020; pp. 198–203. [Google Scholar]
- Betz, V.; Rose, J. VPR: A new packing, placement and routing tool for FPGA research. In International Workshop on Field Programmable Logic and Applications, Proceedings of the 7th International Workshop, FPL ’97, London, UK, 1–3 September 1997; Springer: Cham, Switzerland, 1997; pp. 213–222. [Google Scholar]
- Chen, G.; Cong, J. Simultaneous placement with clustering and duplication. In Proceedings of the 41st Annual Design Automation Conference, San Diego, CA, USA, 7–11 June 2004; pp. 740–772. [Google Scholar]
- Betz, V.; Rose, J. Automatic generation of FPGA routing architectures from high-level descriptions. In Proceedings of the 2000 ACM/SIGDA Eighth International Symposium on Field Programmable Gate Arrays, Monterey, CA, USA, 10–11 February 2000; pp. 175–184. [Google Scholar]
- Yu, L.; Guo, B. Timing-Driven Simulated Annealing for FPGA Placement in Neural Network Realization. Electronics 2023, 12, 3562. [Google Scholar] [CrossRef]
- Maidee, P.; Ababei, C.; Bazargan, K. Timing-driven partitioning-based placement for island style FPGAs. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2005, 24, 395–406. [Google Scholar] [CrossRef]
- Karypis, G.; Kumar, V. Multilevel k-way hypergraph partitioning. In Proceedings of the 36th Annual ACM/IEEE Design Automation Conference, New Orleans, LA, USA, 21–25 June 1999; pp. 343–348. [Google Scholar]
- Fiduccia, C.M.; Mattheyses, R.M. A Linear-Time Heuristic for Improving Network Partitions. Papers on Twenty-Five Years of Electronic Design Automation. 1988, pp. 241–247. Available online: https://dl.acm.org/doi/pdf/10.1145/62882.62910 (accessed on 18 December 2023).
- Gort, M.; Anderson, J.H. Analytical placement for heterogeneous FPGAs. In Proceedings of the 22nd International Conference on Field Programmable Logic and Applications (FPL), Oslo, Norway, 29–31 August 2012; pp. 143–150. [Google Scholar]
- Li, W.; Dhar, S.; Pan, D.Z. UTPlaceF: A routability-driven FPGA placer with physical and congestion aware packing. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2017, 37, 869–882. [Google Scholar] [CrossRef]
- Chen, Y.C.; Chen, S.Y.; Chang, Y.W. Efficient and effective packing and analytical placement for large-scale heterogeneous FPGAs. In Proceedings of the 2014 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, 2–6 November 2014; pp. 647–654. [Google Scholar]
- Meng, Y.; Li, W.; Lin, Y.; Pan, D.Z. elfplace: Electrostatics-based placement for large-scale heterogeneous fpgas. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2021, 41, 155–168. [Google Scholar] [CrossRef]
- Zhu, Z.; Mei, Y.; Deng, K.; He, H.; Chen, J.; Yang, J.; Chang, Y.W. High-performance Placement Engine for Modern Large-scale FPGAs With Heterogeneity and Clock Constraints. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2023. [Google Scholar] [CrossRef]
- Xu, Y.; Khalid, M.A. QPF: Efficient quadratic placement for FPGAs. In Proceedings of the International Conference on Field Programmable Logic and Applications, Tampere, Finland, 24–26 August 2005; pp. 555–558. [Google Scholar]
- Gopalakrishnan, P.; Li, X.; Pileggi, L. Architecture-aware FPGA placement using metric embedding. In Proceedings of the 43rd Annual Design Automation Conference, San Francisco, CA, USA, 24–28 July 2006; pp. 460–465. [Google Scholar]
- Xu, M.; Gréwal, G.; Areibi, S. StarPlace: A new analytic method for FPGA placement. Integration 2011, 44, 192–204. [Google Scholar] [CrossRef]
- Taj, I.; Farooq, U. Towards Machine Learning-Based FPGA Backend Flow: Challenges and Opportunities. Electronics 2023, 12, 935. [Google Scholar] [CrossRef]
- Baig, I.; Farooq, U. Efficient Detailed Routing for FPGA Back-End Flow Using Reinforcement Learning. Electronics 2022, 11, 2240. [Google Scholar] [CrossRef]
- Mirhoseini, A.; Goldie, A.; Yazgan, M.; Jiang, J.W.; Songhori, E.; Wang, S.; Lee, Y.J.; Johnson, E.; Pathak, O.; Nazi, A.; et al. A graph placement methodology for fast chip design. Nature 2021, 594, 207–212. [Google Scholar] [CrossRef] [PubMed]
- Mallappa, U.; Pratty, S.; Brown, D. RLPlace: Deep RL guided heuristics for detailed placement optimization. In Proceedings of the 2022 Design, Automation & Test in Europe Conference & Exhibition (DATE), Antwerp, Belgium, 14–23 March 2022; pp. 120–123. [Google Scholar]
- Lin, Y.; Dhar, S.; Li, W.; Ren, H.; Khailany, B.; Pan, D.Z. Dreamplace: Deep learning toolkit-enabled gpu acceleration for modern vlsi placement. In Proceedings of the 56th Annual Design Automation Conference, Las Vegas, NV, USA, 2–6 June 2019; pp. 1–6. [Google Scholar]
- Rajarathnam, R.S.; Alawieh, M.B.; Jiang, Z.; Iyer, M.; Pan, D.Z. DREAMPlaceFPGA: An open-source analytical placer for large scale heterogeneous FPGAs using deep-learning toolkit. In Proceedings of the 2022 27th Asia and South Pacific Design Automation Conference (ASP-DAC), Taipei, Taiwan, 17–20 January 2022; pp. 300–306. [Google Scholar]
- Goswami, P.; Bhatia, D. Congestion Prediction in FPGA Using Regression Based Learning Methods. Electronics 2021, 10, 1995. [Google Scholar] [CrossRef]
- Levine, J. Flex & Bison: Text Processing Tools; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2009. [Google Scholar]
- Xu, D.; Tian, Y. A comprehensive survey of clustering algorithms. Ann. Data Sci. 2015, 2, 165–193. [Google Scholar] [CrossRef]
- Gabow, H.N.; Kaplan, H.; Tarjan, R.E. Unique maximum matching algorithms. In Proceedings of the Thirty-First Annual ACM Symposium on Theory of Computing, Atlanta, GA, USA, 1–4 May 1999; pp. 70–78. [Google Scholar]
- Zhu, Z.; Chen, J.; Peng, Z.; Zhu, W.; Chang, Y.W. Generalized augmented lagrangian and its applications to VLSI global placement. In Proceedings of the 55th Annual Design Automation Conference, San Francisco, CA, USA, 24–29 June 2018; pp. 1–6. [Google Scholar]
- Churiwala, S.; Hyderabad, I. Designing with Xilinx® FPGAs. In Circuits & Systems; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Wolf, C.; Glaser, J.; Kepler, J. Yosys-a free Verilog synthesis suite. In Proceedings of the 21st Austrian Workshop on Microelectronics (Austrochip), Linz, Austria, 10 October 2013; p. 97. [Google Scholar]
- Meng, L.; Shuai, L.; Yunfei, W.; Huixin, P.; Chunxue, L.; Liang, W. HDLcs1. 0: A Compiler and Simulator Framework for Hardware Description Language. In Proceedings of the 2023 International Symposium of Electronics Design Automation (ISEDA), Nanjing, China, 8–11 May 2023; pp. 93–96. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Liu, M. A co-design method of customized ISA design space exploration and fixed-point library construction for RISC-V dedicated processor. IEICE Electron. Express 2022, 19, 20220244. [Google Scholar] [CrossRef]





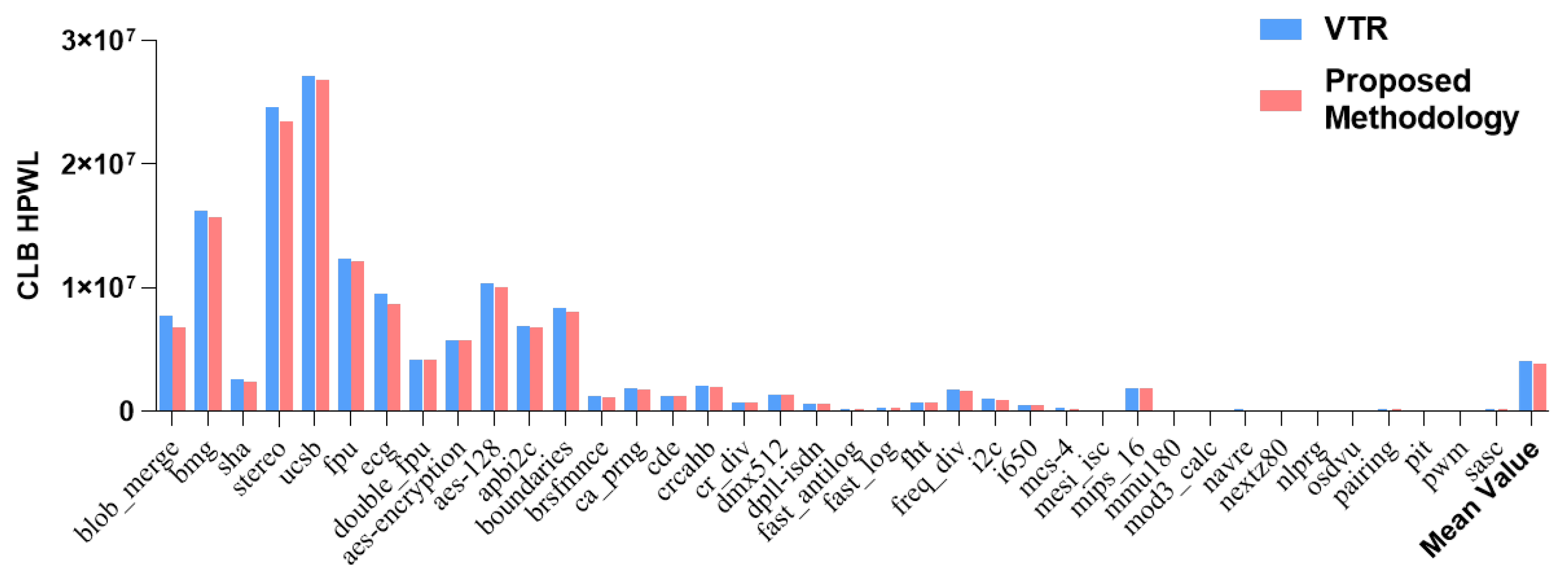

| Benchmarks 1 | VTR | Proposed Methodology | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Packing Time (s) |
Placement Time (s) |
Total Time (s) |
CLB HPWL |
Freq. (MHz) |
CLB Util. |
Packing Time (s) |
Placement Time (s) |
Total Time (s) |
CLB HPWL |
Freq. (MHz) |
CLB Util. | |
| blob_merge | 35.19 | 16.65 | 51.84 | 7706102 | 282.62 | 13.10% | 23.91 | 4.06 | 27.97 | 6819560 | 286.40 | 10.35% |
| bmg | 94.55 | 69.73 | 164.28 | 16182815 | 271.43 | 28.37% | 67.17 | 37.67 | 104.84 | 15711471 | 277.75 | 25.48% |
| sha | 10.77 | 3.63 | 14.40 | 2568701 | 286.15 | 4.21% | 6.52 | 1.32 | 7.84 | 2378427 | 297.58 | 2.17% |
| stereo | 127.15 | 15.81 | 142.96 | 24659527 | 265.89 | 35.82% | 100.64 | 6.07 | 106.71 | 23485264 | 266.74 | 33.24% |
| ucsb | 260.39 | 27.50 | 287.89 | 27125480 | 261.83 | 43.16% | 226.45 | 12.38 | 238.83 | 26856911 | 262.19 | 40.99% |
| fpu | 135.54 | 33.20 | 168.74 | 12329764 | 268.97 | 27.53% | 95.28 | 12.70 | 107.98 | 12088004 | 269.60 | 24.84% |
| ecg | 83.64 | 22.50 | 106.14 | 9484434 | 273.78 | 26.21% | 58.64 | 20.40 | 79.04 | 8701315 | 275.89 | 23.21% |
| double_fpu | 10.54 | 8.21 | 18.75 | 4123667 | 285.63 | 7.12% | 7.40 | 1.89 | 9.29 | 4115436 | 296.52 | 4.97% |
| aes-encryption | 24.64 | 16.32 | 40.96 | 5773133 | 278.36 | 11.86% | 17.46 | 5.76 | 23.22 | 5699046 | 284.69 | 9.17% |
| aes-128 | 148.54 | 30.43 | 178.97 | 10391640 | 269.27 | 27.93% | 99.23 | 8.53 | 107.76 | 9991962 | 278.05 | 26.07% |
| apbi2c | 63.28 | 66.50 | 129.78 | 6927760 | 282.38 | 14.78% | 45.12 | 15.05 | 60.17 | 6725981 | 286.02 | 13.48% |
| boundaries | 289.47 | 100.45 | 389.92 | 8313312 | 263.45 | 42.32% | 201.75 | 18.10 | 219.85 | 8039954 | 263.72 | 40.83% |
| brsfmnce | 16.91 | 14.50 | 31.41 | 1187616 | 287.86 | 10.51% | 11.68 | 3.90 | 15.58 | 1100830 | 297.12 | 8.03% |
| ca_prng | 57.82 | 49.78 | 107.60 | 1900186 | 283.21 | 13.75% | 40.22 | 16.95 | 57.17 | 1881187 | 286.19 | 10.79% |
| cde | 42.99 | 18.43 | 61.42 | 1187616 | 280.43 | 11.40% | 29.95 | 7.29 | 37.24 | 1096672 | 283.68 | 9.28% |
| crcahb | 78.13 | 34.54 | 112.67 | 2018947 | 271.39 | 18.65% | 54.06 | 12.66 | 66.72 | 1927769 | 273.10 | 17.31% |
| cr_div | 11.26 | 32.08 | 43.34 | 747758 | 287.44 | 8.34% | 7.83 | 1.83 | 9.66 | 681233 | 297.36 | 6.01% |
| dmx512 | 47.53 | 28.81 | 76.34 | 1345965 | 279.62 | 12.54% | 33.02 | 7.67 | 40.69 | 1238855 | 282.89 | 11.05% |
| dpll-isdn | 17.42 | 13.42 | 30.84 | 611802 | 286.87 | 9.16% | 12.14 | 2.93 | 15.07 | 565370 | 295.25 | 6.63% |
| fast_antilog | 6.88 | 3.32 | 10.20 | 197356 | 281.92 | 3.25% | 4.79 | 1.98 | 6.77 | 184318 | 299.75 | 1.78% |
| fast_log | 31.77 | 20.70 | 52.47 | 276298 | 280.45 | 12.93% | 22.07 | 9.10 | 31.17 | 276256 | 283.94 | 11.64% |
| fht | 75.22 | 34.70 | 109.92 | 663115 | 278.93 | 14.87% | 51.96 | 12.36 | 64.32 | 620420 | 280.50 | 13.32% |
| freq_div | 162.33 | 100.11 | 262.44 | 1724098 | 267.39 | 28.36% | 112.98 | 25.90 | 138.88 | 1698974 | 268.25 | 27.19% |
| i2c | 97.09 | 89.03 | 186.12 | 1014175 | 277.34 | 25.32% | 67.39 | 25.05 | 92.44 | 977281 | 279.11 | 22.33% |
| i650 | 51.08 | 26.91 | 77.99 | 533776 | 278.53 | 13.83% | 35.52 | 14.63 | 50.15 | 504092 | 282.07 | 10.93% |
| mcs-4 | 28.75 | 15.63 | 44.38 | 242626 | 283.89 | 8.56% | 20.08 | 4.85 | 24.93 | 242039 | 289.91 | 7.32% |
| mesi_isc | 7.44 | 4.20 | 11.64 | 56425 | 285.12 | 5.75% | 5.18 | 1.90 | 7.08 | 53854 | 297.27 | 3.87% |
| mips_16 | 213.02 | 171.78 | 384.80 | 1884581 | 257.28 | 40.43% | 148.00 | 61.50 | 209.50 | 1761781 | 257.91 | 38.15% |
| mmu180 | 18.99 | 16.36 | 35.35 | 31410 | 283.26 | 10.77% | 13.16 | 5.57 | 18.73 | 29221 | 290.67 | 9.40% |
| mod3_calc | 43.21 | 18.43 | 61.64 | 59678 | 281.51 | 11.65% | 30.11 | 7.29 | 37.40 | 57425 | 286.88 | 9.15% |
| navre | 89.07 | 37.37 | 126.44 | 137260 | 278.67 | 14.36% | 62.02 | 15.25 | 77.27 | 127944 | 282.03 | 12.68% |
| nextz80 | 12.56 | 8.46 | 21.02 | 22139 | 288.45 | 7.67% | 8.73 | 2.15 | 10.88 | 21792 | 297.98 | 5.22% |
| nlprg | 46.33 | 28.90 | 75.23 | 79700 | 280.96 | 12.86% | 32.28 | 7.80 | 40.08 | 76753 | 285.94 | 11.17% |
| osdvu | 55.78 | 38.56 | 94.34 | 103609 | 279.16 | 13.43% | 39.00 | 16.15 | 55.15 | 94854 | 283.83 | 10.75% |
| pairing | 107.26 | 43.95 | 151.21 | 165775 | 275.39 | 26.18% | 75.00 | 20.90 | 95.90 | 154530 | 277.10 | 24.42% |
| pit | 19.84 | 13.36 | 33.20 | 31278 | 285.29 | 9.07% | 13.72 | 5.50 | 19.22 | 28968 | 293.94 | 7.51% |
| pwm | 67.55 | 32.31 | 99.86 | 106346 | 277.46 | 14.21% | 46.88 | 18.45 | 65.33 | 97470 | 281.38 | 12.01% |
| sasc | 126.34 | 44.54 | 170.88 | 175471 | 274.23 | 27.17% | 88.68 | 21.22 | 109.90 | 166121 | 275.66 | 25.13% |
| Mean Value | 74.11 | 35.56 | 109.67 | 4002404 | 277.94 | 17.56% | 53.05 | 12.49 | 65.55 | 3849456 | 283.02 | 15.47% |
| Site Type | Available | Used | Utilization |
|---|---|---|---|
| LUTs | 230400 | 217254 | 0.94 |
| FFs | 460800 | 165580 | 0.36 |
| BRAM | 11 | 8 | 0.73 |
| DSP | 1729 | 1340 | 0.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Wang, Y.; Li, S. A Field Programmable Gate Array Placement Methodology for Netlist-Level Circuits with GPU Acceleration. Electronics 2024, 13, 37. https://doi.org/10.3390/electronics13010037
Liu M, Wang Y, Li S. A Field Programmable Gate Array Placement Methodology for Netlist-Level Circuits with GPU Acceleration. Electronics. 2024; 13(1):37. https://doi.org/10.3390/electronics13010037
Chicago/Turabian StyleLiu, Meng, Yunfei Wang, and Shuai Li. 2024. "A Field Programmable Gate Array Placement Methodology for Netlist-Level Circuits with GPU Acceleration" Electronics 13, no. 1: 37. https://doi.org/10.3390/electronics13010037
APA StyleLiu, M., Wang, Y., & Li, S. (2024). A Field Programmable Gate Array Placement Methodology for Netlist-Level Circuits with GPU Acceleration. Electronics, 13(1), 37. https://doi.org/10.3390/electronics13010037





