Current-Prediction-Controlled Quasi-Z-Source Cascaded Multilevel Photovoltaic Inverter
Abstract
:1. Introduction
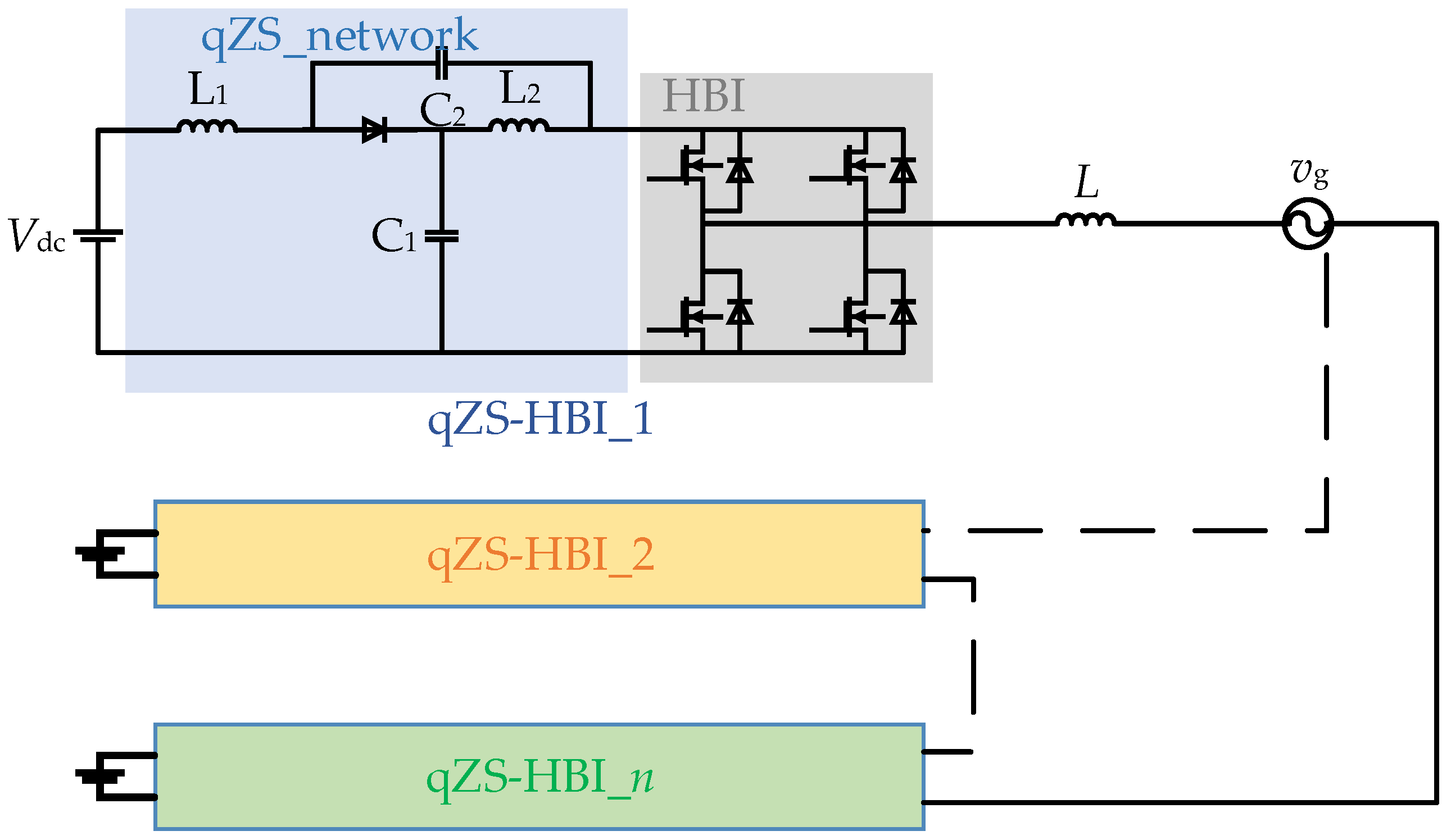
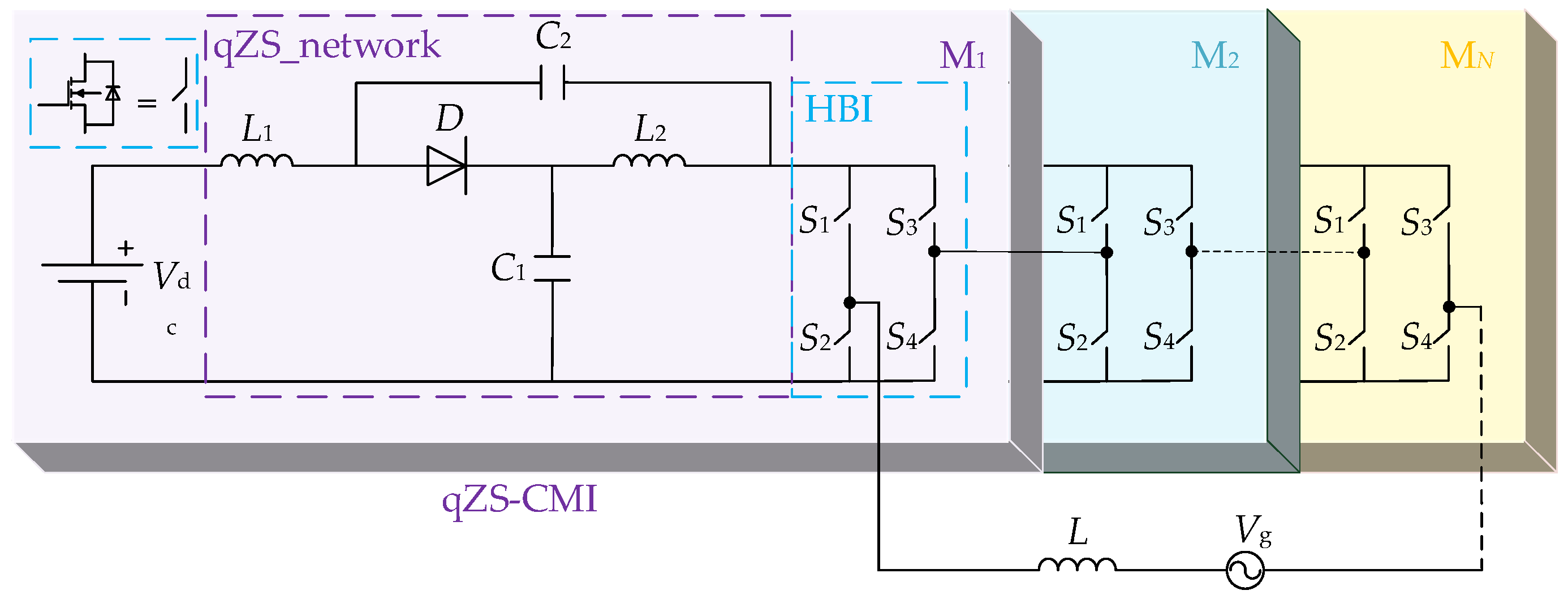
2. Principle of Quasi-Z-Source Cascaded Multilevel Inverter
2.1. Voltage Boost Principle of the Quasi-Z-Source
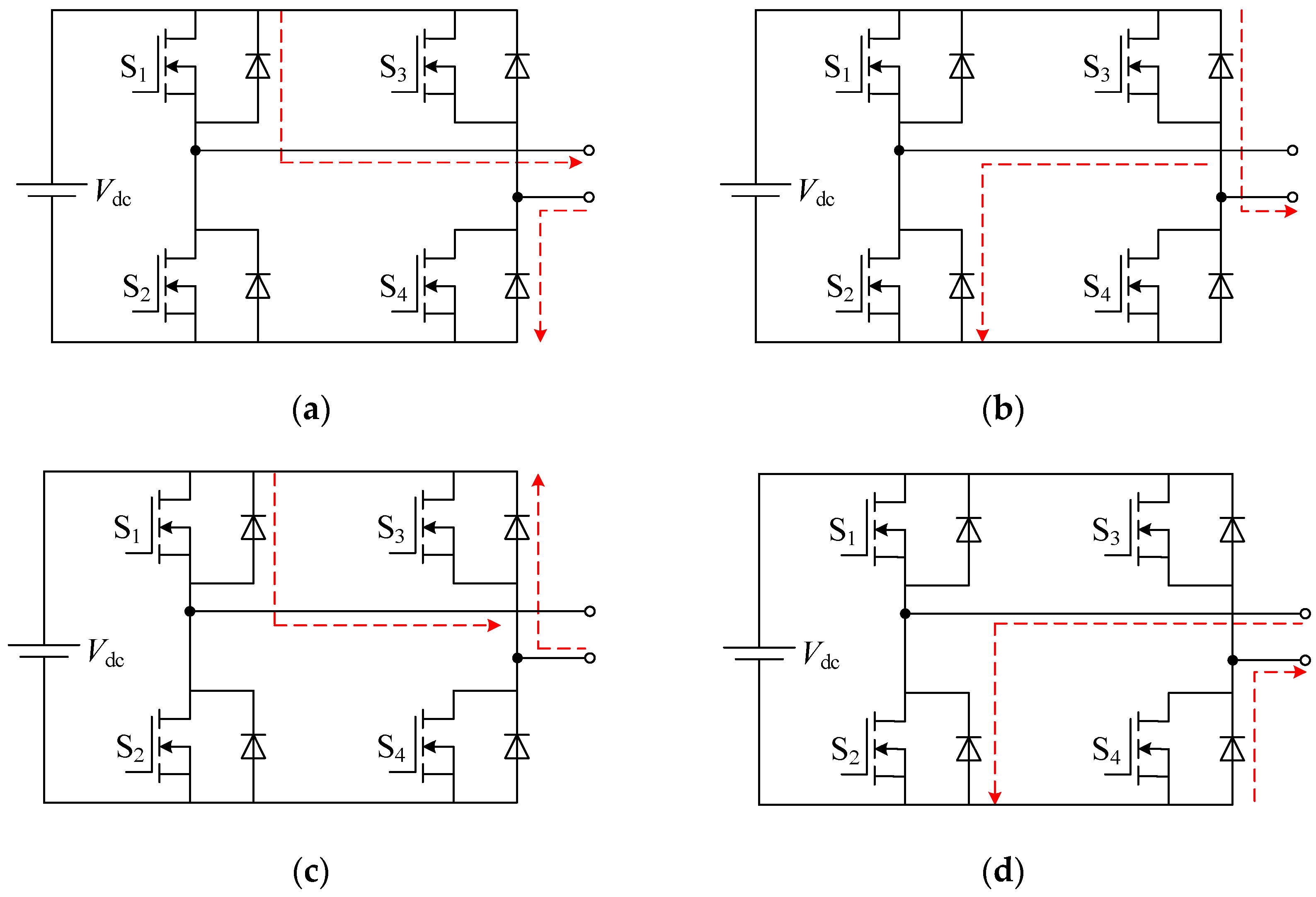
2.2. Principle of Cascaded Multilevel Inverter
2.3. QZS-CMI Mathematical Model
3. Current-Predictive-Control-Improved Deadbeat Current Control
3.1. Principle of Deadbeat Current Control
3.2. Improved Deadbeat Current-Predictive Control
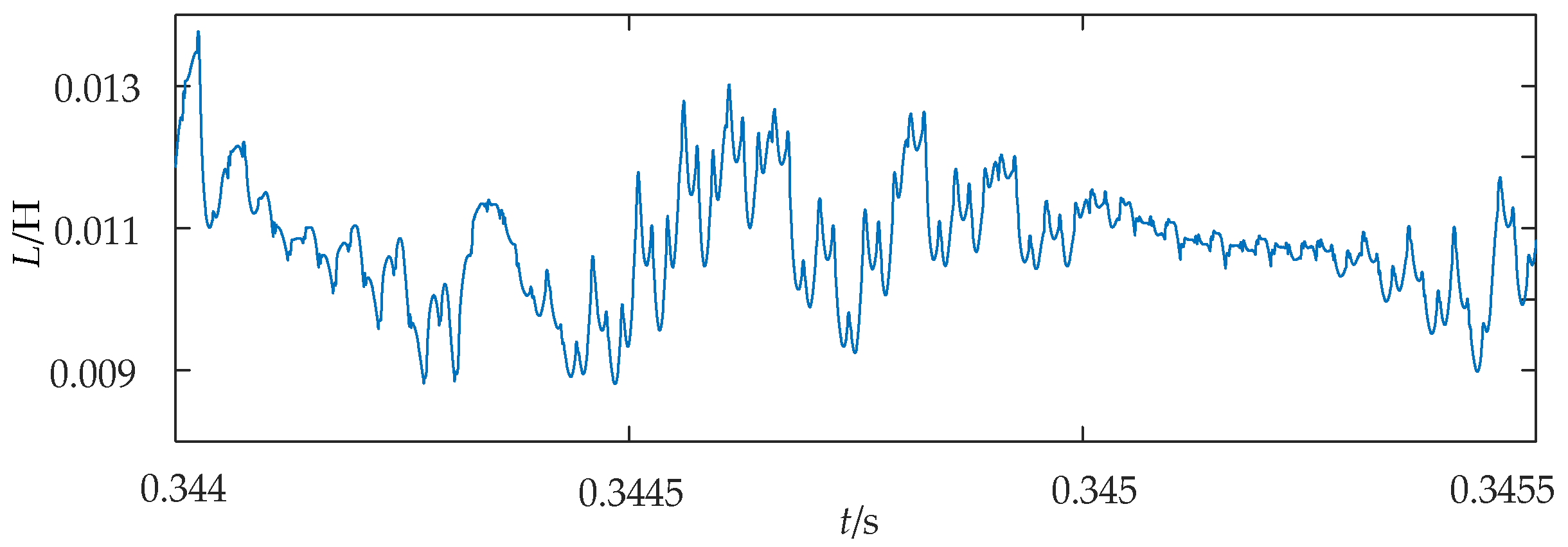
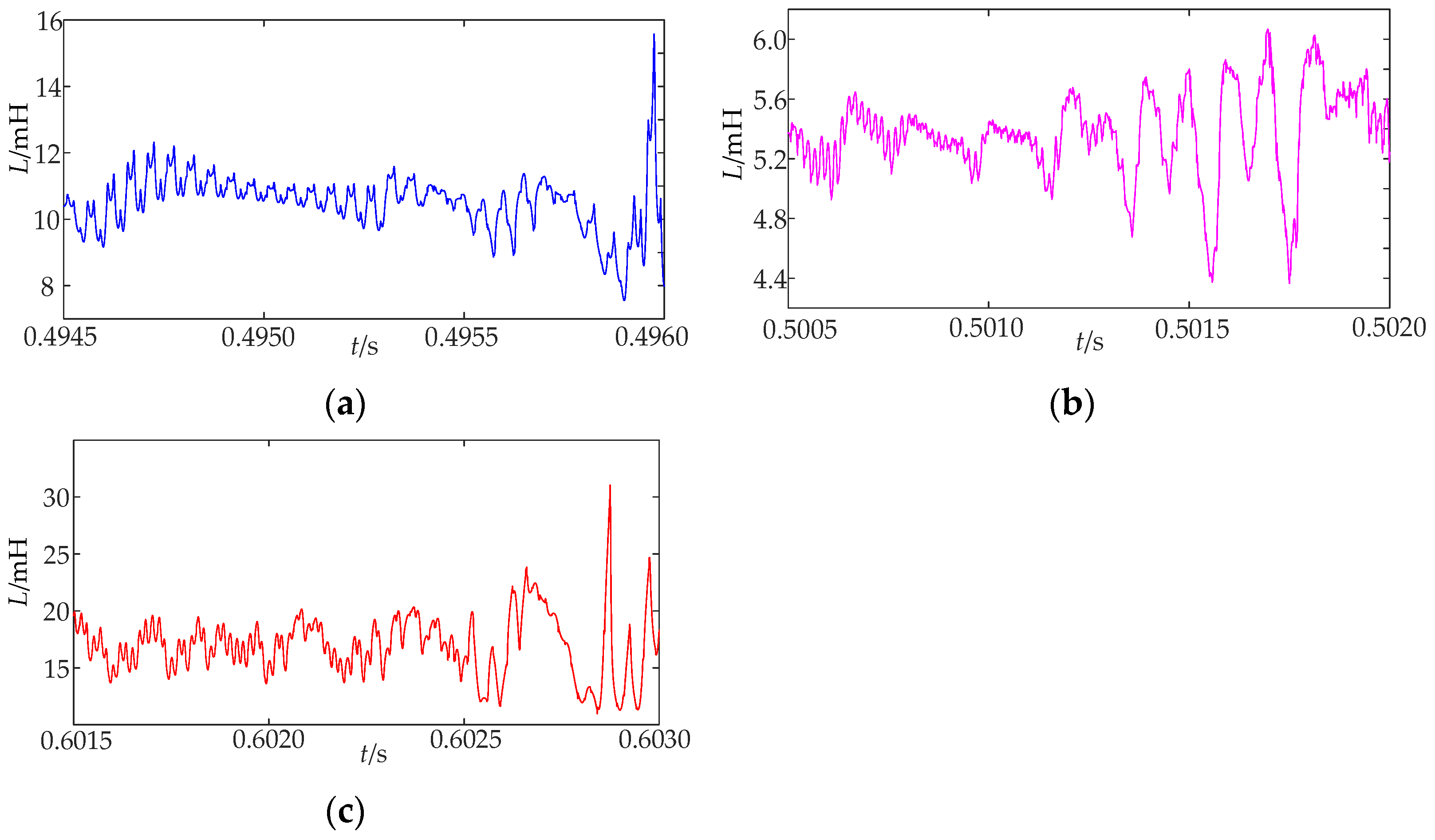
3.3. Parameter Identification of Grid-Side Inductance Based on the Least Squares Method
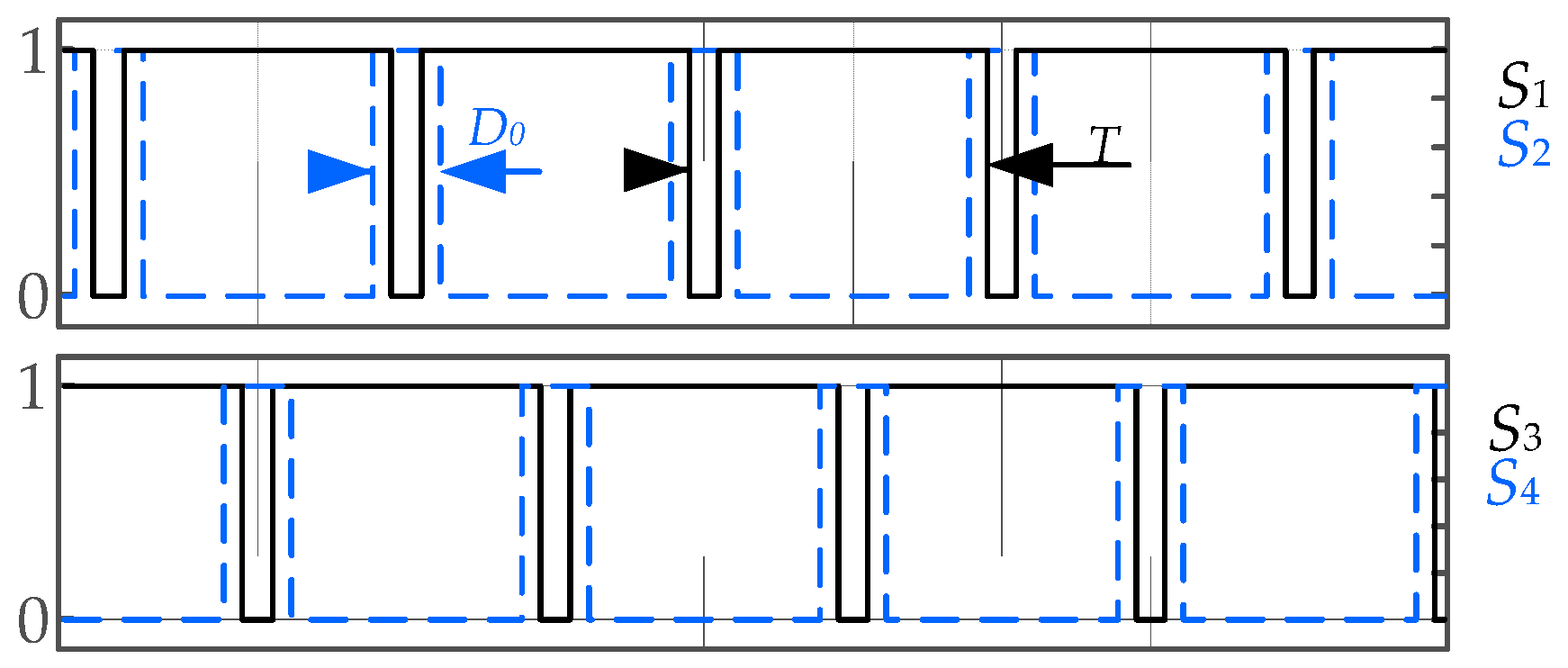
4. Multi-Carrier Phase-Shifted Sinusoidal Pulse Width Modulation
5. Results of the System
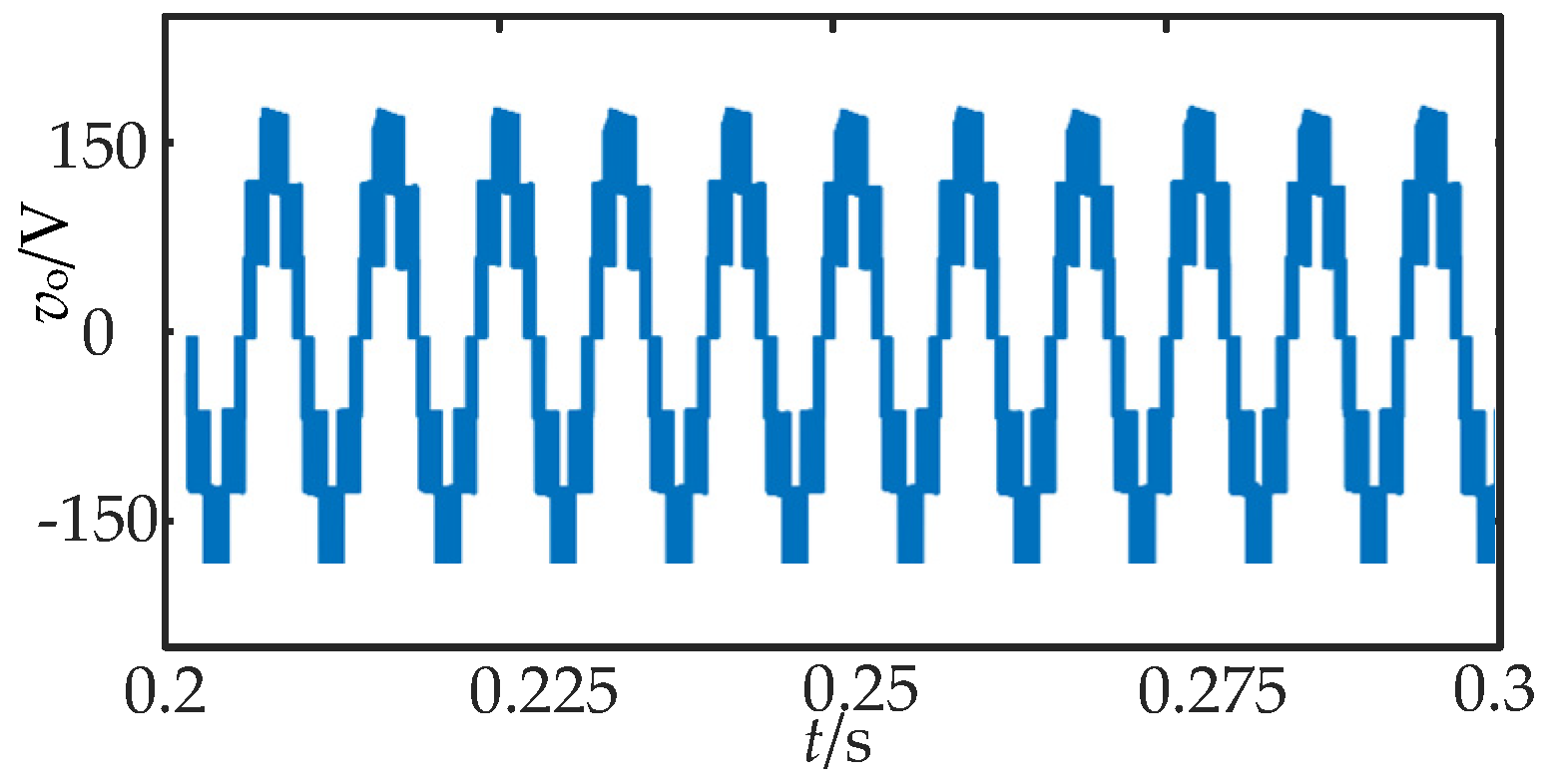
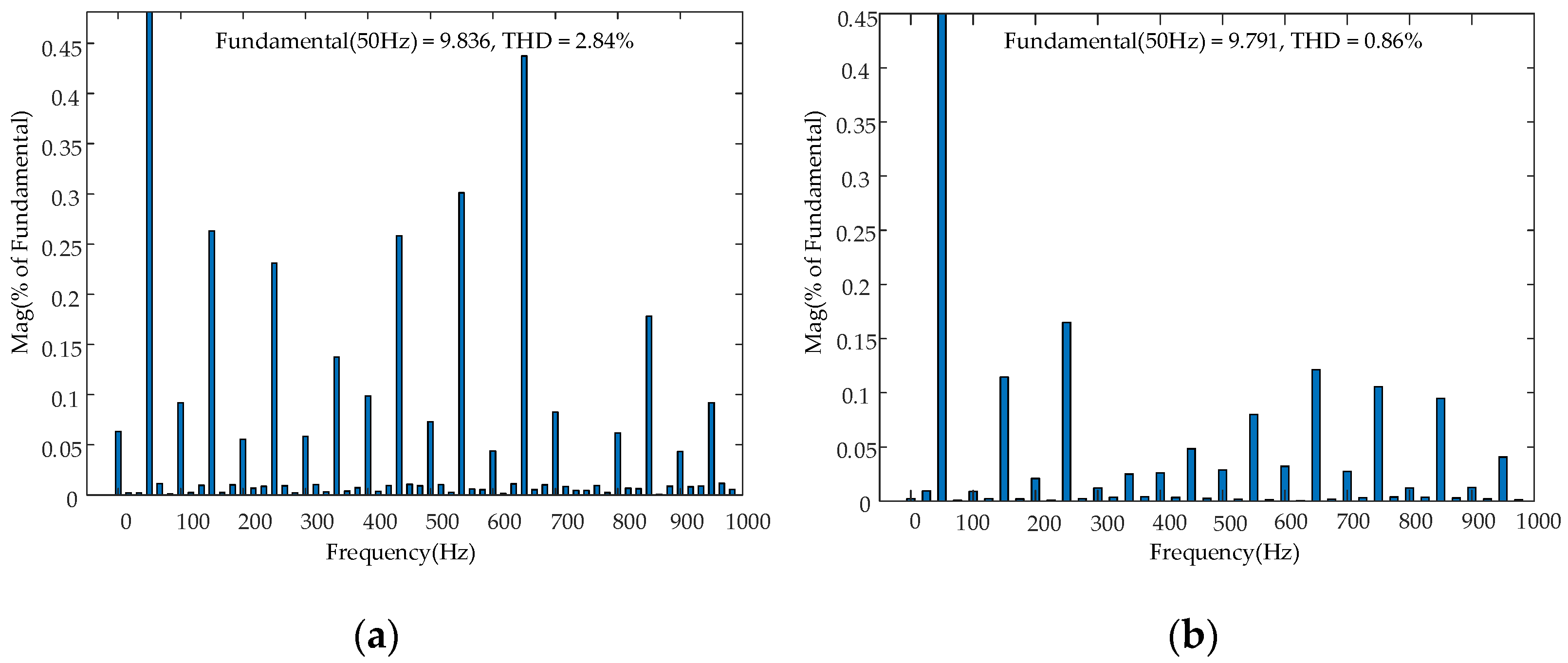
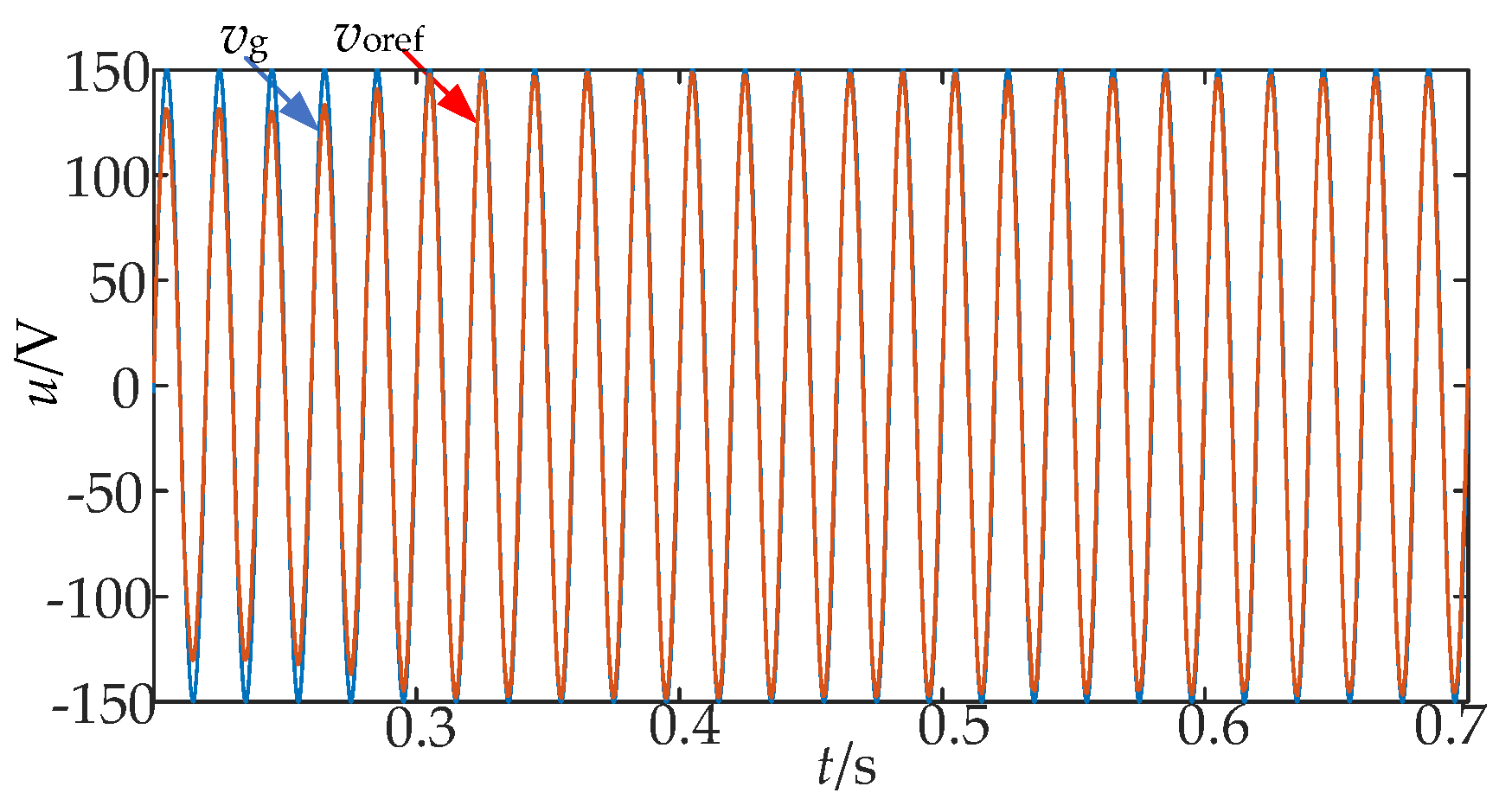
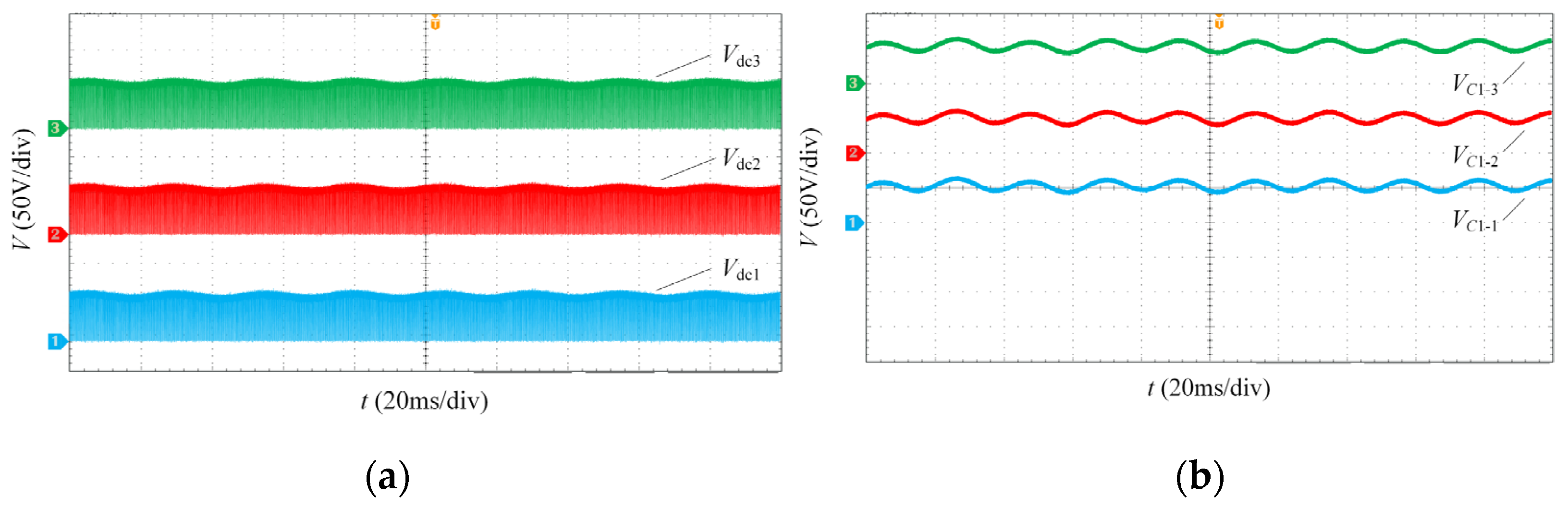
5.1. Analysis of System Steady-State Simulation Results
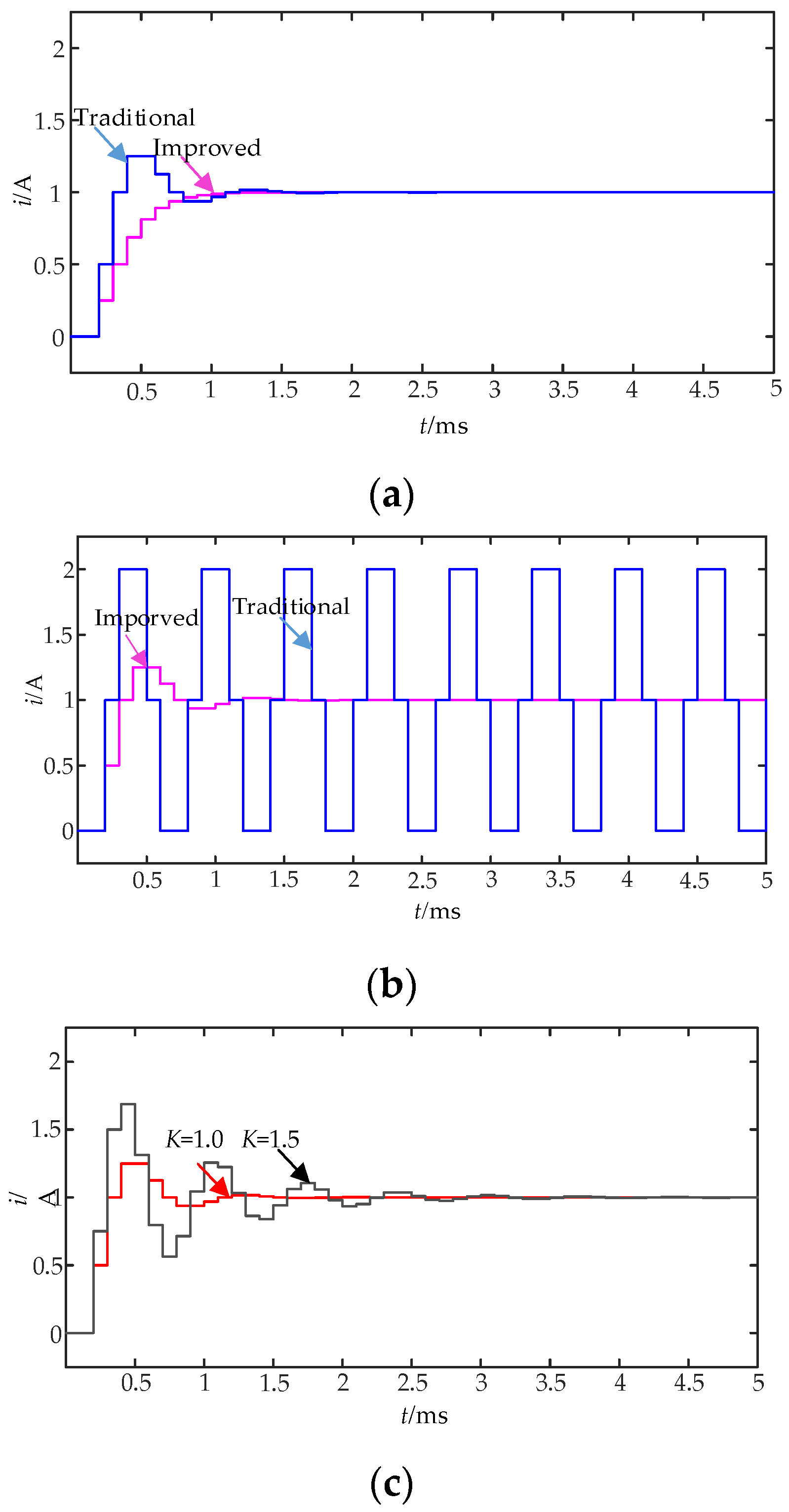
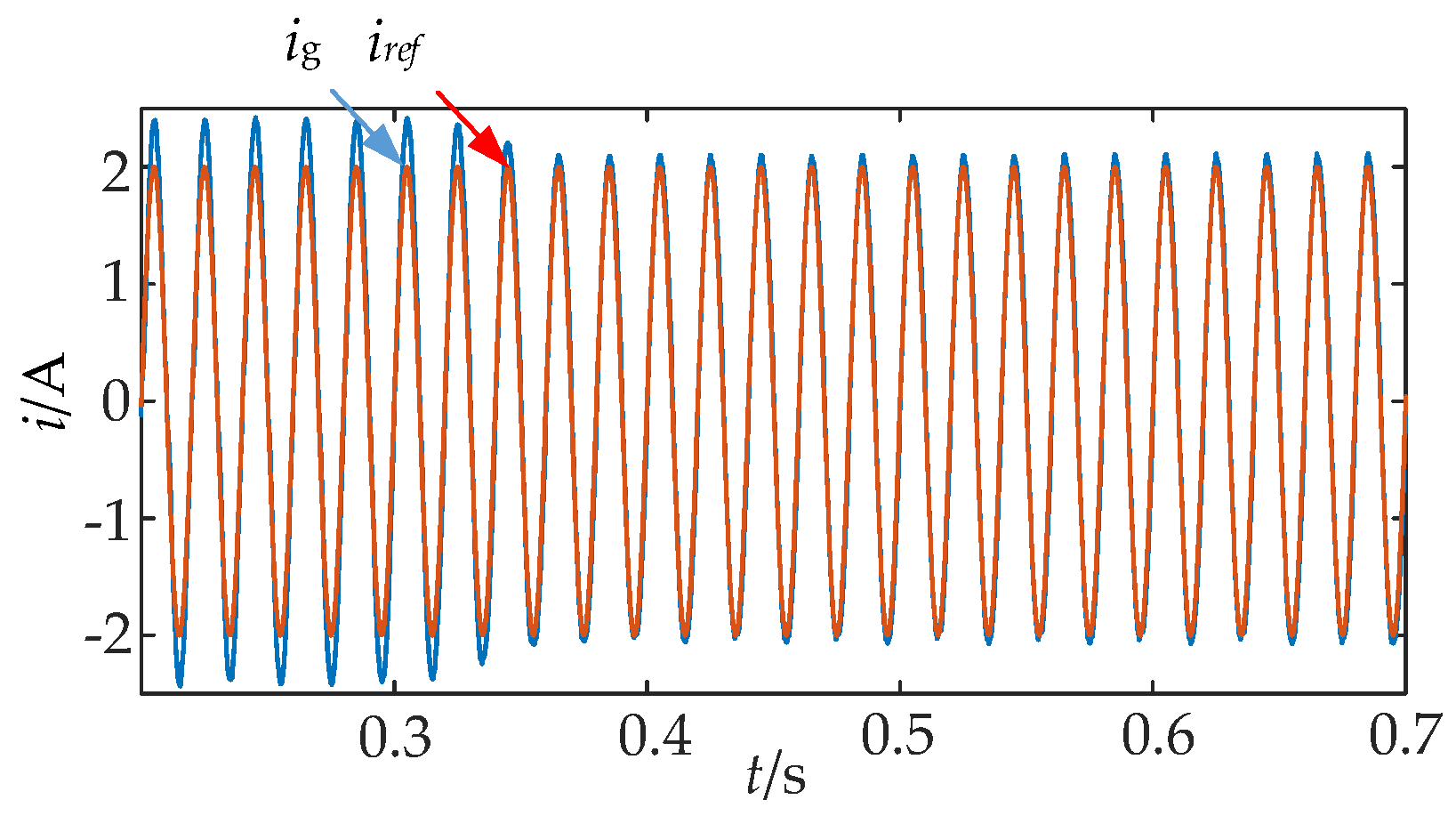
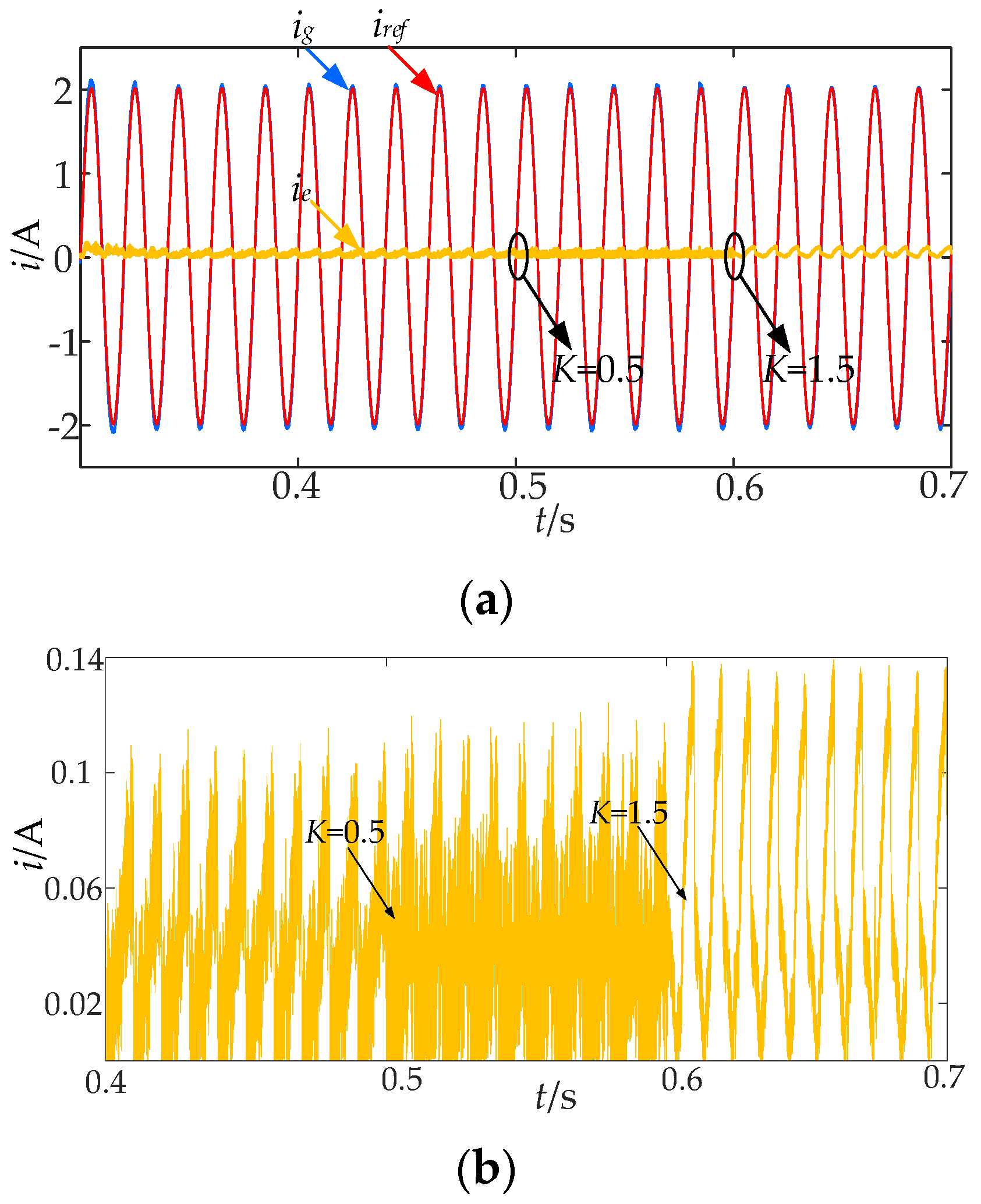
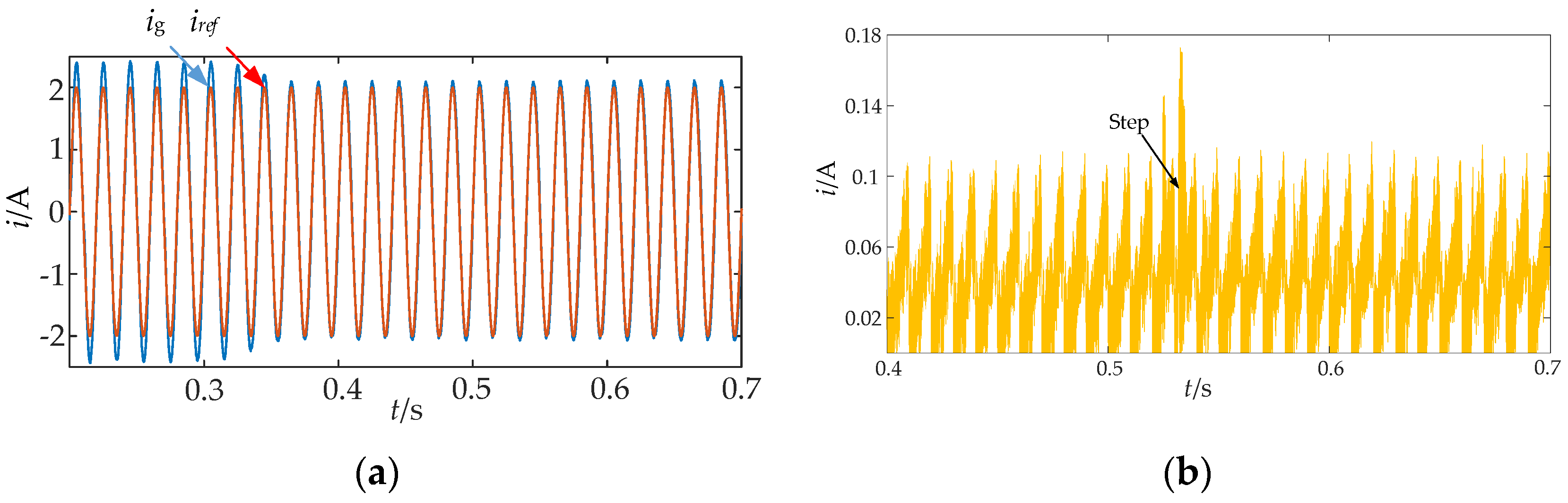
5.2. Analysis of System Dynamic Simulation Results
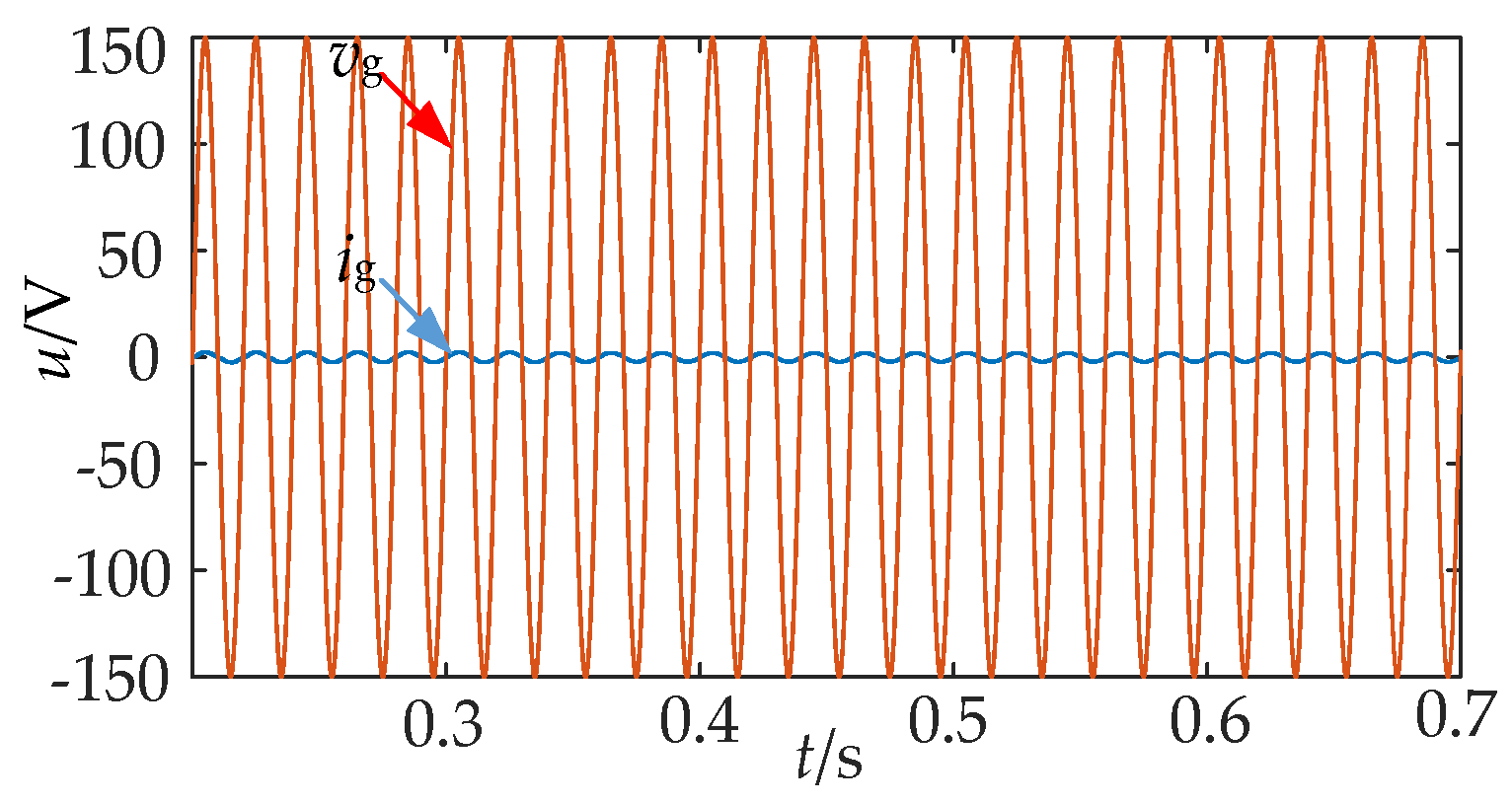
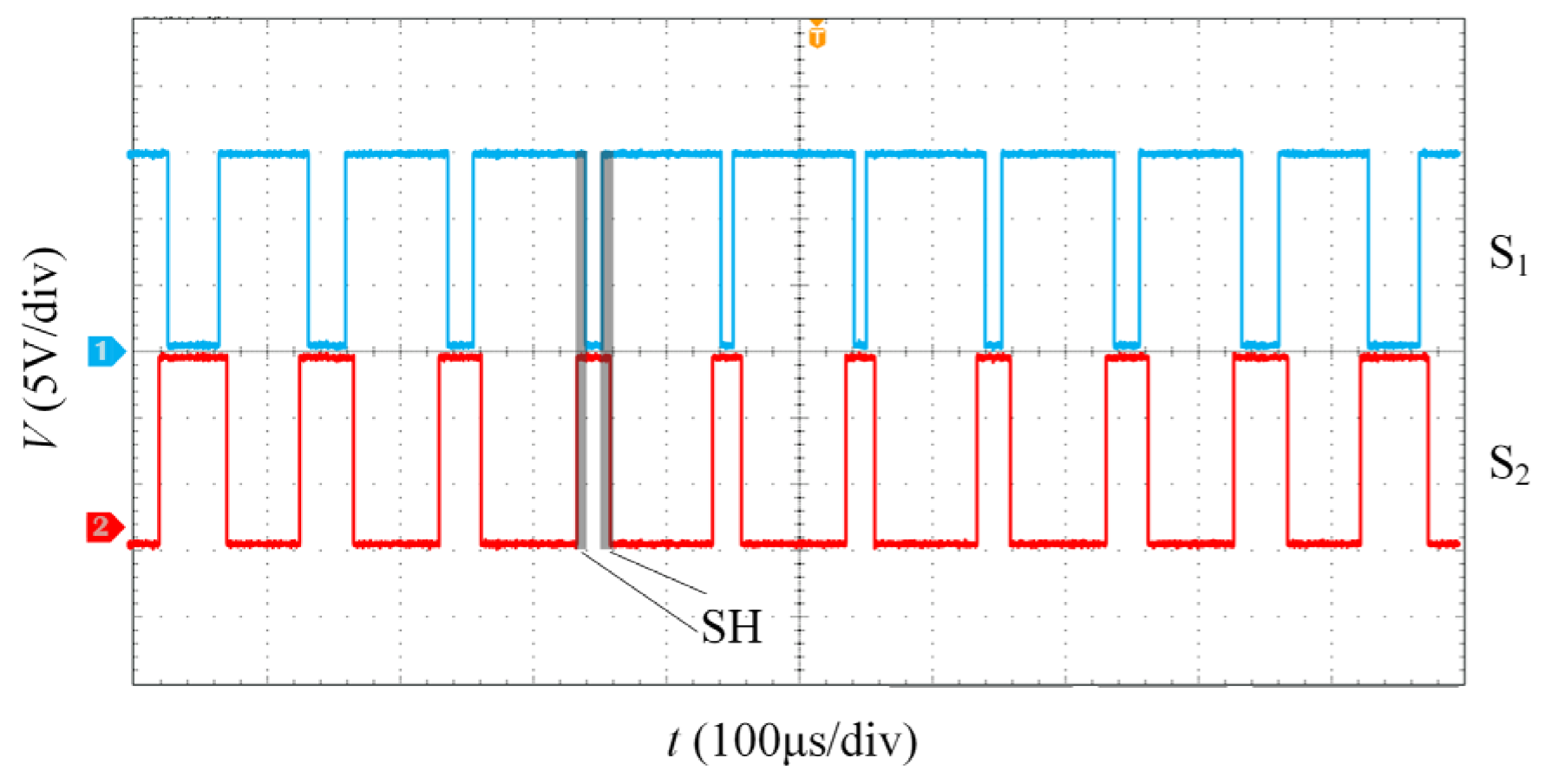
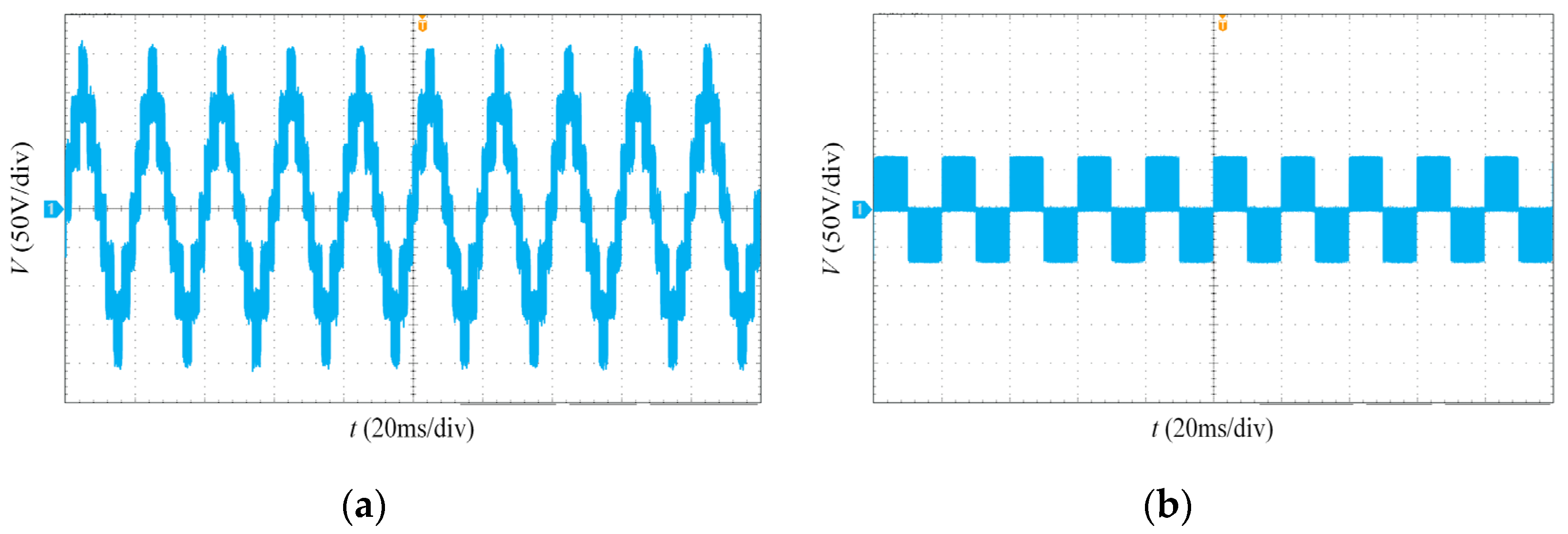
5.3. Analysis of Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Peng, F.Z. Z-source inverter. IEEE Trans. Ind. Appl. 2003, 39, 504–510. [Google Scholar] [CrossRef]
- Lu, H.C. Research on Permanent Magnet Synchronous Motor System Based on Three-Level Inverter and LC Filter; Huazhong University of Science and Technology: Wuhan, China, 2022. [Google Scholar]
- Zhang, C.H.; Zhou, J.W.; Du, C.S.; Chen, A.L. Review of Control Strategies of Single-phase Cascaded H-Bridge Multilevel Inverter for Grid-connected Photovoltaic Systems. J. Power Supply 2017, 15, 1–8. [Google Scholar]
- Xu, J.; Xu, T.L. Research on NPC Single-Phase Inverter Based on Five-Level Control. Sol. Energy 2021, 15, 1–8. [Google Scholar]
- Dong, S.; Zhang, Q.F.; Wang, R.; Wang, H.L.; Cheng, S.K. Development of the Z-Source Inverters and Its Key Technologies: A Review. J. Electr. Eng. 2016, 11, 1–12. [Google Scholar]
- Su, H.S.; Lin, H.J.; Che, Y.L. Comparative Analysis of All Kinds of Z-source Inverters in Properties and Their Application Background. Control Eng. China 2017, 24, 188–196. [Google Scholar]
- Li, S.; Si, W.X.; Chen, Y.; Cui, S. Research on Isolated Quasi-Z-Source Single Phase Photovoltaic Grid Connected Inverter Based on PR Control. Acta Energiae Solaris Sin. 2018, 39, 3081–3089. [Google Scholar]
- Zhang, R.; Li, Y. System Parameter Design and Grid-connected Control Methods for Quasi-Z-Source Cascaded Multilevel Inverter Considering Power Difference of Modules. Proc. CSEE 2018, 48, 4836–4845. [Google Scholar]
- Wang, J.; Zhang, R.; Liu, Y.; Li, Y. A Multi-Modulation Waveform Phase-Shift Sinusoidal Pulse Width Modulation Method of QZS-CHI and Its Output Voltage Analysis. Trans. China Electrotech. Soc. 2020, 35, 3470–3477. [Google Scholar]
- You, Y.F.; Li, Y.; Xiao, X.Y.; Fang, F. Finite control set-model predictive control of single-phase quasi-Z-source cascaded multilevel inverter. Power Syst. Prot. Control 2020, 48, 1–8. [Google Scholar]
- Niu, L.; Yang, M.; Liu, K.S.; Xu, D.G. A Predictive Current Control Scheme for Permanent Magnet Synchronous Motors. Proc. CSEE. 2012, 32, 131–137. [Google Scholar]
- Yang, H.; Yang, L.H.; Chen, Y.M.; Shi, J.Z.; Wang, S.K. Deadbeat Predictive Current Control Strategy Based on Disturbance Compensation for Grid Connected Inverter with LCL Filter. Proc. CSEE 2023, 43, 1–16. [Google Scholar]
- Chen, Y.D.; Luo, A.; Zhou, L.M.; Xie, N.; Jin, G.B.; Lu, Z.P. A Robust Predictive Deadbeat Grid-connected Control Method Based on Power Feed-forward Control. Proc. CSEE 2013, 33, 62–70. [Google Scholar]
- Jiang, Y.; Xu, W.; Mu, C.; Liu, Y. Improved deadbeat predictive current control combined sliding mode strategy for PMSM drive system. IEEE Trans. Veh. Technol. 2017, 67, 251–263. [Google Scholar] [CrossRef]
- Qu, A.W.; Chen, D.L.; Su, Q. Simple Boost Modified Space Vector Modulation Strategy for Three-Phase Quasi-Z-Source Grid-Connected Inverter. Trans. China Electrotech. Soc. 2018, 33, 826–836. [Google Scholar]
- Guo, H.S. Improvement of SVPWM Direct Modulation Strategy for Quasi-Z Source Inverter. Electr. Eng. 2022, 05, 67–70. [Google Scholar]
- You, Y.F.; Li, Y.; Fang, F.; Yang, X.Y. Deadbeat grid-connected control strategy of quasi-Z-source cascaded multilevel inverter and System Parameter Design. Power Syst. Prot. Control 2019, 2022, 47. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Li, B.Y.; Liu, J. Online Inductance Identification of a PWM Rectifier Under Unbalanced and Distorted Grid Voltages. IEEE Trans. Ind. Appl. 2020, 56, 3879–3888. [Google Scholar] [CrossRef]
- Chen, Z.G.; Yang, L.Y.; Zhang, Y.L.; Li, Z.X. A Control Method of PMSM Current-Loop Based on Online Parameter Identification; IEEE Computer Society: Singapore, 2012; pp. 417–422. [Google Scholar]










| Main Parameters | Values |
|---|---|
| Quasi-Z-source Inductance (H) | 0.003 |
| Quasi-Z-source Capacitance (F) | 0.004 |
| Input Voltage (V) | 35 |
| Grid Voltage (V) | 150 |
| Grid Current (A) | 2 |
| Filter Inductance (H) | 0.01 |
| Maximum Shoot-through Duty Ratio | 0.25 |
| Switching Frequency (kHz) | 10 |
| Main Parameters | Values |
|---|---|
| Input Voltage (V) | 35 |
| DC Link Voltage Peak (V) | 70 |
| Peak Output Voltage After Filtered (V) | 150 |
| Peak Output Current (A) | 10 |
| Switching Frequency (kHz) | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, S.; Jin, N.; Jiang, J. Current-Prediction-Controlled Quasi-Z-Source Cascaded Multilevel Photovoltaic Inverter. Electronics 2024, 13, 1824. https://doi.org/10.3390/electronics13101824
Lei S, Jin N, Jiang J. Current-Prediction-Controlled Quasi-Z-Source Cascaded Multilevel Photovoltaic Inverter. Electronics. 2024; 13(10):1824. https://doi.org/10.3390/electronics13101824
Chicago/Turabian StyleLei, Shanshan, Ningzhi Jin, and Jiaxin Jiang. 2024. "Current-Prediction-Controlled Quasi-Z-Source Cascaded Multilevel Photovoltaic Inverter" Electronics 13, no. 10: 1824. https://doi.org/10.3390/electronics13101824
APA StyleLei, S., Jin, N., & Jiang, J. (2024). Current-Prediction-Controlled Quasi-Z-Source Cascaded Multilevel Photovoltaic Inverter. Electronics, 13(10), 1824. https://doi.org/10.3390/electronics13101824





