An Enhanced Power Allocation Strategy for Microgrids Considering Frequency and Voltage Restoration
Abstract
:1. Introduction
2. Microgrid and Issues
2.1. Droop Control in Microgrids
- (1)
- When imbalance and nonlinear loads are connected to the microgrid, imbalance and harmonic power will be generated, which also need to be properly shared.
- (2)
- Real power sharing is a kind of power allocation strategy without considering economic factors of DG units. It mainly considers the operation of inverters.
- (3)
- Droop control has static errors in the frequency and voltage magnitude control. The influence is small in islanded mode, but large in the mode-switching process.
2.2. Power Sharing Analysis
2.3. Preliminaries on Consensus Algorithm
3. Consensus-Based Control Strategy
3.1. I-H Regulator for Imbalance and Harmonic Power Sharing
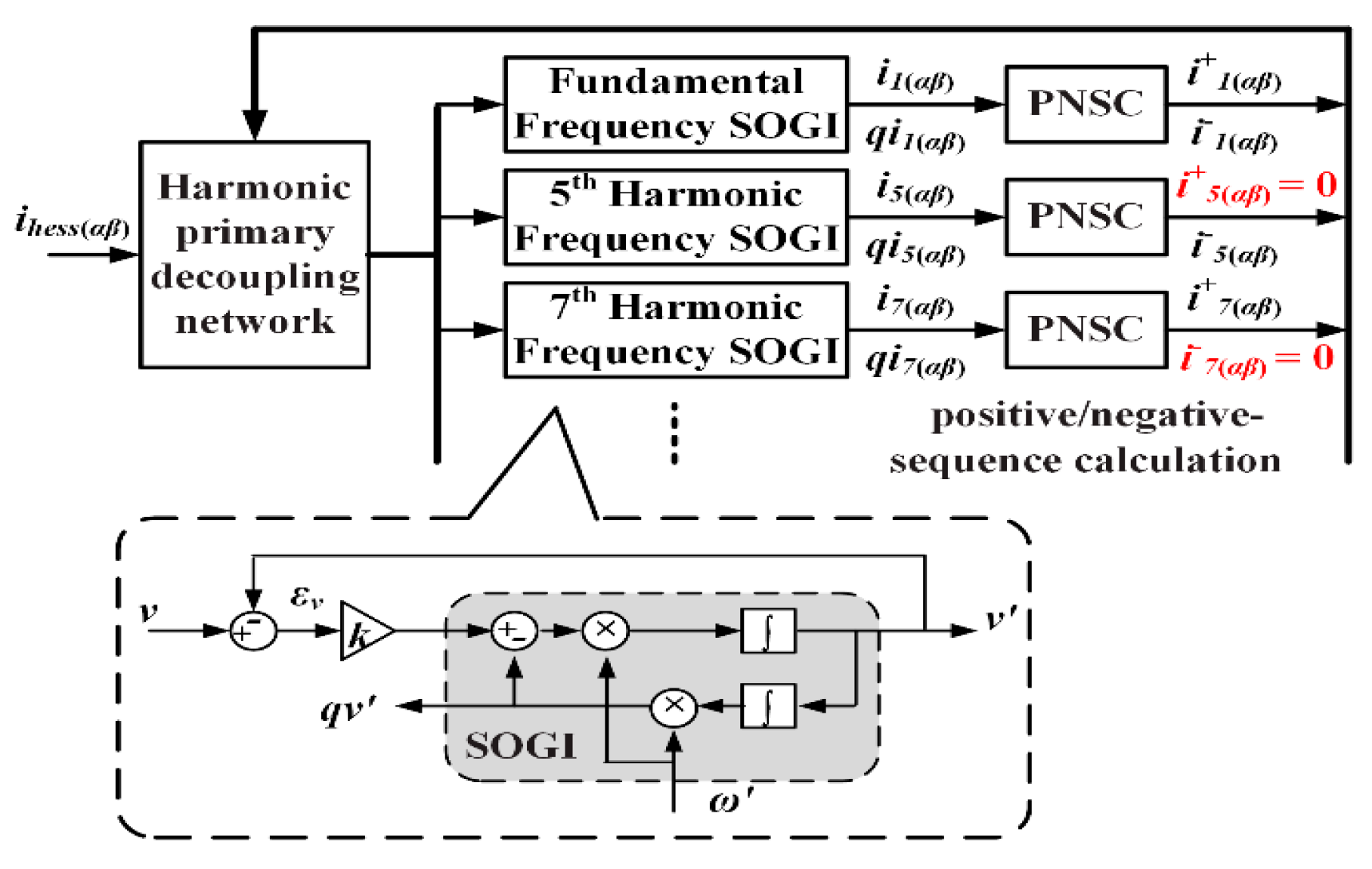
3.1.1. Imbalance and Harmonic Power Detection
3.1.2. Virtual Impedance Control
3.2. P-F Regulator for Real Power Allocation and Frequency Restoration
3.3. Q-V Regulator for Reactive Power Sharing and Voltage Restoration
3.4. Overall Control Diagram
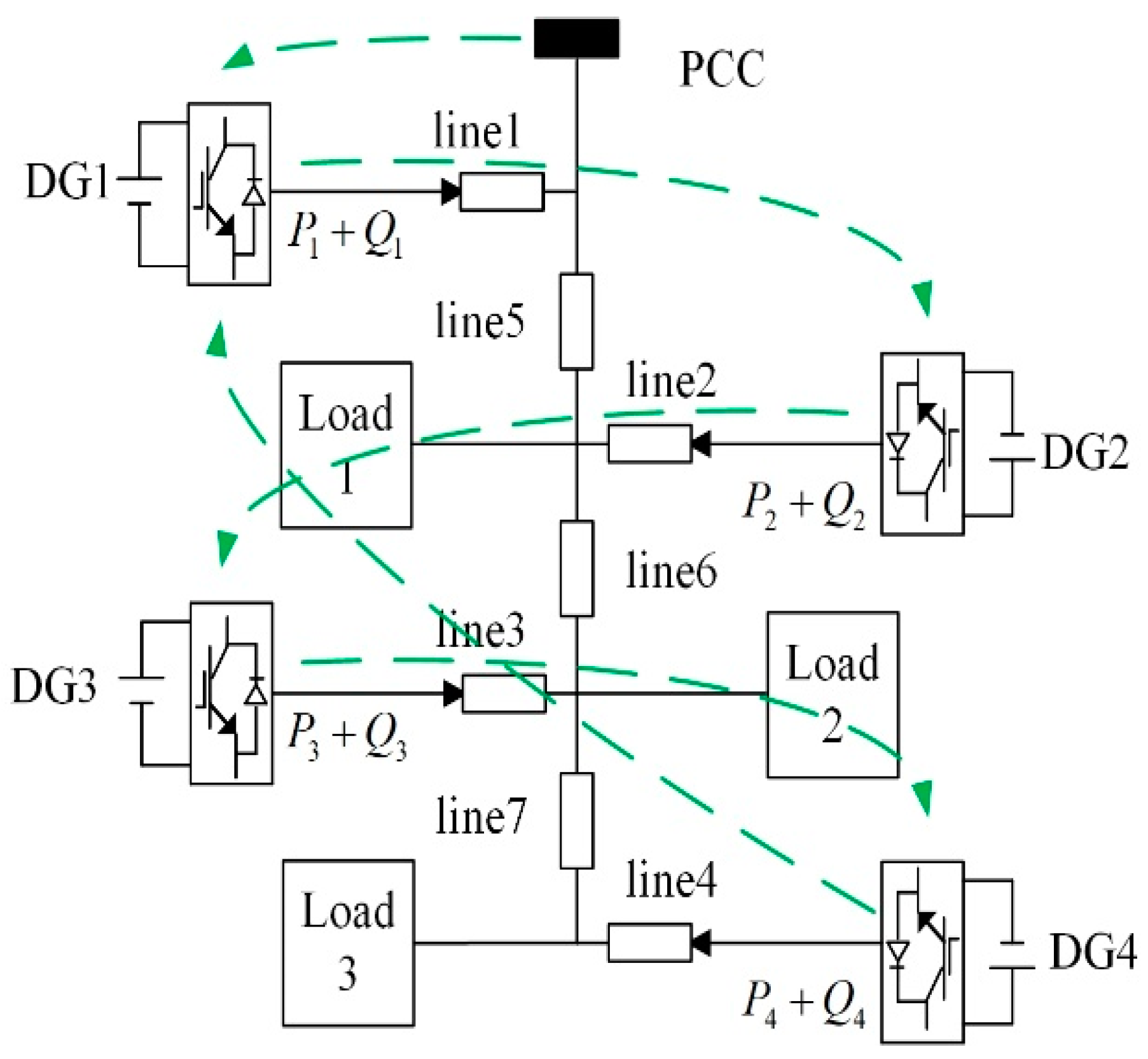
4. Simulation Results
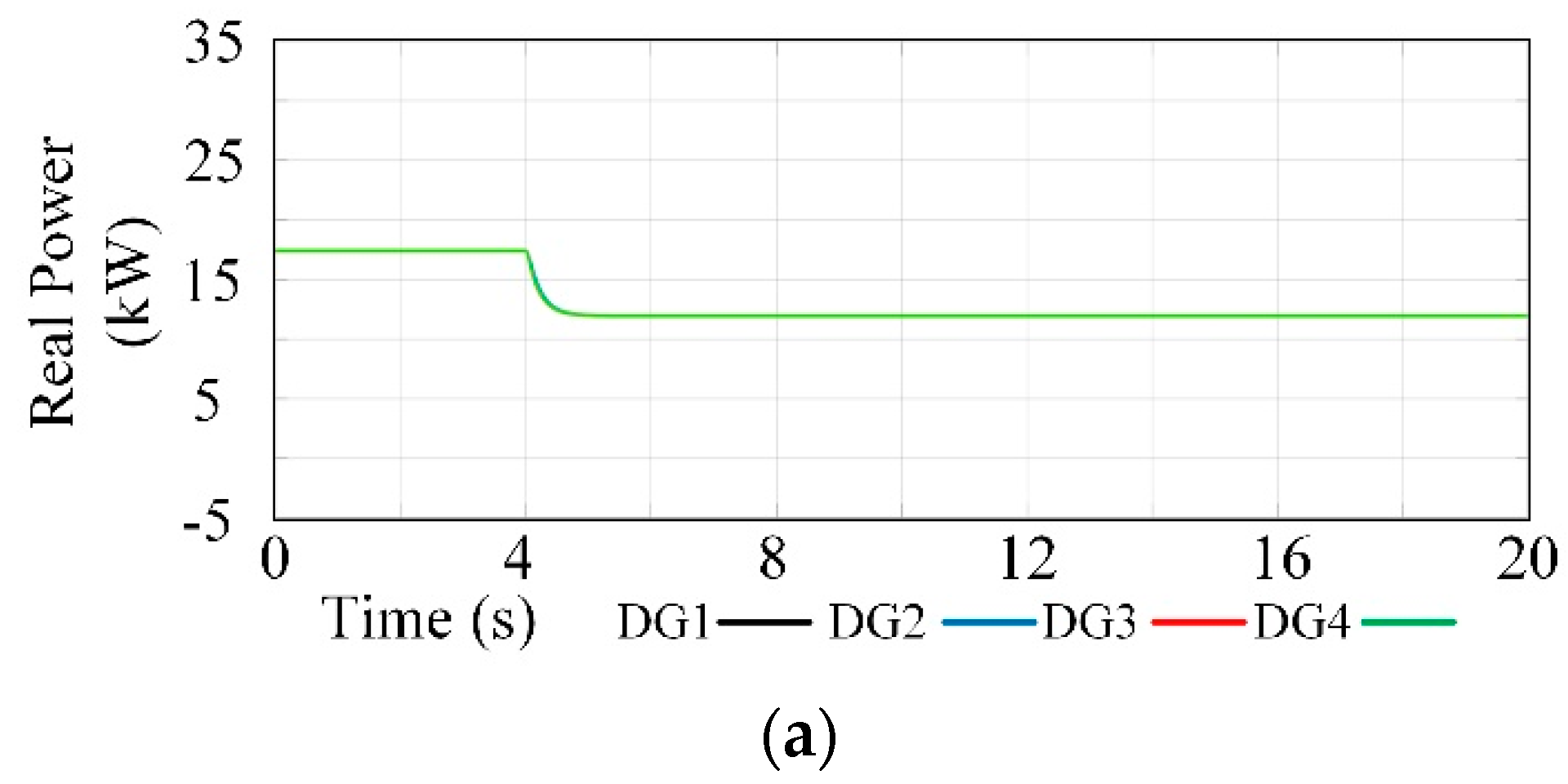
4.1. Economic Operation Test
- (1)
- Case 1: Traditional droop control method:
- (2)
- Case 2: Consensus-based control strategy:
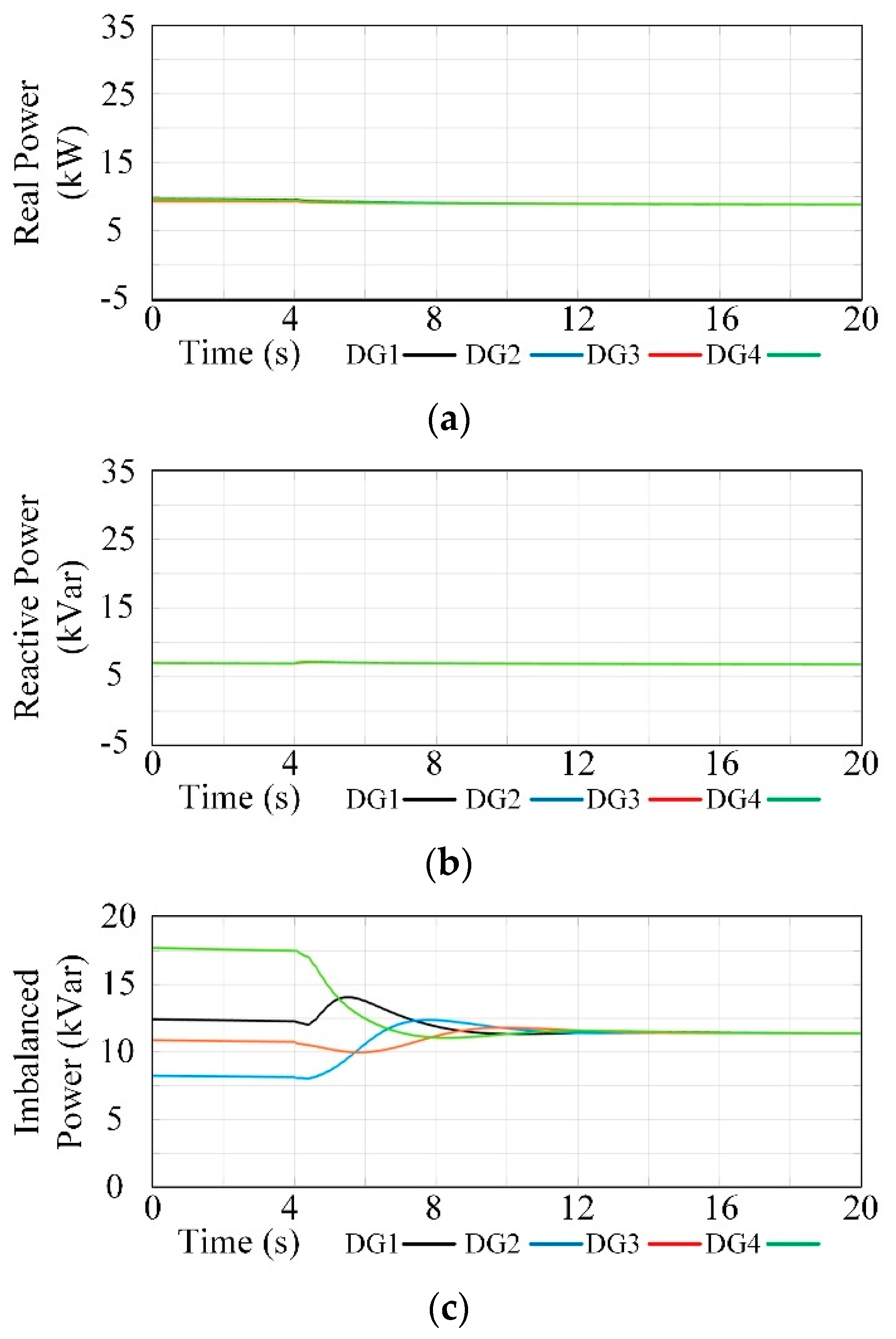
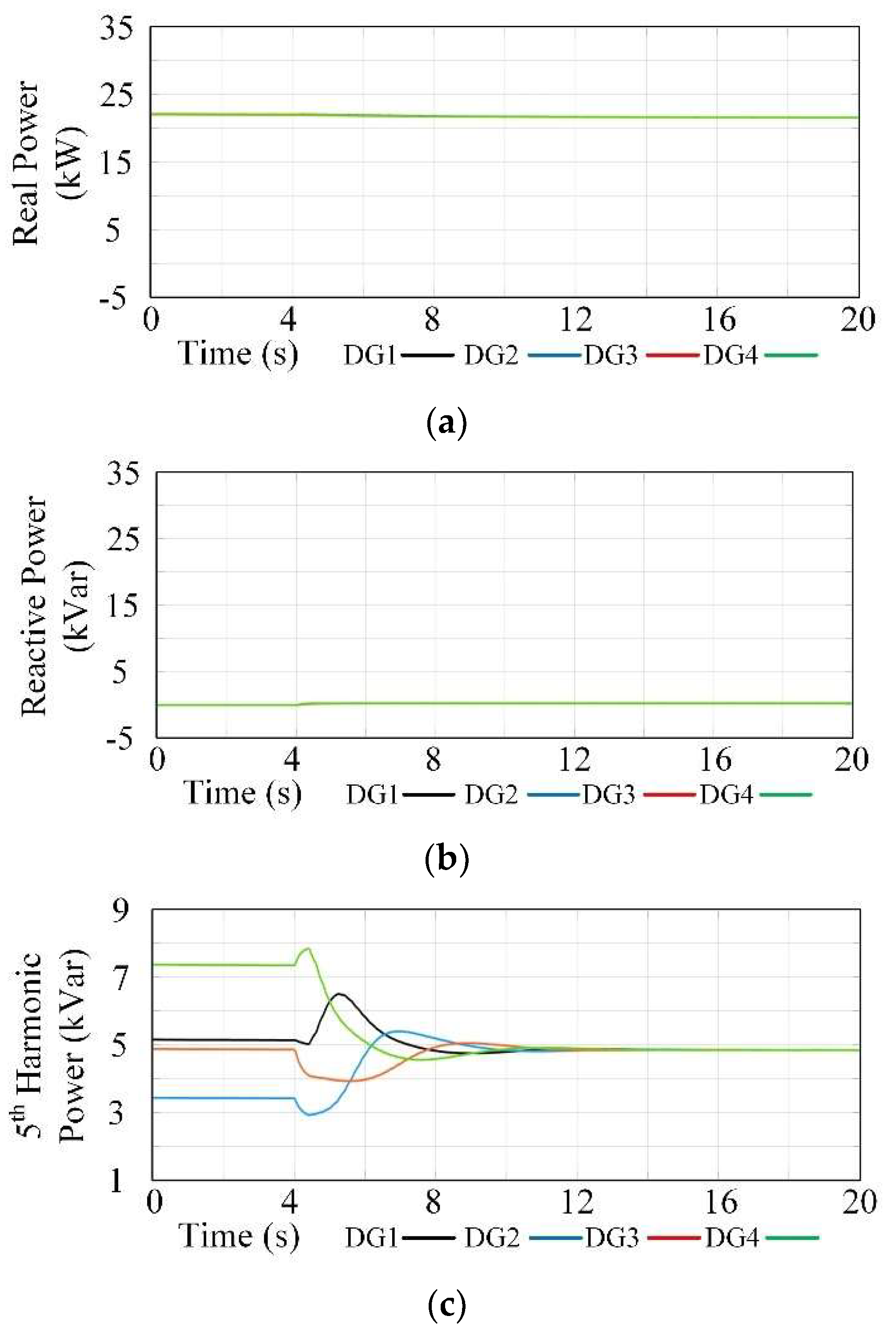
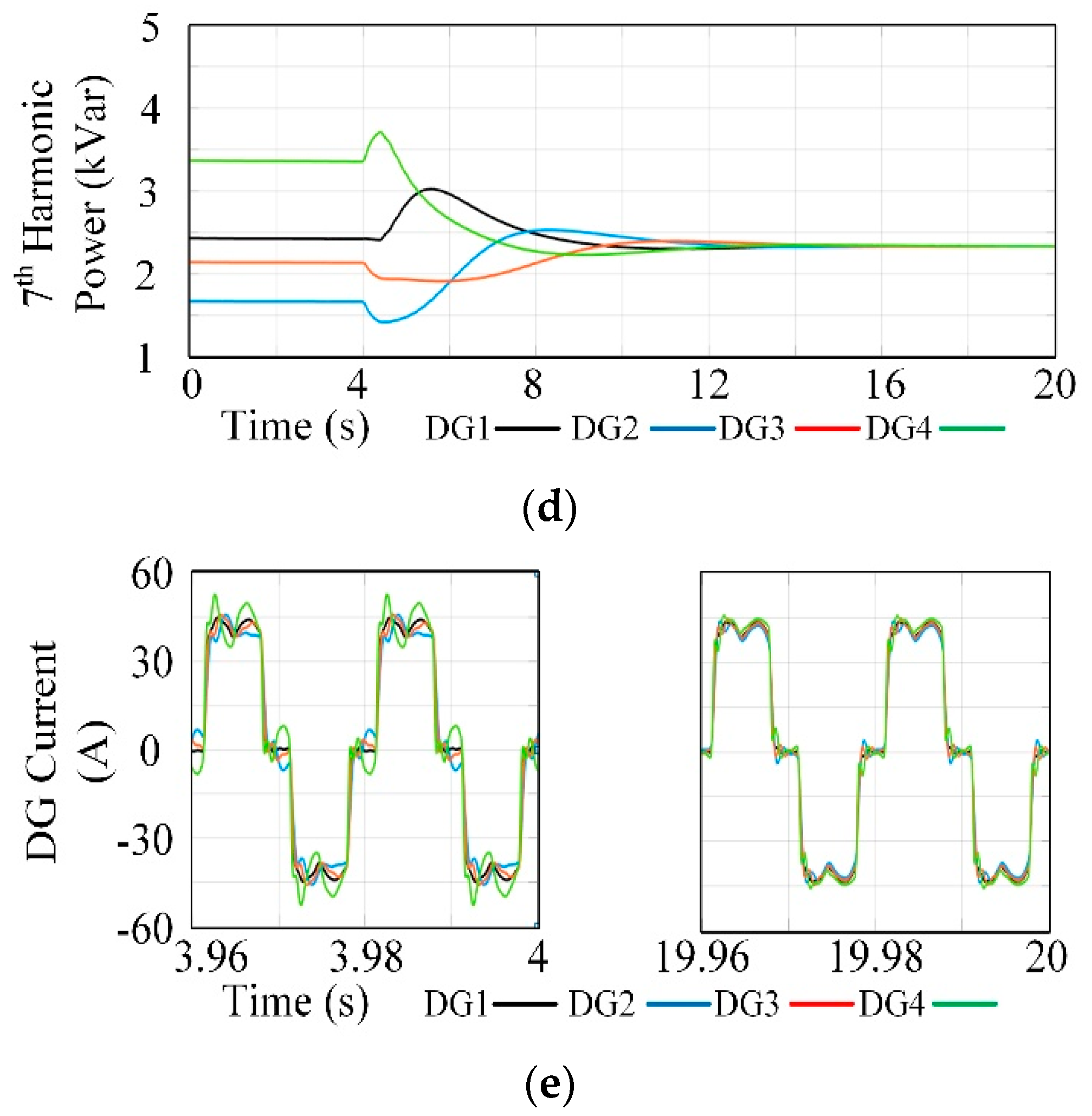
4.2. Current Sharing Test
- (1)
- Case 3: Imbalanced Power Sharing:
- (2)
- Case 4: Harmonic power sharing
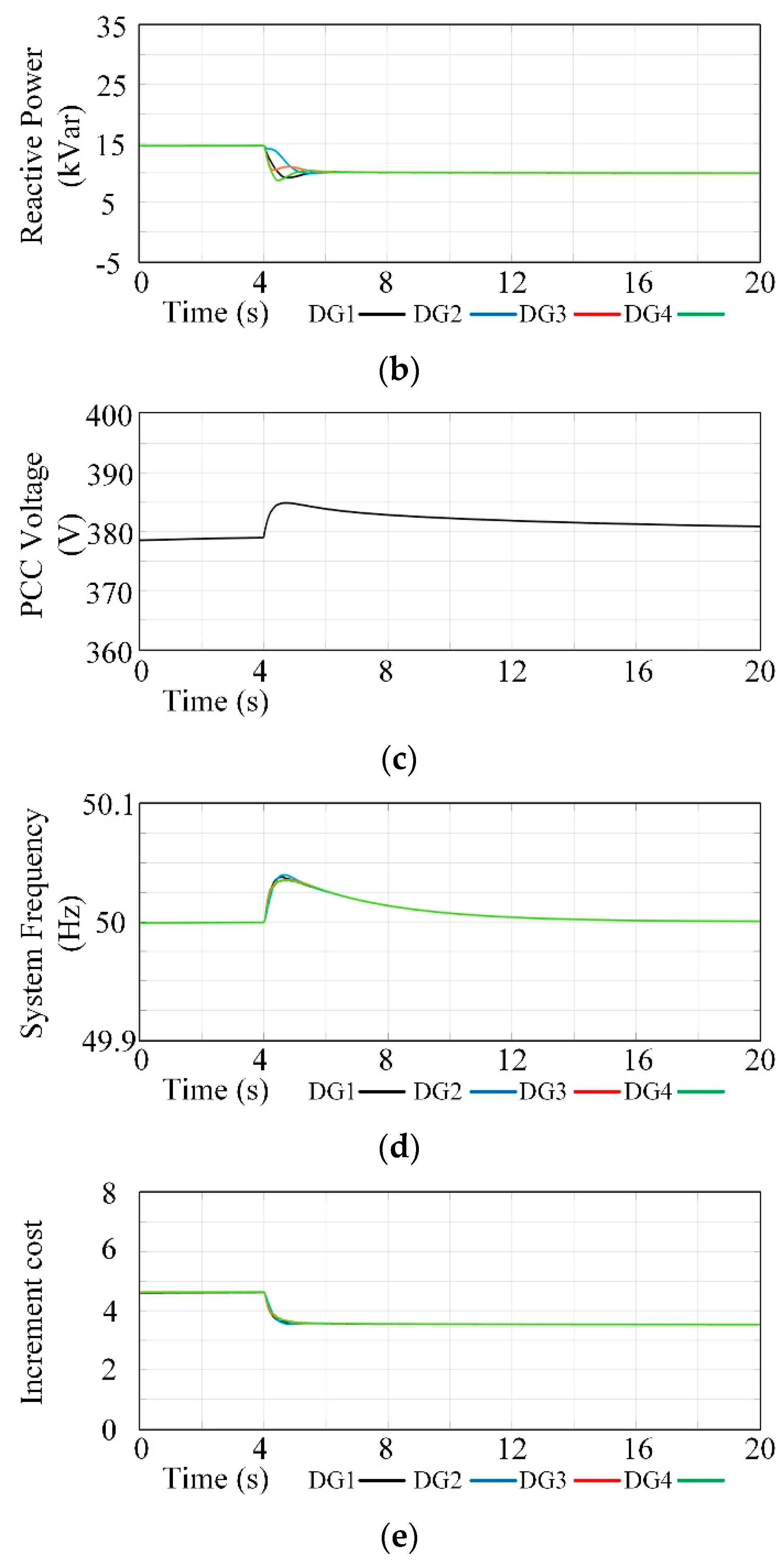
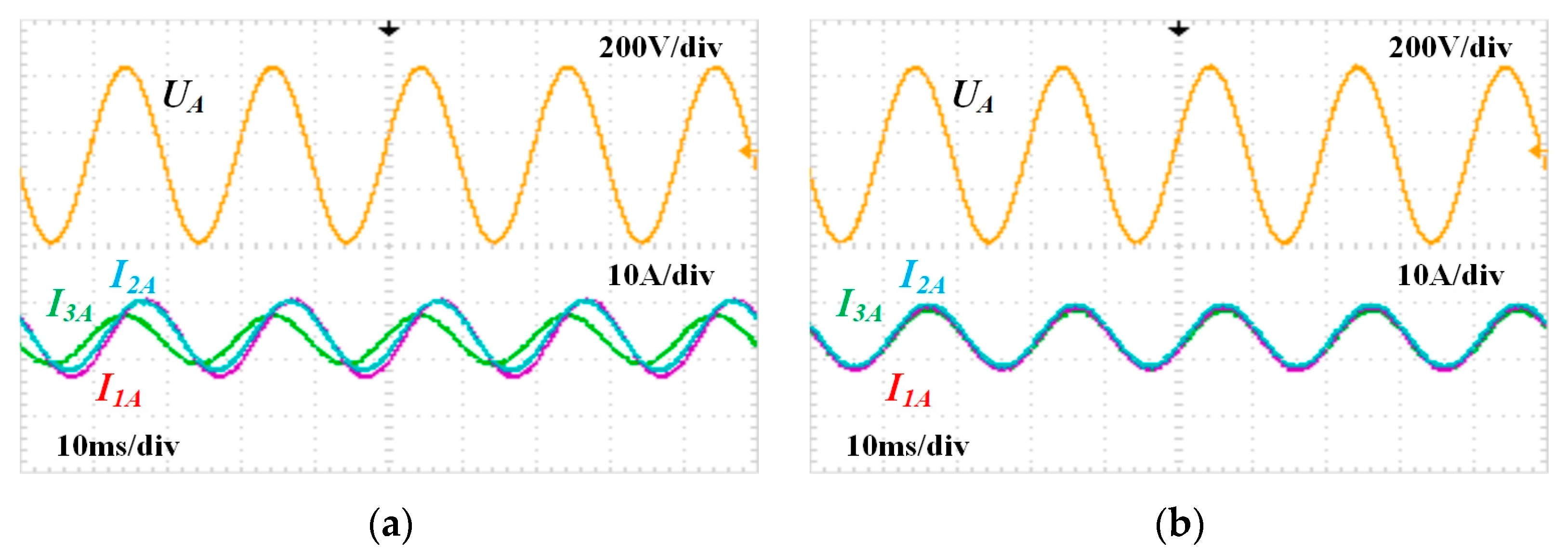
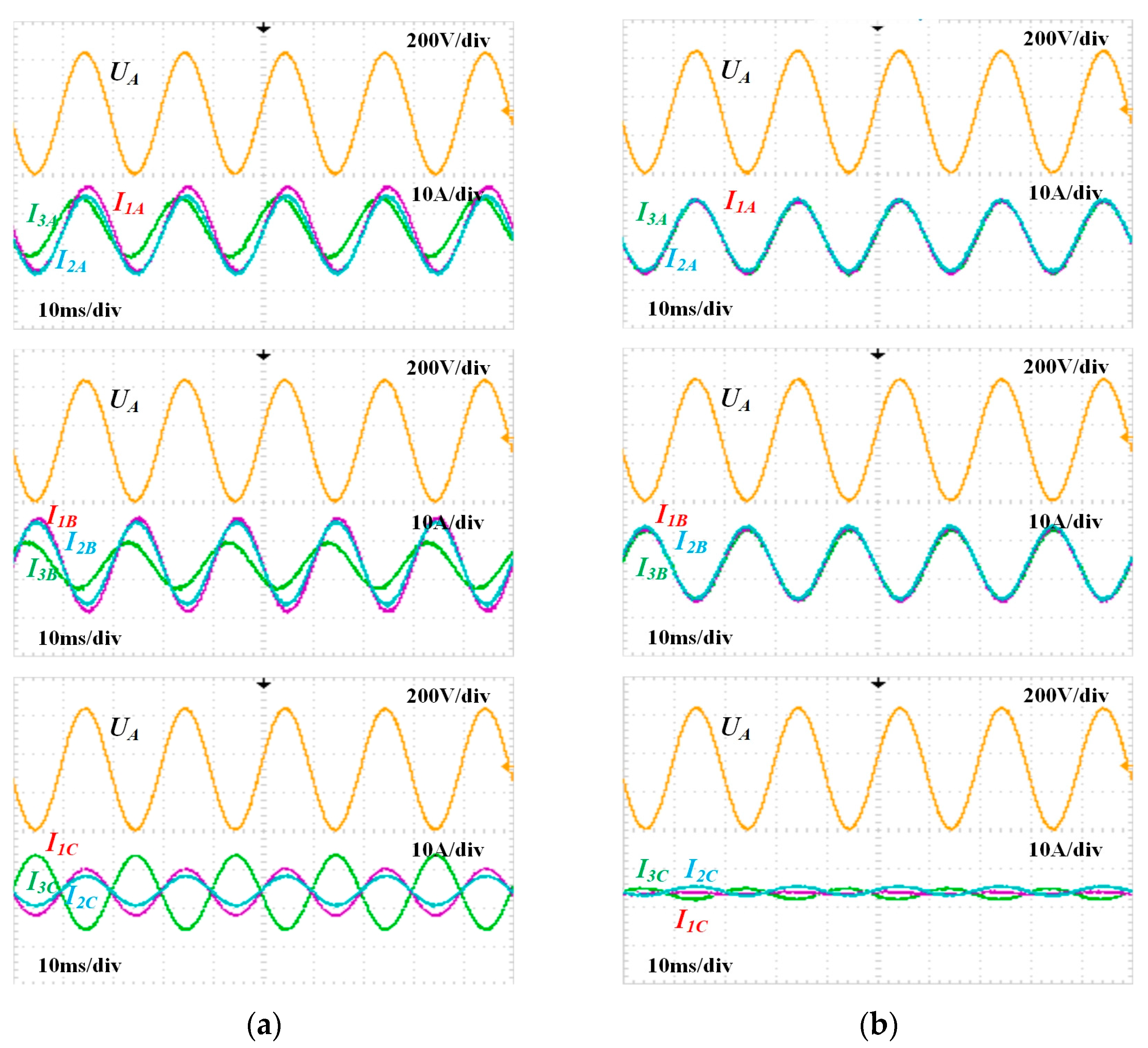
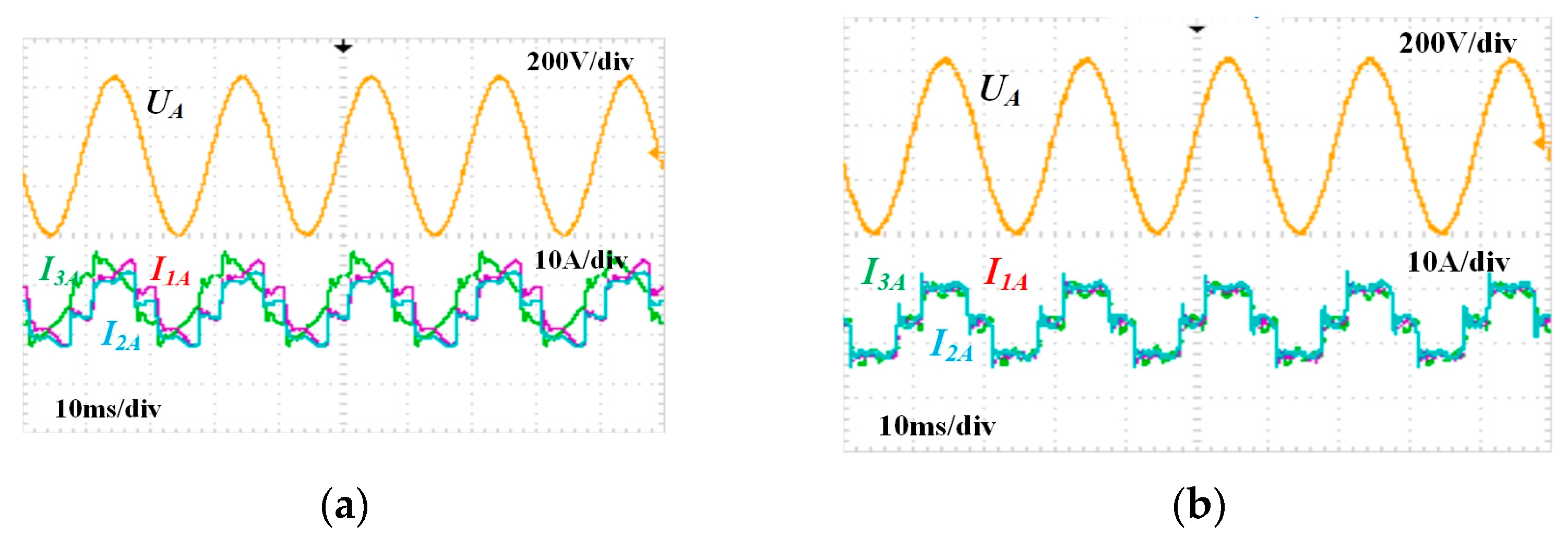
5. Experimental Results
- (1)
- Case 1: Reactive Power Sharing:
- (2)
- Case 2: Imbalanced Power Sharing:
- (3)
- Case 3: Harmonic Power Sharing:
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DG | Distributed Generation |
| SOGI | Second-order Generalized Integrator |
| PCC | Point Of Common Coupling |
| MGCC | Management Of Microgrid Central Controller |
| SCN | Sparse Communication Network |
| EIP | Equal Increment Principle |
| STS | Static Transfer Switch |
| PNSC | Positive/Negative Sequence Calculation |
| PR | Proportional Resonance |
References
- Yin, M.; Li, K.; Yu, J. A data-driven approach for microgrid distributed generation planning under uncertainties. Appl. Energy 2022, 309, 118429. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, X.; Liu, F.; Shi, R.; Yu, C.; Cao, R. A reactive power sharing strategy of VSG based on virtual capacitor algorithm. IEEE Trans. Ind. Electron. 2017, 64, 7520–7531. [Google Scholar] [CrossRef]
- Xiong, L.; Liu, X.; Liu, Y.; Zhuo, F. Modeling and stability issues of voltage-source converter dominated power systems: A review. CSEE J. Power Energy Syst. 2022, 8, 1530–1549. [Google Scholar]
- Liu, X.; Du, Z.; Tan, Y.; Liu, Y. Voltage Optimization Control Strategy for Islanded Microgrid Source-Grid-Load Active-Reactive Power Coordination Based on Collaborative Di-MPC. Front. Energy Res. 2022, 10, 880825. [Google Scholar] [CrossRef]
- Wong, Y.C.C.; Lim, C.S.; Rotaru, M.D.; Cruden, A.; Kong, X. Consensus Virtual Output Impedance Control Based on the Novel Droop Equivalent Impedance Concept for a Multi-Bus Radial Microgrid. IEEE Trans. Energy Convers. 2020, 35, 1078–1087. [Google Scholar] [CrossRef]
- Deng, F.; Yao, W.; Zhang, X.; Tang, Y.; Mattavelli, P. Review of Impedance-Reshaping-Based Power Sharing Strategies in Islanded AC Microgrids. IEEE Trans. Smart Grid. 2023, 14, 1692–1707. [Google Scholar] [CrossRef]
- Deng, F.; Li, Y.; Li, X.; Yao, W.; Zhang, X.; Mattavelli, P. A Decentralized Impedance Reshaping Strategy for Balanced, Unbalanced and Harmonic Power Sharing in Islanded Resistive Microgrids. IEEE Trans. Sustain. Energy 2022, 13, 743–754. [Google Scholar] [CrossRef]
- Zhu, Y.X.; Zhuo, F.; Wan, F.; Liu, B.Q.; Zhao, Y.J. A wireless load sharing strategy for islanded microgrid based on feeder current sensing. IEEE Trans. Power Electron. 2015, 30, 6706–6719. [Google Scholar] [CrossRef]
- He, J.W.; Li, Y.W. An enhanced microgrid load demand sharing strategy. IEEE Trans. Power Electron. 2012, 27, 3984–3995. [Google Scholar] [CrossRef]
- Han, H.; Liu, Y.; Sun, Y.; Su, M.; Guerrero, J.M. An improved droop control strategy for reactive power sharing in islanded microgrid. IEEE Trans. Power Electron. 2015, 30, 3133–3141. [Google Scholar] [CrossRef]
- Liu, S.; Wang, X.; Liu, P.X. Impact of communication delays on secondary frequency control in an islanded microgrid. IEEE Trans. Ind. Electron. 2015, 62, 2021–2031. [Google Scholar] [CrossRef]
- Hoang, T.V.; Lee, H. Accurate power sharing with harmonic power for islanded multi-bus microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 1286–1299. [Google Scholar] [CrossRef]
- Li, S.; Wu, J.; Agundis-Tinajero, G.D.; Chaudhary, S.; Vasquez, J.C.; Guerrero, J.M. A Hierarchical Harmonic Control Method for Wind Power Plants in Microgrids. In Proceedings of the IECON 2023-49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 16–19 October 2023; pp. 1–6. [Google Scholar]
- Chen, L.; Wang, Y.; Lu, X.; Zheng, T.; Wang, J.; Mei, S. Resilient active power sharing in autonomous microgrids using pinning-consensus-based distributed control. IEEE Trans. Smart Grid. 2019, 10, 6802–6811. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, W.; Zhang, B. A fully distributed power dispatch method for fast frequency recovery and minimal generation cost in autonomous microgrids. IEEE Trans. Smart Grid. 2016, 7, 19–31. [Google Scholar] [CrossRef]
- Xiong, L.; Liu, L.; Liu, X.; Liu, Y. Frequency trajectory planning based strategy for improving frequency stability of droop-controlled inverter based standalone power systems. IEEE J. Emerg. Sel. Top. Circuits Syst. 2021, 11, 176–187. [Google Scholar] [CrossRef]
- Schiffer, J.; Seel, T.; Raisch, J.; Sezi, T. Voltage stability and reactive power sharing in inverter-based microgrids with consensus based distributed voltage control. IEEE Trans. Control Syst. Technol. 2016, 24, 96–109. [Google Scholar] [CrossRef]
- Lai, J.; Lu, X.; Li, X.; Tang, R. Distributed multiagent-oriented average control for voltage restoration and reactive power sharing of autonomous microgrids. IEEE Access 2018, 6, 25551–25561. [Google Scholar] [CrossRef]
- Lu, J.; Zhao, M.; Golestan, S.; Dragicevic, T.; Pan, X.; Guerrero, J.M. Distributed Event-Triggered Control for Reactive, Unbalanced, and Harmonic Power Sharing in Islanded AC Microgrids. IEEE Trans. Ind. Electron. 2022, 69, 1548–1560. [Google Scholar] [CrossRef]
- He, J.; Li, Y.W.; Blaabjerg, F. An enhanced islanding microgrid reactive power, imbalance power, and harmonic power sharing scheme. IEEE Trans. Power Electron. 2015, 30, 3389–3401. [Google Scholar] [CrossRef]
- Meng, L.; Zhao, X.; Tang, F.; Dragicevic, T.; Savaghebi, M.; Vasquez, J.C.; Guerrero, J.M. Distributed voltage unbalance compensation in islanded microgrids by using dynamic consensus algorithm. IEEE Trans. Power Electron. 2016, 31, 827–838. [Google Scholar] [CrossRef]
- Guo, F.; Wen, C.; Mao, J.; Chen, J.; Song, Y.D. Distributed cooperative secondary control for voltage unbalance compensation in an islanded microgrid. IEEE Trans. Ind. Inform. 2015, 11, 1078–1088. [Google Scholar] [CrossRef]
- Zhou, J.; Kim, S.; Zhang, H.; Sun, Q.; Han, R. Consensus-based distributed control for accurate reactive, harmonic, and imbalance power sharing in microgrids. IEEE Trans. Smart Grid. 2018, 9, 2453–2467. [Google Scholar] [CrossRef]
- Tang, Z.; Hill, D.J.; Liu, T. A novel consensus-based economic dispatch for microgrids. IEEE Trans. Smart Grid 2018, 9, 3920–3922. [Google Scholar] [CrossRef]
- Zheng, Y.; Song, Y.; Hill, D.J.; Zhan, Y. Multiagent system based microgrid energy management via asynchronous consensus ADMM. IEEE Trans. Energy Conv. 2018, 33, 886–888. [Google Scholar] [CrossRef]
- Wang, R.; Li, Q.; Zhang, B.; Wang, L. Distributed consensus-based algorithm for economic dispatch in a microgrid. IEEE Trans. Smart Grid. 2019, 10, 3630–3640. [Google Scholar] [CrossRef]
- Wu, X.; Shen, C.; Iravani, R. A distributed, cooperative frequency and voltage control for microgrids. IEEE Trans. Smart Grid. 2018, 9, 2764–2776. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Auto. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Li, Z.; Duan, Z.; Chen, G.; Huang, L. Consensus of Multiagent systems and synchronization of complex networks: A unified viewpoint. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 57, 213–224. [Google Scholar]



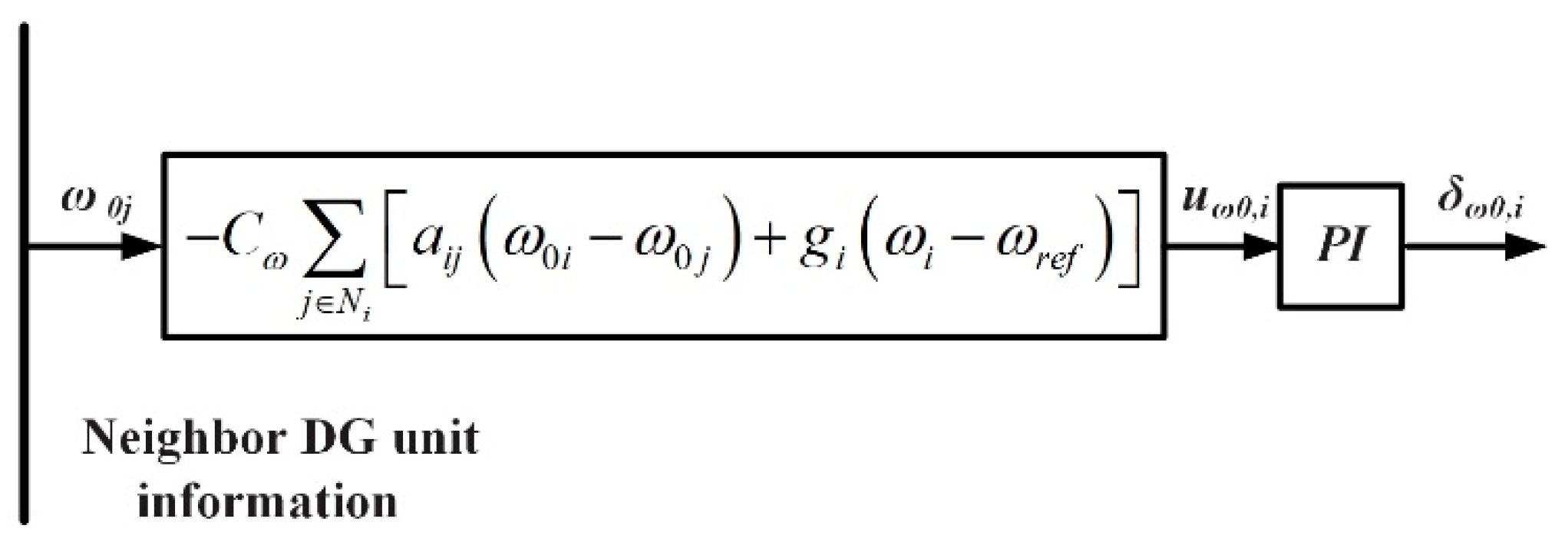





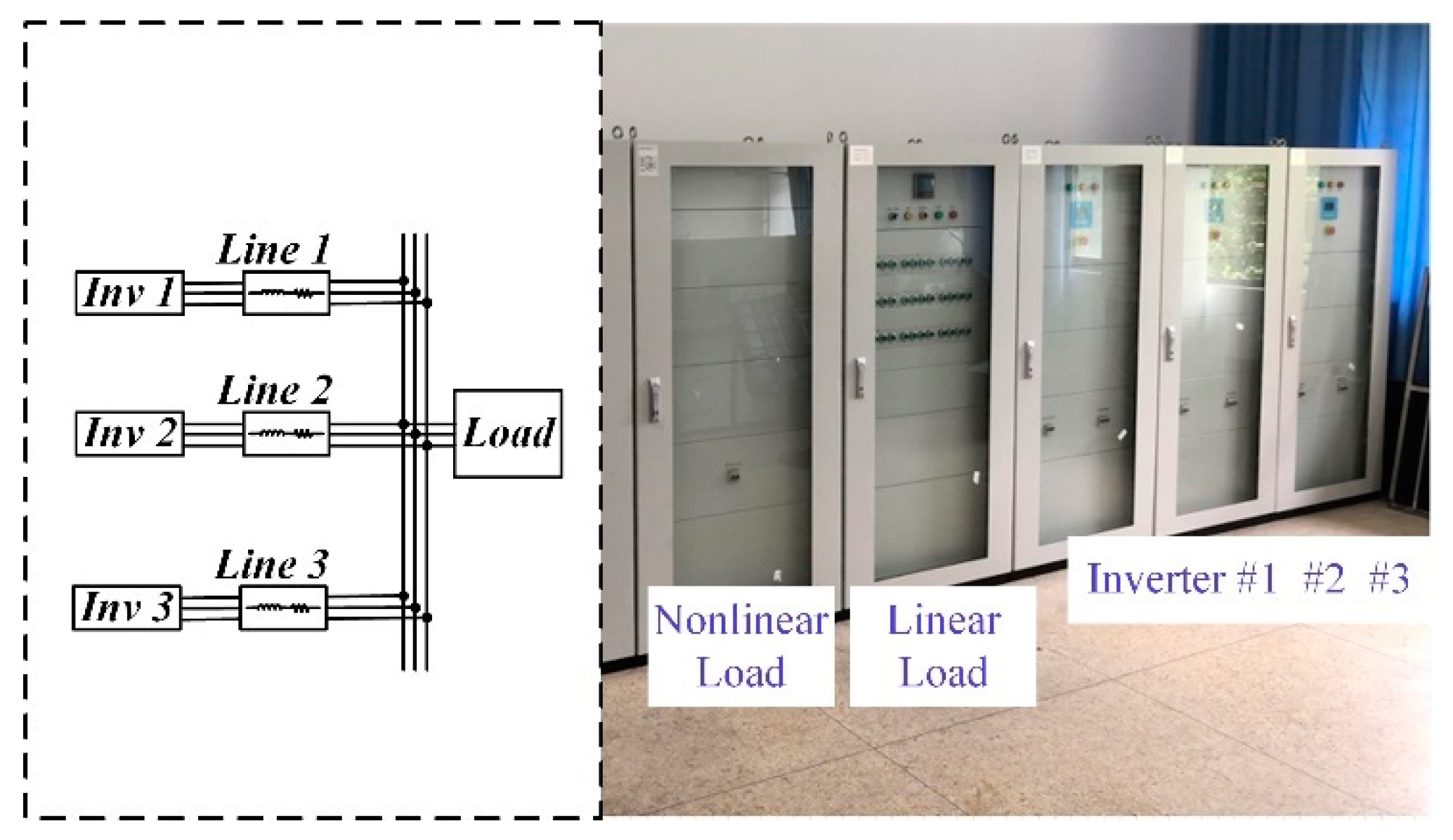
| Circuit Parameters | Values | |
|---|---|---|
| Line 1–7 | Resistance | Rf = [1 1 4 3 1 1 1] * 0.1 Ω |
| Resistance | Xf = [1 1 4 3 1 1 1] * 0.028j Ω | |
| DG 1–4 | LC Filter | Lf = 1.5 mH, Cf = 100 µF |
| Frequency | fs = 10 kHz | |
| Capacity | S = 25 kVA | |
| Load 1–3 | Real power | PL = 25 kW |
| Reactive power | QL = 20 kVar | |
| Droop | Droop Slopes | Dp = 8 × 10−6, Dq = 1 × 10−4 |
| Initial Voltage | E0 = 320 V, F0 = 50.125 Hz | |
| PR | Voltage Controller | kP = 0.1, k1h = 20, k5h = k7h = 15 |
| Current Controller | kP = 0.1 | |
| Consensus | Q regulator | kP = 4 × 10−4, kP = 1.6 × 10−3 |
| V regulator | kP = 0, kI = 0.5 | |
| P-f regulator | kP = 0, kI = 8 × 10−4 | |
| I-H regulator | kP = 0, kI = 2.5 × 10−5 | |
| Load Condition | Remarks | |
| Test 1 | Three-phase balanced Load | Remove Load2 at t = 4 s |
| Test 2 | Imbalanced Load | Remove phase C loads in Test 1 |
| Diode Rectifier | Rd = 8 Ω, Cd = 5 µF | |
| Cost Function | |
|---|---|
| DG 1 | 0.094P2 + 1.22P + 51 |
| DG 2 | 0.078P2 + 3.41P + 31 |
| DG 3 | 0.105P2 + 2.53P + 78 |
| DG 4 | 0.082P2 + 4.02P + 42 |
| Circuit Parameters | Values | |
|---|---|---|
| Feeder Line | Feeder 1 | Rf1 = 0.10 Ω |
| Feeder 2 | Rf2 = 0.05 Ω | |
| Feeder 3 | Rf3 = 0.15 Ω | |
| Inverter | LC Filter | Lf = 0.7 mH, Cf = 50 µF |
| Frequency | fs = 10 kHz | |
| Control Parameters | Values | |
| Inv 1–3 | Droop Slopes | m = 5 × 10−6, n = 5 × 10−5 |
| Initial Voltage | E0 = 315 V, F0 = 50.15 Hz | |
| Voltage Controller | kPV = 7.6, kIV = 76 | |
| Current Controller | kPI = 0.2, kII = 15 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Wu, X.; Song, Q.; Wu, H.; Zhu, Y. An Enhanced Power Allocation Strategy for Microgrids Considering Frequency and Voltage Restoration. Electronics 2024, 13, 1966. https://doi.org/10.3390/electronics13101966
Yang C, Wu X, Song Q, Wu H, Zhu Y. An Enhanced Power Allocation Strategy for Microgrids Considering Frequency and Voltage Restoration. Electronics. 2024; 13(10):1966. https://doi.org/10.3390/electronics13101966
Chicago/Turabian StyleYang, Chunguang, Xue Wu, Qichao Song, Haoyu Wu, and Yixin Zhu. 2024. "An Enhanced Power Allocation Strategy for Microgrids Considering Frequency and Voltage Restoration" Electronics 13, no. 10: 1966. https://doi.org/10.3390/electronics13101966
APA StyleYang, C., Wu, X., Song, Q., Wu, H., & Zhu, Y. (2024). An Enhanced Power Allocation Strategy for Microgrids Considering Frequency and Voltage Restoration. Electronics, 13(10), 1966. https://doi.org/10.3390/electronics13101966






