Design and Optimization of Coil for Transcutaneous Energy Transmission System
Abstract
:1. Introduction
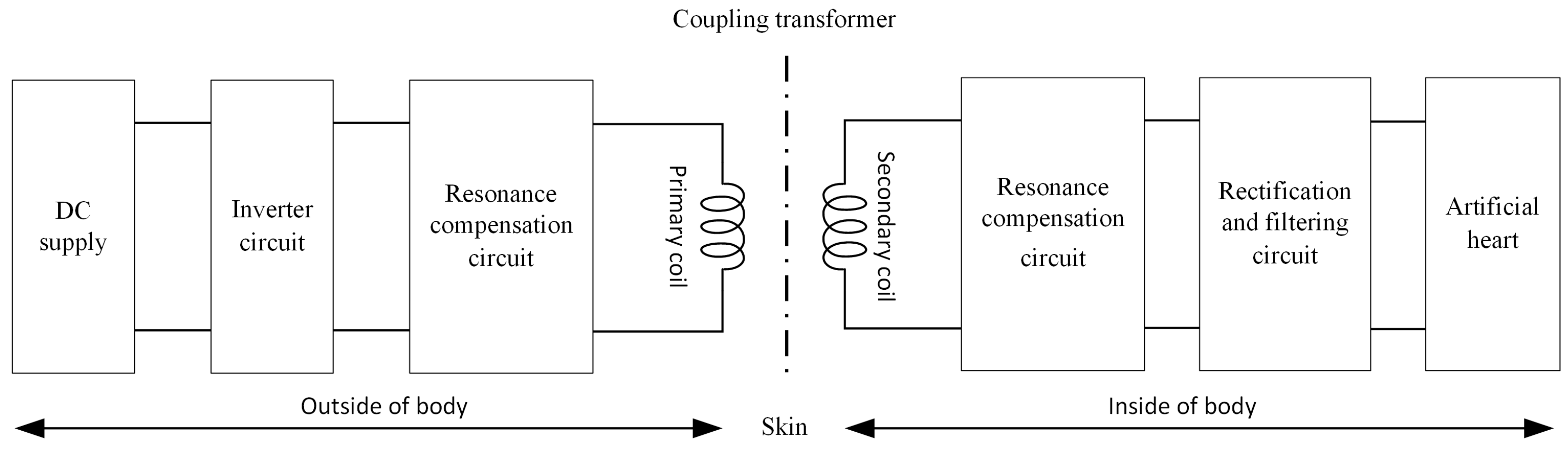
2. System Theoretical Analysis
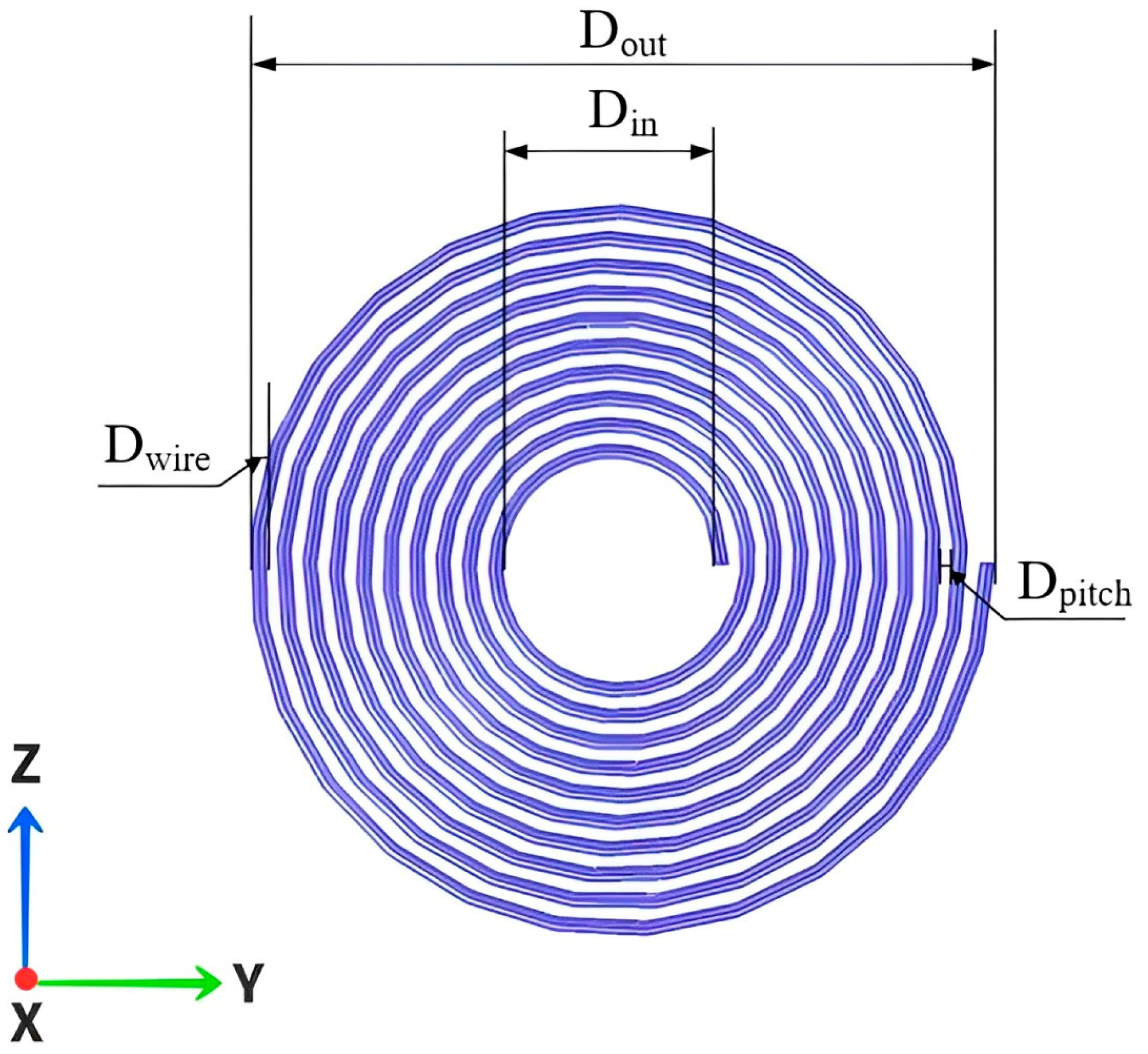
3. Optimization of Coils
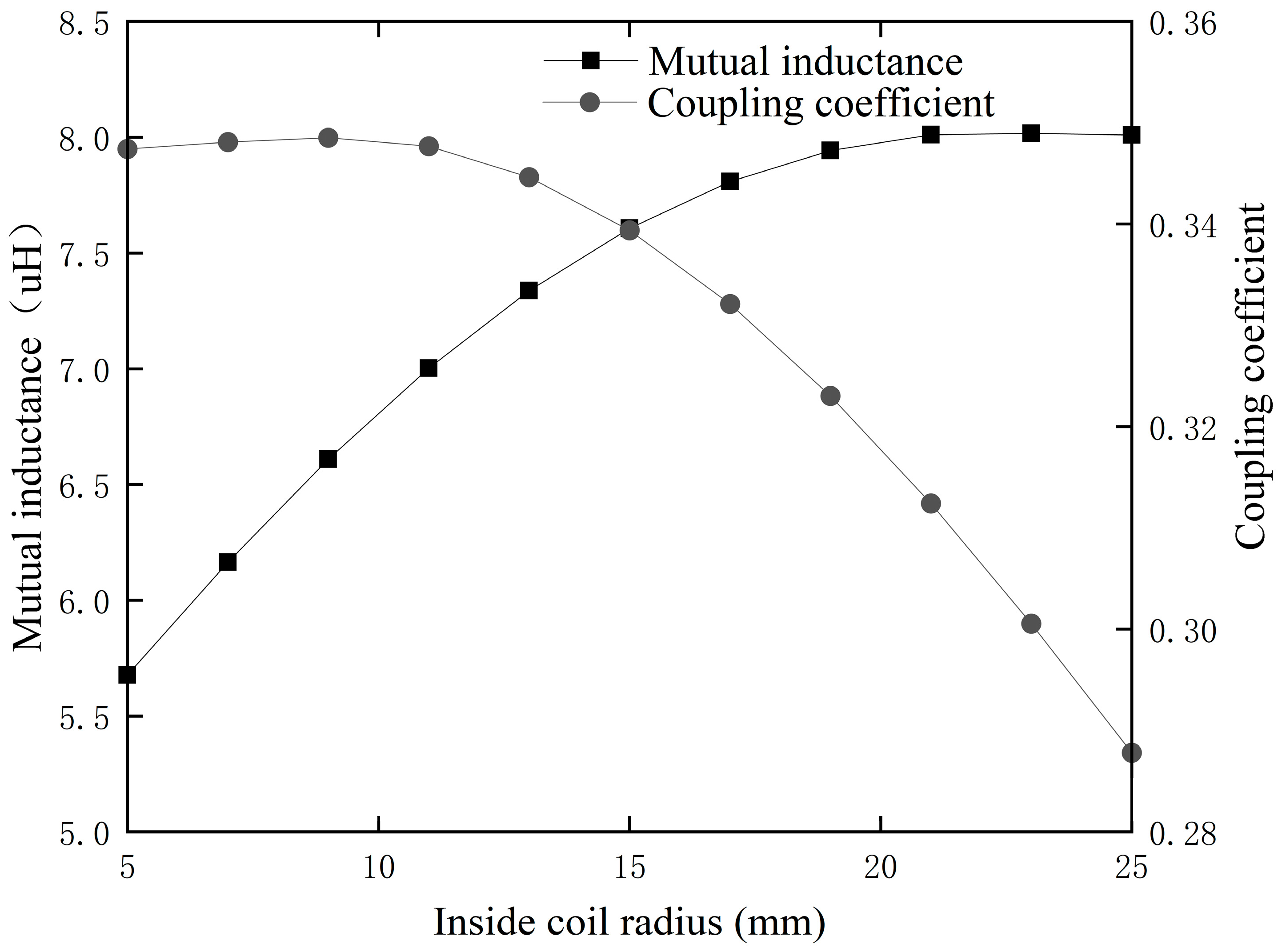
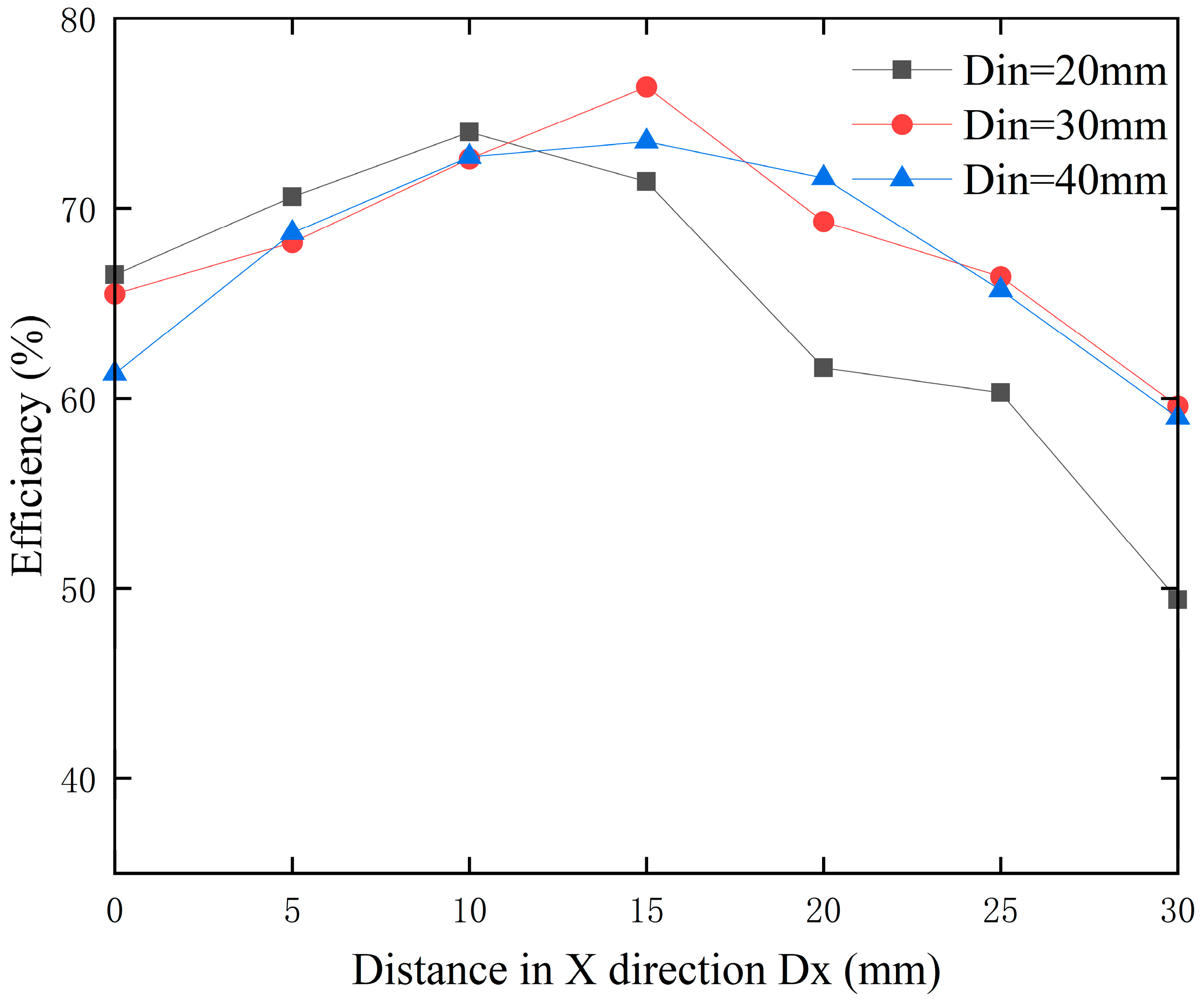
3.1. Optimal Coil Inner Diameter
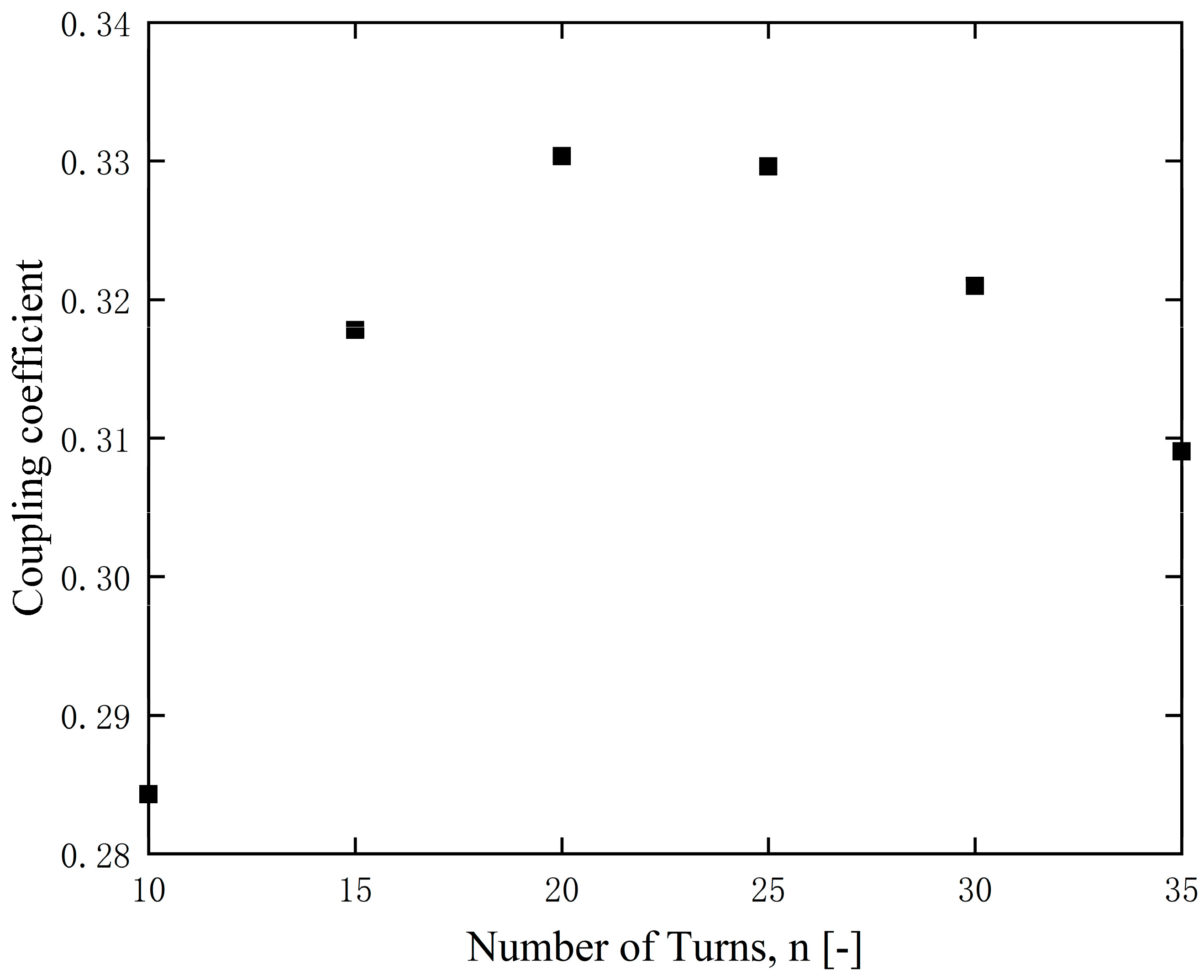
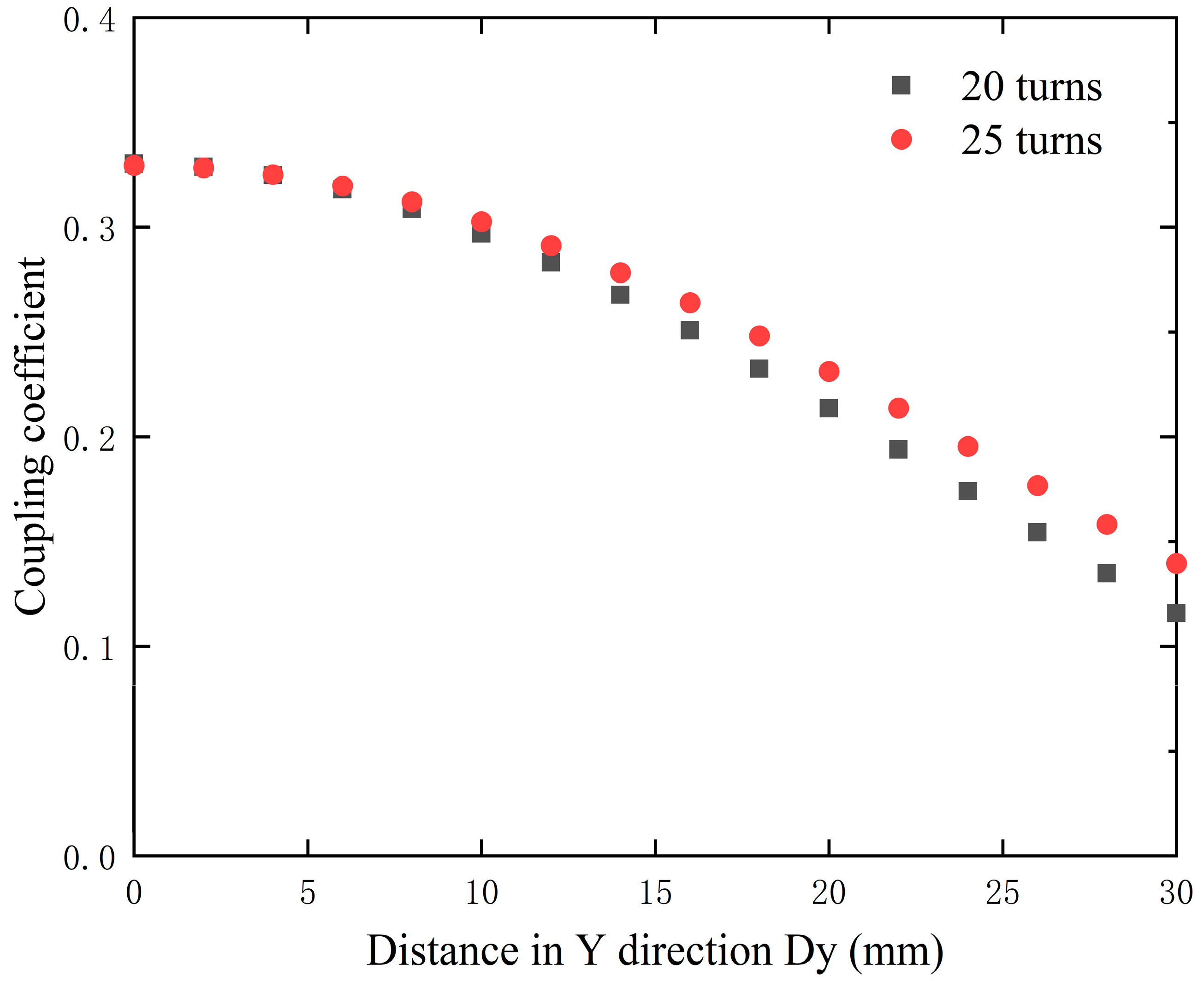
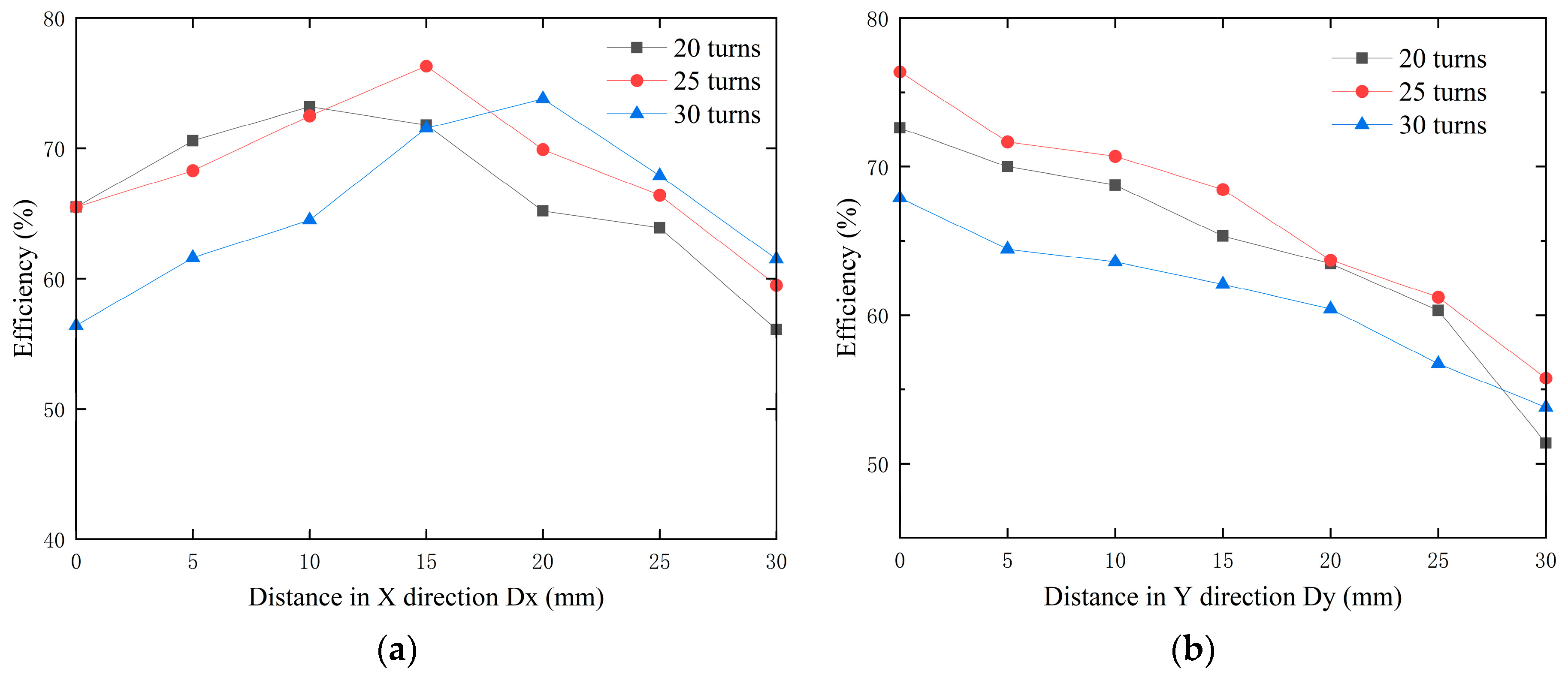
3.2. Optimal Coil Turn
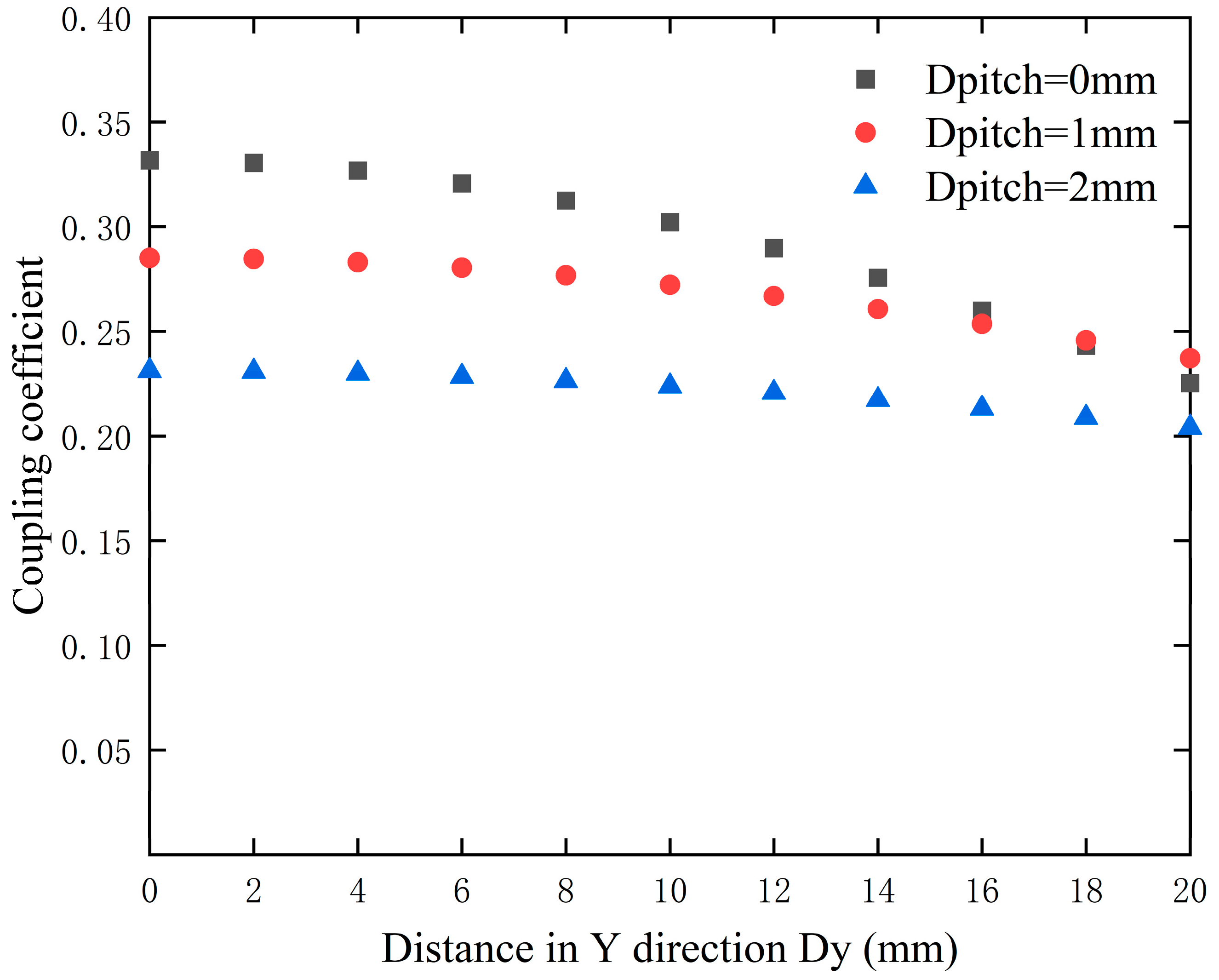
3.3. Optimal Pitch of Turns
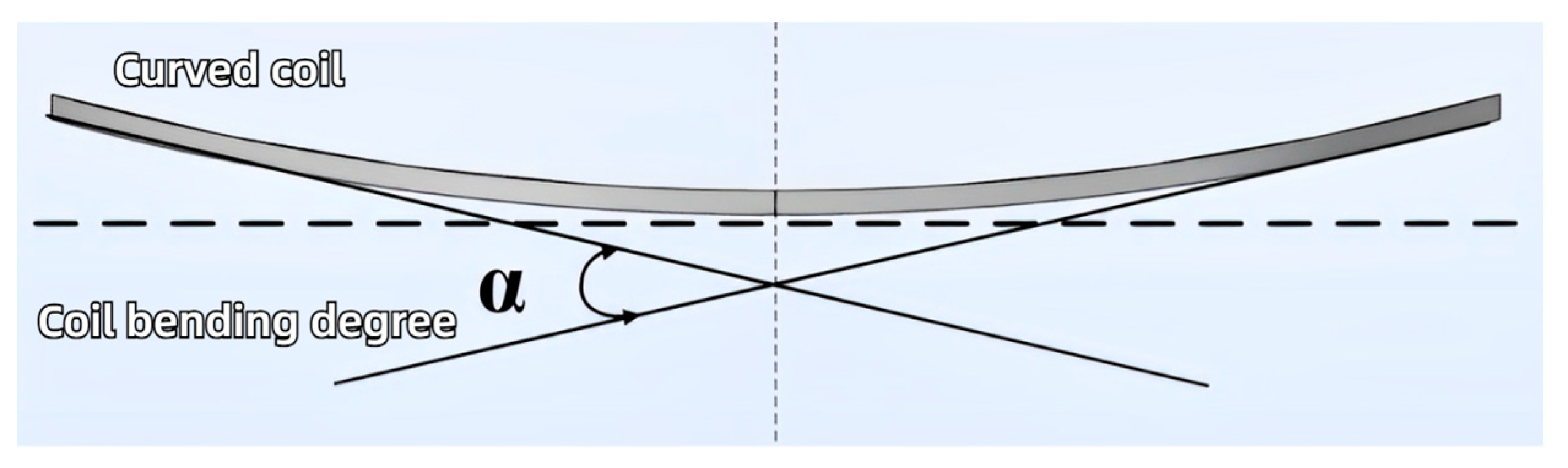
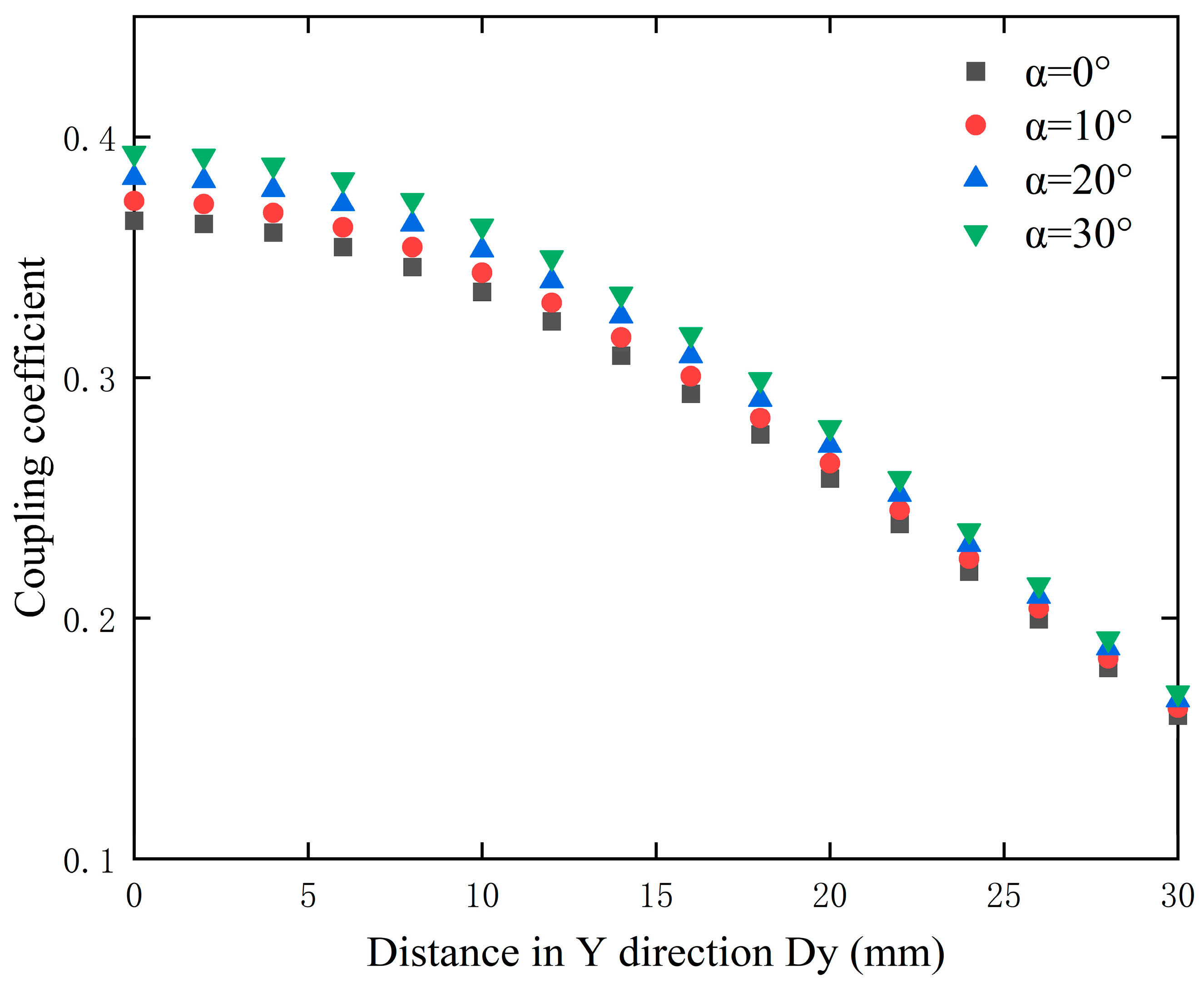
3.4. Optimal Bend Degree
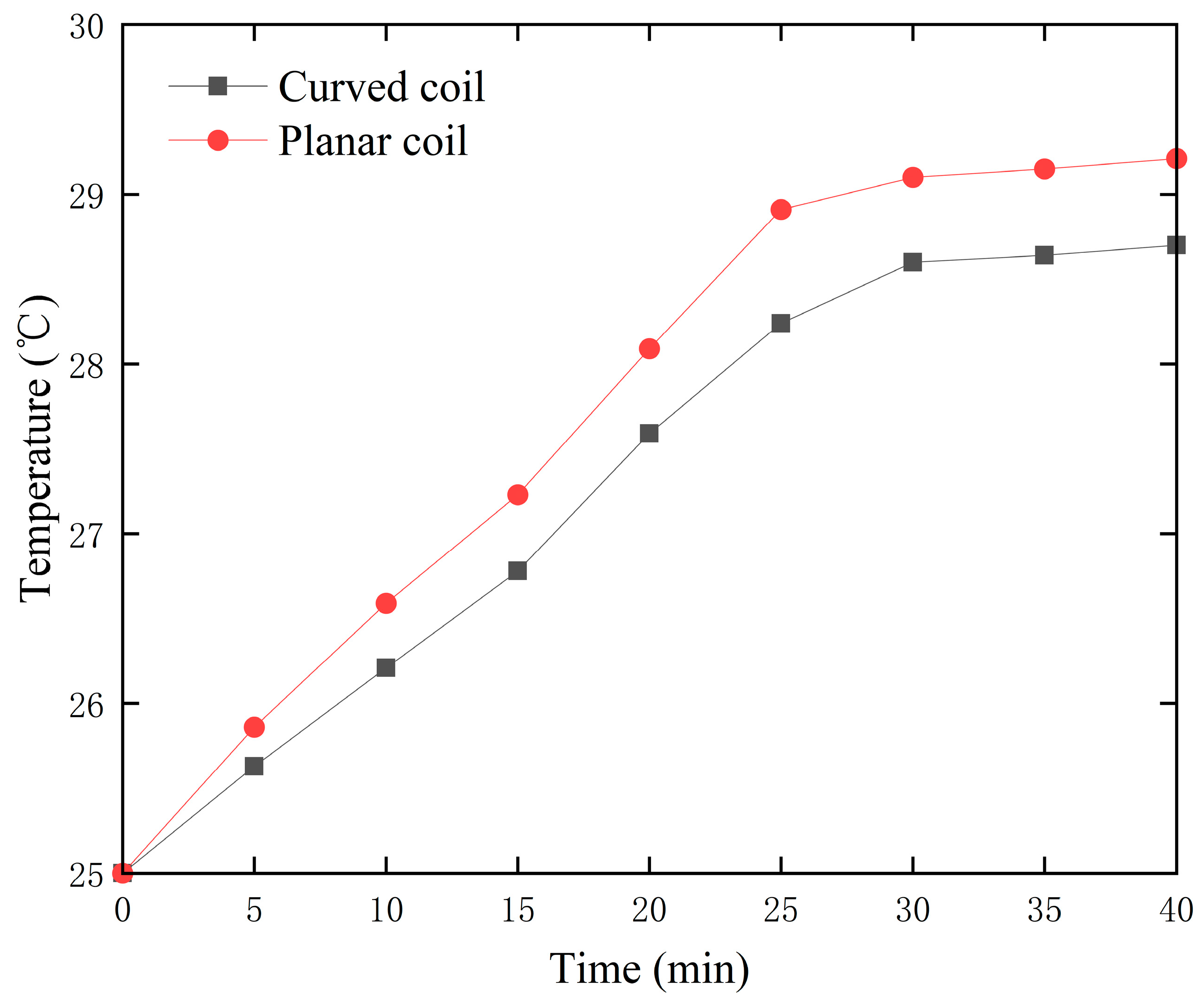
3.5. Temperature Simulation of Coupling Coils
4. Experimental Verification
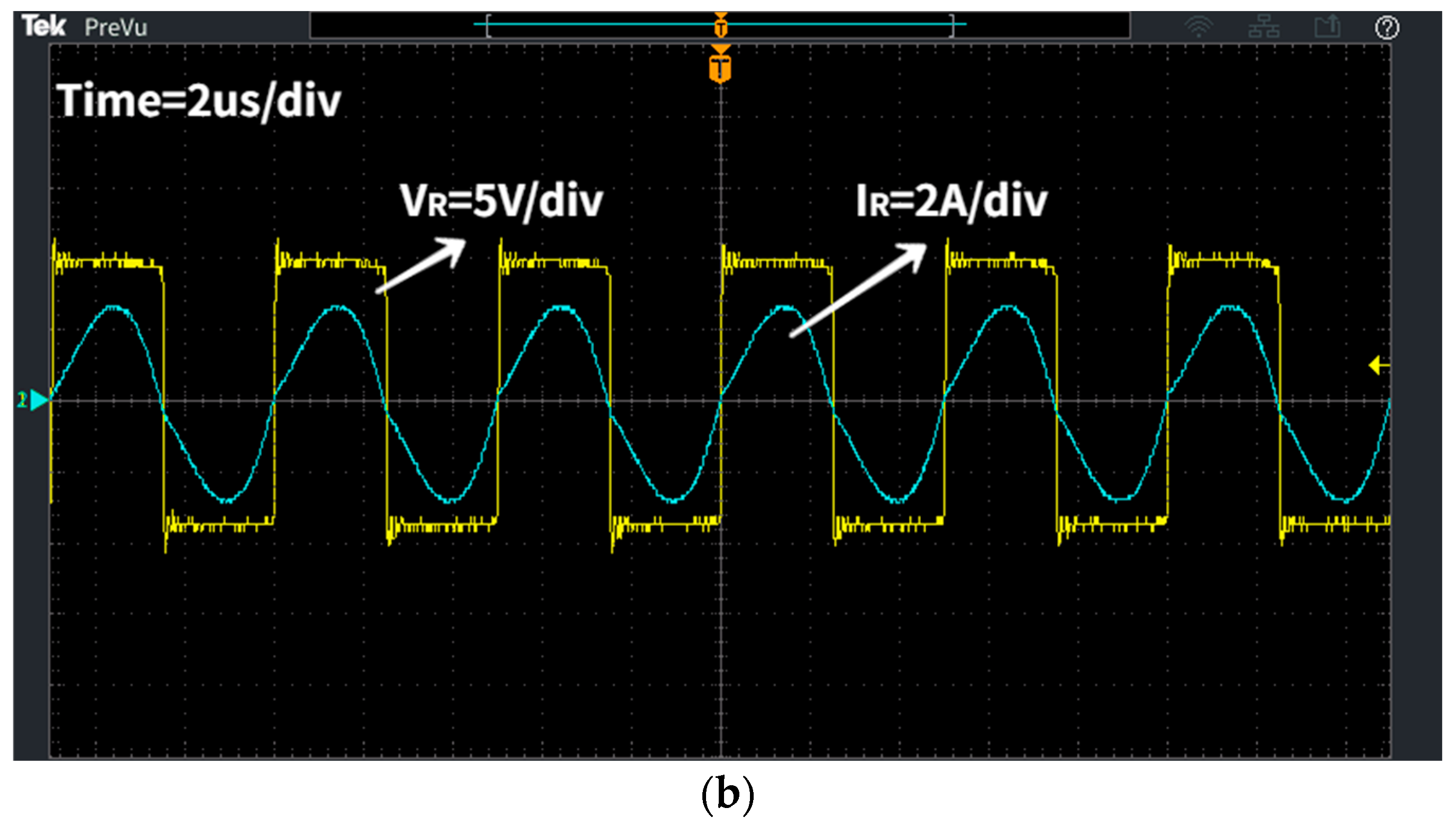
4.1. Experimental Platform
4.2. Result and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alnajar, A.; Frazier, O.H. The State of Artificial Heart Therapy. Tex. Heart Inst. J. 2019, 46, 77–79. [Google Scholar] [CrossRef] [PubMed]
- Itagaki, S.; Toyoda, N.; Egorova, N.; Sun, E.R.; Lee, T.M.Y.; Boateng, P.; Gibson, G.; Moss, N.; Mancini, D.; Adams, D.H.; et al. Total artificial heart implantation as a bridge to transplantation in the United States. J. Thorac. Cardiovasc. Surg. 2024, 167, 15. [Google Scholar] [CrossRef] [PubMed]
- Kothari, P.D.; Ahmad, D.; Topaz, S.R. The NASA artificial heart driver: A pneumatic power source developed for Willem Kolff's artificial heart program. Artif. Organs 2023, 47, 1539–1543. [Google Scholar] [CrossRef] [PubMed]
- Caraffa, R.; Bejko, J.; Carrozzini, M.; Bifulco, O.; Tarzia, V.; Lorenzoni, G.; Bottigliengo, D.; Gregori, D.; Castellani, C.; Bottio, T.; et al. A Device Strategy-Matched Comparison Analysis among Different Intermacs Profiles: A Single Center Experience. J. Clin. Med. 2022, 11, 4901. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.R.; Pavuluri, S.K.; Cummins, G.; Desmulliez, M.P.Y. Wireless Power Transfer Techniques for Implantable Medical Devices: A Review. Sensors 2020, 20, 3487. [Google Scholar] [CrossRef]
- Tsai, C.-C.; Chen, B.-S.; Tsai, C.-M. Design of wireless transcutaneous energy transmission system for totally artificial hearts. In Proceedings of the IEEE APCCAS 2000. 2000 IEEE Asia-Pacific Conference on Circuits and Systems. Electronic Communication Systems, Tianjin, China, 4–6 December 2020; pp. 646–649. [Google Scholar]
- Liang, C.; Zhang, Y.C.; Li, Z.G.; Yuan, F.; Yang, G.; Song, K. Coil Positioning for Wireless Power Transfer System of Automatic Guided Vehicle Based on Magnetic Sensing. Sensors 2020, 20, 5304. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.-K.; Lee, D.-J.; Park, S.-J. The effect of boost coil and alignment of transmitting and receiving coils on transmission efficiency in EV wireless power transfer systems. Energies 2023, 16, 3213. [Google Scholar] [CrossRef]
- Huang, W.C.; Huang, J.Y.; Hu, Y.; Zhu, Y.Q.; Chang, Y.F. Design and Parameter Optimization of Double-Mosquito Combination Coils for Enhanced Anti-Misalignment Capability in Inductive Wireless Power Transfer Systems. Electronics 2024, 13, 838. [Google Scholar] [CrossRef]
- Qing, X.D.; Li, Z.J.; Wu, X.Y.; Liu, Z.; Zhao, L.; Su, Y.G. A Hybrid Wireless Power Transfer System With Constant and Enhanced Current Output Against Load Variation and Coupling Misalignment. IEEE Trans. Power Electron. 2023, 38, 13219–13230. [Google Scholar] [CrossRef]
- Rayan, B.A.; Subramaniam, U.; Balamurugan, S. Wireless Power Transfer in Electric Vehicles: A Review on Compensation Topologies, Coil Structures, and Safety Aspects. Energies 2023, 16, 3084. [Google Scholar] [CrossRef]
- Leng, Y.; Luo, D.R.; Li, Z.Q.; Yu, F. Coupling coefficient calculation and optimization of positive rectangular series coils in wireless power transfer systems. Heliyon 2023, 9, 13. [Google Scholar] [CrossRef]
- Ji, X.X.; Zhao, P.; Wang, H.Y.; Yang, H.Z.; Fu, M.F. Multiple-Receiver Inductive Power Transfer System Based on Multiple-Coil Power Relay Module. IEEE Trans. Circuits Syst. I-Regul. Pap. 2023, 70, 2625–2634. [Google Scholar] [CrossRef]
- Qian, L.B.; Qian, K.F.; Shi, Y.; Xia, H.K.; Wang, J.; Xia, Y.S. TSV Based Orthogonal Coils With High Misalignment Tolerance for Inductive Power Transfer in Biomedical Implants. IEEE Trans. Circuits Syst. II-Express Briefs 2021, 68, 1832–1836. [Google Scholar] [CrossRef]
- Xie, S.; Wu, L.; Zhang, X.; Huang, J.; Li, L. Misalignment-tolerant Wireless Power Transfer System Based on Double-layer Quadrature Double-D Coil with Magnetic Field Control. IEEE Trans. Transp. Electrif. 2024, 38, 4838–4852. [Google Scholar] [CrossRef]
- Domajnko, J.; Prosen, N. A Wireless Power Transfer System Using a Double DD Quadrature Coil Structure. Electronics 2023, 12, 890. [Google Scholar] [CrossRef]
- Inoue, Y.; Inoue, R.; Ueda, H.; Kim, S. Basic Study of a Wireless Power Transmission System Using Superconducting Coil as a Ground-Side Coil for Electric Vehicles. IEEE Trans. Appl. Supercond. 2023, 33, 5. [Google Scholar] [CrossRef]
- Sedwick, R.J. Long range inductive power transfer with superconducting oscillators. Ann. Phys. 2010, 325, 287–299. [Google Scholar] [CrossRef]
- Inoue, R.; Nagasaki, Y.; Tsuda, M.; Miyagi, D. Basic Coil Structure for Rapid Charge in a Low-Frequency and High-Efficiency Wireless Power Transmission System Using High-Temperature Superconducting Coil for Railway Vehicle. IEEE Trans. Appl. Supercond. 2023, 33, 9. [Google Scholar] [CrossRef]
- Oshimoto, N.; Sakuma, K.; Sekiya, N. Improvement in Power Transmission Efficiency of Wireless Power Transfer System Using Superconducting Intermediate Coil. IEEE Trans. Appl. Supercond. 2023, 33, 4. [Google Scholar] [CrossRef]
- Sari, V. Design and Implementation of a Wireless Power Transfer System for Electric Vehicles. World Electr. Veh. J. 2024, 15, 110. [Google Scholar] [CrossRef]
- Chen, Z.C.; Sun, X.D.; Ren, B.Y.; Wang, Z.X.; Liu, J. Analysis of four-coil magnetic resonance coupling wireless power transfer system based on LCC-SSS compensation network. Energy Rep. 2023, 9, 419–427. [Google Scholar] [CrossRef]
- Li, J.G.; Wang, C.; Wang, L.Y.; Ding, Y.S.; Yu, T.Q.; Cheng, Y.Y. A comparative study on transmission performance of multi-stage wireless power transfer systems using SPS compensation and LCC compensation. Int. J. Circuit Theory Appl. 2023, 51, 1625–1641. [Google Scholar] [CrossRef]
- Liu, H.C.; Wang, Y.Z.; Yu, H.Y.; Wu, F.J.; Wheeler, P. A Novel Three-Phase Omnidirectional Wireless Power Transfer System With Zero-Switching-Loss Inverter and Cylindrical Transmitter Coil. IEEE Trans. Power Electron. 2023, 38, 10426–10441. [Google Scholar] [CrossRef]
- Ning, Y.; Lombarte, A.C.; Gong, Y.; Sun, S.; Rong, Z.C.; Middya, S.; Pang, W.; Malliaras, G.; Zhang, M.L. A mm-sized acoustic wireless implantable neural stimulator based on a piezoelectric micromachined ultrasound transducer. Sens. Actuator B-Chem. 2024, 405, 10. [Google Scholar] [CrossRef]
- Tan, L.; Huang, X.; Zhao, J.; Zhao, J.; Wang, W.; Zhou, Y. Optimization design for disc resonators of a wireless power transmission system. Trans. China Electrotech. Soc. 2013, 28, 1–6. [Google Scholar]
- Zhang, W.; Mi, C.C. Compensation topologies of high-power wireless power transfer systems. IEEE Trans. Veh. Technol. 2015, 65, 4768–4778. [Google Scholar] [CrossRef]







| Parameter | Note | Value |
|---|---|---|
| Input voltage | 20 V | |
| Resonant frequency | 200 kHz | |
| Inductance of receiver coil | 11.52 uH | |
| Compensating capacitance | 54.97 nF | |
| Load | 10 Ω |
| Number | Turns | (mm) | ) | ) | Internal Resistance ) | ||
|---|---|---|---|---|---|---|---|
| 1 | 30 | 30 | 0 | 58.12 | 392.5 | 186.3 | 10.81 |
| 2 | 25 | 40 | 0 | 44.95 | 318.3 | 171.0 | 14.09 |
| 3 | 20 | 30 | 0 | 24.19 | 198.3 | 153.9 | 26.27 |
| 4 | 25 | 30 | 30 | 35.54 | 261.3 | 170.4 | 17.81 |
| 5 | 25 | 20 | 0 | 27.11 | 212.5 | 160.8 | 22.73 |
| 6 | 25 | 30 | 0 | 35.43 | 252.5 | 173.6 | 17.82 |
| 7 | 15 | 30 | 0 | 11.52 | 112.1 | 128.3 | 54.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, R.; Li, H.; Chen, J.; Le, Q.; Wang, L.; Huang, F.; Fu, Y. Design and Optimization of Coil for Transcutaneous Energy Transmission System. Electronics 2024, 13, 2157. https://doi.org/10.3390/electronics13112157
Wu R, Li H, Chen J, Le Q, Wang L, Huang F, Fu Y. Design and Optimization of Coil for Transcutaneous Energy Transmission System. Electronics. 2024; 13(11):2157. https://doi.org/10.3390/electronics13112157
Chicago/Turabian StyleWu, Ruiming, Haonan Li, Jiangyu Chen, Qi Le, Lijun Wang, Feng Huang, and Yang Fu. 2024. "Design and Optimization of Coil for Transcutaneous Energy Transmission System" Electronics 13, no. 11: 2157. https://doi.org/10.3390/electronics13112157
APA StyleWu, R., Li, H., Chen, J., Le, Q., Wang, L., Huang, F., & Fu, Y. (2024). Design and Optimization of Coil for Transcutaneous Energy Transmission System. Electronics, 13(11), 2157. https://doi.org/10.3390/electronics13112157






