Abstract
Massive multiple input multiple output (MIMO) enabled grant-free random access (mGFRA) stands out as a promising random access (RA) solution, thus effectively addressing the need for massive access in massive machine-type communications (mMTCs) while ensuring high spectral efficiency and minimizing signaling overhead. However, the bottleneck of mGFRA is mainly dominated by the orthogonal preamble collisions, since the orthogonal preamble pool is small and of a fixed-sized. In this paper, we explore the potential of non-orthogonal preambles to overcome limitations and enhance the success probability of mGFRA without extending the length of the preamble. Given the RA procedure of mGFRA, we analyze the factors influencing the success rate of mGFRA with non-orthogonal preamble and propose to use two types of sequences, namely Gold sequence and Gaussian distribution sequence, as the preambles for mGFRA. Simulation results demonstrate the effectiveness of these two types pf non-orthogonal preambles in improving the success probability of mGFRA. Moreover, the system parameters’ impact on the performance of mGFRA with non-orthogonal preambles is examined and deliberated.
1. Introduction
The rapid advancements in wireless communication technology have enabled wireless connectivity not only for individuals but also for machines and objects, including those within the Internet of Things (IoT) [,]. Machine-to-machine (M2M) communication, serving as a key enabler for the Internet of Things, has garnered significant attention from researchers in recent years. However, the sheer magnitude of RA user equipments (UEs) in M2M scenarios poses a significant challenge for networks to efficiently handle simultaneous massive access [].
The traditional random access (RA) procedure in Long-Term Evolution (LTE) involves a four-step handshake and can only support a limited number of RA UEs []. Despite various modifications and enhancements aimed at supporting mMTC, the challenges posed by signaling overhead and the scarcity of wireless resources remain significant barriers to the performance of mMTC. Alternatively, the grant-free RA approach, where UEs compete directly for uplink data transmission by sending both preambles and data payloads simultaneously, offers a highly efficient means of minimizing signaling overhead [].
To enhance the utilization of wireless resources, non-orthogonal multiple access (NOMA) has emerged as a cutting-edge technology, thus focusing on enabling the coexistence of multiple signals across the same wireless resource by leveraging different power or code domains []. To accommodate the demands of mMTC, grant-free NOMA has emerged as a primary research area in recent times. For instance, ref. [] showed a simplified version of NOMA, referred to as NOMA-assisted random access, which was implemented for grant-free transmission to demonstrate two advantages of NOMA in enhancing channel access opportunities and minimizing user collisions. Ref. [] proposed a low-correlation superimposed pilot grant-free massive access approach, which incorporates a low-correlation zone periodic sequence specifically designed for the superimposed pilot architecture. However, these methods depend on accurate power allocation, and the system access capacity is constrained by the performance of successive interference cancellation.
Massive MIMO represents another promising technology that holds the potential to significantly enhance capacity in future wireless communication systems []. The central concept involves deploying numerous antennas at the base station (BS) to concurrently serve multiple UEs through spatial multiplexing []. By integrating grant-free RA approach with massive MIMO, mGFRA is emerging as a compelling option to meet the demands of massive access while ensuring high spectral efficiency and minimal signaling overhead, but the bottleneck of the success probability of mGFRA turns out to be the preamble collisions [,]. The rationale behind this is that preamble detection and channel estimation in grant-free RA solely depends on the received preambles, thus contrasting sharply with grant-based RA, where preamble detection leverages the contention resolution mechanism through protocol exchanges, and channel estimation occurs during the subsequent non-contention phase. In the case of preamble collisions in grant-free RA, the likelihood of successfully recovering the data from the UEs involved in the collisions is slim.
To decrease preamble collisions, a super-preamble scheme utilizing massive MIMO technology was introduced in [], and it was verified that transforming the preamble into a super-preamble in a massive MIMO environment offers a promising method to decrease the preamble collision rate and enhance the performance of massive grant-free random access (mGFRA). Ref. [] proposed two unique preamble designs, which are the single orthogonal preamble and the concatenated orthogonal preamble in grant-free RA utilizing massive MIMO for the concurrent detection of users and estimation of channels. In [], a composite preamble was designed by utilizing differential phase rotations for grant-free RA, achieved through the aggregation of orthogonal Zadoff–Chu (ZC) sequences and multiple root ZC sequences with differential phase shifts. This approach aims to minimize the likelihood of preamble collisions, thus ultimately enhancing the performance of automatic user detection and channel estimation. The performance of user detection of these preamble design schemes rely on both preamble characteristics and the correlation of user channels. In addition, channel estimation errors will also affect the performance of beamforming and data recovery.
To avoid errors in channel estimation, non-coherent massive MIMO has been proposed and investigated with great potential. Ref. [] introduced a novel constellation design along with a detection algorithm based on multi-symbol joint detection decision tailored for a non-coherent massive single input multiple output (m-SIMO) uplink system that utilizes M-DPSK and is optimized for Rician channels. Affected by the inter-user interference, the number of access users was constrained by the processing complexity at the receiver. To reduce the complexity of the receiver and improve the number of access users, ref. [] proposed a user grouping scheme to avoid the dependence between constellation design and channel fading. This scheme shows great potential to increase the the number of access users with relatively low complexity at the receiver to avoid errors in channel estimation and sheds light on the methods to efficiently utilize resources other than time division and frequency division.
In this paper, we aim to break through the bottleneck caused by preamble collisions of mGFRA and investigate the potential of utilizing non-orthogonal preambles to enhance the success probability of mGFRA. Different from the grant-free NOMA schemes, the proposed scheme does not require complex successive interference cancellation and power allocation. In addition, user detection of the mGFRA with non-orthogonal preambles only depends on preamble cross-correlation, which is more reliable with low detection complexity than the preamble design methods. Different from the scenario of non-coherent massive MIMO schemes, the scenario we consider is grant-free RA for mMTC, where user-initiated access is completely random and uses the same constellation. The BS needs to use the randomly selected preambles transmitted by the RA users to distinguish the number of users accessing randomly and estimate their channels, and then beamforming is utilized with massive MIMO to achieve spatial multiplexing for the following data signals recovery. Specifically, we first model the system of mGFRA and then analyze the elements that affect the likelihood of success for mGFRA when employing non-orthogonal preambles. To provide a large set of preamble sequences at the cost of losing orthogonality, two types of preamble sequences, namely Gold sequence and Gaussian distribution sequence, are respectively considered as non-orthogonal preambles for mGFRA. Simulation outcomes confirm that non-orthogonal preambles can effectively enhance the success probability of mGFRA when the BS is equipped with a sufficient number of antennas. Furthermore, the characteristics of the success probability in relation to various system parameters are revealed and discussed.
The contributions of this paper are summarized as follows. We analyze the success probability of mGFRA when employing non-orthogonal preambles under CB and ZFB and propose to use Gold sequence and Gaussian distribution sequence as the preamble of mGFRA. We present the performances of the proposed non-orthogonal preambles under different system parameters, and the results reveal that both Gold sequence and Gaussian distribution sequence could offer a high success probability for mGFRA particularly when the number of antennas at the base station is considerable, and the preamble collisions no longer becomes a bottleneck. For practical system design, we recommend adopting Gold sequence, since the performance of Gold sequence is close to the performance of Gaussian distribution sequence, and the storage overhead of Gold sequence is much smaller than that of Gaussian distribution sequence, as both the BS and the UEs only need to store the primitive polynomials but not all the preamble sequences.
Notations: Boldface lowercase symbols denote vectors, while boldface uppercase symbols represent matrices. is the identity matrix. The transpose is denoted by , while the conjugate transpose is denoted by . denote the modulus of a complex-valued number x, and denotes the Euclidean norm of a vector . The spaces of complex-valued numbers are denoted by . indicates that is a symmetric complex Gaussian random vector with a zero mean and covariance matrix .
2. System Model
We investigate a single-cell massive MIMO network that comprises an M antenna BS and N single-antenna UEs. As illustrated in Figure 1, N UEs are attempting to perform grant-free random access over the same channel simultaneously, where the preamble transmitted by each UE is followed by a data payload. Assuming that the uplink RA frame’s duration is shorter than the channel coherence interval, we can represent the channel between each UE and the BS as having a constant response throughout a given frame. We further assume that power control is employed to maintain approximately the same level of received power at the BS from all UEs [].
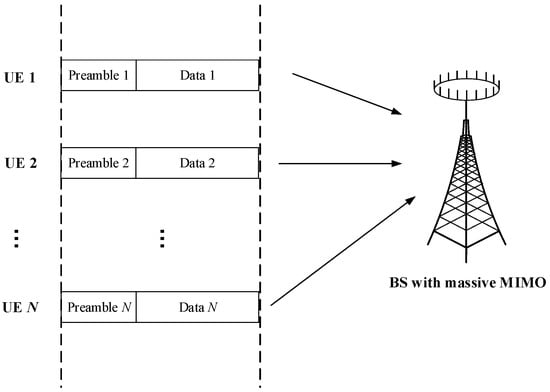
Figure 1.
N UEs perform grant-free RA over the same channel in Massive MIMO system.
In Figure 2, the simplified overview of the grant-free random access process with massive MIMO is outlined. Each UE randomly chooses a preamble sequence from a shared pool of preamble sequences, which comprises a total of K sequences. The pool of preamble sequences is referred to as , where () consists of a preamble sequence composed of L symbols satisfying . Then, the preamble of each UE is transmitted and followed by a data payload.
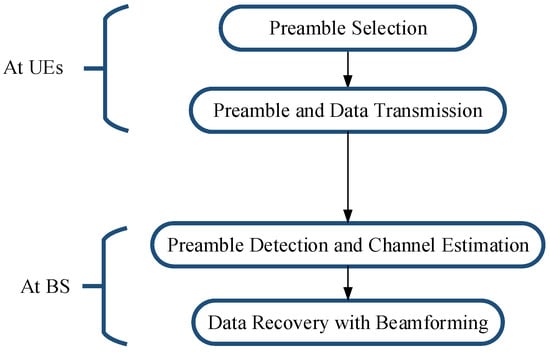
Figure 2.
Procedure of grant-free RA with massive MIMO.
The preamble signal, received at the BS equipped with M antennas, is denoted as and given by
where represents the sample of the lth () symbol captured by the mth () antenna. The matrix comprises the uplink channel responses from the N UEs to the BS, with each column representing the channel response vector between UE n and the BS. Specifically, denotes the channel response between the UE n and the mth antenna of the BS. The matrix represents the preamble sequences transmitted by all UEs, where each row () corresponds to the preamble sequence sent by UE n and aligns with one of the row vectors in . Finally, represents the complex additive white Gaussian noise matrix present at the BS.
We consider least squares (LSs) estimation for the preamble detection and channel estimation. Once the BS has received the preamble signal, it performs a correlation operation between and , which is given by
where .
If is selected by at least one UE as the preamble, it is likely that
where and is a predefined threshold.
Based on (2) and (3), the BS could acquire the estimated channels of all the potential UEs by conducting a thorough search through all K column vectors of . The estimated channels of the potential UEs are given by
where is the number of UEs that are detected by the BS.
After the preamble detection and channel estimation, data recovery is performed. The data signal received at the BS at a target sampling point is given by
where is the data transmitted by UE n at a target sampling point, and represents the vector of complex additive white Gaussian noise received at the BS.
We consider two beamforming methods for data recovery, which are conjugate beamforming (CB) and zero-forcing beamforming (ZFB). The demodulation of data signals under CB of the detected UEs is given by
The demodulation of data signals under ZFB of the detected UEs is as follows:
For an UE to successfully transmit data, it is crucial for the BS to achieve accurate channel estimation for that UE. Additionally, the signal-to-interference-and-noise ratio (SINR) must exceed a pre-established threshold after beamforming.
3. Factors Influencing Success Probability
In this section, we delve into the factors that impact the likelihood of success for mGFRA with non-orthogonal preambles. Considering that the preamble selection of the RA UEs is random and independent and the channels of the RA UEs are also random, we select one UE for the following analysis. For simplicity, we consider UE 1 as a representative case and assume it selects as its preamble. Additionally, we neglect the influence of noise on channel estimation for the sake of brevity.
Given the RA procedure, the success probability of UE 1 could be approximately given by
where represents the likelihood that no preamble collisions occur between UE 1 and the remaining UEs. Here, K denotes the total number of distinct preamble sequences in the pool, thus indicating that there are K different non-orthogonal sequences available for selection.
represents the likelihood that the SINR of UE 1 exceeds the threshold . This probability is conditioned on two factors: (1) the BS has access to the channel response of UE 1; (2) other UEs are concurrently utilizing the same channel resource for data transmission as UE 1.
The system access capacity is expressed by the number of UEs that are successfully accessed at the same time, which could be approximately given by
According to (2) and (3), the channel estimation result of UE 1 is
where , which is the error that results from using a non-orthogonal preamble during channel estimation.
With , utilizing its estimated channel response, the BS retrieves the data of UE 1 through conjugate beamforming. The retrieved signal pertaining to UE 1 is
In massive MIMO systems, M is assumed to be large. Hence, it can be assumed that the channels of any two UEs are approximately orthogonal to each other, i.e., . Then, when M is large, (11) could be approximated as
The SINR of UE 1 is therefore approximately calculated as
where represents the uplink signal-to-noise ratio at the BS for the UE 1 in the random access process. It is noted from (13) that the interference caused by the non-orthogonal preambles in the channel estimation, i.e., , would affect the SINR, and it can not be neglected even when M is large. Moreover, the increase of N in the case of non-orthogonal preamble would result in more loss of the SINR compared to the case of orthogonal preamble.
In addition to the CB, we further analyze the SINR under zero-forcing beamforming (ZFB). The demodulation of data signals under ZFB of the detected UEs is
where is the ZFB signal demodulation matrix at the base station, and represents the channel matrix estimated by the BS, which is given by (4).
To facilitate a more comprehensible derivation in the subsequent steps, is expressed in the following form:
where , is the set of UEs who have selected the sth pilot out of the pilots pool , where .
Based on (14) and (15), the data of UE 1 recovered by the BS under ZFB are defined as
where represents the first row of .
Then, the SINR of UE1 is calculated as
Given (8), (13), and (17), the key factors that affect the success probability of mGFRA could be summarized as (1) the size of the preamble sequence set and the cross-correlation performance between the preamble sequences; (2) the number of antennas at the BS; (3) the uplink signal-to-noise ratio at the BS for the UE 1 in the random access process. Compared to the case of orthogonal preamble, the non-orthogonal preamble could provide a much lower preamble collision probability, but it would result in more loss of the SINR. Thus, there is a compromise to be made between reducing the likelihood of preamble collisions and ensuring a reasonable SINR for successful data recovery.
Based on the analysis, two types of non-orthogonal sequences, which are Gold sequence and Gaussian distribution sequence, have the potential to be the non-orthogonal preamble for mGFRA, since both of them could have a large set size of the preamble sequences and a low cross-correlation. The performance outcomes of mGFRA with the Gold sequence and Gaussian distribution sequence are analyzed in the following simulations.
4. Numerical Results
In this section, the performance outcomes of mGFRA with the Gold sequence and Gaussian distribution sequence are simulated and presented. In the simulations, we considered that each UE randomly chooses a preamble sequence from a shared pool of preamble sequences and performs grant-free random access over the same channel simultaneously in the phase of transmission. In the phase of preamble detection and channel estimation at the BS, LS estimation is used. In the phase of beamforming and data recovery at the BS, CB and ZFB are utilized. It is also assumed that power control is employed to maintain approximately the same level of received power at the BS from all UEs. The simulation parameters are configured as follows.
(1) Gold sequence: A Gold sequence is obtained by the binary addition of a preferred pair of M sequences []. An example of the Gold sequence generator in parallel with six levels of the shift register is shown in Figure 3, where the primitive polynomials are and . By separately changing the initial state of these two shift registers (the values of the shift register cannot be all zeros), different Gold sequences can be generated. Thus, the preamble sequence pool could consists of 3969 different Gold sequences when the length of the preamble is 63.
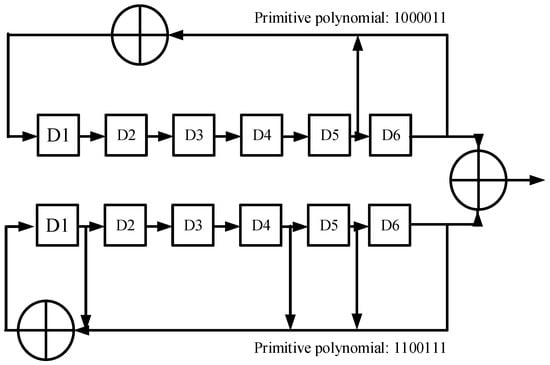
Figure 3.
Gold sequence generator in parallel with 6 levels.
(2) Gaussian distribution sequence: The preamble sequences are composed of entries generated from an independent and identically distributed (i.i.d.) Gaussian distribution with a mean of zero and a variance of one. In other words, each entry of the matrix follows an independent Gaussian distribution having a mean of zero and a variance of one.
The massive MIMO channel model incorporates an independent Rayleigh fading assumption, which characterizes the signal transmission between the M antennas of the base station and the N UEs. This propagation is mathematically represented by a complex matrix with dimensions . Each element of is an independent complex normal random variable with a mean of zero and a variance of one. Consequently, the expected squared norm of the channel vector corresponding to each UE equals M. The key simulation parameters are outlined as follows:
- Length of preamble: 63
- Number of orthogonal sequences: 63
- Number of Gold sequences: 3969
- Number of Gaussian sequences: 3969
- The threshold of preamble dectection ():
- The threshold of SINR (): 0 to 6 dB
In Figure 4, the simulation results of under CB are displayed as a function of M to demonstrate its behavior for each type of preamble. It is observed that with each type of non-orthogonal preamble approached to as M increased. We also see that with orthogonal preamble demonstrated a trend towards saturation as M increased, since the bottleneck of with orthogonal preamble was mainly dominated by the preamble collisions, i.e., the preamble collision probability was . In addition, it is noteworthy that the performance of the non-orthogonal preamble was highly responsive to changes in M. From the observations, we could conclude that when M is sufficiently large, the non-orthogonal preamble is effective in increasing .
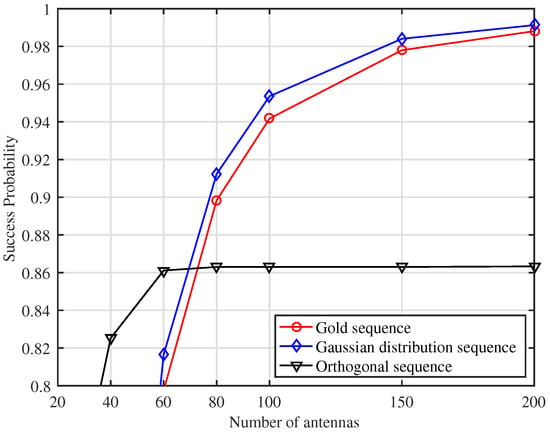
Figure 4.
versus M with and SNR = dB under CB.
Figure 5 shows the simulation results of under ZFB as a function of M. As can be seen, the performance of with non-orthogonal preamble under ZFB improved faster with the increase in the number of antennas compared to the case of CB. In addition, the performance of with the orthogonal preamble was still limited by preamble collisions and could not improve indefinitely with the increase in the number of antennas.
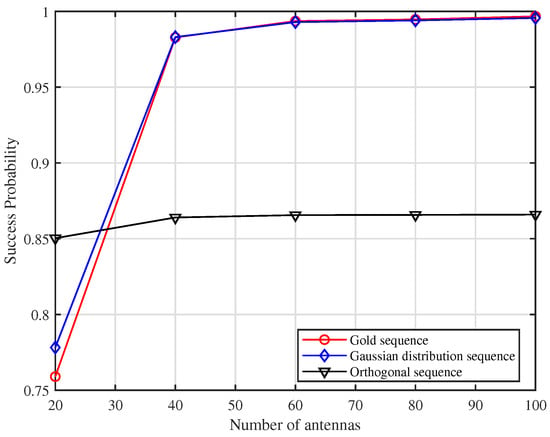
Figure 5.
versus M with and SNR = dB under ZFB.
In Figure 6, the simulation outcomes of are displayed as a function of N under CB when the SINR threshold was set to dB. We see that when N increased, with each type of non-orthogonal preamble showed a faster decline than the case of the orthogonal preamble. It is also observed that when M decreased from 200 to 100, the decline in with each type of non-orthogonal preamble greatly increased. These observations reveal that the performance of the non-orthogonal preamble would be more easy to be affected than that of the orthogonal preamble as N increases. Moreover, when N is large, i.e., , a substantial increase in the number of antennas is needed to ensure high success probability for the case of the non-orthogonal preamble.
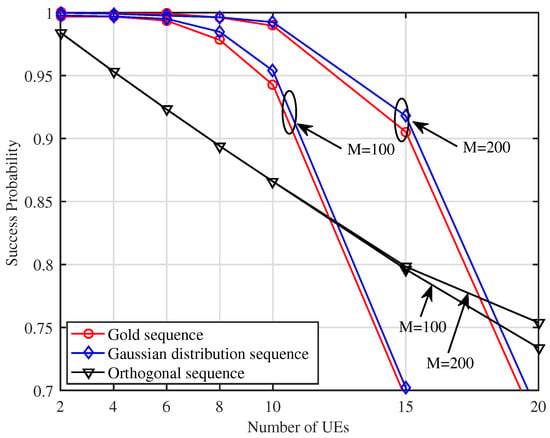
Figure 6.
versus N with dB and SNR = dB under CB.
Figure 7 demonstrates as a function of N under ZFB when the SINR threshold was set to dB. It could be seen that the performance degradation of ZFB was slower with the increase in the number of UEs compared to CB. However, when the number of users exceeded 15, with non-orthogonal preamble under ZFB still exhibited a faster rate of degradation and was lower than that of the orthogonal preamble.
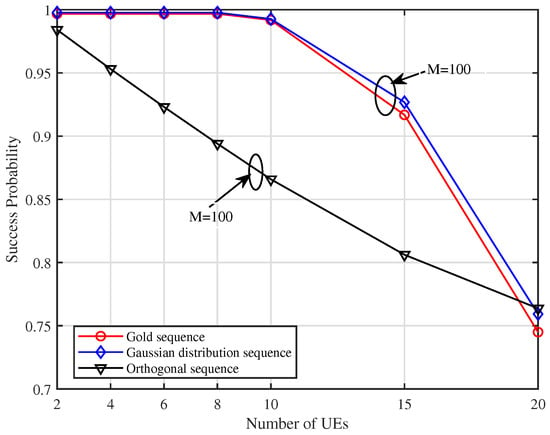
Figure 7.
versus N with dB and SNR = dB under ZFB.
Figure 8 shows the access capacity versus N under ZFB and CB. It can be seen that when the number of RA UEs was less than 10, the access capacity was almost the same as the number of RA UEs under ZFB with non-orthogonal preambles. We can also see that when the number of RA UEs was less than eight, the access capacity was almost the same as the number of RA UEs with non-orthogonal preambles. However, as the number of RA UEs increased, the access capacity decreased rapidly under CB with non-orthogonal preambles. It indicates that CB is more susceptible to channel estimation errors with non-orthogonal preambles. For the orthogonal preamble, only when the number of RA UEs was less than four, the system access capacity was almost the same as the number of RA UEs. The reason is that its performance was mainly limited by preamble collisions.
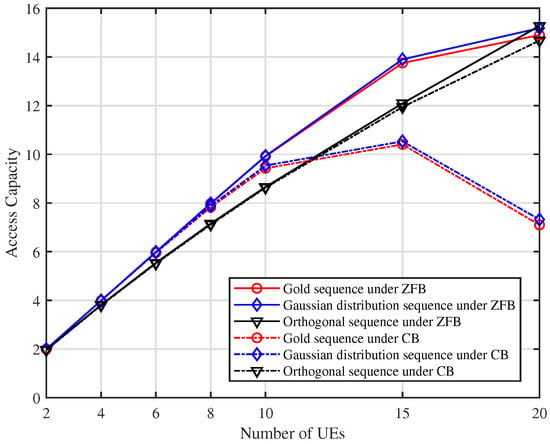
Figure 8.
versus N with dB and SNR = dB under ZFB and CB.
In Figure 9, the simulation results of are exhibited as a function of when M was fixed at 200 for each type of preamble considered under CB. It is observed that with each type of non-orthogonal preamble showed a faster decline as increased. For the orthogonal preamble, remained unchanged as increased. This observation verifies that the non-orthogonal preamble results in more loss of compared to the case of the orthogonal preamble, even when M is large.
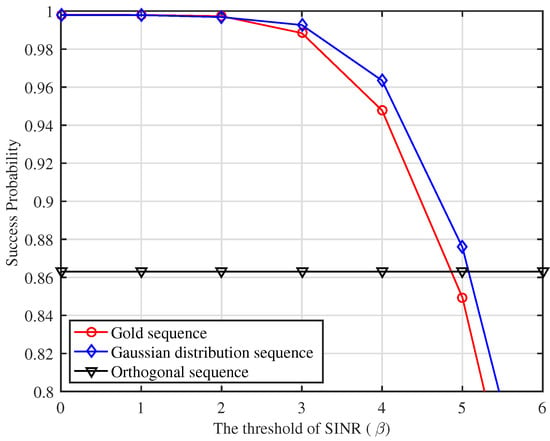
Figure 9.
versus the SINR threshold () with , and SNR = dB.
To assess the performance of non-orthogonal preambles more thoroughly, the simulation results of are presented considering the scenario of imperfect power control in Figure 10 under CB. In the simulation, it is assumed that the expected received power from the UEs is uniformly distributed across a range of to dB or to 0 dB. When the expected received UE power is the lowest, i.e., dB, it results in an SNR of dB. It is evident that imperfect power control has a notable impact on the for each type of non-orthogonal preamble, since with each type of non-orthogonal preamble could almost converge to the under perfect power control, as shown in Figure 4. Furthermore, it becomes apparent that the associated with each type of non-orthogonal preamble was more susceptible to imperfections in power control, as compared to the case where an orthogonal preamble was used.
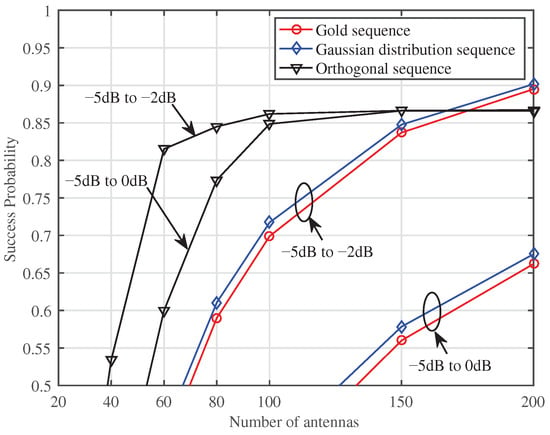
Figure 10.
under imperfect power control.
5. Conclusions
In this paper, we explored the possibility of utilizing non-orthogonal preambles to enhance the success probability of mGFRA without extending the length of the preamble. We delved into the factors that affect the success probability of mGFRA when employing non-orthogonal preambles and suggest the employment of two types of non-orthogonal preambles: the Gold sequence and Gaussian distribution sequence. The performances of the Gold sequence and Gaussian distribution sequence are presented with respect to system parameters.
The results indicate that the two proposed types of non-orthogonal preambles could offer a high success probability for mGFRA, particularly when the number of antennas at the base station is considerable. On the other hand, affected by the errors in channel estimation, the success probability performances with the two proposed types of non-orthogonal preambles showed a faster rate of degradation and would be lower than that of orthogonal preamble when the number of UEs reached a certain point. Therefore, there is a tradeoff among the number of UEs, the number of BS antennas, and the processing complexity at the BS.
Based on the analysis, we recommend adopting non-orthogonal preambles and increasing the number of antennas at the BS to ensure a higher success rate when it is difficult to increase orthogonal preamble resources due to limited time–frequency resources in the system. We also recommend adopting the Gold sequence, since the performance of the Gold sequence is close to the performance of Gaussian distribution sequence, and the storage overhead of the Gold sequence is much smaller than that of the Gaussian distribution sequence, as both the BS and the UEs only need to storage the primitive polynomials but not all the preamble sequences. In addition, effective power control is crucial for non-orthogonal preambles to guarantee a high success probability for mGFRA in practical system applications.
In future research, inspired by the schemes in [,], different constellations and user grouping method in conjunction with mGFRA with non-orthogonal preambles could be investigated to reduce channel estimation error. In addition, the impact of imperfect power control and different channel environments on the success probability performance of mGFRA with non-orthogonal preambles could also be further studied.
Author Contributions
Conceptualization, H.J.; methodology, H.J.; formal analysis, H.J.; investigation, H.J. and H.C.; software, H.J., H.H., and J.D.; validation, H.J., H.H., and J.D.; data curation, H.J.; writing—original draft preparation, H.J.; writing—review and editing, H.J. and H.C.; supervision, H.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China “Cheung Kong Scholars Programme” (No. 21069000222).
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
Author Hao Jiang was employed by the company Guangzhou Digital Technology Group Co., Ltd.; Authors Hao Jiang and Hongming Hu were employed by the company Guangzhou Haige Communications Group Incorporated Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Stankovic, J.A. Research directions for the internet of things. IEEE Internet Things J. 2014, 1, 3–9. [Google Scholar] [CrossRef]
- Schulz, P.; Matthe, M.; Klessig, H.; Simsek, M.; Fettweis, G.; Ansari, J.; Ashraf, S.A.; Almeroth, B.; Voigt, J.; Riedel, I.; et al. Latency critical IoT applications in 5G: Perspective on the design of radio interface and network architecture. IEEE Commun. Mag. 2017, 55, 70–78. [Google Scholar] [CrossRef]
- Dawy, Z.; Saad, W.; Ghosh, A.; Andrews, J.G.; Yaacoub, E. Toward massive machine type cellular communications. IEEE Wirel. Commun. 2016, 24, 120–128. [Google Scholar] [CrossRef]
- De Andrade, T.P.; Astudillo, C.A.; Sekijima, L.R.; Da Fonseca, N.L. The random access procedure in long term evolution networks for the Internet of Things. IEEE Commun. Mag. 2017, 55, 124–131. [Google Scholar] [CrossRef]
- Liu, L.; Larsson, E.G.; Yu, W.; Popovski, P.; Stefanovic, C.; De Carvalho, E. Sparse signal processing for grant-free massive connectivity: A future paradigm for random access protocols in the Internet of Things. IEEE Signal Process. Mag. 2018, 35, 88–99. [Google Scholar] [CrossRef]
- Makki, B.; Chitti, K.; Behravan, A.; Alouini, M.S. A survey of NOMA: Current status and open research challenges. IEEE Open J. Commun. Soc. 2020, 1, 179–189. [Google Scholar] [CrossRef]
- Ding, Z.; Schober, R.; Poor, H.V. Impact of NOMA on age of information: A grant-free transmission perspective. IEEE Trans. Wirel. Commun. 2023, 23, 3975–3989. [Google Scholar] [CrossRef]
- Xu, L.; Jiao, J.; Wang, Y.; Wu, S.; Lu, R.; Zhang, Q. Low-Correlation Superimposed Pilot Grant-free Massive Access for Satellite Internet of Things. IEEE Trans. Commun. 2023, 71, 7087–7101. [Google Scholar] [CrossRef]
- Marzetta, T.L. Noncooperative cellular wireless with unlimited numbers of base station antennas. IEEE Trans. Wirel. Commun. 2010, 9, 3590–3600. [Google Scholar] [CrossRef]
- Lu, L.; Li, G.Y.; Swindlehurst, A.L.; Ashikhmin, A.; Zhang, R. An overview of massive MIMO: Benefits and challenges. IEEE J. Sel. Top. Signal Process. 2014, 8, 742–758. [Google Scholar] [CrossRef]
- Ding, J.; Qu, D.; Jiang, H.; Jiang, T. Success probability of grant-free random access with massive MIMO. IEEE Internet Things J. 2018, 6, 506–516. [Google Scholar] [CrossRef]
- Jiang, H.; Qu, D.; Ding, J.; Wang, Z.; He, H.; Chen, H. Enabling LPWAN massive access: Grant-free random access with massive MIMO. IEEE Wirel. Commun. 2022, 29, 72–77. [Google Scholar] [CrossRef]
- Jiang, H.; Qu, D.; Ding, J.; Jiang, T. Multiple preambles for high success rate of grant-free random access with massive MIMO. IEEE Trans. Wirel. Commun. 2019, 18, 4779–4789. [Google Scholar] [CrossRef]
- Yang, Y.; Song, G.; Liu, H. Joint User Detection and Channel Estimation in Grant-Free Random Access for Massive MIMO Systems. J. Electr. Comput. Eng. 2023, 2023, 1672421. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, W.; Juntti, M.; Lin, J.; Pan, M. Composite preambles based on differential phase rotations for grant-free random access systems. IEEE Internet Things J. 2023, 10, 17035–17046. [Google Scholar] [CrossRef]
- Baeza, V.M.; Armada, A.G. Non-coherent massive SIMO system based on M-DPSK for Rician channels. IEEE Trans. Veh. Technol. 2019, 68, 2413–2426. [Google Scholar] [CrossRef]
- Baeza, V.M.; Armada, A.G. User grouping for non-coherent DPSK massive SIMO with heterogeneous propagation conditions. In Proceedings of the 2021 Global Congress on Electrical Engineering (GC-ElecEng), Valencia, Spain, 10–12 December 2021; pp. 26–30. [Google Scholar]
- Björnson, E.; Larsson, E.G.; Debbah, M. Massive MIMO for maximal spectral efficiency: How many users and pilots should be allocated? IEEE Trans. Wirel. Commun. 2016, 15, 1293–1308. [Google Scholar] [CrossRef]
- Gold, R. Optimal binary sequences for spread spectrum multiplexing (Corresp.). IEEE Trans. Inf. Theory 1967, 13, 619–621. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).