Robust Tensor Learning for Multi-View Spectral Clustering
Abstract
1. Introduction
- With a novel integrated strategy, the weighted tensor nuclear norm-based tensor low-rank constraint, the matrix nuclear norm-based low-rank regularization, and the regularization are integrated into a unified framework, where the WTNN regularization depicts the information among different samples and different views, and the matrix nuclear norm regularization makes each frontal slice of the learned tensor approximately block-diagonal, capturing the geometry of each single view. Thus, the affinity matrix calculated from the latent tensor depicts the intrinsic clustering structure of the multi-view data.
- A column-wise sparse norm, namely, norm, is introduced to enhance the robustness of our model. Compared with the norm, the norm, which is invariant, continuous, and differentiable, can be better in restricting the sparsity property of noised samples.
2. Background and Motivation
3. The Proposed Method
| Algorithm 1 RTL-MSC Algorithm |
Input: Multi-view data sample number n, and cluster number c
|
4. Experiments
4.1. Competitors
4.2. Datasets
4.3. Experimental Process
4.4. Experimental Results and Analysis
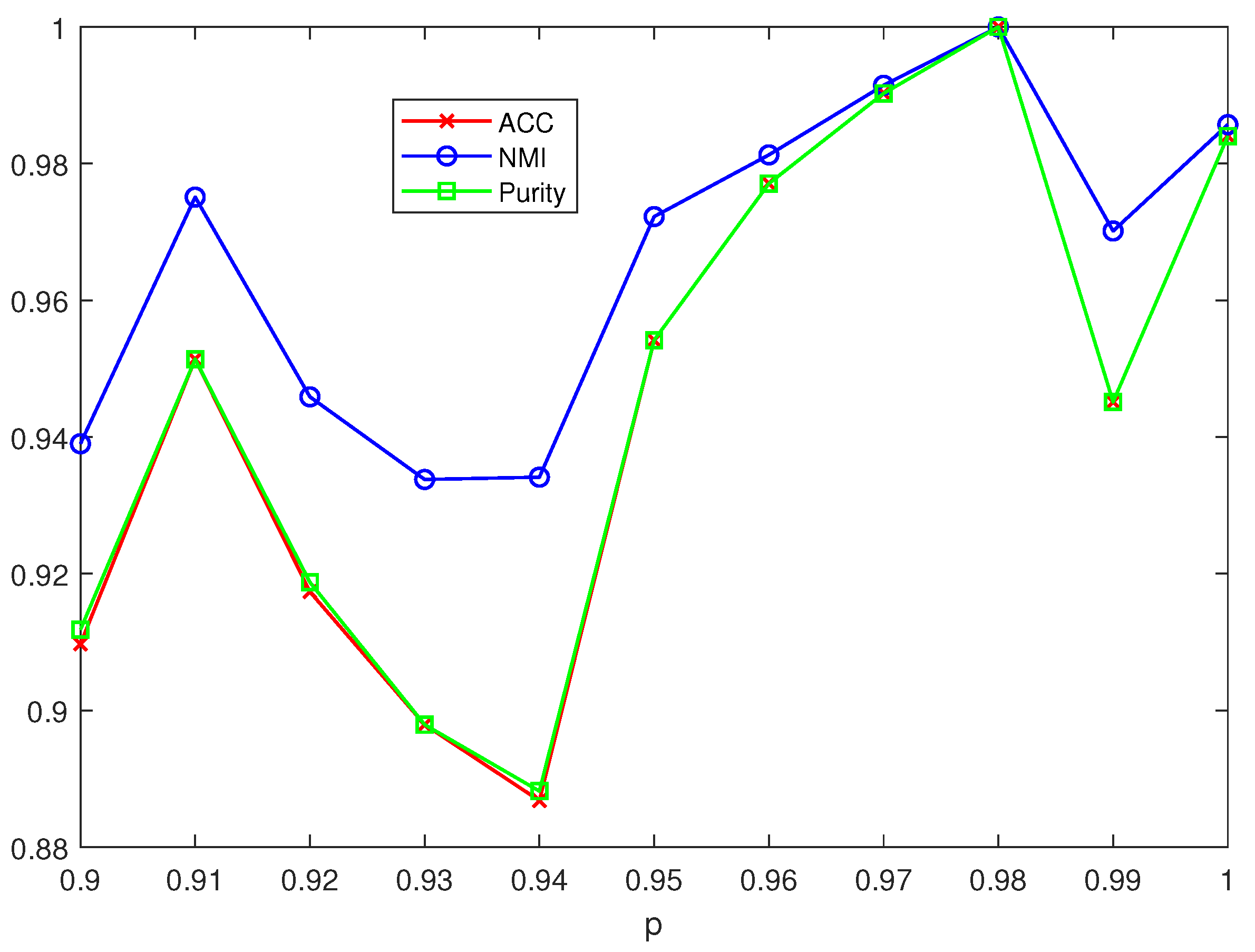
4.5. Ablation Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar]
- Ng, A.; Jordan, M.; Weiss, Y. On spectral clustering: Analysis and an algorithm. Adv. Neural Inf. Process. Syst. 2001, 14, 849–856. [Google Scholar]
- Fan, J.; Tu, Y.; Zhang, Z.; Zhao, M.; Zhang, H. A simple approach to automated spectral clustering. Adv. Neural Inf. Process. Syst. 2022, 35, 9907–9921. [Google Scholar]
- Yan, Y.; Shen, C.; Wang, H. Efficient semidefinite spectral clustering via Lagrange duality. IEEE Trans. Image Process. 2014, 23, 3522–3534. [Google Scholar] [CrossRef] [PubMed]
- Meila, M.; Shi, J. Learning segmentation by random walks. Adv. Neural Inf. Process. Syst. 2000, 13, 837–843. [Google Scholar]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Elhamifar, E.; Vidal, R. Sparse subspace clustering: Algorithm, theory, and applications. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2765–2781. [Google Scholar] [CrossRef] [PubMed]
- Nie, F.; Cai, G.; Li, X. Multi-view clustering and semi-supervised classification with adaptive neighbours. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar]
- Zhou, S.; Liu, X.; Liu, J.; Guo, X.; Zhao, Y.; Zhu, E.; Zhai, Y.; Yin, J.; Gao, W. Multi-view spectral clustering with optimal neighborhood Laplacian matrix. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 6965–6972. [Google Scholar]
- Alzate, C.; Suykens, J.A. Multiway spectral clustering with out-of-sample extensions through weighted kernel PCA. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 32, 335–347. [Google Scholar] [CrossRef] [PubMed]
- Xia, T.; Tao, D.; Mei, T.; Zhang, Y. Multiview spectral embedding. IEEE Trans. Syst. Man, Cybern. Part B Cybern. 2010, 40, 1438–1446. [Google Scholar]
- Lu, C.; Yan, S.; Lin, Z. Convex sparse spectral clustering: Single-view to multi-view. IEEE Trans. Image Process. 2016, 25, 2833–2843. [Google Scholar] [CrossRef]
- El Hajjar, S.; Dornaika, F.; Abdallah, F. Multi-view spectral clustering via constrained nonnegative embedding. Inf. Fusion 2022, 78, 209–217. [Google Scholar] [CrossRef]
- Zong, L.; Zhang, X.; Liu, X.; Yu, H. Weighted multi-view spectral clustering based on spectral perturbation. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Nie, F.; Li, J.; Li, X. Parameter-free auto-weighted multiple graph learning: A framework for multiview clustering and semi-supervised classification. In Proceedings of the IJCAI, New York, NY, USA, 9–15 July 2016; Volume 9, pp. 1881–1887. [Google Scholar]
- Zhan, K.; Zhang, C.; Guan, J.; Wang, J. Graph learning for multiview clustering. IEEE Trans. Cybern. 2017, 48, 2887–2895. [Google Scholar] [CrossRef] [PubMed]
- Xie, D.; Zhang, X.; Gao, Q.; Han, J.; Xiao, S.; Gao, X. Multiview clustering by joint latent representation and similarity learning. IEEE Trans. Cybern. 2019, 50, 4848–4854. [Google Scholar] [CrossRef] [PubMed]
- Kang, Z.; Shi, G.; Huang, S.; Chen, W.; Pu, X.; Zhou, J.T.; Xu, Z. Multi-graph fusion for multi-view spectral clustering. Knowl.-Based Syst. 2020, 189, 105102. [Google Scholar] [CrossRef]
- Zhong, G.; Shu, T.; Huang, G.; Yan, X. Multi-view spectral clustering by simultaneous consensus graph learning and discretization. Knowl.-Based Syst. 2022, 235, 107632. [Google Scholar] [CrossRef]
- Tang, C.; Li, Z.; Wang, J.; Liu, X.; Zhang, W.; Zhu, E. Unified one-step multi-view spectral clustering. IEEE Trans. Knowl. Data Eng. 2022, 35, 6449–6460. [Google Scholar] [CrossRef]
- Houthuys, L.; Langone, R.; Suykens, J.A. Multi-view kernel spectral clustering. Inf. Fusion 2018, 44, 46–56. [Google Scholar] [CrossRef]
- Huang, Z.; Zhou, J.T.; Peng, X.; Zhang, C.; Zhu, H.; Lv, J. Multi-view Spectral Clustering Network. In Proceedings of the IJCAI, Macao, 10–16 August 2019; Volume 2, p. 4. [Google Scholar]
- Zhao, M.; Yang, W.; Nie, F. Deep multi-view spectral clustering via ensemble. Pattern Recognit. 2023, 144, 109836. [Google Scholar] [CrossRef]
- Wang, Q.; Cheng, J.; Gao, Q.; Zhao, G.; Jiao, L. Deep multi-view subspace clustering with unified and discriminative learning. IEEE Trans. Multimed. 2020, 23, 3483–3493. [Google Scholar] [CrossRef]
- Tao, Q.; Tonin, F.; Patrinos, P.; Suykens, J.A. Tensor-based multi-view spectral clustering via shared latent space. Information Fusion 2024, 108, 102405. [Google Scholar] [CrossRef]
- Goldfarb, D.; Qin, Z. Robust low-rank tensor recovery: Models and algorithms. SIAM J. Matrix Anal. Appl. 2014, 35, 225–253. [Google Scholar] [CrossRef]
- Chen, Y.; Xiao, X.; Peng, C.; Lu, G.; Zhou, Y. Low-rank tensor graph learning for multi-view subspace clustering. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 92–104. [Google Scholar] [CrossRef]
- Wu, J.; Lin, Z.; Zha, H. Essential tensor learning for multi-view spectral clustering. IEEE Trans. Image Process. 2019, 28, 5910–5922. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Yang, W.; Liu, B.; Ke, G.; Pan, Y.; Yin, J. Multi-view spectral clustering via tensor-SVD decomposition. In Proceedings of the 2017 IEEE 29th International Conference on Tools with Artificial Intelligence (ICTAI), Boston, MA, USA, 6–8 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 493–497. [Google Scholar]
- Wang, S.; Chen, Y.; Cen, Y.; Zhang, L.; Wang, H.; Voronin, V. Nonconvex low-rank and sparse tensor representation for multi-view subspace clustering. Appl. Intell. 2022, 52, 14651–14664. [Google Scholar] [CrossRef]
- Gao, Q.; Xia, W.; Wan, Z.; Xie, D.; Zhang, P. Tensor-SVD based graph learning for multi-view subspace clustering. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 3930–3937. [Google Scholar]
- Jia, Y.; Liu, H.; Hou, J.; Kwong, S.; Zhang, Q. Multi-view spectral clustering tailored tensor low-rank representation. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 4784–4797. [Google Scholar] [CrossRef]
- Gao, Q.; Zhang, P.; Xia, W.; Xie, D.; Gao, X.; Tao, D. Enhanced tensor RPCA and its application. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 2133–2140. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Xiao, X.; Hua, Z.; Zhou, Y. Adaptive transition probability matrix learning for multiview spectral clustering. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 4712–4726. [Google Scholar] [CrossRef]
- Wang, S.; Chen, Y.; Jin, Y.; Cen, Y.; Li, Y.; Zhang, L. Error-robust low-rank tensor approximation for multi-view clustering. Knowl.-Based Syst. 2021, 215, 106745. [Google Scholar] [CrossRef]
- Xia, R.; Pan, Y.; Du, L.; Yin, J. Robust multi-view spectral clustering via low-rank and sparse decomposition. In Proceedings of the AAAI Conference on Artificial Intelligence, Québec City, QC, Canada, 27–31 July 2014; Volume 28. [Google Scholar]
- Xie, D.; Gao, Q.; Deng, S.; Yang, X.; Gao, X. Multiple graphs learning with a new weighted tensor nuclear norm. Neural Netw. 2021, 133, 57–68. [Google Scholar] [CrossRef]
- Yang, M.; Luo, Q.; Li, W.; Xiao, M. Multiview clustering of images with tensor rank minimization via nonconvex approach. SIAM J. Imaging Sci. 2020, 13, 2361–2392. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Liu, G.; Lin, Z.; Yu, Y. Robust subspace segmentation by low-rank representation. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 663–670. [Google Scholar]
- Cai, J.F.; Candès, E.J.; Shen, Z. A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]


| Methods | ACC | NMI | Purity | F-score | AVE |
|---|---|---|---|---|---|
| 0.3737 ± 0.020 | 0.3975 ± 0.017 | 0.3916 ± 0.017 | 0.2637 ± 0.008 | 2.4604 ± 0.027 | |
| RMSC | 0.3796 ± 0.015 | 0.4167 ± 0.008 | 0.3982 ± 0.015 | 0.2685 ± 0.008 | 2.3890 ± 0.032 |
| MSCAN | 0.4585 ± 0.001 | 0.5070 ± 0.001 | 0.4852 ± 0.002 | 0.3164 ± 0.002 | 2.1405 ± 0.009 |
| ETL-MSC | 0.9108 ± 0.034 | 0.9114 ± 0.016 | 0.9167 ± 0.028 | 0.8626 ± 0.033 | 0.3693 ± 0.068 |
| ATPML-MSC | 0.9772 ± 0.001 | 0.9661 ± 0.002 | 0.9772 ± 0.001 | 0.9554 ± 0.004 | 0.1395 ± 0.010 |
| MGL-WTNN | 0.9811 ± 0.001 | 0.9703 ± 0.001 | 0.9811 ± 0.001 | 0.9628 ± 0.001 | 0.1215 ± 0.003 |
| RTL-WTNN | 0.9874 ± 0.001 | 0.9800 ± 0.001 | 0.9874 ± 0.001 | 0.9753 ± 0.001 | 0.0818 ± 0.003 |
| Methods | ACC | NMI | Purity | F-score | AVE |
|---|---|---|---|---|---|
| 0.6886 ± 0.026 | 0.8131 ± 0.010 | 0.7276 ± 0.019 | 0.6609 ± 0.025 | 0.8388 ± 0.048 | |
| RMSC | 0.7026 ± 0.020 | 0.8022 ± 0.006 | 0.7101 ± 0.011 | 0.6628 ± 0.015 | 0.8668 ± 0.031 |
| MSCAN | 0.8061 ± 0.022 | 0.9299 ± 0.005 | 0.8481 ± 0.016 | 0.7441 ± 0.030 | 0.4266 ± 0.044 |
| ETL-MSC | 0.8730 ± 0.021 | 0.9204 ± 0.009 | 0.8811 ± 0.015 | 0.8510 ± 0.020 | 0.3518 ± 0.040 |
| ATPML-MSC | 0.9513 ± 0.038 | 0.9795 ± 0.016 | 0.9616 ± 0.031 | 0.9481 ± 0.041 | 0.0990 ± 0.078 |
| MGL-WTNN | 0.8853 ± 0.023 | 0.9300 ± 0.006 | 0.8919 ± 0.015 | 0.8645 ± 0.016 | 0.3098 ± 0.032 |
| RTL-WTNN | 0.9769 ± 0.028 | 0.9866 ± 0.011 | 0.9806 ± 0.020 | 0.9695 ± 0.027 | 0.0627 ± 0.053 |
| Methods | ACC | NMI | Purity | F-score | AVE |
|---|---|---|---|---|---|
| 0.2338 ± 0.008 | 0.1095 ± 0.004 | 0.2457 ± 0.007 | 0.1361 ± 0.002 | 3.1950 ± 0.016 | |
| RMSC | 0.2962 ± 0.004 | 0.1556 ± 0.004 | 0.3035 ± 0.004 | 0.1758 ± 0.003 | 3.029 ± 0.013 |
| MSCAN | 0.2493 ± 0.005 | 0.1972 ± 0.004 | 0.2643 ± 0.005 | 0.1739 ± 0.001 | 3.0376 ± 0.012 |
| ETL-MSC | 0.6906 ± 0.001 | 0.7007 ± 0.001 | 0.6927 ± 0.001 | 0.6243 ± 0.001 | 1.078 ± 0.004 |
| ATPML-MSC | 0.9286 ± 0.001 | 0.8844 ± 0.001 | 0.9286 ± 0.001 | 0.8658 ± 0.002 | 0.4062 ± 0.005 |
| MGL-WTNN | 0.8787 ± 0.001 | 0.7774 ± 0.001 | 0.8787 ± 0.001 | 0.7791 ± 0.001 | 0.7990 ± 0.003 |
| RTL-WTNN | 0.9441 ± 0.001 | 0.8976 ± 0.001 | 0.9441 ± 0.001 | 0.8933 ± 0.001 | 0.3650 ± 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, D.; Li, Z.; Sun, Y.; Song, W. Robust Tensor Learning for Multi-View Spectral Clustering. Electronics 2024, 13, 2181. https://doi.org/10.3390/electronics13112181
Xie D, Li Z, Sun Y, Song W. Robust Tensor Learning for Multi-View Spectral Clustering. Electronics. 2024; 13(11):2181. https://doi.org/10.3390/electronics13112181
Chicago/Turabian StyleXie, Deyan, Zibao Li, Yingkun Sun, and Wei Song. 2024. "Robust Tensor Learning for Multi-View Spectral Clustering" Electronics 13, no. 11: 2181. https://doi.org/10.3390/electronics13112181
APA StyleXie, D., Li, Z., Sun, Y., & Song, W. (2024). Robust Tensor Learning for Multi-View Spectral Clustering. Electronics, 13(11), 2181. https://doi.org/10.3390/electronics13112181





