Wearable Loops for Dynamic Monitoring of Joint Flexion: A Machine Learning Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Overview of the Approach
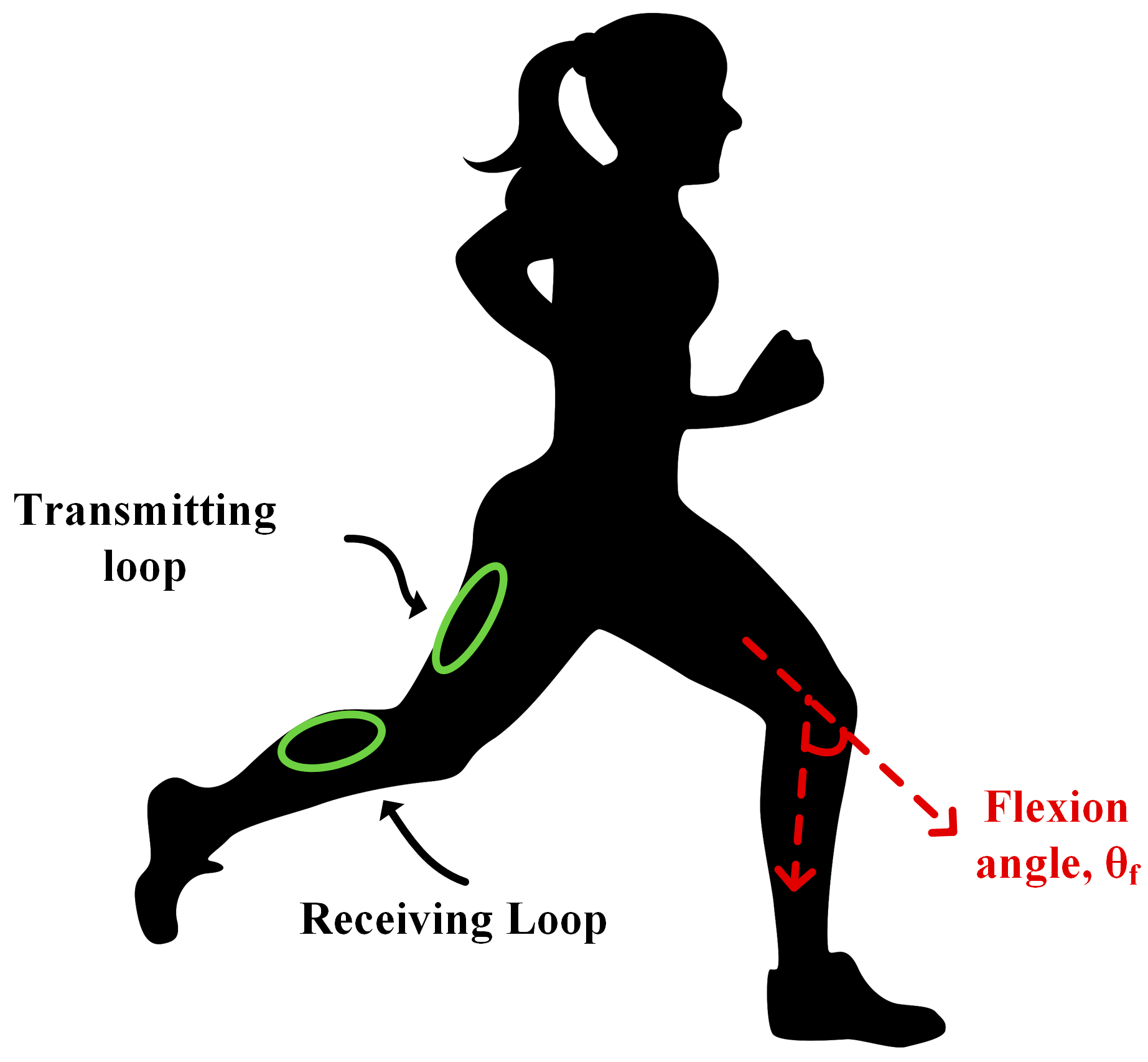
2.2. Data Acquisition System and Methods
2.2.1. Experimental Setup
2.2.2. Data Collection
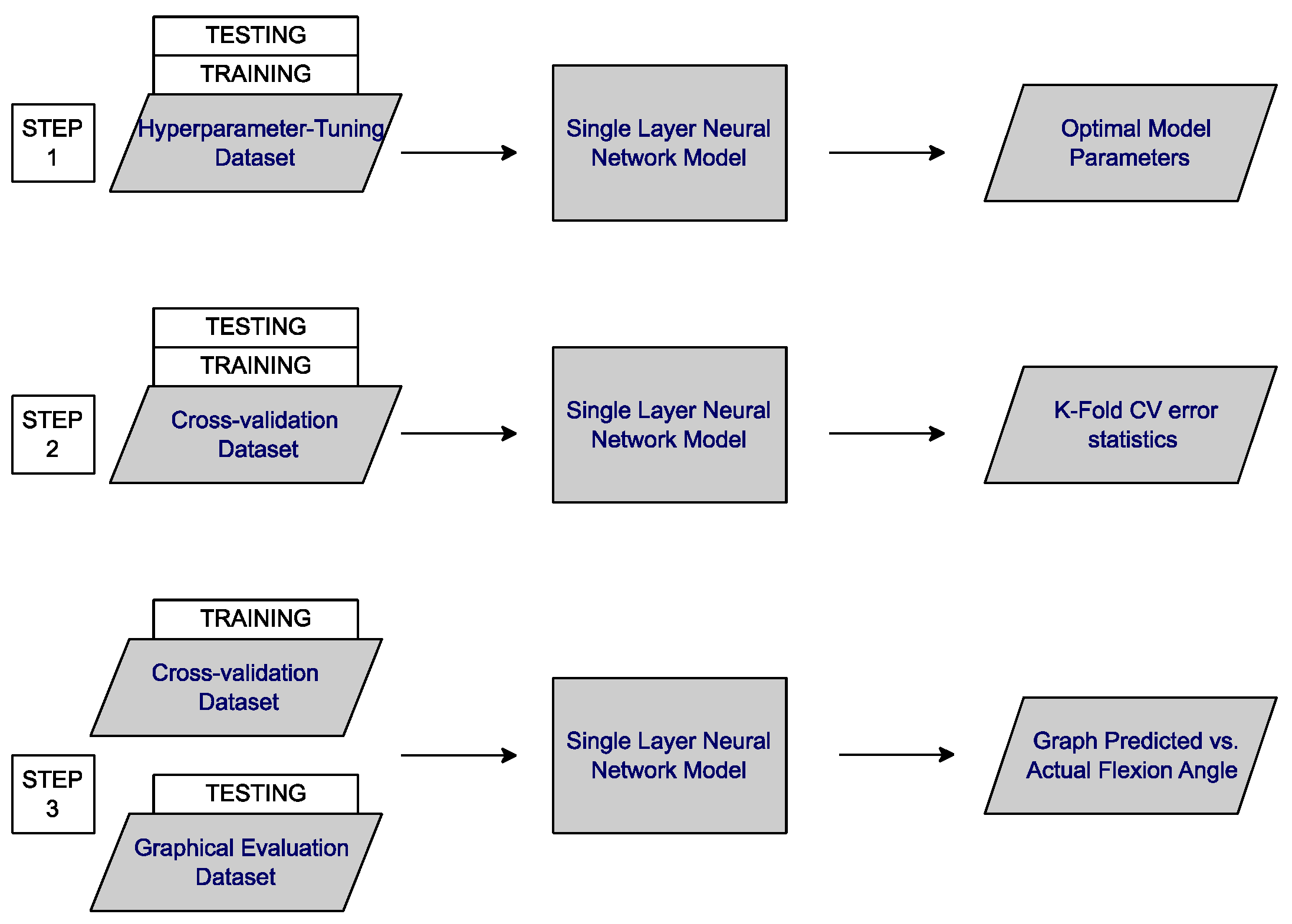
2.3. Machine Learning Framework
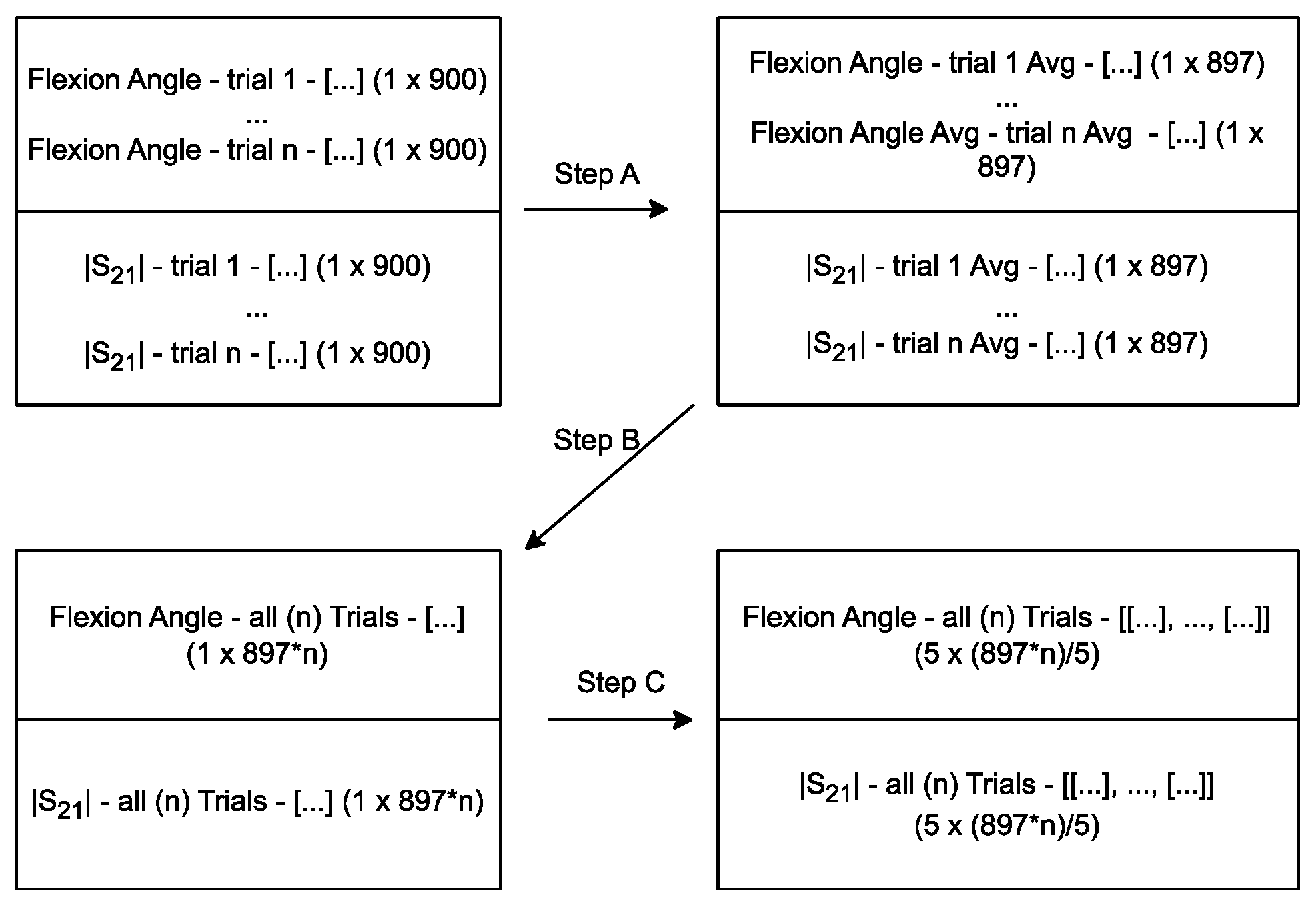
2.3.1. Data Preprocessing
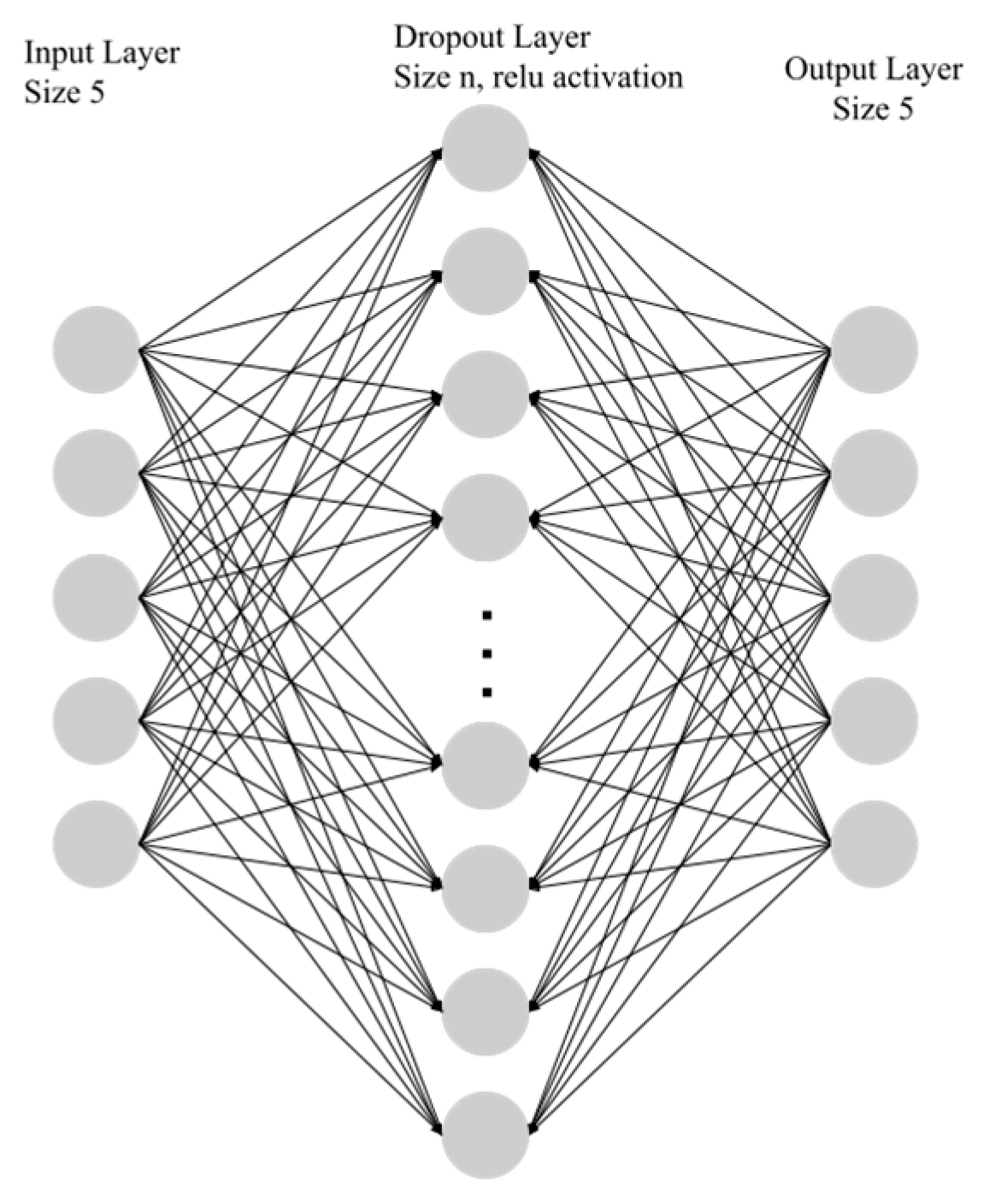
2.3.2. Architecture of the Artificial Neural Network
2.3.3. Hyperparameters Tuning
3. Results
3.1. Evaluation Criteria
3.2. Assessing Optimal Network Structure and Parameters
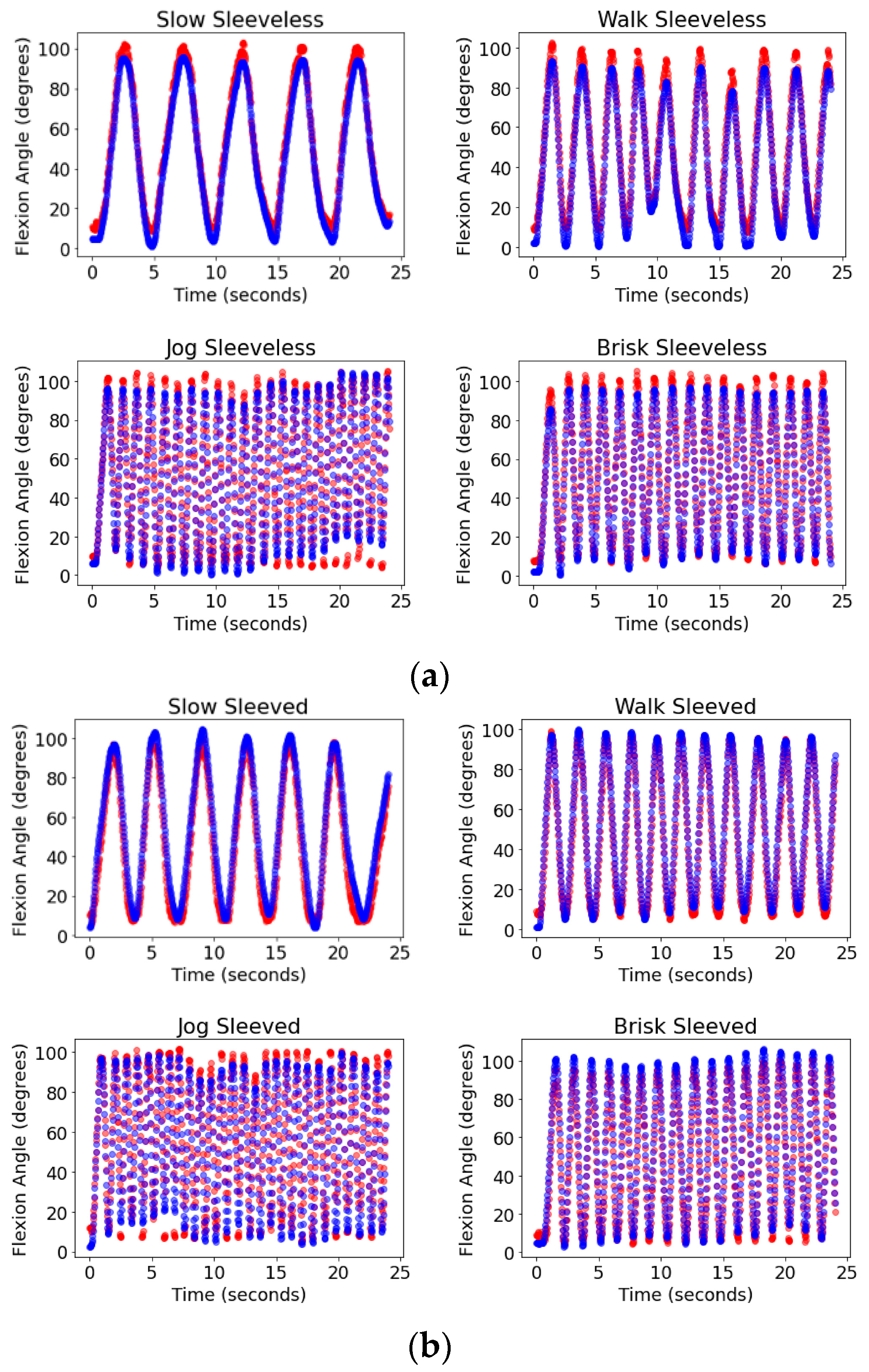
3.3. Assessing Network Performance
3.4. Comparison to Approaches without Machine Learning
4. Discussion
4.1. Summary of Reported Phantom-Based Study
4.2. Translation to Human Subjects
4.3. Other Study Limitations
4.4. Potential Applications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rovini, E.; Maremmani, C.; Cavallo, F. How Wearable Sensors Can Support Parkinson’s Disease Diagnosis and Treatment: A Systematic Review. Front. Neurosci. 2017, 11, 288959. [Google Scholar] [CrossRef] [PubMed]
- Oh, J.; Ripic, Z.; Signorile, J.F.; Andersen, M.S.; Kuenze, C.; Letter, M.; Best, T.M.; Eltoukhy, M. Monitoring joint mechanics in anterior cruciate ligament reconstruction using depth sensor-driven musculoskeletal modeling and statistical parametric mapping. Med. Eng. Phys. 2022, 103, 103796. [Google Scholar] [CrossRef] [PubMed]
- Sevick, M.; Eklund, E.; Mensch, A.; Foreman, M.; Standeven, J.; Engsberg, J. Using Free Internet Videogames in Upper Extremity Motor Training for Children with Cerebral Palsy. Behav. Sci. 2016, 6, 10. [Google Scholar] [CrossRef] [PubMed]
- Gasparutto, X.; van der Graaff, E.; van der Helm, F.C.T.; Veeger, D.H.E.J. Influence of biomechanical models on joint kinematics and kinetics in baseball pitching. Sports Biomech. 2018, 20, 96–108. [Google Scholar] [CrossRef] [PubMed]
- Luu, T.P.; He, Y.; Brown, S.; Nakagome, S.; Contreras-Vidal, J.L. Gait adaptation to visual kinematic perturbations using a real-time closed-loop brain–computer interface to a virtual reality avatar. J. Neural Eng. 2016, 13, 036006. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Zhang, Z.; Beck, A.; Yuan, J.; Thalmann, D. Human–Robot Interaction by Understanding Upper Body Gestures. Presence Virtual Augment. Real. 2014, 23, 133–154. [Google Scholar] [CrossRef]
- Jamsrandorj, A.; Kumar, K.S.; Arshad, M.Z.; Mun, K.-R.; Kim, J. Deep Learning Networks for View-independent Knee and Elbow Joint Angle Estimation. In Proceedings of the 2022 44th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Glasgow, UK, 11–15 July 2022; pp. 2703–2707. [Google Scholar] [CrossRef]
- Metcalf, C.D.; Robinson, R.; Malpass, A.J.; Bogle, T.P.; Dell, T.A.; Harris, C.; Demain, S.H. Markerless Motion Capture and Measurement of Hand Kinematics: Validation and Application to Home-Based Upper Limb Rehabilitation. IEEE Trans. Biomed. Eng. 2013, 60, 2184–2192. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Zhu, M.; Pavlakos, G.; Leonardos, S.; Derpanis, K.G.; Daniilidis, K. MonoCap: Monocular Human Motion Capture using a CNN Coupled with a Geometric Prior. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 901–914. [Google Scholar] [CrossRef] [PubMed]
- Sabale, A.S.; Vaidya, Y.M. Accuracy Measurement of Depth Using Kinect Sensor. In Proceedings of the 2016 Conference on Advances in Signal Processing (CASP), Pune, India, 9–11 June 2016; Available online: https://ieeexplore.ieee.org/document/7746156 (accessed on 7 March 2023).
- Shin, S.; Li, Z.; Halilaj, E. Markerless Motion Tracking with Noisy Video and IMU Data. IEEE Trans. Biomed. Eng. 2023, 70, 3082–3092. [Google Scholar] [CrossRef]
- Bartlett, H.L.; Goldfarb, M. A Phase Variable Approach for IMU-Based Locomotion Activity Recognition. IEEE Trans. Biomed. Eng. 2018, 65, 1330–1338. [Google Scholar] [CrossRef] [PubMed]
- Veron-Tocquet, E.; Leboucher, J.; Burdin, V.; Savean, J.; Remy-Neris, O. A Study of Accuracy for a Single Time of Flight Camera Capturing Knee Flexion Movement. In Proceedings of the 2014 IEEE Healthcare Innovation Conference (HIC), Seattle, WA, USA, 8–10 October 2014; Available online: https://ieeexplore.ieee.org/document/7038944 (accessed on 7 March 2023).
- Fursattel, P.; Placht, S.; Balda, M.; Schaller, C.; Hofmann, H.; Maier, A.; Riess, C. A Comparative Error Analysis of Current Time-of-Flight Sensors. IEEE Trans. Comput. Imaging 2016, 2, 27–41. [Google Scholar] [CrossRef]
- Oubre, B.; Daneault, J.-F.; Boyer, K.; Kim, J.H.; Jasim, M.; Bonato, P.; Lee, S.I. A Simple Low-Cost Wearable Sensor for Long-Term Ambulatory Monitoring of Knee Joint Kinematics. IEEE Trans. Biomed. Eng. 2020, 67, 3483–3490. [Google Scholar] [CrossRef] [PubMed]
- Sanca, A.S.; Rocha, J.C.; Eugenio, K.J.S.; Nascimento, L.B.P.; Alsina, P.J. Characterization of Resistive Flex Sensor Applied to Joint Angular Displacement Estimation. In Proceedings of the 2018 Latin American Robotic Symposium, 2018 Brazilian Symposium on Robotics (SBR) and 2018 Workshop on Robotics in Education (WRE), Joȧo Pessoa, Brazil, 6–10 November 2018; Available online: https://ieeexplore.ieee.org/document/8588523 (accessed on 7 March 2023).
- Kim, D.; Kwon, J.; Han, S.; Park, Y.-L.; Jo, S. Deep Full-Body Motion Network for a Soft Wearable Motion Sensing Suit. IEEE/ASME Trans. Mechatron. 2019, 24, 56–66. [Google Scholar] [CrossRef]
- Li, X.; Wen, R.; Shen, Z.; Wang, Z.; Luk, K.D.K.; Hu, Y. A Wearable Detector for Simultaneous Finger Joint Motion Measurement. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 644–654. [Google Scholar] [CrossRef] [PubMed]
- Kobashi, S.; Tsumori, Y.; Imawaki, S.; Yoshiya, S.; Hata, Y. Wearable Knee Kinematics Monitoring System of MARG Sensor and Pressure Sensor Systems. In Proceedings of the 2009 IEEE International Conference on System of Systems Engineering (SoSE), Albuquerque, NM, USA, 30 May–3 June 2009; pp. 1–6. [Google Scholar]
- Dai, Z.; Jing, L. Lightweight Extended Kalman Filter for MARG Sensors Attitude Estimation. IEEE Sens. J. 2021, 21, 14749–14758. [Google Scholar] [CrossRef]
- Tian, Y.; Wei, H.; Tan, J. An Adaptive-Gain Complementary Filter for Real-Time Human Motion Tracking with MARG Sensors in Free-Living Environments. IEEE Trans. Neural Syst. Rehabil. Eng. 2013, 21, 254–264. [Google Scholar] [CrossRef] [PubMed]
- Kun, L.; Inoue, Y.; Shibata, K.; Enguo, C. Ambulatory Estimation of Knee-Joint Kinematics in Anatomical Coordinate System Using Accelerometers and Magnetometers. IEEE Trans. Biomed. Eng. 2011, 58, 435–442. [Google Scholar] [CrossRef] [PubMed]
- Mishra, V.; Kiourti, A. Wearable Electrically Small Loop Antennas for Monitoring Joint Kinematics: Guidelines for Optimal Frequency Selection. In Proceedings of the 2020 IEEE International Symposium on Antennas and Propagation and North American Radio Science Meeting, Montreal, QC, Canada, 5–10 July 2020; Available online: https://ieeexplore.ieee.org/document/9329988 (accessed on 7 March 2023).
- Mishra, V.; Kiourti, A. Wrap-Around Wearable Coils for Seamless Monitoring of Joint Flexion. IEEE Trans. Biomed. Eng. 2019, 66, 2753–2760. [Google Scholar] [CrossRef] [PubMed]
- Ketola, R.; Mishra, V.; Kiourti, A. Modeling Fabric Movement for Future E-Textile Sensors. Sensors 2020, 20, 3735. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Mishra, V.; Kiourti, A. Denoising Textile Kinematics Sensors: A Machine Learning Approach. In Proceedings of the 3rd URSI Atlantic/Asia-Pacific Radio Science Meeting (URSI AT-AP-RASC), Gran Canaria, Spain, 29 May–3 June 2022; Available online: https://par.nsf.gov/servlets/purl/10354091 (accessed on 9 March 2023).
- Zheng, T.; Chen, Z.; Ding, S.; Luo, J. Enhancing RF Sensing with Deep Learning: A Layered Approach. IEEE Commun. Mag. 2021, 59, 70–76. [Google Scholar] [CrossRef]
- Bashar, S.K.; Han, D.; Zieneddin, F.; Ding, E.; Fitzgibbons, T.P.; Walkey, A.J.; McManus, D.D.; Javidi, B.; Chon, K.H. Novel Density Poincare Plot Based Machine Learning Method to Detect Atrial Fibrillation from Premature Atrial/Ventricular Contractions. IEEE Trans. Biomed. Eng. 2021, 68, 448–460. [Google Scholar] [CrossRef] [PubMed]
- Fitzpatrick, K.; Brewer, M.A.; Turner, S. Another Look at Pedestrian Walking Speed. Transp. Res. Rec. J. Transp. Res. Board 2006, 1982, 21–29. [Google Scholar] [CrossRef]
- Barreira, T.V.; Rowe, D.A.; Kang, M. Parameters of Walking and Jogging in Healthy Young Adults. Int. J. Exerc. Sci. 2010, 3, 2. Available online: https://digitalcommons.wku.edu/ijes/vol3/iss1/2/ (accessed on 7 March 2023).
- Jia, P.; Liu, H.; Wang, S.; Wang, P. Research on a Mine Gas Concentration Forecasting Model Based on a GRU Network. IEEE Access 2020, 8, 38023–38031. [Google Scholar] [CrossRef]
- Panwar, M.; Biswas, D.; Bajaj, H.; Jobges, M.; Turk, R.; Maharatna, K.; Acharyya, A. Rehab-Net: Deep Learning Framework for Arm Movement Classification Using Wearable Sensors for Stroke Rehabilitation. IEEE Trans. Biomed. Eng. 2019, 66, 3026–3037. [Google Scholar] [CrossRef] [PubMed]
- Stetter, B.J.; Krafft, F.C.; Ringhof, S.; Stein, T.; Sell, S. A Machine Learning and Wearable Sensor Based Approach to Estimate External Knee Flexion and Adduction Moments During Various Locomotion Tasks. Front. Bioeng. Biotechnol. 2020, 8, 9. [Google Scholar] [CrossRef] [PubMed]
- Halilaj, E.; Rajagopal, A.; Fiterau, M.; Hicks, J.L.; Hastie, T.J.; Delp, S.L. Machine learning in human movement biomechanics: Best practices, common pitfalls, and new opportunities. J. Biomech. 2018, 81, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Xie, J.; Wang, Q. Benchmarking Machine Learning Algorithms on Blood Glucose Prediction for Type I Diabetes in Comparison with Classical Time-Series Models. IEEE Trans. Biomed. Eng. 2020, 67, 3101–3124. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Caccese, J.B.; Kiourti, A. Wearable Loop Sensor for Bilateral Knee Flexion Monitoring. Sensors 2024, 24, 1549. [Google Scholar] [CrossRef] [PubMed]
- Büttner, C.; Milani, T.L.; Sichting, F. Integrating a Potentiometer into a Knee Brace Shows High Potential for Continuous Knee Motion Monitoring. Sensors 2021, 21, 2150. [Google Scholar] [CrossRef]
- Slade, P.; Habib, A.; Hicks, J.L.; Delp, S.L. An open-source and wearable system for measuring 3D human motion in real-time. IEEE Trans. Biomed. Eng. 2022, 69, 678–688. [Google Scholar] [CrossRef] [PubMed]
- Zhong, J.; Kiourti, A.; Sebastian, T.; Bayram, Y.; Volakis, J.L. Conformal Load-Bearing Spiral Antenna on Conductive Textile Threads. IEEE Antennas Wirel. Propag. Lett. 2016, 16, 230–233. [Google Scholar] [CrossRef]
- Toivonen, M.; Bjorninen, T.; Sydanheimo, L.; Ukkonen, L.; Rahmat-Samii, Y. Impact of Moisture and Washing on the Performance of Embroidered UHF RFID Tags. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 1590–1593. [Google Scholar] [CrossRef]
- Mishra, V.; Kiourti, A. Wearable Electrically Small Loop Antennas for Monitoring Joint Flexion and Rotation. IEEE Trans. Antennas Propag. 2020, 68, 134–141. [Google Scholar] [CrossRef]



| Camera-Based [7,8,9,10] | IMUs [11] | Time-of-Flight [13,14] | Retractable String [15] | Bending Sensors [16,17,18] | MARG Sensor System [19,20,21] | Magnetometer [22] | Loop-Based Sensors (Our Previous Work) [23,24] | Loop-Based Sensors with Machine Learning (Proposed) | |
|---|---|---|---|---|---|---|---|---|---|
| Works in unconfined environment | × | ✓ | ✓ | ✓ | ✓ | ✓ | × | ✓ | ✓ |
| Seamless | ✓ | × | × | × | ✓ | × | × | ✓ | ✓ |
| Insensitive to line of sight | × | ✓ | × | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Allows natural motion | ✓ | ✓ | ✓ | × | × | ✓ | ✓ | ✓ | ✓ |
| Reliable vs. time | ✓ | × | ✓ | ✓ | × | × | × | ✓ | ✓ |
| Low error during dynamic motion | ✓ | × | ✓ | × | × | × | × | × | ✓ |
| Motion Type | Motion Speed [m/min] | Number of Flexes |
|---|---|---|
| Slow | N/A | 3–5 |
| Walking | 64 | 9–13 |
| Brisk Walking | 80 | 17–19 |
| Jogging | 110 | 25–30 |
| Hyperparameter | Searched Values |
|---|---|
| Learning Rate | 0.001, 0.01, 0.1 |
| Batch Size | 2, 4, 5 |
| Epochs | 20, 40 |
| Layer Size | 1500, 1700, 2000, 2200 |
| Hyperparameter | Chosen Val |
|---|---|
| Learning Rate | 0.001 |
| Batch Size | 2 |
| Epochs | 40 |
| Layer Size | 2200 |
| Motion Type | RMSE (deg) | rRMSE | R |
|---|---|---|---|
| Brisk Sleeved | 9.41 ± 1.00 | 0.17 ± 0.02 | 0.98 ± 0.01 |
| Brisk Sleeveless | 5.90 ± 0.86 | 0.12 ± 0.02 | 0.99 ± 0.00 |
| Jog Sleeved | 7.79 ± 0.42 | 0.14 ± 0.01 | 0.98 ± 0.00 |
| Jog Sleeveless | 5.44 ± 0.22 | 0.11 ± 0.01 | 0.99 ± 0.00 |
| Walk Sleeved | 7.21 ± 0.85 | 0.13 ± 0.02 | 0.99 ± 0.00 |
| Walk Sleeveless | 6.11 ± 0.88 | 0.13 ± 0.02 | 0.99 ± 0.00 |
| Slow Sleeved | 8.97 ± 0.80 | 0.17 ± 0.02 | 0.99 ± 0.00 |
| Slow Sleeveless | 5.90 ± 0.80 | 0.12 ± 0.02 | 0.99 ± 0.00 |
| All Trials | 7.26 ± 0.15 | 0.14 ± 0.003 | 0.98 ± 0.00 |
| Motion Type | RMSE (deg) | rRMSE | R |
|---|---|---|---|
| Brisk Sleeved | 7.07 | 0.13 | 0.99 |
| Brisk Sleeveless | 4.83 | 0.10 | 0.99 |
| Jog Sleeved | 5.82 | 0.11 | 0.99 |
| Jog Sleeveless | 4.62 | 0.09 | 0.99 |
| Walk Sleeved | 6.30 | 0.12 | 0.99 |
| Walk Sleeveless | 6.87 | 0.16 | 0.99 |
| Slow Sleeved | 8.21 | 0.16 | 0.99 |
| Slow Sleeveless | 5.14 | 0.11 | 0.99 |
| Motion Type | RMSE (deg) |
|---|---|
| Brisk Sleeved | 52.00 |
| Brisk Sleeveless | 46.71 |
| Jog Sleeved | 51.08 |
| Jog Sleeveless | 56.53 |
| Walk Sleeved | 52.15 |
| Walk Sleeveless | 54.19 |
| Slow Sleeved | 35.07 |
| Slow Sleeveless | 44.26 |
| All Trials | 49.92 |
| Approach | RMSE (deg) | rRMSE | R |
|---|---|---|---|
| Human Trials | 6.62 ± 0.49 | 0.15 ± 0.01 | 0.97 ± 0.003 |
| Phantom Trials | 7.26 ± 0.15 | 0.14 ± 0.003 | 0.98 ± 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saltzman, H.; Rajaram, R.; Zhang, Y.; Islam, M.A.; Kiourti, A. Wearable Loops for Dynamic Monitoring of Joint Flexion: A Machine Learning Approach. Electronics 2024, 13, 2245. https://doi.org/10.3390/electronics13122245
Saltzman H, Rajaram R, Zhang Y, Islam MA, Kiourti A. Wearable Loops for Dynamic Monitoring of Joint Flexion: A Machine Learning Approach. Electronics. 2024; 13(12):2245. https://doi.org/10.3390/electronics13122245
Chicago/Turabian StyleSaltzman, Henry, Rahul Rajaram, Yingzhe Zhang, Md Asiful Islam, and Asimina Kiourti. 2024. "Wearable Loops for Dynamic Monitoring of Joint Flexion: A Machine Learning Approach" Electronics 13, no. 12: 2245. https://doi.org/10.3390/electronics13122245
APA StyleSaltzman, H., Rajaram, R., Zhang, Y., Islam, M. A., & Kiourti, A. (2024). Wearable Loops for Dynamic Monitoring of Joint Flexion: A Machine Learning Approach. Electronics, 13(12), 2245. https://doi.org/10.3390/electronics13122245








