Assessment of the Winding Mechanical Condition Based on Transformer Vibration during Transient Processes
Abstract
1. Introduction
- (1)
- Resolution Problem. The free vibration period is generally less than 0.1 s. The traditional OMA approach uses only the free vibration, which yields a spectrum with poor frequency resolution, making it challenging to identify the modal frequencies and evaluate the mechanical condition of the transformer.
- (2)
- Separation Problem. To overcome the resolution problem, some researchers have used the whole vibration signal instead. However, this vibration signal includes forced and modal vibration components, making it challenging to separate the modal frequencies from the other frequencies [15].
- (3)
- Generalization Capability Problem. An in-service power transformer is generally subjected to various transient operation conditions. An OMA approach that could be used under different operation conditions would be highly valuable since it could serve different maintenance purposes, including condition evaluation after strong short-circuit impacts and daily maintenance that could be conducted during the power-off condition. Therefore, the generalization capability of the OMA method is important. Unfortunately, all methods proposed in published works have been designed for a particular operation condition, and their generalization capabilities have been tested very rarely.
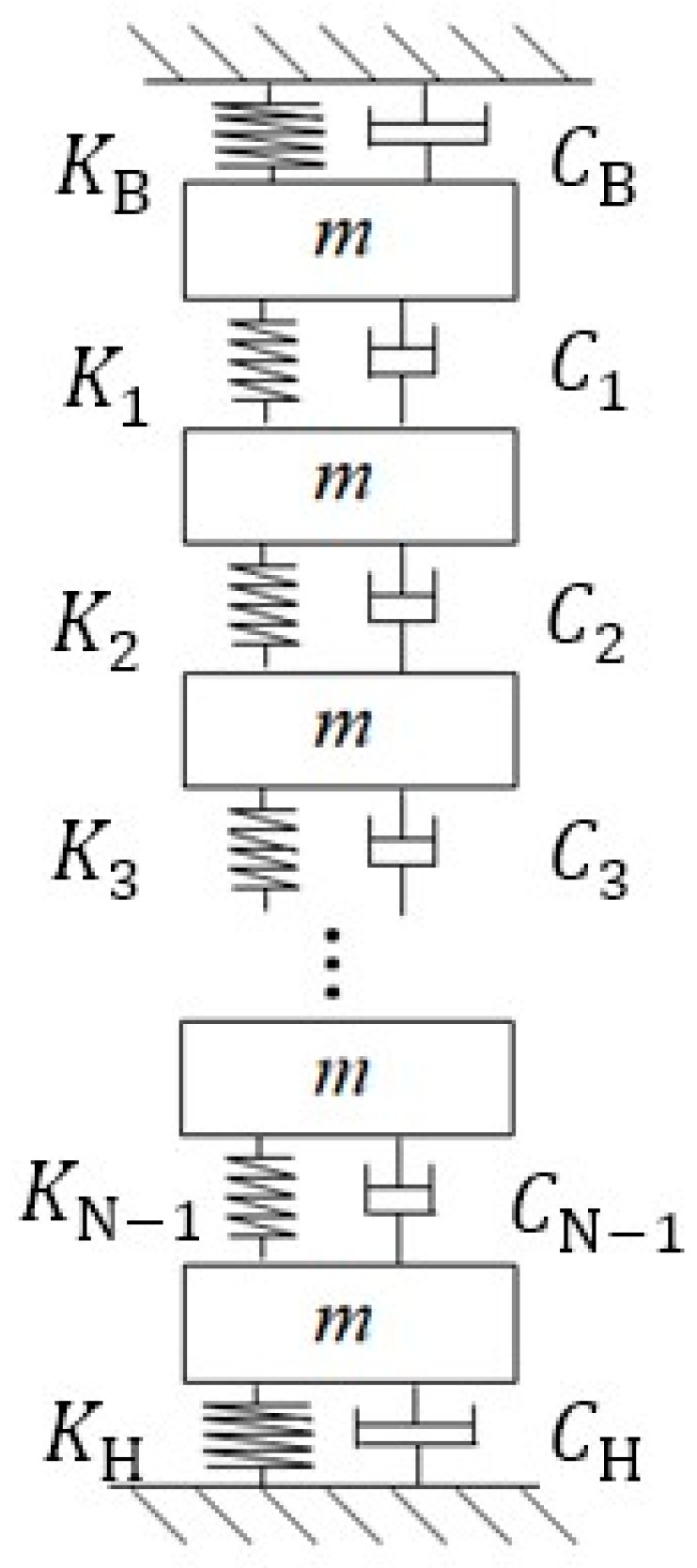
2. Vibration Model during Transient Process
3. Transient Vibration Modal Spectrum Recognition Method for Transformers
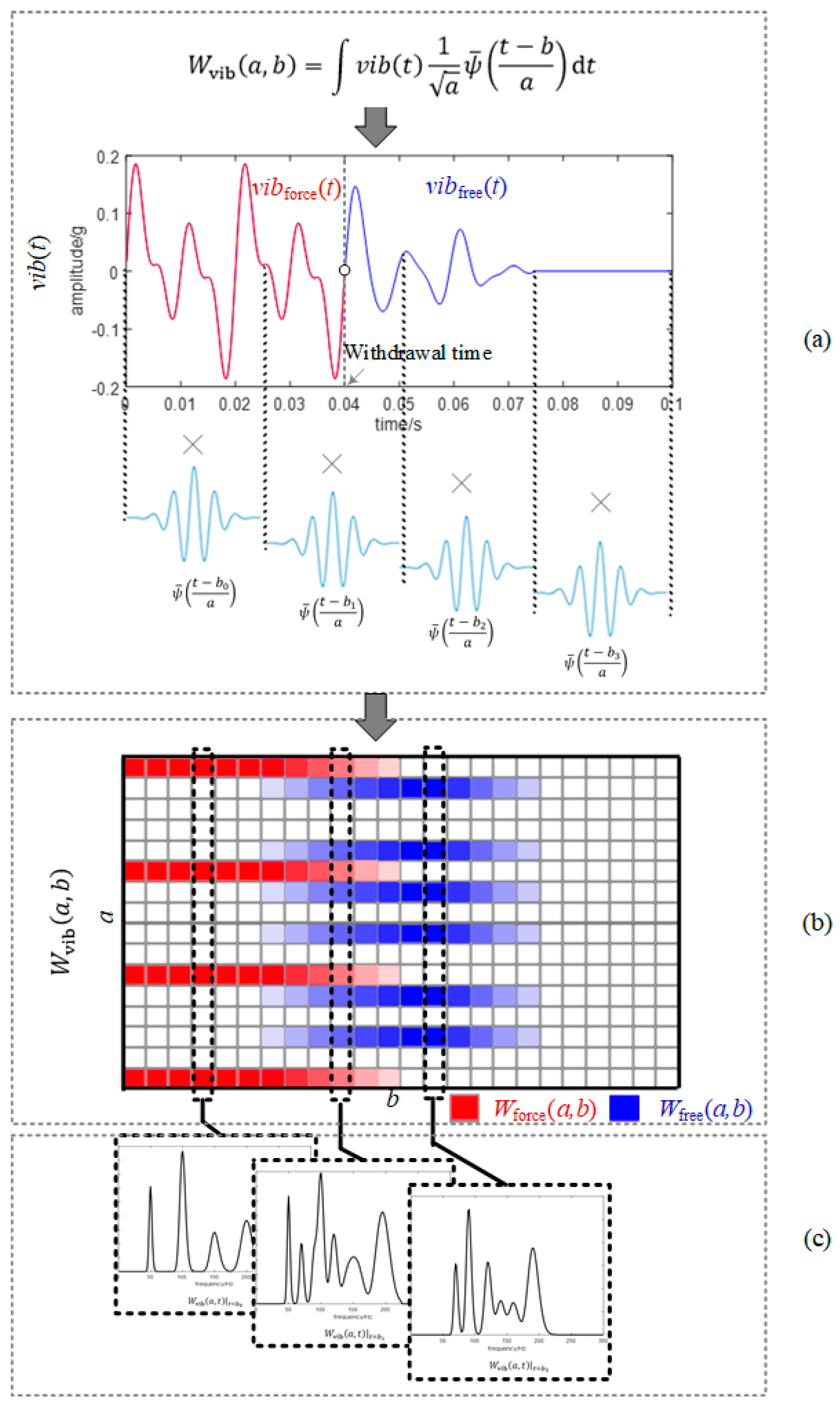
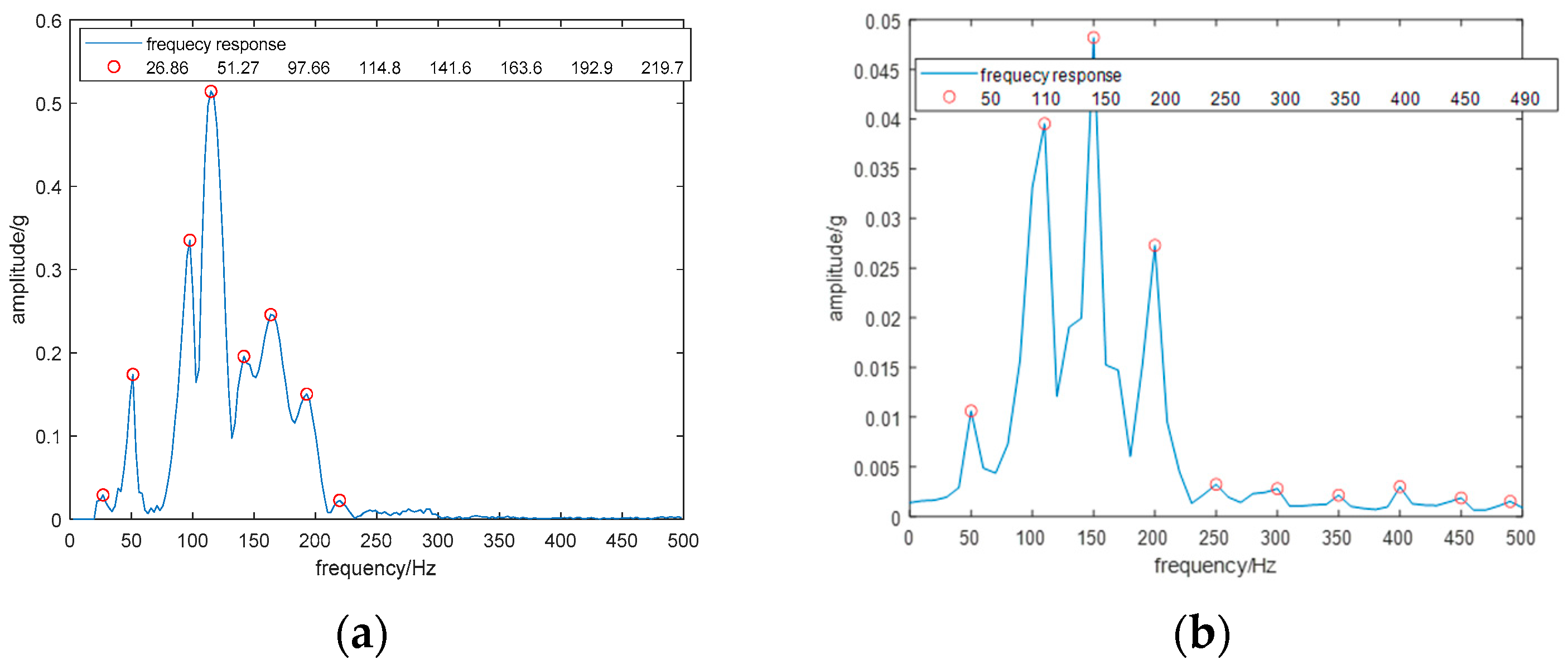
3.1. Time–Frequency Domain Characteristics of Vibration Signature
3.2. Identification of Modal Frequencies Based on the Time–Frequency Domain Characteristics
3.3. A Vibration-Based OMA Approach for Transformer Condition Assessment
- Step 1: Collect transformer vibration before and after a transient operation.
- Step 2: Compute the CWT of the transformer’s vibration signal .
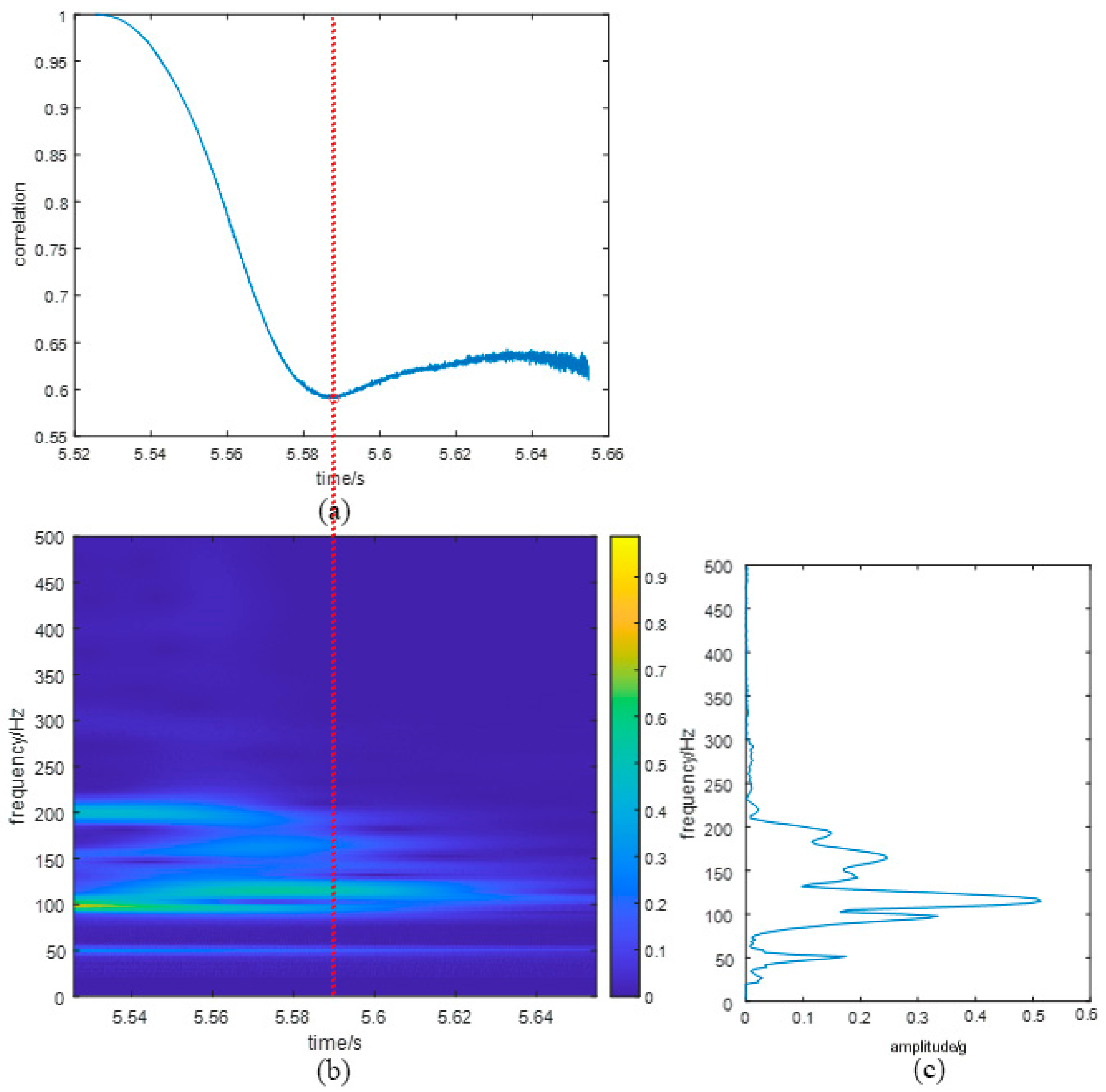
- Step 3: Calculate the similarity coefficient as a function of time based on Equation (14).
- Step 4: Determine the time point by selecting a minimum value at the turning point of . Regard as the moment when the modal frequency components have the highest proportion.
- Step 5: Extract the instantaneous frequency spectrum at this time point as the modal spectrum.
- Step 6: Calculate a measure of similarity between the estimated modal spectrum and the initial modal spectrum obtained under a healthy state.
- Step 7: Determine the condition of the transformer using that proposed indicator.
4. Case Study
4.1. Case 1: Winding Looseness Assessment under Power-Off Condition
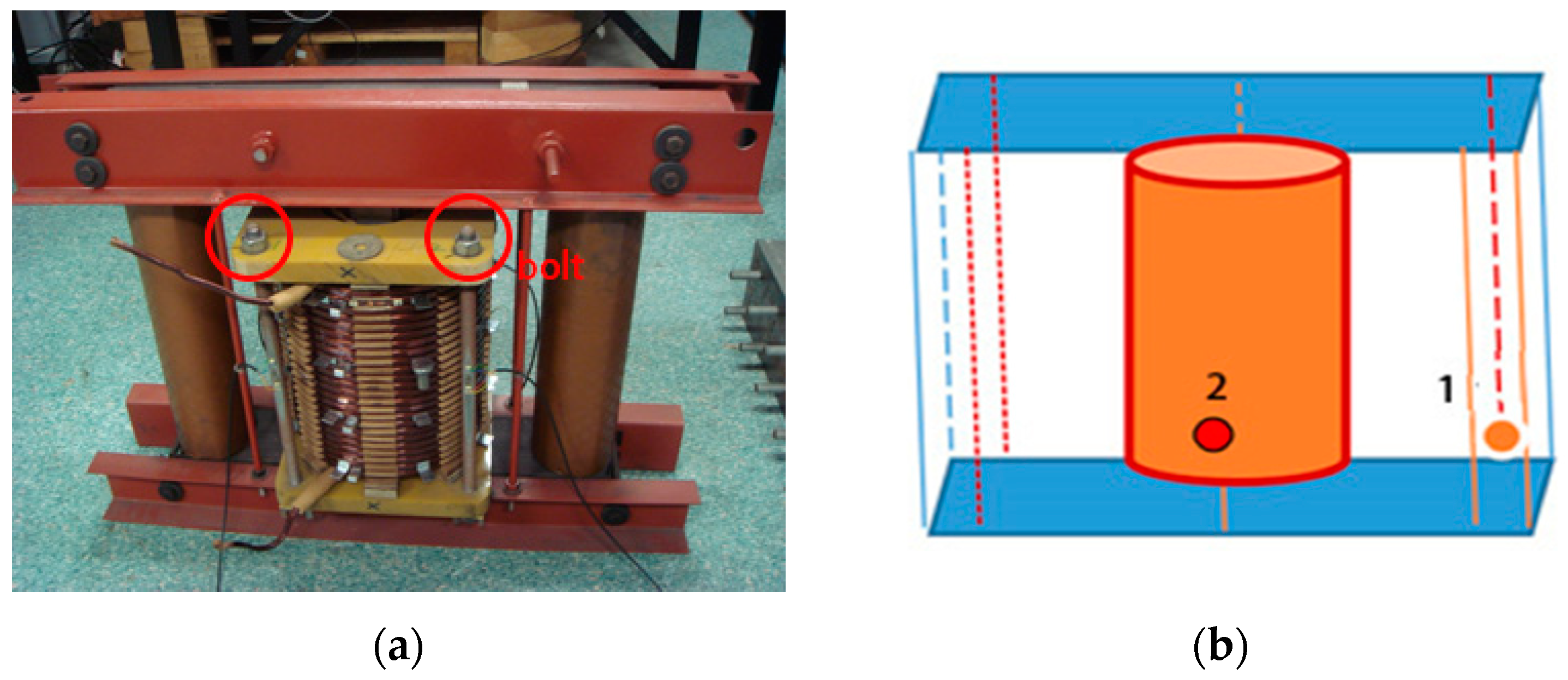
4.1.1. Experimental Setup
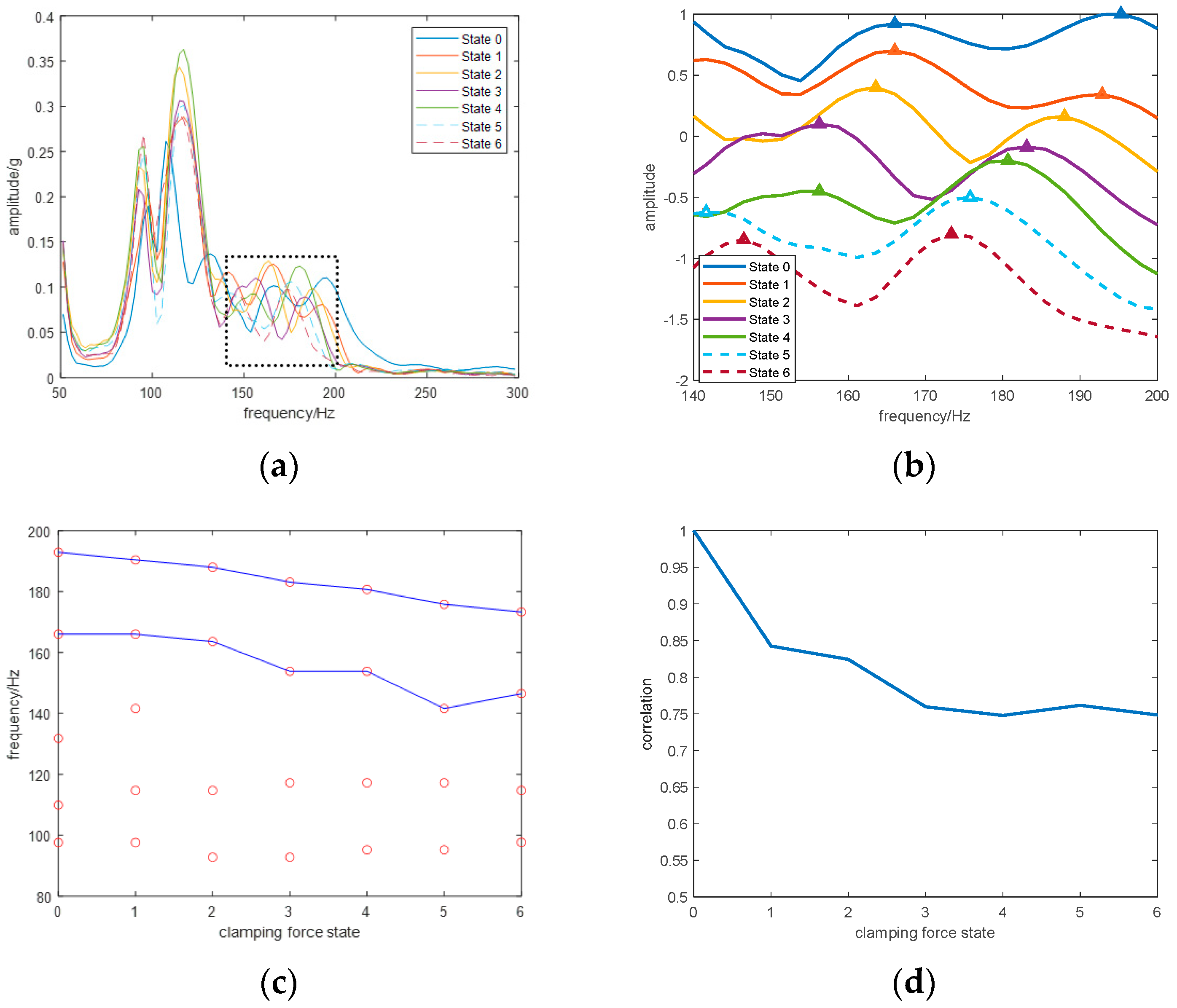
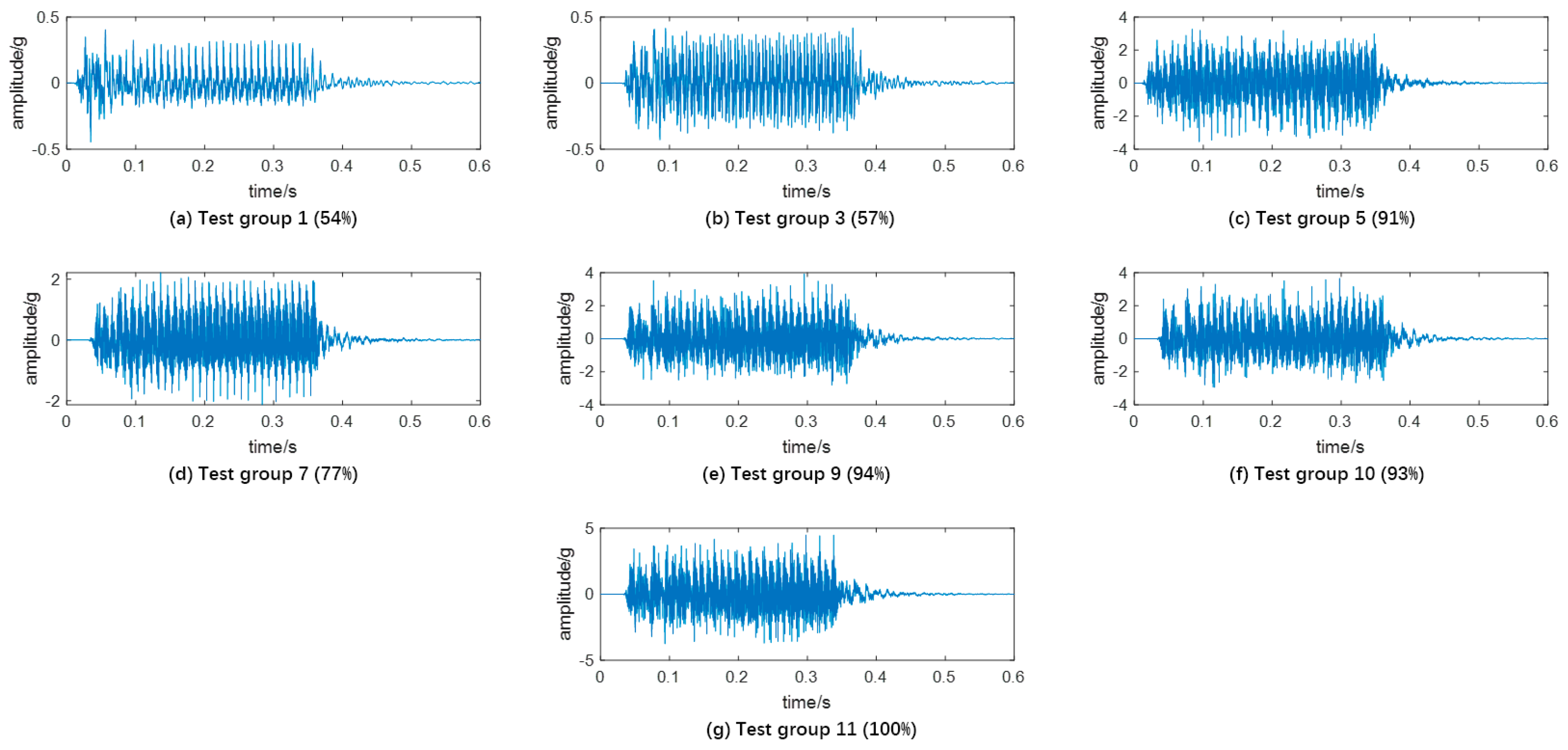
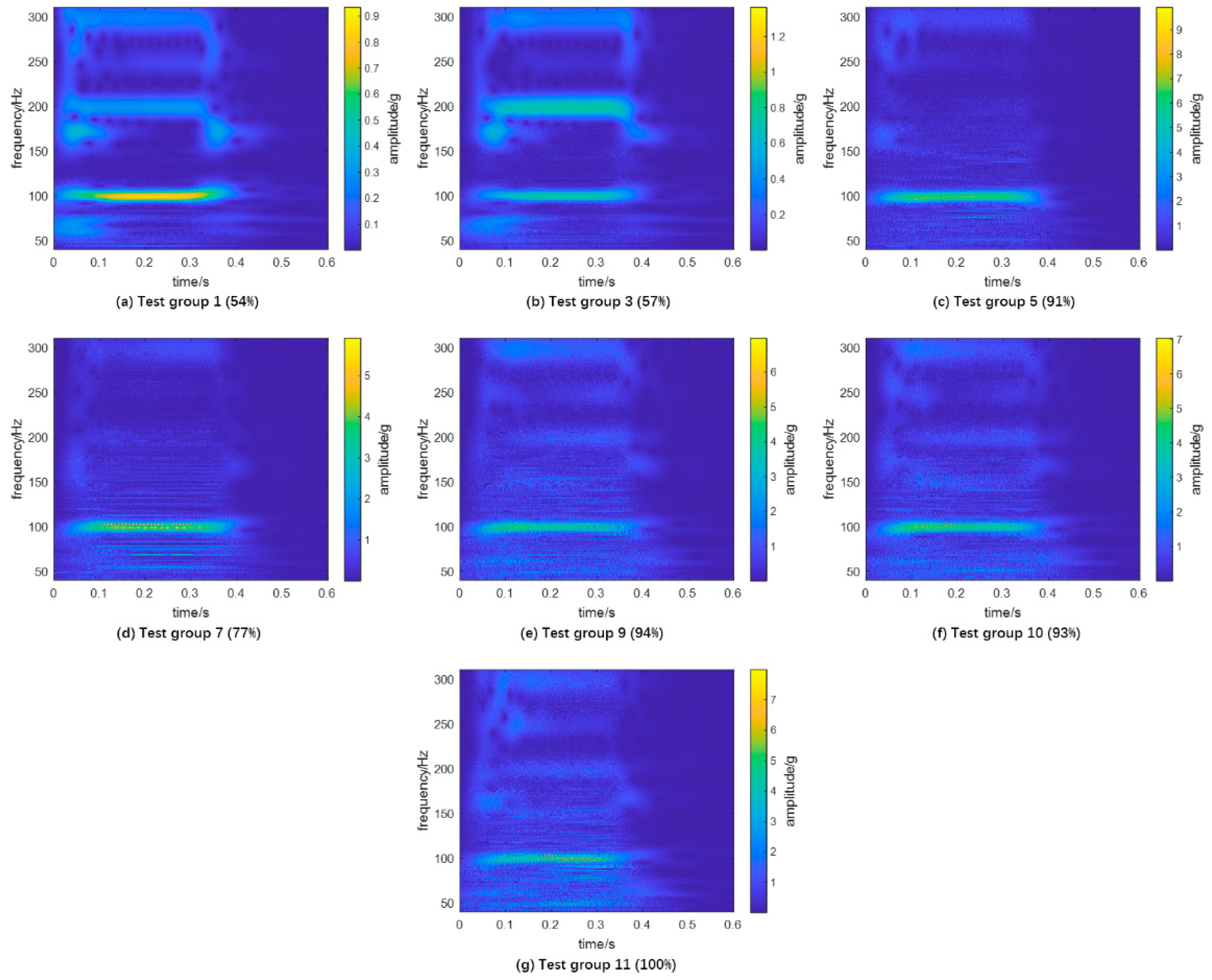
4.1.2. Results
4.1.3. Discussion
- (1)
- The proposed algorithm is proven to be able to extract the modal frequency spectrum from the vibration signal with high-frequency resolution.
- (2)
- According to Equation (11), a decrease in stiffness due to the loosening of the winding clamping force will cause the natural frequencies of the winding to decrease. As a result, the extracted modal frequency spectrum changes as the looseness of the winding clamping force changes. Some frequencies, especially higher modal frequencies, gradually shift toward lower frequencies as the clamping force loosens.
- (3)
- Changes in the clamping force looseness cause changes in the results at both measurement points. This is because changes in the mechanical properties of the winding are included in the vibration transmission path of the core as a consequence of the coupling between the core and the winding. The results at the measurement point on the winding show a higher sensitivity to changes in mechanical properties than the results at the measurement point on the core.
- (4)
- Compared with the damping ratio, the proposed indicator demonstrates better sensitivity, accuracy, and robustness in detecting looseness in winding clamping force.
4.2. Case 2: Winding Deformation Detection under Multiple Short-Circuit Conditions
4.2.1. Experimental Setup
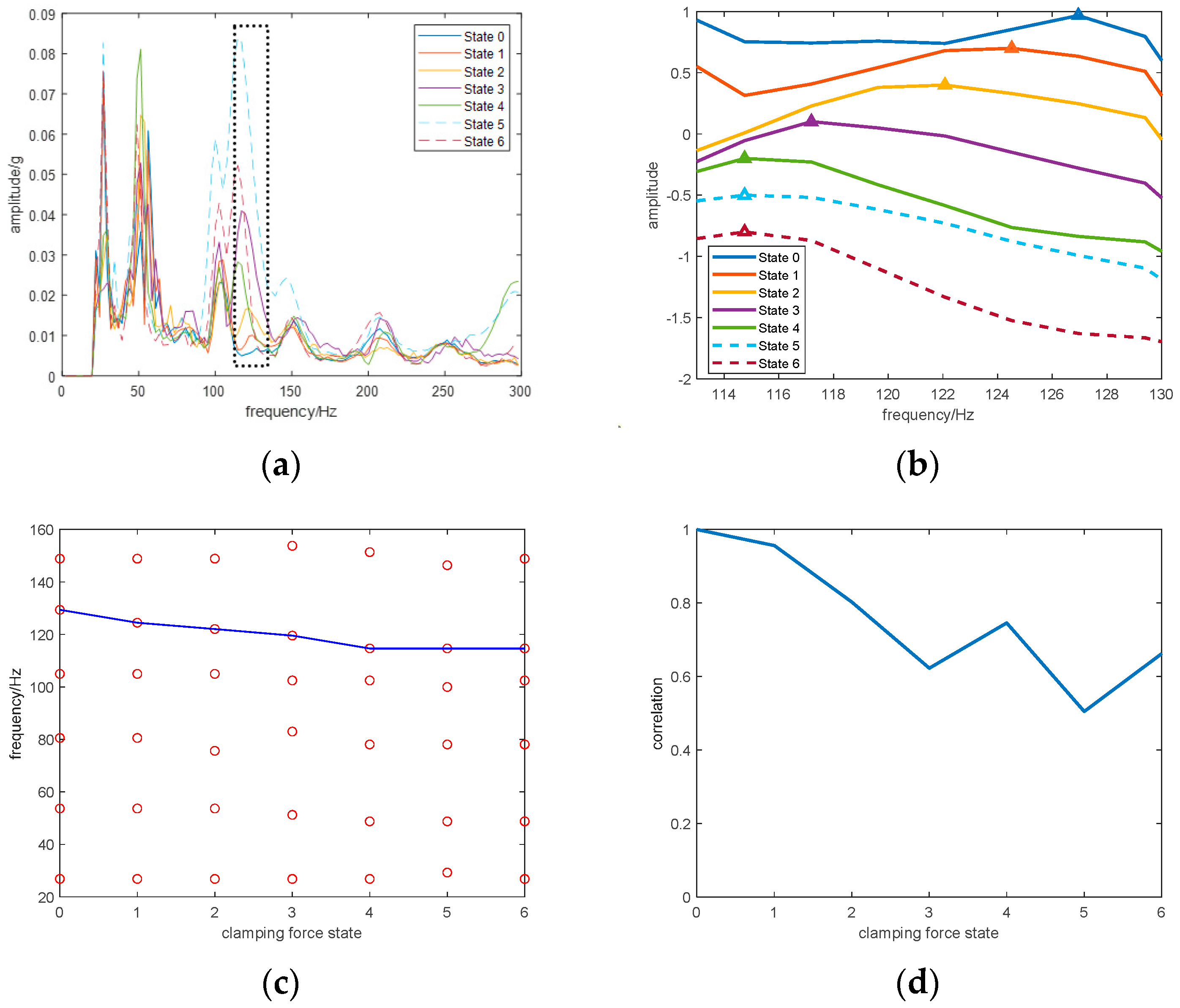
4.2.2. Results
4.2.3. Discussion
- (1)
- The proposed algorithm has been proven to be able to extract the modal frequency spectrum from the vibration signal under short-circuit conditions.
- (2)
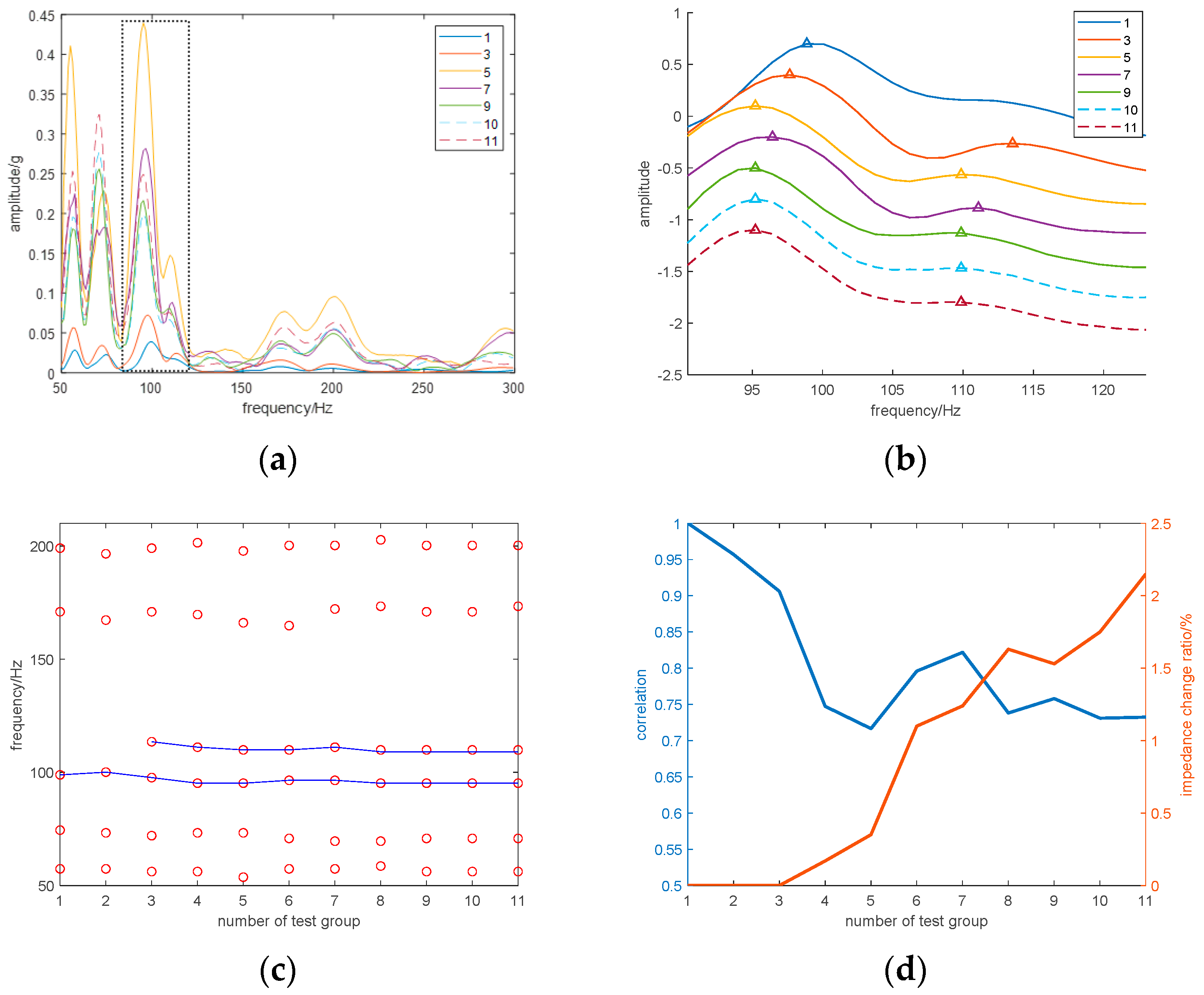
- Although the measurement points are located on the tank surface, the estimated modal frequency spectrums of vibration vary with the repetition of the short-circuit test. Compared with the decrease of modal frequency caused by the clamping force looseness, the change in modal frequency caused by the short-circuit impacts exhibits diverse characteristics, including an increase, decrease, and splitting of modal frequencies.
- (3)
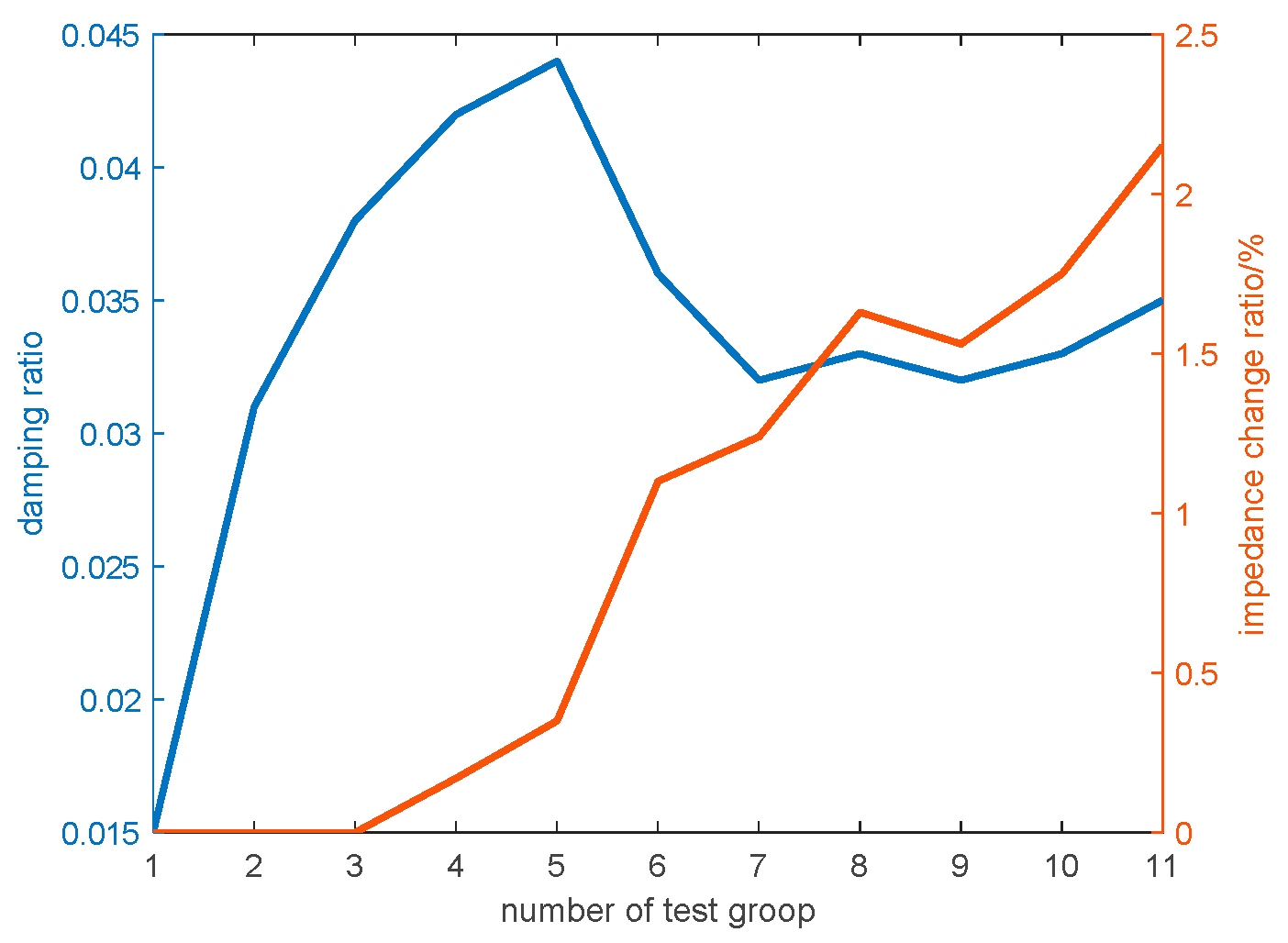
- The change of the similarity coefficient is opposite to the change of the impedance change ratio, which means the similarity coefficient is also a reliable index to evaluate the winding condition.
- (4)
- As the short-circuit impact test is repeated, some modal frequencies undergo significant changes while others change slightly. Therefore, it is necessary to consider the entire modal spectrum in condition assessment rather than solely based on changes in individual modal frequencies.
- (5)
- The winding deformation causes changes in the results at both measurement points. This is because the changes in the mechanical properties of the winding are also included in the vibration transmission paths to the tank surface. However, the results at the measurement point near the deformed winding show higher sensitivity to changes in the mechanical properties than the results at the other measurement point.
- (6)
- The proposed indicator demonstrates greater accuracy than the damping ratio in detecting winding deformation.
5. Conclusions
- In order to obtain a higher frequency resolution, the vibration before and during a transient process is used, which includes both force vibration and modal vibration components. A time–frequency analysis-based algorithm is proposed to separate the modal vibration and forced vibration components. The proposed algorithm is proven to be able to extract the modal frequency spectrum during transient processes.
- When the winding is loosened, changes are observed in the extracted modal frequency spectrum. Some frequencies, especially higher modal frequencies, gradually shift toward lower frequencies as the clamping force loosens. It seems that higher modal frequencies are much more sensitive to the looseness of the winding clamping force. Besides the decrease of the frequencies, disappearances of frequencies are also observed in the modal frequency spectrum. This observation clearly supports the idea that the entire spectrum distribution should be considered in condition assessment. Furthermore, the proposed indicator is used to describe the difference between the modal frequency spectrums and the initial spectrum. The indicator decreases as the clamping force decreases, offering a sensitive and accurate measure of the winding’s mechanical condition.
- A cumulative effect is generated when the transformer suffers multiple short circuit impacts, which will lead to changes in the mechanical condition of the windings. With repetition of the short-circuit test, the extracted modal frequency spectrum undergoes significant changes. Compared with the decrease of modal frequency caused by the clamping force looseness, the change in modal frequencies caused by the short-circuit impacts exhibits diverse patterns. This once again illustrates the importance of analyzing the entire spectrum distribution. In addition, the proposed indicator, which is used to describe changes in the modal frequency spectrum, decreases with the repetition of the short-circuit test. The results are consistent with the change of the impedance change ratio, enabling the analysis of the cumulative effect of the transformer.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Usha, K.; Joseph, J.; Usa, S. Location of Faults in Transformer Winding using SFRA. In Proceedings of the IEEE 1st International Conference on Condition Assessment Techniques in Electrical Systems (IEEE CATCON), Kolkata, India, 6–8 December 2013. [Google Scholar]
- Wang, Y.; Xu, D.; Li, Y.; Zhang, C. A Study on Instrumentation Techniques in LVI Method for Detecting Transformer Winding Deformation. High Volt. Eng. 1998, 03, 24–34. (In Chinese) [Google Scholar]
- Li, Z.; He, Y.; Xing, Z.; Chen, M. Minor Fault Diagnosis of Transformer Winding using Polar Plot based on Frequency Response Analysis. Int. J. Electr. Power Energy Syst. 2023, 152, 109173. [Google Scholar] [CrossRef]
- Li, C.; Chen, J.; Yang, C.; Yang, J.; Liu, Z.; Davari, P. Convolutional Neural Network-Based Transformer Fault Diagnosis Using Vibration Signals. Sensors 2023, 23, 4781. [Google Scholar] [CrossRef] [PubMed]
- Han, S.; Wang, B.; Liao, S.; Gao, F.; Chen, M. Defect Identification Method for Transformer End Pad Falling Based on Acoustic Stability Feature Analysis. Sensors 2023, 23, 3258. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhou, G.; Zeng, C.; Zhang, W.; Ren, Y.; Ke, Y.; Chu, H.; Suo, C. Research on On-Line Detection Method of Transformer Winding Deformation Based on VFTO. Sensors 2021, 21, 7386. [Google Scholar] [CrossRef] [PubMed]
- Huerta-Rosales, J.R.; Granados-Lieberman, D.; Garcia-Perez, A.; Camarena-Martinez, D.; Amezquita-Sanchez, J.P.; Valtierra-Rodriguez, M. Short-Circuited Turn Fault Diagnosis in Transformers by Using Vibration Signals, Statistical Time Features, and Support Vector Machines on FPGA. Sensors 2021, 21, 3598. [Google Scholar] [CrossRef] [PubMed]
- Hong, K.; Wang, L.; Xu, S. A Variational Mode Decomposition Approach for Degradation Assessment of Power Transformer Windings. IEEE Trans. Instrum. Meas. 2019, 68, 1221–1229. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, J. Comparison of Mechanically and Electrically Excited Vibration Frequency Responses of a Small Distribution Transformer. IEEE Trans. Power Deliv. 2017, 32, 1173–1180. [Google Scholar] [CrossRef]
- Zhang, F.; Ji, S.; Ma, H.; Saha, T.K. Operational Modal Analysis of Transformer Windings. IEEE Trans. Power Deliv. 2020, 35, 1285–1298. [Google Scholar] [CrossRef]
- Li, X.; Yue, X.; Huang, W.; Dong, X.; Peng, Z. Vibration Response Transmissibility and Operational Modal Analysis Methods: A Review and Comparative Study. J. Vib. Shock. 2019, 38, 24–34+45. [Google Scholar]
- Shao, Y.; Xu, J.; Rao, Z.; Jin, Z.; Jiang, Y.; Fu, J. On-line diagnosis for a transformer winding’s state under short-circuit shock. J. Vib. Shock. 2011, 30, 173–176. [Google Scholar]
- Wang, F.; Li, Q.; Jin, Z. On-line Monitoring the Winding Condition of Power Transformer Under Sudden Short-circuit Based on the Vibration Analysis Method. Control Eng. China 2011, 18, 596–599. [Google Scholar]
- Zhang, K.; Wang, F.; Liao, T.; Jin, Z. Detection of Transformer Winding Deformation under Sudden Short-Circuit Impact Based on Complex Wavelet Algorithm. Diangong Jishu Xuebao/Trans. China Electrotech. Soc. 2014, 29, 327–332. [Google Scholar]
- Soria, L.; Peeters, B.; Auweraer, H.V.D. Automatic in-Operation Modal Analysis for the continuous monitoring of high-speed railway bridges. In Proceedings of the 8th International Conference on Structural Dynamics (EURODYN 2011), Leuven, Belgium, 4–6 July 2011. [Google Scholar]
- Lin, C.; Ou, X.; Yang, X.; Sun, W.; Rao, Z.; He, H.; Zhan, C. Vibration Characteristics and Detection of Inter-turn Short-circuit Fault Under Transformer Suffering Short-circuit Impact. High Volt. Eng. 2018, 44, 3569–3576. [Google Scholar]
- Wang, Y.; Pan, J. Applications of Operational Modal Analysis to a Single-Phase Distribution Transformer. IEEE Trans. Power Deliv. 2015, 30, 2061–2063. [Google Scholar] [CrossRef]
- Hu, Y. Research on Fault Diagnosis Method of Transformer Windings Based on Spatial Vibration Distribution and Operational Modal Analysis. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2020. (In Chinese). [Google Scholar] [CrossRef]
- Hong, K.; Huang, X.; Xu, S. A Study of Nonlinear Behavior of Transformer Windings in Structural Degradation Detection. J. Vib. Acoust. 2020, 142, 011020. [Google Scholar] [CrossRef]
- Zhou, H.; Hong, K.; Huang, H.; Zhou, J. Transformer Winding Fault Detection by Vibration Analysis Methods. Appl. Acoust. 2016, 114, 136–146. [Google Scholar] [CrossRef]
- Hong, K. Research on the On-Line Detection Method of Mechanical Stability of Power Transformer Windings Based on Vibration Analysis. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2016. (In Chinese). [Google Scholar]
- Cao, S.; Zhang, W.; Xiao, L. Modal Analysis of Vibrating Structures: Theory, Experiment, and Application; Tianjin University Press: Tianjin, China, 2001. [Google Scholar]
- Qian, G. IEEE In Detecting Transformer Winding Deformation Fault Types Based on Continuous Wavelet Transform. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Harbin, China, 7–10 August 2016; pp. 1886–1891. [Google Scholar]
- Blackburn, G.A. Wavelet decomposition of hyperspectral data: A novel approach to quantifying pigment concentrations in vegetation. Int. J. Remote Sens. 2007, 11–12, 2831–2855. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, J.; Huang, H. An experimental study of winding vibration of a single-phase power transformer using a laser Doppler vibrometer. Appl. Acoust. 2015, 87, 30–37. [Google Scholar] [CrossRef]
- Xu, F.; Shao, Y.; Jin, Z.; Guan, H. Experimental Study of Measuring Point Selection for Transformer Vibration Detection. East China Electr. Power 2012, 40, 274–277. [Google Scholar]
- IEC 60076-5; Power Transformers—Part 5: Ability to Withstand Short Circuit. IEC (International Electrotechnical Commission): Geneva, Switzerland, 2006.



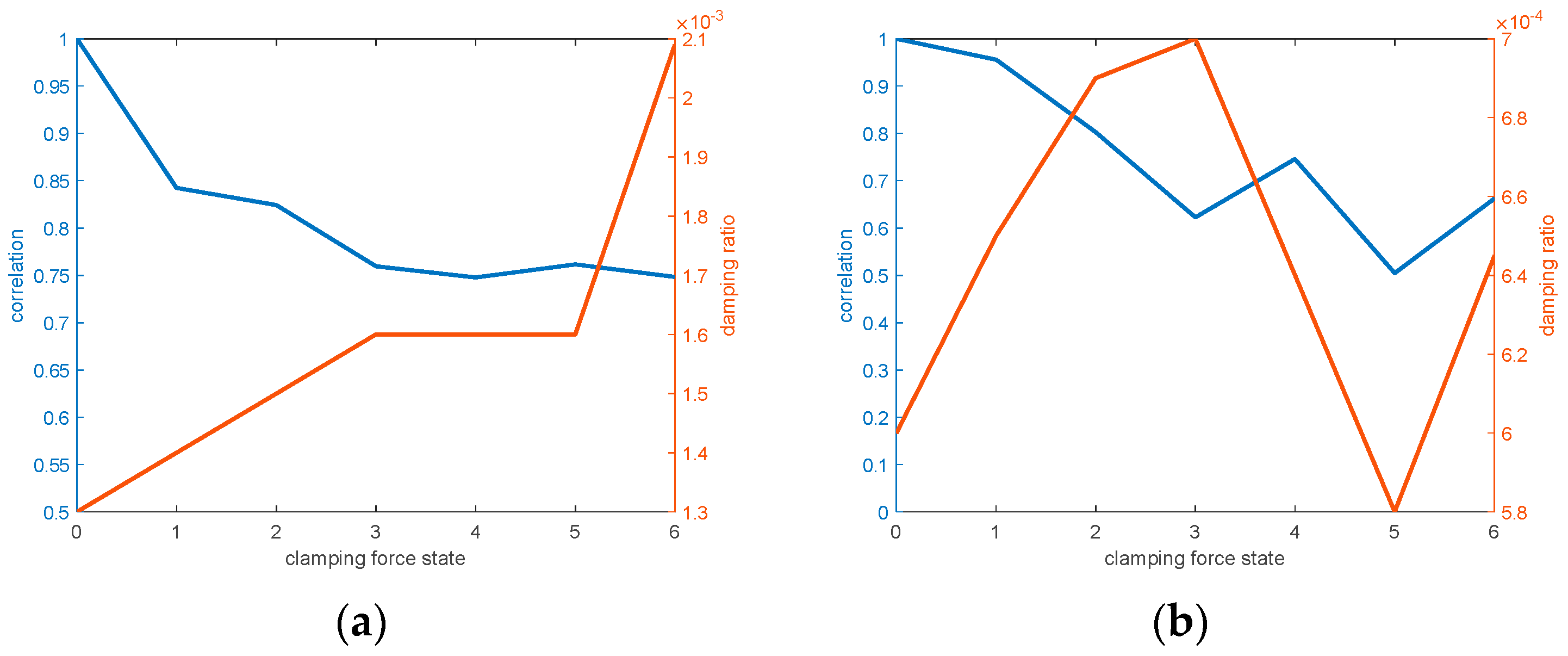



| Clamping Force State | Number of Turns Loosened |
|---|---|
| State 0 | 0 |
| State 1 | 1/4 |
| State 2 | 1/2 |
| State 3 | 3/4 |
| State 4 | 1 |
| State 5 | 5/4 |
| State 6 | 3/2 |
| Test Group Number (Short-Circuit Current Percentage) | Impedance Change Ratio (%) |
|---|---|
| 1 (54%) | 0.00 |
| 2 (75%) | 0.00 |
| 3 (57%) | 0.00 |
| 4 (83%) | 0.17 |
| 5 (91%) | 0.35 |
| 6 (77%) | 1.10 |
| 7 (77%) | 1.24 |
| 8 (94%) | 1.63 |
| 9 (94%) | 1.53 |
| 10 (93%) | 1.75 |
| 11 (100%) | 2.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Y.; Zhao, J.; Hong, K.; Wang, N.; Zheng, J. Assessment of the Winding Mechanical Condition Based on Transformer Vibration during Transient Processes. Electronics 2024, 13, 2519. https://doi.org/10.3390/electronics13132519
Yuan Y, Zhao J, Hong K, Wang N, Zheng J. Assessment of the Winding Mechanical Condition Based on Transformer Vibration during Transient Processes. Electronics. 2024; 13(13):2519. https://doi.org/10.3390/electronics13132519
Chicago/Turabian StyleYuan, Yao, Jiafeng Zhao, Kaixing Hong, Ning Wang, and Jing Zheng. 2024. "Assessment of the Winding Mechanical Condition Based on Transformer Vibration during Transient Processes" Electronics 13, no. 13: 2519. https://doi.org/10.3390/electronics13132519
APA StyleYuan, Y., Zhao, J., Hong, K., Wang, N., & Zheng, J. (2024). Assessment of the Winding Mechanical Condition Based on Transformer Vibration during Transient Processes. Electronics, 13(13), 2519. https://doi.org/10.3390/electronics13132519






