Double-Timescale Multi-Agent Deep Reinforcement Learning for Flexible Payload in VHTS Systems
Abstract
:1. Introduction
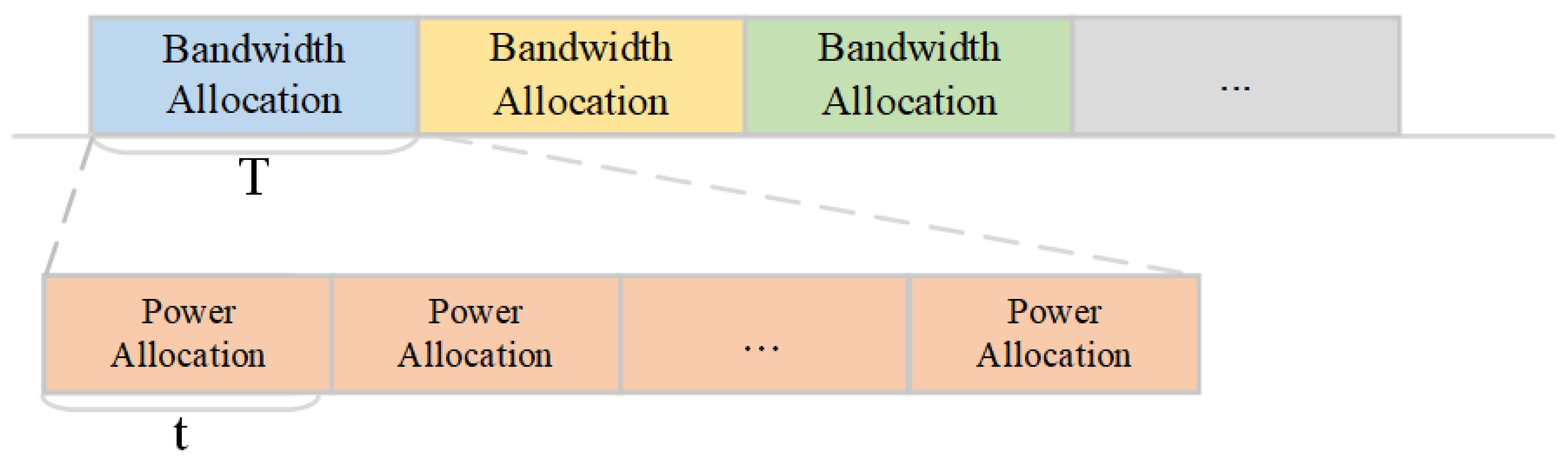
- A double-timescale framework is proposed in this paper to accommodate uneven time-varying traffic demands in aviation-type scenarios. In this framework, we allocate bandwidth and power on a large timescale, and subsequently allocate power on multiple small timescales. Compared to simultaneously adjusting the bandwidth and power resources, the double-timescale resource management approach enables us to fully and flexibly utilize all resources without compromising system stability, allowing for the better adaptation to the specific changes in aviation demands.
- The MADRL-based DT-BPA algorithm is employed to construct a two-layer network for addressing the DRM problem, which is low in complexity for offline training and online decision making. We model the DRM problem as a Markov decision process (MDP) and utilize DRL networks for offline training, which reduces the complexity of online execution to meet aviation demands in real time. Additionally, multi-agent method is used to cope with the exponential growth of the action space with the number of beams.
- We conduct extensive simulation experiments to evaluate the performance of the proposed scheme. The numerical results demonstrate that, when compared with the benchmark scheme, the proposed strategy can better match the multi-beam traffic demands over a long-time scale. The proposed scheme effectively utilizes the double-timescale resource management framework, enabling the better adaptation to time-varying traffic demands. On the premise of meeting the demand-matching degree, the power consumption of the system is also reduced, so the resource utilization and overall performance of the system are improved to a certain extent.
2. Related Work
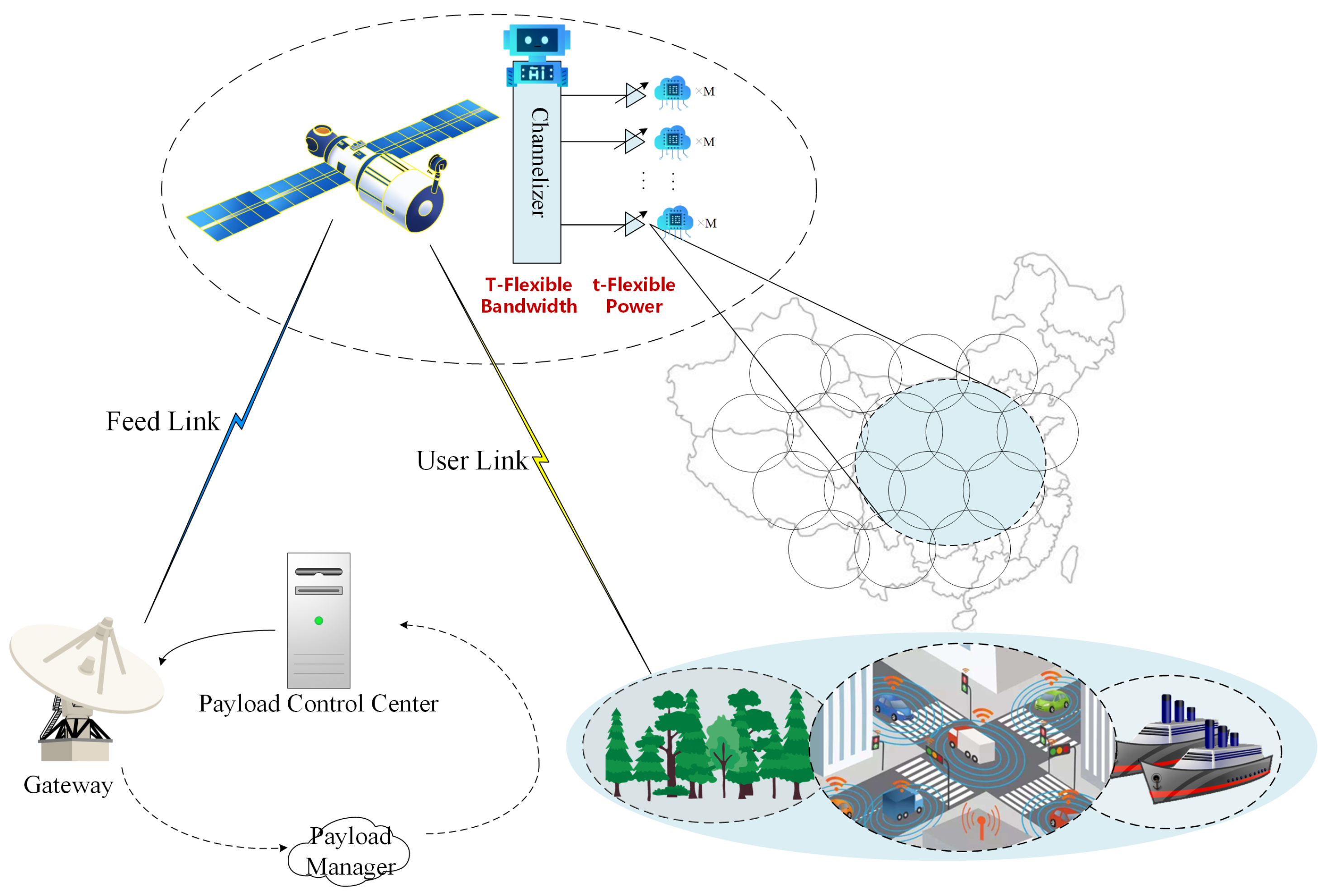
3. System Model and Problem Formulation
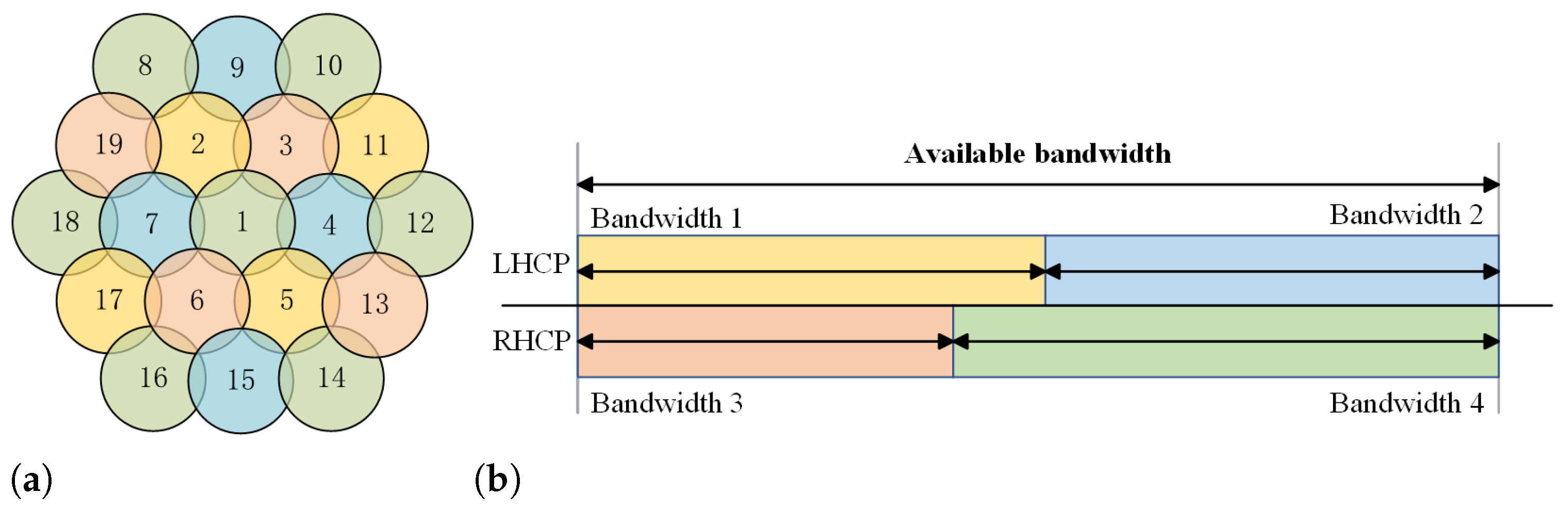
3.1. System Model
3.2. Link Budget
3.3. Problem Formulation
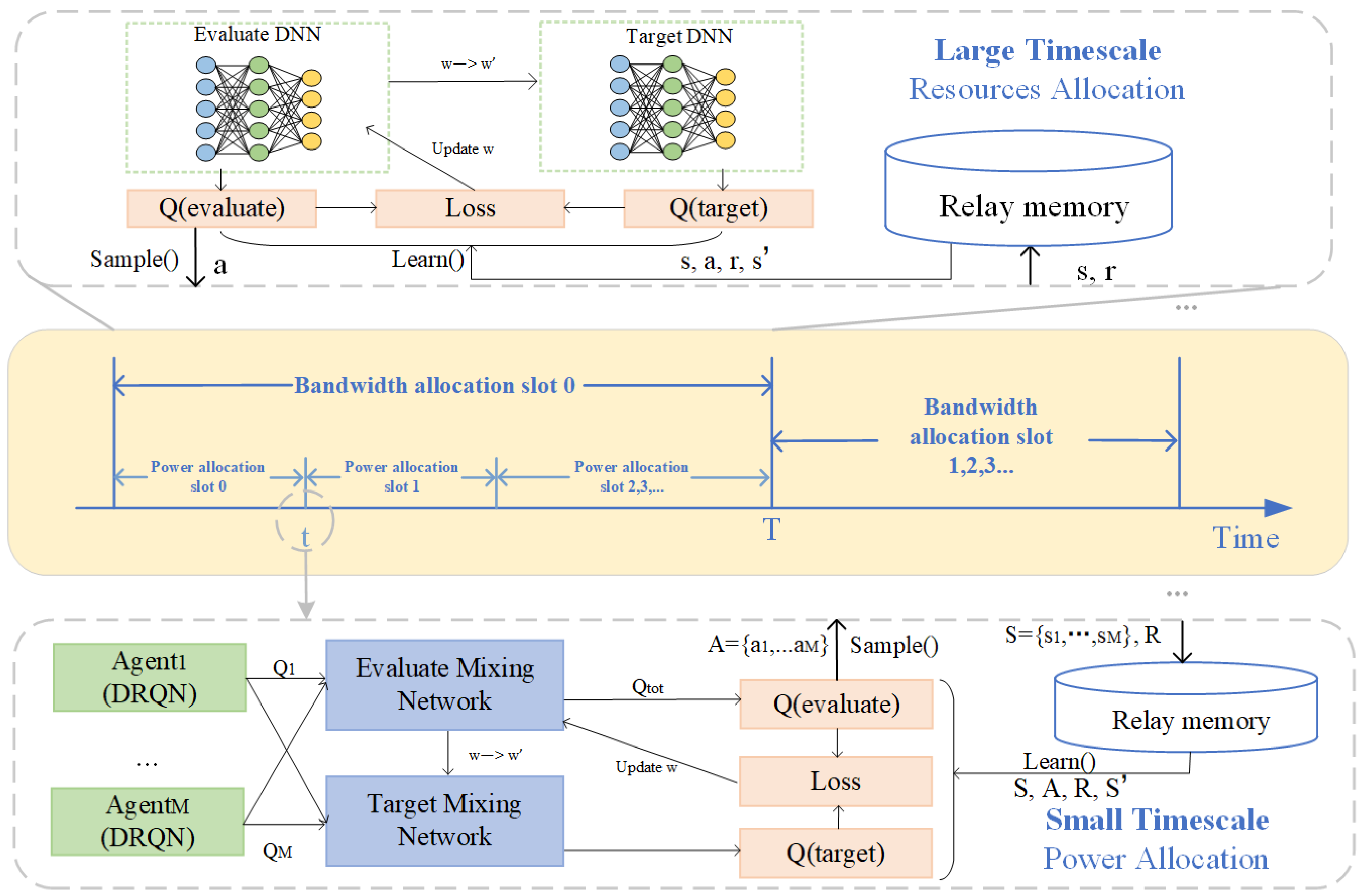
4. Double-Timescale MADRL Algorithm
4.1. Small-Timescale Power Allocation Strategy
- State space
- 2.
- Action space
- 3.
- Reward
- 4.
- Value function
| Algorithm 1 QMIX-based power allocation algorithm. |
| Input: network parameters and system parameters. Output: power allocation strategy.
|
4.2. Large-Timescale Resources Allocation Strategy
- State space
- 2.
- Action space
- 3.
- Reward
| Algorithm 2 DQN-based resources allocation algorithm. |
| Input: network parameters and system parameters. Output: bandwidth and power allocation strategy.
|
5. Performance Evaluation
5.1. Simulation Setting
- Single-timescale management of bandwidth and power: For the change in the traffic demands during a period, only the bandwidth and power resources are managed at the same time on a large timescale.
- Proportional allocation of bandwidth and power (PABP): For the difference in traffic demand of each beam, the power and bandwidth resources are allocated according to the proportion of demand.
- QMIX [39]: Each agent manages the bandwidth of each frequency color and the power of all beams using the bandwidth, and uses the QMIX algorithm for training.
- DQN [40]: Single agent manages the bandwidth of all frequency colors and the power of all beams in the system, and uses the DQN algorithm for training.
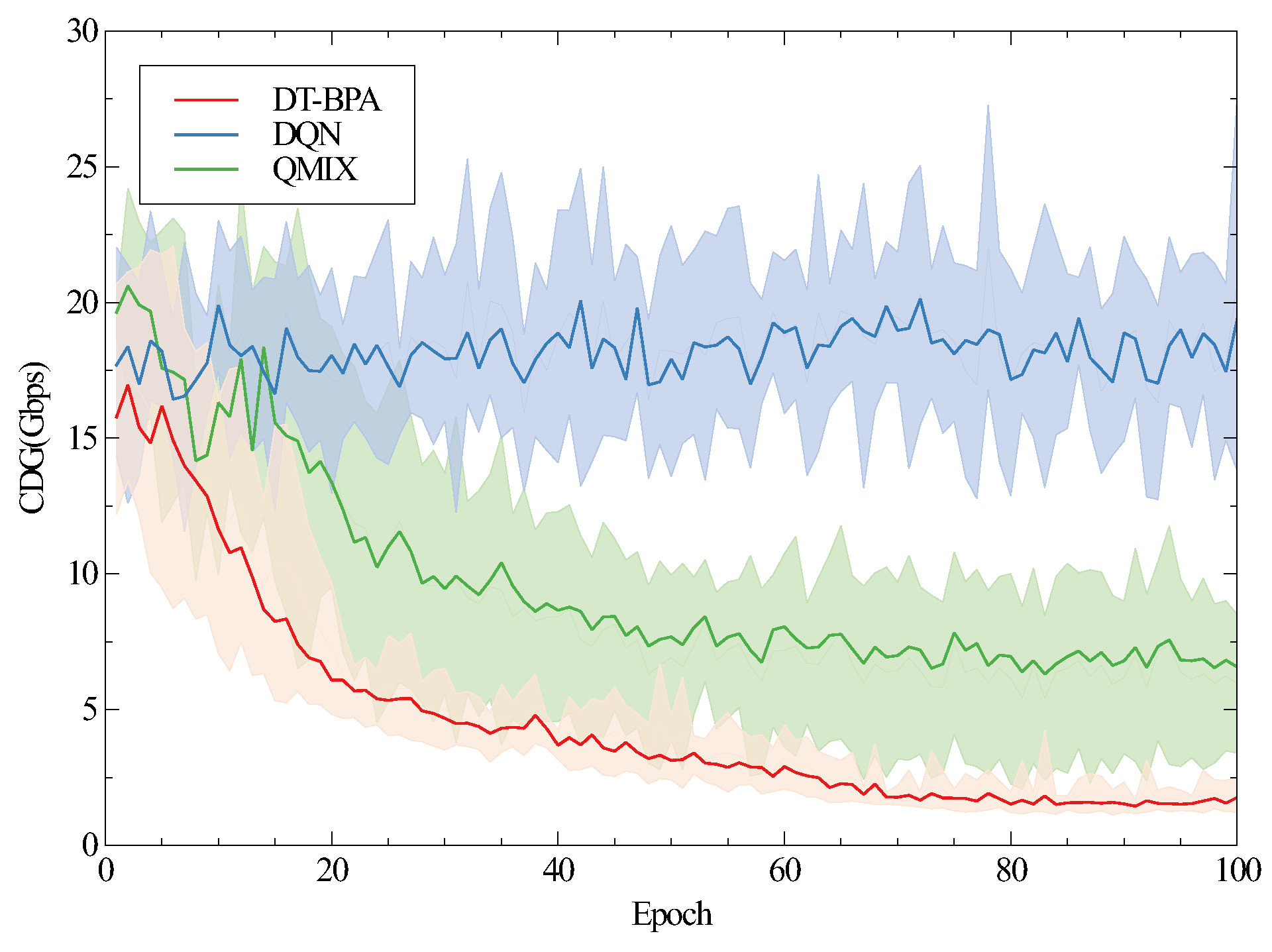
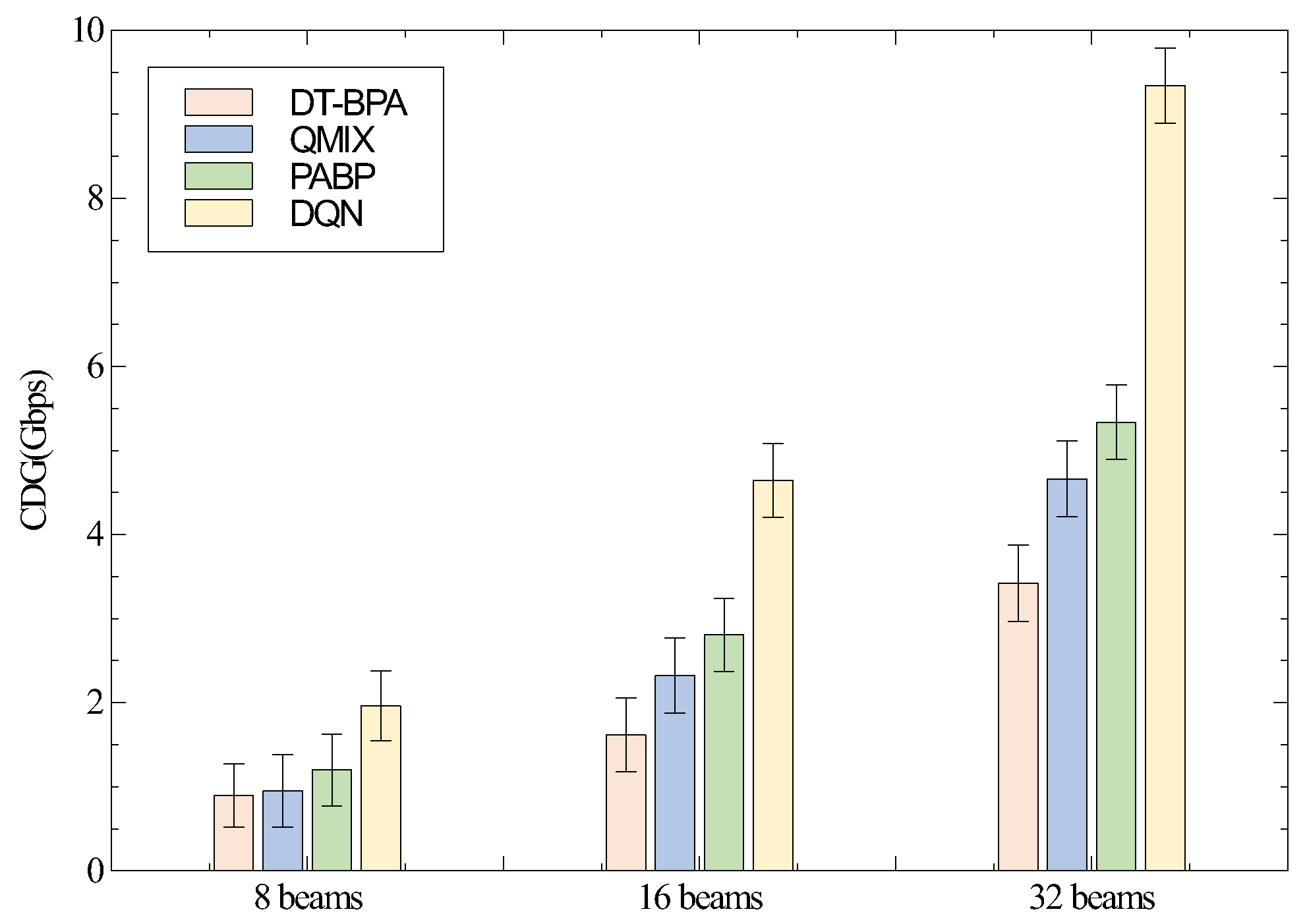
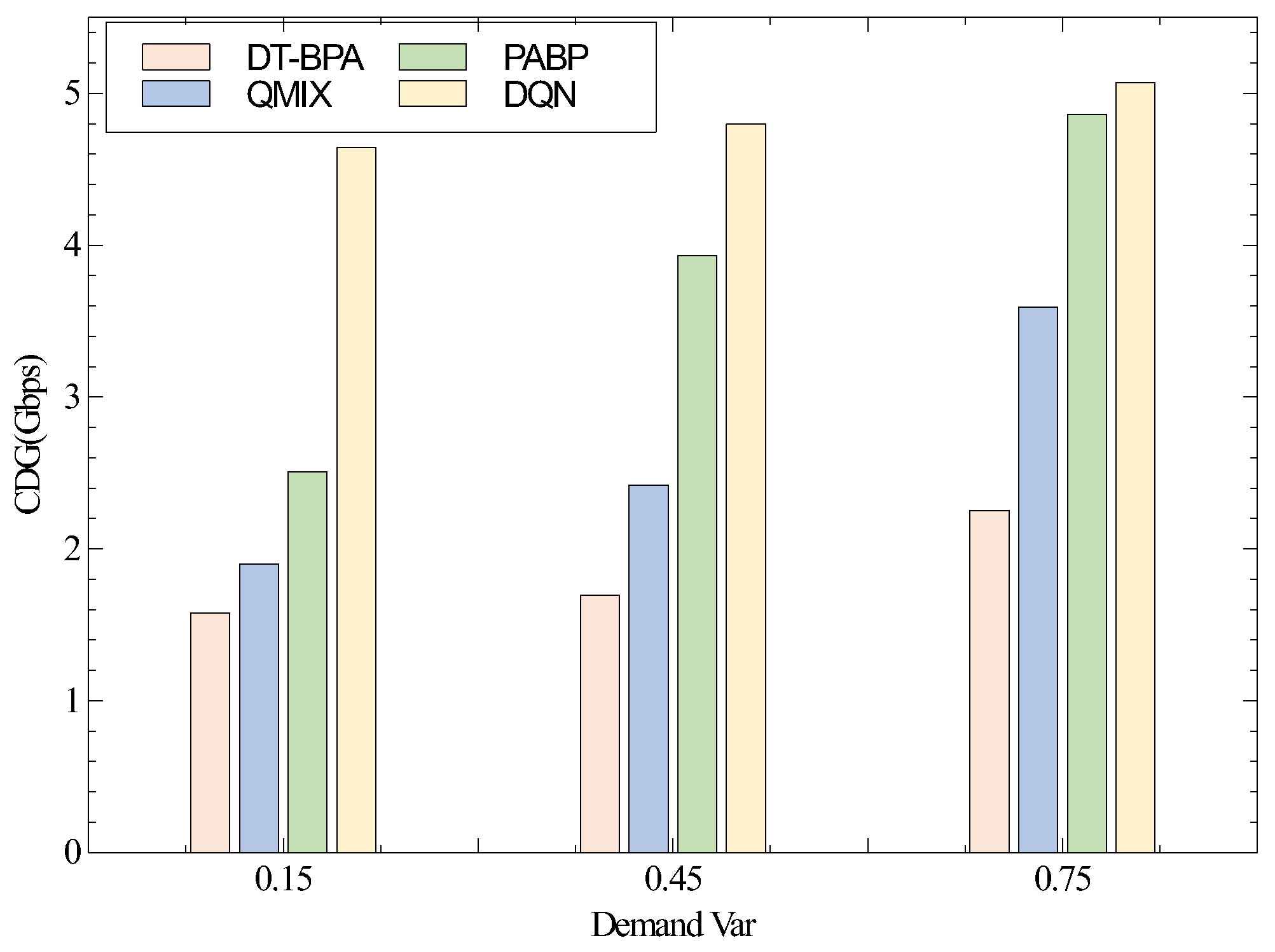
5.2. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Saad, W.; Bennis, M.; Chen, M. A vision of 6G wireless systems: Applications, trends, technologies, and open research problems. IEEE Netw. 2019, 34, 134–142. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiao, Y.; Ma, Z.; Xiao, M.; Ding, Z.; Lei, X.; Karagiannidis, G.K.; Fan, P. 6G wireless networks: Vision, requirements, architecture, and key technologies. IEEE Veh. Technol. Mag. 2019, 14, 28–41. [Google Scholar] [CrossRef]
- Tataria, H.; Shafi, M.; Molisch, A.F.; Dohler, M.; Sjöland, H.; Tufvesson, F. 6G wireless systems: Vision, requirements, challenges, insights, and opportunities. Proc. IEEE 2021, 109, 1166–1199. [Google Scholar] [CrossRef]
- Yang, P.; Xiao, Y.; Xiao, M.; Li, S. 6G wireless communications: Vision and potential techniques. IEEE Netw. 2019, 33, 70–75. [Google Scholar] [CrossRef]
- Giordani, M.; Zorzi, M. Non-terrestrial networks in the 6G era: Challenges and opportunities. IEEE Netw. 2020, 35, 244–251. [Google Scholar] [CrossRef]
- Giordani, M.; Zorzi, M. Satellite communication at millimeter waves: A key enabler of the 6G era. In Proceedings of the International Conference on Computing, Networking and Communications (ICNC), Big Island, HI, USA, 19–22 February 2020; pp. 383–388. [Google Scholar]
- Zhu, X.; Jiang, C. Integrated satellite-terrestrial networks toward 6G: Architectures, applications, and challenges. IEEE Internet Things J. 2021, 9, 437–461. [Google Scholar] [CrossRef]
- Vidal, O.; Verelst, G.; Lacan, J.; Alberty, E.; Radzik, J.; Bousquet, M. Next generation high throughput satellite system. In Proceedings of the IEEE First AESS European Conference on Satellite Telecommunications (ESTEL), Rome, Italy, 2–5 October 2012; pp. 1–7. [Google Scholar]
- Le Kernec, A.; Canuet, L.; Maho, A.; Sotom, M.; Matter, D.; Francou, L.; Edmunds, J.; Welch, M.; Kehayas, E.; Perlot, N.; et al. The H2020 VERTIGO project towards tbit/s optical feeder links. In Proceedings of the SPIE International Conference on Space Optics, Virtual, 6–11 March 2021; pp. 508–519. [Google Scholar]
- Guan, Y.; Geng, F.; Saleh, J.H. Review of high throughput satellites: Market disruptions, affordability-throughput map, and the cost per bit/second decision tree. IEEE Aerosp. Electron. Syst. Mag. 2019, 34, 64–80. [Google Scholar] [CrossRef]
- Jia, H.; Wang, Y.; Wu, W. Dynamic Resource Allocation for Remote IoT Data Collection in SAGIN. IEEE Internet Things J. 2024, 11, 20575–20589. [Google Scholar] [CrossRef]
- Al-Hraishawi, H.; Lagunas, E.; Chatzinotas, S. Traffic simulator for multibeam satellite communication systems. In Proceedings of the Advanced Satellite Multimedia Systems Conference and Signal Processing for Space Communications Workshop (ASMS/SPSC), Graz, Austria, 20–21 October 2020; pp. 1–8. [Google Scholar]
- De Gaudenzi, R.; Angeletti, P.; Petrolati, D.; Re, E. Future technologies for very high throughput satellite systems. Int. J. Satell. Commun. Netw. 2020, 38, 141–161. [Google Scholar] [CrossRef]
- Hasan, M.; Bianchi, C. Ka band enabling technologies for high throughput satellite (HTS) communications. Int. J. Satell. Commun. Netw. 2016, 34, 483–501. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W.; Wu, Q.; Cao, H.; Wang, K.; Li, J. Robust beamforming design and time allocation for IRS-assisted wireless powered communication networks. IEEE Trans. Commun. 2022, 70, 2838–2852. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W.; Cao, H.; Tang, H.; Wang, K.; Li, J. Joint communication and trajectory design for intelligent reflecting surface empowered UAV SWIPT networks. IEEE Trans. Veh. Technol. 2022, 71, 12840–12855. [Google Scholar] [CrossRef]
- Hu, X.; Liao, X.; Liu, Z.; Liu, S.; Ding, X.; Helaoui, M.; Wang, W.; Ghannouchi, F.M. Multi-agent deep reinforcement learning-based flexible satellite payload for mobile terminals. IEEE Trans. Veh. Technol. 2020, 69, 9849–9865. [Google Scholar] [CrossRef]
- Wang, H.; Liu, A.; Pan, X.; Li, J. Optimization of power allocation for a multibeam satellite communication system with interbeam interference. J. Appl. Math. 2014, 2014, 1–8. [Google Scholar] [CrossRef]
- Abdu, T.S.; Kisseleff, S.; Lagunas, E.; Chatzinotas, S. Flexible resource optimization for GEO multibeam satellite communication system. IEEE Trans. Wirel. Commun. 2021, 20, 7888–7902. [Google Scholar] [CrossRef]
- Durand, F.R.; Abrão, T. Power allocation in multibeam satellites based on particle swarm optimization. AEU Int. J. Electron. Commun. 2017, 78, 124–133. [Google Scholar] [CrossRef]
- Cocco, G.; De Cola, T.; Angelone, M.; Katona, Z.; Erl, S. Radio resource management optimization of flexible satellite payloads for DVB-S2 systems. IEEE Trans. Broadcast. 2017, 64, 266–280. [Google Scholar] [CrossRef]
- Paris, A.; Del Portillo, I.; Cameron, B.; Crawley, E. A genetic algorithm for joint power and bandwidth allocation in multibeam satellite systems. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; pp. 1–15. [Google Scholar]
- Zhang, P.; Wang, X.; Ma, Z.; Liu, S.; Song, J. An online power allocation algorithm based on deep reinforcement learning in multibeam satellite systems. Int. J. Satell. Commun. Netw. 2020, 38, 450–461. [Google Scholar] [CrossRef]
- Liao, X.; Hu, X.; Liu, Z.; Ma, S.; Xu, L.; Li, X.; Wang, W.; Ghannouchi, F.M. Distributed intelligence: A verification for multi-agent DRL-based multibeam satellite resource allocation. IEEE Commun. Lett. 2020, 24, 2785–2789. [Google Scholar] [CrossRef]
- Fenech, H.; Amos, S.; Hirsch, A.; Soumpholphakdy, V. VHTS systems: Requirements and evolution. In Proceedings of the European Conference on Antennas and Propagation (EUCAP), Paris, France, 19–24 March 2017; pp. 2409–2412. [Google Scholar]
- Aravanis, A.I.; MR, B.S.; Arapoglou, P.D.; Danoy, G.; Cottis, P.G.; Ottersten, B. Power allocation in multibeam satellite systems: A two-stage multi-objective optimization. IEEE Trans. Wirel. Commun. 2015, 14, 3171–3182. [Google Scholar] [CrossRef]
- Pachler, N.; Luis, J.J.G.; Guerster, M.; Crawley, E.; Cameron, B. Allocating power and bandwidth in multibeam satellite systems using particle swarm optimization. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–11. [Google Scholar]
- Ortiz-Gomez, F.G.; Tarchi, D.; Rodriguez-Osorio, R.M.; Vanelli-Coralli, A.; Salas-Natera, M.A.; Landeros-Ayala, S. Supervised machine learning for power and bandwidth management in VHTS systems. In Proceedings of the 10th Advanced Satellite Multimedia Systems Conference and the 16th Signal Processing for Space Communications Workshop (ASMS/SPSC), Graz, Austria, 20–21 October 2020; pp. 1–7. [Google Scholar]
- Luis, J.J.G.; Guerster, M.; del Portillo, I.; Crawley, E.; Cameron, B. Deep reinforcement learning for continuous power allocation in flexible high throughput satellites. In Proceedings of the IEEE Cognitive Communications for Aerospace Applications Workshop (CCAAW), Cleveland, OH, USA, 25–26 June 2019; pp. 1–4. [Google Scholar]
- Hu, X.; Zhang, Y.; Liao, X.; Liu, Z.; Wang, W.; Ghannouchi, F.M. Dynamic beam hopping method based on multi-objective deep reinforcement learning for next generation satellite broadband systems. IEEE Trans. Broadcast. 2020, 66, 630–646. [Google Scholar] [CrossRef]
- Bi, S.; Huang, L.; Wang, H.; Zhang, Y.J.A. Stable online computation offloading via Lyapunov-guided deep reinforcement learning. In Proceedings of the IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; pp. 1–7. [Google Scholar]
- Liu, S.; Hu, X.; Wang, W. Deep reinforcement learning based dynamic channel allocation algorithm in multibeam satellite systems. IEEE Access 2018, 6, 15733–15742. [Google Scholar] [CrossRef]
- Ferreira, P.V.R.; Paffenroth, R.; Wyglinski, A.M.; Hackett, T.M.; Bilén, S.G.; Reinhart, R.C.; Mortensen, D.J. Multiobjective reinforcement learning for cognitive satellite communications using deep neural network ensembles. IEEE J. Sel. Areas. Commun. 2018, 36, 1030–1041. [Google Scholar] [CrossRef]
- Ortiz-Gomez, F.G.; Tarchi, D.; Martínez, R.; Vanelli-Coralli, A.; Salas-Natera, M.A.; Landeros-Ayala, S. Cooperative multi-agent deep reinforcement learning for resource management in full flexible VHTS systems. IEEE Trans. Cognit. Commun. Netw. 2021, 8, 335–349. [Google Scholar] [CrossRef]
- Sharma, S.K.; Borras, J.Q.; Maturo, N.; Chatzinotas, S.; Ottersten, B. System modeling and design aspects of next generation high throughput satellites. IEEE Commun. Lett. 2020, 25, 2443–2447. [Google Scholar] [CrossRef]
- Gonthier, G. Formal proof—The four-color theorem. Notices AMS 2008, 55, 1382–1393. [Google Scholar]
- Qiuyang, Z.; Ying, W.; Xue, W. A double-timescale reinforcement learning based cloud-edge collaborative framework for decomposable intelligent services in industrial Internet of Things. China Commun. 2024, 2024, 1–19. [Google Scholar] [CrossRef]
- Bachir, A.F.B.A.; Zhour, M.; Ahmed, M. Modeling and Design of a DVB-S2X system. In Proceedings of the International Conference on Optimization and Applications (ICOA), Kenitra, Morocco, 25–26 April 2019; pp. 1–5. [Google Scholar]
- Rashid, T.; Samvelyan, M.; De Witt, C.S.; Farquhar, G.; Foerster, J.; Whiteson, S. Monotonic value function factorisation for deep multi-agent reinforcement learning. J. Mach. Learn. Res. 2020, 21, 7234–7284. [Google Scholar]
- Hu, X.; Liu, S.; Chen, R.; Wang, W.; Wang, C. A deep reinforcement learning-based framework for dynamic resource allocation in multibeam satellite systems. IEEE Commun. Lett. 2018, 22, 1612–1615. [Google Scholar] [CrossRef]




| Type | Objective | Algorithm Classification | Concrete Algorithm | Demand Matching | Bandwidth Flexibility | Frequency Reuse | Power Flexibility | Literature |
|---|---|---|---|---|---|---|---|---|
| Single- objective | AFI | Convex optimization | Lagrange dual theory | × | × | × | ✓ | [18] |
| USC, TPC, TBC | Convex optimization | DC, SCA | ✓ | ✓ | × | ✓ | [19] | |
| TPC | Heuristics | PSO | × | × | × | ✓ | [20] | |
| CDG, AFI | Heuristics | SA | ✓ | ✓ | × | ✓ | [21] | |
| USC | Heuristics | GA | ✓ | ✓ | ✓ | ✓ | [22] | |
| TPC | Deep reinforcement learning | DRL-DPA | × | × | × | ✓ | [23] | |
| CDG, AFI | Deep reinforcement learning | DRL-DBA | ✓ | ✓ | × | × | [24] | |
| Multi- objective | USC, TPC | Heuristics | GA-SA, NSGA-II | ✓ | × | × | ✓ | [26] |
| USC, TPC | Heuristics | PSO-GA, NSGA-II | ✓ | ✓ | × | ✓ | [27] | |
| CDG, TPC, TBC | Machine learning | SL | ✓ | ✓ | × | ✓ | [28] | |
| USC, TPC | Deep reinforcement learning | PPO | ✓ | × | × | ✓ | [29] |
| SE | Threshold | SE | Threshold |
|---|---|---|---|
| 0.83 | 1.8 | 2.22 | 5.6 |
| 1 | 2.2 | 2.5 | 6.3 |
| 1.11 | 2.6 | 2.67 | 6.8 |
| 1.25 | 3 | 2.78 | 7.2 |
| 1.33 | 3.4 | 3.13 | 7.8 |
| 1.39 | 3.8 | 3.33 | 8.5 |
| 1.5 | 3.9 | 3.47 | 8.9 |
| 1.67 | 4.6 | 3.7 | 10.1 |
| 1.88 | 5.4 | 3.75 | 10.4 |
| Parameters | Values |
|---|---|
| Satellite altitude h | 35,786 km |
| Beam number B | 16 |
| System total power | 1600 W |
| Amplifier maximum power | 400 W |
| System total bandwidth | 2 GHz |
| Beamwidth | 0.6° |
| Link loss | 210 dB |
| Amplifier backlash | 3 dB |
| UT receiving | 22 dB/K |
| Boltzmann constant k | −228.6 dB |
| Amplifier number | 4 |
| Frequency color number M | 4 |
| Frequency polar number | 2 |
| Parameters | Values |
|---|---|
| Step number (Qmix) | 100 |
| Epoch number (Qmix) | 100 |
| Episode number (Qmix) | 10 |
| Step number (DQN) | 50 |
| Epoch number (DQN) | 50 |
| Episode number (DQN) | 12 |
| Update frequency | 100 |
| Learning rate | 0.001 |
| Discount factor | 0.98 |
| Batch size | 32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, L.; Zhang, C.; Zhang, Q.; Zeng, L.; Qin, P.; Wang, Y. Double-Timescale Multi-Agent Deep Reinforcement Learning for Flexible Payload in VHTS Systems. Electronics 2024, 13, 2764. https://doi.org/10.3390/electronics13142764
Feng L, Zhang C, Zhang Q, Zeng L, Qin P, Wang Y. Double-Timescale Multi-Agent Deep Reinforcement Learning for Flexible Payload in VHTS Systems. Electronics. 2024; 13(14):2764. https://doi.org/10.3390/electronics13142764
Chicago/Turabian StyleFeng, Linqing, Cheng Zhang, Qiuyang Zhang, Lingchao Zeng, Pengfei Qin, and Ying Wang. 2024. "Double-Timescale Multi-Agent Deep Reinforcement Learning for Flexible Payload in VHTS Systems" Electronics 13, no. 14: 2764. https://doi.org/10.3390/electronics13142764
APA StyleFeng, L., Zhang, C., Zhang, Q., Zeng, L., Qin, P., & Wang, Y. (2024). Double-Timescale Multi-Agent Deep Reinforcement Learning for Flexible Payload in VHTS Systems. Electronics, 13(14), 2764. https://doi.org/10.3390/electronics13142764






