Determination of Parameters of Radio Frequency Identification Transponder Antennas Dedicated to IoTT Systems Located on Non-Planar Objects
Abstract
:1. Introduction
2. Materials and Methods
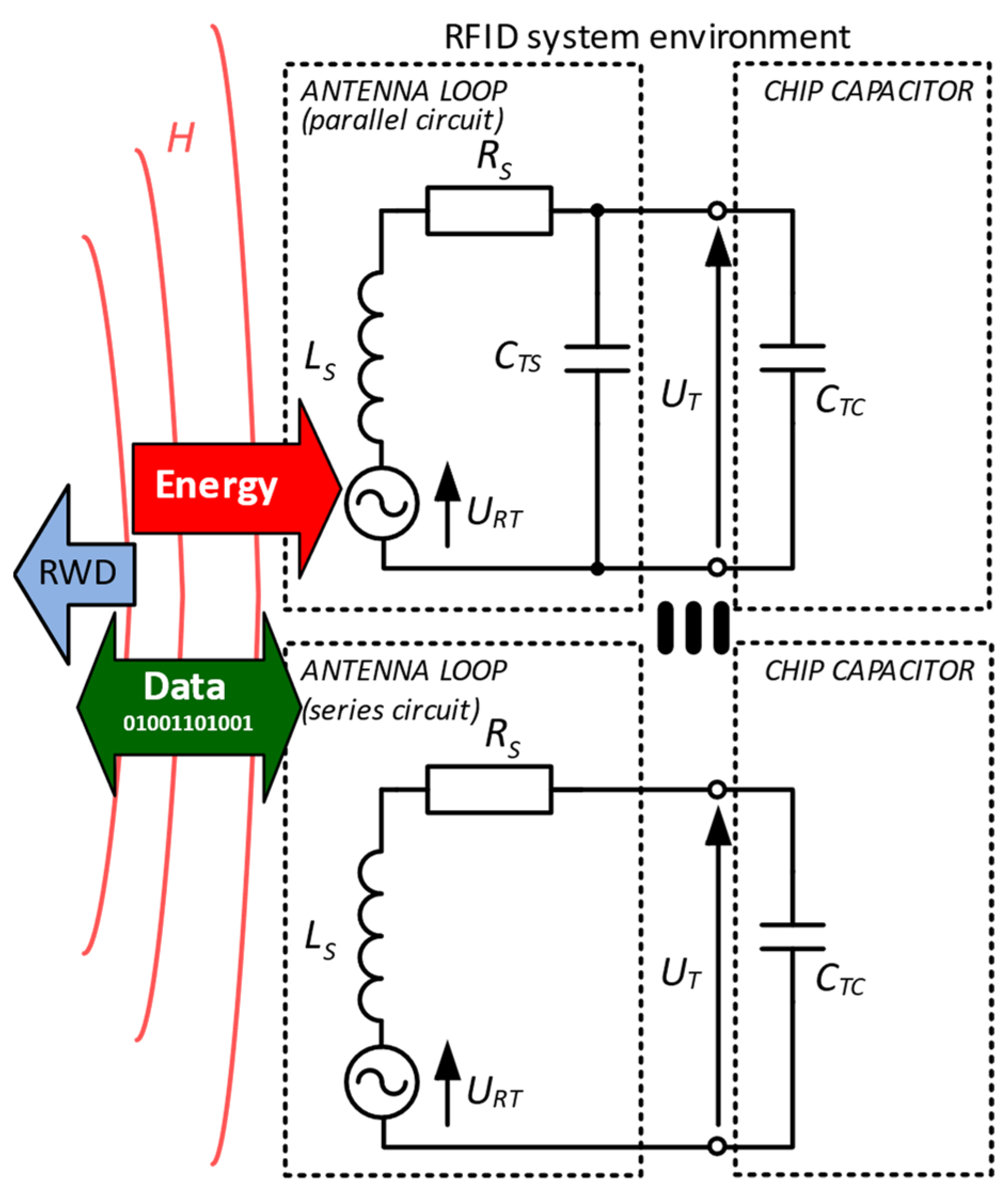
2.1. HF RFID Transponder Textile Antenna
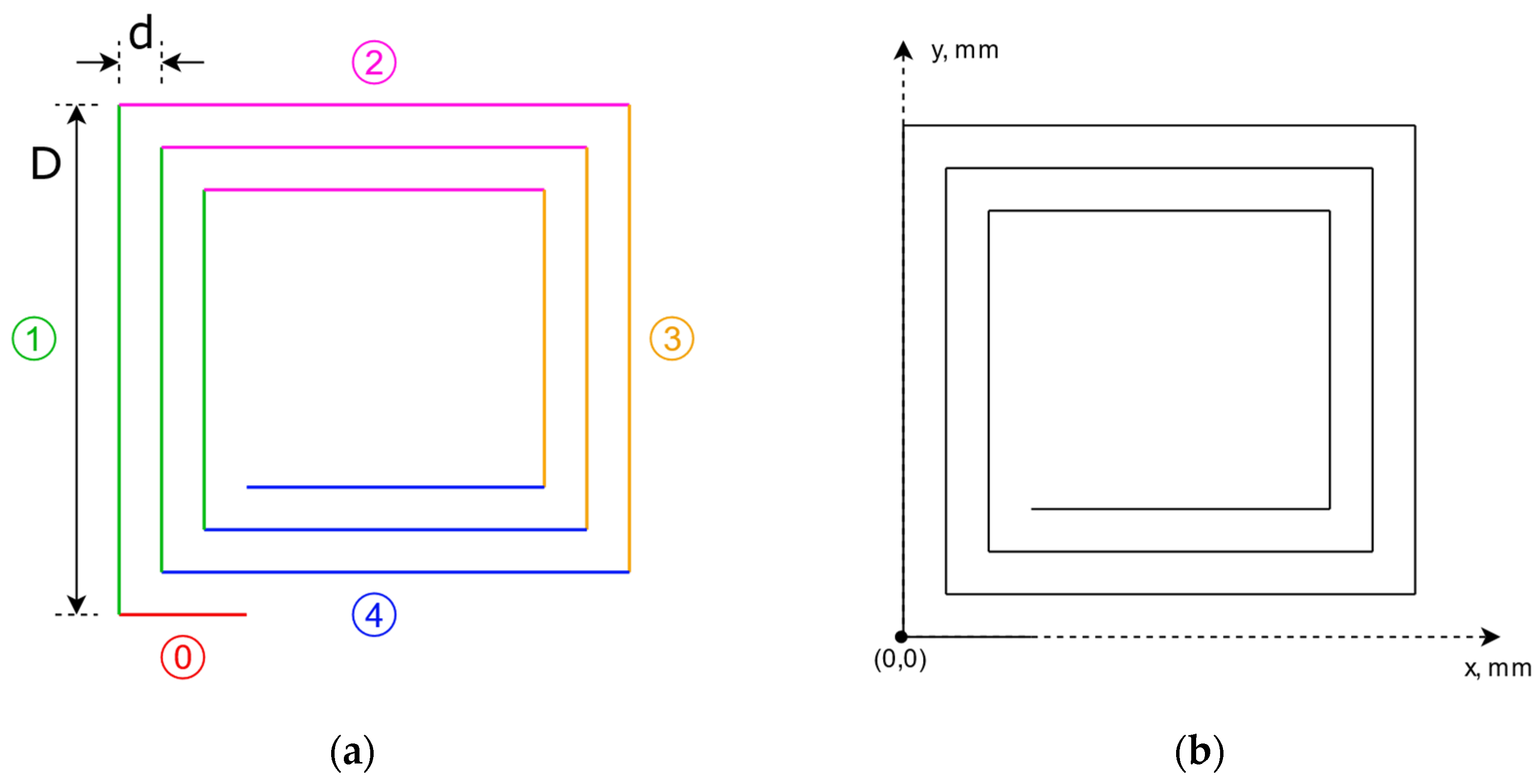
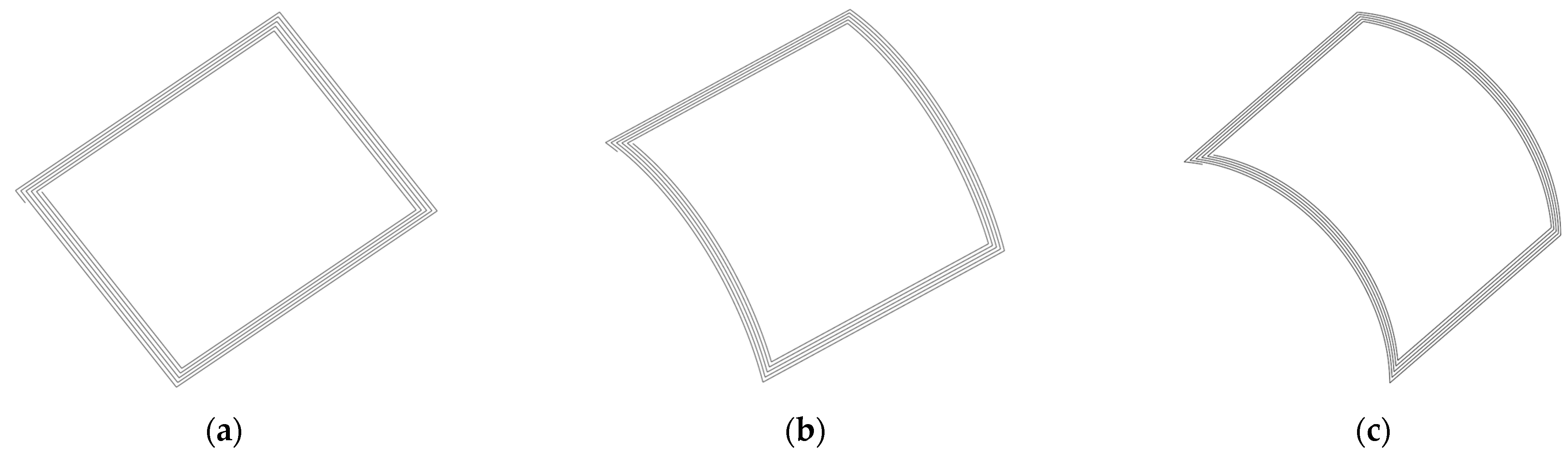
2.2. Parametric Model
3. Results
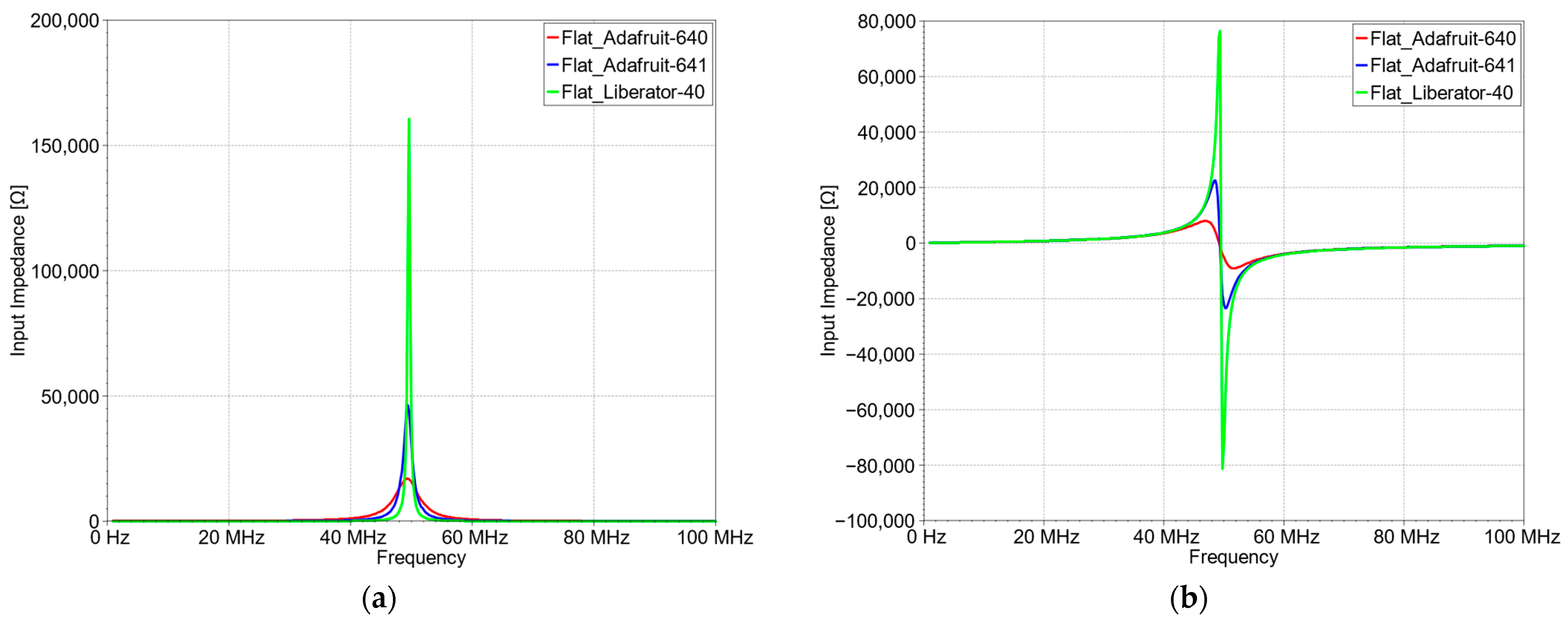
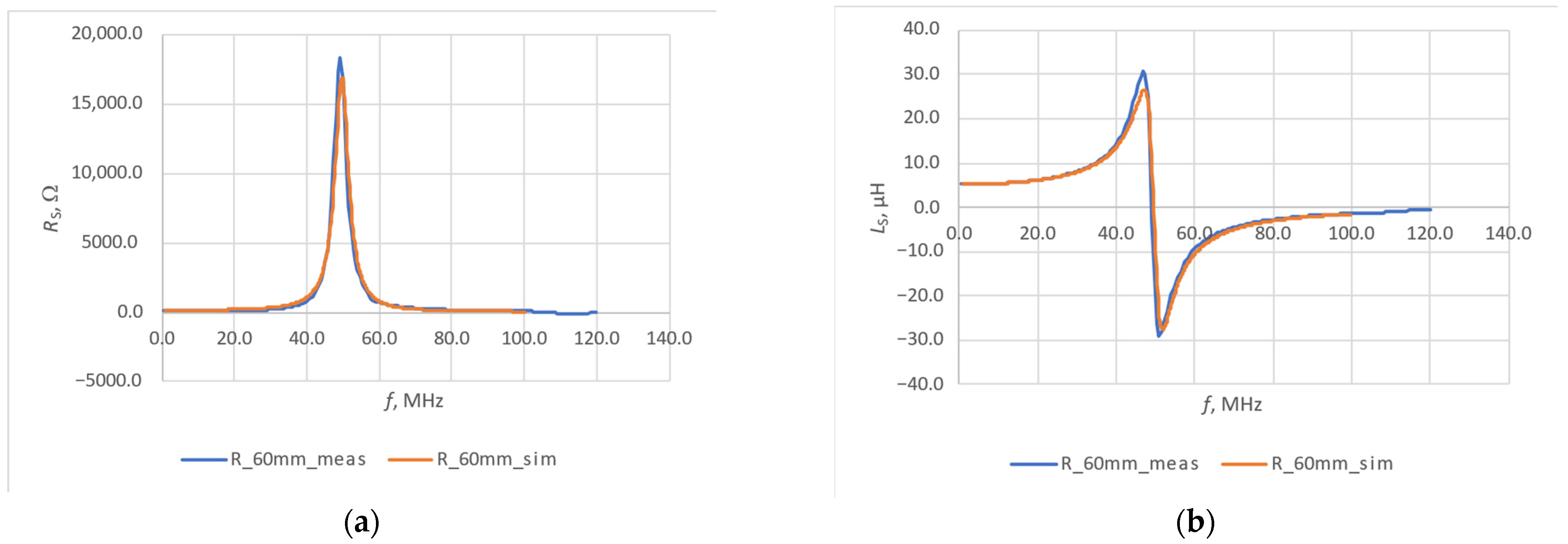
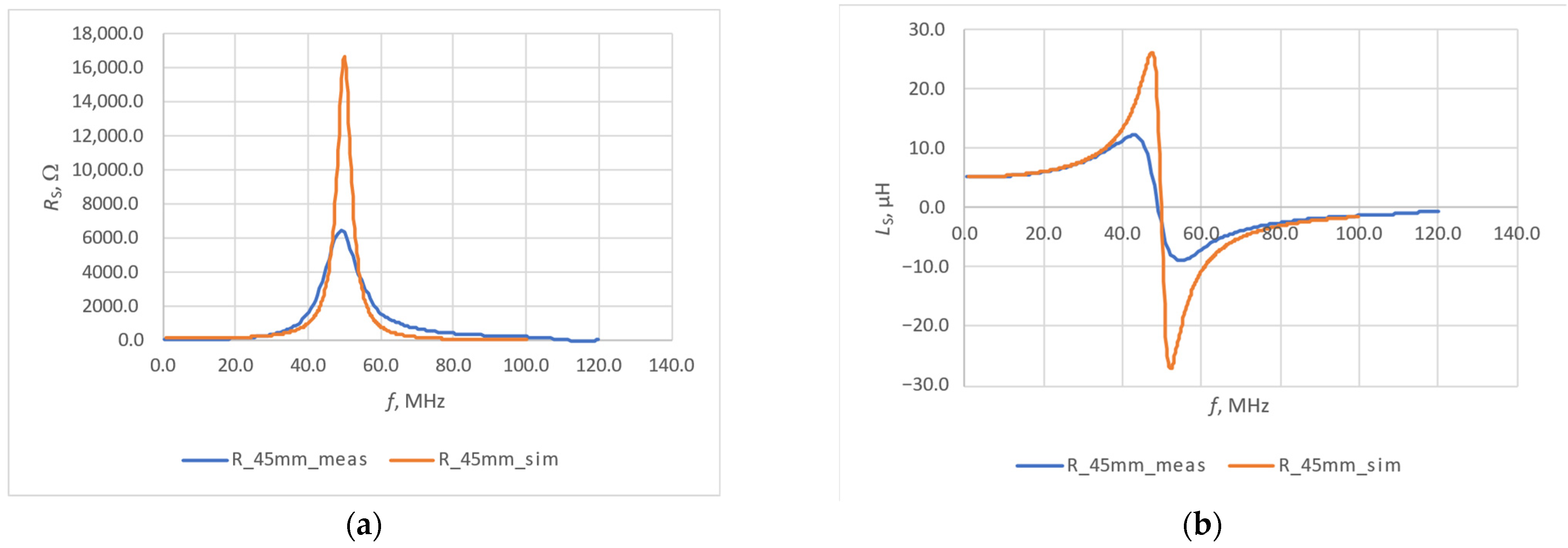
3.1. Simulation Test
3.2. Experimental Verification
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lombardi, M.; Pascale, F.; Santaniello, D. Internet of Things: A General Overview between Architectures, Protocols and Applications. Information 2021, 12, 87. [Google Scholar] [CrossRef]
- Tawalbeh, L.; Muheidat, F.; Tawalbeh, M.; Quwaider, M. IoT Privacy and Security: Challenges and Solutions. Appl. Sci. 2020, 10, 4102. [Google Scholar] [CrossRef]
- Padma, A.; Seth, B.; Ramachandran, G. Analysis of Current Smart Wearable Trends Using Internet of Medical Things. In Proceedings of the 3rd International Conference on Artificial Intelligence and Smart Energy, ICAIS, Coimbatore, India, 2–4 February 2023. [Google Scholar]
- Vital, D. A Biomimetic Resonator for Fabric-Based Wireless Power Transfer, Harvesting, and Charging of Sensors and Internet of Medical Things. In Proceedings of the 2022 IEEE 12th International Conference on RFID Technology and Applications, RFID-TA, Cagliari, Italy, 12–14 September 2022. [Google Scholar]
- Chit, T.W.; Ning, L.; Paliath, N.A.; Long, Y.M.; Akhtar, H.; Shanshan, Y. IIoT-Enabled and Data-Driven Sustainability Evaluation Framework for Textile Supply Chain. In Proceedings of the 16th IEEE Conference on Industrial Electronics and Applications, ICIEA, Chengdu, China, 1–4 August 2021. [Google Scholar]
- Li, X.; Pan, W.; An, J.; Wan, P. The Application Research on Military Internet of Things. In Proceedings of the 2020 17th International Computer Conference on Wavelet Active Media Technology and Information Processing, ICCWAMTIP, Chengdu, China, 17–19 December 2021. [Google Scholar]
- Donghao, C.; Bohua, Z.; Chaomin, O.; Zhiyu, C. Research on Military Internet of Things Technology Application in the Context of National Security. In Proceedings of the 2021 2nd International Conference on Electronics, Communications and Information Technology, CECIT, Sanya, China, 27–29 December 2021. [Google Scholar]
- Bing, L.; Gu, Y.; Hu, L.; Bowen, L.; Lihua, Y.; Wang, J.; Yin, Y. Ultra Reliability and Massive Connectivity Provision in Integrated Internet of Military Things (IoMT) Based on Tactical Datalink. Def. Technol. 2024, 33, 386–398. [Google Scholar] [CrossRef]
- Loncar, P. Internet of Musical Things and Music Data Visualization. In Proceedings of the 2022 45th Jubilee International Convention on Information, Communication and Electronic Technology, MIPRO, Opatija, Croatia, 23–27 May 2022. [Google Scholar]
- Turchet, L.; Casari, P. Latency and Reliability Analysis of a 5G-Enabled Internet of Musical Things System. IEEE Internet Things J. 2024, 11, 1228–1240. [Google Scholar] [CrossRef]
- Bouhassoune, I.; Chaibi, H.; Chehri, A.; Saadane, R. A Review of RFID-Based Internet of Things in the Healthcare Area, the New Horizon of RFID. In Proceedings of the Procedia Computer Science, Zurich, Switzerland, 14–17 June 2022; Volume 207. [Google Scholar]
- Sahukara, K.V.; Ammisetty, M.B.; Devi, G.S.K.G.; Prathyusha, S.; Nikhita, T.S. COVID-SAFE: IoT Based Health Monitoring System Using RFID in Pandemic Life. In Proceedings of the 2021 IEEE International Conference on RFID Technology and Applications, RFID-TA 2021, Delhi, India, 6–8 October 2021. [Google Scholar]
- Almalki, H.; Rankin, A.C.; Juette, A.; Youssef, M.M.G. Radio-Frequency Identification (RFID) Tag Localisation of Non-Palpable Breast Lesions a Single Centre Experience. Breast 2023, 69, 417–421. [Google Scholar] [CrossRef] [PubMed]
- Varriale, V.; Cammarano, A.; Michelino, F.; Caputo, M. Integrating Blockchain, RFID and IoT within a Cheese Supply Chain: A Cost Analysis. J. Ind. Inf. Integr. 2023, 34, 100486. [Google Scholar] [CrossRef]
- Tan, W.C.; Sidhu, M.S. Review of RFID and IoT Integration in Supply Chain Management. Oper. Res. Perspect. 2022, 9, 100229. [Google Scholar] [CrossRef]
- Bianco, G.M.; Panunzio, N.; Pintaudi, A.; Santamaria, S.; Faustino, F.; Occhiuzzi, C.; Marrocco, G. RFID Labeling of Police Equipment. In Proceedings of the 2021 IEEE International Conference on RFID Technology and Applications, RFID-TA 2021, Delhi, India, 6–8 October 2021. [Google Scholar]
- Yaman, O.; Tuncer, T.; Ertam, F. Automated Book Location and Classification Method Using RFID Tags for Smart Libraries. Microprocess. Microsyst. 2021, 87, 104388. [Google Scholar] [CrossRef]
- Jakub, D.; Filip, L. Comparison of the Difficulty Overcoming of RFID Electronic Access Control Systems and Overcoming of Pin Tumbler Locks. In Proceedings of the Transportation Research Procedia, Online, 28 June–2 July 2021; Volume 55. [Google Scholar]
- Chen, Y.; Zhao, H.; Li, Z.; Lan, S.; Dai, X. Design of RFID Access Control System Based on 51 Microcontroller. In Proceedings of the Proceedings—2023 International Conference on Computers, Information Processing and Advanced Education, CIPAE, Ottawa, ON, Canada, 26–28 August 2023. [Google Scholar]
- Jankowski-Mihułowicz, P.; Węglarski, M.; Chamera, M.; Pyt, P. Textronic Uhf Rfid Transponder. Sensors 2021, 21, 1093. [Google Scholar] [CrossRef] [PubMed]
- Jankowski-Mihułowicz, P.; Węglarski, M.; Pyt, P.; Skrobacz, K.; Karpiński, K. UHF Textronic RFID Transponder with Bead-Shaped Microelectronic Module. Electronics 2023, 12, 4873. [Google Scholar] [CrossRef]
- Peters, S.; Hangmann, C.; Wüllner, I.; Traupe, J.; John, T.; Weigel, R.; Scheiner, B. Low-Cost and High Performance Antenna Setup for Updating EPaper Displays on Curved RFID SmartTags Used in Pharmaceutical Studies. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, San Diego, CA, USA, 11–16 June 2023. [Google Scholar]
- Garg, M.; Sharma, A.; Garcia Zuazola, I.J.; Gupta, A. Compact UHF RFID Balun-like Integrated Tag Antenna for Long Range Detection of Water Bottles. IET Microw. Antennas Propag. 2023, 17, 909–919. [Google Scholar] [CrossRef]
- He, S.; Zhang, Y.; Li, L.; Lu, Y.; Zhang, Y.; Liu, H. High Performance UHF Rfid Tag Antennas on Liquid-Filled Bottles. Prog. Electromagn. Res. 2019, 165, 83–92. [Google Scholar] [CrossRef]
- Ozek, E.A.; Tanyeli, S.; Yapici, M.K. Flexible Graphene Textile Temperature Sensing RFID Coils Based on Spray Printing. IEEE Sens. J. 2021, 21, 26382–26388. [Google Scholar] [CrossRef]
- Biswas, B.; Karmakar, A.; Chandra, V. Miniaturised Wideband Ingestible Antenna for Wireless Capsule Endoscopy. IET Microw. Antennas Propag. 2020, 14, 293–301. [Google Scholar] [CrossRef]
- Tong, Y.; Meng, F.; Zhang, Y.; Hu, J. The Impact of Contextual Factors on the Performance of Human Breath Monitoring Using Flexible UHF RFID Temperature Sensing Yarn and Its Underlying Mechanisms. Sens. Actuators A Phys. 2024, 375, 115522. [Google Scholar] [CrossRef]
- El Bakkali, M.; Martinez-Estrada, M.; Fernandez-Garcia, R.; Gil, I.; Mrabet, O. El Effect of Bending on a Textile UHF-RFID Tag Antenna. In Proceedings of the 14th European Conference on Antennas and Propagation, EuCAP 2020, Copenhagen, Denmark, 15–20 March 2020. [Google Scholar]
- Zaidi, N.I.; Abd Rahman, N.H.; Yahya, M.F.; Nordin, M.S.A.; Subahir, S.; Yamada, Y.; Majumdar, A. Analysis on Bending Performance of the Electro-Textile Antennas with Bandwidth Enhancement for Wearable Tracking Application. IEEE Access 2022, 10, 31800–31820. [Google Scholar] [CrossRef]
- Jeong, S.; Kim, T.W.; Lee, S.; Sim, B.; Park, H.; Son, K.; Son, K.; Kim, S.; Shin, T.; Kim, Y.C.; et al. Analysis of Repetitive Bending on Flexible Wireless Power Transfer (WPT) PCB Coils for Flexible Wearable Devices. IEEE Trans. Compon. Packag. Manuf. Technol. 2022, 12, 1748–1756. [Google Scholar] [CrossRef]
- Jankowski-Mihułowicz, P.; Węglarski, M. Textronic RFID Transponder. Patent PL 231291 B1, 19 March 2019. [Google Scholar]





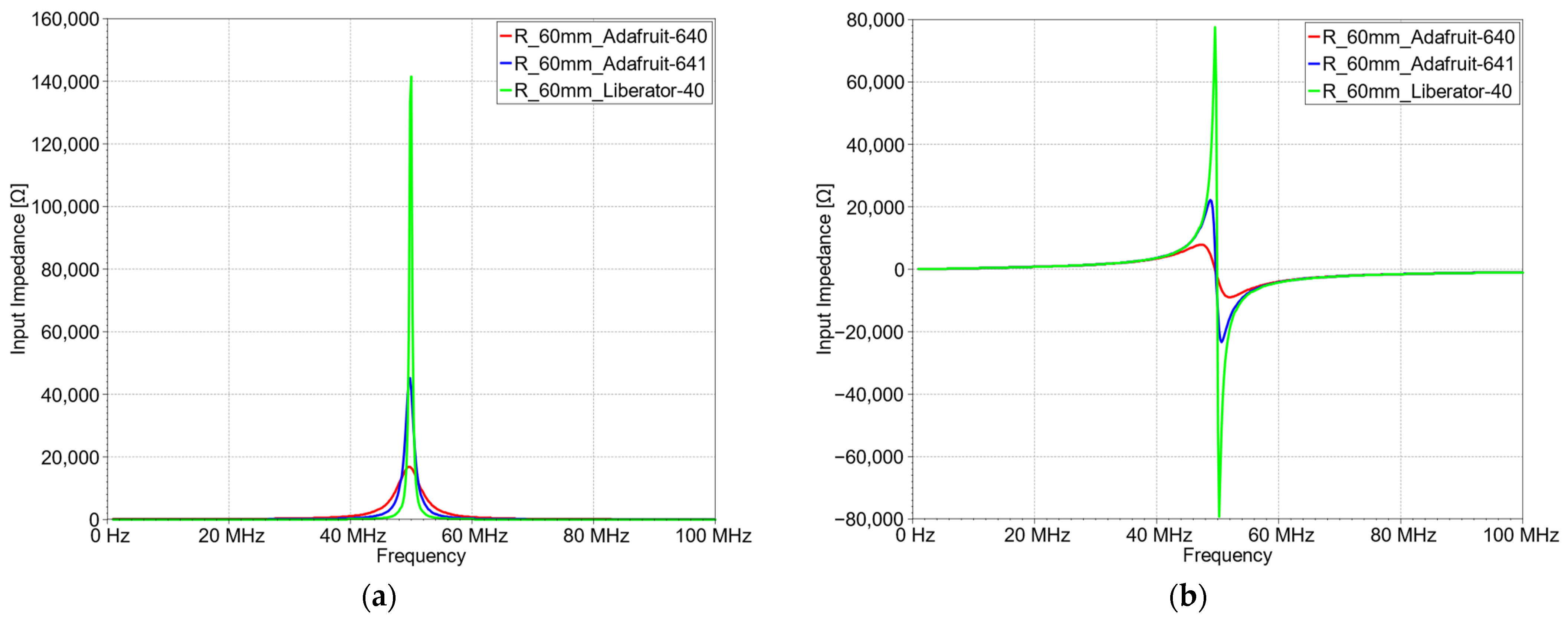
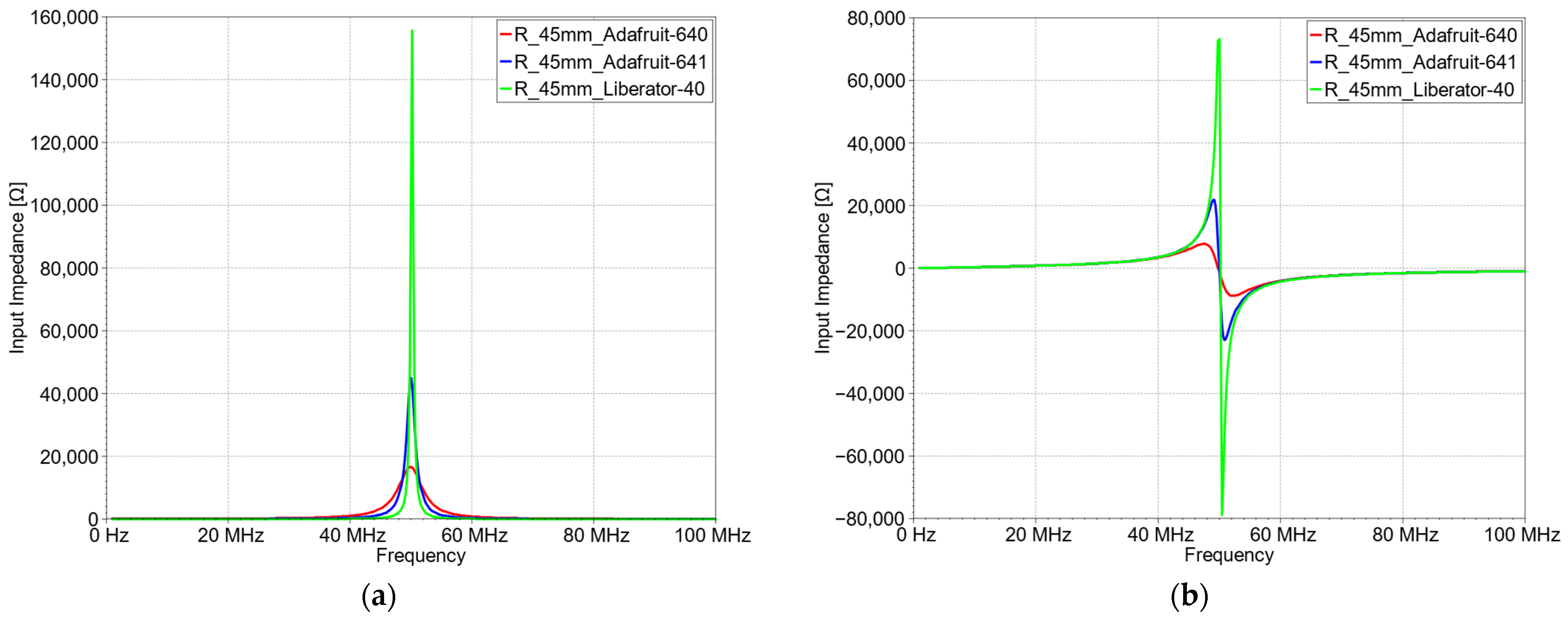
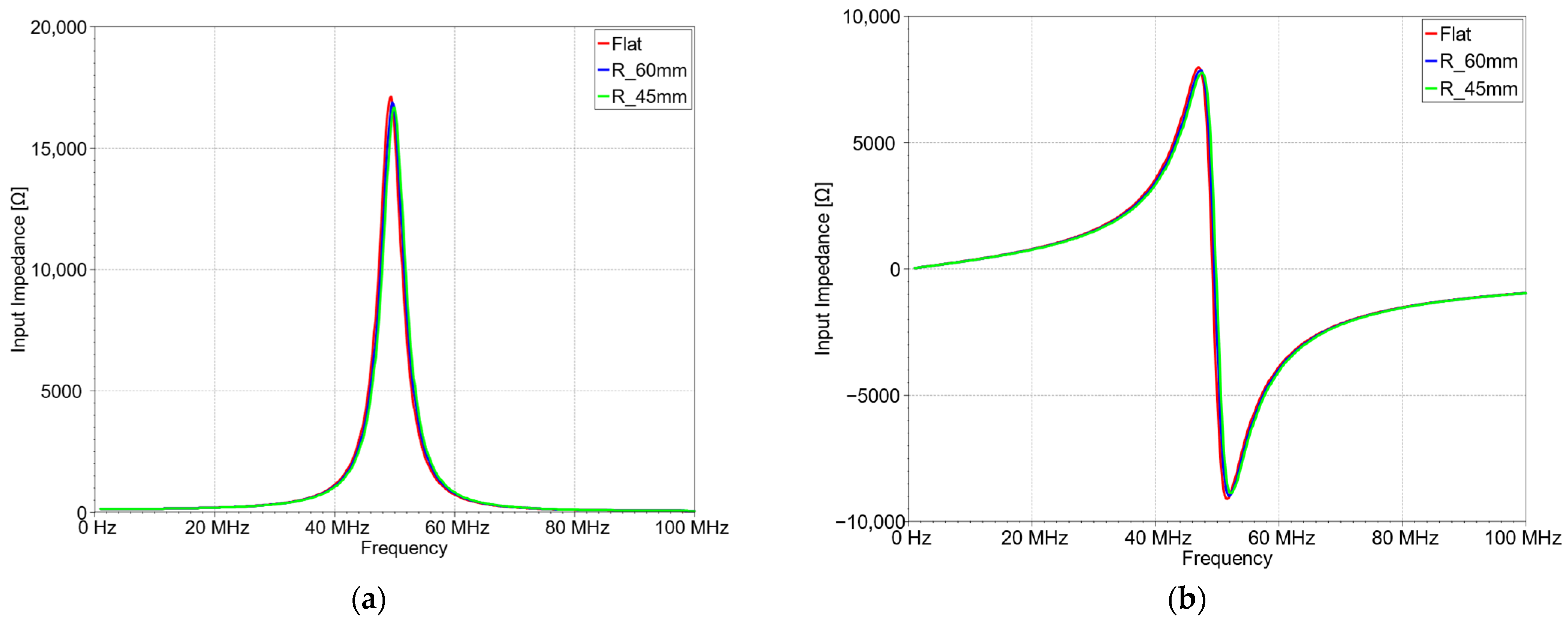





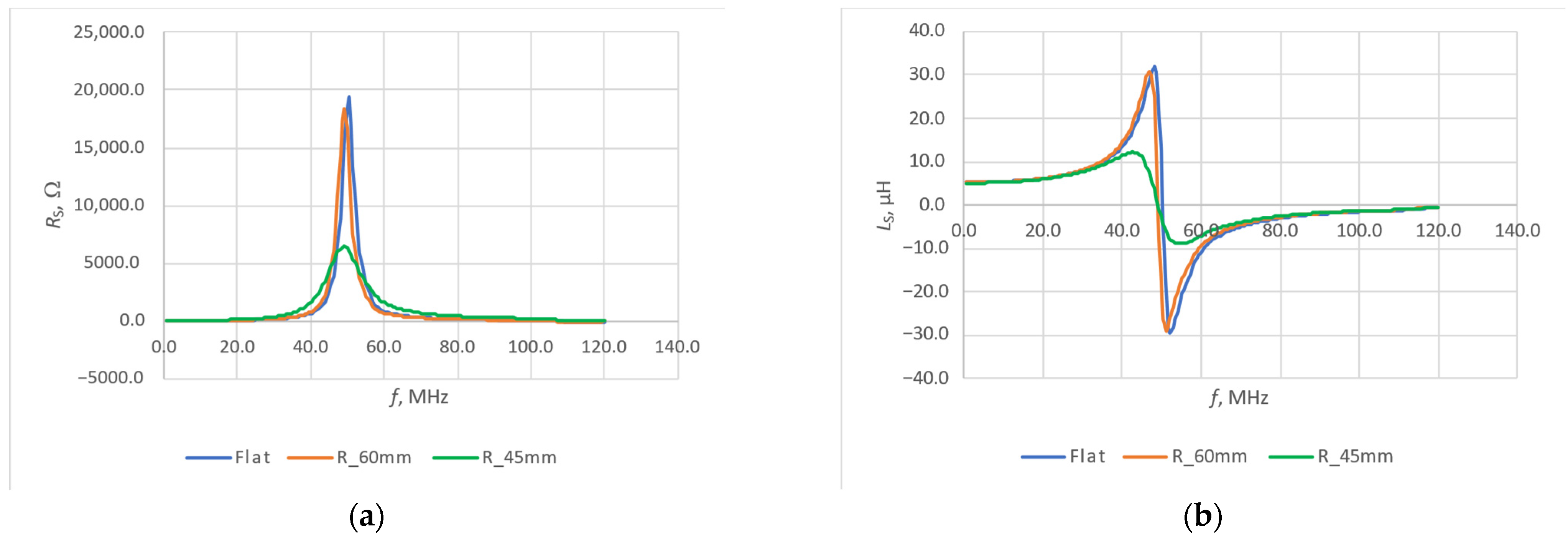

| Thread | Measured Resistance, Ω/m | Calculated Conductance, S/m |
|---|---|---|
| Adafruit 640 | 58.1 | 8.77 · 104 |
| Adafruit 641 | 20.1 | 2.53 ∙ 105 |
| Liberator 40 | 2.86 | 1.78 ∙ 106 |
| Thread | Flat Model | Curved Model (R = 60 mm) | Curved Model (R = 45 mm) | |||
|---|---|---|---|---|---|---|
| RS, Ω | LS, µH | RS, Ω | LS, µH | RS, Ω | LS, µH | |
| Adafruit 640 | 160.50 | 5.68 | 160.12 | 5.59 | 159.83 | 5.53 |
| Adafruit 641 | 55.97 | 5.72 | 55.83 | 5.63 | 55.73 | 5.57 |
| Liberator 40 | 9.85 | 5.71 | 9.83 | 5.63 | 9.81 | 5.56 |
| RS, Ω | LS, µH | |
|---|---|---|
| Flat model | 84.663 | 5.5954 |
| Curved model (R = 60 mm) | 84.554 | 5.5616 |
| Curved model (R = 45 mm) | 101.93 | 5.4647 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nizioł, M.; Jankowski-Mihułowicz, P.; Węglarski, M. Determination of Parameters of Radio Frequency Identification Transponder Antennas Dedicated to IoTT Systems Located on Non-Planar Objects. Electronics 2024, 13, 2800. https://doi.org/10.3390/electronics13142800
Nizioł M, Jankowski-Mihułowicz P, Węglarski M. Determination of Parameters of Radio Frequency Identification Transponder Antennas Dedicated to IoTT Systems Located on Non-Planar Objects. Electronics. 2024; 13(14):2800. https://doi.org/10.3390/electronics13142800
Chicago/Turabian StyleNizioł, Magdalena, Piotr Jankowski-Mihułowicz, and Mariusz Węglarski. 2024. "Determination of Parameters of Radio Frequency Identification Transponder Antennas Dedicated to IoTT Systems Located on Non-Planar Objects" Electronics 13, no. 14: 2800. https://doi.org/10.3390/electronics13142800
APA StyleNizioł, M., Jankowski-Mihułowicz, P., & Węglarski, M. (2024). Determination of Parameters of Radio Frequency Identification Transponder Antennas Dedicated to IoTT Systems Located on Non-Planar Objects. Electronics, 13(14), 2800. https://doi.org/10.3390/electronics13142800






