Capacitance Evaluation of Metallized Polypropylene Film Capacitors Considering Cumulative Self-Healing Damage
Abstract
:1. Introduction
2. Measurement Setup and Characterization
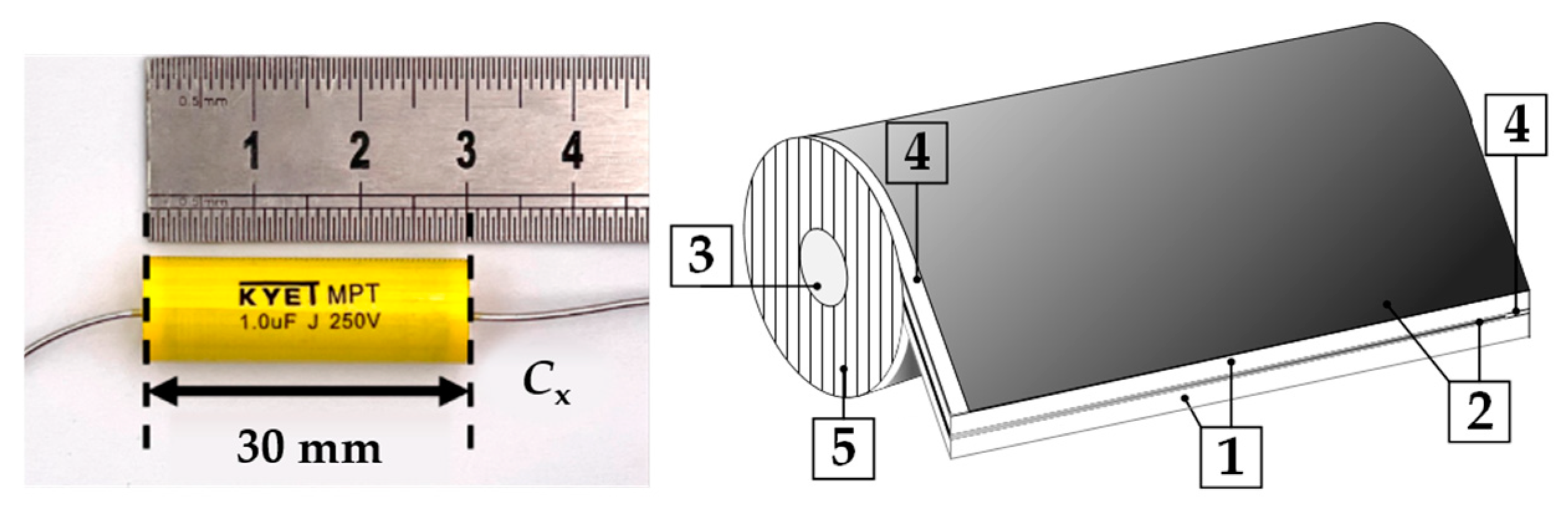
2.1. Specification of MPPFCs
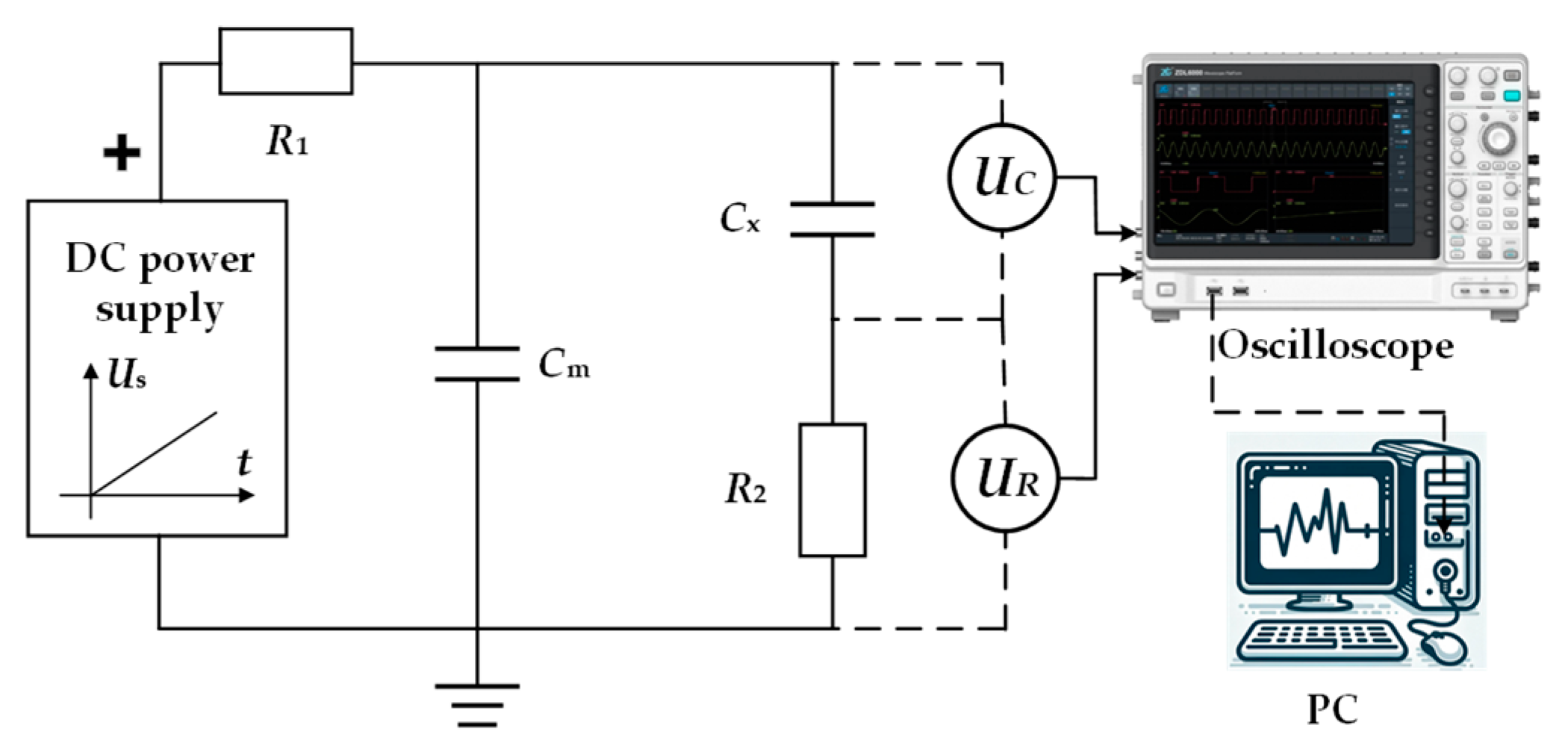
2.2. Measurement Setup
2.3. Feature Parameter Extraction
3. Results and Discussion
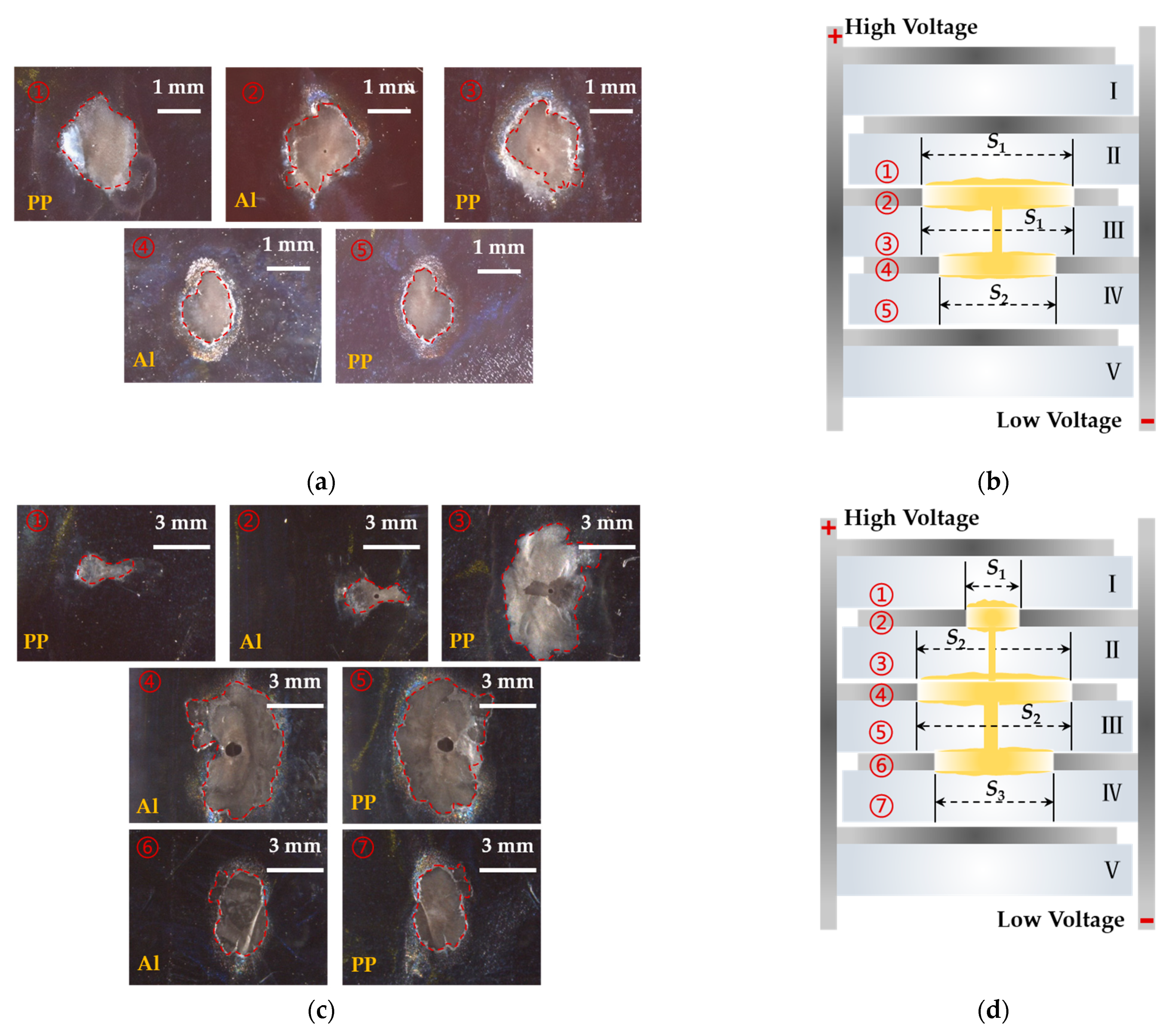
3.1. SH Electrochemical Behavior for Al Electrode and PP Dielectric
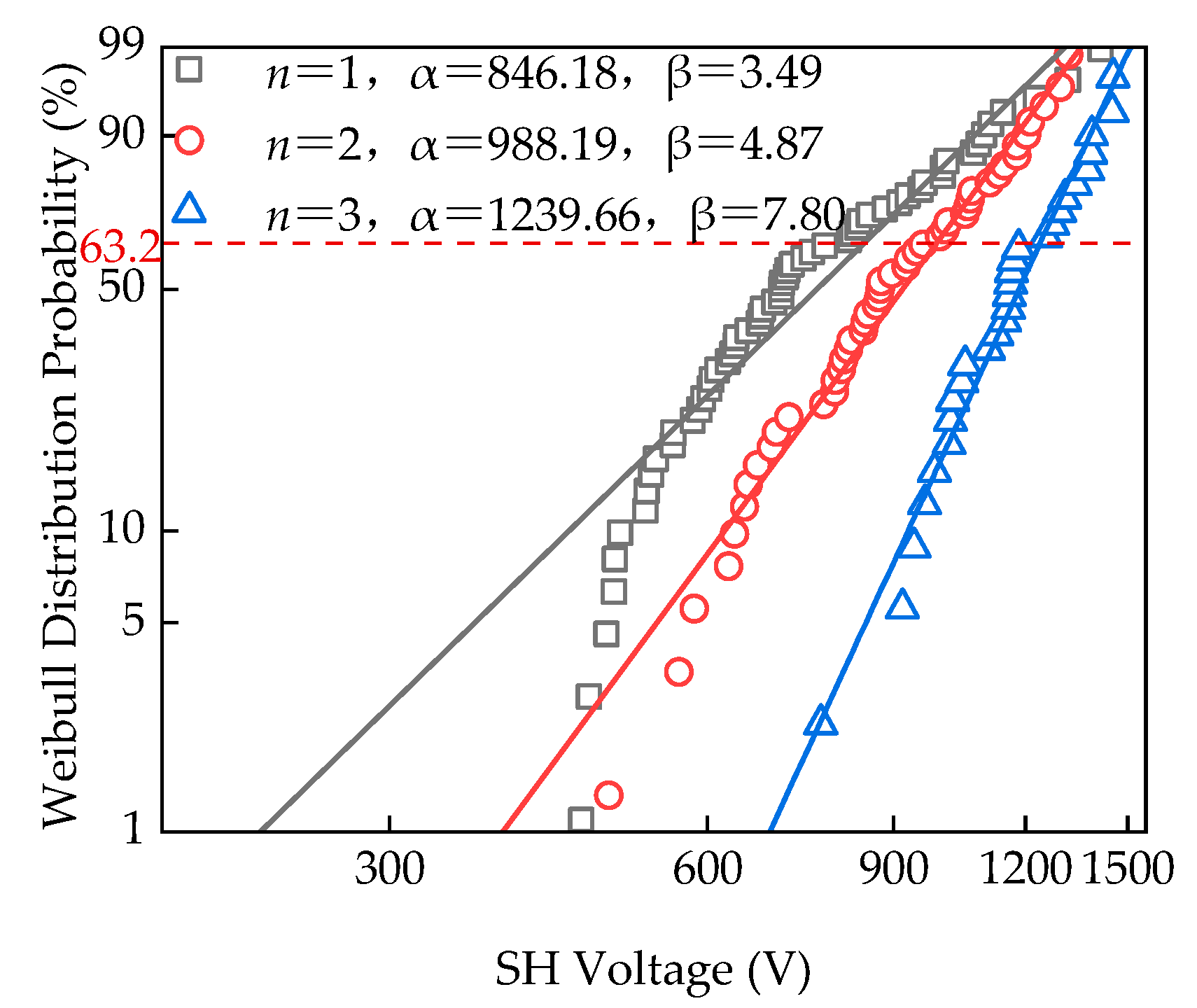
3.2. SH Voltage Distribution
3.3. Correlation between Total Electrode Evaporated Area and SH Energy
3.4. Cumulative SH Damage Feature Parameters Analysis
3.5. Capacitance Loss Analysis under Single SH
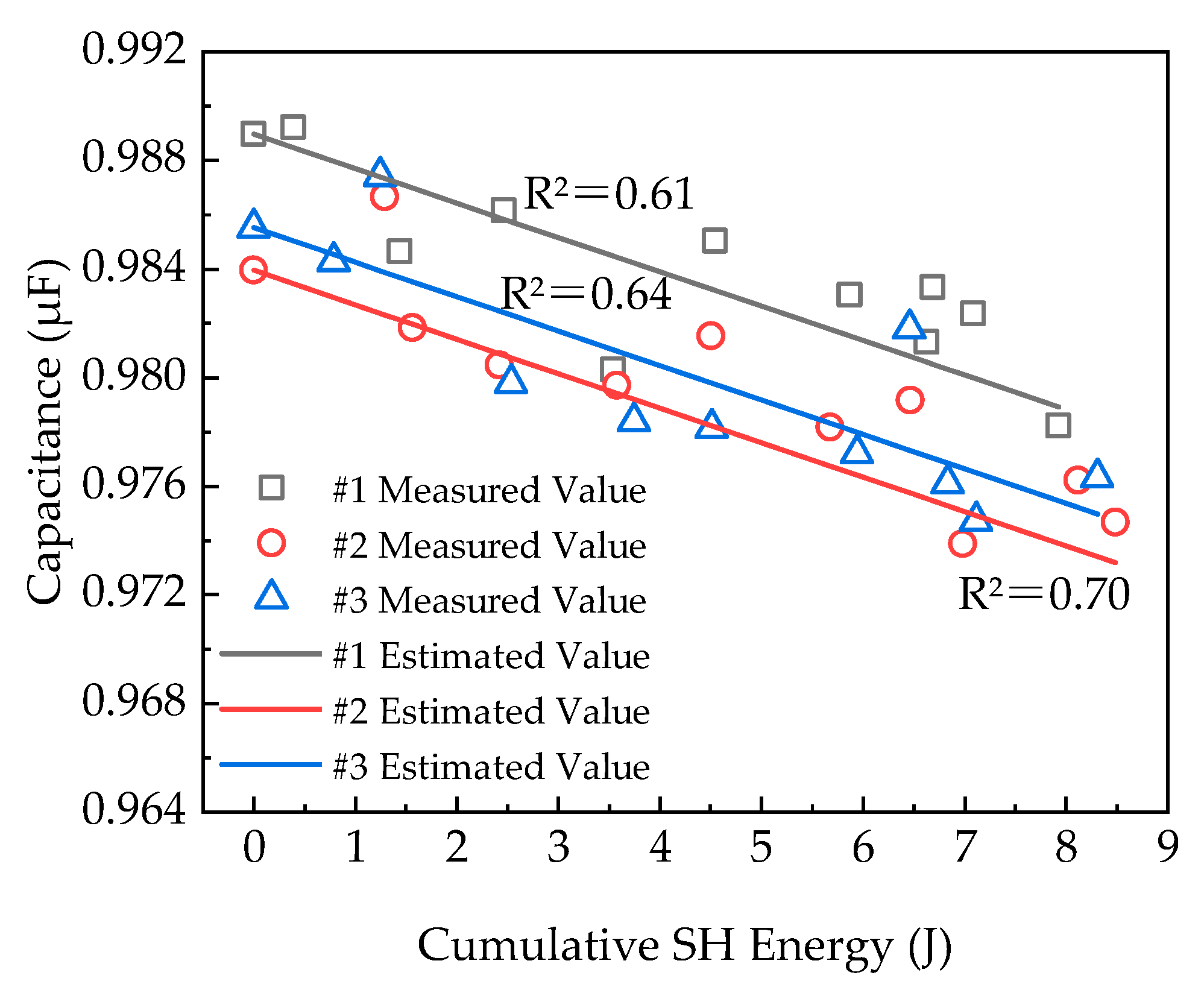
3.6. Capacitance Evaluation Method under Cumulative SH
4. Conclusions
- The Al electrode and PP dielectric in an MPPFC undergo electrochemical behavior during SH, altering their morphologies—the Al electrode is cleared and the PP dielectric is decomposed. As the SH voltage increases, the number of SH-breakdown film layers during a single SH event rises, leading to a significant increase in SH energy. The electrode also incurs losses due to high-temperature evaporation. Under cumulative SH conditions, there is a positive correlation between the SH number and the total number of SH-breakdown film layers, and the linear regression model has a slope close to 1. The average single SH energy decreases exponentially with SH number. As the SH number increases, the probability of SH breaking only one layer of film in each event rises;
- Capacitance loss calculations need to account for the winding structure of the capacitor. It was observed that capacitance loss is nonlinearly related to the total electrode evaporation area. Under single SH conditions, capacitance loss is determined by both the SH-breakdown film layers and the electrode evaporation area. Therefore, an improved equation for capacitance loss calculation was proposed;
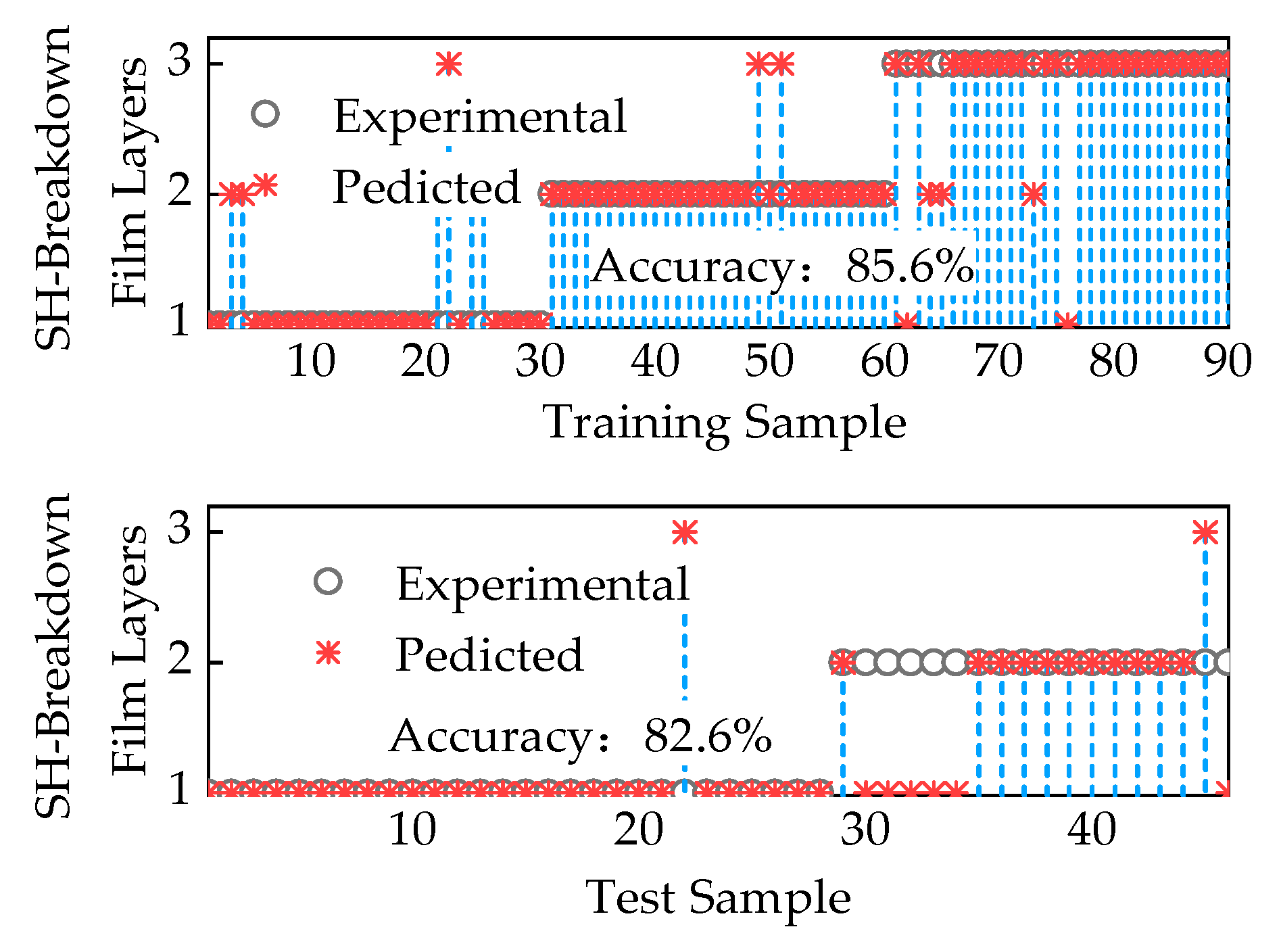
- Based on the distribution patterns of SH voltage and SH energy for different numbers of SH-breakdown film layers during SH, it was found that these characteristic parameters can be used to construct a feature parameter set. Thus, this study employed the SVM algorithm to classify the feature parameter set and identify the SH-breakdown film layers and the total electrode evaporation area during each SH event, and the model classification accuracy was 82.6%. A capacitance evaluation method for cumulative SH in MPPFC was proposed. Comparative analysis with measured data indicates the effectiveness of the evaluation method.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lei, W.; Liu, J.; Lv, G.; Cao, R. Review of Reliability Comprehensive Analysis and Evaluation Methods for Key Components and System of Large Capacity Power Electronic Equipment. High Volt. Eng. 2020, 46, 3353–3361. [Google Scholar] [CrossRef]
- Li, Q.; Li, M. High-temperature Polymer Dielectrics for Film Capacitors: Review and Prospect. High Volt. Eng. 2021, 47, 3105–3123. [Google Scholar] [CrossRef]
- Du, B.; Ran, Z.; Liu, H.; Xiao, M. Research Progress of Dielectric Properties and Improvement Methods of Polypropylene Film for Dry-Type Capacitor. Trans. China Electrotech. Soc. 2023, 38, 1363–1374. [Google Scholar] [CrossRef]
- Tai, Y.; Chen, P.; Jian, Y.; Fang, Q.; Xu, D.; Cheng, J. Failure Mechanism and Life Estimate of Metallized Film Capacitor under High Temperature and Humidity. Microelectron. Reliab. 2022, 137, 114755. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, C.; Pan, L.; Du, Y.; Zhu, L. Study on Aging Mechanism of Metallized Film Capacitor Based on Surface Analysis. Guangdong Electr. Power 2019, 32, 119–125. Available online: https://kns.cnki.net/kcms/detail/44.1420.TM.20190827.1428.030.html (accessed on 9 July 2024).
- Xu, Z.; Cheng, L.; Liu, H.; Wang, J.; Ma, Y.; Li, Z.; Liu, W.; Guo, J. Ageing characteristics of metallized film capacitor under ultra-high DC field. Insul. Mater. 2023, 56, 55–62. [Google Scholar] [CrossRef]
- Sarjeant, W.J.; Zirnheld, J.; MacDougall, F.W. Capacitors. IEEE Trans. Plasma Sci. 1998, 26, 1368–1392. [Google Scholar] [CrossRef]
- Picci, G.; Rabuffi, M. Status Quo and Future Prospects for Metallized Polypropylene Energy Storage Capacitors. In Proceedings of the IEEE Conference Record—Abstracts. PPPS-2001 Pulsed Power Plasma Science 2001. 28th IEEE International Conference on Plasma Science and 13th IEEE International Pulsed Power Conference (Cat. No.01CH37255), Las Vegas, NV, USA, 17–22 June 2001; p. 374. [Google Scholar]
- Zhu, J.; Tong, H.; Cao, S.; Liu, J.; Peng, W. Study on self-healing properties of metallized high-temperature dielectric films for capacitors. Adv. Technol. Electr. Eng. Energy 2024, 43, 1–13. [Google Scholar] [CrossRef]
- Ho, J.S.; Greenbaum, S.G. Polymer Capacitor Dielectrics for High Temperature Applications. ACS Appl. Mater. Interfaces 2018, 10, 29189–29218. [Google Scholar] [CrossRef]
- Huan, T.D.; Boggs, S.; Teyssedre, G.; Laurent, C.; Cakmak, M.; Kumar, S.; Ramprasad, R. Advanced Polymeric Dielectrics for High Energy Density Applications. Prog. Mater. Sci. 2016, 83, 236–269. [Google Scholar] [CrossRef]
- Tan, D.Q.; Wu, X. A Case Study of High-Temperature Polyetherimide Film Capacitor Fabrication. Mater. Today Energy 2022, 30, 101167. [Google Scholar] [CrossRef]
- Ma, Y.; Shen, H.; Pei, C.; Zhang, H.; Junaid, M.; Wang, Y. Detection of Self-Healing Discharge in Metallized Film Capacitors Using an Ultrasonic Method. Electronics 2020, 9, 1893. [Google Scholar] [CrossRef]
- Belko, V.; Glivenko, D.; Emelyanov, O.; Ivanov, I.; Plotnikov, A. Current Pulse Polarity Effect on Metallized Film Capacitors Failure. IEEE Trans. Plasma Sci. 2017, 45, 1020–1025. [Google Scholar] [CrossRef]
- Li, H.; Wang, B.; Li, Z.; Liu, D.; Li, H.; Zhang, Q.; Lin, F.; Chen, Y. Effect of Pulsed Discharge Current on Lifetime Performance of Metallized Polypropylene Film Capacitors. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 957–963. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Xu, Z.; Wang, X.; Cheng, L.; Liu, W. Self-healing Characteristics and Life Prediction of Metallized Film Capacitor under DC Voltage. High Volt. Eng. 2023, 49, 2929–2937. [Google Scholar] [CrossRef]
- Sarjeant, W.J.; MacDougall, F.W.; Larson, D.W.; Kohlberg, I. Energy Storage Capacitors: Aging, and Diagnostic Approaches for Life Validation. IEEE Trans. Magn. 1997, 33, 501–506. [Google Scholar] [CrossRef]
- Lv, C.; Liu, J.; Zhang, Y.; Lei, W.; Cao, R. An Improved Lifetime Prediction Method for Metallized Film Capacitor Considering Harmonics and Degradation Process. Microelectron. Reliab. 2020, 114, 113892. [Google Scholar] [CrossRef]
- He, Y.; Su, Q.; Liu, D.; Xia, L.; Huang, X.; Lan, D.; Liu, Y.; Huang, Y.; Zhong, B. Surface Engineering Strategy for MXene to Tailor Electromagnetic Wave Absorption Performance. Chem. Eng. J. 2024, 491, 152041. [Google Scholar] [CrossRef]
- Belko, V.O.; Emelyanov, O.A.; Ivanov, I.O.; Plotnikov, A.P. Self-Healing Processes of Metallized Film Capacitors in Overload Modes-Part 1: Experimental Observations. IEEE Trans. Plasma Sci. 2021, 49, 1580–1587. [Google Scholar] [CrossRef]
- Hu, Y.; Ye, X.; Zheng, B.; Zhao, Z.; Zhai, G. Degradation Mechanisms-Based Reliability Modeling for Metallized Film Capacitors under Temperature and Voltage Stresses. Microelectron. Reliab. 2022, 138, 114609. [Google Scholar] [CrossRef]
- Li, Z.; Sun, B.; He, D.P. Fault Analysis and Improvement Measure for 10 kV Dry Type Self-healing Capacitor. High Volt. Eng. 2005, 82–83, 82–83. [Google Scholar] [CrossRef]
- Tan, D.; Wang, Q.; Li, M.; Song, L.; Zhang, F.; Min, Z.; Wang, H.; Zhu, Y.; Zhang, R.; Lan, D.; et al. Magnetic Media Synergistic Carbon fiber@Ni/NiO Composites for High-Efficiency Electromagnetic Wave Absorption. Chem. Eng. J. 2024, 492, 152245. [Google Scholar] [CrossRef]
- Yang, X.; Xuan, L.; Men, W.; Wu, X.; Lan, D.; Shi, Y.; Jia, H.; Duan, Y. Carbonyl Iron/Glass Fiber Cloth Composites: Achieving Multi-Spectrum Stealth in a Wide Temperature Range. Chem. Eng. J. 2024, 491, 151862. [Google Scholar] [CrossRef]
- Dai, X.; Lin, F.; Li, J.; Yao, Z.; Wang, N. Influence Factors for the Self-Healing of Metallized Polypropylene Capacitors. In Proceedings of the 2000 Annual Report Conference on Electrical Insulation and Dielectric Phenomena (Cat. No.00CH37132), Victoria, BC, Canada, 15–18 October 2000; Volume 2, pp. 461–465. [Google Scholar] [CrossRef]
- Zhang, G.; Li, H.; Lan, J.; Li, H.; Li, Z.; Lin, F.; Zhang, Q. Study on the Dynamic Process and Extinguishing Criterion of Metallized Film Self-Healing Arc. In Proceedings of the 2023 IEEE Electrical Insulation Conference (EIC), Quebec City, QC, Canada, 18–21 June 2023; pp. 1–4. [Google Scholar]
- Bel’ko, V.O.; Bondarenko, P.N.; Emel’yanov, O.A. The Dynamic Characteristics of Self-Healing Processes in Metal Film Capacitors. Russ. Electr. Eng. 2007, 78, 138–142. [Google Scholar] [CrossRef]
- Cheng, L.; Li, Z.; Wang, J.; Liu, W.; Li, S. Mechanism Study on the Failure of Metalized Film Capacitor Under HVDC Field Superimposed Harmonics. Proc. CSEE. 2023, 43, 8955–8965. [Google Scholar] [CrossRef]
- Makdessi, M.; Sari, A.; Venet, P. Metallized Polymer Film Capacitors Ageing Law Based on Capacitance Degradation. Microelectron. Reliab. 2014, 54, 1823–1827. [Google Scholar] [CrossRef]
- He, Y.; Wang, F.; Du, G.; Pan, L.; Wang, K.; Kong, D.; Zhang, X. From Independent to Related: Voltage Ramp Rate Effects on Self-Healing Scaling in Metallized Polypropylene Film Capacitors. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 2189–2198. [Google Scholar] [CrossRef]
- Kammermaier, J.; Rittmayer, G.; Birkle, S. Modeling of Plasma-Induced Self-Healing in Organic Dielectrics. J. Appl. Phys. 1989, 66, 1594–1609. [Google Scholar] [CrossRef]
- Kammermaier, J. Chemical Prpcesses During Electrical Breakdown in an Organic Dielectric with Evaporated Thin Electrodes. IEEE Trans. Electr. Insul. 1987, EI-22, 145–149. [Google Scholar] [CrossRef]
- Hauschild, W.; Mosch, W. Statistical Techniques for High-Voltage Engineering; IET Digital Library: London, UK, 1992; ISBN 978-1-84919-429-7. [Google Scholar]
- Li, H.; Zhang, M.; Lin, F.; Cheng, Y.; Lv, F.; Li, Z.; Peng, B. Study on Theory and Influence Factors of Self-Healing in Metallized Film Capacitors. Trans. China Electrotech. Soc. 2012, 27, 218–223+230. [Google Scholar] [CrossRef]
- Tortai, J.H.; Denat, A.; Bonifaci, N. Self-Healing of Capacitors with Metallized Film Technology: Experimental Observations and Theoretical Model. J. Electrost. 2001, 53, 159–169. [Google Scholar] [CrossRef]
- Pan, L.; Wang, F.; He, Y.; Sun, X.; Du, G.; Zhou, Q.; Zhang, J.; Zhang, Z.; Li, J. Reassessing Self-Healing in Metallized Film Capacitors: A Focus on Safety and Damage Analysis. IEEE Trans. Dielectr. Electr. Insul. 2024. [Google Scholar] [CrossRef]
- Li, C.; Wang, B. A Knowledge Graph Method towards Power System Fault Diagnosis and Classification. Electronics 2023, 12, 4808. [Google Scholar] [CrossRef]
- Lin, S.-L. Application of Machine Learning to a Medium Gaussian Support Vector Machine in the Diagnosis of Motor Bearing Faults. Electronics 2021, 10, 2266. [Google Scholar] [CrossRef]
- Haripriya, M.; Manimekala, T.; Dharmalingam, G.; Minakshi, M.; Sivasubramanian, R. Asymmetric Supercapacitors Based on ZnCo2O4 Nanohexagons and Orange Peel Derived Activated Carbon Electrodes. Chem. Asian J. 2024, 19, e202400202. [Google Scholar] [CrossRef] [PubMed]



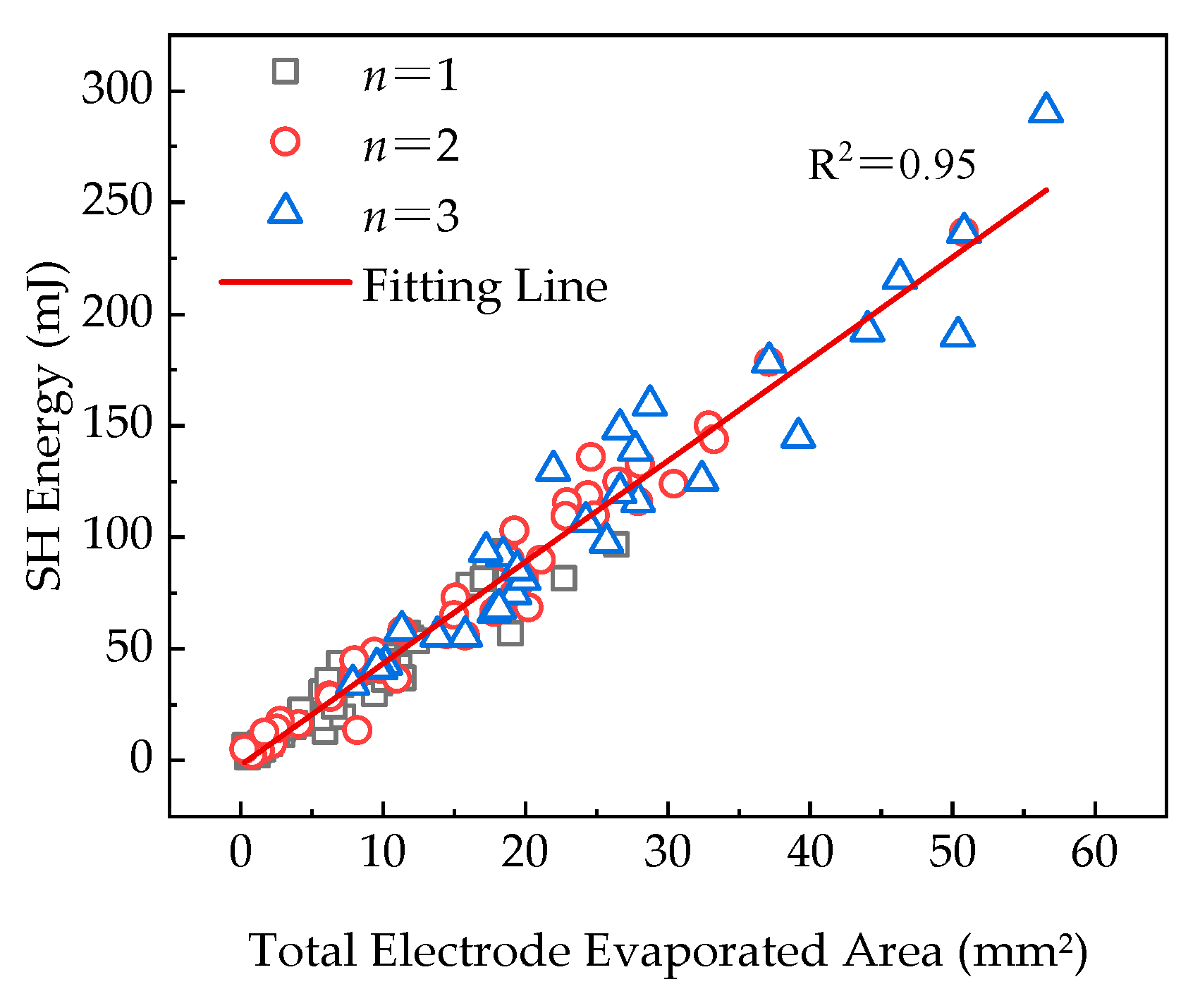
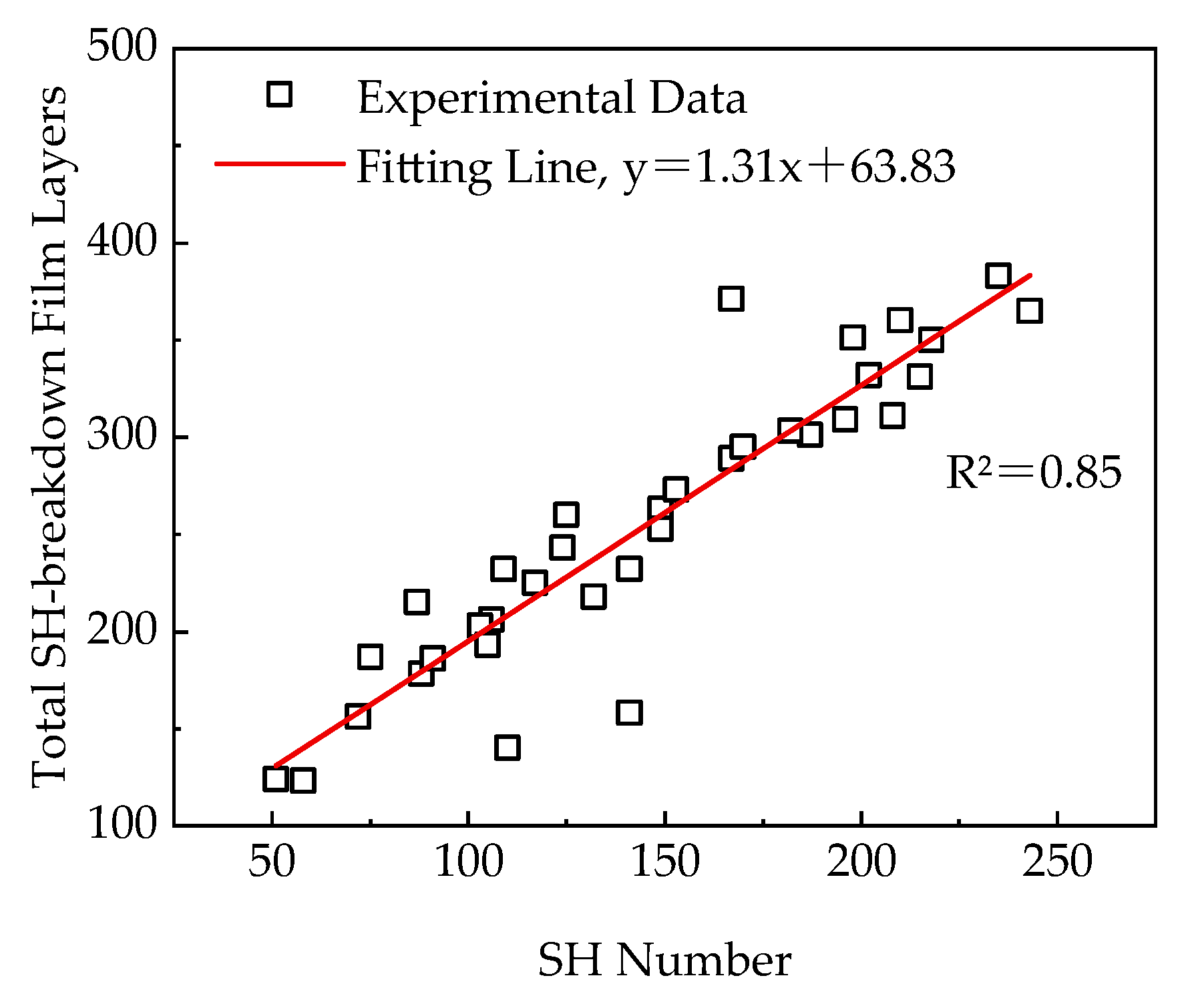
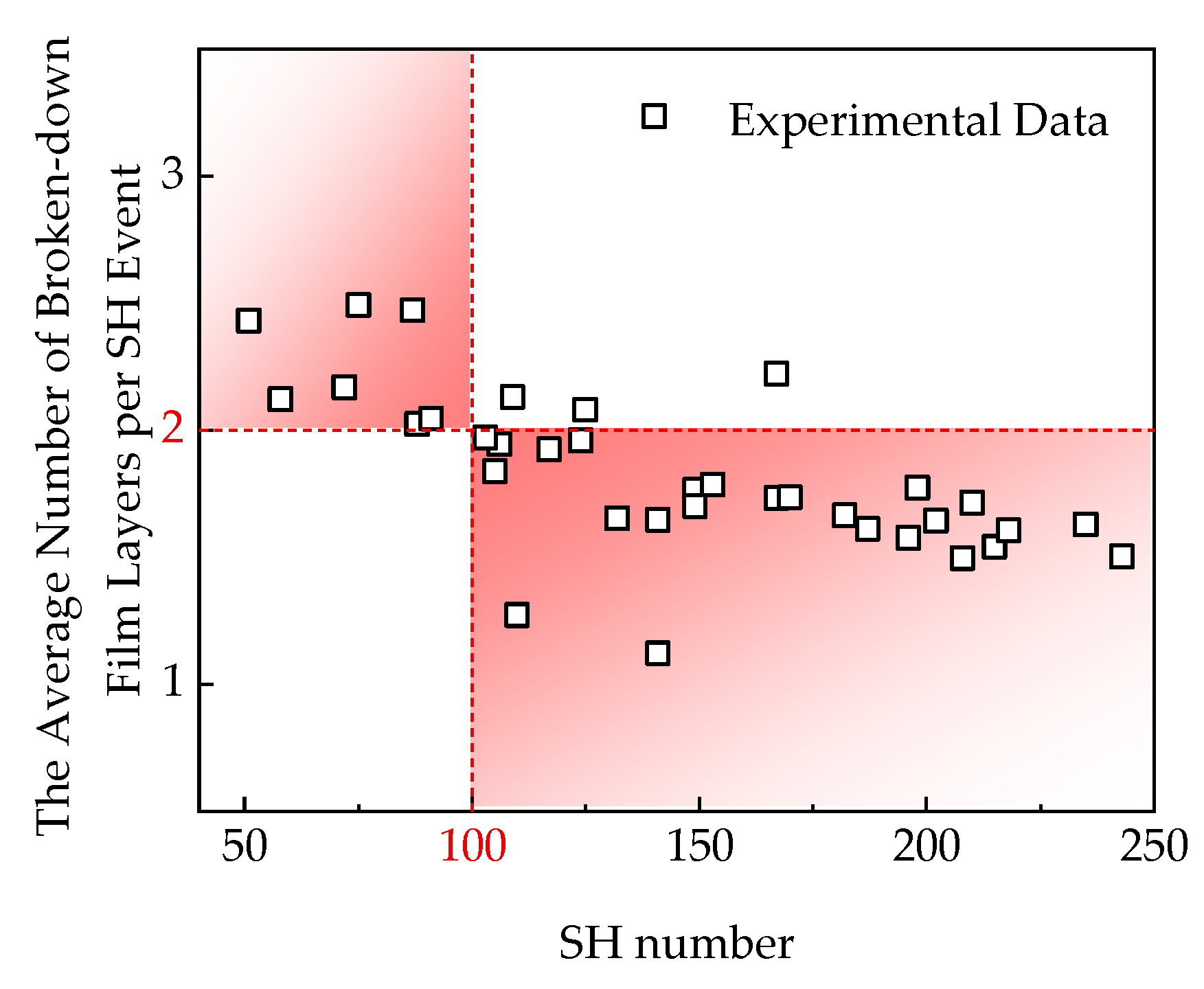


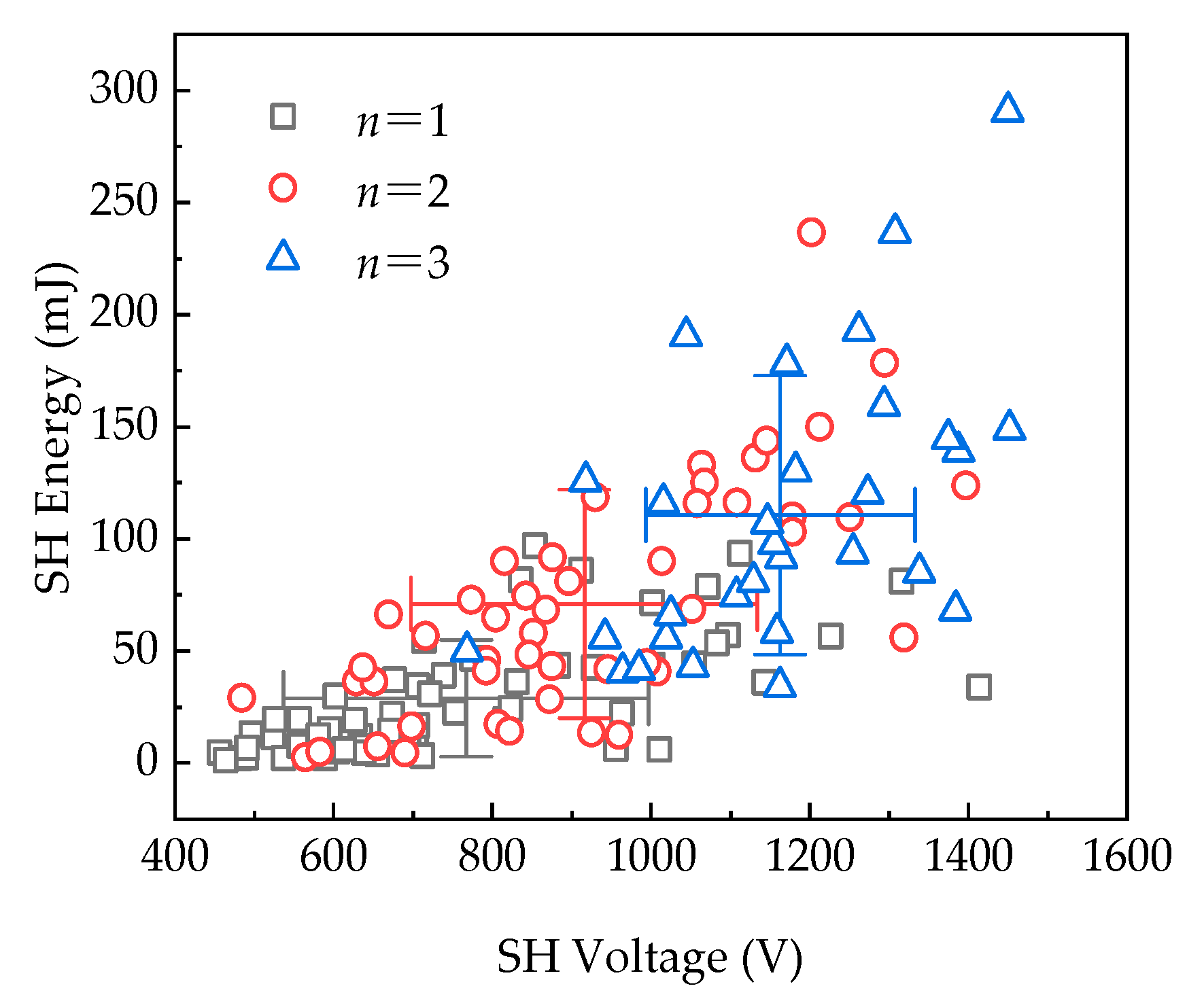


| Plastic Film | ε | Maximum Operating Temperature [°C] | Breakdown Filed [V·μm−1] | Dissipation Factor % 1 kHz | Energy Density [J·cm−3] | References |
|---|---|---|---|---|---|---|
| Biaxially oriented polypropylene | 2.2~2.25 | 105 | 640~764 | ≤0.02 | 1~1.2 | [8,9,10,11] |
| Polyester | 3.2~3.3 | 125 | 570 | <0.5 | 1~1.5 | [8,10,11] |
| Polycarbonate | 2.8~2.9 | 125 | 528 | <0.15 | 0.5~1 | [8,10,11] |
| Polyvinylidene fluoride | 12 | 125 | 590 | <1.8 | 2.4 | [8] |
| Polyethylene naphlate | 3~3.2 | 125 | 500~559 | <0.15 | 1~1.5 | [8,9,10,11,12] |
| Polyphenylene-sulfide (PPS) | 3 | 200 | 550 | <0.03 | 1~1.5 | [8,10,11] |
| Ether ether ketone (PEEK) | 2.97 | / | 446 | 0.25 | / | [9,10,12] |
| Total Dielectric Thermal Damage Area/mm² | Total Electrode Evaporation Area/mm² | |
|---|---|---|
| SH Breakdown in Single-Film Layer | 7.22 | 4.42 |
| SH Breakdown in Two-Film Layer | 57.13 | 39.65 |
| SH Breakdown in Three-Film Layer | 63.48 | 44.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, G.; Zhang, J. Capacitance Evaluation of Metallized Polypropylene Film Capacitors Considering Cumulative Self-Healing Damage. Electronics 2024, 13, 2886. https://doi.org/10.3390/electronics13142886
Du G, Zhang J. Capacitance Evaluation of Metallized Polypropylene Film Capacitors Considering Cumulative Self-Healing Damage. Electronics. 2024; 13(14):2886. https://doi.org/10.3390/electronics13142886
Chicago/Turabian StyleDu, Guoqiang, and Jie Zhang. 2024. "Capacitance Evaluation of Metallized Polypropylene Film Capacitors Considering Cumulative Self-Healing Damage" Electronics 13, no. 14: 2886. https://doi.org/10.3390/electronics13142886
APA StyleDu, G., & Zhang, J. (2024). Capacitance Evaluation of Metallized Polypropylene Film Capacitors Considering Cumulative Self-Healing Damage. Electronics, 13(14), 2886. https://doi.org/10.3390/electronics13142886





