A Secure Data-Sharing Model Resisting Keyword Guessing Attacks in Edge–Cloud Collaboration Scenarios

Abstract

In edge–cloud collaboration scenarios, data sharing is a critical technological tool, yet smart devices encounter significant challenges in ensuring data-sharing security. Attribute-based keyword search (ABKS) is employed in these contexts to facilitate fine-grained access control over shared data, allowing only users with the necessary privileges to retrieve keywords. The implementation of secure data sharing is threatened since most of the current ABKS protocols cannot resist keyword guessing attacks (KGAs), which can be launched by an untrusted cloud server and result in the exposure of sensitive personal information. Using attribute-based encryption (ABE) as the foundation, we build a secure data exchange paradigm that resists KGAs in this work. In our paper, we provide a secure data-sharing framework that resists KGAs and uses ABE as the foundation to achieve fine-grained access control to resources in the ciphertext. To avoid malicious guessing of keywords by the cloud server, the edge layer computes two encryption session keys based on group key agreement (GKA) technology, which are used to re-encrypt the data user’s secret key of the keyword index and keyword trapdoor. The model is implemented using the JPBC library. According to the security analysis, the model can resist KGAs in the random oracle model. The model’s performance examination demonstrates its feasibility and lightweight nature, its large computing advantages, and lower storage consumption.

1. Introduction

Since the edge–cloud collaboration scenario is developing so quickly, its data-sharing technology has been applied to the Industrial Internet of Things [1], intelligent transportation systems [2], and the Medical Internet of Things [3]. Additionally, resource-constrained intelligent terminals in the edge–cloud collaboration scenario can realize improved computing power elasticity, and the core data-sharing technology satisfies the entity users in the scenario to carry out high-precision, fast-response, low-latency transmission, and safe information exchange. In an edge–cloud scenario, data users can efficiently lower terminal communication costs and realize resource rationalization by outsourcing data to the cloud server. However, sensitive data are contained in the stored data [4,5,6], and data security is readily jeopardized. As a result, maintaining data security becomes an important and difficult responsibility [7].

Sensitive data must first be encrypted before being uploaded to the cloud to enable secure data sharing in edge–cloud scenarios. Users who meet the requirements for keyword information matching can then access the relevant ciphertext information. Unfortunately, fine-grained access control to cloud-stored data cannot be achieved by using public key encryption with keyword search. This is because when more users access cloud-stored data, the cloud generates a significant volume of private data simultaneously. Additionally, there is a greater frequency of information interaction between data users and the cloud. To access the relevant data, users must jointly negotiate a session key, which consumes a lot of computational power and results in inefficient access authorization from the users. The scheme in [8] suggests using ABE in conjunction with keyword search to address this issue. In this method, the data owner encrypts private information using an access policy, creates a secure index for the keyword, and then, outsources the work to the cloud. Only authorized data users who comply with the access policy can verify the keyword trapdoor on the cloud server. Upon successful verification, the cloud server retrieves the corresponding ciphertext and calculation parameters and sends them directly to the authorized data user for decryption. However, a semi-trusted cloud server that uses protocols with keyword-searchable encryption is vulnerable to internal and external KGAs [9,10]. In these attacks, adversaries with probabilistic polynomial-time capabilities can use the captured query message to learn more about a particular keyword and use that information to launch KGAs during a data user’s search.

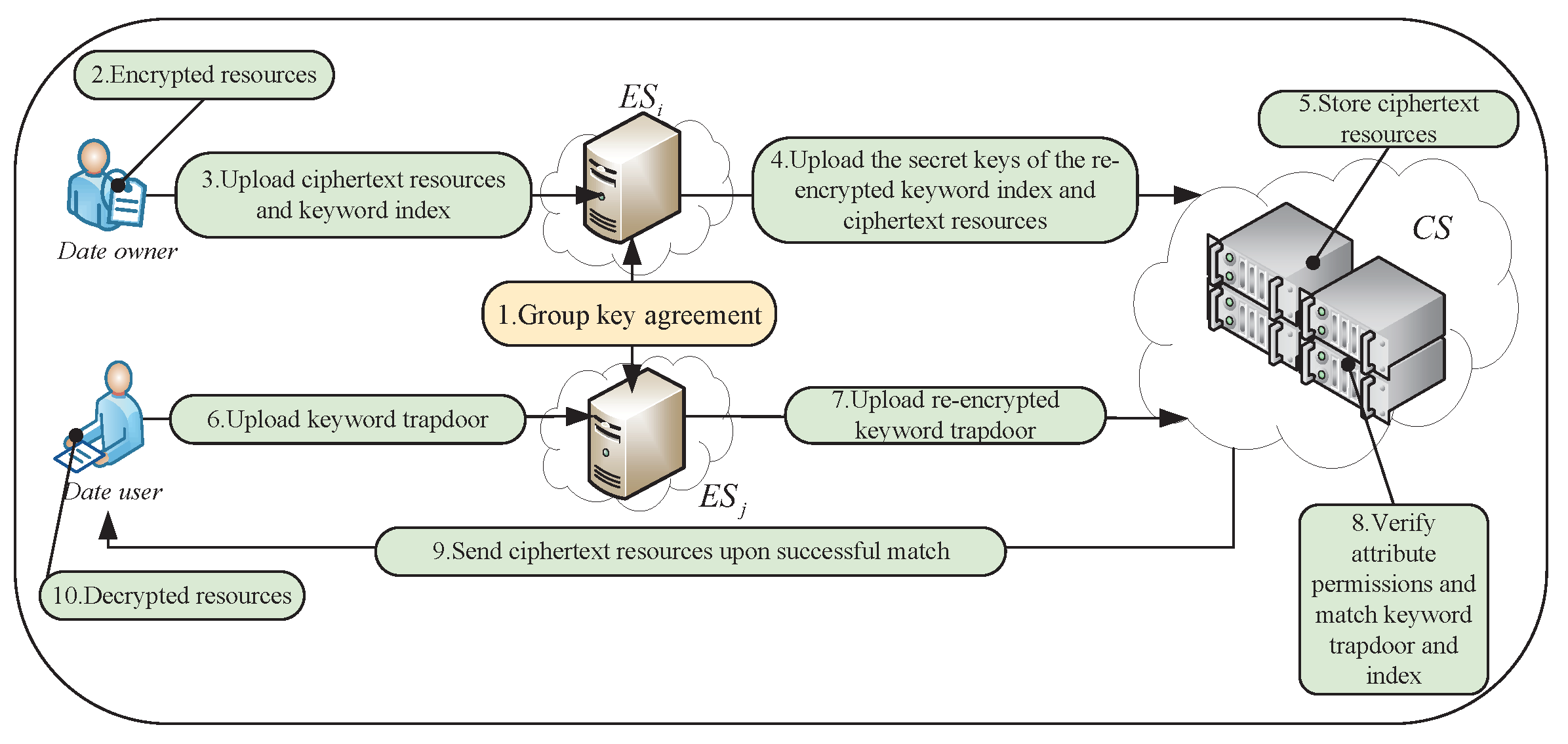
Thus, it is necessary to pay attention to resist KGAs to safeguard the privacy of sensitive data stored in the cloud. This paper aims to tackle the issue of privacy leakage by developing a secure data-sharing model that withstands KGAs in edge–cloud collaboration scenarios. To achieve this goal, the edge layer generates two inversely related session keys based on GKA technology. One is used to re-encrypt the data owner’s secret key of the keyword index to prevent tampering during the upload to the cloud, and the other is used to re-encrypt the keyword trapdoor information to prevent its leakage to the cloud server. The data owner transmits the ciphertext and keyword index parameters to the edge layer, where the edge server managing the domain has the corresponding attribute permissions of the data owner and computes the data user’s decryption key factor based on these permissions. The edge layer uses one of its session keys to re-encrypt the secret key of the keyword index, and then, sends the ciphertext and other parameters to the cloud for secure storage and data sharing. To prevent the cloud server from launching KGAs, the keyword trapdoor is re-encrypted by the edge server managing the domain after the data user computes and sends the keyword trapdoor to it. Only when the keyword trapdoor of the data user, who meets the access policy, successfully matches the keyword index stored in the cloud, does the data user have the authority to access the ciphertext resources. The cloud server searches the ciphertext and sends it along with the decryption key factor to the data user based on their ip address. The data user then uses the decryption key factor and the Lagrange interpolating polynomial to compute the decryption key and decrypt the ciphertext, thereby obtaining the corresponding resources and completing flexible and secure cross-domain data sharing. The re-encrypted keyword trapdoor can resist KGAs initiated by the cloud server in this model and prevent sensitive privacy leakage and tampering. The simplified process of the appeal is shown in Figure 1.

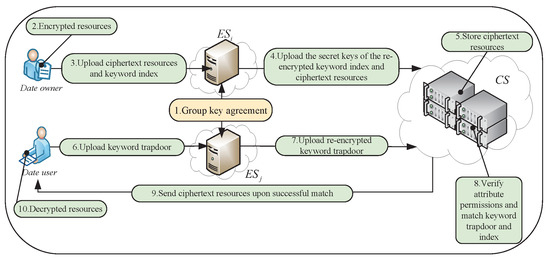
Figure 1. Simplified process for our model.

2. Related Work

Song et al. [11] were the first to propose the keyword-searchable encryption (SE) technique, which allows data users to securely search ciphertexts stored in the cloud while providing concealed keyword querying. Building on Song’s scheme, Li et al. [12] introduced searchable symmetric encryption (SSE) with forward search privacy. This approach enhances security by enabling the addition of new documents without revealing any information about previous queries, proving to be more effective than previous techniques according to test data. To counteract adversaries with arbitrary background knowledge, Chen et al. [13] developed a framework for SSE systems based on differential privacy approaches, offering verifiable security guarantees. However, experimental investigations have shown that even advanced leakage suppression techniques in SSE schemes are insufficient to defend against new inference attacks. Gui et al. [14] proposed a novel inference attack capable of performing efficient, scalable, and accurate query reconstruction against end-to-end SSE systems, revealing that the existing SSE framework cannot prevent such attacks.

Public-key encryption with keyword search (PEKS) was introduced by Boneh et al. [15] to facilitate data exchange between users. In this scheme, the data provider encrypts the chosen keyword within the ciphertext before outsourcing it to the cloud for storage. The data user generates a list of keywords, searches for them on the cloud server, and utilizes a test function in the cloud to verify the presence of the keywords in each ciphertext. If a match is found, the corresponding ciphertext can be returned to the data user. With this technique, security and privacy could be readily jeopardized if the cloud server is hostile. Most current PEKS systems cannot simultaneously achieve high search efficiency and robust security. To address this challenge, Chen et al. [16] proposed a method for parallel and forward private searchable encryption with cloud data sharing. This approach ensures forward privacy and parallelism, with experimental results demonstrating its effectiveness and applicability. Through comparative analysis and experimental results, Lu et al. [17] proposed an effective PKES scheme featuring flexible keyword-free domain multi-keyword search, and forward ciphertext retrieval. This scheme effectively guards against KGAs and unauthorized ciphertext retrieval, demonstrating security in the random oracle model and outperforming existing schemes. Cheng et al. [18] introduced a server-assisted public-key authentication searchable encryption scheme with constant ciphertext and constant trapdoor sizes, combining sender and receiver servers. In this scheme, the sender only needs to encrypt the keyword once, and the constant sizes of the ciphertext and trapdoor ensure scalability, enabling multi-scenario applications.

Bethencourt, Sahai, and Waters [19] initially introduced ABE with a ciphertext policy to establish access control for cloud data. In this approach, data users determine access based on the specified access policy. Goyal [20] proposed a key-policy attribute-based encryption (KP-ABE) method, featuring a key-associative access control structure. Waters et al. [21] later introduced a ciphertext-policy attribute-based encryption (CP-ABE) approach, enabling one-to-many fine-grained sharing. Subsequently, numerous traditional ABE systems and variations were proposed [22]. To prevent dishonest searches by the data user’s cloud, Zheng and Xu et al. [23] proposed VABKS (verifiable attribute-based keyword search) for outsourced encrypted data. This method can verify whether the cloud has performed honest searches. Combining ABE with SE, ABSE offers advantages over traditional PKES. However, as the cloud is not entirely trustworthy, Liu et al. [24] proposed a key-policy attribute-based searchable encryption (KP-ABSE) method to enhance practicality. This approach can successfully verify the accuracy and integrity of data files stored in the cloud. Since the cloud holds a public key for re-encrypting keyword ciphertexts, it can effectively fend off offline KGAs. Nevertheless, hostile adversaries can fabricate the cloud’s public key, compromising user data privacy.

Liang and Susilo [25] employed attribute-based proxy re-encryption capabilities and ABKS to facilitate data sharing and keyword upgrading. The approach verifies that it is chosen-ciphertext-safe in the random oracle and guarantees that the ciphertexts’ keyword search functionality can be maintained after ciphertext sharing. A verifiable keyword search for encrypted cloud data in smart cities was proposed by Miao [26]. This allows the data user to confirm the search results and also demonstrates the security of the scheme against targeted keyword attacks (CKAs). A verified attribute-based keyword search with fine-grained owner-enforced search authorization in the cloud was proposed by Sun et al. [27] Multiple data owners and users are supported by this method. Large-scale systems may scale more easily thanks to the user owner’s enforced search authorization, and the user revocation process is more effective and resilient to targeted keyword attacks.

Cui et al. [28] proposed an attribute-based keyword search with an effective revocation scheme (AKSER). AKSER achieves fine-grained authorization of search under a distributed multi-attribute authority institution. It also ensures keyword semantic security, keyword confidentiality, trapdoor unlinkability, and collision resistance. In contrast to ciphertext-policy attribute-based encryption schemes, Wang et al. [29] introduced the first hierarchical attribute-based encryption scheme for document collections, which uses fewer ciphertext storage resources. They also developed a depth-first search algorithm for ARF trees, enhancing search efficiency, which can be further improved through parallel computing. The search algorithm only requires one keyword to be the same in two keyword sets to output the corresponding correlation, reflecting the number of identical keywords in these sets. Meng et al. [30] proposed an attribute-based encryption and dynamic keyword search method in fog computing that shifts the majority of computational overhead from resource-constrained users to fog nodes, reducing the computational load on the endpoints. Current CP-ABKS methods are designed for non-shared multi-owner configurations and are not immediately applicable to shared multi-owner configurations.

To improve monitoring of hostile users for selective security and resistance to offline keyword guessing attacks, Miao et al. [31] presented privacy-preserving attribute-based keyword searches in shared owner settings. Most earlier techniques are vulnerable to offline KGAs when the keyword space is polynomial. To address these issues, Zhang et al. [32] proposed an attribute-based encryption scheme with searchable and verifiable multiple keywords based on cloud data. Their experimental results demonstrate the scheme’s effectiveness, achieving selective security against offline keyword guessing attacks and ensuring the unforgeability of signatures.

Li et al. [33] proposed an attribute-based keyword search strategy that prevents keyword guessing attacks by signing the keyword with the data owner’s private key before generating the keyword ciphertext. To combat data tampering, Zhang et al. [34] introduced a blockchain-based anonymous attribute searchable encryption scheme for data sharing. This scheme leverages blockchain technology to conceal the attributes of the access policy while ensuring tamper resistance, integrity verification, and non-repudiation. Experimental results demonstrate the scheme’s practicality and efficiency. Ge et al. [35] proposed an attribute-based proxy re-encryption scheme with a direct revocation mechanism for data sharing in the cloud. This mechanism allows the cloud server to directly revoke users in the original shared set involved in the re-encryption key. Additionally, Ge et al. [36] proposed a secure keyword search and data-sharing mechanism for cloud computing, addressing the need for users to quickly search and return results without compromising data confidentiality. This mechanism supports attribute-based keyword search and attribute-based data sharing simultaneously, and it has been shown to be secure against chosen-ciphertext attacks in random oracle models and CKAs.

Upon perusing the above references, it is evident that researchers have made significant contributions to the attainment of secure data sharing. However, there exist certain limitations. Specifically, the majority of schemes are susceptible to KGAs, and in the event of a probabilistic polynomial-time adversary of a semi-trusted cloud server, they can obtain specific keyword information through the captured query information, thereby compromising privacy. In the edge–cloud collaboration scenario, we propose a secure data-sharing model based on an anti-keyword guessing attack to counter the appeal attack. The model is lightweight and highly appropriate for resource-constrained smart terminals, as it achieves resistance to keyword guessing attacks through key negotiation at the edge layer, and safe in terms of privacy for end users. Comparative investigations indicate that this model performs better than existing schemes.

Methodology

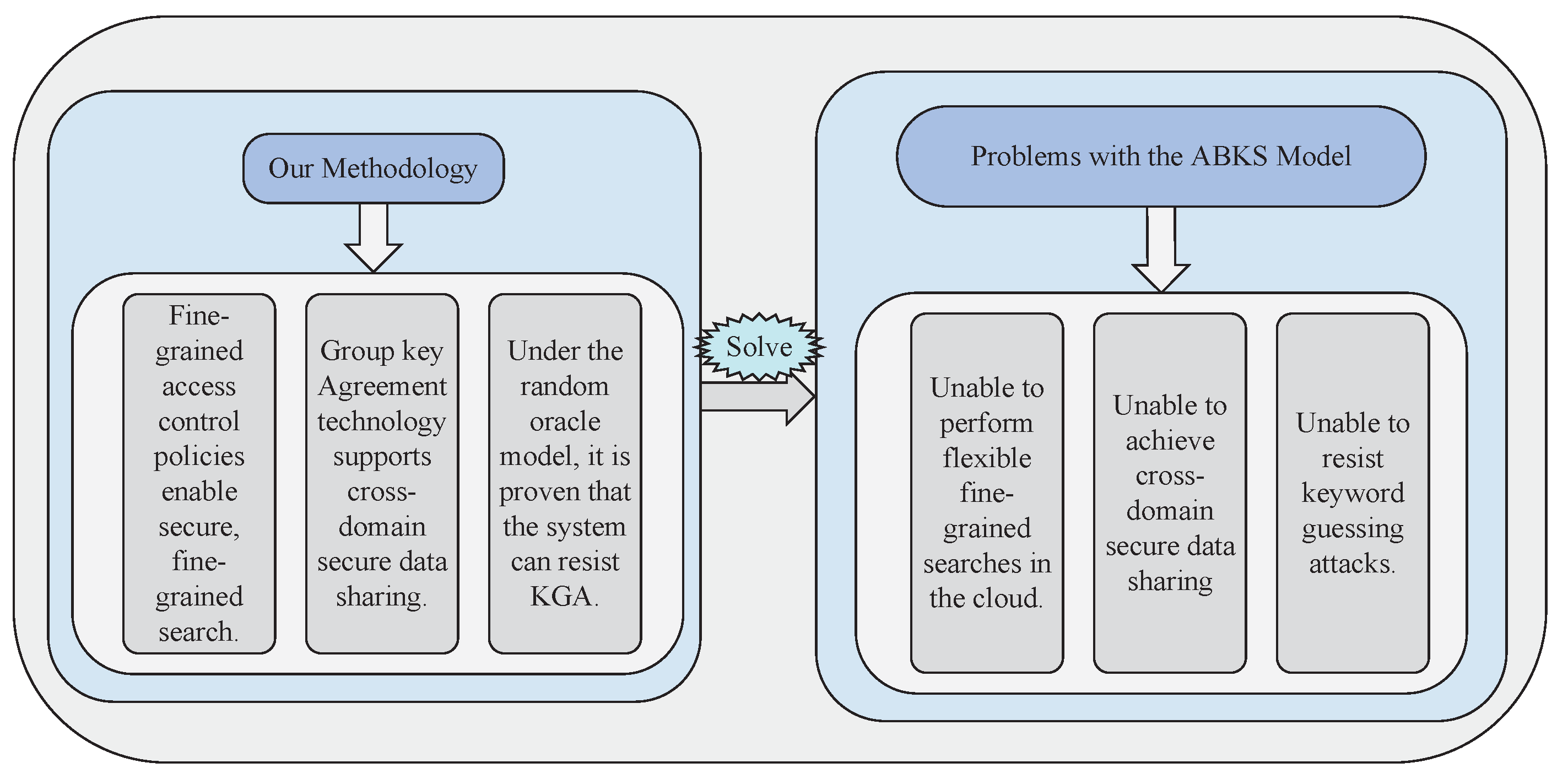
We propose a secure data-sharing model that resists keyword guessing attacks in edge–cloud collaboration scenarios (SDSM-KGA). The methodology of this paper is as follows, and the problems addressed are illustrated in Figure 2.

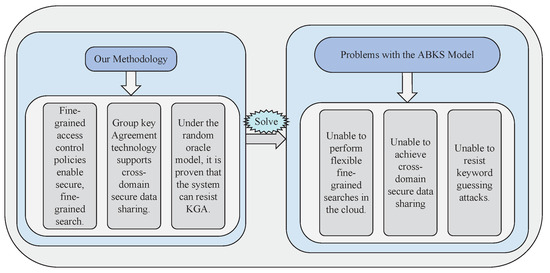
Figure 2. Problems solved by the methodology.

(1)

This paper extends the traditional attribute-based keyword search (ABKS) model by proposing a new flexible, fine-grained access control mechanism. This mechanism allows data users with identical attribute permissions to perform fine-grained searches on ciphertext based on specific access policies, enabling flexible and secure data sharing. If a data user’s attribute permissions do not meet the requirements of the access policy, they are not able to access the shared ciphertext. This access control strategy enhances the efficiency and security of data sharing among users.

(2)

The ABKS model we propose supports cross-domain data sharing and can effectively resist KGAs initiated by cloud servers. In traditional models, keyword trapdoor information is public in the cloud, and is therefore vulnerable to attacks by external attackers or malicious cloud servers. To prevent such attacks, we implement a key negotiation method at the edge layer. This allows the edge layer to re-encrypt the keys of the data owner’s keyword index and keyword trapdoor key stored in the cloud to prevent other entities from identifying them.

(3)

We define a new security model and prove its ability to resist KGAs under the random oracle model, and implement our scheme using the JPBC library. The experimental evaluation proves the practicality and high performance of the scheme compared with other traditional schemes.

3. Basic Knowledge

3.1. Bilinear Map

Let ${\mathbb{G}}_1$ be an additive group and g be a ${\mathbb{G}}_1$ generator. ${\mathbb{G}}_T$ represents a multiplicative cyclic group. ${\mathbb{G}}_1$ and ${\mathbb{G}}_T$ have the same prime order q. We can say $e:{\mathbb{G}}_1\times {\mathbb{G}}_1\to {\mathbb{G}}_T$ is a bilinear pairing if it meets the following properties:

(1)

Bilinearity: For all $\forall a,b\in {\mathbb{Z}}_q^{*}$ and $g_1,g_2\in {\mathbb{G}}_1$, we have $e(a{g}_1,b{g}_2)=e{(g_1,g_2)}^{ab}$.

(2)

Non-degenerate: $\exists g_1\in {\mathbb{G}}_1$, $e(g_1,g_1)\ne 1$.

(3)

Computability: $\forall g_1,g_2\in {\mathbb{G}}_1$; there exist efficient algorithms in polynomial time that can compute the $e(g_1,g_2)$.

3.2. Access Structure

Let $P=\{P_1,P_2,...,P_n\}$ denote the set of participants, and let $2^P=\left\{A\right|A\subseteq P=\{P_1,P_2,...,P_n\}\}$. For $\forall B,C\subseteq P$, if $B\subseteq \mathbb{A}$ and $B\subseteq C$, then $C\subseteq \mathbb{A}$. If $\mathbb{A}$ is a non-empty subset of $P=\{P_1,P_2,...,P_n\}$, then $\mathbb{A}$ is called an access structure. For any set D, if $D\subseteq \mathbb{A}$, then D is an authorized set; otherwise, it is an unauthorized set.

3.3. Linear Secret-Sharing Scheme

The set of participants is $P=\{P_1,P_2,...,P_n\}$, where the access structure is $\mathbb{A}=<M,F>$. Here, M is a matrix with n rows and m columns. For all $\forall 1\le i\le n$, $F_i$ is a mapping function that maps each row of the matrix to different attributes. If $\Pi$ satisfies the following conditions, then $\Pi$ is a linear secret-sharing scheme (LSSS) defined over P.

(1)

Given a secret value $s\in {\mathbb{Z}}_q^{*}$, randomly select $l_2,l_3,..,l_n\in {\mathbb{Z}}_q^{*}$; construct the column vector $\overrightarrow{v}={(s,l_2,l_3,...,l_n)}^T$. Then, compute $h_i={\left(M\overrightarrow{v}\right)}_i$, where $h_i$ represents the secret share held by $F_i$.

(2)

There exists a set of vectors ${\{{\omega }_i\in {\mathbb{Z}}_q^{*}\}}_{i\in I}$ such that ${\sum }_{i\in I}{\omega }_i{M}_i=(1,0,...,0)$. The secret value s can be reconstructed as $s={\sum }_{i\in I}{\omega }_i{M}_i·\overrightarrow{v}={\sum }_{i\in I}{\omega }_i{h}_i$, where $\left\{h_i\right\}(1\le i\le r)$ are valid secret shares of the secret value.

This scheme is based on the algorithm idea of scheme [37], using the elements in the access matrix to encrypt the information, and decrypting according to ${\sum }_{i\in I}{\omega }_i{M}_i={(1,0,...,0)}^T$, which can ensure that ${\prod }_{j=1}^n{\sum }_{i\in I}{M}_{i,j}{\omega }_i=1$.

3.4. Decisional Bilinear Diffie–Hellman Assumption

Considering the bilinear mapping elements ${\mathbb{G}}_1,{\mathbb{G}}_T,g,e,q$ and random elements $a,b,c\in {\mathbb{Z}}_q^{*}$, we see that adversary $\mathcal{B}$ is unable to discriminate between the tuples $(ag,bg,cg,Z)$ and $(ag,bg,cg,abcg)$, where Z is chosen at random from ${\mathbb{G}}_1$. Consequently, there is no probabilistic polynomial time (PPT). The advantage $\epsilon$ of $\mathcal{B}$ in resolving the DBDH problem is described as follows, assuming the following equations hold.

$$\left|Pr\left[\mathcal{B}\left(\right(ag,bg,cg,abcg\left)\right)=1\right]\right|-\left|Pr\left[\mathcal{B}\left(\right(ag,bg,cg,Z\left)\right)=1\right]\right|<\epsilon .$$

(1)

3.5. Security Model

Init: The simulator $\mathcal{B}$ ensures that the keyword index secret key $s_0$ remains secret. The value $s_{0}g$ is sent by $\mathcal{B}$ to the attacker $\mathcal{A}$. Attacker $\mathcal{A}$ challenges the access structure $\mathbb{A}$ and randomly selects attributes to form a set $\left\{at{t}_1^{*},at{t}_2^{*},\dots ,at{t}_r^{*}\right\}$, which is then sent to the simulator $\mathcal{B}$. The simulator $\mathcal{B}$ computes the corresponding attribute permissions $\{{\rho }_1^{*},{\rho }_2^{*},\dots ,{\rho }_r^{*}\}$ and sends them to $\mathcal{A}$. The attacker $\mathcal{A}$ subsequently computes the attribute permission key $s_1^{*}={\sum }_{i=1}^r{H}_2\left({\rho }_i^{*}\right)modq$ for the challenge.

Phase 1: $\mathcal{A}$ executes a polynomially limited number of queries in an adaptive manner, which means that each query may depend on the response to previous queries.

(1)

Attribute permissions secret-key extraction query: $\mathcal{A}$ chooses an attribute permissions secret key $s_{1,i}^{*}$, then sends $s_{1,i}^{*}$ to simulator $\mathcal{B}$ to verify whether the private key is legal or not; the verification succeeds in computing the key $E_i$, then runs the re-encryption attribute permissions private key to obtain $E_i^{\stackrel{`}{ }}$, and then, returns $E_i^{\stackrel{`}{ }}$ to $\mathcal{A}$.

(2)

Keyword trapdoor extraction query: $\mathcal{A}$ randomly selects a keyword $k{w}_i$ from the keyword dictionary, then $\mathcal{A}$ sends $k{w}_i$ to $\mathcal{B}$; simulator $\mathcal{B}$ calculates the keyword trapdoor $Y_i$ of the searchable keyword $k{w}_i$, then runs to re-encrypt the trapdoor $Y_i^{\prime }$ and returns $Y_i^{\prime }$ to $\mathcal{A}$.

Challenge: $\mathcal{A}$ decides when the first stage will end. $\mathcal{A}$ generates two keywords $k{w}_1$ and $k{w}_0$ of the same length that it wants to be challenged. The simulator $\mathcal{B}$ randomly selects bits $coin\in \{0,1\}$, computes the trapdoor for keyword $k{w}_{*}$ as $Y_i^{*}$, and then, runs the re-encryption trapdoor to obtain $Y_i^{*\stackrel{`}{ }}=<\beta ,Y_i^{*}>$. $\mathcal{B}$ re-encrypts the attribute permissions private key $E_i^{*}$ to obtain $E_i^{*\stackrel{`}{ }}=<\alpha ,E_i^{*}>$, and sends $(Y_i^{*\stackrel{`}{ }},E_i^{*\stackrel{`}{ }})$ as the challenged parameters to $\mathcal{A}$. If the encryption of the trapdoor for the target keyword $k{w}_{*}$ fails, then $\mathcal{A}$ aborts the game.

Phase 2: $\mathcal{A}$ can make a polynomially bounded number of adaptive queries as in phase 1, except that it cannot make private-key extraction queries and trapdoor extraction queries for $s_1^{*}$ and $k{w}_1,k{w}_0$.

$\mathcal{A}$ outputs the result ${coin}^{\prime }$, if ${coin}^{\prime }=coin$ will win the game. We define the advantage of $\mathcal{A}$ in attacking the scheme as $Ad{v}_{\mathcal{A}}^{IND-KGA}=\left|Pr[{coin}^{\prime }=coin]-1/2\right|$.

4. System Model and Initialization

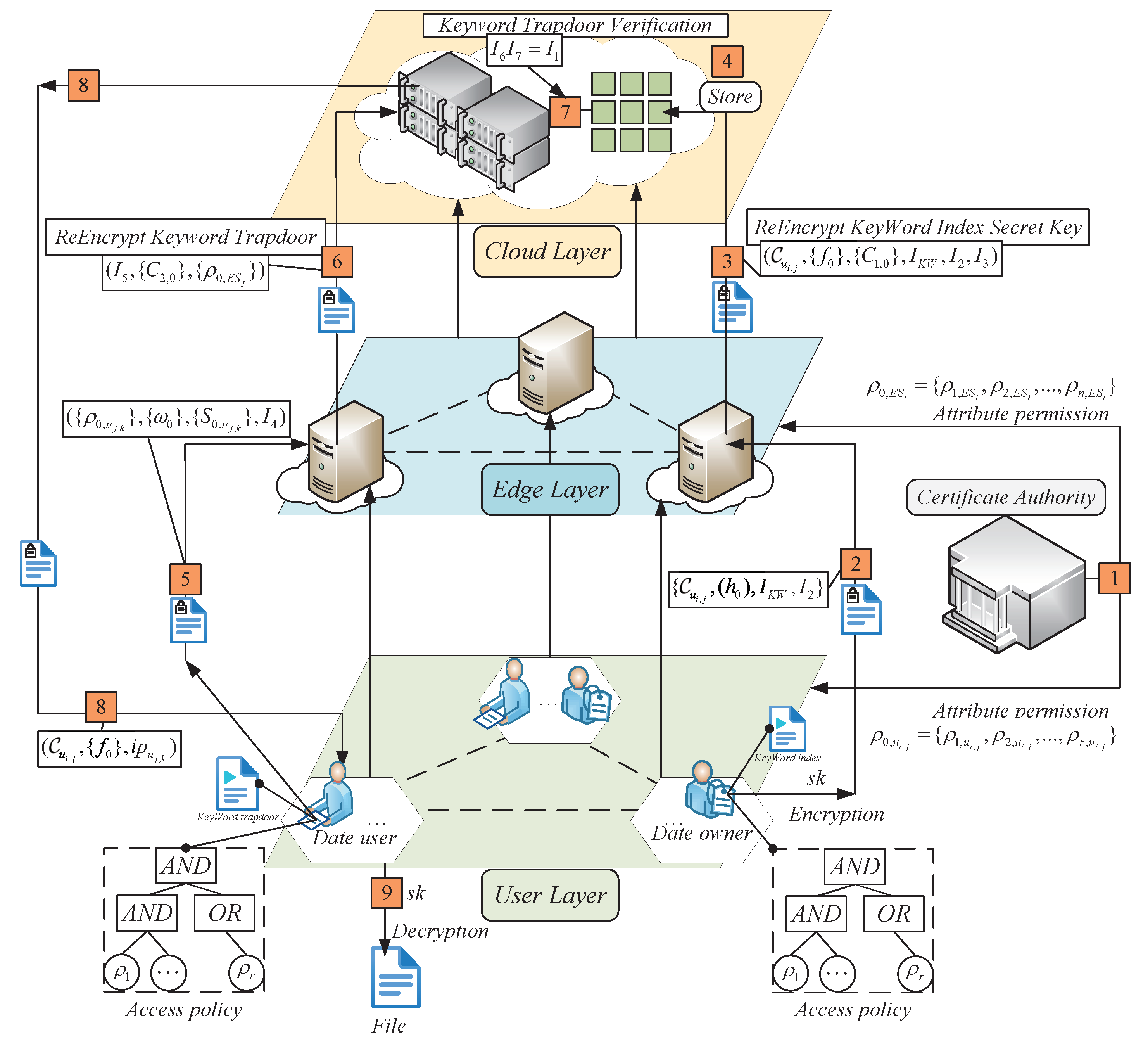
In this paper, we propose a secure data-sharing model to resist keyword guessing attacks in the edge–cloud collaboration scenario. The system model is shown in Figure 3, which mainly has certification authority, cloud layer, edge layer, and data user layer.

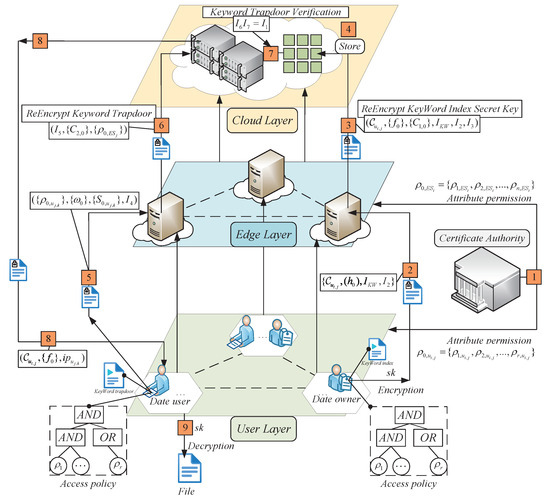
Figure 3. System model.

4.1. System Model

CA Authentication Center: The center is responsible for implementing system parameter settings, generating the system’s master and public keys, registering user attributes, determining attribute permissions, and distributing attributes to data users and edge servers.

Cloud service layer: Comprised of a cloud server, the primary purpose of this layer is to store and validate the private key and re-encrypted keyword trapdoor data sent by the edge layer. Upon successful verification, ciphertext resources are sent to data users who comply with the access policy. This layer also offers higher storage capacity, high scalability, and flexibility, while handling complex calculations and tasks from the edge layer and providing a secure channel for data sharing.

Edge layer: The edge layer primarily handles the negotiation of session keys, one is used to re-encrypt the data owner’s secret key of the keyword index to prevent tampering during the upload to the cloud, and the other is used to re-encrypt the keyword trapdoor information to prevent its leakage to the cloud server. This layer facilitates collaborative computation, enhances data resource-sharing security, and reduces processing times. By decreasing latency and improving security, it ensures efficient collaborative computation.

User layer: This layer consists of mobile data users and data owners. The data owner is the one who uploads the shared resources. For a data user to access the decrypted key factor and ciphertext resources, their attribute permission set must match the access policy. Additionally, only when the keyword index and trapdoor are successfully verified by the cloud server will ciphertext resources be accessible.

4.2. System Initialization

The CA authentication center generates a bilinear mapping $e:{\mathbb{G}}_1\times {\mathbb{G}}_1\to {\mathbb{G}}_T$, where ${\mathbb{G}}_1$ is an addition group, ${\mathbb{G}}_T$ is a multiplicative cyclic group, the prime order is q, and g is a generating element of ${\mathbb{G}}_1$. Then, it selects a random number $s{k}_{CA}\in {\mathbb{Z}}_q^{*}$, and computes $p{k}_{CA}=s{k}_{CA}g$, where $(p{K}_{CA},s{k}_{CA})$ is the CA’s public/private key pair, and the CA selects a hash function $H_1:{\{0,1\}}^{*}\to {\mathbb{Z}}_q^{*},H_2:{\mathbb{G}}_1\to {\mathbb{Z}}_q^{*},H_3:{\mathbb{Z}}_q^{*}\to {\mathbb{G}}_1$, and the CA sets the system’s public parameters $\{g,q,{\mathbb{G}}_1,{\mathbb{G}}_T,e,H_1,H_2,H_3,P{K}_{CA}\}$.

4.3. System Entity Key Generation

Assume there are N edge servers $E{S}_i(1\le i\le N)$, each edge server manages $E{S}_i$ the corresponding domain and the number of data users in each domain is at most n. For example, data user $u_{i,j}$ is the j-th user in the i-th domain, and the identity set of data users in the i-th domain is $I{D}_i=\{i{d}_{u_{i,1}},i{d}_{u_{i,2}},i{d}_{u_{i,j}},...,i{d}_{u_{i,n}}\}$. Using data user $u_{i,j}$ who is controlled by edge server $E{S}_i$ as an example, the CA broadcasts system parameters $\{g,q,{\mathbb{G}}_1,{\mathbb{G}}_T,e,H_1,H_2,H_3,p{k}_{CA}\}$ in the following ways:

1.

The data user $u_{i,j}$, whose identity is $i{d}_{u_{i,j}}$, receives the system parameters $\{g,q,{\mathbb{G}}_1,{\mathbb{G}}_T,$$e,H_1,H_2,H_3,p{k}_{CA}\}$ that the CA broadcasts, $u_{i,j}$ chooses a positive number $s{k}_{u_{i,j}}\in {\mathbb{Z}}_q^{*}$ at random, $u_{i,j}$ computes public key $p{k}_{u_{i,j}}=s{k}_{u_{i,j}}g$ and ${\eta }_0=H_1(i{d}_{u_{i,j}}\left|\right|p{k}_{u_{i,j}})p{k}_{CA}$. After that, the CA receives argument $\{u_{i,j},i{d}_{u_{i,j}},{\eta }_0,p{k}_{u_{i,j}}\}$.

2.

After receiving the parameter $\{u_{i,j},i{d}_{u_{i,j}},{\eta }_0,p{k}_{u_{i,j}}\}$, the CA checks whether the public key $p{k}_{u_{i,j}}$ and the user’s identity $i{d}_{u_{i,j}}$ correspond using equation $e(p{k}_{u_{i,j}},{\eta }_0)=e(s{k}_{CA}p{k}_{u_{i,j}},H_1(i{d}_{u_{i,j}}\left|\right|p{k}_{u_{i,j}}\left)g\right)$ to verify its legitimacy. If valid, the CA publishes the valid public key $p{k}_{u_{i,j}}$ of $u_{i,j}$. The procedure mentioned above provides the identified public-key information to the data user $u_{i,j}$, enabling them to create their own public/private key pair $(p{k}_{u_{i,j}}/s{k}_{u_{i,j}})$.

The process of creating the public/private key pair for the cloud server (CS) and the edge server $E{S}_i(1\le i\le N)$ is the same. The entity’s CS generated the public/private key pair $(p{k}_{CS},s{k}_{CS})$ through the above process. The $E{S}_i$ of the i management domain generated the public/private key pair $(p{k}_{E{S}_i},s{k}_{E{S}_i})$.

4.4. Acquisition of Data User Attribute Permissions

For network resource access, the CA authentication center defines the system attribute set ${SA}_{set}=\{At{t}_1,At{t}_2,...,At{t}_n\}$. The attribute serial number corresponding to each attribute is $\{S_1,S_2,...,S_n\}$. It also generates the corresponding attribute parameter $b_i\in {\mathbb{Z}}_q^{*}(1\le i\le n)$ for each attribute to form the attribute parameter set $At{t}_{set}=\{b_1,b_2,...,b_n\}$, and the terminal members receive the attribute set that is available for authentication. Assuming that the attribute set of $u_{i,j}(1\le i\le N,1\le j\le n)$ is expressed as $\{at{t}_{1,u_{i,j}},at{t}_{2,u_{i,j}},...,at{t}_{r,u_{i,j}}\}\subseteq S{A}_{set}(1\le r\le n)$, where $at{t}_{r,u_{i,j}}\subseteq S{A}_{set}(1\le r\le n)$, attribute registration for arbitrary terminals and acquisition of attribute privileges are as follows:

1.

$u_{i,j}$ When carrying out the process of attribute authentication, the terminal $u_{i,j}$ obtains the set $SA$ of authentication attributes announced by the CA, randomly chooses ${\gamma }_{1,u_{i,j}}\in {\mathbb{Z}}_q^{*}$, computes $o_{1,u_{i,j}}={\gamma }_{1,u_{i,j}}g$, ${\vartheta }_{1,u_{i,j}}=H_1\left(at{t}_{1,u_{i,j}}\right)p{k}_{CA}$, ${\vartheta }_{2,u_{i,j}}=H_1\left(at{t}_{2,u_{i,j}}\right)p{k}_{CA}$,…,${\vartheta }_{r,u_{i,j}}=H_1\left(at{t}_{r,u_{i,j}}\right)p{k}_{CA}(1\le r\le n)$, ${\eta }_{1,u_{i,j}}$ as the signature message, ${\eta }_{1,u_{i,j}}=s{k}_{u_{i,j}}^{-1}{\gamma }_{1,u_{i,j}}{H}_1(at{t}_{1,u_{i,j}}\left|\right|at{t}_{2,u_{i,j}}\left|\right|...\left|\right|at{t}_{r,u_{i,j}}\left|\right|p{k}_{u_{i,j}})g$, where ${\vartheta }_{0,u_{i,j}}=\{{\vartheta }_{1,u_{i,j}},{\vartheta }_{2,u_{i,j}},...,{\vartheta }_{r,u_{i,j}}\}$, and then, sends the parameters $\{o_{1,u_{i,j}},\left\{{\vartheta }_{0,u_{i,j}}\right\},{\eta }_{1,u_{i,j}},p{k}_{u_{i,j}}\}$ to the CA.

2.

After receiving the parameters $\{o_{1,u_{i,j}},\left\{{\vartheta }_{0,u_{i,j}}\right\},{\eta }_{1,u_{i,j}},p{k}_{u_{i,j}}\}$ from $u_{i,j}$, the CA computes $l_1=s{k}_{CA}^{-1}{\vartheta }_{1,u_{i,j}}$$,l_2=s{k}_{CA}^{-1}{\vartheta }_{2,u_{i,j}}$,…,$l_r=s{k}_{CA}^{-1}{\vartheta }_{r,u_{i,j}}(1\le r\le n)$ and $L_1=H_1\left(At{t}_1\right)g$, $L_2=H_1\left(At{t}_2\right)g$,…, $L_r=H_1\left(At{t}_r\right)g$ by comparing the sets $l_0=\{l_1,l_2,...l_r\}$ and $L_0=\{L_1,L_2,...,L_r\}$ to see if they are equal; the CA can determine the set of attributes and the corresponding attribute sequence numbers of the attributes $S_0=\{S_1,S_2,...,S_r\}$. The CA computes ${\eta }_2=H_1(At{t}_1\left|\right|At{t}_2...\left|\right|At{t}_r\left|\right|p{k}_{u_{i,j}})g$, verifies the signature of $u_{i,j}$ by Equation $e({\eta }_{1,u_{i,j}},p{k}_{u_{i,j}})=e({\eta }_2,o_{1,u_{i,j}})$, and determines whether the equation is valid. The CA can determine $\{at{t}_1^{u_{i,j}},at{t}_2^{u_{i,j}},...,at{t}_r^{u_{i,j}}\}$ the set of attributes $u_{i,j}$ has, and the CA selects the corresponding attribute parameters according to the corresponding attributes to compute for $u_{i,j}$ the set of attribute authority factors for the set ${\chi }_{1,u_{i,j}}=b_1{H}_2\left(at{t}_{1,u_{i,j}}\right)p{k}_{u_{i,j}}$, ${\chi }_{2,u_{i,j}}=b_1{H}_2\left(at{t}_{2,u_{i,j}}\right)p{k}_{u_{i,j}}$…${\chi }_{r,u_{i,j}}=b_r{H}_2\left(at{t}_{r,u_{i,j}}\right)p{k}_{u_{i,j}}$, ${\chi }_{0,u_{i,j}}=\{{\chi }_{1,u_{i,j}},{\chi }_{2,u_{i,j}},...,{\chi }_{r,u_{i,j}}\}$. The CA chooses ${\gamma }_2\in {\mathbb{Z}}_q^{*}$ randomly, computes $o_2={\gamma }_{2}g$, ${\eta }_{3,u_{i,j}}={\gamma }_{2}s{k}_{CA}^{-1}{H}_2({\chi }_{1,u_{i,j}}\left|\right|{\chi }_{2,u_{i,j}}\left|\right|...\left|\right|{\chi }_{r,u_{i,j}}\left|\right|p{k}_{CA})g$, and then, sends the parameters $(\left\{{\chi }_{0,u_{i,j}}\right\},{\eta }_{3,u_{i,j}},o_2,p{k}_{CA})$ to $u_{i,j}$.

3.

$u_{i,j}$ receives the public parameters $(\left\{{\chi }_{0,u_{i,j}}\right\},{\eta }_{3,u_{i,j}},o_2,p{k}_{CA})$ sent by the CA, computes ${\eta }_{4,u_{i,j}}=H_2({\chi }_{1,u_{i,j}}\left|\right|{\chi }_{2,u_{i,j}}\left|\right|...\left|\right|{\chi }_{r,u_{i,j}}\left|\right|p{k}_{CA})g$, verifies if the CA’s signature is valid through equation $e({\eta }_{3,u_{i,j}},p{k}_{CA})=e(o_2,{\eta }_{4,u_{i,j}})$, accepts the parameters if valid, and then, calculates the attribute permissions through the attribute factor ${\rho }_{1,u_{i,j}}=s{k}_{u_{i,j}}^{-1}{\chi }_{1,u_{i,j}}$, ${\rho }_{2,u_{i,j}}=s{k}_{u_{i,j}}^{-1}{\chi }_{2,u_{i,j}},...,{\rho }_{r,u_{i,j}}=s{k}_{u_{i,j}}^{-1}{\chi }_{r,u_{i,j}}$. Thus, the set of attribute permissions is ${\rho }_{0,u_{i,j}}=\{{\rho }_{1,u_{i,j}},{\rho }_{2,u_{i,j}},...,{\rho }_{r,u_{i,j}}\}$, where ${\rho }_{i,u_{i,j}}=b_i{H}_1\left(at{t}_{i,u_{i,j}}\right)g\left(1\le i\le r\right)$. The attribute permissions set $\{{\rho }_{1,u_{i,j}},{\rho }_{2,u_{i,j}},...,{\rho }_{r,u_{i,j}}\}$ corresponds to the attribute set $\{at{t}_{1,u_{i,j}},at{t}_{2,u_{i,j}},....,at{t}_{r,u_{i,j}}\}$.

The edge server $E{S}_i(1\le i\le n)$ is specialized and is considered to have all the attributes of the system attribute set $S{A}_{set}=\{At{t}_1,At{t}_2,...,At{t}_n\}$ as well as the attribute sequence numbers $\{S_1,S_2,...,S_n\}$ corresponding to the attributes, and all the attribute permission sets ${\rho }_{0,E{S}_i}=\{{\rho }_{1,E{S}_i},{\rho }_{2,E{S}_i},...,{\rho }_{r,E{S}_i}\}$ are obtained according to the above process, where ${\rho }_{i,E{S}_i}=b_i{H}_1\left(At{t}_i\right)g(1\le i\le r)$. The CA carries out the division of the management domain according to the $u_{i,j}$ address of $u_{i,j}$ and the $i{p}_{E{S}_i}$ of the edge server $E{S}_i(1\le i\le N)$.

4.5. Edge Server Session Key Establishment

Each edge server in the system manages different domains. In order to enable secure cross-domain data access, the edge servers use a ring data structure. This structure facilitates the negotiation of the session private key $\alpha$ and the calculation of the inverse session private key $\beta$ by the edge server based on GKA technology. Each edge server is connected to its neighboring edge servers, and authentication is performed through signing and calculating the session key factor. The specific steps are as follows:

1.

Using the edge server $E{S}_1$ as an example, $E{S}_1$ computes the session factor about the key to the neighboring edge server $E{S}_2$. $E{S}_1$ randomly selects ${\gamma }_{3,E{S}_1}\in {\mathbb{Z}}_q^{*}$, and computes parameters $ss{k}_1=s{k}_{E{S}_1}$, $T_{1,E{S}_1}={\gamma }_{3,E{S}_1}g$, $ss{k}_{1}g$, and the signature ${\theta }_{1,E{S}_1}={\gamma }_{3,E{S}_1}{H}_3(T_{1,E{S}_1}\left|\right|{\rho }_{1,E{S}_1}\left|\right|{\rho }_{2,E{S}_1}\left|\right|...\left|\right|{\rho }_{r,E{S}_1}\left|\right|p{k}_{E{S}_1}\left|\right|i{p}_{E{S}_1}\left|\right|ss{k}_{1}g)s{k}_{E{S}_1}^{-1}g$. The parameter set $({\theta }_{1,E{S}_1},T_{1,E{S}_1},p{k}_{E{S}_1},i{p}_{E{S}_1},ss{k}_{1}g)$ is sent to the edge server $E{S}_2$.

2.

Edge server $E{S}_2$ receives the parameters $({\theta }_{1,E{S}_1},T_{1,E{S}_1},p{k}_{E{S}_1},i{p}_{E{S}_1},ss{k}_{1}g)$, $E{S}_2$ computes ${\xi }_{1,E{S}_2}=H_3(T_{1,E{S}_1}\left|\right|{\rho }_{1,E{S}_2}\left|\right|{\rho }_{2,E{S}_2}\left|\right|...\left|\right|{\rho }_{r,E{S}_2}\left|\right|p{k}_{E{S}_1}\left|\right|i{p}_{E{S}_1}\left|\right|ss{k}_{1}g)g$ and verifies the signature through equation $e({\theta }_{1,E{S}_1},p{k}_{E{S}_1})=e({\xi }_{1,E{S}_2},T_{1,E{S}_1})$, if the equation holds $E{S}_2$ computes the session key factor $ss{k}_{2}ss{k}_{1}g$, in which $ss{k}_2=s{k}_{E{S}_2}$. $E{S}_2$ randomly selects ${\gamma }_{4,E{S}_1}\in {\mathbb{Z}}_q^{*}$ and computes ${\theta }_{2,E{S}_2}={\gamma }_{4,E{S}_1}{H}_3(T_{2,E{S}_2}\left|\right|{\rho }_{1,E{S}_2}\left|\right|{\rho }_{2,E{S}_2}\left|\right|...\left|\right|{\rho }_{r,E{S}_2}\left|\right|p{k}_{E{S}_2}\left|\right|i{p}_{E{S}_2}\left|\right|ss{k}_{2}ss{k}_{1}g)s{k}_{E{S}_2}^{-1}g$.

3.

Following the steps of the appeal, $E{S}_n$ sends message $({\theta }_{n,E{S}_n},T_{n,E{S}_n},p{k}_{E{S}_n},i{p}_{E{S}_n},ss{k}_n...ss{k}_{2}ss{k}_{1}g)$ to $E{S}_1$. Then, $E{S}_1$ computes ${\xi }_{n,E{S}_1}=H_3(T_{n,E{S}_n}\left|\right|{\rho }_{1,E{S}_1}\left|\right|{\rho }_{2,E{S}_1}\left|\right|...\left|\right|{\rho }_{r,E{S}_1}\left|\right|p{k}_{E{S}_n}\left|\right|i{p}_{E{S}_n}\left|\right|ss{k}_n...ss{k}_{2}ss{k}_{1}g)g$, where $ss{k}_0=ss{k}_n...ss{k}_{2}ss{k}_{1}g$, $E{S}_1$ verifies the signature by equation $e({\theta }_{n,E{S}_n},p{k}_{E{S}_n})=e({\xi }_{n,E{S}_1},T_{n,E{S}_n})$, and if the equation holds $E{S}_1$ computes $\alpha =H_2\left(H_2\left(ss{k}_0\right)g\right)$ as the session key for the system edge servers layer, then $E{S}_1$ sends the parameters $\{(H_2\left(ss{k}_0\right)p{k}_{E{S}_2},i{p}_{E{S}_2}),(H_2\left(ss{k}_0\right)p{k}_{E{S}_3},i{p}_{E{S}_3}),...(H_2\left(ss{k}_0\right)p{k}_{E{S}_n},i{p}_{E{S}_n})\}$ to the corresponding edge servers based on the $ip$ address. When the edge servers $E{S}_i(2\le i\le n)$ have all accepted the parameter to compute $\alpha =H_2\left(s{k}_{E{S}_i}^{-1}{H}_2\left(ss{k}_0\right)p{k}_{E{S}_i}\right)$$=H_2\left(H_2\left(ss{k}_0\right)g\right)$, there exists $\alpha \beta =1modq$.

5. The Construction of Our Model

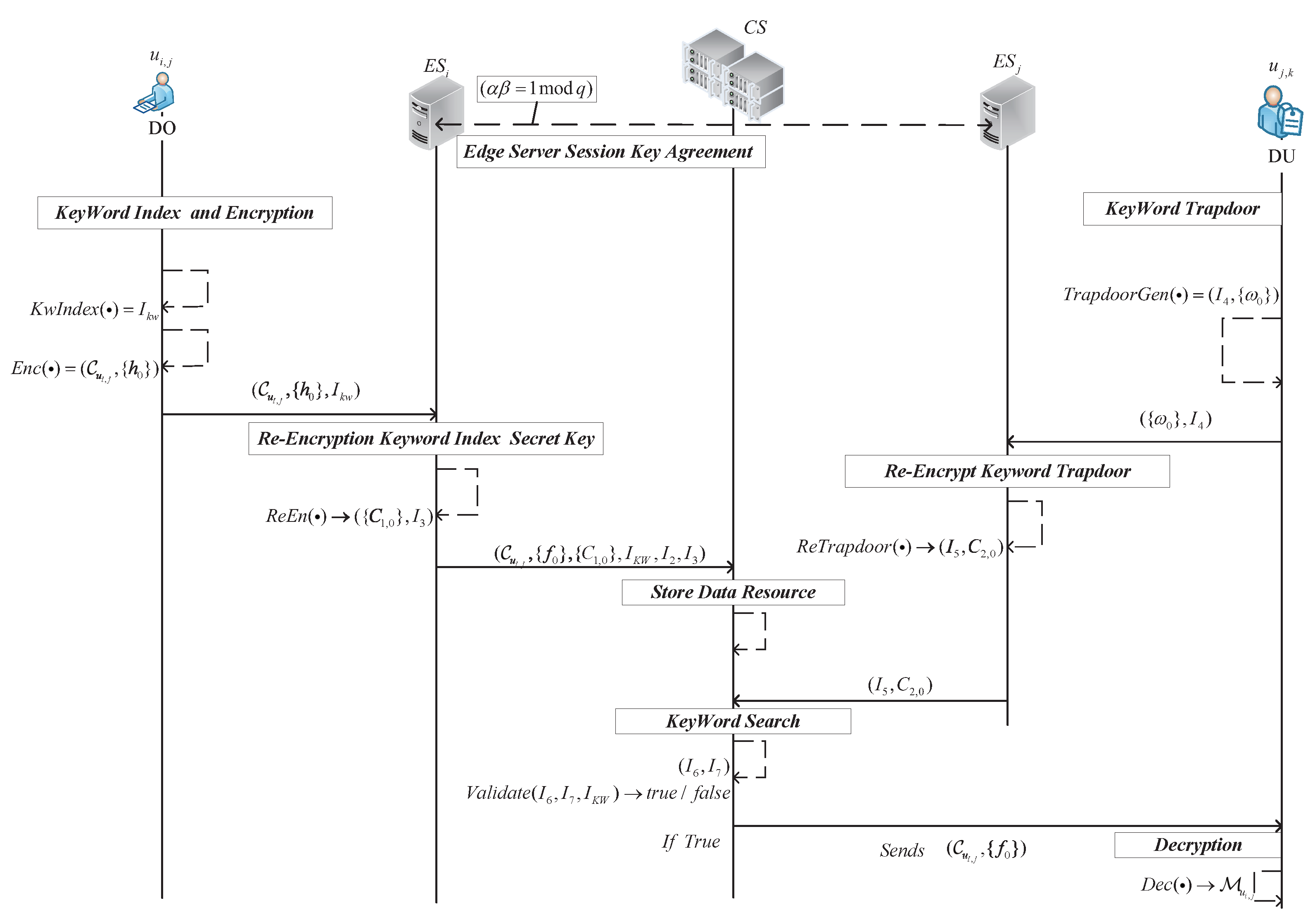
Taking the data owner $u_{i,j}$ in the management domain of the edge server $E{S}_i$ as an example, the related algorithm interaction process is depicted in Figure 4.

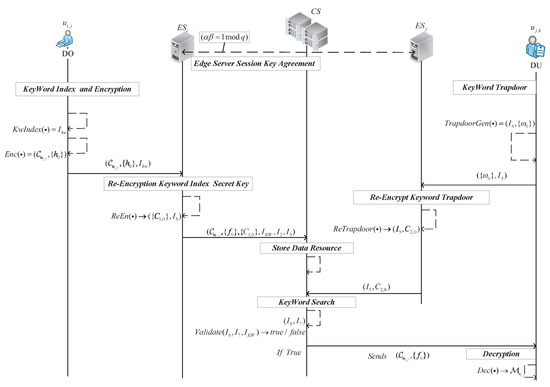
Figure 4. Interaction process of different SDSM-KGA algorithms.

5.1. Keyword Index Generation

$KwIndex(H_2\left(k{w}_i\right),{\rho }_{i,u_{i,j}})\to I_{kw}$: If the data owner $u_{i,j}$ wants to share the data ${\mathcal{M}}_{u_{i,j}}$, $u_{i,j}$ randomly selects a keyword from the keyword dictionary $(k{w}_i\in {\{0,1\}}^{*})$. The keyword $k{w}_1$ is the extraction information of the shared data ${\mathcal{M}}_{u_{i,j}}$. $u_{i,j}$ computes $H_1\left(k{w}_1\right)g$, where ${\rho }_{i,u_{i,j}}$ is the universal element of set $\{{\rho }_{1,u_{j,k}},{\rho }_{2,u_{j,k}},...,{\rho }_{r,u_{j,k}}\}$ that satisfies the access policy, the attribute permissions secret key $s_1={\displaystyle \sum _{i=1}^r}{H}_2\left({\rho }_{i,u_{i,j}}\right)modq$. $u_{i,j}$ randomly selects $s_0,z_1\in {\mathbb{Z}}_q^{*}$ and computes the signature parameters ${\psi }_1=z_{1}g$, ${\psi }_2=p{k}_{E{S}_i}{z}_1$. The keyword index of $u_{i,j}$ is $I_{KW}=e(H_2\left(k{w}_1\right)g,H_3\left(s_1\right)s_0)e(g,s_{0}g)$, with $s_0$ as the secret key of the keyword index.

5.2. Data Owner Encryption

$Enc({\mathcal{M}}_{u_{i,j}},H_2\left(z_{1}g\right),F(\cdot ))\to ({\mathcal{C}}_{u_{i,j}},\left\{h_0\right\})$: Data owner $u_{i,j}$ computes $I_2=s_{0}g$. According to Section 3.3, $u_{i,j}$ randomly selects $l_i\in {\mathbb{Z}}_q^{*}(2\le i\le r)$ to combine into secret vectors $\overrightarrow{v}={[s_0,l_2,l_3,...l_n]}^T$. $u_{i,j}$ to encrypt the plaintext message ${\mathcal{M}}_{u_{i,j}}$, to obtain the ciphertext ${\mathcal{C}}_{u_{i,j}}=e(g,H_2\left(z_{1}g\right)g){\mathcal{M}}_{u_{i,j}}$. $u_{i,j}$ computes the share of the randomized secret value from this matrix $h_i=M_i\overrightarrow{v}=M_i{[s_0,l_2,l_3,...l_n]}^T(1\le i\le r)$, the secret key of the keyword index share parameter and the signature information $h_0=\{h_{1}g,h_{2}g,...h_{r}g\}$ and ${\sigma }_{1,u_{i,j}}=z_1{H}_1({\mathcal{C}}_{u_{i,j}}\left|\right|S_0\left|\right|{\psi }_2\left|\right|p{k}_{u_{i,j}}\left|\right|h_{1}g\left|\right|h_{2}g\left|\right|...\left|\right|h_{r}g\left|\right|I_{KW}\left|\right|I_2)p{k}_{E{S}_i}$. The attribute sequence number is $S_{0,u_{i,j}}=\{S_1,S_2,...,S_r\}$, whose parameters $({\sigma }_{1,u_{i,j}},{\mathcal{C}}_{u_{i,j}},\left\{h_0\right\},{\psi }_2,I_{KW},I_2,p{k}_{u_{i,j}},S_{0,u_{i,j}})$ will be sent over a secure channel to the edge server that manages the domain $E{S}_i$.

5.3. Edge Server $E{S}_i$ Re-Encrypts Secret Key of Keyword Index

$ReEnc(\alpha ,\left\{h_0\right\},I_2)\to (\left\{C_{1,0}\right\},I_3)$: When the edge server $E{S}_i$ receives the parameters $({\sigma }_{1,u_{i,j}},{\mathcal{C}}_{u_{i,j}},\left\{h_0\right\},{\psi }_2,I_{KW},I_2,p{k}_{u_{i,j}},S_{0,u_{i,j}})$, it computes ${\varphi }_{1,E{S}_i}=H_1({\mathcal{C}}_{u_{i,j}}$$\left|\right|S_{0,u_{i,j}}\left|\right|{\psi }_2\left|\right|p{k}_{u_{i,j}}\left|\right|h_{1}g\left|\right|h_{2}g\left|\right|...h_{r}g\left|\right|I_{KW}\left|\right|I_2)g$, determines whether the equation is valid by $e({\sigma }_{1,u_{i,j}},s{k}_{u_{i,j}}^{-1}g)=e({\varphi }_{1,E{S}_i},{\psi }_2)$, and accepts the parameters if it is valid, and computes ${\psi }_3=s{k}_{E{S}_i}^{-1}{\psi }_2$, $d_0=H_2\left({\psi }_3\right)$. $E{S}_i$ obtains the corresponding attribute permissions based on the set of permission numbers $S_{0,u_{i,j}}$ sent by $u_{i,j}$ to access the ciphertext, constructs a polynomial $P_1\left(x\right)=d_{r-1}{x}^{r-1}+d_{r-2}{x}^{r-2}+...+d_{1}x+d_0$ of degree $r-1$, and then, substitutes the attribute values $\{H_2\left({\rho }_{1,E{S}_i}\right)modq,H_2\left({\rho }_{1,E{S}_i}\right)modq,...,H_2\left({\rho }_{1,E{S}_i}\right)modq\}$ into the polynomial $P_1\left(x\right)$. Respectively, $E{S}_i$ obtains the r function value $f_0=\{f_1,f_2,...,f_r\}$, the encryption factor of the key reconstruction. $E{S}_i$ re-encrypts the secret key of keyword index $I_3=\alpha I_2$ and re-encrypts the secret key of keyword index share $C_{1,0}=\{C_{1,1}=\alpha h_{1}g,C_{1,2}=\alpha h_{2}g,...C_{1,r}=\alpha h_{r}g\}$. Then, $E{S}_i$ randomly selects $z_2\in {\mathbb{Z}}_q^{*}$ and computes ${\psi }_4=z_{2}g$ and ${\sigma }_{2,E{S}_i}=z_2{H}_2(f_1\left|\right|f_2\left|\right|...\left|\right|f_r\left|\right|I_{KW}\left|\right|I_2\left|\right|I_3\left|\right|p{k}_{E{S}_i}\left|\right|{\psi }_4)p{k}_{CS}$. Then, $E{S}_i$ sends the parameters $({\mathcal{C}}_{u_{i,j}},{\sigma }_{2,E{S}_i},{\psi }_4,\left\{f_0\right\},I_{KW},I_2,I_3,\left\{C_{1,0}\right\},p{k}_{E{S}_i})$ to the cloud server for storage.

5.4. Cloud Server Ciphertext Resource Store

The cloud server receives the parameters $({\mathcal{C}}_{u_{i,j}},{\sigma }_{2,E{S}_i},{\psi }_4,\left\{f_0\right\},\left\{C_{1,0}\right\},I_{KW},I_2,I_3,p{k}_{E{S}_i})$, $CS$ computes ${\varphi }_{2,CS}=H_3(f_1\left|\right|f_2\left|\right|...\left|\right|f_r\left|\right|I_{KW}\left|\right|I_2\left|\right|I_3\left|\right|p{k}_{E{S}_i}\left|\right|{\psi }_4)g$ and verifies the equation $e({\sigma }_{2,E{S}_i},s{k}_{CS}^{-1}g)=e({\varphi }_{2,CS},{\psi }_4)$. If the equation holds, $CS$ stores the ciphertext and keyword index.

5.5. Data User’s Trapdoor Generation

$TrapdoorGen(\Pi ,\left\{{\rho }_{0,u_{j,k}}\right\},s_1)\to I_4$: Taking the data user demander $u_{j,k}$ in the management domain of $E{S}_j$ as an example, assume that $u_{j,k}$ has the attribute permission of ${\rho }_{0,u_{j,k}}=\{{\rho }_{1,u_{j,k}},{\rho }_{2,u_{j,k}},...,{\rho }_{r,u_{j,k}}\}$ and the corresponding attribute sequence of $S_{0,u_{j,k}}=\{S_1,S_2,...,S_r\}$. According to the corresponding access policy to obtain the matrix M, according to Section 3.3, we can obtain ${\displaystyle \sum _{i=1}^r}{\omega }_i{M}_i={[1,0,0,...,0]}^T$; $u_{j,k}$ obtains $\{{\omega }_1,{\omega }_2,...,{\omega }_r\}$. $u_{j,k}$ computes ${\omega }_0=({\omega }_{1}g,{\omega }_{2}g,...,{\omega }_{r}g)$ and attribute permissions secret $s_1={\displaystyle \sum _{i=1}^r}{H}_2\left({\rho }_{i,u_{j,k}}\right)$, $modq$, where ${\rho }_{i,u_{j,k}}$ is the universal element of set $\{{\rho }_{1,u_{j,k}},{\rho }_{2,u_{j,k}},...,{\rho }_{r,u_{j,k}}\}$ that satisfies the access policy. $u_{j,k}$ randomly selects $z_3,z_4\in {\mathbb{Z}}_q^{*}$ and computes ${\psi }_5=z_{3}g$. Then, $u_{j,k}$ selects the keyword from the keyword dictionary and computes the parameter of the keyword trapdoor $I_4=H_3\left(s_1\right)H_1\left(k{w}_{i,u_{j,k}}\right)$. The signature information is ${\sigma }_{3,u_{j,k}}=z_{3}p{k}_{E{S}_j}{H}_3({\rho }_{1,u_{j,k}}\left|\right|{\rho }_{2,u_{j,k}}\left|\right|...$$\left|\right|{\rho }_{r,u_{j,k}}\left|\right|{\omega }_{1}g\left|\right|{\omega }_{2}g\left|\right|...\left|\right|{\omega }_{r}g\left|\right|p{k}_{u_{j,k}})$, $u_{j,k}$ sends the parameters $({\sigma }_{3,u_{j,k}},\left\{{\rho }_{0,u_{j,k}}\right\},\left\{{\omega }_0\right\},\left\{S_{0,u_{j,k}}\right\}$, $p{k}_{u_{j,k}}$, $i{p}_{u_{j,k}}$, $I_4)$ to the edge server managing the domain $E{S}_j$.

5.6. Edge Server $E{S}_j$ Re-Encrypts Keyword Trapdoor

$ReTrapdoor(\beta ,I_4)\to I_5$: $E{S}_j$ according to the serial number $S_{0,u_{j,k}}=\{S_1,S_2,...,S_r\}$ to find the corresponding attribute permissions, and then, computes ${\varphi }_{3,E{S}_j}=H_3({\rho }_{1,E{S}_j}\left|\right|{\rho }_{2,E{S}_j}\left|\right|...\left|\right|{\rho }_{r,E{S}_j}\left|\right|{\omega }_{1}g\left|\right|{\omega }_{2}g\left|\right|...\left|\right|{\omega }_{r}g\left|\right|p{k}_{u_{j,k}})g$ based on the serial number sent. If the equation $e({\sigma }_{3,u_{j,k}},s{k}_{E{S}_j}^{-1}g)=e({\varphi }_{3,E{S}_j},{\psi }_5)$ holds, $E{S}_j$ re-encrypts the keyword trapdoor $I_5=\beta I_4$ and the keyword index secret-key share parameter $C_{2,0}=(C_{2,1}=\beta {\omega }_{1}g$, $C_{2,2}=\beta {\omega }_{2}g,...,$$C_{2,r}=\beta {\omega }_{r}g)$. $E{S}_j$ computes parameters ${\psi }_6=z_{4}g$ and ${\varphi }_{4,E{S}_j}=z_4{H}_3(C_{2,1}\left|\right|C_{2,2}\left|\right|...\left|\right|C_{2,r}\left|\right|{\rho }_{1,E{S}_j}\left|\right|{\rho }_{2,E{S}_j}\left|\right|...\left|\right|{\rho }_{r,E{S}_j}\left|\right|p{k}_{E{S}_j})g$. Then, $E{S}_j$ sends parameters $(\left\{C_{2,0}\right\},\left\{{\rho }_{0,E{S}_j}\right\},p{k}_{E{S}_i},i{p}_{u_{i,j}},{\varphi }_{4,E{S}_j},{\psi }_6,I_5)$ to the $CS$.

5.7. Cloud Server Keyword Search

$Verify(I_6,I_7,I_{KW})\to true/false$: After the $CS$ receives parameters $(\left\{C_{2,0}\right\},\left\{{\rho }_{0,E{S}_j}\right\},p{k}_{E{S}_i},i{p}_{u_{i,j}},{\varphi }_{4,E{S}_j},{\psi }_6,I_5)$, the $CS$ computes ${\varphi }_{5,E{S}_j}=H_3(C_{2,1}\left|\right|C_{2,2}\left|\right|...\left|\right|C_{2,r}\left|\right|{\rho }_{1,E{S}_j}\left|\right|{\rho }_{2,E{S}_j}\left|\right|...$$\left|\right|{\rho }_{r,E{S}_j}\left|\right|p{k}_{E{S}_j})g$ if the equation $e({\varphi }_{5,E{S}_j},{\psi }_6)=e({\varphi }_{4,E{S}_j},g)$ is true. And, if it is true $CS$ computes $I_6=e(C_{1,1},C_{2,1})e(C_{1,2},C_{2,2})...e(C_{1,r},C_{2,r})=e{(g,g)}^{\sum _{i=1}^r{h}_i{\omega }_i}=e(g,s_{0}g)$ and $I_7=e(I_5,I_3)$. $CS$ matches the keyword trapdoor information by equation $I_6{I}_7=I_{KW}$. $CS$ verifies if the equation holds true, if the equation holds it means that the keyword information is matched successfully. Then, the $CS$ retrieves the corresponding ciphertext resources and computes ${\sigma }_{4,CS}=H_2(f_1\left|\right|f_2\left|\right|...\left|\right|f_r\left|\right|i{p}_{u_{j,k}}\left|\right|p{k}_{u_{j,k}})p{k}_{u_{j,k}}$, the ciphertext parameters $({\mathcal{C}}_{u_{i,j}}{\sigma }_{4,CS},\left\{f_0\right\},i{p}_{u_{j,k}})$ are sent directly to $u_{j,k}$ through the $i{p}_{u_{j,k}}$.

5.8. Data User Decryption

$Dec({\mathcal{C}}_{u_{i,j}},\left\{f_0\right\},P_1\left(x\right))\to {\mathcal{M}}_{u_{i,j}}$: After receiving the parameters $\{{\mathcal{C}}_{u_{i,j}}{\sigma }_4^{CS},\left(f_0\right),i{p}_{u_{j,k}}\}$, $u_{j,k}$ decrypts and computes ${\varphi }_6^{u_{j,k}}=H_2(f_1\left|\right|f_2\left|\right|...\left|\right|f_r\left|\right|i{p}_{u_{j,k}}\left|\right|p{k}_{u_{j,k}})g$. By verifying the equation $e({\sigma }_4^{CS},s{k}_{u_{j,k}}^{-1}g)=e({\varphi }_6^{u_{j,k}},g)$, if true, the decryption key is then computed. $u_{j,k}$ uses the encryption key factors $(f_1,f_2,...,f_r)$ of ${\mathcal{C}}_{u_{i,j}}$, along with the attribute permissions $\{{\rho }_1^{u_{j,k}},{\rho }_2^{u_{j,k}},...,{\rho }_r^{u_{j,k}}\}$ it possesses, and parameters $\{x_1,x_2,...,x_r\}$, where $x_i=H_2\left({\rho }_i^{u_{j,k}}\right)modq$ (for $1\le i\le r$). For data users $u_{j,k}$ who satisfy the access policy, based on the Lagrange interpolation theorem they reconstruct the polynomial $P_1\left(x\right)$ using the parameters $\{(x_1,f_1),(x_2,f_2),...,(x_r,f_r)\}$ and the equation $P\left(x\right)={\displaystyle \sum _{i=1}^r}{f}_i{\ell }_i\left(x\right)$, where ${\ell }_i\left(x\right)=p_i\left(x\right)={\displaystyle \prod _{j=1,j\ne i}^r}{\displaystyle \frac{x-x_j}{x_i-x_j}}$. The polynomial $P_1\left(x\right)=d_{r-1}{x}^{r-1}+d_{r-2}{x}^{r-2}+...+d_{1}x+d_0$ is reconstructed. $P_1\left(0\right)=d_0$ serves as the decryption key for the shared resource. The data user decrypts the resource ${\mathcal{M}}_{u_{i,j}}$ as ${\mathcal{M}}_{u_{i,j}}={\mathcal{C}}_{u_{i,j}}/e(g,d_{0}g)$ to obtain the plaintext data.

6. Security Analysis

This scheme proposes a cross-domain secure data-sharing model to resist keyword guessing attacks. To demonstrate the correctness and security of the model, this section discusses the security analysis of the model.

Theorem 1.

If a probabilistic polynomial-time (PPT) adversary $\mathcal{A}$ can break the KGA security of our scheme with non-negligible advantage, then the simulator $\mathcal{B}$ can break the assumption of the DBDH problem with advantage ε.

Proof of Theorem 1.

We are assuming the existence of an adversary $\mathcal{A}$ that can break our protocol in polynomial time t by a non-negligible advantage $\epsilon$$(t,\epsilon )$ in the IND-KGA security model; we construct a simulator $\mathcal{B}$ to solve the DBDH problem. Given an instance $(g,ag,bg,cg,Z)$ of the problem on a bilinear pair of groups $\mathbb{P}\mathbb{G}$, where g is a generator of an additive group ${\mathbb{G}}_1$, $a,b\in {\mathbb{Z}}_q^{*}$ is randomly chosen, and let $coin$ be a random bit 0 or 1, when $coin=0$, Z in this case can be equal to $abcg$ and when $coin=1$, Z is a random element in ${\mathbb{G}}_1$; the interaction between the challenger and the adversary is as follows.

Init: Initialize the secret key of the keyword index as $s_0=a$; the challenger enters the public parameters $[g,ag]$ to send to the attacker $\mathcal{A}$; the attacker selects the challenge access structure $\mathbb{A}$ and the set of challenged attributes $\{at{t}_1^{*},at{t}_2^{*},...,at{t}_r^{*}\}$ to send to $\mathcal{B}$; $\mathcal{B}$ randomly selects $t_i^{*}\in {\mathbb{Z}}_q^{*}(1\le i\le r)$ and computes the attribute permissions ${\rho }_1^{*}=t_1^{*}{H}_1\left(at{t}_1^{*}\right)g,{\rho }_2^{*}=t_2^{*}{H}_1\left(at{t}_2^{*}\right)g,...,{\rho }_r^{*}=t_r^{*}{H}_1\left(at{t}_r^{*}\right)g$, ${\rho }_0^{*}=\{{\rho }_1^{*},{\rho }_2^{*},...,{\rho }_r^{*}\}$ and sends them to $\mathcal{A}$.

Phase 1: $\mathcal{A}$ can query oracles that can be simulated by $\mathcal{B}$ as follows.

Hash query: The adversary performs a private-key hash query in this phase, the attacker computes the attribute permission secret key $s_1^{*}={\displaystyle \sum _{i=1}^r}{H}_2\left({\rho }_i^{*}\right)modq(1\le i\le r)$, using j to represent the number of queries, where $j\in [1,Q_{H_3}]$ and $k\in [1,Q_{H_1}]$, where $Q_{H_1}$ and $Q_{H_3}$ represent the number of queries to the random oracles $H_1$ and $H_3$, respectively. The simulator $\mathcal{B}$ creates two hash lists to record all queries and responses, and the hash lists are initialized to be empty.

1.

Let the j-th query of $H_3$ be $s_{1,j}^{*}$; if the hash list already has $s_{1,j}^{*}$ corresponding options, the simulator $\mathcal{B}$ answers the query according to the hash list; otherwise, the simulator $\mathcal{B}$ randomly chooses $a_j\in {\mathbb{Z}}_q^{*}$, tosses a biased coin where $coin\in \{0,1\}$, where $Pr[coin=0]=\delta$, and when $coin=1$, set $H_3\left(s_{1,j}^{*}\right)=a_{j}g$; when $coin=0$, $H_3\left(s_{1,j}^{*}\right)=bg$. The simulator $\mathcal{B}$ then marks $H_3\left(s_{1,j}^{*}\right)$ as the should for that query and adds the corresponding tuple $<j,s_{1,j}^{*},a_j,H_3\left(s_{1,j}^{*}\right)>$ to the hash table.

2.

The adversary $\mathcal{A}$ randomly selects keyword $k{w}_k$ from the keyword dictionary for each query; if there is already an item corresponding to $k{w}_k$ in the hash list, simulator $\mathcal{B}$ answers the query based on the hash list; otherwise, simulator $\mathcal{B}$ randomly selects $Y_k\in {\mathbb{G}}_1$ (the k-th query $H_1\left(k{w}_k\right)$ of $H_1$ is $y_k$, when $coin=1$, $y_k{a}_{j}g=Y_k$; when $coin=0$, $y_{k}bg=Y_k$), and adds the tuple $<g,k{w}_k,Y_k>$ to the hash list.

Attribute permissions secret-key extraction query: The adversary performs private-key interrogation in this phase. $\mathcal{A}$ queries the attribute permissions secret key of $s_{1,j}^{*}$ such that $<j,s_{1,j}^{*},a_j,H\left(s_{1,j}^{*}\right)>$ is the corresponding tuple; it randomly tosses a coin and aborts if $coin=1$; otherwise, according to the simulation process, and computes $E_j=a_{j}ag=a{H}_3\left(s_{1,j}^{*}\right)$, so that $H_3\left(s_{1,j}^{*}\right)$ is a valid intermediate parameter, and randomly choosing ${\alpha }_j\in {\mathbb{Z}}_q^{*}$, computes the re-encryption attribute permissions secret key $E_j^{\prime }={\alpha }_{j}ag$ and adds $E_j^{\prime }$ to this tuple $<j,s_{1,j}^{*},a_j,H_3\left(s_{1,j}^{*}\right),E_j,E_j^{\prime }>$.

Keyword trapdoor extraction query: The adversary $\mathcal{A}$ makes a keyword trapdoor query in this phase to respond to the keyword trapdoor extraction query; the simulator $\mathcal{B}$ maintains a list keyword trapdoor $<g,y_k,k{w}_k>$; $\mathcal{A}$ selects the keyword $k{w}_k$ to be queried, and if $coin=0$, aborts; if $coin=1$, the simulation $\mathcal{B}$ process calculates that $Y_k=y_k{a}_{j}g$, and therefore, $Y_k$ is a valid trapdoor corresponding to the keyword, and selects ${\beta }_k\in {\mathbb{Z}}_q^{*}$, where ${\alpha }_j{\beta }_k=1modq$, and re-encrypts the keyword trapdoor $Y_k^{\prime }={\beta }_k{y}_k{a}_{j}g$. $\mathcal{B}$ adds $Y_k^{\prime }$ to that tuple $<g,k{w}_k,Y_k,Y_k^{\prime }>$.

Challenge phase: Challenge phase: the adversary $\mathcal{A}$ selects two equal-length keywords $k{w}_0,k{w}_1\in {\{0,1\}}^{*}$ and a challenge attribute permission secret key $s_{1,j}^{*}$ in the $H_3,H_1$ hash list, $s_{1,j}^{*}$ corresponding to the tuple $<j,s_{1,j}^{*},a_j,H_3\left(s_{1,j}^{*}\right),E_j^{\prime },Y_k^{\prime }>$, if $coin=1$, it reports a failure and an abort; otherwise, if $coin=0$, it can obtain $H_3\left(s_{1,i}^{*}\right)=bg$. $k{w}_0$ corresponding to the tuple $<g,k{w}_0,Y_0,Y_0^{\prime }>$, $k{w}_1$ corresponding to the tuple $<g,k{w}_1,Y_1,Y_1^{\prime }>$, and the simulator $\mathcal{B}$ randomly selects $coin\in \{0,1\}$ again, and if $coin=1$, the simulator $\mathcal{B}$ reports a failure and an abort; if $coin=0$, the simulator $\mathcal{A}$ can compute the challenge keyword information as $I^{*}=e(g,ag)Z$, where $Z\in {\mathbb{G}}_1$. If we make $H_1\left(k{w}_{coin}\right)=c$, we can compute $Z=e(E_k^{\prime },Y_j^{\prime })=e({\beta }_{k}cbg,{\alpha }_{j}ag)=e(cbg,ag)=e{(g,g)}^{abc}$, then we can obtain the challenge keyword trapdoor information $I_{KW}^{*}=e{(g,g)}^{a}e{(g,g)}^{abc}$, and therefore, this challenge keyword parameter $I^{*}$ is the correct parameter corresponding to the attribute permission ${\rho }_0^{*}$ and keyword trapdoor information $k{w}_{coin}$.

Phase 2: $\mathcal{A}$ can adaptively interrogate queries for a polynomial a bounded number of times as in phase 1, but it cannot perform an attribute permissions secret-key extraction query for $s_{1,i}^{*}$ and a keyword trapdoor extraction query for $k{w}_0$ and $k{w}_1$, where $k{w}_{*}\ne \{k{w}_0,k{w}_1\}$.

Guess: Adversary $\mathcal{A}$ outputs a guess about the result of $coin$, $coin=coi{n}^{\prime }$, the simulator outputs $True$; otherwise, it outputs $False$. We use $event$ to denote that the simulator reports failed and aborted events during the game, and from the process above we can see that there are two cases: $even{t}_1$ denotes that $\mathcal{B}$ reports failed and aborted events during attribute permissions secret-key extraction queries and keyword trapdoor extraction queries, $even{t}_2$ denotes that $\mathcal{B}$ reports failed and aborted events during the generation of challenge permissions during the challenge phase and during the challenge trapdoor, $Pr\left(\overline{even{t}_1}\right)={(1-\delta )}^{Q_{H_3}+Q_{H_1}}$, $Pr\left(\overline{even{t}_2}\right)=1-{(1-\delta )}^2$ because of $Pr\left(\overline{event}\right)=Pr\left(\overline{even{t}_1}\right)·Pr\left(\overline{even{t}_2}\right)$. It can be computed when $\delta =1-\sqrt{{\displaystyle \frac{Q_{H_3}+Q_{H_1}}{2+Q_{H_3}+Q_{H_1}}}}$, $Pr{\left(\overline{event}\right)}_{max}={\left({\displaystyle \frac{Q_{H_3}+Q_{H_1}}{Q_{H_3}+Q_{H_1}+2}}\right)}^{{\displaystyle \frac{Q_{H_3}+Q_{H_1}}{2}}}·{\displaystyle \frac{Q_{H_3}+Q_{H_1}}{Q_{H_3}+Q_{H_1}+2}}\approx {\displaystyle \frac{1}{(Q_{H_3}+Q_{H_1})e}}(e\approx 2.72)$. It can be shown that the $Pr\left[\overline{event}\right]$ probability is non-negligible. □

The time cost of the simulation process is $T_s=O(Q_{H_1}+Q_{H_3})$. According to Equation (1), the probability that the simulator $\mathcal{B}$ can solve the DBDH problem is $|Pr[coin=coi{n}^{\stackrel{`}{ }}]-{\displaystyle \frac{1}{2}}|={\displaystyle \frac{\epsilon }{2}}Pr\left[\overline{event}\right]$. If $\epsilon$ is non-negligible, simulator $\mathcal{B}$ will be able to solve the DBDH problem with $(t+T_s,{\displaystyle \frac{\epsilon }{2}}Pr\left[\overline{event}\right])$. Since the DBDH problem is difficult, no attacker can break the IND-KGA security of our protocol.

7. Performance Analysis

In this section, we evaluate the performance aspects of the scheme, which we compare with the most advanced schemes [30,31,32,33,38,39,40,41]. We evaluate the performance of our scheme. In terms of theoretical performance, we mainly analyze the aspect of computational complexity. Then, we perform experimental comparisons using real datasets to demonstrate the feasibility and effectiveness of our scheme.

7.1. Functional Comparison

Before analyzing the performance of our scheme, we first compare the functionality of our scheme with several state-of-the-art schemes in Table 1. All the schemes in Table 1 satisfy fine-grained keyword search; Refs. [30,33,38] are based on the structural construction of an access tree, Ref. [39] is based on the structural construction of a hidden AND-tree; Ref. [32] and the present scheme are based on the structural construction of LSSS; all the schemes are efficient in terms of expressiveness. Refs. [30,32,39] cannot resist keyword guessing attacks; Refs. [30,33,38,39] cannot realize cross-domain data sharing; and only the present scheme supports resisting keyword guessing attack and cross-domain data sharing of the above schemes.

Table 1. Functional comparison of various schemes.

Scheme	Function 1 1	Function 2 2	Function 3 3	Function 4 4
ABDKS [30]	✓	Tree	✗	✗
MKS-VABKS [32]	✓	LSSS	✗	✗
HP-CPABKS [39]	✓	AND-gates	✓	✗
LFGS [38]	✓	Tree	✗	✗
ABKS-SKGA [33]	✓	Tree	✓	✗
Ours	✓	LSSS	✓	✓

¹ Function 1: fine-grained keyword search. ² Function 2: access structure. ³ Function 3: keyword guessing attacks. ⁴ Function 4: cross-domain data share.

7.2. Theoretical Performance

The existing schemes’ computational times and storage costs are shown in Table 2 and Table 3, respectively, taking into account certain time-consuming operations. The bilinear pairing operation is denoted by $T_{bp}$, the point addition operation is denoted by $T_{pa}$ in the additive group ${\mathbb{G}}_1$, and the exponential operation is denoted by $T_{exp}$ in the multiplication cyclic group ${\mathbb{G}}_T$. In addition, we consider $|{\mathbb{Z}}_q^{*}|$ to denote the length of an element in ${\mathbb{Z}}_q^{*}$, and $|{\mathbb{G}}_1|$ denotes the length of an element in group ${\mathbb{G}}_1$; $|{\mathbb{G}}_T|$ denotes the size of an element in group ${\mathbb{G}}_T$.

Table 2. Computational costs in various schemes.

Algorithm	Our Scheme	MKS-VABKS [32]	HP-CPABKS [39]	LFGS [38]	ABKS-SM [31]	ABCKS [40]	CABKS-CRF [41]
KeyGen	$(2r+6)T_{pa}$+$(2r+2)T_{inv}$+$6T_{bp}$	$(2r+6)T_{exp}$	$(2r+2)T_{exp}$	$(r+5)T_{exp}$	$(6+2r)T_{exp}$	$3r{T}_{exp}$	$(r+1)T_{exp}$
$r=40$	78.75 ms	854.07 ms	814.35 ms	446.90 ms	854.07 ms	1191.73 ms	407.18 ms
Encryption	$(r-1)T_{exp}$+$(2r+11)T_{pa}$+$7T_{bp}$	$(2r+6)T_{exp}$	$(2r+2)T_{exp}$	$(r+5)T_{exp}$+$T_{bp}$	$(7+2r)T_{exp}$	$(r+5)T_{exp}$	$(8T_{exp}+3T_{bp})(r+1)$
$r=40$	477.24 ms	854.07 ms	814.35 ms	448.96 ms	864.01 ms	446.90 ms	4740.05 ms
Trapdoor Gen	$2T_{bp}$+$(2r+7)T_{pa}$	$(2r+1)T_{exp}$	$(2r+1)T_{exp}$	$(3r+2)T_{exp}$	$(2r+1)T_{exp}$	$(2r+3)T_{exp}$	$(4r+2)T_{exp}$
$r=40$	29.38 ms	804.42 ms	804.42 ms	1211.59 ms	804.42 ms	824.28 ms	1608.84 ms
Search	$(r+3)T_{bp}$+$2T_{pa}$	$(2r+1)T_{bp}$+$T_{exp}$	$(2r+1)T_{bp}$+$T_{exp}$	$(r+1)T_{bp}$+$2T_{exp}$	$(1+2r)T_{bp}$+$T_{exp}$	$(2r+3)T_{bp}$	$(r+1)T_{bp}+T_{exp}$
$r=40$	518.60 ms	986.60 ms	986.60 ms	514.23 ms	986.60 ms	1000.80 ms	504.30 ms
Decryption	$T_{pa}$+$3T_{bp}$+$(r-1)T_{exp}$	$(2r+1)T_{bp}$		$(r+3)T_{bp}$	$2r{T}_{exp}$+$3T_{bp}$	$T_{exp}$
$r=40$	423.55 ms	976.67 ms		518.48 ms	830.66 ms	9.93 ms

Table 3. Storage costs of various schemes.

Algorithm	Our Scheme	MKS-VABKS [32]	HP-CPABKS [39]	LFGS [38]	ABKS-SM [31]	ABCKS [40]	CABKS-CRF [41]
KeyGen	$(2r+4)|{\mathbb{G}}_1|$+$|{\mathbb{Z}}_q^{*}|$	$(2r+5)|{\mathbb{G}}_T|$+$(r+3)|{\mathbb{Z}}_q^{*}|$	$(2r+1)|{\mathbb{G}}_1|$+$(r+2)|{\mathbb{Z}}_q^{*}|$	$(3r+9)|{\mathbb{G}}_T|$+$2|{\mathbb{Z}}_q^{*}|$	$(2r+5)|{\mathbb{G}}_T|$+$(r+3)|{\mathbb{Z}}_q^{*}|$	$3r|{\mathbb{G}}_T|+r|{\mathbb{Z}}_q^{*}|$	$\left(\right|{\mathbb{G}}_T|+|{\mathbb{Z}}_q^{*}\left|\right)(r+1)$
$r=40$	5.27 kb	5.98 kb	5.72 kb	8.09 kb	5.98 kb	8.13 kb	3.20 kb
Encryption	$(2r+9)|{\mathbb{G}}_1|$+$(r+3)|{\mathbb{Z}}_q^{*}|$+$3|{\mathbb{G}}_T|$	$(2r+1)|{\mathbb{G}}_T|$+$2|{\mathbb{Z}}_q^{*}|$	$(2r+1)|{\mathbb{G}}_T|$+$(r+1)|{\mathbb{Z}}_q^{*}|$	$(2r+8)|{\mathbb{G}}_T|$+$(2r+1)|{\mathbb{Z}}_q^{*}|$	$(2r+6)|{\mathbb{G}}_T|$+$(r+2)|{\mathbb{Z}}_q^{*}|$	$(2r+2)|{\mathbb{G}}_T|+|{\mathbb{Z}}_q^{*}|$	$(5r+4)|{\mathbb{G}}_T|+2|{\mathbb{Z}}_q^{*}|$
$r=40$	6.42 kb	6.09 kb	5.70 kb	6.77 kb	6.03 kb	5.14 kb	12.78 kb
Trapdoor Gen	$2|{\mathbb{Z}}_q^{*}|$+$(2r+7)|{\mathbb{G}}_1|$+$2|{\mathbb{G}}_T|$	$(2r+1)|{\mathbb{G}}_T|$+$2|{\mathbb{Z}}_q^{*}|$	$(2r+1)|{\mathbb{G}}_T|$+$2|{\mathbb{Z}}_q^{*}|$	$(4r+3)|{\mathbb{G}}_T|$+$4|{\mathbb{Z}}_q^{*}|$	$(2r+1)|{\mathbb{G}}_T|$+$2|{\mathbb{Z}}_q^{*}|$	$3r|{\mathbb{G}}_T|+|{\mathbb{Z}}_q^{*}|$	$(2r+1)|{\mathbb{G}}_T|+2|{\mathbb{Z}}_q^{*}|$
$r=40$	5.59 kb	5.09 kb	5.09 kb	10.25 kb	5.09 kb	7.52 kb	5.09 kb
Search	$2|{\mathbb{G}}_T|+2|{\mathbb{G}}_1|$	$4|{\mathbb{G}}_T|$	$4|{\mathbb{G}}_T|$	$(r+1)|{\mathbb{G}}_T|$	$4|{\mathbb{G}}_T|$	$5|{\mathbb{G}}_T|$	$|{\mathbb{G}}_T|$
$r=40$	0.25 kb	0.25 kb	0.25 kb	2.56 kb	0.25 kb	0.3125 kb	0.0625 kb
Decryption	$2|{\mathbb{G}}_1|$	$2|{\mathbb{G}}_T|$		$(r+2)|{\mathbb{G}}_T|$+$|{\mathbb{Z}}_q^{*}|$	$(r+1)|{\mathbb{G}}_T|$	$|{\mathbb{G}}_T|$
$r=40$	0.125 kb	0.125 kb		2.64 kb	2.56 kb	0.0625

Key generation: Data users in our scheme need to obtain public and private key pairs and attribute permissions, and our scheme has a very significant reduction in computational overhead compared to the schemes in [31,32,38,39,40,41]. The data user obtains the corresponding attribute privileges by CA authentication computation for randomly selected attributes from the attribute collection, and our scheme significantly outperforms the compared schemes. Our scheme has slightly higher storage overhead compared to the scheme in [41], but it is superior to the schemes in [31,32,38,39,40]. It offers certain advantages in terms of storage overhead and shows significant advantages for data users with limited resources.

Encryption: Our scheme has a similar computational cost to the schemes in [38,40]. However, compared to the schemes in [31,32,39,41], our scheme has a lower overhead cost, making it more suitable for resource-constrained terminal devices. The storage overhead of our scheme is better than that of the schemes in [38,41], but higher than that of the schemes in [31,32,39]. However, since most of the storage overhead in our scheme is handled by the edge server, it does not impose any additional resource burden on data users.

Trapdoor generation: Our scheme has a lower overhead cost compared to the schemes in [31,32,38,39,40,41], because the trapdoor is generated based on the number of attribute permissions of the attribute endpoints that satisfy the access structure. In contrast, the schemes in [31,32,39,40] require $2r$ exponential operations, the scheme in [38] requires $(3r+2)$ exponential operations, and the scheme in [41] requires $(4r+2)$ exponential operations. The storage cost of our scheme is slightly higher than that of the schemes in [31,32,39,41], but better than the schemes in [38,40]. Additionally, at this stage our scheme offloads part of the computation to the edge server, thereby reducing the actual storage costs for data users.

Keyword search: Our scheme’s efficiency in the search phase is comparable to the schemes in [38,41], but significantly better than the comparison schemes in [31,32,39,40]. This is because those comparison schemes incur time overhead due to $2r$ bilinear pair operations, whereas our scheme only requires r bilinear pair operations, resulting in less overhead during the verification process. In terms of storage overhead, our scheme is on par with the comparison schemes in [31,32,39], and all are lower than those of the schemes in [38,40]. Although the scheme in [41] has certain advantages, our scheme performs searches in the cloud, ensuring that no extra storage space is occupied.

Decryption: In our scheme, data users decrypt based on an interpolated polynomial reduction key during the decryption process. The time overhead in this phase is highly efficient compared to the comparison schemes in [31,32]. Although it is higher than the scheme in [40], the computational overhead remains acceptable. Our scheme has the same storage overhead as the comparison scheme in [32], is lower than the schemes in [31,38], and is slightly higher than the scheme in [40]. Additionally, it does not incur any extra storage overhead.

7.3. Actual Performance

In this section, we tested on an Android device with 8.0 GB + 2.0 GB (HONOR RAM Turbo) of RAM and 256 GB of storage space, using the JPBC encryption library (version JPBC-2.0.0) in Java to measure the computational time for the processes used, as shown in Table 2 and Table 3. The process of testing the algorithm time is divided into two steps. First, the APK file is generated in Android Studio, and then, the APK file is run on the Android phone to obtain the corresponding algorithm time. The obtained calculation data are shown in Table 4.

Table 4. Time of operation execution.

Computation Type	Operational Time (ms)
$T_{bp}$ 1	$T_{bp}\approx 12.0577$
$T_{exp}$ 2	$T_{exp}\approx 9.9311$
$T_{pa}$ 3	$T_{pa}\approx 0.0605$
$T_{inv}$ 4	$T_{inv}\approx 0.0146$

¹ Bilinear pair operation. ² Exponential operations. ³ Point addition on elliptic curves. ⁴ Modular inversion operation.

We consider $|{\mathbb{Z}}_q^{*}|$ = 128 bit to denote the length of the elements in ${\mathbb{Z}}_q^{*}$, $|{\mathbb{G}}_1|=$ 512 bit to denote the length of the elements in ${\mathbb{G}}_1$, $|{\mathbb{G}}_T|$ = 512 bit to denote the length of the elements in ${\mathbb{G}}_T$, and for ease of description, we assume that the range of the attributes is $r\in [10,40]$. In this paper, we show the performance characteristics of some of the main algorithms, key generation, encryption, trapdoor generation, keyword search, and decryption.

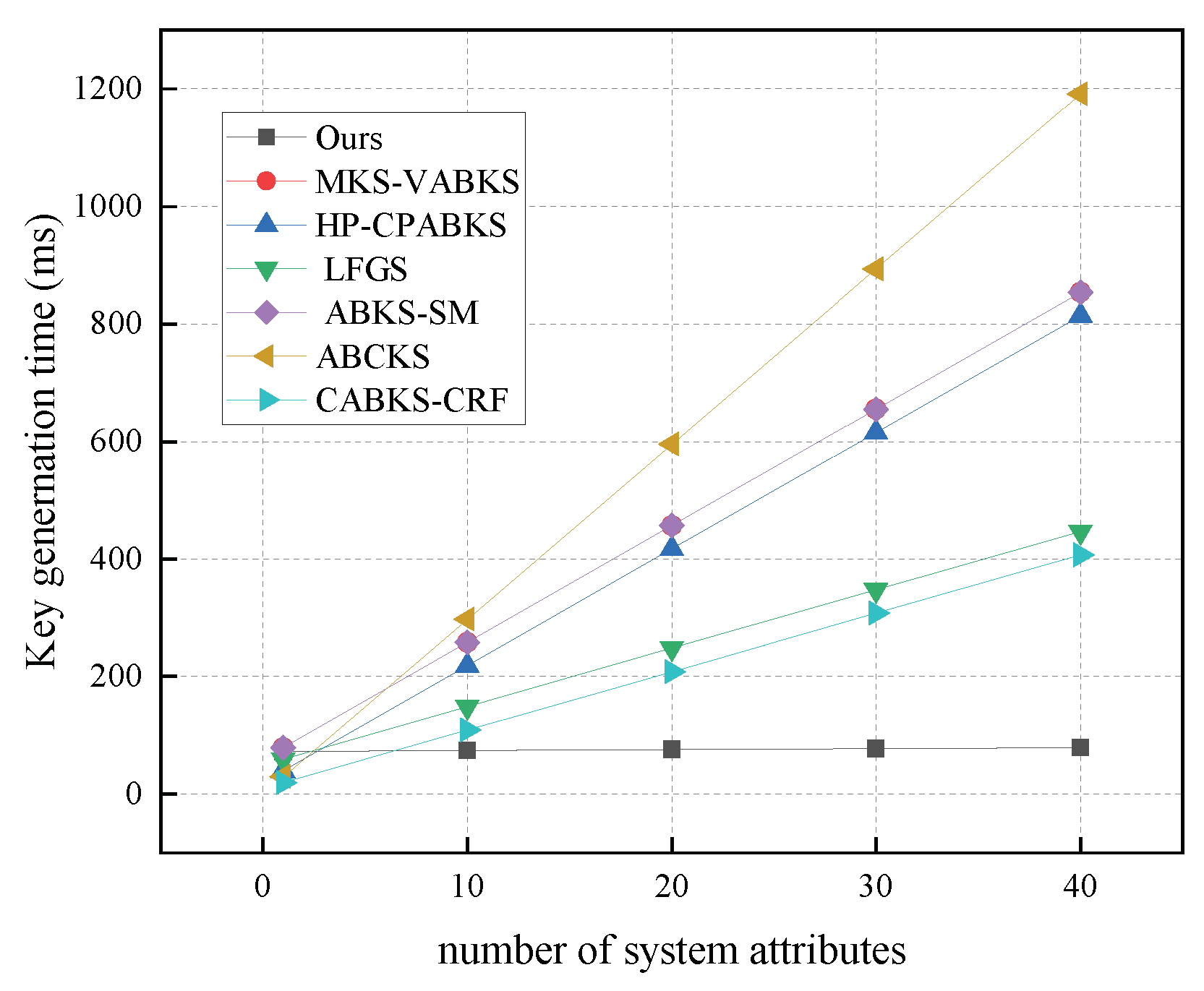
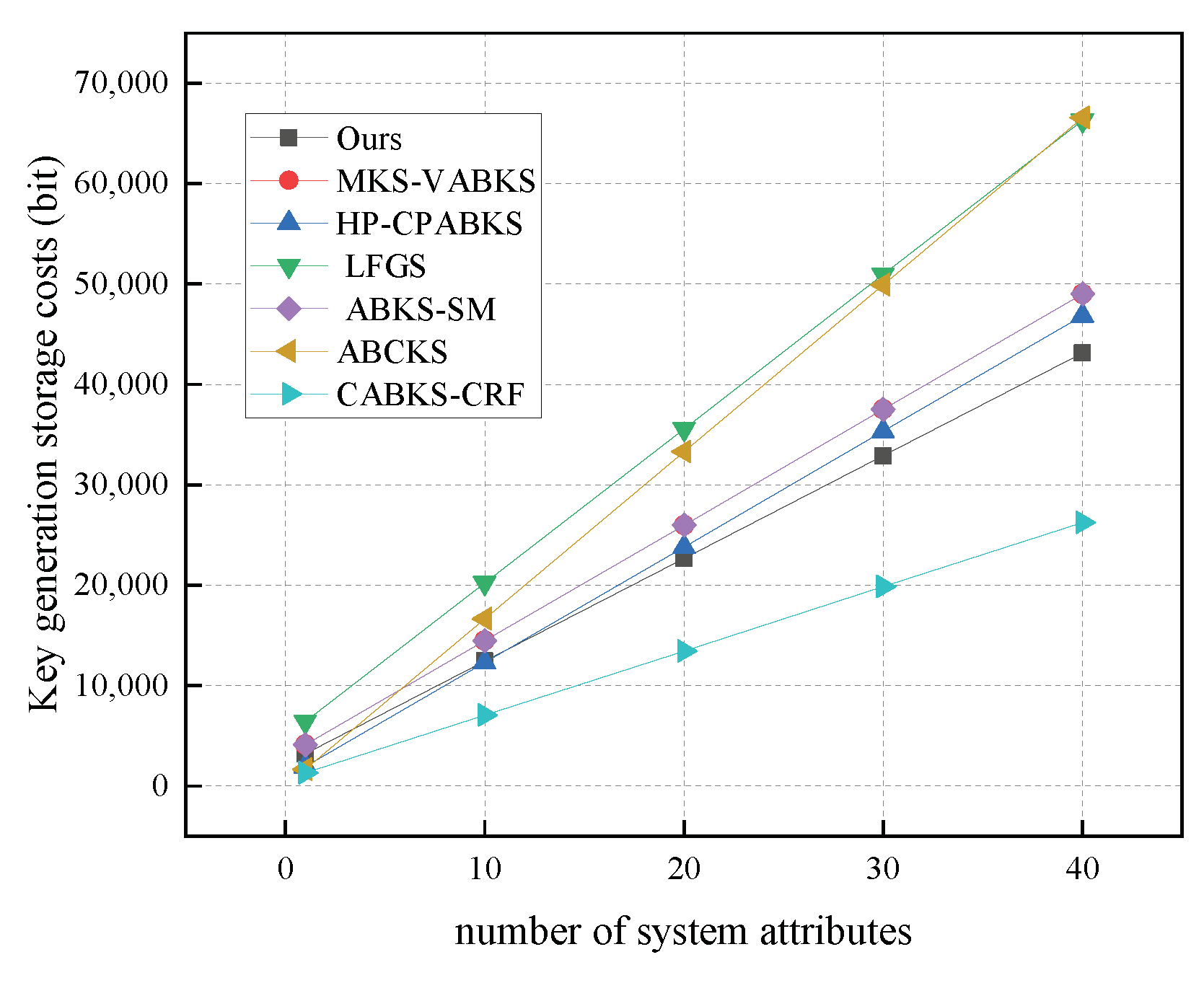
In Figure 5, we present the computational costs of key generation algorithms, illustrating variations in time consumption across the comparison schemes with r set to 10, 20, 30, and 40. When the number of attributes is 40, our scheme consistently exhibits the lowest computational cost, approximately 78.75 ms. In contrast, the time consumption of the comparison schemes in [31,32,39] is around 850 ms, while the scheme in [40] has the highest time consumption at 1191.73 ms, and the scheme in [41] shows a time consumption of 407.18 ms. In Figure 6, we analyze the storage overhead of key generation algorithms. Our scheme demonstrates the lowest storage consumption at 5.27 kb, highlighting a clear advantage over the schemes in [31,32,38,39,40]. Although the scheme in [41] has a lower storage overhead of 3.20 kb in key generation, our scheme still has an advantage over the storage overhead of other algorithms.

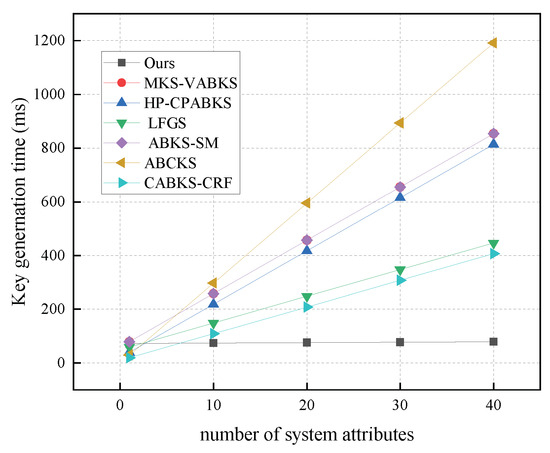
Figure 5. Computational costs in KeyGen. (The red line of MKS-VABKS overlaps with the purple line of ABKS-SM).

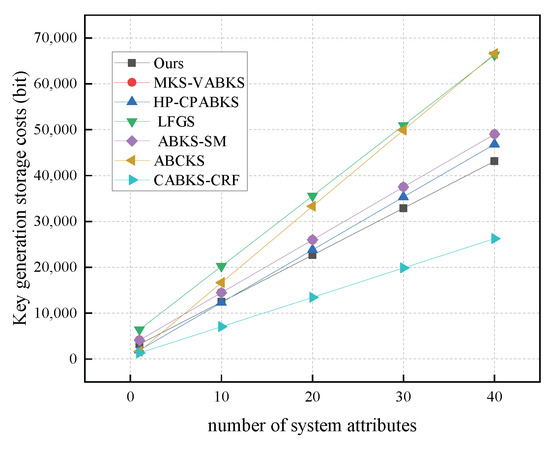
Figure 6. Storage costs in KeyGen. (The red line of MKS-VABKS overlaps with the purple line of ABKS-SM).

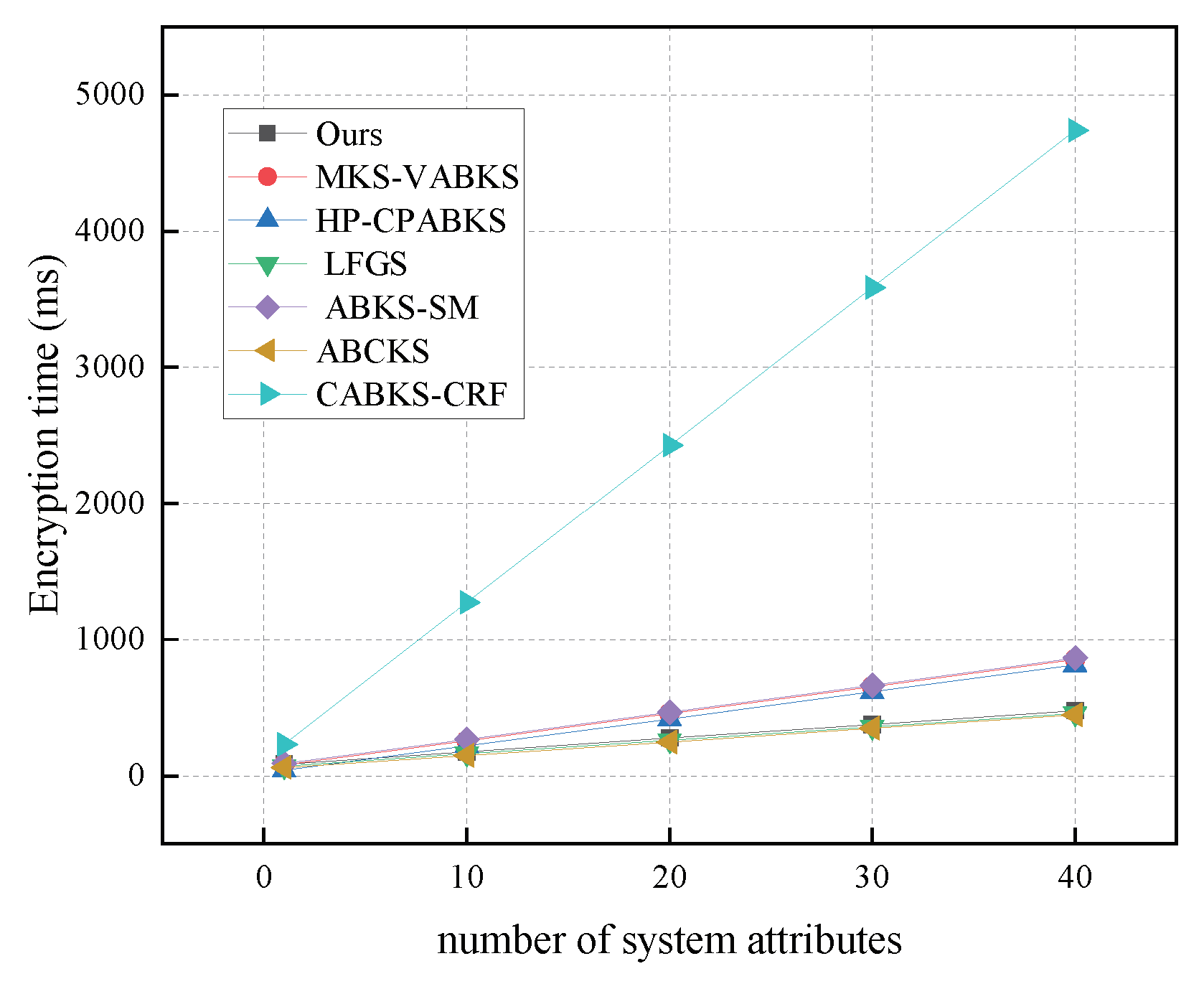
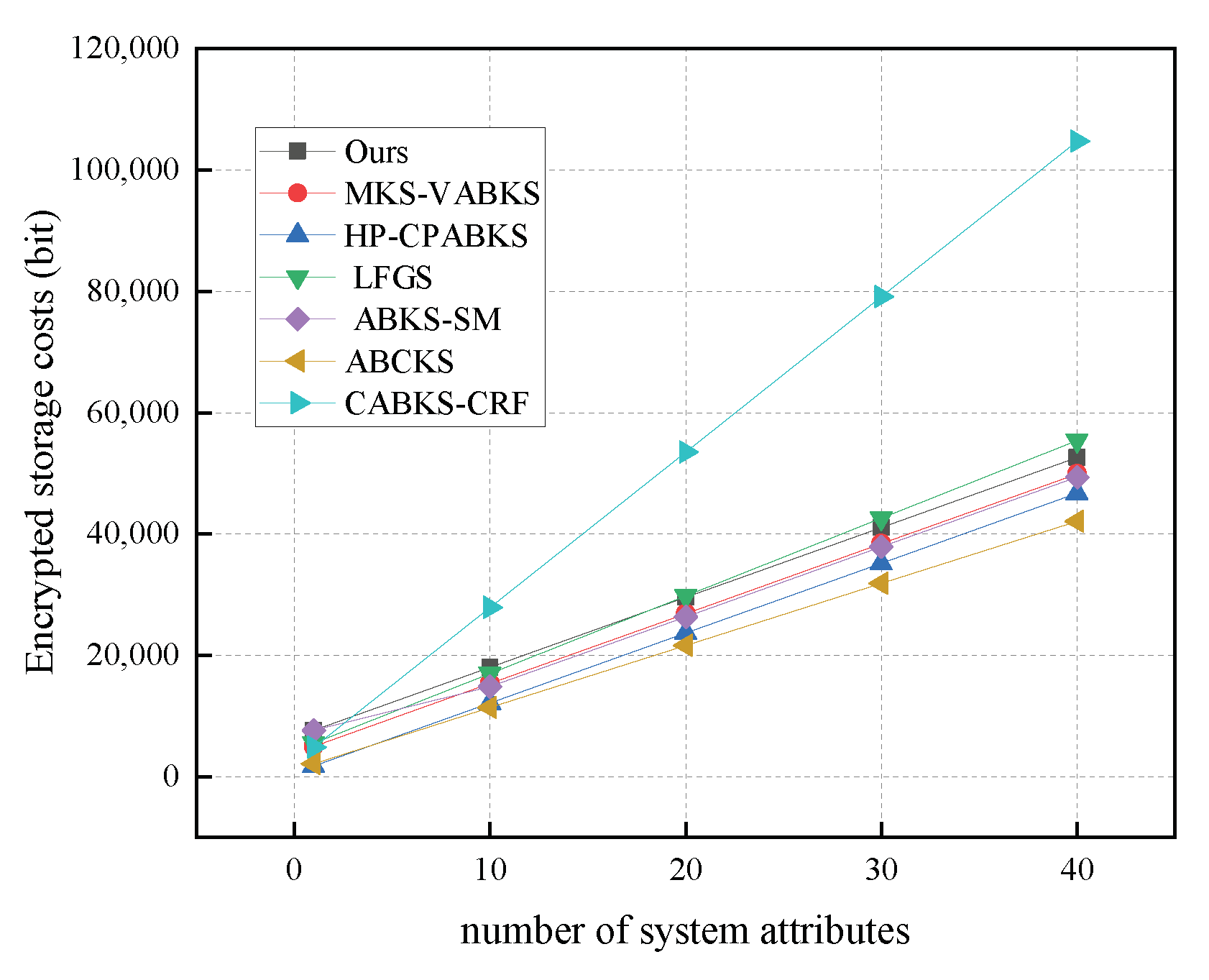
In Figure 7, we maintain r values from 10 to 40 to compare encryption algorithms. Our scheme demonstrates a time consumption of 477.24 ms, while the scheme from Ref. [38] shows 458.96 ms, and the scheme in [40] shows 446.89 ms. All of these schemes significantly outperform the schemes in [31,32,39,41]. In Figure 8, we analyze the storage overhead of the encryption algorithms. Our scheme has a storage consumption of 6.42 kb, which is slightly higher than the schemes in [31,32,39,40], but better than the storage overhead of the schemes in [38,41].

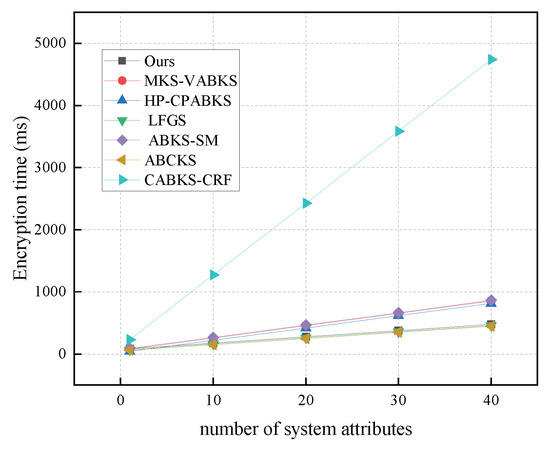
Figure 7. Computational costs in Enc.

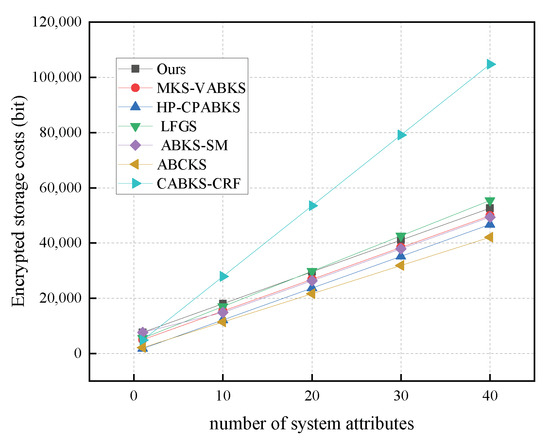
Figure 8. Storage costs in Enc.

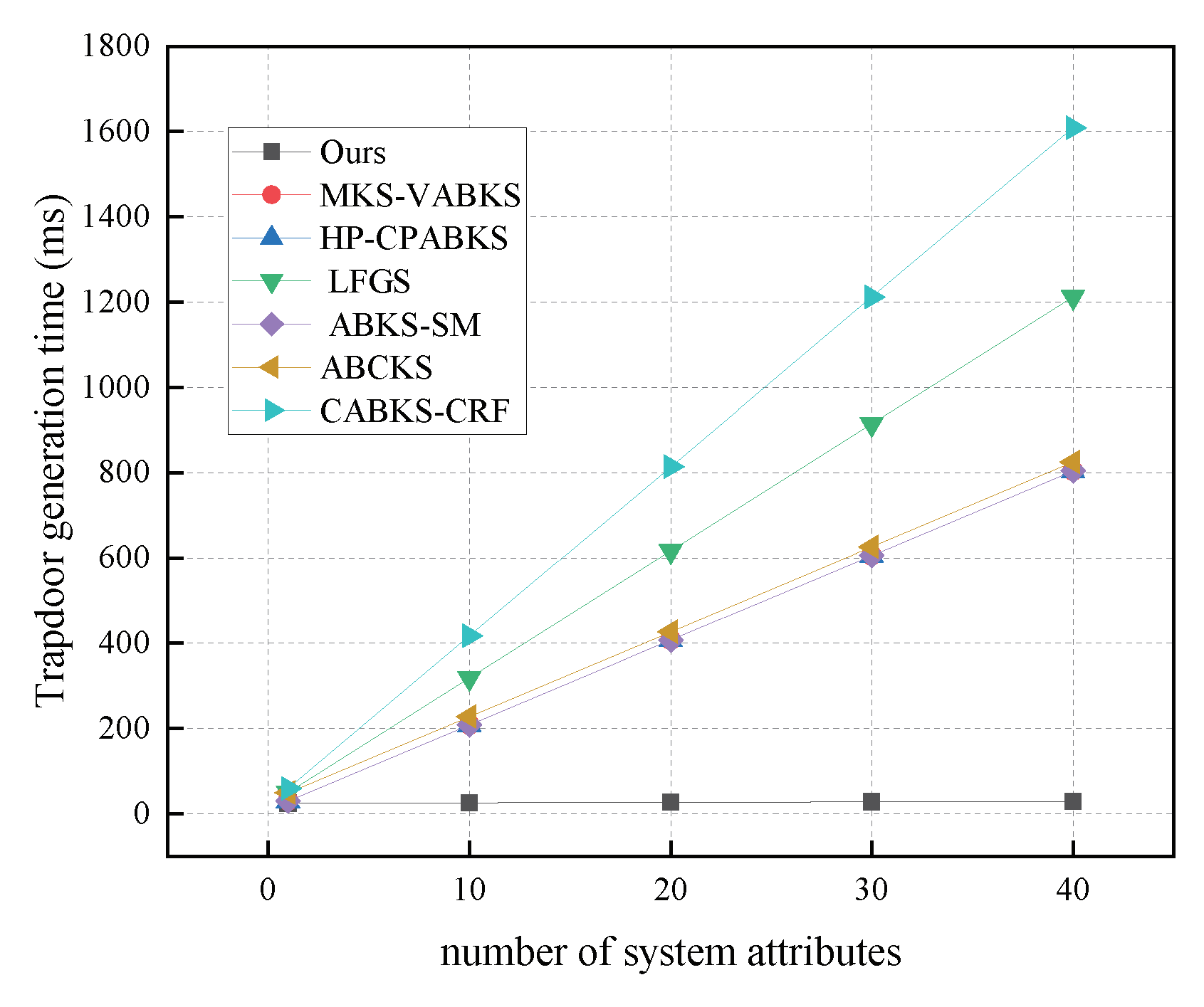
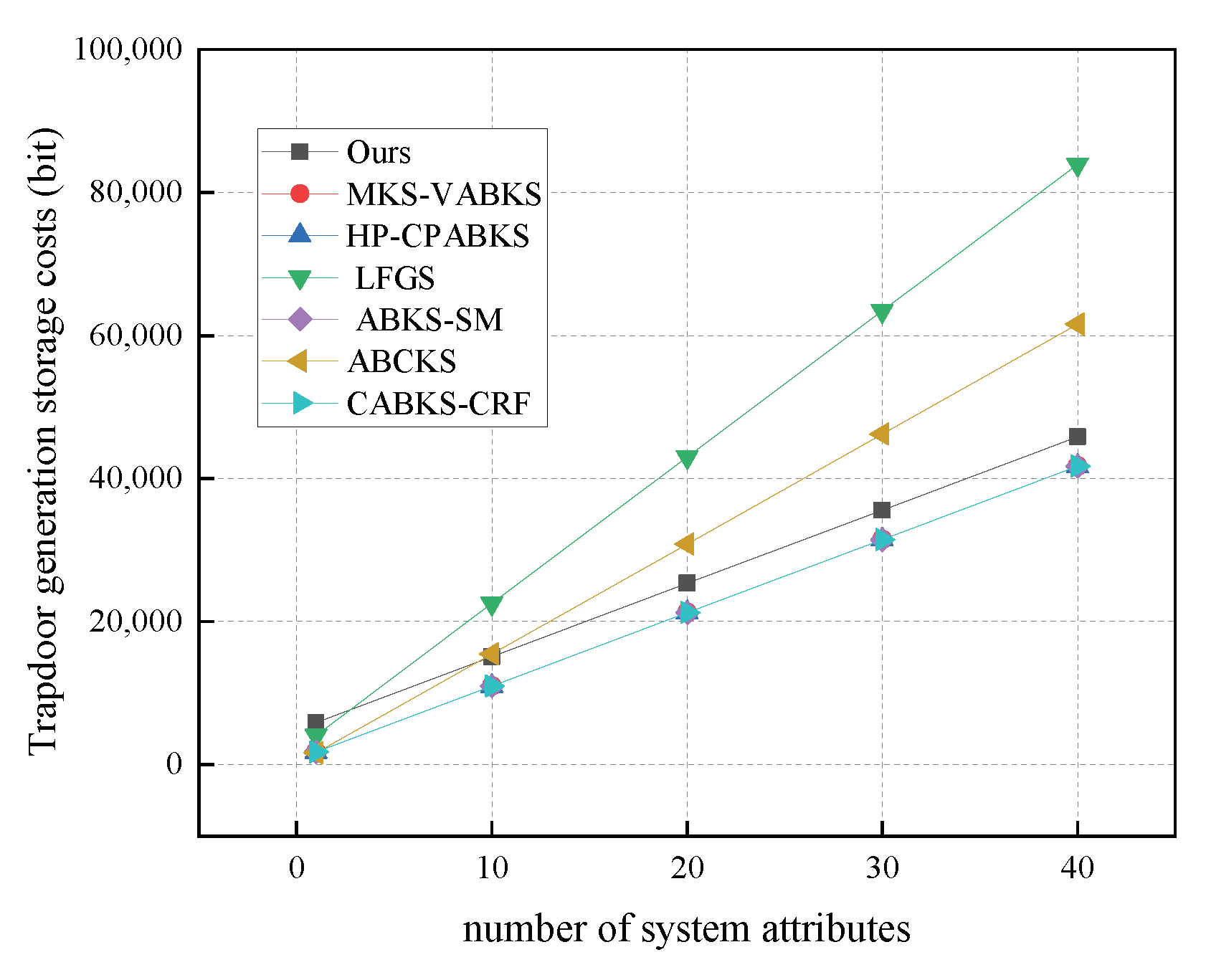
In Figure 9, we compare the computational costs of the trapdoor generation algorithms among the schemes in [31,32,39]. The time consumption for these three schemes is consistently 804.42 ms, while the scheme in [41] exhibits the highest time expenditure at approximately 1608.84 ms. Our scheme, with a time overhead of only 29.38 ms, demonstrates a significant advantage. In Figure 10, we analyze the storage overhead of the trapdoor algorithms. Our scheme has a storage overhead of 5.59 kb, which is slightly higher than the 5.09 kb overhead of the comparison schemes in [31,32,39], and the scheme in [41], but lower than the 10.25 kb overhead of the scheme in [38].

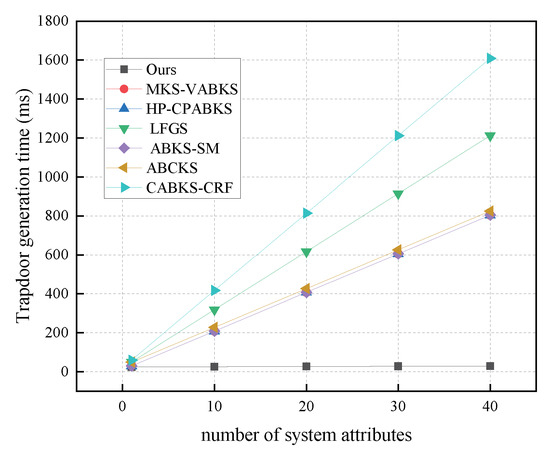
Figure 9. Computational costs in TrapdoorGen. (The red line of MKS-VABKS and the blue line of HP-CPABKS overlap with the purple line of ABKS-SM.)

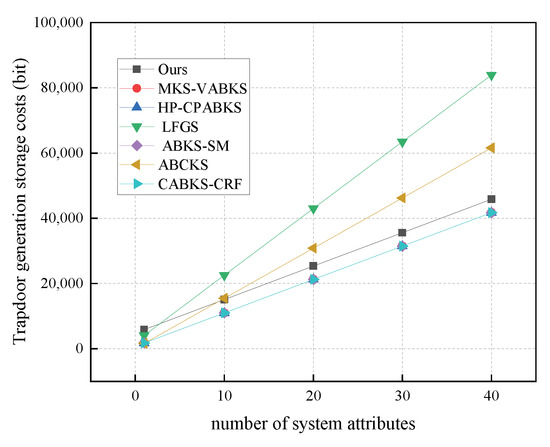
Figure 10. Storage costs in TrapdoorGen. (The red line of MKS-VABKS, the blue line of HP-CPABKS, and the purple line of ABKS-SM overlap with the cyan line of CABKS-CRF.)

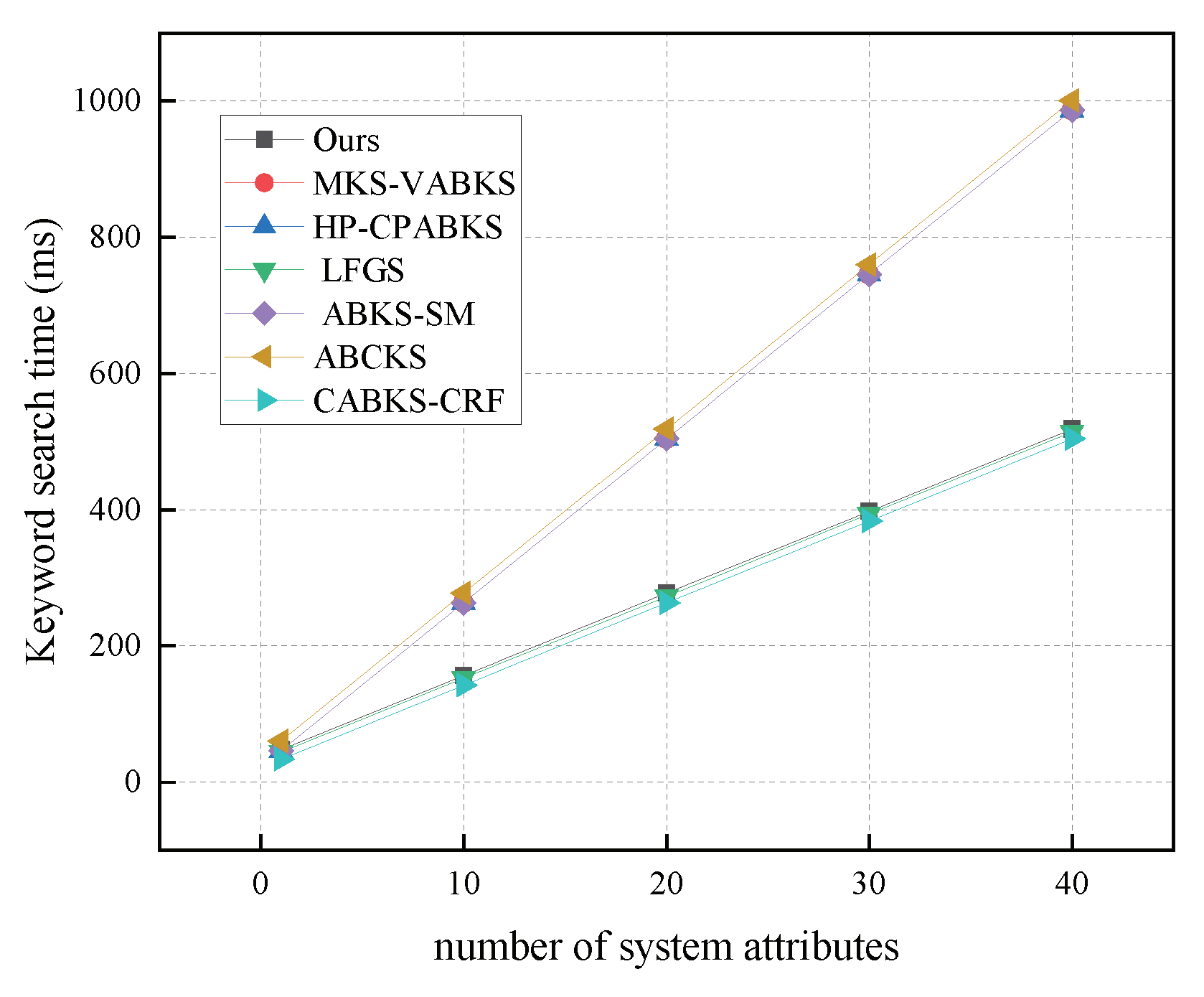
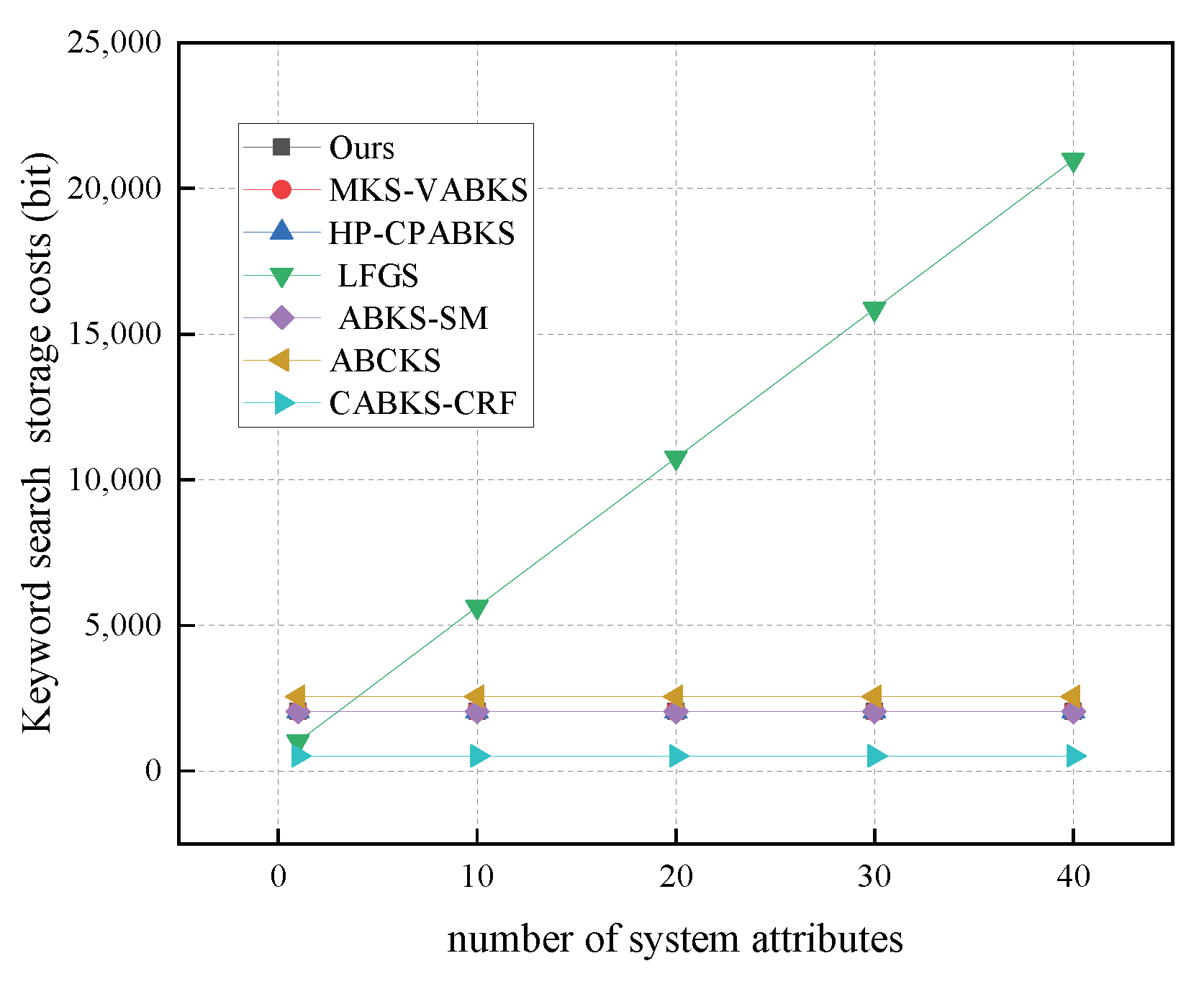
In Figure 11, we analyze the computational overhead of the keyword search algorithms. The schemes in [31,32,39] all have a time overhead of 986.6 ms. Our scheme shows a time overhead of 518.60 ms, which is comparable to the scheme in [38] with 514.23 ms and the scheme in [41] with 504.30 ms. The scheme in [40] has the highest time overhead at 1000.79 ms, ensuring efficient search for ciphertext information by data users. In Figure 12, we analyze the storage overhead of keyword search algorithms. Our scheme and the comparison schemes in [31,32,39] all have a storage overhead of 0.25 kb. Although the scheme in [41] has a lower storage overhead of 0.0625 kb, our scheme overall provides better performance. The scheme in [38] has the highest storage overhead at 2.56 kb.

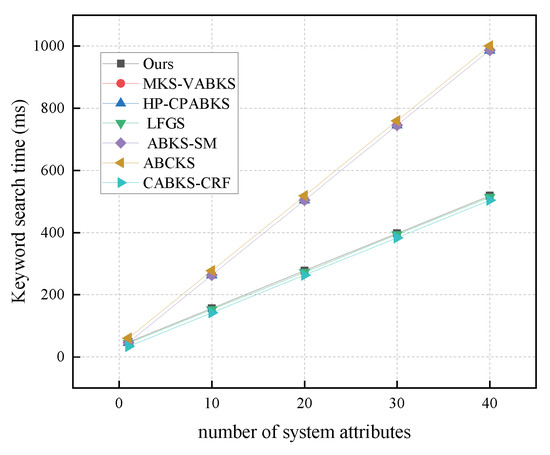
Figure 11. Computational costs in Keyword Search. (The red line of MKS-VABKS and the blue line of HP-CPABKS overlap with the purple line of ABKS-SM.)

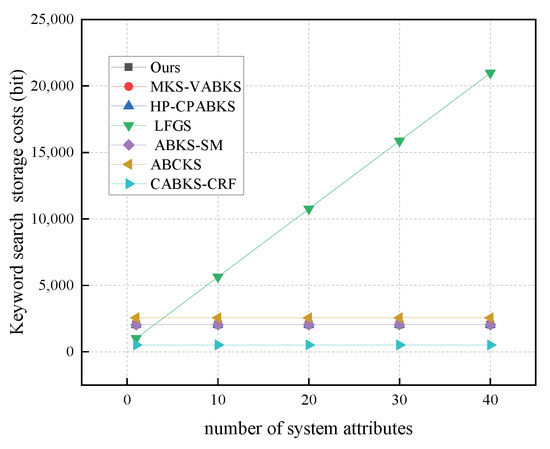
Figure 12. Storage costs in Keyword Search. (The gray line of our scheme, the red line of MKS-VABKS, and the blue line of HP-CPABKS overlap with the purple line of ABKS-SM.)

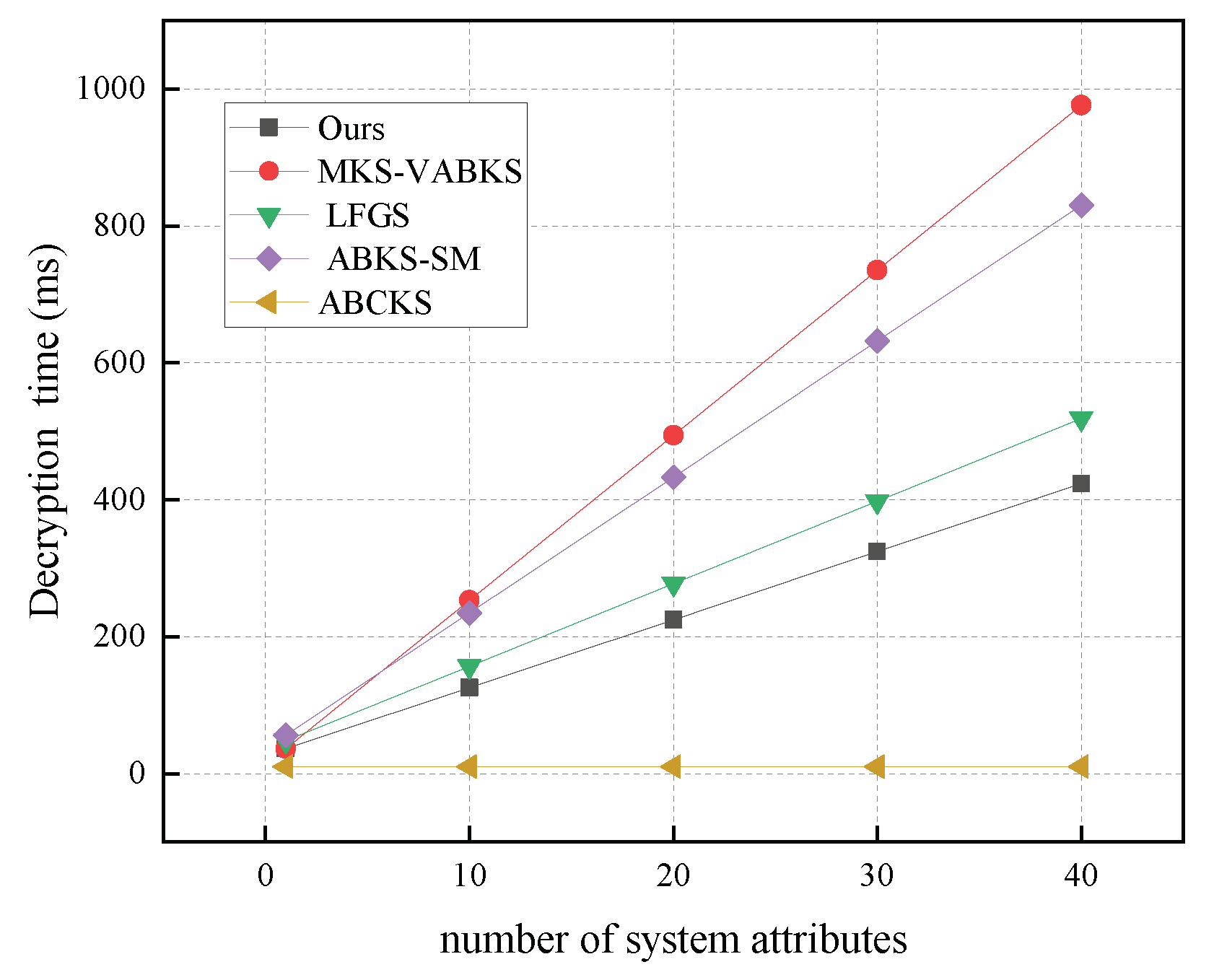
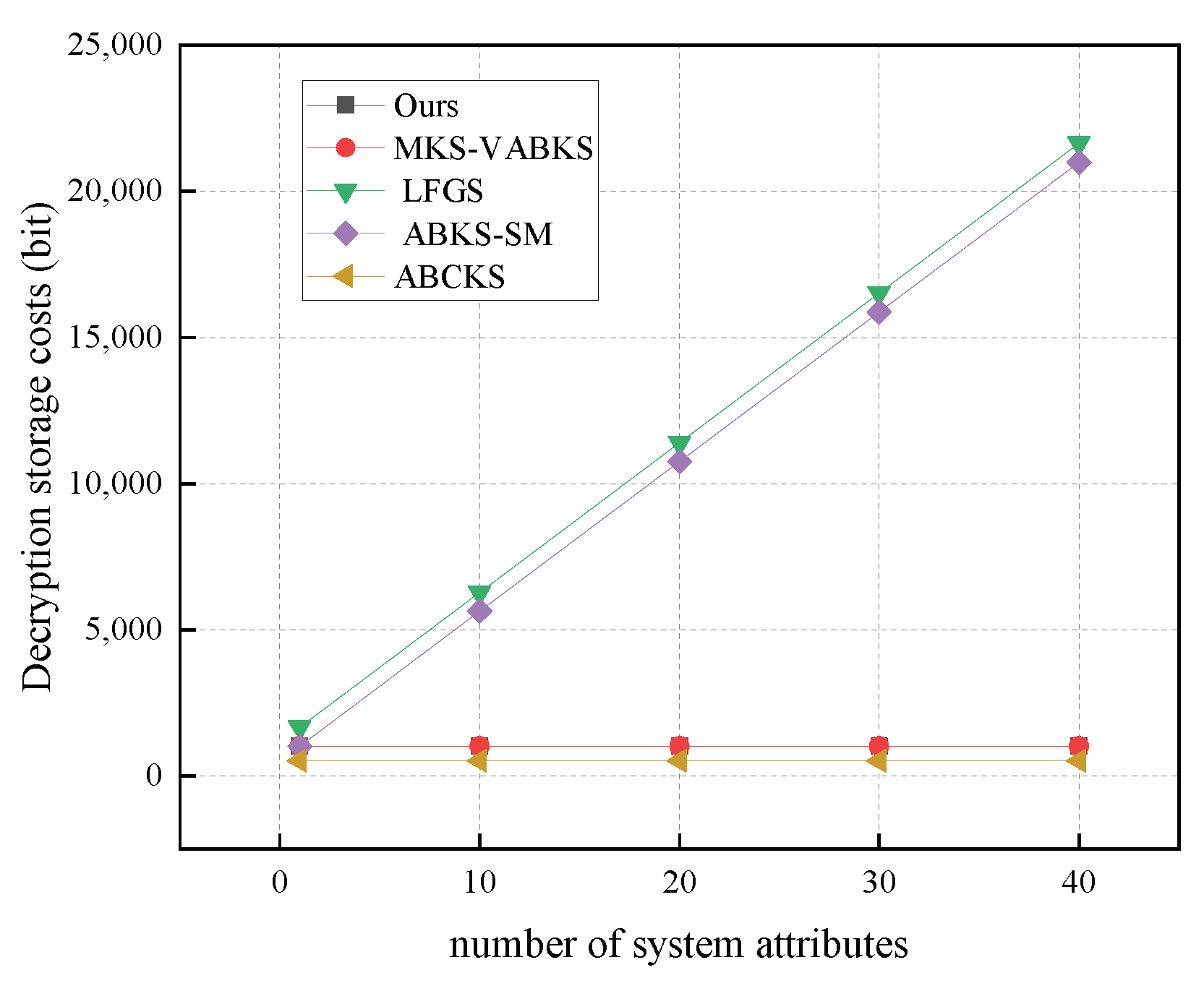
In Figure 13, we analyze the computational overhead of the decryption algorithms. The scheme in [31] exhibits a computational overhead of 830.66 ms, while the schemes in [32,38] show time overheads of 976.67 ms and 518.48 ms, respectively. Our scheme achieves a time overhead of 423.55 ms, and although the scheme in [40] has a time overhead of 9.93 ms, our scheme still significantly outperforms it in overall computational cost. In Figure 14, we analyze the storage overhead of decryption algorithms with the number of system attributes set to 40. Both our scheme and the comparison scheme in [32] have the same storage overhead of 0.125 kb. In contrast, the schemes in [31,38] have storage overheads of 2.64 kb and 2.56 kb, respectively. Our scheme demonstrates a clear storage advantage in this phase, making it suitable for resource-constrained terminal devices.

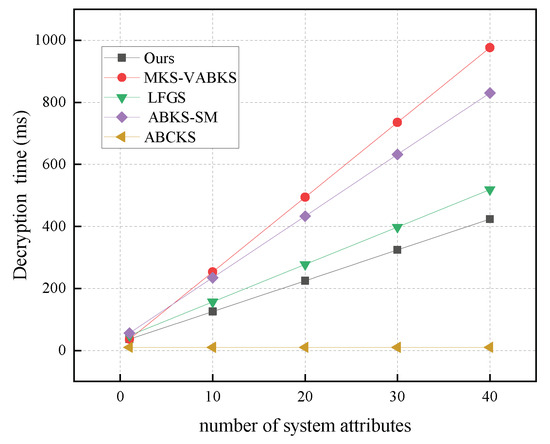
Figure 13. Computational costs in Dec.

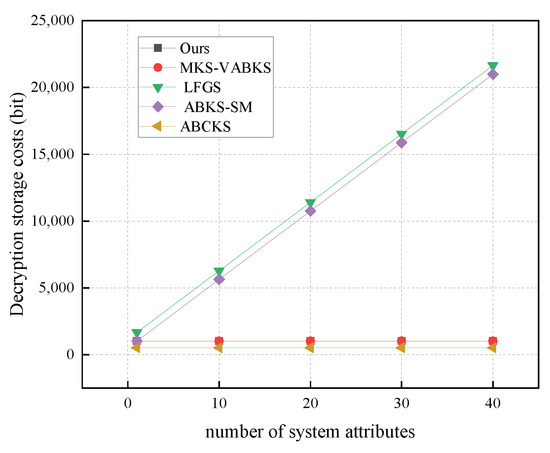
Figure 14. Storage costs in Dec. (The gray line of our scheme overlaps with the red line of MKS-VABKS.)

8. Discussion

We have designed a new secure data-sharing model that uses an edge–cloud server architecture to enable secret resource sharing between data users across different domains. First, this model consists of algorithms with five stages, and compared to other schemes it shows significant advantages in terms of overall computational performance and storage consumption. The model supports fine-grained search characteristics during keyword searches in the cloud, and its lower computational overhead allows for faster responses in real-world environments. Second, the edge layer of the model uses group key agreement technology to re-encrypt ciphertext and keyword information, preventing keyword trapdoor guessing in the cloud and further enhancing security. Third, the model is based on the computational difficulty of the Decisional Bilinear Diffie–Hellman (DBDH) problem, and its security under the random oracle model is proven, ensuring theoretical completeness.

However, our model also has some drawbacks, such as handling attribute updates and revocations, updating and revoking data users, and whether it can allow data users to authenticate without a CA. A decentralized secure data-sharing model, where users authenticate themselves using their own public and private keys, could be explored. Currently, using a CA for authentication may impose a heavy computational burden on the CA. For future work, we will continue to explore attribute-based keyword search, focusing on flexible attribute updates, revocations, and traceability. In practical applications, both data users and attribute sets are dynamically changing. If user attributes are updated, how can secure data sharing be ensured? Thus, we need to address several challenges, such as revoking user permissions at specific attribute levels to allow secure data sharing and tracking malicious users’ identities. If a user’s identity is found to be malicious, it can be directly revoked to enhance the model’s robustness. Additionally, we aim to develop a decentralized secure data-sharing model that does not rely on CA authentication centers. Therefore, we will further optimize our model to improve its efficiency and adaptability across various environments.

For future work, we will continue to work on attribute-based keyword search, including flexible attribute updates, revocations, and traceability. In practical applications, data users and attribute sets are dynamically changing. If user attributes are updated, how to ensure secure data sharing? Therefore, some challenges need to be addressed, such as revoking the permissions of a user at a specific attribute level so that the user can still share data securely, and tracking the identity of malicious users. If the user identity is malicious, it can be directly revoked to make the model more complete. Therefore, in the future, SDSM-KGA will be further optimized to improve efficiency so that it can be used in various environments.

9. Conclusions

In this work, we propose the secure data-sharing model resisting keyword guessing attacks in edge–cloud collaboration scenarios (SDSM-KGA). On the one hand, SDSM-KGA can greatly reduce the computation and storage burden through the edge layer without leaking sensitive information. On the other hand, the SDSM-KGA supports fine-grained keyword search and resists keyword guessing attacks in the cloud. Furthermore, standard security analyses demonstrate that it is capable of resisting keyword guessing attacks (KGAs) in the random oracle model. This empirical experiment using a cryptographic database illustrates the efficiency and feasibility of SDSM-KGA.