3DRecNet: A 3D Reconstruction Network with Dual Attention and Human-Inspired Memory
Abstract
1. Introduction
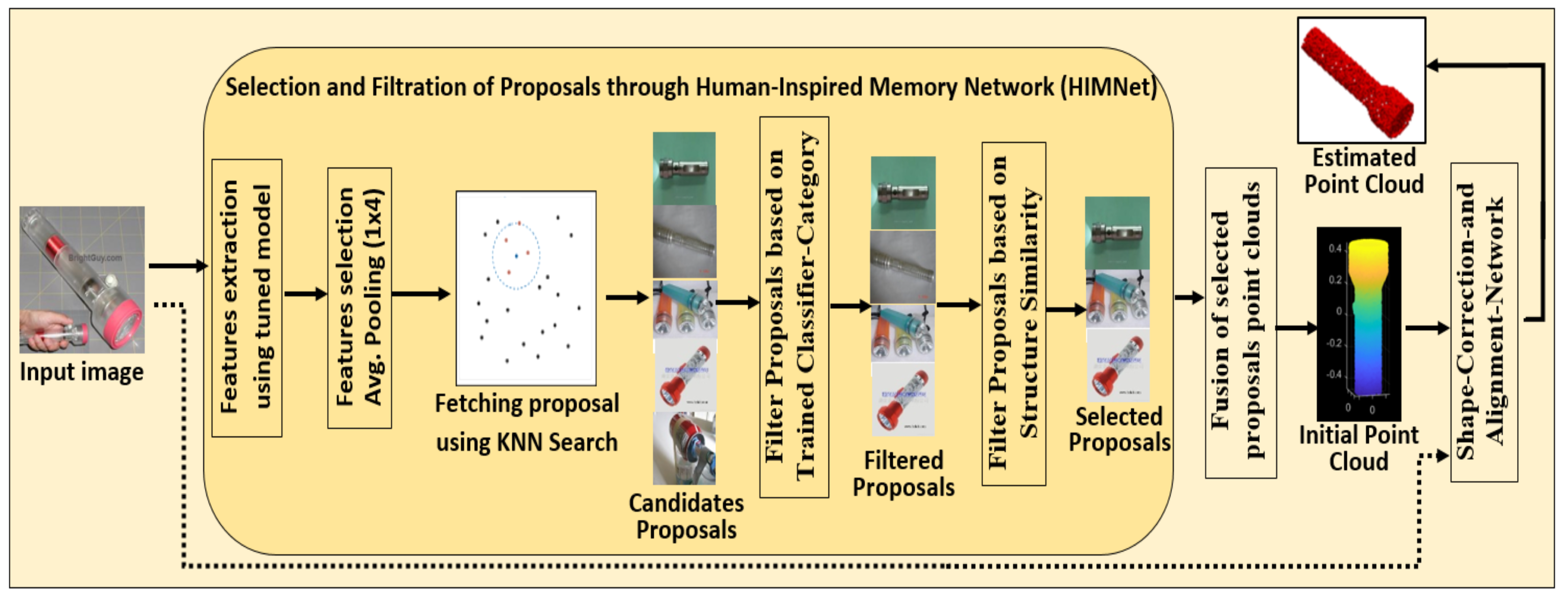
- The Human-Inspired Memory Network (HIMNet) is proposed, drawing inspiration from the human brain’s ability to remember and utilize past experiences. HIMNet retains crucial spatial information regarding an object’s category, shape, and geometry, even in complex and occluded regions. This capability significantly enhances the accuracy and completeness of 3D reconstruction within the end-to-end learning framework of 3DRecNet.
- A deep attention-based fusion mechanism is presented for the intelligent fusion of image-encoded features with the initial point cloud features from HIMNet. This approach helps to learn complex object shapes and geometries, enhancing learning accuracy and reducing feature loss.
- Extensive experiments are conducted and the results analyzed while tuning different hyperparameters to make the architecture more adaptable and accurate.
2. Related Work
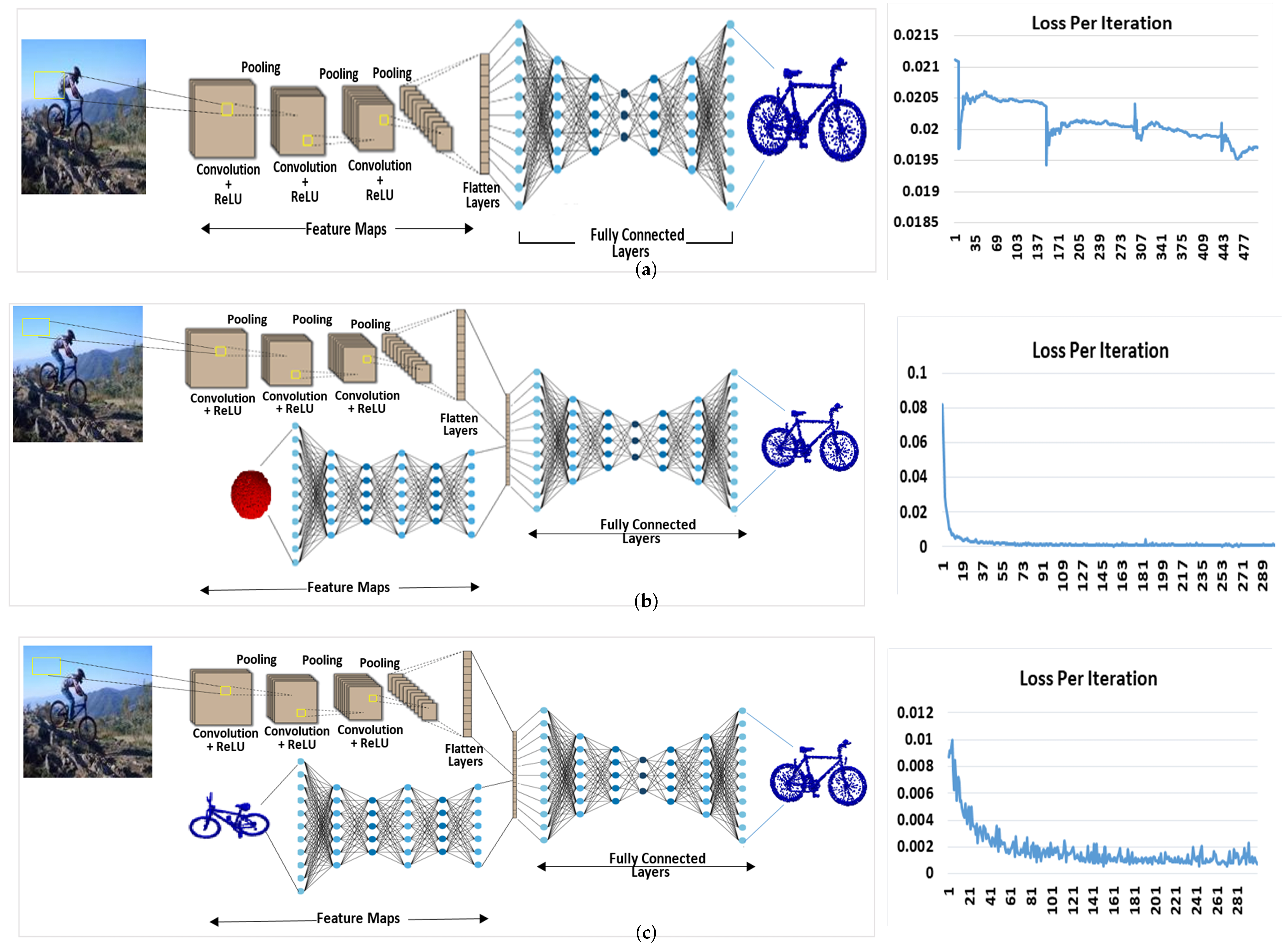
3. Proposed Method
- I.
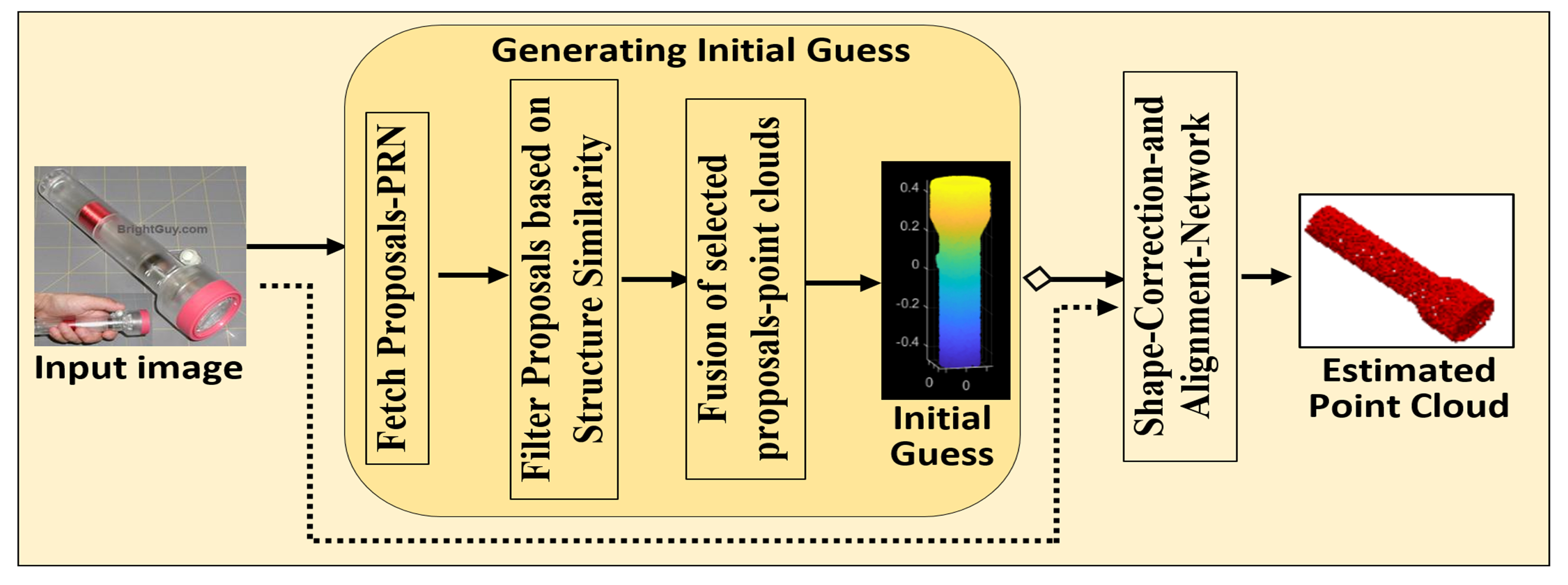
- Human-Inspired Memory Network (HIMNet): Preserves critical spatial information by searching for similar-structure proposals within the same category, generating an initial guess of the point clouds.
- II.
- Image Encoder: Extracts high-level features from the input image.
- III.
- 3D Encoder: Processes HIMNet’s proposals to extract high-level 3D features.
- IV.
- Dual Attention-based Feature Fusion: Fuses features from the Image and 3D Encoders using a dual attention mechanism.
- V.
- Decoder Branch: Transforms the fused features into a 3D representation.
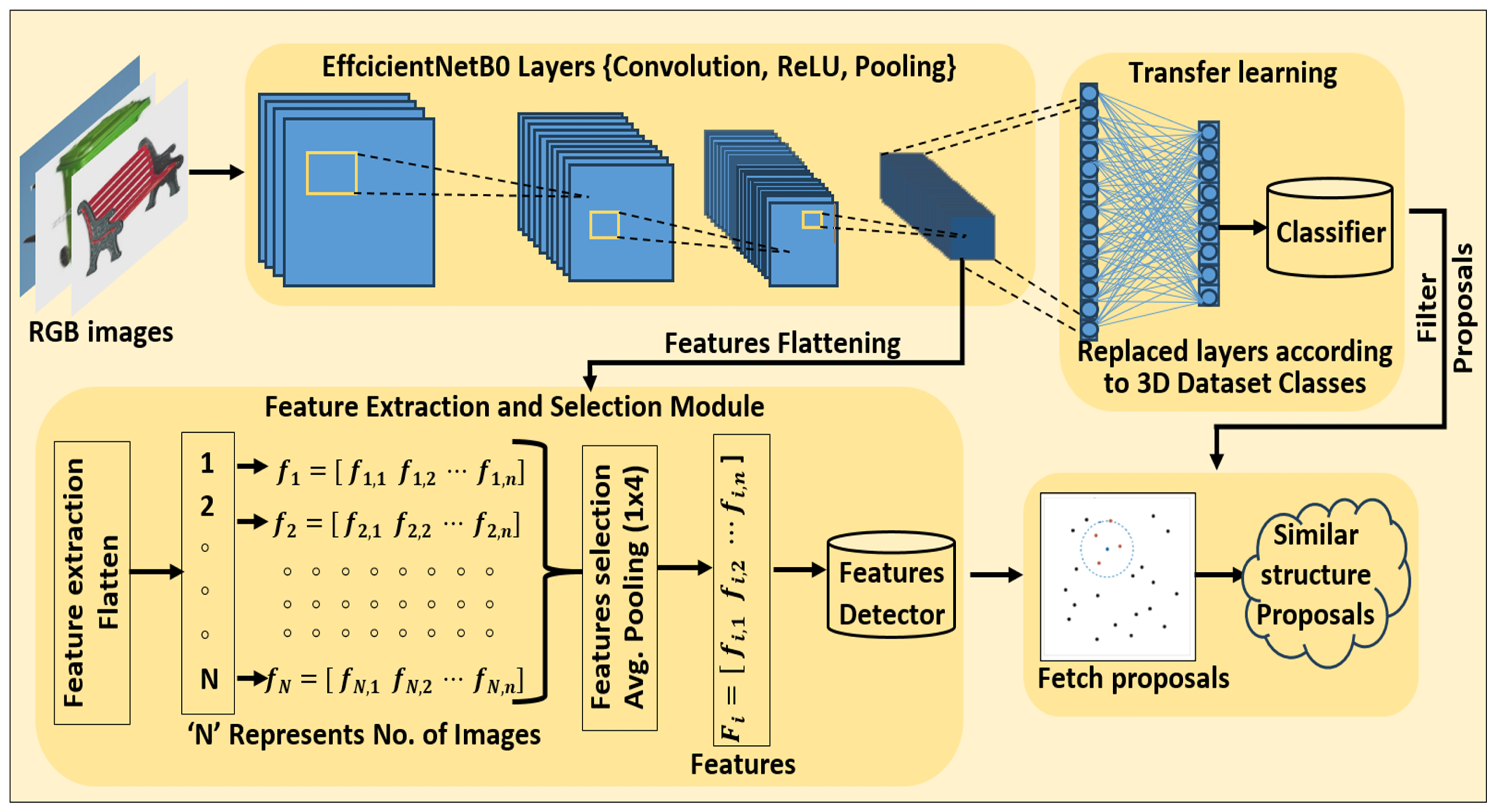
3.1. Human-Inspired Memory Network-HIMNet
3.1.1. Image Analysis: Preprocessing, Feature Extraction, and Representation
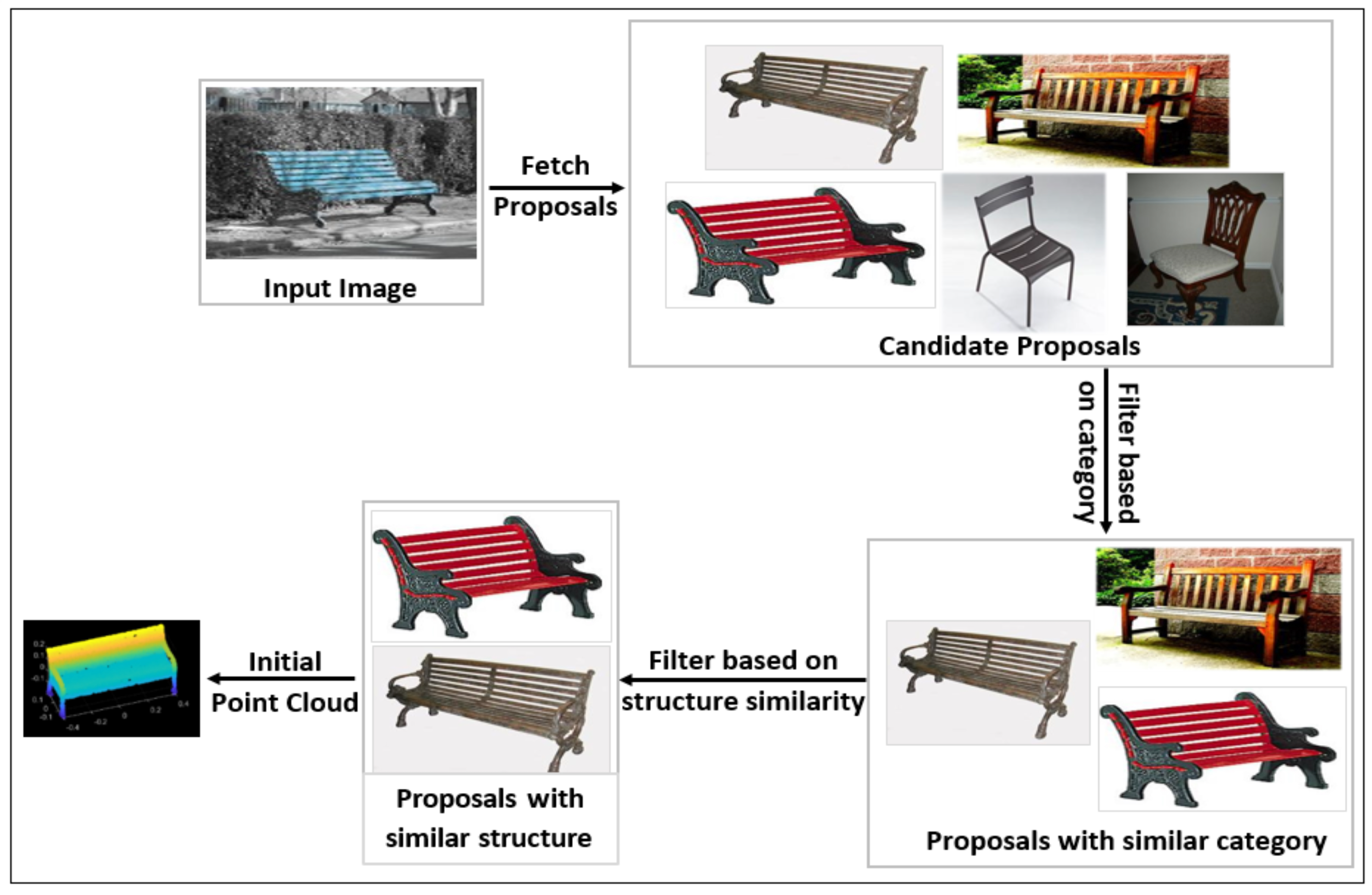
3.1.2. Memory Design Using Structural Similarity Proposals and Metrics
3.1.3. Time Complexity of HIMNet
- Convolutional Layers: Each convolutional layer executes convolutions across the input image or feature maps. The time complexity for a single convolutional layer is , where K is the kernel size (e.g., ), is the number of input channels, is the number of output channels, and H and W are the height and width of the input feature map, respectively.
- Batch Normalization: This layer normalizes the output of the convolutional layers to stabilize and accelerate training. Its time complexity is .
- ReLU Activation: The ReLU function introduces an element-wise non-linearity. The time complexity for ReLU is .
- Depthwise Separable Convolutions: Depthwise Separable Convolutions significantly reduce the computational cost compared to standard convolutions by decomposing the operation into a depthwise convolution, which filters each input channel separately, followed by a pointwise convolution that combines these outputs across channels. The time complexity for depthwise convolution is , and for pointwise convolution, it is .
- Feature Comparison: After feature extraction, comparing features with those of other images using cosine similarity has a time complexity of , where N is the number of images compared, and d is the dimensionality of the feature vectors.
3.2. Image Encoder
Time Complexity Analysis: Image Encoder Branch
- Convolutional Layers: Image Encoder branch has 17 convolutional layers (when including layers within residual blocks). The time complexity for these layers is where and are the input and output channels for layer i, is the kernel size, and are the dimensions of the feature maps at layer i.
- Batch Normalization Layers: Each convolutional layer is typically followed by a batch normalization layer, contributing to the time complexity
- ReLU Activation Layers: ReLU activation follows each batch normalization layer, with the same complexity:
- Max Pooling Layers: Image Encoder Branch has one max pooling layer after the initial convolutional layer, reducing the spatial dimensions: where is the number of channels after the first pooling layer, and are the reduced dimensions.
3.3. 3D Encoding Branch
3.4. Dual Attention-Based Feature Fusion
3.5. Decoder Branch
3.6. Summary and Aggregated Time Complexity
4. Experimentation and Results
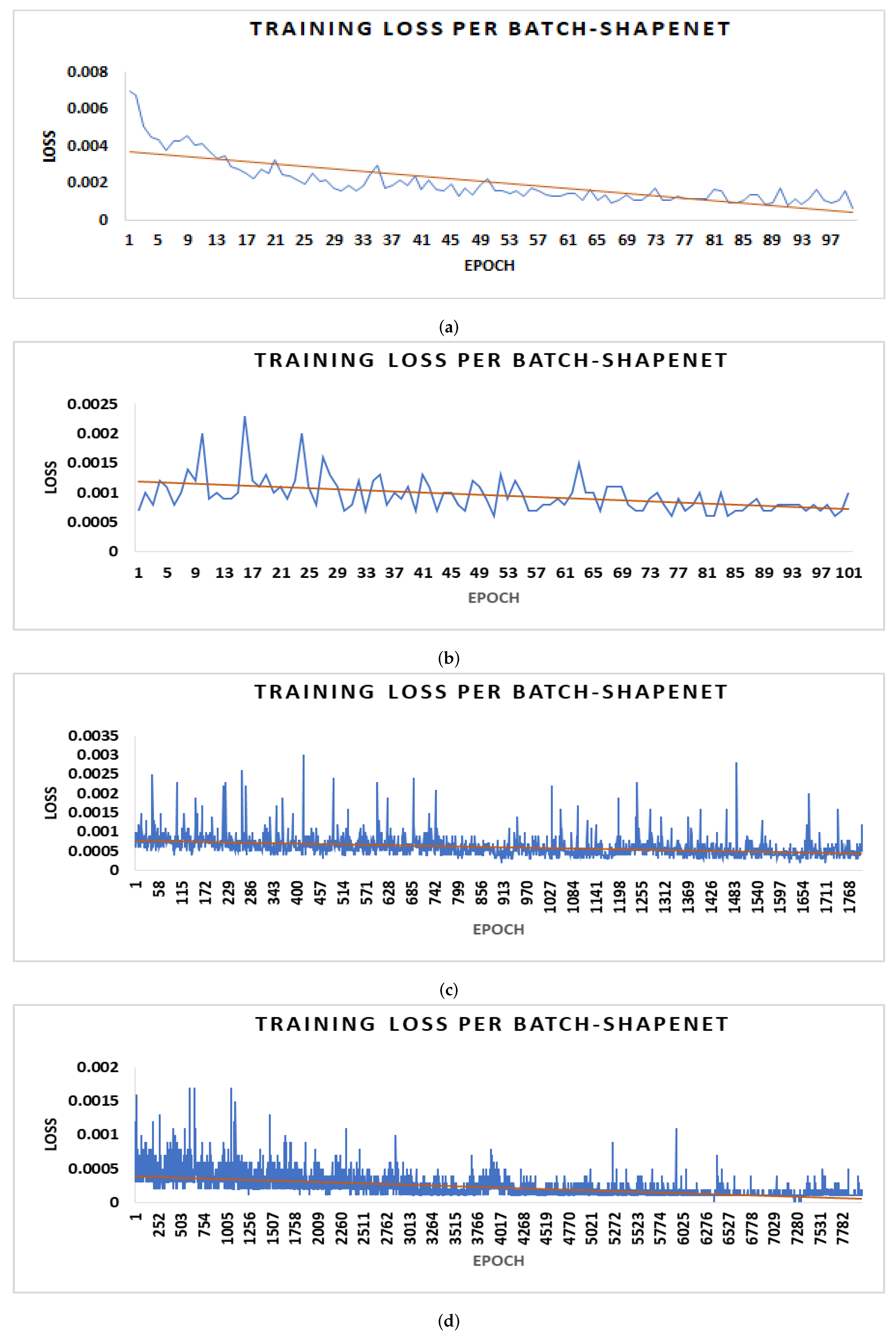
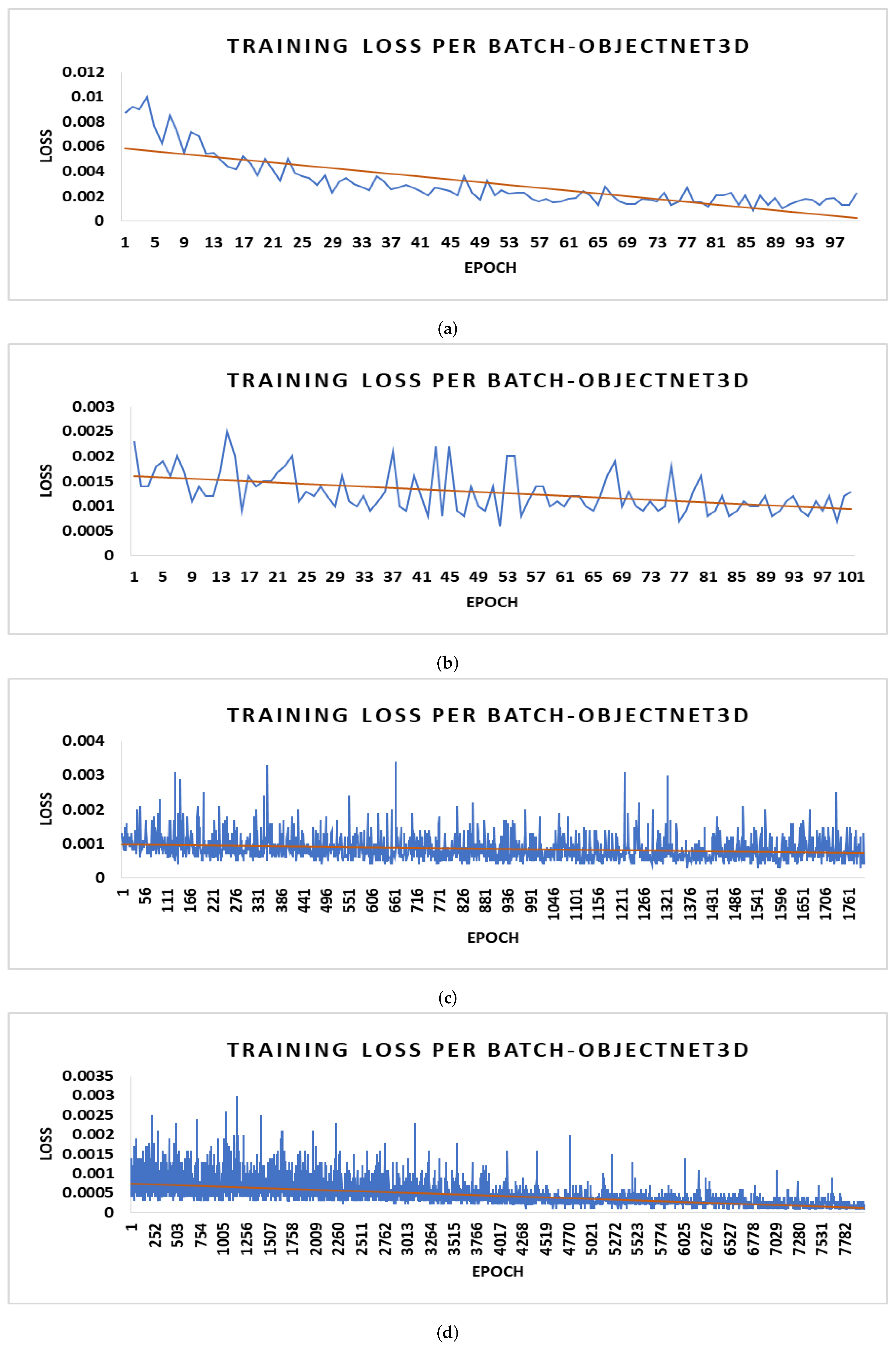
4.1. 3D Datasets
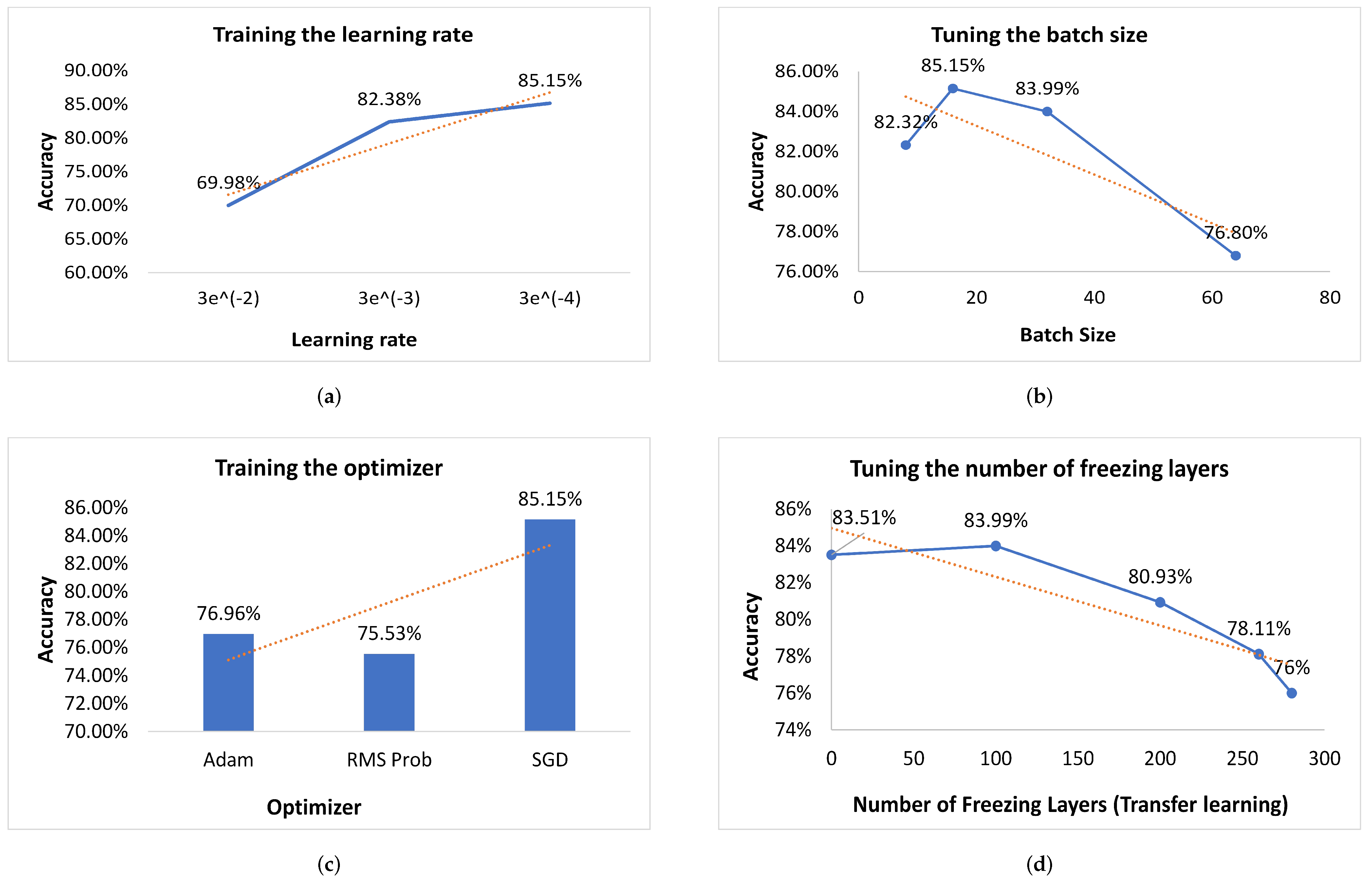
4.2. Experimentation Settings
4.3. Ablation Study
4.3.1. Impact of Memory Integration on 3DRecNet Performance
4.3.2. Handling Inter-Class and Intra-Class Variations
4.3.3. Impact of Attention-Based Fusion
4.4. Parameter Optimization and Gradient Loss
4.5. Time Complexity
| CD Comparison | Methods | ||||||
|---|---|---|---|---|---|---|---|
| PSGN | 3D-LMNet | 3D-ARNet | 3D-ReconstNet | 3D-FEGNet | Proposed | ||
| [12] | [32] | [36] | [30] | [34] | |||
| Category | Chair | 8.05 | 7.35 | 7.22 | 5.59 | 5.66 | 5.16 |
| Sofa | 8.45 | 8.18 | 8.13 | 6.14 | 6.23 | 5.91 | |
| Table | 10.85 | 11.2 | 10.31 | 7.04 | 7.58 | 6.22 | |
| CD Comparison | Methods | ||||
|---|---|---|---|---|---|
| PSGN [12] | Real-Point3D [31] | EGN [37] | Proposed | ||
| Category | Sofa | 2.0 | 1.95 | 1.82 | 0.98 |
| Aeroplane | 1.0 | 0.79 | 0.77 | 0.41 | |
| Bench | 2.51 | 2.11 | 2.18 | 1.29 | |
| Car | 1.28 | 1.26 | 1.25 | 0.72 | |
| Chair | 2.38 | 2.13 | 1.97 | 1.22 | |
| EMD Comparison | Methods | ||||||
|---|---|---|---|---|---|---|---|
| PSGN | 3D-LMNet | 3D-ARNet | 3D-ReconstNet | 3D-FEGNet | Proposed | ||
| [12] | [32] | [36] | [30] | [34] | |||
| Category | Chair | 12.55 | 9.14 | 7.94 | 5.99 | 8.24 | 6.15 |
| Sofa | 9.16 | 7.22 | 6.69 | 5.02 | 6.77 | 4.79 | |
| Table | 15.16 | 12.73 | 10.42 | 7.60 | 11.40 | 7.43 | |
| EMD Comparison | Methods | ||||||
|---|---|---|---|---|---|---|---|
| PSGN | 3D-LMNet | 3D-VENet | 3D-FEGNet | 3D-CDRNet | Proposed | ||
| [12] | [32] | [33] | [34] | [26] | |||
| Category | Airplane | 6.38 | 4.77 | 3.56 | 2.67 | 2.98 | 2.54 |
| Bench | 5.88 | 4.99 | 4.09 | 3.75 | 3.65 | 2.92 | |
| Cabinet | 6.04 | 6.35 | 4.69 | 4.75 | 4.47 | 3.38 | |
| Car | 4.87 | 4.1 | 3.57 | 3.4 | 3.21 | 2.91 | |
| Chair | 9.63 | 8.02 | 6.11 | 4.52 | 4.65 | 4.17 | |
| Lamp | 16.17 | 15.8 | 9.97 | 6.11 | 7.26 | 5.41 | |
| Monitor | 7.59 | 7.13 | 5.63 | 4.88 | 4.65 | 4.11 | |
| Rifle | 8.48 | 6.08 | 4.06 | 2.91 | 3.31 | 2.17 | |
| Sofa | 7.42 | 5.65 | 4.8 | 4.56 | 4.04 | 3.71 | |
| Speaker | 8.7 | 9.15 | 6.78 | 6.24 | 5.73 | 4.22 | |
| Table | 8.4 | 7.82 | 6.1 | 4.62 | 4.32 | 3.66 | |
| Telephone | 5.07 | 5.43 | 3.61 | 3.39 | 3.08 | 2.67 | |
| Vessel | 6.18 | 5.68 | 4.59 | 4.09 | 3.59 | 2.88 | |
| CD Comparison | Methods | ||||||
|---|---|---|---|---|---|---|---|
| PSGN | 3D-LMNet | 3D-VENet | 3D-FEGNet | 3D-CDRNet | Proposed | ||
| [12] | [32] | [33] | [34] | [26] | |||
| Category | Airplane | 3.74 | 3.34 | 3.09 | 2.36 | 2.22 | 1.94 |
| Bench | 4.63 | 4.55 | 4.26 | 3.6 | 3.38 | 3.01 | |
| Cabinet | 6.98 | 6.09 | 5.49 | 4.84 | 4.08 | 3.57 | |
| Car | 5.2 | 4.55 | 4.3 | 3.57 | 3.05 | 3.46 | |
| Chair | 6.39 | 6.41 | 5.76 | 4.35 | 4.17 | 4.09 | |
| Lamp | 6.33 | 7.1 | 6.07 | 5.13 | 5.07 | 4.36 | |
| Monitor | 6.15 | 6.4 | 5.76 | 4.67 | 4.08 | 4.02 | |
| Rifle | 2.91 | 2.75 | 2.67 | 2.45 | 1.91 | 1.35 | |
| Sofa | 6.98 | 5.85 | 5.34 | 4.56 | 4 | 3.89 | |
| Speaker | 8.75 | 8.1 | 7.28 | 6 | 5.05 | 4.45 | |
| Table | 6 | 6.05 | 5.46 | 4.42 | 3.8 | 3.14 | |
| Telephone | 4.56 | 4.63 | 4.2 | 3.5 | 2.53 | 2.19 | |
| Vessel | 4.38 | 4.37 | 4.22 | 3.75 | 2.95 | 2.42 | |
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, X.F.; Laga, H.; Bennamoun, M. Image-based 3D object reconstruction: State-of-the-art and trends in the deep learning era. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 43, 1578–1604. [Google Scholar] [CrossRef] [PubMed]
- Sra, M.; Garrido-Jurado, S.; Schmandt, C.; Maes, P. Procedurally generated virtual reality from 3D reconstructed physical space. In Proceedings of the 22nd ACM Conference on Virtual Reality Software and Technology, Munich, Germany, 2–4 November 2016; pp. 191–200. [Google Scholar]
- Montefusco, L.B.; Lazzaro, D.; Papi, S.; Guerrini, C. A fast compressed sensing approach to 3D MR image reconstruction. IEEE Trans. Med. Imaging 2010, 30, 1064–1075. [Google Scholar] [CrossRef]
- Pang, H.E.; Biljecki, F. 3D building reconstruction from single street view images using deep learning. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102859. [Google Scholar] [CrossRef]
- Yang, S.; Xu, M.; Xie, H.; Perry, S.; Xia, J. Single-view 3D object reconstruction from shape priors in memory. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 3152–3161. [Google Scholar]
- Li, B.; Zhu, S.; Lu, Y. A single stage and single view 3D point cloud reconstruction network based on DetNet. Sensors 2022, 22, 8235. [Google Scholar] [CrossRef] [PubMed]
- Schonberger, J.L.; Frahm, J.M. Structure-from-motion revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, present, and future of simultaneous localization and mapping: Toward the robust-perception age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef]
- Huang, Q.; Wang, H.; Koltun, V. Single-view reconstruction via joint analysis of image and shape collections. ACM Trans. Graph. TOG 2015, 34, 87–91. [Google Scholar] [CrossRef]
- Choy, C.B.; Xu, D.; Gwak, J.; Chen, K.; Savarese, S. 3D-R2N2: A unified approach for single and multi-view 3D object reconstruction. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 628–644. [Google Scholar]
- Girdhar, R.; Fouhey, D.F.; Rodriguez, M.; Gupta, A. Learning a predictable and generative vector representation for objects. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 484–499. [Google Scholar]
- Fan, H.; Su, H.; Guibas, L.J. A point set generation network for 3D object reconstruction from a single image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 605–613. [Google Scholar]
- Feng, Y.; Wu, F.; Shao, X.; Wang, Y.; Zhou, X. Joint 3D face reconstruction and dense alignment with position map regression network. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 534–551. [Google Scholar]
- Sinha, A.; Unmesh, A.; Huang, Q.; Ramani, K. Surfnet: Generating 3D shape surfaces using deep residual networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6040–6049. [Google Scholar]
- Xiang, Y.; Kim, W.; Chen, W.; Ji, J.; Choy, C.; Su, H.; Mottaghi, R.; Guibas, L.; Savarese, S. Objectnet3D: A large scale database for 3D object recognition. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 160–176. [Google Scholar]
- Sun, X.; Wu, J.; Zhang, X.; Zhang, Z.; Zhang, C.; Xue, T.; Tenenbaum, J.B.; Freeman, W.T. Pix3D: Dataset and methods for single-image 3D shape modeling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2974–2983. [Google Scholar]
- Richter, S.R.; Roth, S. Matryoshka networks: Predicting 3D geometry via nested shape layers. In Proceedings of the IEEE Conference on Computer vision And Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1936–1944. [Google Scholar]
- Wu, J.; Wang, Y.; Xue, T.; Sun, X.; Freeman, B.; Tenenbaum, J. Marrnet: 3D shape reconstruction via 2.5 D sketches. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Wu, J.; Zhang, C.; Zhang, X.; Zhang, Z.; Freeman, W.T.; Tenenbaum, J.B. Learning shape priors for single-view 3D completion and reconstruction. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 646–662. [Google Scholar]
- Tahir, R.; Sargano, A.B.; Habib, Z. Voxel-based 3D object reconstruction from single 2D image using variational autoencoders. Mathematics 2021, 9, 2288. [Google Scholar] [CrossRef]
- Xie, H.; Yao, H.; Sun, X.; Zhou, S.; Zhang, S. Pix2vox: Context-aware 3D reconstruction from single and multi-view images. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–3 November 2019; pp. 2690–2698. [Google Scholar]
- Han, Z.; Qiao, G.; Liu, Y.S.; Zwicker, M. SeqXY2SeqZ: Structure learning for 3D shapes by sequentially predicting 1D occupancy segments from 2D coordinates. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; pp. 607–625. [Google Scholar]
- Kniaz, V.V.; Knyaz, V.A.; Remondino, F.; Bordodymov, A.; Moshkantsev, P. Image-to-voxel model translation for 3D scene reconstruction and segmentation. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 105–124. [Google Scholar]
- Peng, K.; Islam, R.; Quarles, J.; Desai, K. Tmvnet: Using transformers for multi-view voxel-based 3D reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 222–230. [Google Scholar]
- Afifi, A.J.; Magnusson, J.; Soomro, T.A.; Hellwich, O. Pixel2Point: 3D object reconstruction from a single image using CNN and initial sphere. IEEE Access 2020, 9, 110–121. [Google Scholar] [CrossRef]
- Tong, Y.; Chen, H.; Yang, N.; Menhas, M.I.; Ahmad, B. 3D-CDRNet: Retrieval-based dense point cloud reconstruction from a single image under complex background. Displays 2023, 78, 102438. [Google Scholar] [CrossRef]
- Chang, A.X.; Funkhouser, T.; Guibas, L.; Hanrahan, P.; Huang, Q.; Li, Z.; Savarese, S.; Savva, M.; Song, S.; Su, H.; et al. Shapenet: An information-rich 3D model repository. arXiv 2015, arXiv:1512.03012. [Google Scholar]
- Pumarola, A.; Popov, S.; Moreno-Noguer, F.; Ferrari, V. C-flow: Conditional generative flow models for images and 3D point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7949–7958. [Google Scholar]
- Mueed Hafiz, A.; Alam Bhat, R.U.; Parah, S.A.; Hassaballah, M. SE-MD: A Single-encoder multiple-decoder deep network for point cloud generation from 2D images. arXiv 2021, arXiv:2106.15325. [Google Scholar]
- Li, B.; Zhang, Y.; Zhao, B.; Shao, H. 3D-ReConstnet: A single-view 3D-object point cloud reconstruction network. IEEE Access 2020, 8, 83782–83790. [Google Scholar] [CrossRef]
- Xia, Y.; Wang, C.; Xu, Y.; Zang, Y.; Liu, W.; Li, J.; Stilla, U. RealPoint3D: Generating 3D point clouds from a single image of complex scenarios. Remote Sens. 2019, 11, 2644. [Google Scholar] [CrossRef]
- Mandikal, P.; Navaneet, K.; Agarwal, M.; Babu, R.V. 3D-LMNet: Latent embedding matching for accurate and diverse 3D point cloud reconstruction from a single image. arXiv 2018, arXiv:1807.07796. [Google Scholar]
- Ping, G.; Esfahani, M.A.; Chen, J.; Wang, H. Visual enhancement of single-view 3D point cloud reconstruction. Comput. Graph. 2022, 102, 112–119. [Google Scholar] [CrossRef]
- Wang, E.; Sun, H.; Wang, B.; Cao, Z.; Liu, Z. 3D-FEGNet: A feature enhanced point cloud generation network from a single image. IET Comput. Vis. 2023, 17, 98–110. [Google Scholar] [CrossRef]
- Tatarchenko, M.; Dosovitskiy, A.; Brox, T. Octree generating networks: Efficient convolutional architectures for high-resolution 3d outputs. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2088–2096. [Google Scholar]
- Chen, H.; Zuo, Y. 3D-ARNet: An accurate 3D point cloud reconstruction network from a single-image. Multimed. Tools Appl. 2022, 81, 12127–12140. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Z.; Liu, T.; Peng, B.; Li, X. RealPoint3D: An efficient generation network for 3D object reconstruction from a single image. IEEE Access 2019, 7, 57539–57549. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shoukat, M.A.; Sargano, A.B.; You, L.; Habib, Z. 3DRecNet: A 3D Reconstruction Network with Dual Attention and Human-Inspired Memory. Electronics 2024, 13, 3391. https://doi.org/10.3390/electronics13173391
Shoukat MA, Sargano AB, You L, Habib Z. 3DRecNet: A 3D Reconstruction Network with Dual Attention and Human-Inspired Memory. Electronics. 2024; 13(17):3391. https://doi.org/10.3390/electronics13173391
Chicago/Turabian StyleShoukat, Muhammad Awais, Allah Bux Sargano, Lihua You, and Zulfiqar Habib. 2024. "3DRecNet: A 3D Reconstruction Network with Dual Attention and Human-Inspired Memory" Electronics 13, no. 17: 3391. https://doi.org/10.3390/electronics13173391
APA StyleShoukat, M. A., Sargano, A. B., You, L., & Habib, Z. (2024). 3DRecNet: A 3D Reconstruction Network with Dual Attention and Human-Inspired Memory. Electronics, 13(17), 3391. https://doi.org/10.3390/electronics13173391









