A Unified Model of a Virtual Synchronous Generator for Transient Stability Analysis
Abstract
:1. Introduction
- (1)
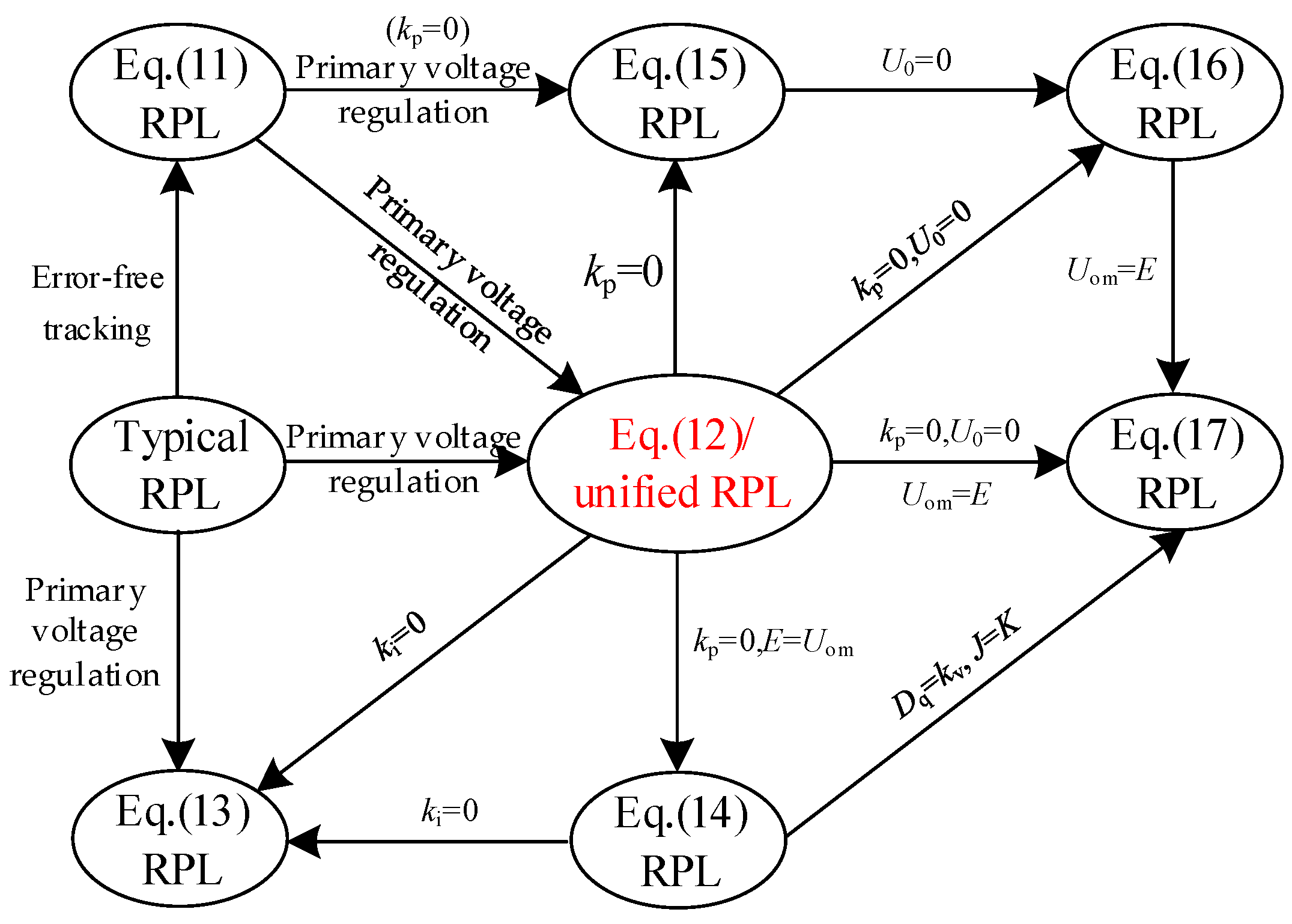
- By comparing and analyzing the evolution characteristics of APL types and RPL types, a representative unified VSG model is established, and the parametric equivalent correspondences between the APL of unified VSG and other types of APLs and between the RPL of unified VSG and other types of RPLs are established.
- (2)
- A large-signal model of unified VSG is established, and based on this model, the influence of unified VSG control parameters on transient stability is analyzed.
- (3)
- Based on the analysis of the influence of different action links on the transient stability of VSG, the transient stability between VSG control with different types of APLs and the transient stability between VSG control with different types of RPLs are compared. It is pointed out that under the same control parameters, the primary frequency regulation in APLs, the reactive power voltage regulation and the reactive power error-free tracking in RPLs are the essential reasons for the different transient stabilities of different types of VSG.
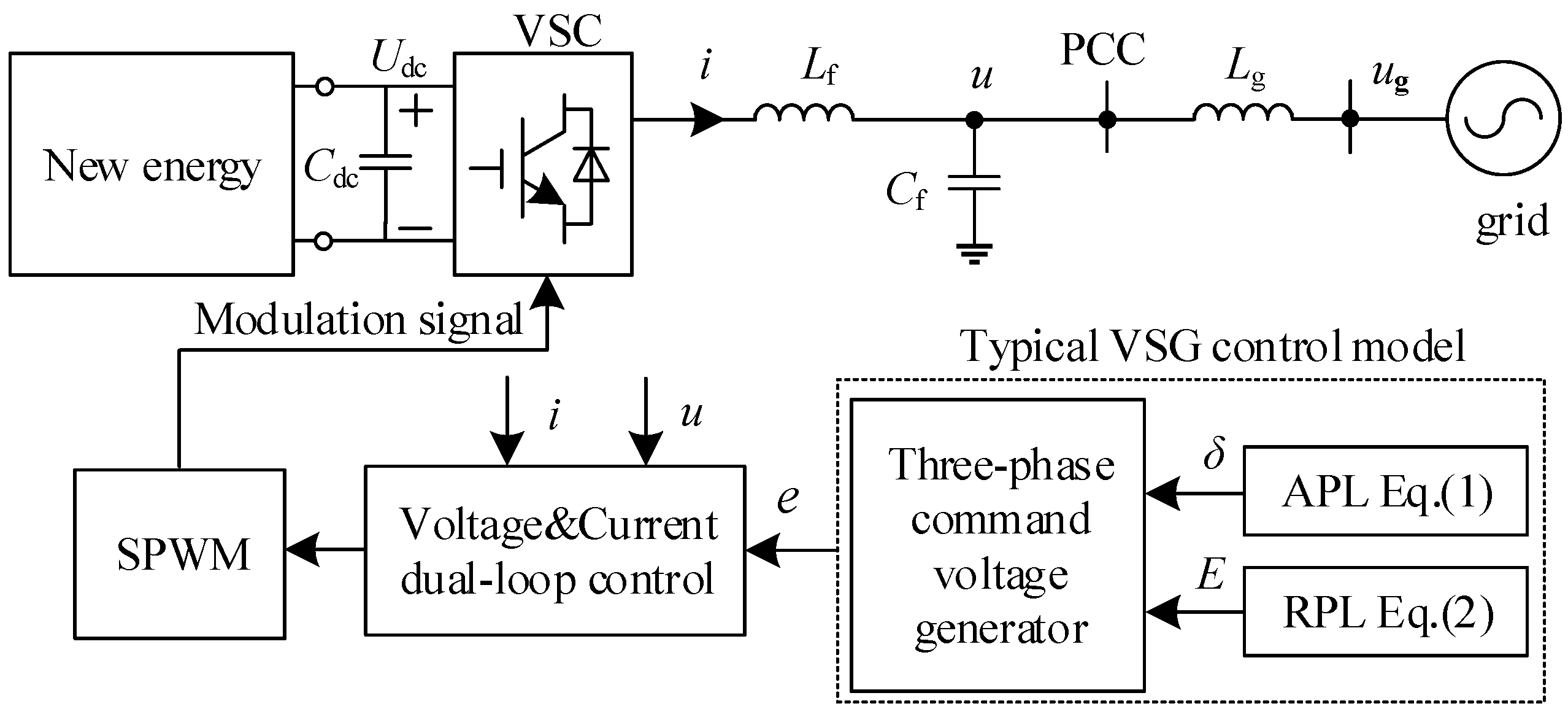
2. Typical Model of Virtual Synchronous Generator Control
3. Models and Characteristics Analysis of Different VSG Controls
3.1. Type and Evolution Characteristics Analysis of APL
- (1)
- A VSG control in which the dΔω/dt of the APL is replaced by dω/dt is proposed in [29], which is expressed as
- (2)
- A VSG control APL in the form of power loop is proposed in [30], which is expressed as
- (3)
- A VSG control APL with primary frequency regulation is proposed in [31], which is expressed as
- (4)
- The APL in the power form of the typical VSG control model is proposed in [32], and its expression is
3.2. Type and Evolution Characteristics Analysis of RPL
- (1)
- An RPL with a reactive power tracking link in VSG control is proposed in [33]. The RPL is designed to eliminate the reactive power tracking error, which is expressed as
- (2)
- On the basis of Equation (11), an RPL with a reactive voltage regulation link in VSG control is proposed in [6]. The RPL enables VSC to actively participate in grid voltage regulation when grid voltage disturbance occurs, which is expressed as
- (3)
- An RPL consisting of reactive power regulation and voltage regulation in VSG control is proposed in [34]. The RPL not only enables VSC to have reactive power regulation capability but also enables VSC to actively participate in grid voltage regulation capability when grid voltage disturbance occurs, which is expressed as
- (4)
- An RPL like an APL in VSG control is proposed in [35]. The RPL makes the relationship between the reactive power and the output voltage of VSG like the relationship between inertia and damping of APL, which is expressed as
- (5)
- Similar to Equation (13), an RPL with the difference between the actual value Uom and U0 of the PCC point voltage as the damping term in VSG control is proposed in [36], which is expressed as
- (6)
- Analogous to the excitation regulation characteristics of SG, an integral form of an RPL with the sum of reactive power and voltage regulation in VSG control is proposed in [37], which is expressed as follows:
- (6)
- An RPL with reactive voltage regulation characteristics like Equation (16) is proposed in [27], which is expressed as
4. Large-Signal Model and Transient Stability Analysis of VSG Unified Model
4.1. Large-Signal Model of VSG Unified Model
4.2. Transient Stability Analysis of VSG Unified Model
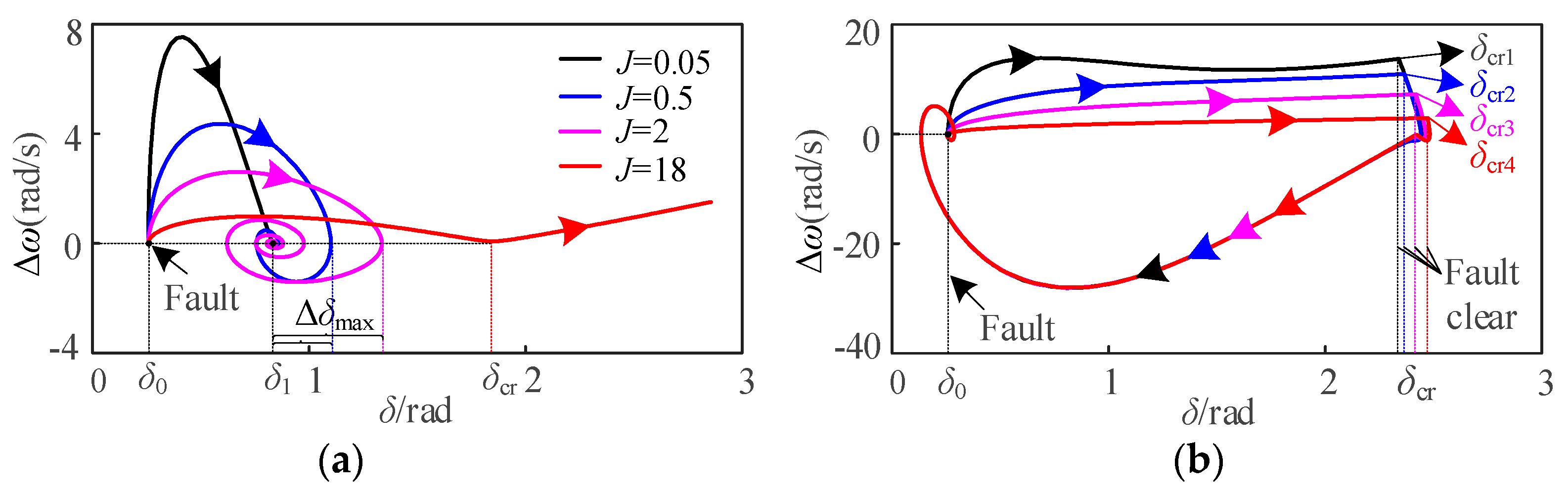
4.2.1. Influence of J Variation on Transient Stability of Unified VSG
4.2.2. Influence of D Variation on Transient Stability of Unified VSG
4.2.3. Influence of kp Variation on Transient Stability of Unified VSG
4.2.4. Influence of ki Variation on Transient Stability of Unified VSG
4.2.5. Influence of Dq Variation on Transient Stability of Unified VSG
- (1)
- For the APL of the VSG unified model, the effect of J on the transient stability of VSG is related to fault type, while the effect of D on the transient stability of VSG is independent of fault type. Specifically, the increase of J will weaken the transient stability under fault I and enhance the transient stability under fault II, and the increase of D is beneficial to enhance the transient stability.
- (2)
- For the RPL of the VSG unified model, the influence of parameters kp, ki and Dq on transient stability of VSG is independent of fault type. Specifically, the increase of kp and Dq is beneficial to enhance transient stability, but the increase of ki will deteriorate the transient stability.
5. Comparative Analysis of Transient Stability of Different VSG Control Models
5.1. Influence of Different Action Links on Transient Stability of VSG
- (1)
- Influence of primary frequency regulation on transient stability
- (2)
- Influence of primary reactive power voltage regulation on transient stability
- (3)
- Influence of reactive power error-free tracking on transient stability
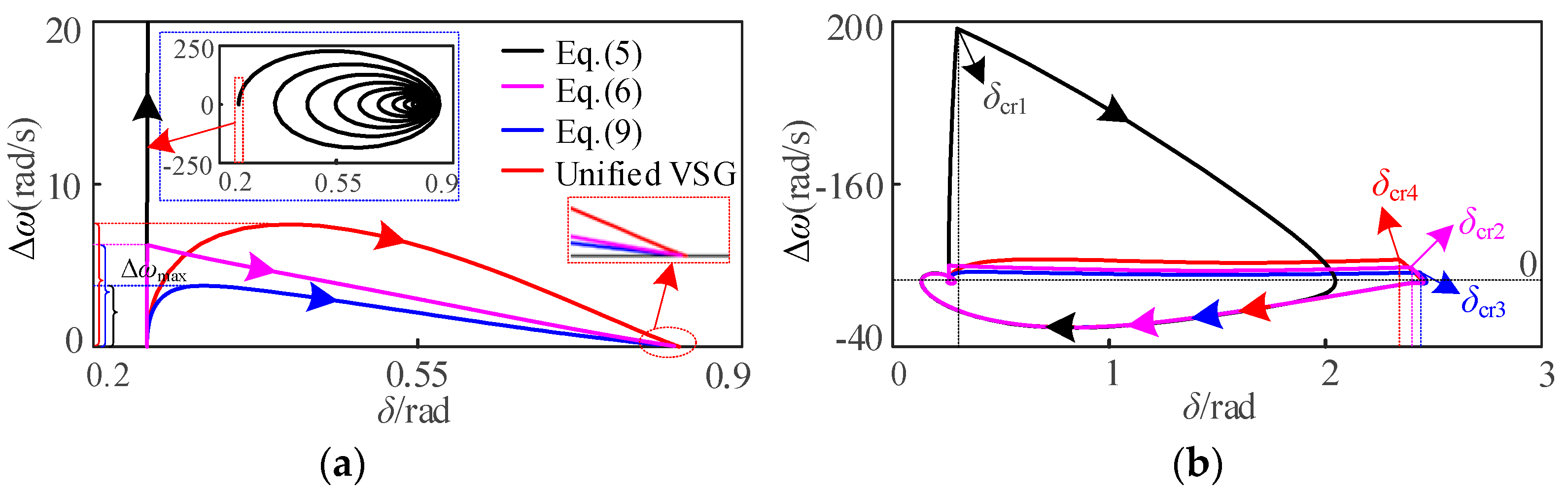
5.2. Influence of Different Types of APL on Transient Stability of VSG
- (1)
- For the APL VSG of the power type, the transient stability and fault adaptability of the APL VSG with the primary frequency regulation link are stronger than those without the primary frequency regulation link. Its influence on transient stability is independent of fault type because introducing the primary frequency modulation link is equivalent to increasing D, and the influence of D on transient stability is independent of fault type.
- (2)
- For the APL VSG of torque type, the transient stability and fault adaptability of APL VSG with the primary frequency regulation link are stronger than those without the primary frequency regulation link, and its influence on transient stability is independent of fault type.
- (3)
- The transient stability and fault adaptability of VSG with different APL types depend not only on the primary frequency regulation link but also on the APL type and are related to the fault type because different APL types lead to different equivalent inertia and damping coefficients.
5.3. Influence of Different Types of RPL on Transient Stability of VSG
- (1)
- The influence of VSG on transient stability of different types of RPLs is independent of fault type; that is to say, the influence of different types of RPLs on transient stability is consistent under two types of faults.
- (2)
- For VSG with different types of RPLs, introducing primary reactive voltage regulation is beneficial to improve transient stability, while introducing a reactive power error-free tracking link is dependent on kp and ki.
- (3)
- For VSG with the same type of RPL, its transient stability is only determined by the corresponding RPL parameters, and the transient stability of VSG can be compared only according to the influence law of RPL parameters on transient stability; for VSG with different types, its transient stability is not only determined by RPL parameters, but also by the primary reactive voltage regulation link and reactive power error-free tracking link in VSG. Under the conditions of the same action link, a transient stability comparison can be carried out according to the parameters.
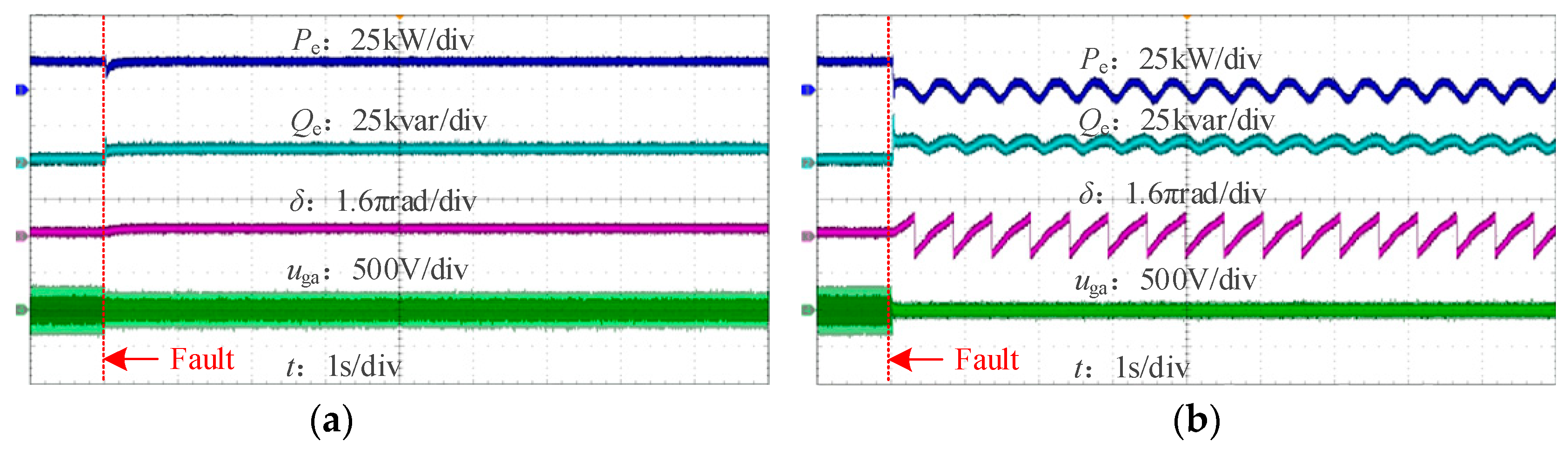
6. Experimental Verification
7. Conclusions
- (1)
- The evolution characteristics of APLs and RPLs controlled by mainstream VSGs are mainly represented by whether primary frequency modulation is introduced into APLs and reactive voltage regulation and reactive power error-free tracking are introduced into RPLs, and these three links are also the fundamental reasons for the different transient stability of different VSG control models.
- (2)
- For the unified VSG control model, all the control parameters are independent of fault type except the influence of J on transient stability.
- (3)
- For different VSG control models, the transient stability of VSG can be enhanced by introducing primary frequency regulation and primary reactive power voltage regulation, while the transient stability of VSG can be deteriorated by introducing reactive power error-free tracking. In addition, the torque-type VSG has stronger transient stability and stronger fault adaptability than the power-type VSG.
- (4)
- The method and principle for comparing the transient stability of different types of APL VSG are given. Under the same RPL conditions, for APL VSGs of the same form, the transient stability of the APL VSG with the primary frequency modulation link is stronger. For APL VSGs of different forms, it is necessary to consider the primary frequency regulation link, APL form and fault type when comparing transient stability and fault adaptability.
- (5)
- The method and principle for comparing the transient stability of different types of RPL VSG are given. Under the same RPL conditions, for different types of RPL VSGs, the transient stability of the RPL with the primary reactive voltage regulation link is stronger. For RPL VSGs of the same form, its transient stability is only determined by the RPL parameters; while for VSGs of different forms, its transient stability is not only determined by the RPL parameters but also by the primary reactive voltage regulation link and reactive power error-free tracking link in the VSG.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luo, C.; Liu, T.; Wang, X.; Ma, X. Design-Oriented Analysis of DC-Link Voltage Control for Transient Stability of Grid-Forming Inverters. IEEE Trans. Ind. Electron. 2024, 71, 3698–3707. [Google Scholar] [CrossRef]
- Tu, C.; Yang, W.; Xiao, F.; Guo, Q.; He, X. Transient power angle stability control method of VSG considering fault current limitation. Electr. Power Autom. Equip. 2023, 43, 55–62. [Google Scholar]
- Ge, P.; Tu, C.; Xiao, F.; Guo, Q.; Gao, J. Design-Oriented Analysis and Transient Stability Enhancement Control for a Virtual Synchronous Generator. IEEE Trans. Ind. Electron. 2023, 70, 2675–2684. [Google Scholar] [CrossRef]
- Hu, X.; Li, Z.; Pan, C.; Li, H.; Liang, Y. An Adaptive Virtual-Impedance-Based Current-Limiting Method with the Functionality of Transient Stability Enhancement for Grid-Forming Converter. Electronics 2024, 13, 2750. [Google Scholar] [CrossRef]
- Lou, G.; Yang, Q.; Gu, W.; Zhang, J. An Improved Control Strategy of Virtual Synchronous Generator Under Symmetrical Grid Voltage Sag. Int. J. Electr. Power Energy Syst. 2020, 121, 106093. [Google Scholar] [CrossRef]
- Zhao, F.; Shuai, Z.; Huang, W.; Shen, Y.; Shen, Z.J.; Shen, C. A Unified Model of Voltage-Controlled Inverter for Transient Angle Stability Analysis. IEEE Trans. Power Deliv. 2022, 37, 2275–2288. [Google Scholar] [CrossRef]
- Yang, W.; Tu, C.; Xiao, F.; Guo, Q. A combined regulation method of transient power angle stability control and fault current suppression for VSG. Int. J. Electr. Power Energy Syst. 2024, 156, 109702. [Google Scholar] [CrossRef]
- Shuai, Z.K.; Huang, W.; Shen, C.; Ge, J.; Shen, Z.J. Characteristics and restraining method of fast transient inrush fault currents in synchronverters. IEEE Trans. Ind. Electron. 2017, 64, 7487–7497. [Google Scholar] [CrossRef]
- Li, Z.; Chan, K.W.; Hu, J.; Or, S.W. An adaptive fault ride-through scheme for grid-forming inverters under asymmetrical grid faults. IEEE Trans. Ind. Electron. 2022, 69, 12912–12923. [Google Scholar] [CrossRef]
- Koiwa, K.; Inoo, K.; Zanma, T.; Liu, K.-Z. Virtual voltage control of VSG for overcurrent suppression under symmetrical and asymmetrical voltage dips. IEEE Trans. Ind. Electron. 2022, 69, 11177–11186. [Google Scholar] [CrossRef]
- Li, M.; Huang, W.; Tai, N.; Yang, L.; Duan, D.; Ma, Z. A Dual-Adaptivity Inertia Control Strategy for Virtual Synchronous Generator. IEEE Trans. Power Syst. 2020, 35, 594–604. [Google Scholar] [CrossRef]
- Guo, J.; Chen, Y.D.; Wang, L.; Wu, W.H.; Wang, X.Y. Impedance analysis and stabilization of virtual synchronous generators with different DC-link voltage controllers under weak grid. IEEE Trans. Power Electron. 2021, 36, 11397–11408. [Google Scholar] [CrossRef]
- Sun, K.; Yao, W.; Wen, J.; Jiang, L. A Two-Stage Simultaneous Control Scheme for the Transient Angle Stability of VSG Considering Current Limitation and Voltage Support. IEEE Trans. Power Syst. 2022, 37, 2137–2150. [Google Scholar] [CrossRef]
- Xiong, X.; Wu, C.; Blaabjerg, F. An Improved Synchronization Stability Method of Virtual Synchronous Generators Based on Frequency Feedforward on Reactive Power Control Loop. IEEE Trans. Power Electron. 2021, 36, 9136–9148. [Google Scholar] [CrossRef]
- Pan, D.; Wang, X.; Liu, F.; Shi, R. Transient Stability of Voltage-Source Converters with Grid-Forming Control: A Design-Oriented Study. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1019–1033. [Google Scholar] [CrossRef]
- Huang, L.; Xin, H.H.; Li, Z.Y.; Ju, P.; Yuan, H. Grid-Synchronization stability analysis and loop shaping for PLL-Based power converters with different reactive power control. IEEE Trans. Smart Grid 2020, 11, 501–516. [Google Scholar] [CrossRef]
- Shuai, Z.; Shen, C.; Liu, X.; Li, Z.; Shen, Z. Transient Angle Stability of Virtual Synchronous Generators Using Lyapunov’s Direct Method. IEEE Trans. Smart Grid 2019, 10, 4648–4661. [Google Scholar] [CrossRef]
- Pan, D.; Wang, X.; Liu, F.; Shi, R. Transient stability impact of reactive power control on grid-connected converters. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 4311–4316. [Google Scholar]
- Chen, M.; Zhou, D.; Blaabjerg, F. Enhanced Transient Angle Stability Control of Grid-Forming Converter Based on Virtual Synchronous Generator. IEEE Trans. Ind. Electron. 2022, 69, 9133–9144. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Chen, Y.C.; Liu, K.X.; Han, Y. Influence of control parameters on synchronization stability of virtual synchronous generator. Arch. Electr. Eng. 2022, 71, 811–828. [Google Scholar]
- Luo, S.; Han, H.; Chen, S.; Shi, G.; Ou, J.; Luo, Z. A Mode Switching Method for Transient Stability Enhancement of VSG. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–5. [Google Scholar]
- Oureilidis, K.O.; Demoulias, C.S. A fault clearing method in converter-dominated microgrids with conventional protection means. IEEE Trans. Power Electron. 2016, 31, 4628–4640. [Google Scholar] [CrossRef]
- Kuang, Y.; Xu, Q. A Current-Limiting Scheme for Voltage-Controlled Inverter Using Instantaneous Current to Generate Virtual Impedance. IEEE J. Emerg. Sel. Top. Circuits Syst. 2023, 13, 524–535. [Google Scholar]
- Qoria, T.; Gruson, F.; Colas, F.; Kestelyn, X.; Guillaud, X. Current limiting algorithms and transient stability analysis of grid-forming VSCs. Electr. Power Syst. Res. 2020, 189, 106726. [Google Scholar] [CrossRef]
- Han, X.; Deng, C.P.; Dai, L.Y.; Zheng, M.Y.; Ling, Z.B. VSG Transient Power Angle Stabilization Strategy Considering Current Limiting. In Proceedings of the 2022 Asian Conference on Frontiers of Power and Energy (ACFPE), Chengdu, China, 21–23 October 2022; pp. 472–477. [Google Scholar]
- Luo, C.; Chen, Y.D.; Xu, Y.C.; Wang, Z.L.; Liao, S.H.; Xie, Z.W. Two-Stage Transient Control for VSG Considering Fault Current Limitation and Transient Angle Stability. IEEE Trans. Ind. Electron. 2024, 71, 7169–7179. [Google Scholar] [CrossRef]
- Zhang, G.; Zhan, L.; Wang, J.; Ke, X.; Ren, C.; Nian, H. Effect of Different Reactive Power Control Structures of Voltage Source Converters on Transient Stability. In Proceedings of the 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 12–14 May 2023; pp. 472–477. [Google Scholar]
- Zhao, F.; Shuai, Z.; Shen, C.; Cheng, H.; Shen, Y. Comparison of Transient Angle Stability Between Different Virtual Synchronous Generators. In Proceedings of the 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2), Changsha, China, 8–10 November 2019; pp. 2529–2533. [Google Scholar]
- Wu, W.H.; Zhou, L.M.; Chen, Y.D.; Luo, A.; Zhou, X.P.; He, Z.X.; Yang, L.; Liu, J.M. Stability Comparison and Analysis Between the Virtual Synchronous Generator and the Traditional Grid-connected Inverter in the View of Sequence Impedance. Proc. CSEE 2019, 39, 1411–1420. (In Chinese) [Google Scholar]
- Liu, J.; Miura, Y.; Ise, T. Fixed-Parameter Damping Methods of Virtual Synchronous Generator Control Using State Feedback. IEEE Access 2019, 7, 99177–99190. [Google Scholar] [CrossRef]
- Meng, X.; Liu, J.; Liu, Z. A Generalized Droop Control for Grid-Supporting Inverter Based on Comparison Between Traditional Droop Control and Virtual Synchronous Generator Control. IEEE Trans. Power Electron. 2019, 34, 5416–5438. [Google Scholar] [CrossRef]
- Tu, C.M.; Xie, W.J.; Xiao, F.; Lan, Z. Influence Analysis of Control Parameters of Parallel System with Multiple Virtual Synchronous Generators on Stability. Autom. Electr. Power Syst. 2020, 44, 77–86. (In Chinese) [Google Scholar]
- Meng, X.; Liu, Z.; Liu, J.; Wang, S.K.; Liu, B.X.; An, R.H. Comparison between inverters based on virtual synchronous generator and droop control. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 4077–4084. [Google Scholar]
- Lv, Z.P.; Sheng, W.X.; Zhong, Q.C.; Liu, H.T.; Zheng, Z.; Yang, L.; Lan, L. Virtual Synchronous Generator and Its Applications in Micro-grid. Proc. CSEE 2014, 34, 2591–2603. (In Chinese) [Google Scholar]
- Wen, T.; Zou, X.; Zhu, D.; Guo, X.; Li, P.; Kang, Y. Comprehensive perspective on virtual inductor for improved power decoupling of virtual synchronous generator control. IET Renew. Power Gener. 2020, 14, 485–494. [Google Scholar] [CrossRef]
- Cheema, K.M. A comprehensive review of virtual synchronous generator. Int. J. Electr. Power Energy Syst. 2020, 120, 106006. [Google Scholar] [CrossRef]
- Tu, C.M.; Lan, Z.; Xiao, F.; Shuai, Z.K.; Meng, Y. Study on Cascaded H-bridge Photovoltaic Power Systems with Synchronous Generator Characteristics. Proc. CSEE 2017, 37, 433–443. (In Chinese) [Google Scholar]

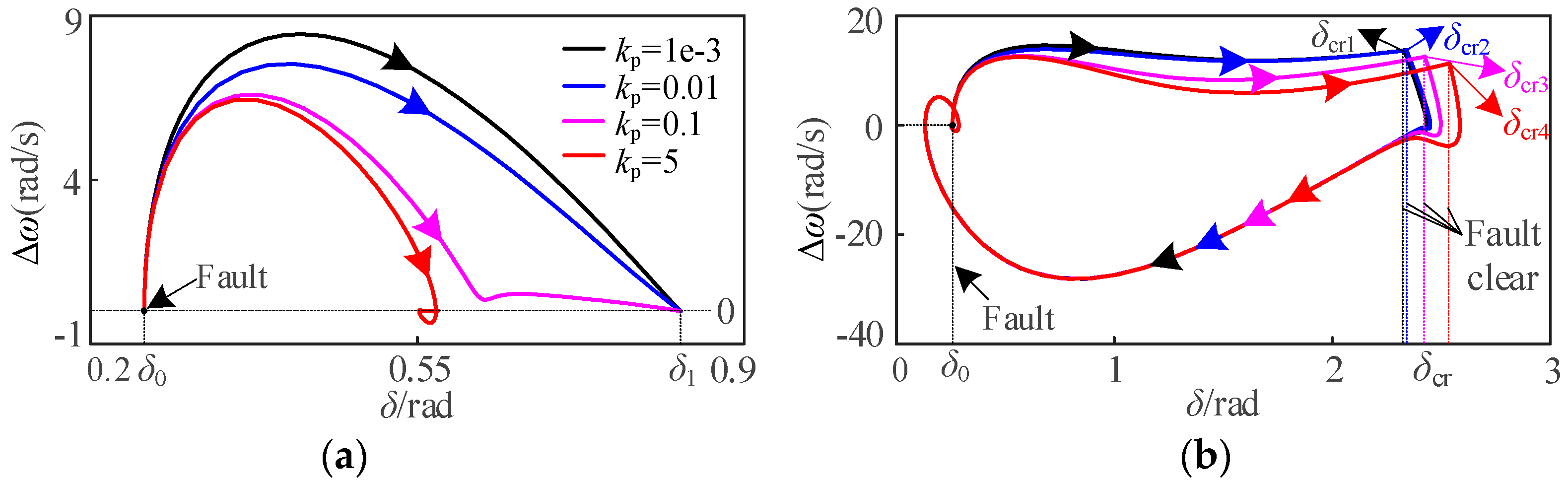
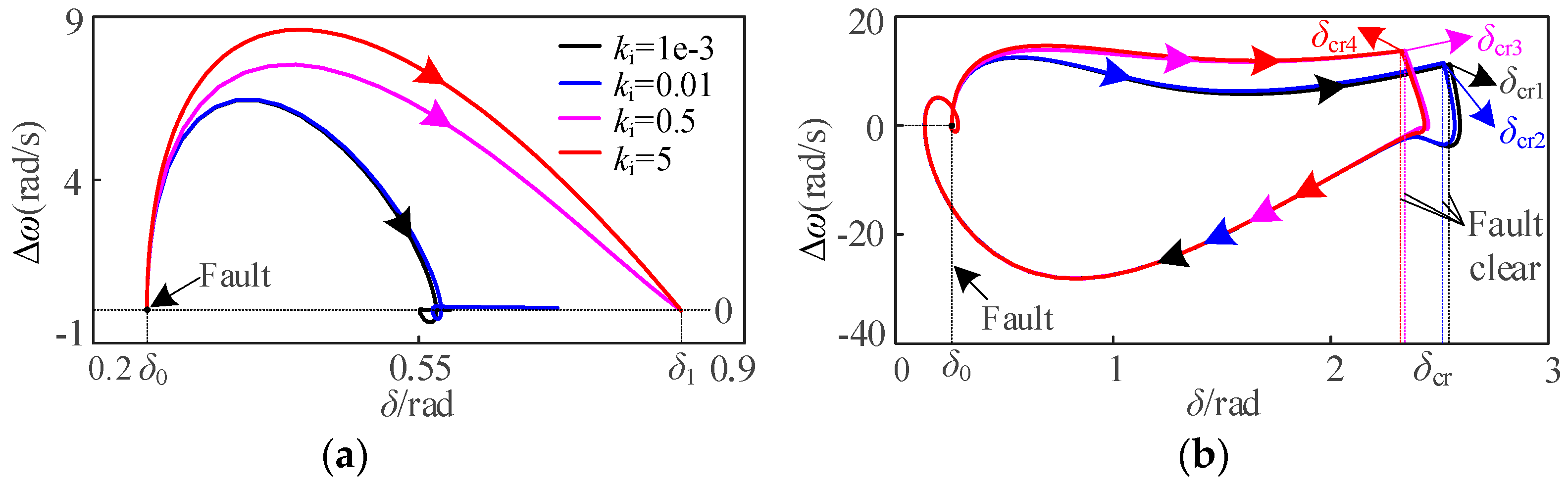




| APL Type | J | D |
|---|---|---|
| Equation (1) | Jeq | Deq |
| Equation (4) | Jeq | Deq |
| Equation (5) | Jeqω0 | Deqω0 |
| Equation (6) | Jeqω0 | Deqω0-kf |
| Equation (9) | Jeqω0 | Deq-kf/ω0 |
| Equation (10) | Jeq | Deq |
| RPL Type | kp | ki | Dq | Jq | K | kv | kq |
|---|---|---|---|---|---|---|---|
| Equation (2) | kq | 0 | 0 | - | - | - | kp |
| Equation (11) | kp | ki | 0 | - | - | - | - |
| Equation (12) | kp | ki | Dq | - | - | - | - |
| Equation (13) | kq | 0 | - | - | - | kpDq | kp |
| Equation (14) | 0 | 1/Jq | Dq | 1/ki | - | - | - |
| Equation (15) | 0 | 1/Jq | Dq | 1/ki | - | - | - |
| Equation (16) | 0 | 1/K | kv | - | 1/ki | Dq | - |
| Equation (17) | 0 | 1/K | kv | - | 1/ki | Dq | - |
| Parameter Changes | Transient Stability under Fault I | Transient Stability under Fault II | Whether It Depends on the Fault Type Types |
|---|---|---|---|
| J↑ | ↓ | ↑ | yes |
| D↑ | ↑ | ↑ | no |
| kp↑ | ↑ | ↑ | no |
| ki↑ | ↓ | ↓ | no |
| Dq↑ | ↑ | ↑ | no |
| APL Type | Characteristics | Transient Stability under Faults I and II | Fault Adaptability |
|---|---|---|---|
| Equation (5) | Power type, without primary frequency modulation | weak | weak |
| Unified VSG | Torque type, without primary frequency modulation | strong | strong |
| Equation (6) | Power type, with primary frequency modulation | stronger | stronger |
| Equation (9) | Torque type, with primary frequency modulation | stronger | stronger |
| RPL Type | Characteristics | Transient Stability under Faults I and II | Fault Adaptability |
|---|---|---|---|
| Equation (2) | ki = 0, without primary reactive power voltage regulation and reactive power error-free tracking | stronger | stronger |
| Equation (13) | |||
| Equation (11) | only with reactive power error-free tracking | weak | weak |
| Unified VSG | with primary reactive power voltage regulation and reactive power error-free tracking | strong | strong |
| Equation (14) | kp = 0, with primary reactive power voltage regulation and reactive power error-free tracking | strong | strong |
| Equation (15) | |||
| Equation (16) | |||
| Equation (17) |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Pm | 20 kW | ω0 | 314 rad/s |
| Qm | 5 kvar | Ts | 1 × 10−5 s |
| Udc | 800 V | J | 0.05 kg/m2 |
| UgN | 311 V | D | 5 N.m.s/rad |
| U0 | 311 V | kq | 0.001 V/kvar |
| Lf | 3 mH | kp | 0.001 |
| Cf | 40 μF | ki | 0.05 |
| Lg | 11.5 mH | Dq | 160 kvar/V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Wei, C.; Zhao, R.; Lu, J.; Chen, Y.; Yang, W. A Unified Model of a Virtual Synchronous Generator for Transient Stability Analysis. Electronics 2024, 13, 3560. https://doi.org/10.3390/electronics13173560
Li M, Wei C, Zhao R, Lu J, Chen Y, Yang W. A Unified Model of a Virtual Synchronous Generator for Transient Stability Analysis. Electronics. 2024; 13(17):3560. https://doi.org/10.3390/electronics13173560
Chicago/Turabian StyleLi, Ming, Chengzhi Wei, Ruifeng Zhao, Jiangang Lu, Yizhe Chen, and Wanli Yang. 2024. "A Unified Model of a Virtual Synchronous Generator for Transient Stability Analysis" Electronics 13, no. 17: 3560. https://doi.org/10.3390/electronics13173560
APA StyleLi, M., Wei, C., Zhao, R., Lu, J., Chen, Y., & Yang, W. (2024). A Unified Model of a Virtual Synchronous Generator for Transient Stability Analysis. Electronics, 13(17), 3560. https://doi.org/10.3390/electronics13173560






