A Unified-Mode Analysis Method for Symmetric Networks and Its Application to Balun Design
Abstract
1. Introduction
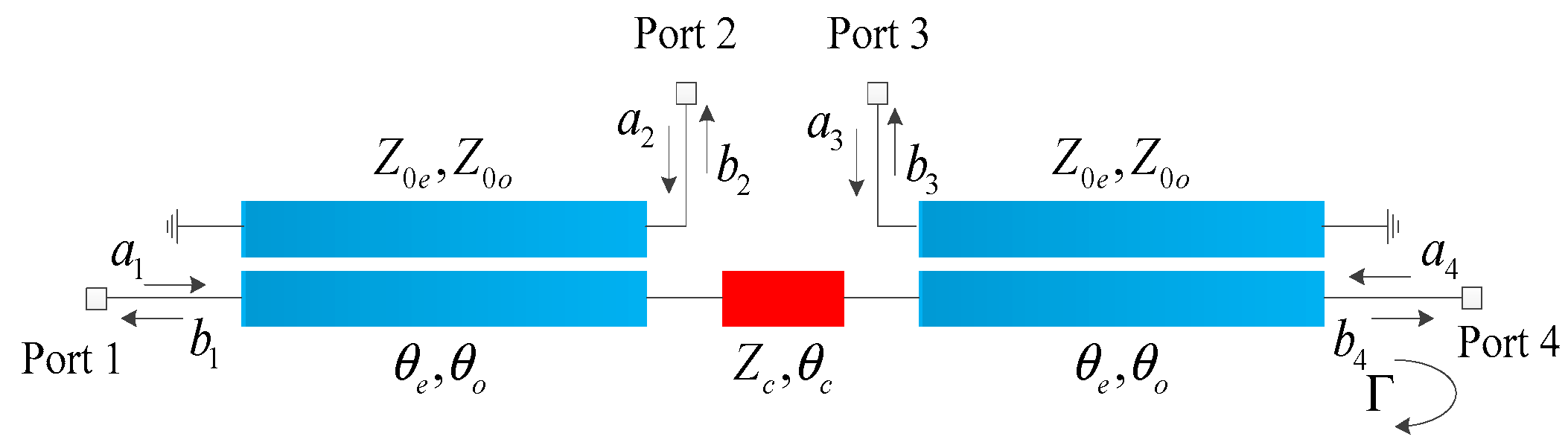
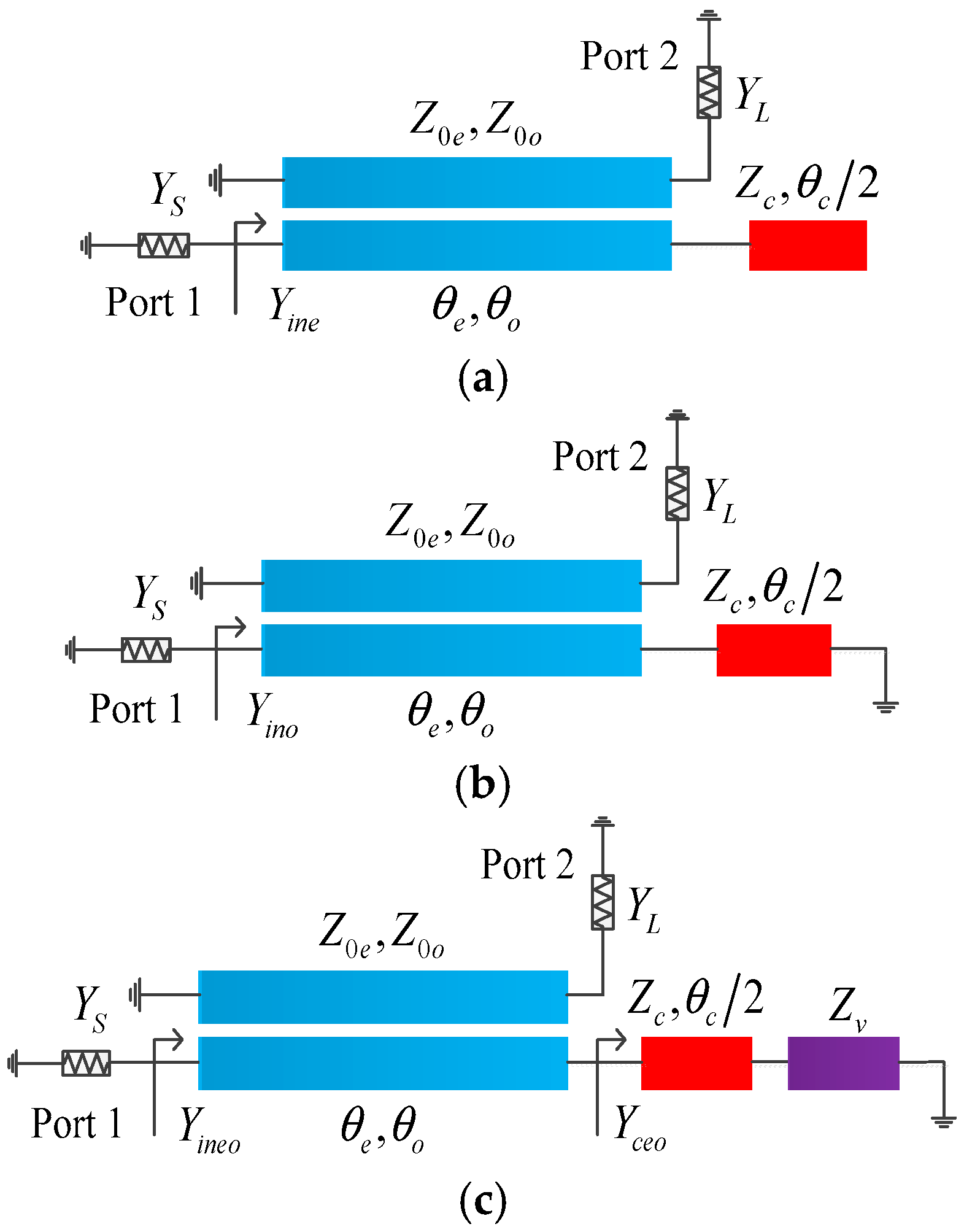
2. Unified Mode Analysis
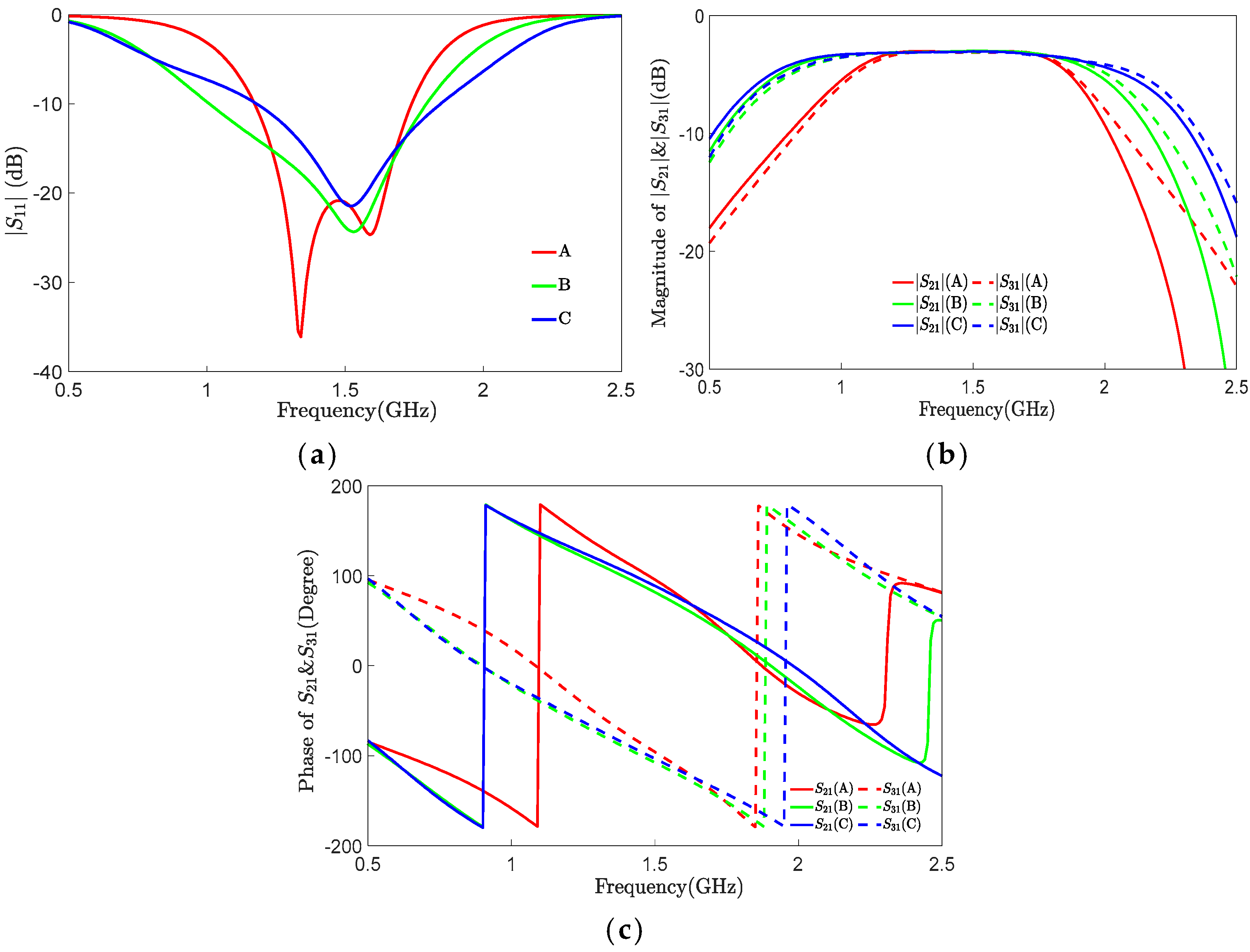
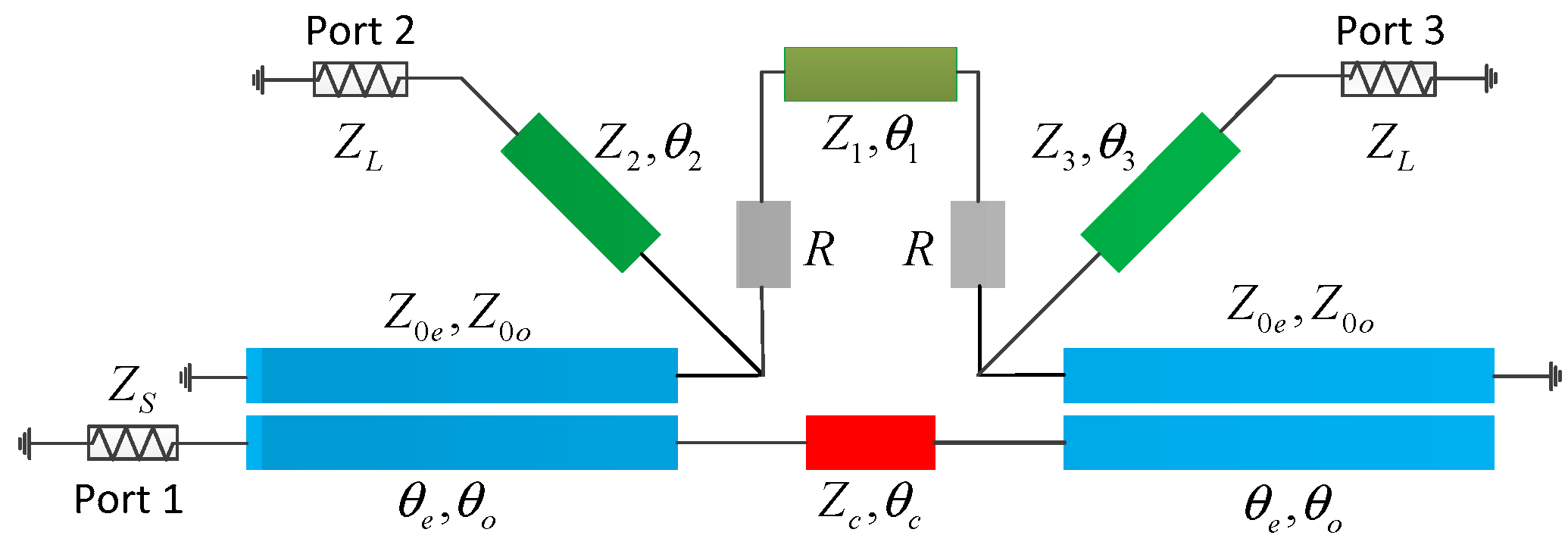
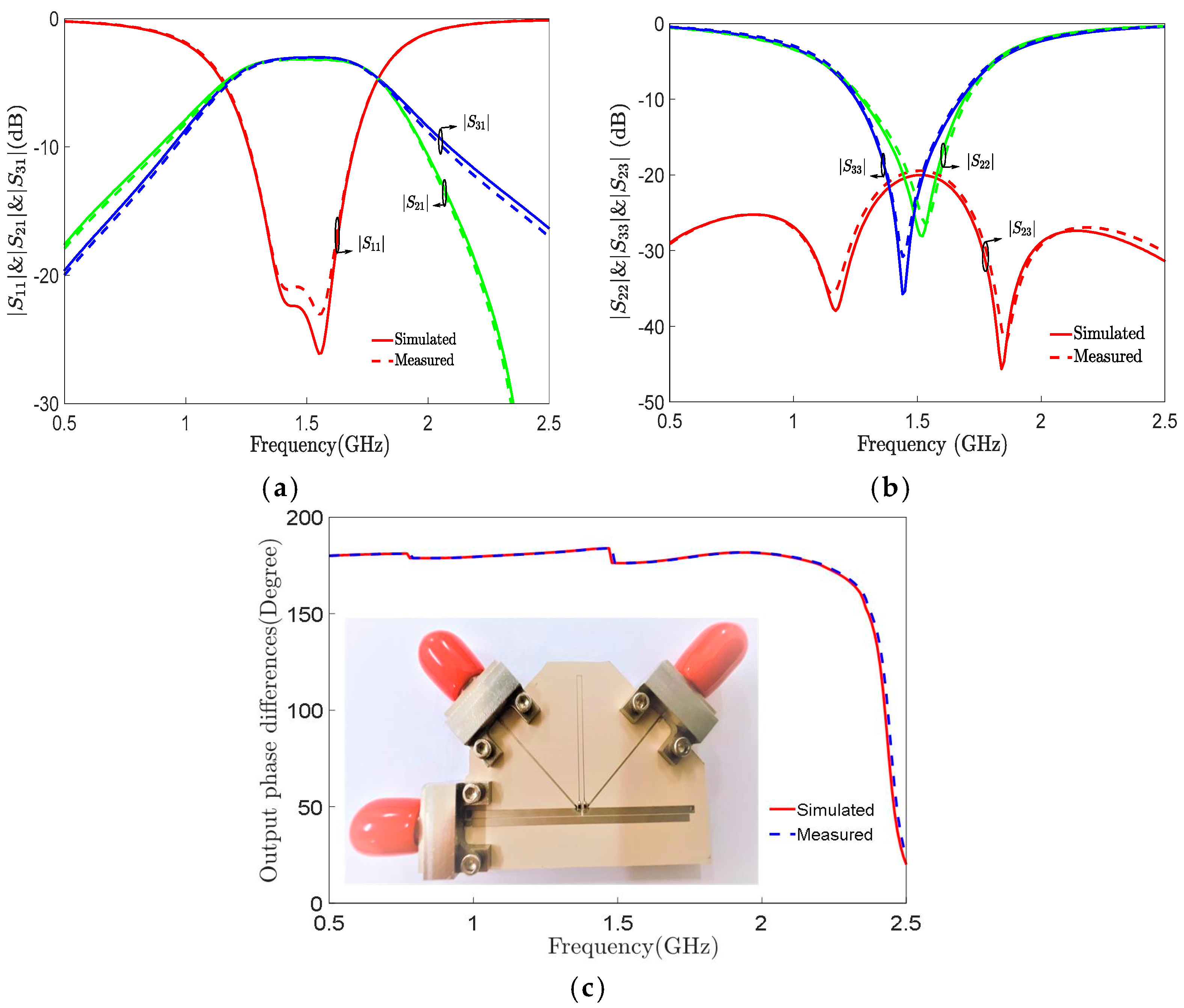
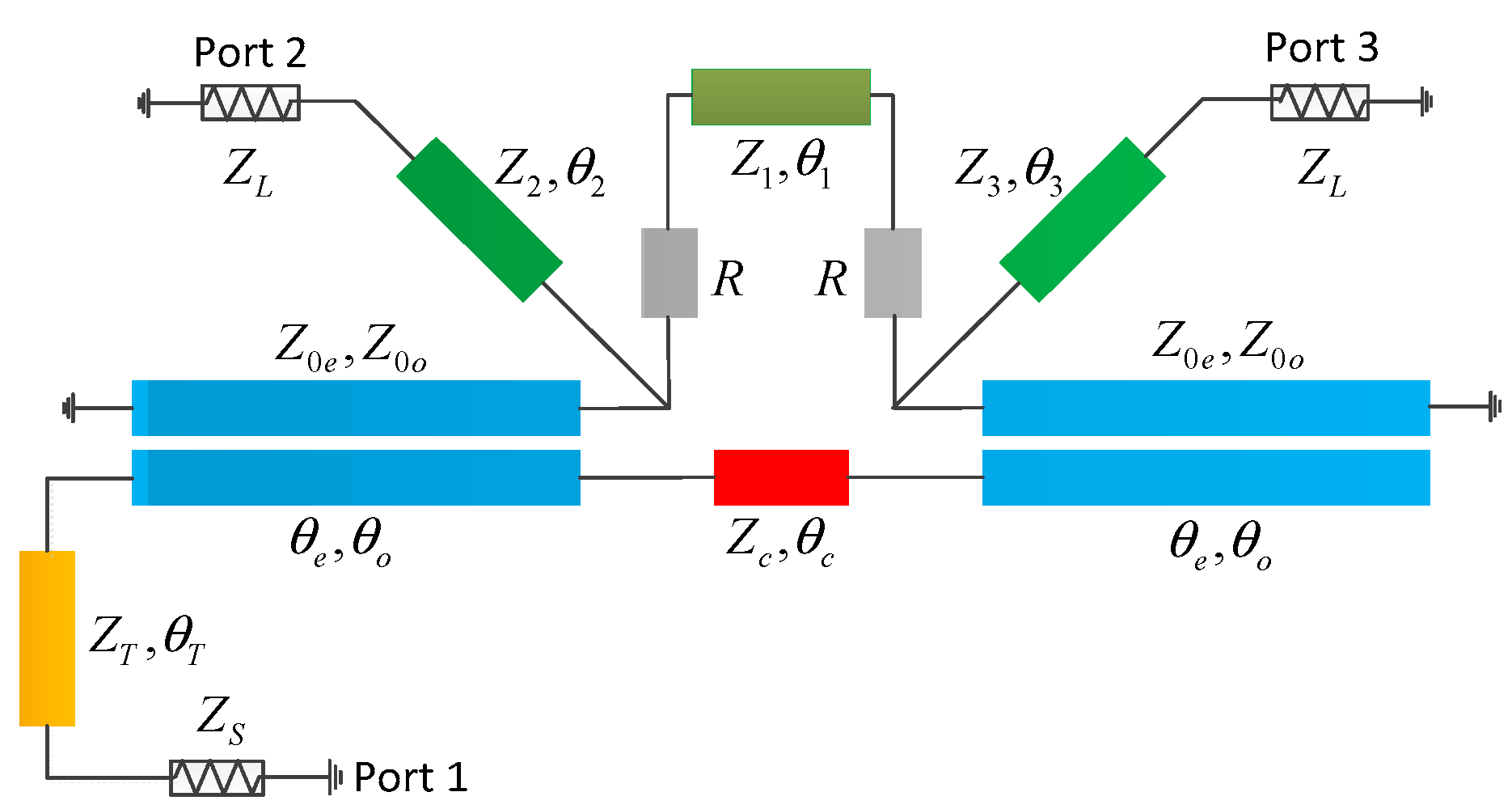
3. Marchand Balun with Matching and Isolation
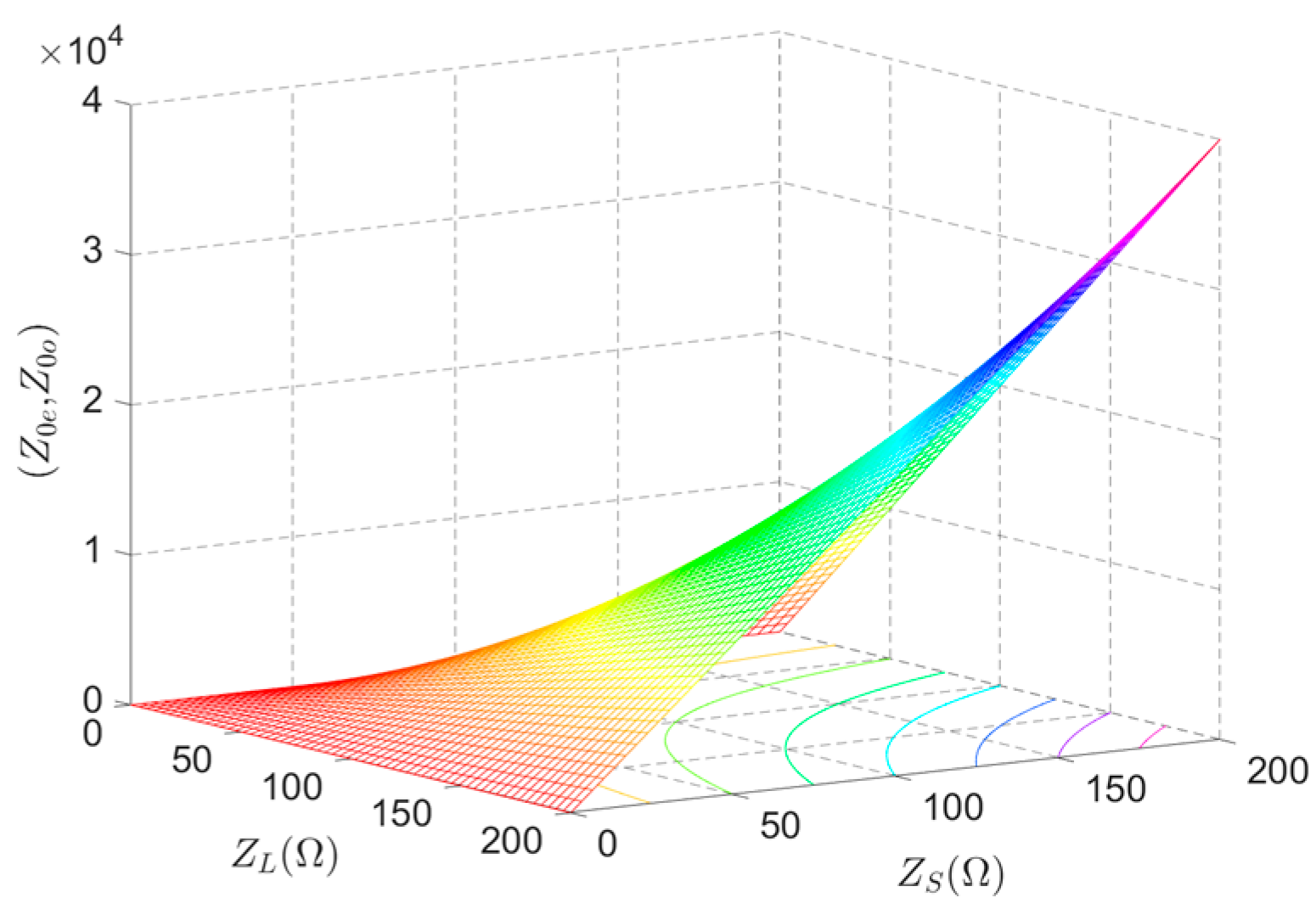
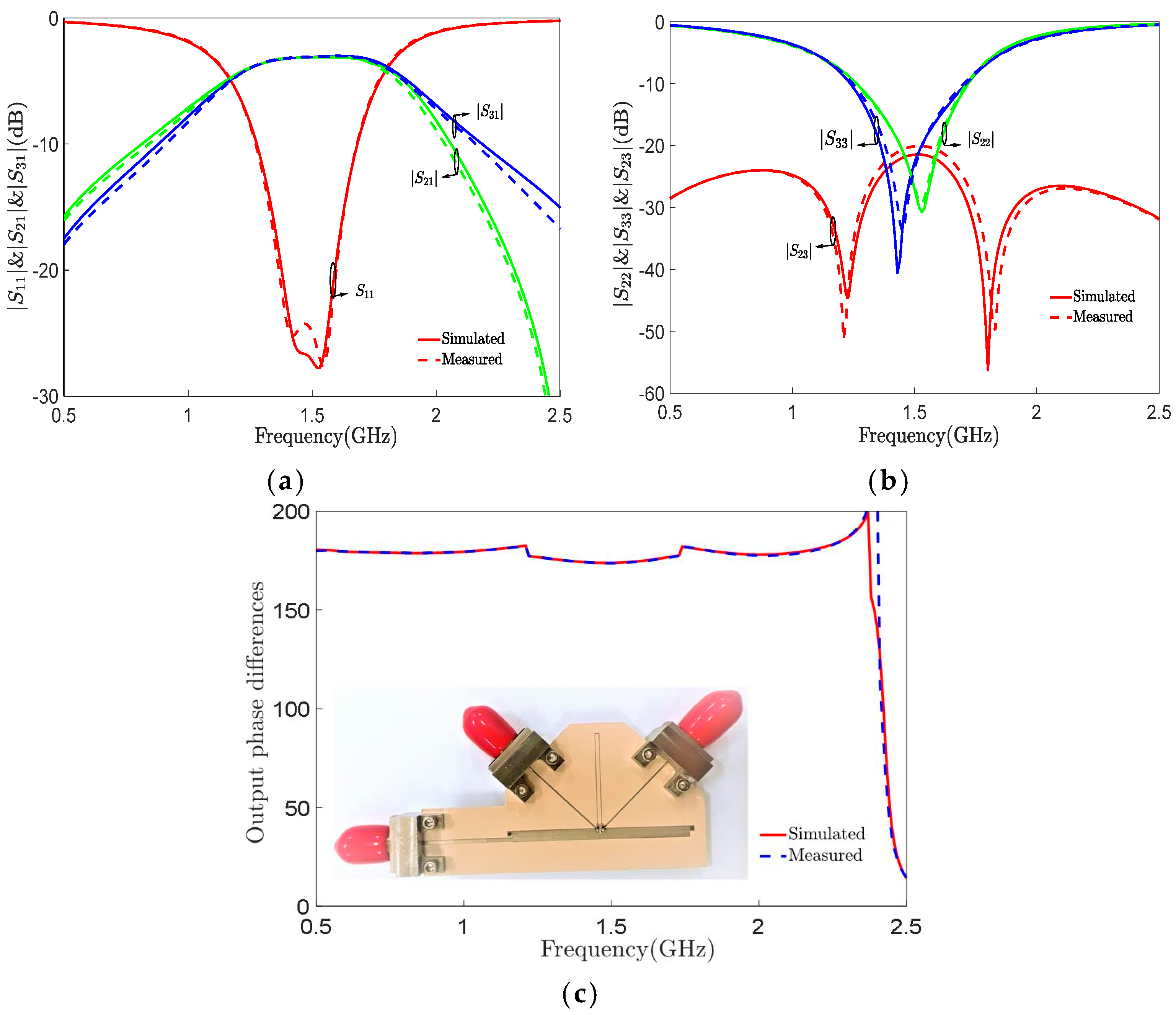
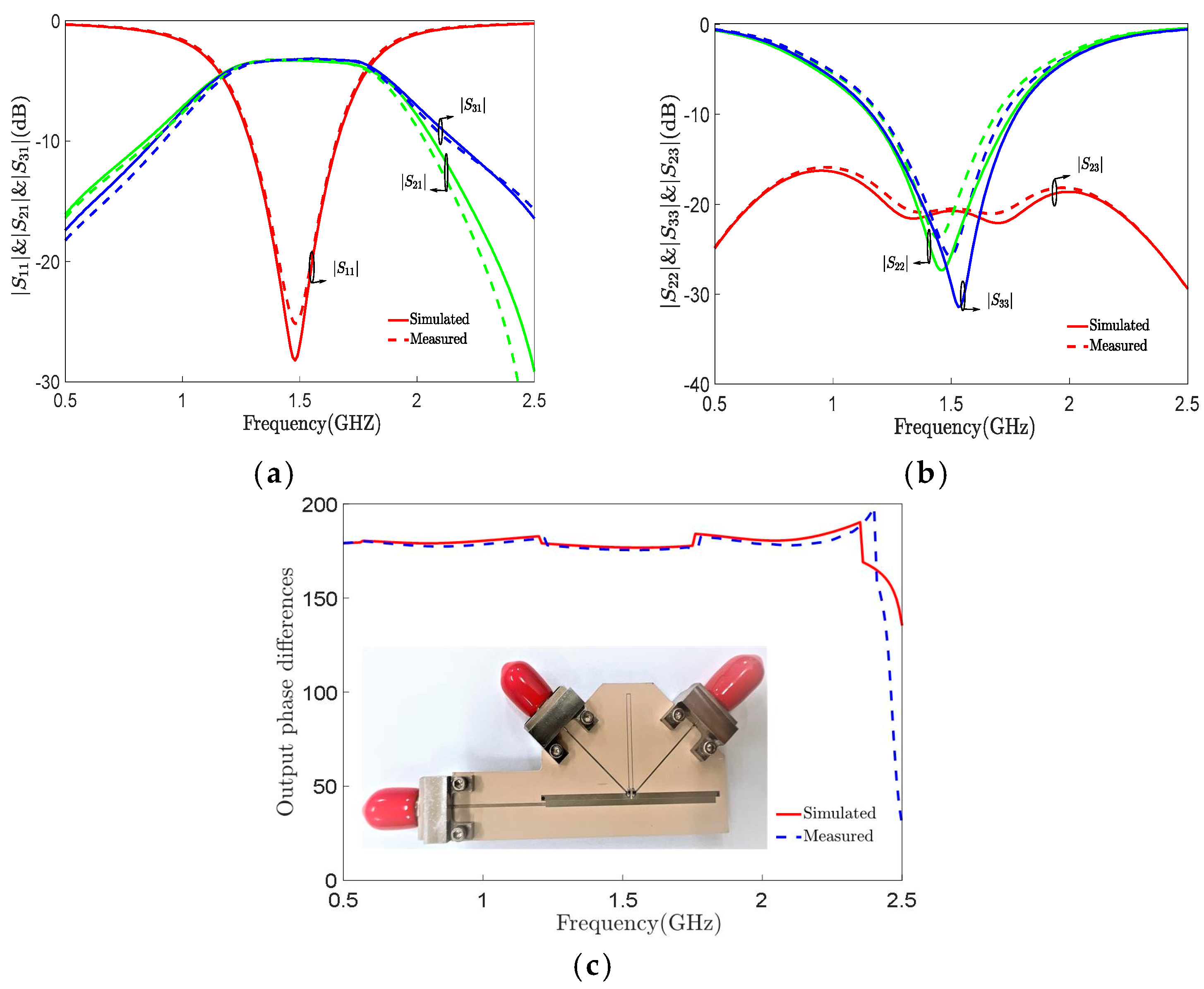
4. Flexible Impedance Transformation Design
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, X.; Li, Y.C.; Xue, Q.; Wu, D.-S.; Wong, S.-W. Dual-mode filtering baluns based on hybrid cavity-microstrip structures. IEEE Trans. Microw. Theory Tech. 2020, 68, 1637–1645. [Google Scholar] [CrossRef]
- Shin, D.; Lee, K.; Kwon, K. A Blocker-tolerant receiver front end employing dual-band n-path balun-lna for 5g new radio cellular applications. IEEE Trans. Microw. Theory Tech. 2022, 70, 1715–1724. [Google Scholar] [CrossRef]
- Martelius, M.; Stadius, K.; Lemberg, J.; Roverato, E.; Nieminen, T.; Antonov, Y.; Anttila, L.; Valkama, M.; Kosunen, M.; Ryynanen, J. A Class-D Tri-Phasing CMOS power amplifier with an extended marchand-balun power combiner. IEEE Trans. Microw. Theory Tech. 2020, 68, 1022–1034. [Google Scholar] [CrossRef]
- Wu, Y.-C.; Hwang, Y.-J.; Chiong, C.-C.; Lu, B.-Z.; Wang, H. An innovative joint-injection mixer with broadband if and rf for advanced heterodyne receivers of millimeter-wave astronomy. IEEE Trans. Microw. Theory Tech. 2020, 68, 5408–5422. [Google Scholar] [CrossRef]
- Chakraborty, S.; Milner, L.-E.; Zhu, X.; Hall, L.-T.; Sevimli, O.; Heimlich, M.-C. A K-band frequency doubler with 35-dB fundamental rejection based on novel transformer balun in 0.13-µm SiGe technology. IEEE Electron Device Lett. 2016, 37, 1375–1378. [Google Scholar] [CrossRef]
- An, W.; Hong, L.; Luo, Y.; Ma, K.; Ma, J.; Huang, X. A Wideband dual-function solar cell dipole antenna for both energy harvesting and wireless communications. IEEE Trans. Antennas Propag. 2021, 69, 544–549. [Google Scholar] [CrossRef]
- Yao, W.; Gao, H.; Tian, Y. Compact wideband and variable impedance transformation ratio balun for folded dipole. IEEE Trans. Antennas Propag. 2022, 70, 5935–5940. [Google Scholar] [CrossRef]
- Zhang, T.; Li, L.; Zhu, Z.; Cui, T.J. A broadband planar balun using aperture-coupled microstrip-to-siw transition. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 532–534. [Google Scholar] [CrossRef]
- Yang, G.; Wang, Z.; Li, Z.; Li, Q.; Liu, F. Balance-compensated asymmetric marchand baluns on silicon for MMICs. IEEE Microw. Wirel. Compon. Lett. 2014, 24, 391–393. [Google Scholar] [CrossRef]
- Zimmer, T.; Fregonese, S. Graphene transistor-based active balun architectures. IEEE Trans. Electron Devices 2015, 62, 3079–3083. [Google Scholar] [CrossRef]
- Kuylenstierna, D.; Linner, P. Design of broad-band lumped-element baluns with inherent impedance transformation. IEEE Trans. Microw. Theory Tech. 2004, 52, 2739–2745. [Google Scholar] [CrossRef]
- Frank, M.; Thorsell, M.; Enoksson, P. Design equations for lumped element balun with inherent complex impedance transformation. IEEE Trans. Microw. Theory Tech. 2017, 65, 5162–5170. [Google Scholar] [CrossRef]
- Ye, Y.; Li, L.-Y.; Gu, J.-Z.; Sun, X.-W. A bandwidth improved broadband compact lumped-element balun with tail inductor. IEEE Microw. Wirel. Compon. Lett. 2013, 23, 415–417. [Google Scholar] [CrossRef]
- Marchand, N. Transmission line conversion transformers. Electronics 1944, 17, 142–145. [Google Scholar]
- Ang, K.S.; Robertson, I. Analysis and design of impedance-transforming planar Marchand baluns. IEEE Trans. Microw. Theory Tech. 2001, 49, 402–406. [Google Scholar] [CrossRef]
- Lin, C.-H.; Wu, C.-H.; Zhou, G.-T.; Ma, T.-G. General compensation method for a marchand balun with an arbitrary connecting segment between the balance ports. IEEE Trans. Microw. Theory Tech. 2013, 61, 2821–2830. [Google Scholar] [CrossRef]
- Wang, Y.; Lee, J.-C. A miniaturized marchand balun model with short-end and capacitive feeding. IEEE Access 2018, 6, 26653–26659. [Google Scholar] [CrossRef]
- Barik, R.K.; Kumar, K.V.P.; Karthikeyan, S.S. Design of a quad-band branch line balun using extended pi-shaped coupled lines. IEEE Microw. Wirel. Compon. Lett. 2016, 26, 771–773. [Google Scholar] [CrossRef]
- Barik, R.-K.; Kumar, K.-V.-P.; Karthikeyan, S.-S. A new design procedure for single-layer and two-layer three-line baluns. IEEE Microw. Wirel. Compon. Lett. 1998, 46, 2514–2519. [Google Scholar]
- Michaelsen, R.; Johansen, T.; Tamborg, K.; Zhurbenko, V. A Modified marchand balun configuration with tunable phase balance. IEEE Microw. Wirel. Compon. Lett. 2013, 23, 66–68. [Google Scholar] [CrossRef]
- Chen, A.C.; Pham, A.-V.; Leoni, R. A novel broadband even-mode matching network for marchand baluns. IEEE Trans. Microw. Theory Tech. 2009, 57, 2973–2980. [Google Scholar] [CrossRef]
- Jung, K.; Andrews, M.F.; Hayden, L.A. Rat-race hybrid ring realized in two-layer printed process. IEEE Microw. Wirel. Compon. Lett. 2016, 26, 768–770. [Google Scholar] [CrossRef]
- Yan, J.-M.; Zhou, H.-Y.; Cao, L.-Z. A novel filtering balun and improvement of its isolation performance. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 1056–1058. [Google Scholar] [CrossRef]
- Ang, K.-S.; Leong, Y.-C. Converting baluns into broad-band impedance-transforming 180º hybrids. IEEE Trans. Microw. Theory Techn. 2002, 50, 1990–1995. [Google Scholar]
- Rao, S.G.; Frounchi, M.; Cressler, J.D. Triaxial balun with inherent harmonic reflection for millimeter-wave frequency doublers. IEEE Trans. Microw. Theory Tech. 2021, 69, 2822–2831. [Google Scholar] [CrossRef]
- Tseng, C.-H.; Hsiao, Y.-C. A new broadband marchand balun using slot-coupled microstrip lines. IEEE Microw. Wirel. Compon. Lett. 2010, 20, 157–159. [Google Scholar] [CrossRef]
- Jia, M.; Zhang, J.; Dong, Y. A compact and broadband balun based on multilayer SIW. IEEE Microw. Wirel. Compon. Lett. 2022, 32, 105–108. [Google Scholar] [CrossRef]
- Zhu, F.; Hong, W.; Chen, J.-X.; Wu, K. Ultra-wideband single and dual baluns based on substrate integrated coaxial line technology. IEEE Trans. Microw. Theory Tech. 2012, 60, 3062–3070. [Google Scholar] [CrossRef]
- Zhou, J.; Qian, H.J.; Ren, J.; Luo, X. Reconfigurable wideband filtering balun with tunable dual-notched bands using cpw-to-slot transition and varactor-loaded shorted-slot. IEEE Access 2019, 7, 36761–36771. [Google Scholar] [CrossRef]
- MartÍn, F.; Zhu, L.; Hong, J.-S.; Medina, F. Balanced Microwave Filters; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Wang, J.; He, S.; You, F.; Shi, W.; Peng, J.; Li, C. Codesign of high-efficiency power amplifier and ring-resonator filter based on a series of continuous modes and even–odd-mode analysis. IEEE Trans. Microw. Theory Tech. 2018, 66, 2867–2878. [Google Scholar] [CrossRef]
- Pozar, D.-M. Microwave Engineering, 4th ed.; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Reed, J.; Wheeler, G. A Method of analysis of symmetrical four-port networks. IEEE Trans. Microw. Theory Tech. 1956, 4, 246–252. [Google Scholar] [CrossRef]
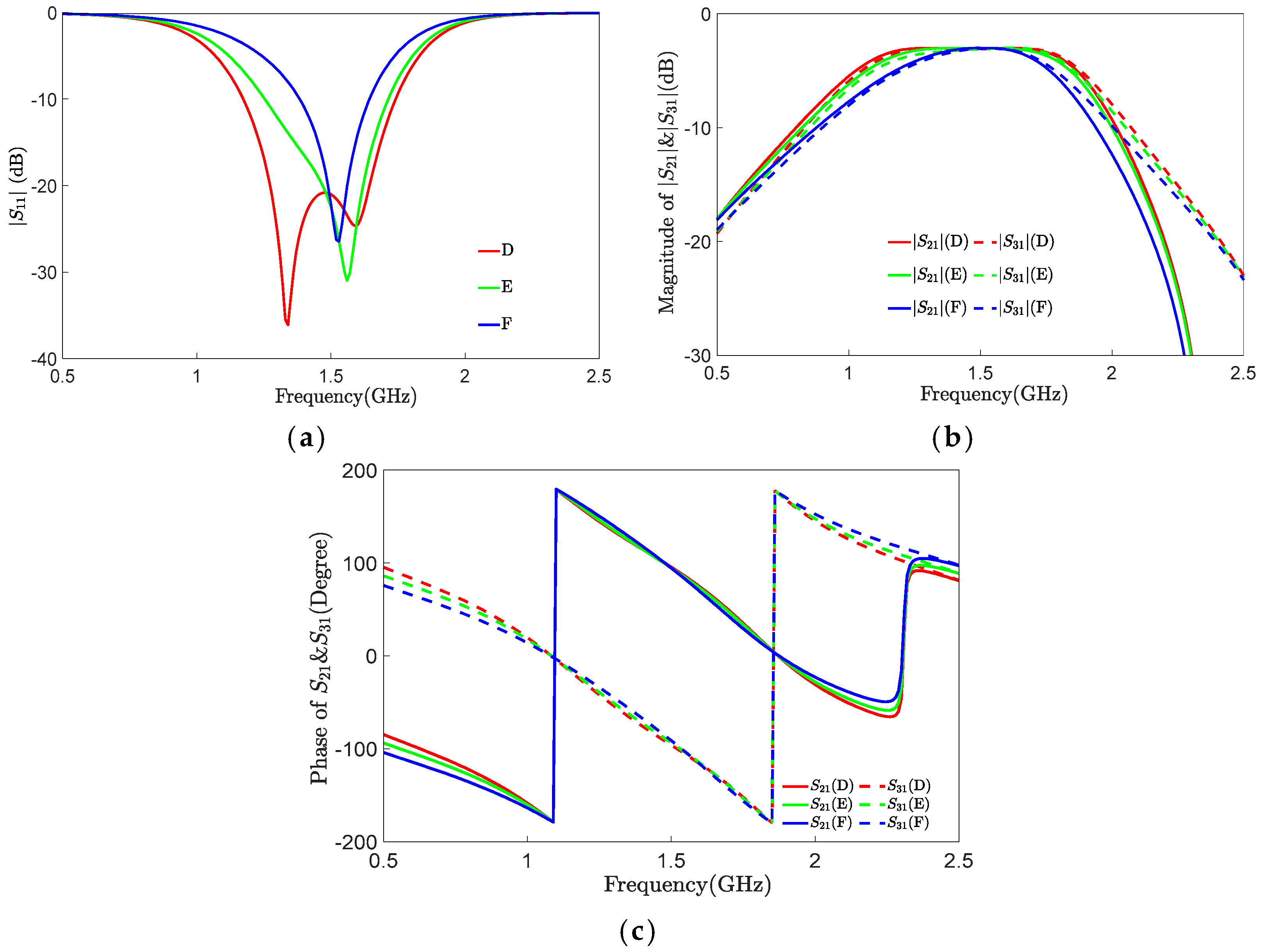
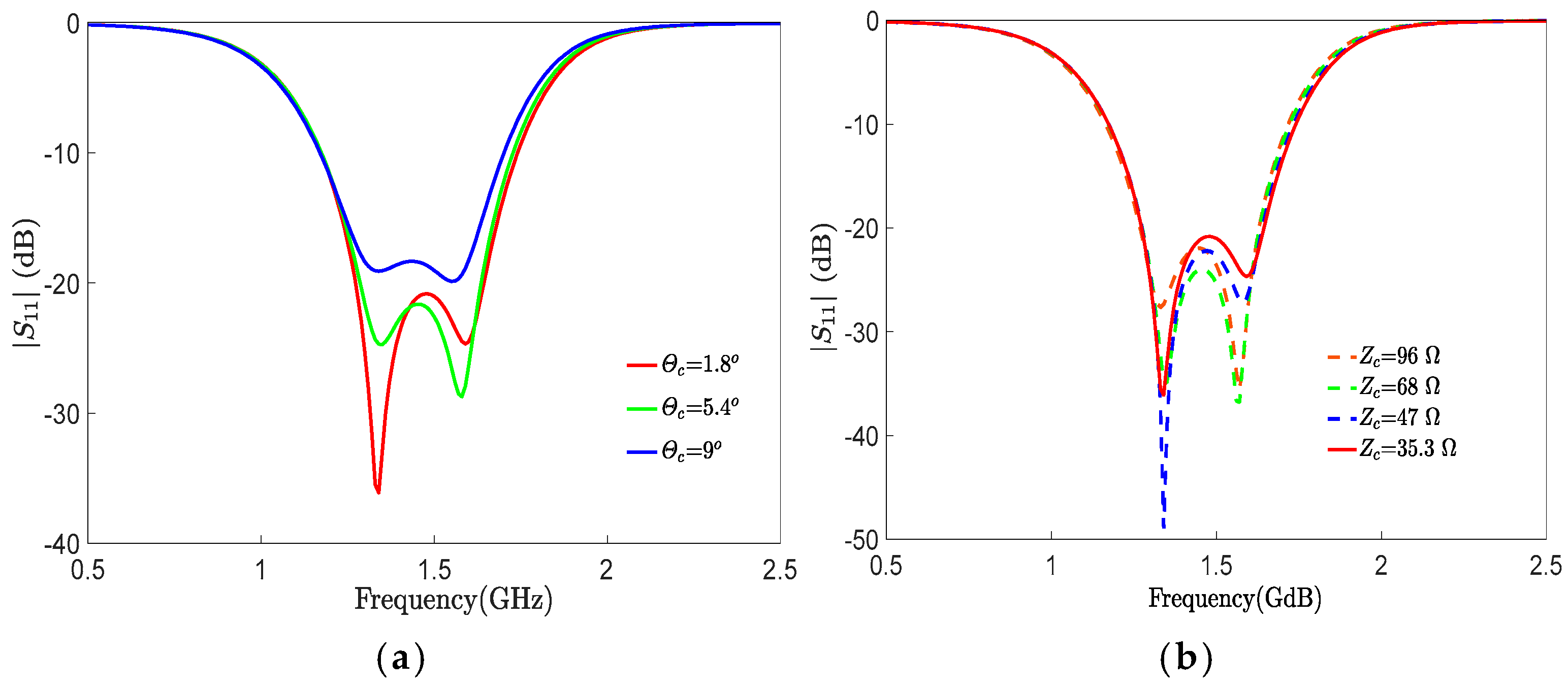
| A | B | C | |
|---|---|---|---|
| , () | 42.40, 22.95 | 98.36, 37.74 | 133.61, 46.25 |
| () | 100 | 150 | 200 |
| D | E | F | |
|---|---|---|---|
| 50 | 70 | 100 | |
| 100 | 70 | 50 |
| Characteristic Impedance and Isolation Resistances () | ||||||
|---|---|---|---|---|---|---|
| , | ||||||
| 42.40, 22.95 | 35.33 | 96.03 | 69.66 | 69.66 | 100 | |
| Electrical Length (Degree) | ||||||
| , | ||||||
| 94.48, 82.73 | 1.8 | 180.93 | 90.06 | 90.06 | ||
| , | Characteristic Impedance and Isolation Resistances | Electrical Length (Degree) | ||
|---|---|---|---|---|
| 35 | 50 | 42.10 | 100 | 91.55 |
| 35 | 75 | 51.03 | 70 | 94.61 |
| Ref. | f0 (GHz) | Methodology | IL (dB) | All-Port Matching | All-Frequency Isolation (dB) |
|---|---|---|---|---|---|
| [12] | 0.9 G | even–odd mode | 0.8 | no | no |
| [8] | 61.75 | equivalent circuit | 2.5 | no | no |
| [27] | 14.88 | electric field | 1.1 | no | <−7.5 dB |
| [16] | 1.8 | voltage wave | 0.84 | no | no |
| [17] | 2.45 | circuit theory | 0.62 | no | no |
| [23] | 2.42 | coupling matrix | 1.5 | yes | <−13 dB |
| [15] | 2 | voltage wave | 0.5 | yes | <−10 dB |
| This Work | 1.5 | UMAM | 0.39 | yes | <−19.5 dB |
| This Work (with FIT) | 1.5 | UMAM | 0.4 | yes | <−20.2 dB (35–50 Ω) <−15.9 dB (35–75 Ω) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Li, Q.; Shen, Z.; Wu, W. A Unified-Mode Analysis Method for Symmetric Networks and Its Application to Balun Design. Electronics 2024, 13, 3925. https://doi.org/10.3390/electronics13193925
Li L, Li Q, Shen Z, Wu W. A Unified-Mode Analysis Method for Symmetric Networks and Its Application to Balun Design. Electronics. 2024; 13(19):3925. https://doi.org/10.3390/electronics13193925
Chicago/Turabian StyleLi, Lei, Qingbo Li, Zhongxiang Shen, and Wen Wu. 2024. "A Unified-Mode Analysis Method for Symmetric Networks and Its Application to Balun Design" Electronics 13, no. 19: 3925. https://doi.org/10.3390/electronics13193925
APA StyleLi, L., Li, Q., Shen, Z., & Wu, W. (2024). A Unified-Mode Analysis Method for Symmetric Networks and Its Application to Balun Design. Electronics, 13(19), 3925. https://doi.org/10.3390/electronics13193925






