A Low Profile Wideband Linear to Circular Polarization Converter Metasurface with Wide Axial Ratio and High Ellipticity
Abstract
1. Introduction
2. Design of the Metasurface
3. Stokes Theorem
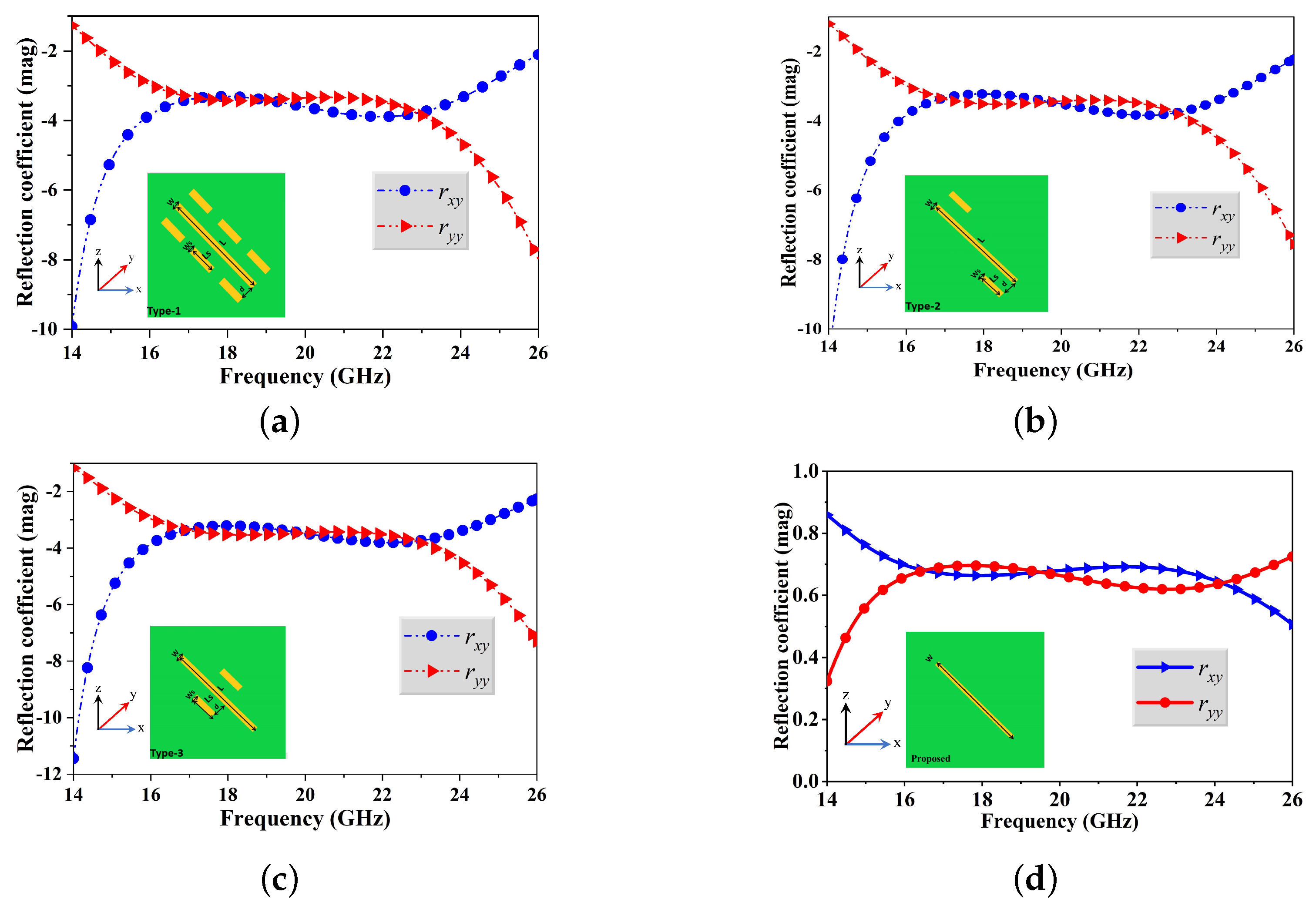
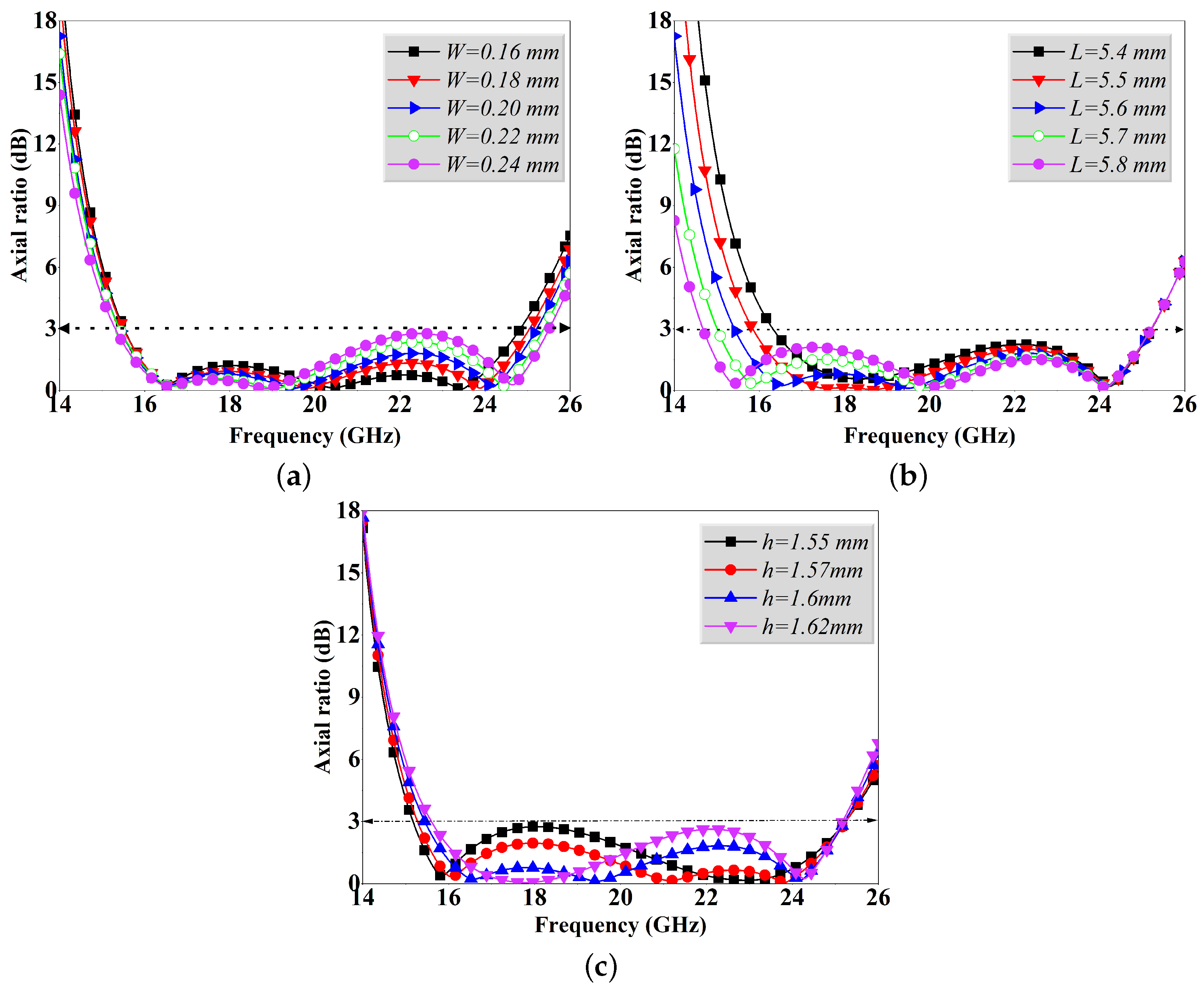
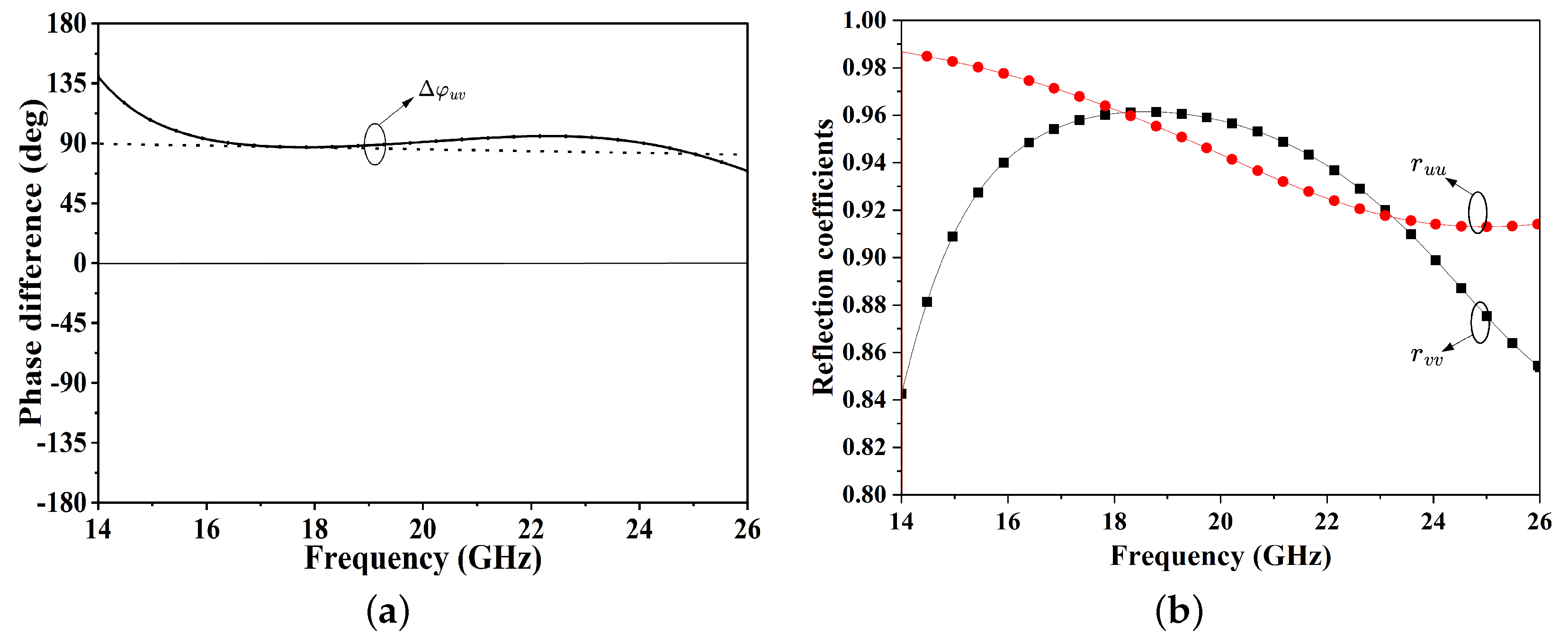
4. Parameters Analysis
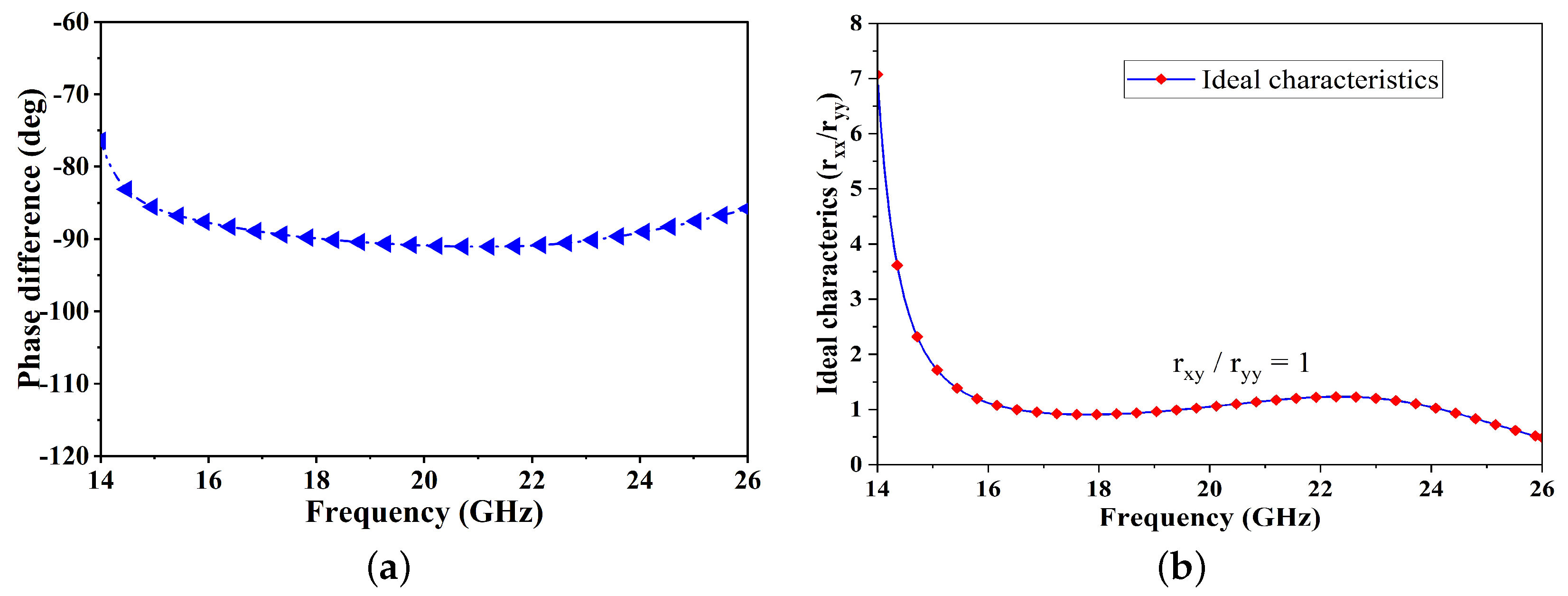
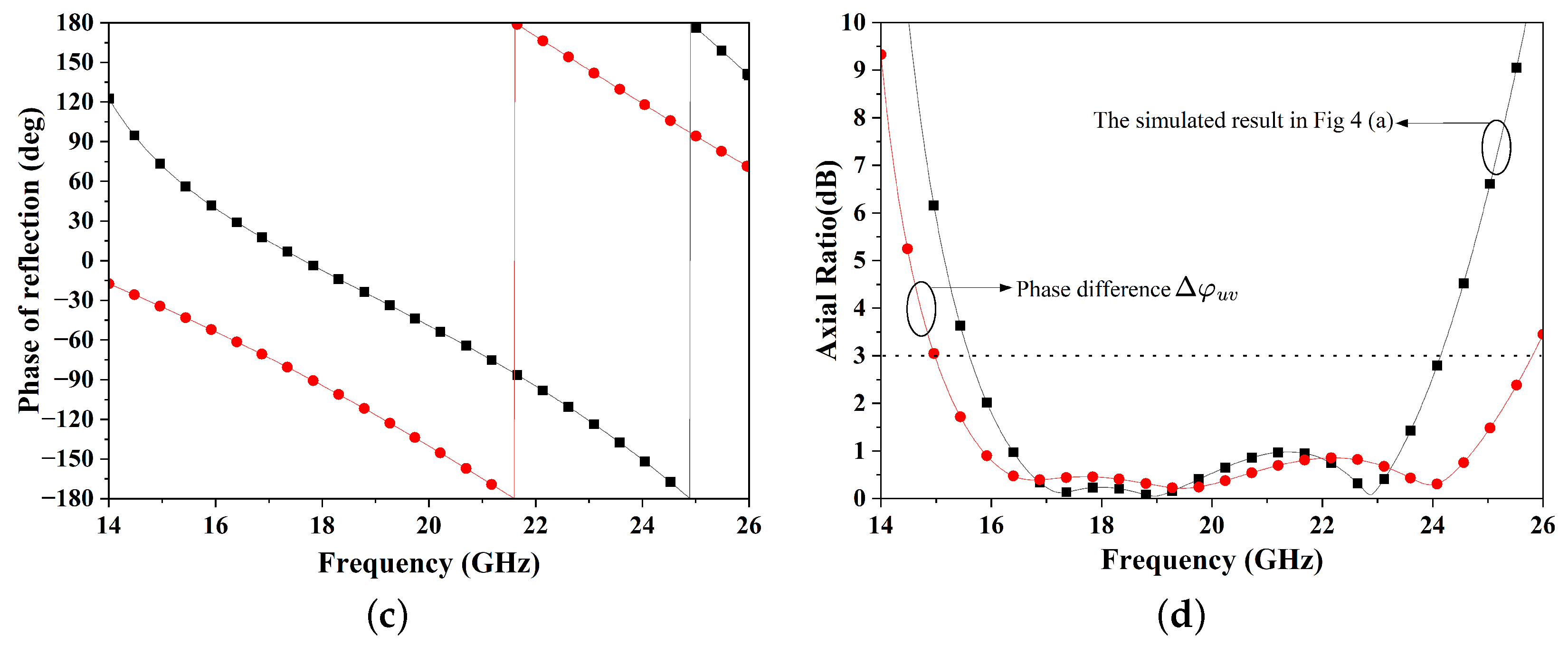
5. Theoretical Analysis
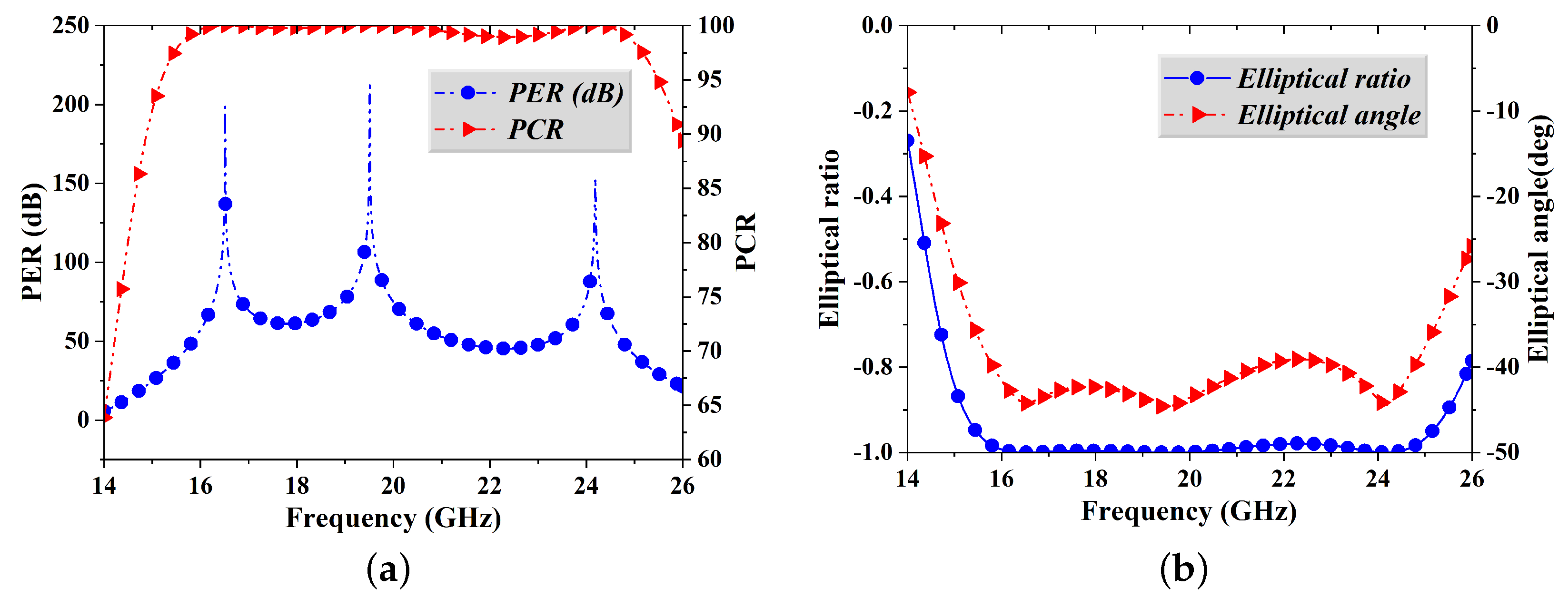
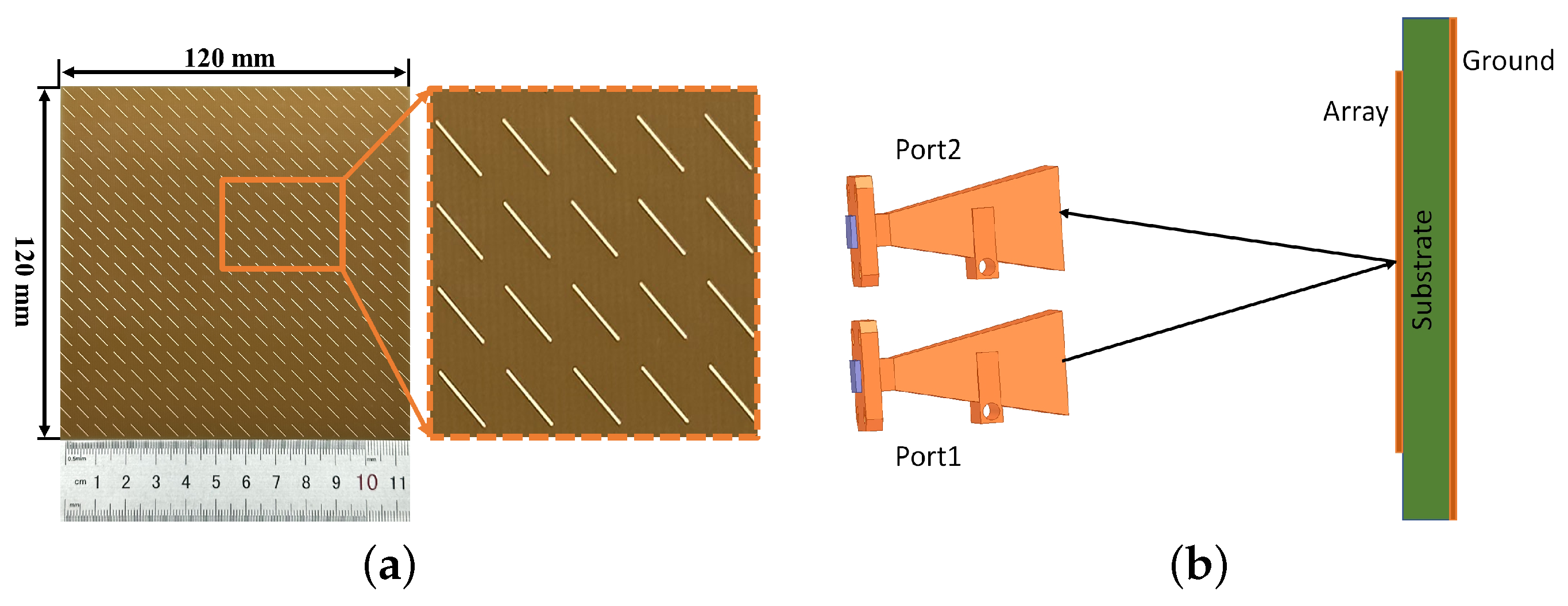
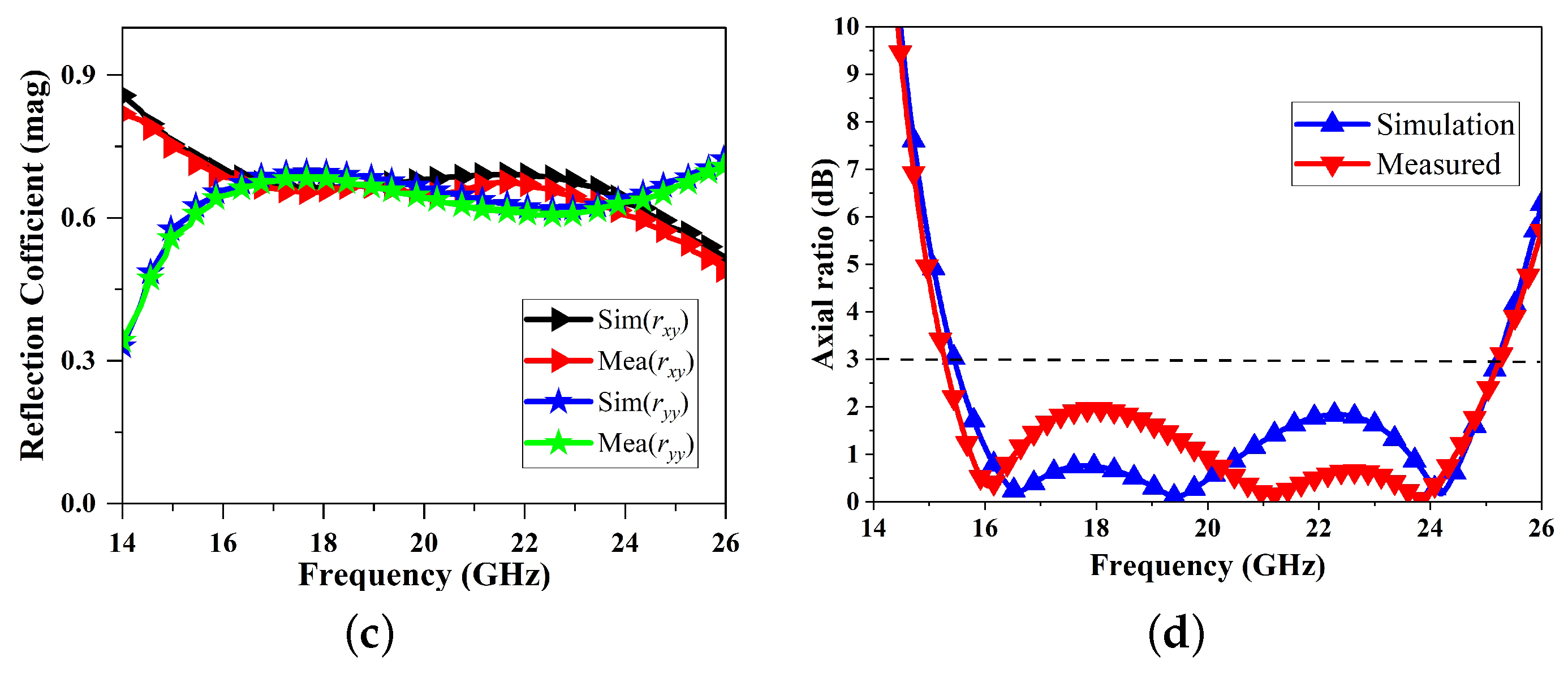
6. Experimental Work
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luo, X. Engineering optics 2.0: A revolution in optical materials, devices, and systems. ACS Photonics 2018, 5, 4724–4738. [Google Scholar] [CrossRef]
- Fahad, A.K.; Ruan, C.; Nazir, R.; Hassan, B. Transmissive Polarizer Metasurfaces: From Microwave to Optical Regimes. Nanomaterials 2022, 12, 1705. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Sun, S.; Xiao, S.; Zhou, L. High-efficiency metasurfaces: Principles, realizations, and applications. Adv. Opt. Mater. 2018, 6, 1800415. [Google Scholar] [CrossRef]
- Jorwal, S.; Dubey, A.; Gupta, R.; Agarwal, S. A Review: Advancement in Metamaterial Based RF and Microwave Absorbers. Sens. Actuators A Phys. 2023, 354, 114283. [Google Scholar] [CrossRef]
- Santonocito, A.; Patrizi, B.; Toci, G. Recent Advances in Tunable Metasurfaces and Their Application in Optics. Nanomaterials 2023, 13, 1633. [Google Scholar] [CrossRef]
- Tumakov, D.; Chikrin, D.; Kokunin, P. Miniaturization of a Koch-type fractal antenna for Wi-Fi applications. Fractal Fract. 2020, 4, 25. [Google Scholar] [CrossRef]
- Li, A.; Singh, S.; Sievenpiper, D. Metasurfaces and their applications. Nanophotonics 2018, 7, 989–1011. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J.; Fu, X.; Jia, Y.; Chen, H.; Feng, M.; Zhu, R.; Qu, S. Single-layer metasurface for ultra-wideband polarization conversion: Bandwidth extension via Fano resonance. Sci. Rep. 2021, 11, 585. [Google Scholar] [CrossRef]
- Khan, M.I.; Khalid, Z.; Tahir, F.A. Linear and circular-polarization conversion in X-band using anisotropic metasurface. Sci. Rep. 2019, 9, 4552. [Google Scholar] [CrossRef]
- Li, J.; Liu, J.; Yue, Z.; Li, J.; Zheng, C.; Yang, F.; Li, H.; Zhang, Y.; Zhang, Y.; Yao, J. Polarization variable terahertz metasurface along the propagation path. Fundam. Res. 2023, in press. [CrossRef]
- Wu, P.C.; Sokhoyan, R.; Shirmanesh, G.K.; Cheng, W.H.; Atwater, H.A. Near-Infrared Active Metasurface for Dynamic Polarization Conversion. Adv. Opt. Mater. 2021, 9, 2100230. [Google Scholar] [CrossRef]
- Khan, S.; Eibert, T.F. A dual-band metasheet for asymmetric microwave transmission with polarization conversion. IEEE Access 2019, 7, 98045–98052. [Google Scholar] [CrossRef]
- Ahmed, A.; Cao, Q.; Khan, M.I.; Sajjad, M.; Ahmed, F. An ultra-thin multifunctional chiral metasurface with asymmetric transmission, cross-polarization conversion, and circular dichroism for Ku-and K-band applications. J. Phys. D Appl. Phys. 2023, 57, 035001. [Google Scholar] [CrossRef]
- Cui, Z.; Xiao, Z.; Chen, M.; Lv, F.; Xu, Q. A transmissive linear polarization and circular polarization cross polarization converter based on all-dielectric metasurface. J. Electron. Mater. 2021, 50, 4207–4214. [Google Scholar] [CrossRef]
- Doumanis, E.; Goussetis, G.; Gomez-Tornero, J.L.; Cahill, R.; Fusco, V. Anisotropic impedance surfaces for linear to circular polarization conversion. IEEE Trans. Antennas Propag. 2011, 60, 212–219. [Google Scholar] [CrossRef]
- Rashid, A.; Murtaza, M.; Zaidi, S.A.A.; Zaki, H.; Tahir, F.A. A single-layer, wideband and angularly stable metasurface based polarization converter for linear-to-linear cross-polarization conversion. PLoS ONE 2023, 18, e0280469. [Google Scholar] [CrossRef]
- Fu, X.; Liang, H.; Li, J. Metalenses: From design principles to functional applications. Front. Optoelectron. 2021, 14, 170–186. [Google Scholar] [CrossRef]
- Gao, Z.; Shi, Y.; Li, M.; Song, J.; Liu, X.; Wang, X.; Yang, F. Tunable extraordinary optical transmission with graphene in terahertz. ACS Omega 2021, 6, 29746–29751. [Google Scholar] [CrossRef]
- Wang, H.B.; Cheng, Y.J.; Chen, Z.N. Wideband and wide-angle single-layered-substrate linear-to-circular polarization metasurface converter. IEEE Trans. Antennas Propag. 2019, 68, 1186–1191. [Google Scholar] [CrossRef]
- Gao, X.; Li, K.; Wu, X.; Xue, C.; Wang, G.; Xie, X.; Qin, M. Ultra-wideband linear-to-circular polarizer realized by bi-layer metasurfaces. Opt. Express 2022, 30, 18392–18401. [Google Scholar] [CrossRef]
- Zhang, X.; Ye, H.; Zhao, Y.; Zhang, H. Linear-to-circular polarization converter with adjustable bandwidth realized by the graphene transmissive metasurface. Plasmonics 2022, 17, 1079–1089. [Google Scholar] [CrossRef]
- Lin, B.Q.; Lv, L.T.; Guo, J.X.; Wang, Z.L.; Huang, S.Q.; Wang, Y.W. Ultra-wideband linear-to-circular polarization conversion metasurface. Chin. Phys. B 2020, 29, 104205. [Google Scholar] [CrossRef]
- Cerveny, M.; Ford, K.L.; Tennant, A. Reflective switchable polarization rotator based on metasurface with PIN diodes. IEEE Trans. Antennas Propag. 2020, 69, 1483–1492. [Google Scholar] [CrossRef]
- Qin, Z.; Li, Y.; Wang, H.; Wan, W.; Li, C.; Zhu, Z.; Cheng, Y.; Li, S.; Chen, H.; Wang, J.; et al. Polarization meta-converter for dynamic polarization states shifting with broadband characteristic. Opt. Express 2022, 30, 20014–20025. [Google Scholar] [CrossRef] [PubMed]
- Bikkuri, S.D.P.; Alapati, S. Design of Low Profile Multiband Reflective Polarization Converter for Both Linear and Circular Polarized Waves. Prog. Electromagn. Res. Lett. 2021, 97, 61–68. [Google Scholar] [CrossRef]
- Zhang, B.; Zhu, C.; Zhang, R.; Yang, X.; Wang, Y.; Liu, X. Ultra-Broadband Angular-Stable Reflective Linear to Cross Polarization Converter. Electronics 2022, 11, 3487. [Google Scholar] [CrossRef]
- Wang, J.; Yang, R.; Ma, R.; Tian, J.; Zhang, W. Reconfigurable multifunctional metasurface for broadband polarization conversion and perfect absorption. IEEE Access 2020, 8, 105815–105823. [Google Scholar] [CrossRef]
- Long, F.; Yu, S.; Kou, N.; Zhang, C.; Ding, Z.; Zhang, Z. Efficient broadband linear polarization conversion metasurface based on%-shape. Microw. Opt. Technol. Lett. 2020, 62, 226–232. [Google Scholar] [CrossRef]
- Feng, Q.Y.; Yan, D.X.; Li, X.J.; Li, J.N. Realization of absorption, filtering, and sensing in a single metamaterial structure combined with functional materials. Appl. Opt. 2022, 61, 4336–4343. [Google Scholar] [CrossRef]
- Ahmed, F.; Hassan, T.; Tamoor, T.; Shoaib, N. A Multi-Functional Metasurface for Polarization Transformation Applications. In Proceedings of the 2020 IEEE International Symposium on Antennas and Propagation and North American Radio Science Meeting, Toronto, ON, Canada, 5–10 July 2020; IEEE: New Yrok, NY, USA, 2020; pp. 861–862. [Google Scholar]
- Zhao, J.; Li, N.; Cheng, Y. All-dielectric InSb metasurface for broadband and high-efficient thermal tunable terahertz reflective linear-polarization conversion. Opt. Commun. 2023, 536, 129372. [Google Scholar] [CrossRef]
- Wu, J.; Wang, X.; Xiao, H.; Wang, Y.; Fan, Z.; Zhang, H. A wide-incidence-angle insensitive multi-polarization converter based on reflective metasurface. J. Phys. D Appl. Phys. 2023, 56, 415103. [Google Scholar] [CrossRef]
- Kamal, B.; Chen, J.; Yingzeng, Y.; Ren, J.; Ullah, S.; Khan, W.U.R. High efficiency and ultra-wideband polarization converter based on an L-shaped metasurface. Opt. Materials Express 2021, 5, 1343–1352. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, L.; Wang, J.; Akwuruoha, C.N.; Cao, W. Ultra-wideband high-efficiency reflective linear-to-circular polarization converter based on metasurface at terahertz frequencies. Opt. Express 2017, 25, 27616–27623. [Google Scholar] [CrossRef] [PubMed]
- Majeed, A.; Zhang, J.; Awan, Z.A.; Memon, S.; Ishfaq, M.; Wang, C. A high-efficiency dual-band linear-to-circular polarization converter based on rectangular-slot reflective metasurface. Appl. Sci. 2022, 12, 9172. [Google Scholar] [CrossRef]
- Zheng, Q.; Guo, C.; Ding, J. Wideband metasurface-based reflective polarization converter for linear-to-linear and linear-to-circular polarization conversion. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1459–1463. [Google Scholar] [CrossRef]
- Wu, J.L.; Lin, B.Q.; Da, X.Y.; Wu, K. A linear-to-circular polarization converter based on I-shaped circular frequency selective surfaces. Chin. Phys. B 2017, 26, 094201. [Google Scholar] [CrossRef]
- Ahmed, F.; Khan, M.I.; Tahir, F.A. A multifunctional polarization transforming metasurface for C-, X-, and K-band applications. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 2186–2190. [Google Scholar] [CrossRef]



| Ref. | Unit (P) | Operating BW (GHz) | Substrate Thickness | Type of (PC) | PCR | Mode |
|---|---|---|---|---|---|---|
| [34] | 9 | 4.7–21.7 | 2 | LP-CP | N/A | surface current |
| [35] | 6 | 16.49–23.54 | 1.6 | LP-CP | 98 | N/A |
| [36] | 8.1 | 13.70–15.60 | 3.5 | LP-CP | N/A | surface current |
| [37] | 12 | 5.86–7.34 | 1.8 | LP-CP | N/A | N/A |
| [38] | 8.25 | 5.1–5.2 | 2 | LP-CP | N/A | surface current |
| This work | 6 | 15.41–25.23 | 1.6 | LP-CP | 98 | surface current |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayat, B.; Zhang, J.; Majeed, A.; Ishfaq, M.; Khan, A.; Ahmad, S. A Low Profile Wideband Linear to Circular Polarization Converter Metasurface with Wide Axial Ratio and High Ellipticity. Electronics 2024, 13, 352. https://doi.org/10.3390/electronics13020352
Hayat B, Zhang J, Majeed A, Ishfaq M, Khan A, Ahmad S. A Low Profile Wideband Linear to Circular Polarization Converter Metasurface with Wide Axial Ratio and High Ellipticity. Electronics. 2024; 13(2):352. https://doi.org/10.3390/electronics13020352
Chicago/Turabian StyleHayat, Babar, Jinling Zhang, Abdul Majeed, Muhammad Ishfaq, Adil Khan, and Shabeer Ahmad. 2024. "A Low Profile Wideband Linear to Circular Polarization Converter Metasurface with Wide Axial Ratio and High Ellipticity" Electronics 13, no. 2: 352. https://doi.org/10.3390/electronics13020352
APA StyleHayat, B., Zhang, J., Majeed, A., Ishfaq, M., Khan, A., & Ahmad, S. (2024). A Low Profile Wideband Linear to Circular Polarization Converter Metasurface with Wide Axial Ratio and High Ellipticity. Electronics, 13(2), 352. https://doi.org/10.3390/electronics13020352








