Localization Optimization Algorithm Based on Phase Noise Compensation

Abstract

Phase noise is a consequence of the instability inherent in the operation of oscillators, making it impossible to entirely eliminate. For low-cost internet of things (IoT) devices, this type of noise can be particularly pronounced, posing a challenge in providing high-quality localization services. To tackle this issue, this paper introduces an improved localization algorithm that includes phase noise compensation. The proposed algorithm enhances the direction of arrival (DoA) estimation for each base station by employing the EM–MUSIC method, subsequently forming a non-convex optimization problem based on the mean square error (MSE) of the estimated DoA results. Finally, a closed-form solution is derived through rational assumptions and approximations. Results show that this algorithm effectively minimizes localization errors and achieves accuracy levels within the sub-meter range.

1. Introduction

As the development of smart cities and the internet of things (IoT) progresses, the functionality and efficiency of IoT systems have been increasing significantly [1]. Current IoT networks consist of a wide range of communication devices, which primarily support short-range communication protocols like Bluetooth [2] and Wi-Fi [3]. Such networks enable continuous data collection and transmission, facilitating diverse applications in smart cities, healthcare, and industrial automation. However, traditional IoT systems focus mainly on data transmission rather than environmental perception. According to the planning for 6G/B6G, the future IoT, by leveraging existing communication signals, can support sensing tasks, allowing for the simultaneous collection of data and perception of physical surroundings [4]. This dual functionality not only improves the efficiency of IoT applications but also reduces the need for dedicated sensing hardware, thereby supporting the development of energy-efficient, multi-functional IoT networks in 6G and beyond. As an indispensable part of sensing capabilities, integrating localization capacity into IoT networks opens up new dimensions for real-time and context-aware applications [5,6].

Localization refers to the process of determining the location of objects or individuals in physical environments [7]. This technology plays a crucial role in various applications [8], including navigation, asset tracking, and emergency response. Although localization accuracy may vary with the needs of applications, improving localization accuracy is an everlasting goal for relevant researchers. Currently, the primary technologies for outdoor localization include global positioning systems (GPS) [9], cellular networks [10], and hybrid systems combining multiple signals [11]. Among them, low power consumption is a crucial point of research and applications. Low power consumption means lower signal-to-noise ratio (SNR) and interference from various systems in the industrial, scientific, and medical (ISM) band. However, challenges remain in reducing energy consumption and addressing environmental interference, particularly in enhancing accuracy. In this case, increasing the precision of location becomes increasingly challenging.

Based on the physical quantities measured, existing localization technologies can be categorized as methods based on distance estimation and methods based on angle estimation [12]. The former method relies on the principle that received signal strength (RSS) decreases as distance increases. This approach is applicable in systems such as Wi-Fi and Bluetooth. Another distance-based method calculates the distance between the transmitter and receiver based on the time of arrival (ToA) of the signal [13]. As an example application, localization systems with ultra-wideband (UWB) technology, which transmit distinct pulse signals that are easy to identify, commonly use this method. Angle-based localization has lower requirements on waveforms compared to UWB’s pulse but requires a large array of antennas, corresponding radio frequency channels, and other hardware resources.

In the theoretical research on DoA estimation, the multiple signal classification (MUSIC) algorithm is generally considered a significant breakthrough in direction estimation [14]. This algorithm uses eigenvalue decomposition to partition the space of covariance matrix, then leverages the orthogonality between the signal subspace and the noise subspace to distinguish the estimation result. However, the main issue with the MUSIC algorithm is its high computational complexity, which makes it difficult to apply in systems with limited computational resources. To address this problem, the Root-MUSIC algorithm was introduced, which reduces the computational load but sacrifices some estimation accuracy. Later, the estimating signal parameters via rotational invariance techniques (ESPRIT) algorithm, which exploits the rotational invariance of subspaces, eliminates the need for spectral search, thereby reducing computational complexity significantly [15]. The Capon algorithm is another classic spectral estimation method and one of the common DoA estimation techniques. It can be used to estimate the DoA of multiple signals received without knowing the number of signal sources [16]. In recent years, the advent of new technologies has introduced novel tools for localization research. Reconfigurable intelligent surface (RIS) can improve DoA estimation algorithms by enhancing signal quality and offering more diverse propagation paths. It also focuses signals in specific directions, reducing noise and interference, which helps achieve more precise DoA estimation. Furthermore, RIS facilitates collaborative positioning and network optimization by providing multiple signal paths, leading to more accurate localization [17,18].

The accuracy of the localization system is not only determined by the chosen localization algorithm. Factors like the number of base stations, their spatial distribution, and signal interference also play a role. To improve the performance of multiple base station systems based on angle estimation, reference [12] assumed that the angle of arrival (AoA) estimation or direction of arrival (DoA) results of all base stations have an identical level of error. This simplifies localization calculations into a least squares problem. However, when interference levels significantly vary among base stations, this assumption becomes unreasonable and can lead to severe localization errors. Reference [19] proposed a localization algorithm that integrates multiple features, such as signal strength and phase, which reduces estimation errors as the number of base stations increases. Nevertheless, unlimitedly increasing the number of base stations implies higher hardware costs, which is against the goal of being energy-efficient and is not suitable for IoT systems. Furthermore, such methods do not fully exploit the information provided by signals that are subject to greater interference. Mathematically, we can model these non-ideal factors as additive white Gaussian noise (AWGN) [20], multipath effects [21], correlation between antennas [22], and signal frequency offsets [23]. Despite the mentioned research providing some insights, the impact of phase noise on localization systems is overlooked. Considering that the actual hardware system has limited cost, many receivers use time division multiplexing to achieve multi-antenna reception. In this scenario, the control of the switching time slots and the instability of the crystal oscillator, along with thermal noise at the sampling moments, can all affect the received signals. This impact can be further categorized into multiplicative phase noise and additive white Gaussian noise. However, for billions of low-cost, low-power IoT devices, noise levels can be even more significant, posing a critical bottleneck that affects localization accuracy.

In this paper, a multiple base station optimization algorithm with phase noise estimation and compensation is proposed. Based on the expectation–maximization (EM) algorithm framework, the proposed algorithm optimizes the DoA estimation results affected by phase noise iteratively and constructs a non-convex optimization problem based on the root mean square error (RMSE) of each DoA estimation result. Then the optimal position estimation is solved by reasonable approximation and iteration.

2. Problem Description

2.1. Existing DoA Estimation Models

A single-input multiple-output (SIMO) localization system is shown in Figure 1. The transmitting device can be an arbitrary signal generator, and the receiver consists of an array with M antennas. The signals received by each array element are connected to the subsequent receiving module through a radio frequency switch. This type of receiver, which employs time division multiplexing of the antennas, is referred to as a switched antenna array (SAA) [24]. Assuming that each antenna element is evenly distributed as a uniform linear array (ULA), the steering vectors can be expressed as

$$\mathbf{A}\left(\varphi \right)={[a_1\left(\varphi \right),\dots ,a_M\left(\varphi \right)]}^T,$$

(1)

where $a_m\left(\varphi \right)=e^{j(m-1)\varphi },m=1,\dots ,M$. $\varphi$ represents the relative phase difference of the signals received by the antennas, and the relationship between the inter-element spacing d and the angle $\beta$ can be expressed as

$$\varphi ={\displaystyle \frac{2\pi d}{\lambda }}cos\beta .$$

(2)

Based on this relationship, DoA estimation is essentially the estimation of $\varphi$ from the received signal.

The existing signal reception models generally formulate the thermal noise of devices as additive white Gaussian noise on DoA estimation. Thus, the received signal sample at the m-th antenna for the n-th sample can be represented as

$$y_m\left(n\right)=a_m\left(\varphi \right)s\left(n\right)+v_m\left(n\right),n=1,\dots ,N,$$

(3)

where the transmitted signal $s\left(n\right)$ can be an arbitrary communication signal. For convenience in subsequent calculations, the entire signal received by the antenna array can be expressed as

$$\mathbf{Y}=\mathbf{A}\left(\varphi \right)\mathbf{S}+\mathbf{V},$$

(4)

where $\mathbf{Y}={[y_1,\dots ,y_m,\dots ,y_M]}^T\in {\mathbb{C}}^{M\times N}$ represents N received signal samples from M antennas, $y_m=[y_m\left(1\right),y_m\left(2\right),\dots ,y_m\left(N\right)]\in {\mathbb{C}}^{1\times N}$ represents the signal vector, $\mathbf{V}$ represents the thermal noise matrix, and $\mathbf{S}\in {\mathbb{C}}^{1\times N}$ is the transmitted signal vector.

2.2. DoA Estimation Model Affected by Phase Noise

The above model does not consider the phase noise [25], which represents the distortion in the phase of the received signal [26]. In the domain of signal processing, there are two commonly employed modeling approaches: Gaussian and Wiener phase noise models. This paper considers a common Wiener phase noise. The Wiener process is non-stationary, and the differences between adjacent moments follow a normal distribution, making it a Markov process. Wiener phase noise exhibits a variance that increases over time, indicating that the longer the operation period, the greater the variation in phase noise. This characteristic makes the Wiener phase noise model particularly suitable for low-cost, low-power IoT devices, where such assumptions align well with practical conditions. Figure 2 is a diagram of Wiener phase noise, which shows that the phase noise is highly irregular and can have a significant impact on the analysis. The four different colors in the figure represent four antennas. It can be observed that the phase noise changes continuously, and under time-division multiplexing, the phase noise experienced by the signals received by different antennas may vary. The discrete Wiener phase noise can be expressed as [27]

$$\phi (n+1)=\phi \left(n\right)+{\omega }_{\phi }\left(n\right),$$

(5)

where ${\omega }_{\phi }\left(n\right)\sim \mathcal{N}(0,{\sigma }_{\phi }^2)$. Then, the phase noise of the single-antenna array is defined as

$${\mathit{\phi }}_m=[{\phi }_m\left(1\right),\dots ,{\phi }_m\left(n\right),\dots ,{\phi }_m\left(N\right)]\in {\mathbb{C}}^{1\times N}.$$

(6)

When the phase noise is incorporated into the received signal, Equations (3) and (4) can be transformed to

$$y_m\left(n\right)=a_m\left(\varphi \right)s\left(n\right)e^{j{\phi }_m\left(n\right)}+v_m\left(n\right),$$

(7)

$$\mathbf{Y}=\mathbf{A}\left(\varphi \right)\mathbf{S}\odot \mathbf{\Phi }+\mathbf{V},$$

(8)

where $\mathbf{\Phi }={[{\mathit{\phi }}_1,\dots ,{\mathit{\phi }}_m,\dots ,{\mathit{\phi }}_M]}^T\in {\mathbb{C}}^{M\times N}$ represents the phase noise of the entire antenna array.

2.3. The Impact of Phase Noise on DoA Estimation in SAA Systems

The following describes the impact of the MUSIC algorithm [14] on DoA estimation in a communication system. The first step of the MUSIC algorithm is to compute the correlation matrix of the received signal:

$${\mathbf{R}}_{yy}=\mathbb{E}\left[\mathbf{Y}\left(n\right){\mathbf{Y}}^H\left(n\right)\right]=\mathbf{A}\left(\varphi \right){\mathbf{R}}_{ss}{\mathbf{A}}^H\left(\varphi \right)\odot \mathbf{\Omega }+{\sigma }_v^2\mathbf{I},$$

(9)

where $\mathbb{E}[·]$ denotes expectation, and ${\mathbf{R}}_{ss}=\mathbb{E}\left[s\left(n\right)s^H\left(n\right)\right]$. ${\sigma }_v^2$ is the thermal noise power, and $\mathbf{I}$ is the identity matrix. Compared with the commonly seen expressions of the MUSIC algorithm in existing literature, it can be observed that Equation (9) includes an additional term related to phase noise, which can be expressed as

$$\mathbf{\Omega }=\mathbb{E}\left[\begin{array}{cccc}{g}_{1,1}& g_{1,2}& \cdots & g_{1,M}\\ g_{2,1}& g_{2,2}& \cdots & g_{2,M}\\ ⋮& ⋮& \ddots & ⋮\\ g_{M,1}& g_{M,2}& \cdots & g_{M,M}\end{array}\right],$$

(10)

where $g_{m_1,m_2}\left(n\right)=exp\left(j\left[{\phi }_{m_1}\left(n\right)-{\phi }_{m_2}\left(n\right)\right]\right)$. For convenience of expression, in Equation (10), $g_{m_1,m_2}\left(n\right)$ is denoted as $g_{m_1,m_2}$. Since the communication system receives signals through the SAA, the spatial parallel signals are converted into time-series signals. Due to the characteristics of phase noise, the phase noise values at different moments are different, so the phase noise of the received signals at each antenna cannot be canceled out, which means ${\mathit{\phi }}_{m_1}\ne {\mathit{\phi }}_{m_2}$.

Due to the existence of $\mathbf{\Omega }$, the signal subspace formed by the steering vector $\mathbf{A}\left(\varphi \right)$ is distorted, which in turn affects the eigenvalue decomposition and spectrum search of the MUSIC algorithm, ultimately leading to a significant increase in the DoA estimation error. Phase noise has a similar impact on other DoA estimation algorithms, which can be derived through simple reasoning, so it will not be elaborated further here.

The above discussion clearly demonstrates that phase noise has a significant impact on the direction-finding algorithm in the antenna array switching process. Moreover, the existing phase noise compensation methods rarely focus on the localization algorithm performance and are unable to accurately estimate phase noise without precise DoA. To improve the accuracy of DoA estimation, we formulate an estimation model for DoA and phase noise as follows:

$$\widehat{\varphi },\widehat{\phi }=arg\underset{\varphi ,\phi }{min}\sum _{m=1}^M\sum _{n=1}^N|y_m\left(n\right)-a_m\left(\varphi \right)s\left(n\right)e^{j{\phi }_m\left(n\right)}|.$$

(11)

The optimization problem seeks to minimize the difficulty inherent in the phase noise $\widehat{\phi }$, which is a type of random noise and can affect the received signal in the same dimension.

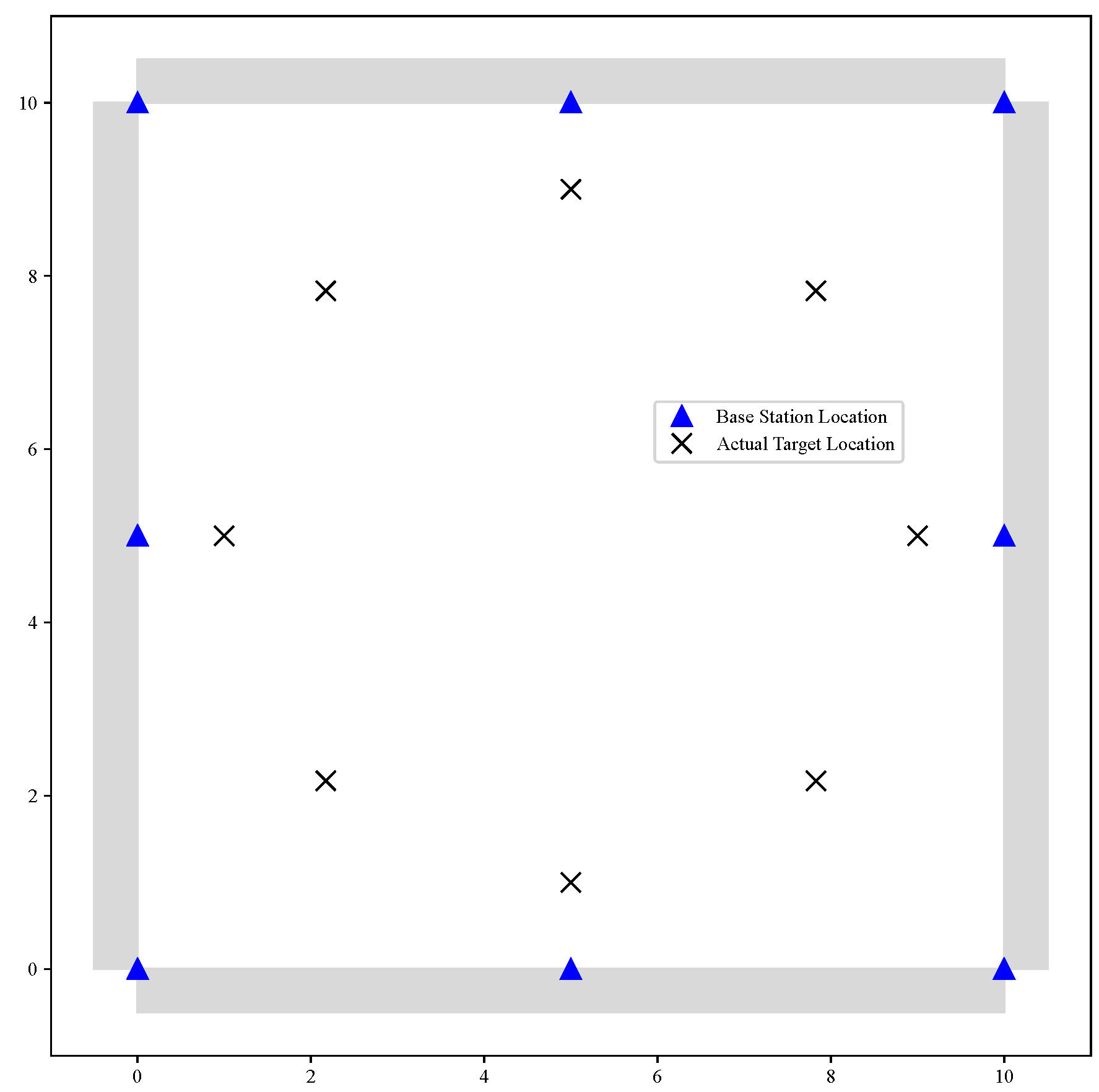
2.4. Localization Optimization Problem for Multiple Base Stations

After obtaining the DoA estimation results from each base station by solving Equation (11), the basic principle of triangulation requires at least two base stations to calculate the position of the device based on angle measurements. As shown in Figure 3, where the red dot represents the real location of the target, and each base station has a certain error in DoA estimation result. Therefore, it is difficult to determine its final position. For the i-th base station with coordinates ${\mathbf{z}}_i=[x_{i,1},x_{i,2}]$ and the transmitting end coordinates $\mathbf{z}=[x_1,x_2]$, the relationship with the angle is as follows:

$$tan{\beta }_i={\displaystyle \frac{x_2-x_{i,2}}{x_1-x_{i,1}}},i=1,\cdots ,N_b,$$

(12)

where $N_b$ is the total number of base stations, and ${\beta }_i$ is the actual angle from the transmitter to the i-th base station.

By solving Equation (11), the impact of phase noise on DoA estimation is reduced. However, there are still errors in the actual direction-finding system, and the error levels of each base station are often different. This paper proposes an optimization algorithm to improve the multiple base stations localization results. Firstly, an optimization problem is constructed based on the error levels of the DoA estimates from each base station:

$$\overline{\mathbf{z}}=argmin\sum _{i=1}^{N_b}{\displaystyle \frac{{({\overline{\beta }}_i-{\widehat{\beta }}_i)}^2}{{\sigma }_i^2}},$$

(13)

where $\overline{\mathbf{z}}=[{\overline{x}}_1,{\overline{x}}_2]$ is the position coordinate estimation result optimized from the DoA estimation of multiple base stations, ${\overline{\beta }}_i$ is the actual DoA value corresponding to the coordinate $\overline{\mathbf{z}}$, ${\widehat{\beta }}_i$ is the DoA estimation value obtained from the signal processing algorithm at each base station, and ${\sigma }_i^2$ is the variance of the angle estimation error at each base station. It can be the Cramér–Rao bound (CRB) derived theoretically or the mean square error (MSE) obtained experimentally. In this paper, we utilize the latter approach. From Equation (12), it can be seen that the conversion of DoA to coordinates is a nonlinear relationship, and ${\sigma }_i^2$ is a term whose relationship with location can vary depending on the specific algorithm used for DoA, making problem (13) a non-convex optimization problem.

3. Algorithm Description

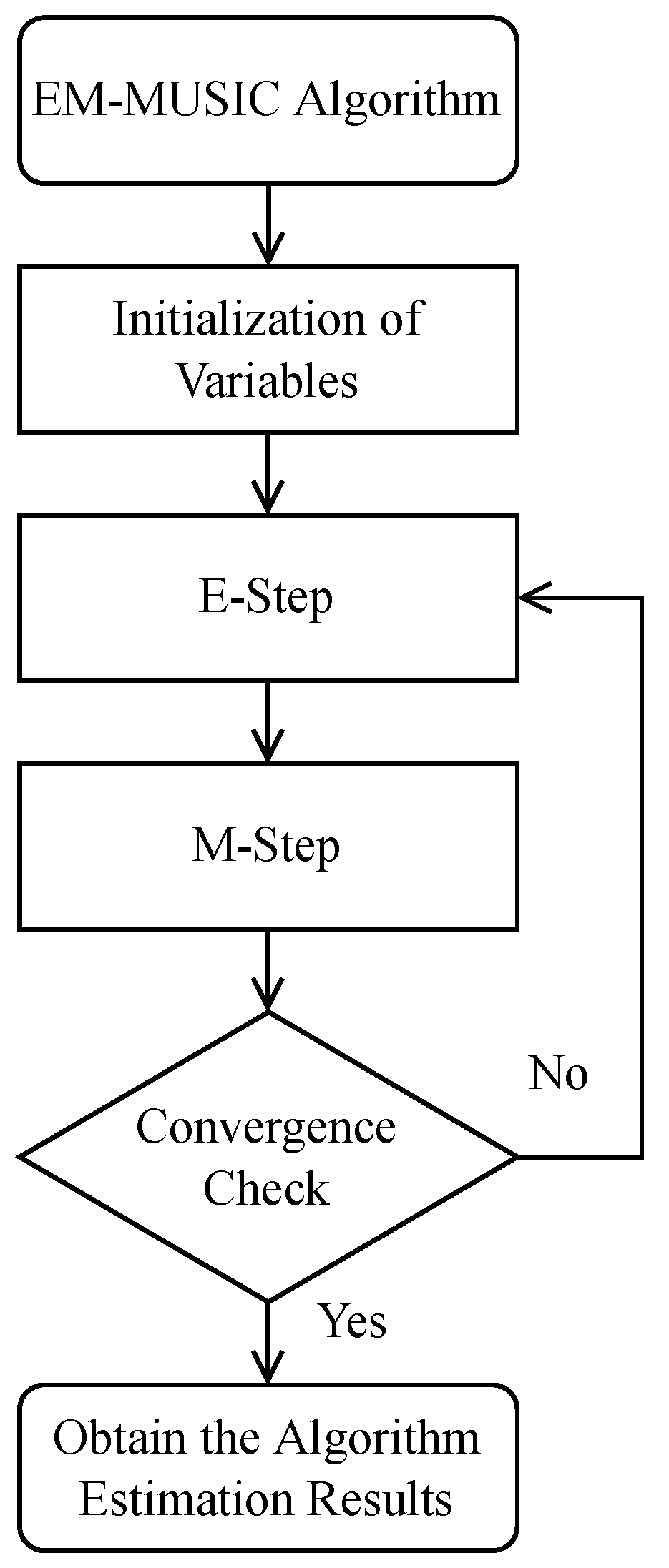
3.1. EM–MUSIC Algorithm

The EM algorithm is a widely used iterative algorithm that can find the maximum likelihood or maximum a posteriori estimates of model parameters in situations with missing data or unobservable variables [28]. The algorithm alternates between the expectation step (E-step) and the maximization step (M-step).

The approach used in this paper is not a strict EM algorithm but rather an extension within this framework [28,29]. EM-type algorithms can employ different methods for different problems, and the core idea is to continuously approximate the optimal result by alternately estimating the parameters of the problem. In the estimation problem of phase noise and DoA, the former is an unobservable latent variable, while the DoA is the desired final result. Therefore, the EM algorithm used in this paper estimates phase noise in the E-step and estimates DoA in the M-step. The algorithm flow is shown in Figure 4, with detailed calculations referenced in [14,27,30].

The expectation–maximization (EM) algorithm, a well-established framework for estimation, and the MUSIC algorithm, a classic method for angle estimation, serve as the foundation for the advanced EM–MUSIC algorithm used in DoA estimation. This algorithm operates within the EM framework, mitigating the effects of phase noise during the E-step through an extended Kalman filter (EKF) and subsequently employing the MUSIC algorithm for angle estimation, refining results through iterative optimization. In the E-step, the algorithm estimates the expected values of unobservable or hidden variables based on the observed data and the values of the model parameters. The result of this step is a temporary assignment of values to the unobservable variables, with each variable taking the estimated value corresponding to its highest probability. At the same time, estimating the phase noise is a crucial part of the solution. It can be achieved using a linear minimum mean squared error (LMMSE) estimator, specifically the EKF. The working principle of the Kalman filter is to compute an LMMSE estimate of the system’s current state, given the past estimates and the current observations. In the M-step, the algorithm uses the estimates from the E-step to update the model parameter estimates. This step typically uses maximum likelihood estimation to maximize the expected log-likelihood of the observed data.

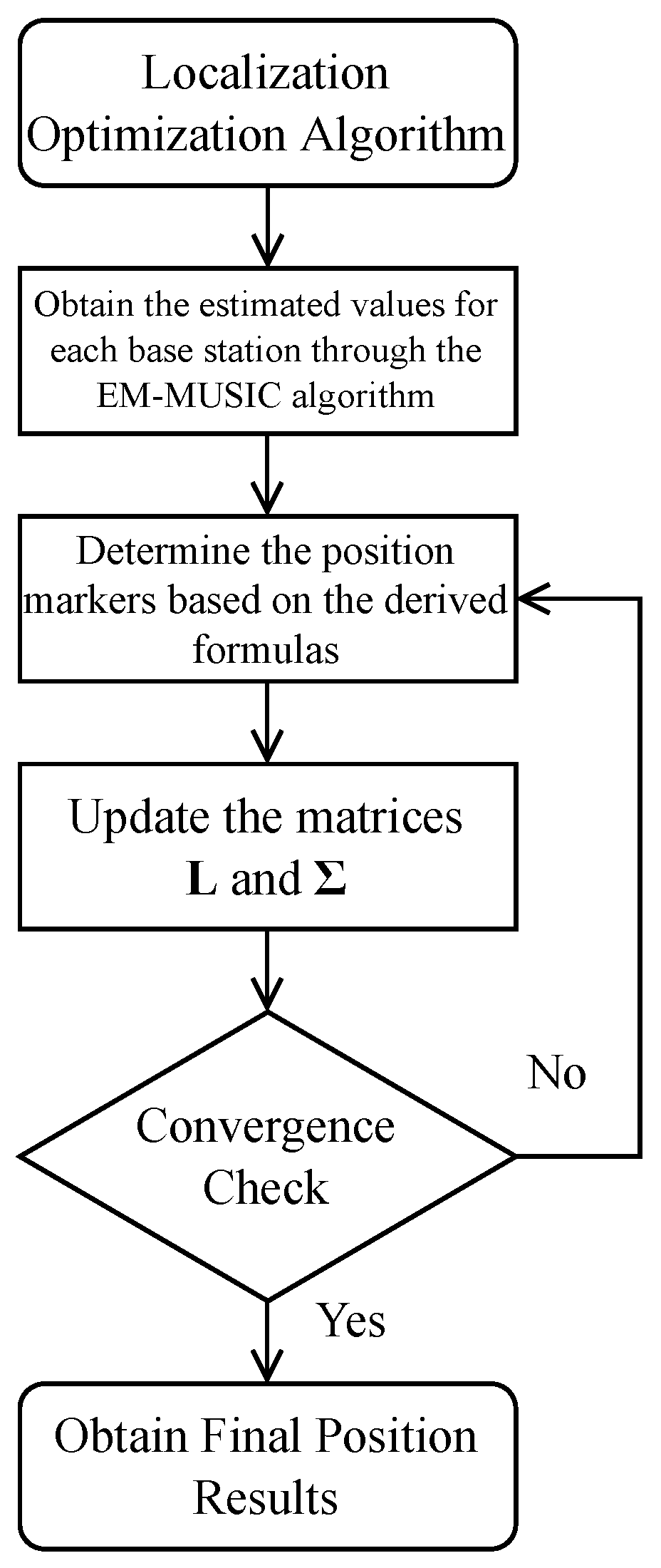
3.2. Optimization Algorithm for Multiple Base Stations

For the optimization problem (13), the general solution method assumes that the DoA estimation errors of each base station are identical, which means ${\sigma }_{i_1}^2={\sigma }_{i_2}^2$, thus transforming the problem into a least-squares problem [12]. Some base stations may receive signals that are severely interfered with. The quality of their received signals, measured by SNR, is significantly worse than that of others. As a result, the errors in their angle estimation are larger, thereby leading to poorer localization results. There are also methods that involve filtering to select higher-quality signals to participate in the localization computation, while the information from signals with poorer quality is not effectively utilized.

This paper assumes that the angle estimation error is not very large. Specifically, the effects of terms beyond the first-order term in the Taylor expansion can be ignored. In this case, according to the Taylor expansion formula, we can obtain that $({\widehat{\beta }}_i-{\beta }_i)\approx sin({\widehat{\beta }}_i-{\beta }_i)$. At this point, based on the geometric relationships and the sum-to-product formulas for trigonometric functions:

$$l_i=\sqrt{{(x_1-x_{i,1})}^2+{(x_2-x_{i,2})}^2},$$

(14)

$$\begin{array}{cc}\hfill sin({\overline{\beta }}_i-{\widehat{\beta }}_i)& =sin{\overline{\beta }}_{i}cos{\widehat{\beta }}_i-cos{\overline{\beta }}_{i}sin{\widehat{\beta }}_i\hfill \\ \hfill & ={\displaystyle \frac{({\overline{x}}_2-x_{i,2})cos{\widehat{\beta }}_i-({\overline{x}}_1-x_{i,1})sin{\widehat{\beta }}_i}{d_i}},\hfill \end{array}$$

(15)

where $d_i$ is the distance from the target to base station i. At this point, the optimization problem is transformed into

$$\begin{array}{cc}\hfill \overline{\mathbf{z}}& =argmin\sum _{i=1}^{N_b}{\displaystyle \frac{{\left[({\overline{x}}_2-x_{i,2})cos{\widehat{\beta }}_i-({\overline{x}}_1-x_{i,1})sin{\widehat{\beta }}_i\right]}^2}{{\sigma }_i^2{d}_i^2}}\hfill \\ \hfill & =argmin{(\mathbf{G}\overline{\mathbf{z}}-\mathbf{k})}^T{\mathbf{L}}^{-1}{\mathbf{\Sigma }}^{-1}(\mathbf{G}\overline{\mathbf{z}}-\mathbf{k}),\hfill \end{array}$$

(16)

where

$$\mathbf{G}=\left[\begin{array}{cc}sin{\widehat{\beta }}_1& -cos{\widehat{\beta }}_i\\ ⋮& ⋮\\ sin{\widehat{\beta }}_{N_b}& -cos{\widehat{\beta }}_{N_b}\end{array}\right],$$

(17)

$$\mathbf{k}=\left[\begin{array}{c}{x}_{1,1}sin{\widehat{\beta }}_1-x_{1,2}cos{\widehat{\beta }}_i\\ ⋮\\ x_{N_b,1}sin{\widehat{\beta }}_{N_b}-x_{N_b,2}cos{\widehat{\beta }}_{N_b}\end{array}\right],$$

(18)

$$\mathbf{L}=\mathrm{diag}\{l_1^2,\dots ,l_{N_b}^2\},$$

(19)

$$\mathbf{\Sigma }=\mathrm{diag}\{{\sigma }_1^2,\dots ,{\sigma }_{N_b}^2\}.$$

(20)

This separation of variables simplifies the optimization process. However, strictly speaking, this optimization problem cannot be solved directly. The matrices $\mathbf{L}$ and $\mathbf{\Sigma }$ change according to the estimation results of the DoA. These results vary for different base stations as the localization outcomes differ. Moreover, the relationship between these two matrices and the coordinates is nonlinear, which makes the calculation further complex. However, if $\mathbf{L}$ and $\mathbf{\Sigma }$ are considered as constants, the optimization problem becomes a well-conditioned convex function. It should be noted that in this case, the changes in $\mathbf{L}$ and $\mathbf{\Sigma }$ with respect to the optimization results are not significant. Specifically, in the scenario of Figure 3, the position is always within the range of the shadow area formed by the base stations. Therefore, the changes in distance to each base station are minor and do not significantly affect the entire solution. As a result, the algorithm adopts this strategy: treat $\mathbf{L}$ and $\mathbf{\Sigma }$ as constants to simplify the calculation process and then iteratively update these matrices in further optimization steps. At this point, the solution to this problem is given by

$$\overline{\mathbf{z}}={\left({\mathbf{G}}^T{\mathbf{L}}^{-1}{\mathbf{\Sigma }}^{-1}\mathbf{G}\right)}^{-1}{\mathbf{G}}^T{\mathbf{L}}^{-1}{\mathbf{\Sigma }}^{-1}\mathbf{k}.$$

(21)

As the optimization results converge further, the changes in $\mathbf{L}$ and $\mathbf{\Sigma }$ become smaller, meeting the conditions of the proposed assumptions. The summary of the multiple base stations optimization localization algorithm based on angle estimation is shown in Figure 5.

3.3. Complexity Analysis

In this section, we provide a brief analysis of the algorithm’s complexity. Initially, the computational complexities associated with several common matrix operations are presented as follows. Multiplying an $M\times N$ matrix by an $N\times P$ matrix has a complexity of $\mathcal{O}\left(MNP\right)$, while multiplying an $M\times N$ matrix by a diagonal $N\times N$ matrix has a complexity of $\mathcal{O}\left(MN\right)$. The eigenvalue decomposition (EVD) of an $M\times M$ matrix has a complexity of $\mathcal{O}\left(M^3\right)$, and matrix inversion exhibits a slightly higher complexity than EVD, but it remains $\mathcal{O}\left(M^3\right)$. It is worth emphasizing that M represents the number of antennas and N represents the number of snapshots.

The EM–MUSIC algorithm consists of the EKF as the E-step and the MUSIC algorithm as the M-step. For phase noise compensation, the EKF operating on a single data sample involves scalar multiplication with $\mathcal{O}\left(1\right)$ complexity, while the EKF applied to all data samples has a complexity of $\mathcal{O}\left(MN\right)$.

For DoA estimation, the MUSIC algorithm includes three stages: constructing the autocorrelation matrix (with complexity $\mathcal{O}\left(M^{2}N\right)$), performing EVD ($\mathcal{O}\left(M^3\right)$), and forming the spatial spectrum function ($\mathcal{O}\left(M^5\right)$). The Capon algorithm differs from MUSIC by replacing EVD with matrix inversion and the spatial spectrum construction, resulting in a higher computational complexity. The ESPRIT algorithm, which divides the antenna array into two sub-arrays and computes the phase differences of the signals, reduces M to half of its value in MUSIC and Capon and eliminates the need for spatial spectrum searching, leading to a lower computational complexity of $\mathcal{O}\left(M^{2}N\right)$ and $\mathcal{O}\left(M^3\right)$. Overall, the total complexity of the EM–MUSIC algorithm is dominated by the MUSIC algorithm. And the above analysis can be summarized in

Table 1. Computational complexity of DoA estimation algorithms.

DoA Estimation Algorithms	Computational Complexity
EM–MUSIC	$\mathcal{O}\left(M^{2}N\right)+\mathcal{O}\left(M^5\right)$
Capon	$\mathcal{O}\left(M^{2}N\right)+\mathcal{O}\left(M^5\right)$
MUSIC	$\mathcal{O}\left(M^{2}N\right)+\mathcal{O}\left(M^5\right)$
ESPRIT	$\mathcal{O}\left(M^{2}N\right)+\mathcal{O}\left(M^3\right)$

.

For the localization optimization algorithm, the computational operations in a single optimization iteration involve four inversions of a diagonal matrix of dimension $N_b\times N_b$ with complexity $\mathcal{O}\left(N_b\right)$, the inversion of a $2\times 2$ matrix with complexity $\mathcal{O}\left(1\right)$, and remaining matrix multiplications with complexity $\mathcal{O}\left(N_b^3\right)$. Consequently, the overall computational complexity of the localization optimization algorithm is $\mathcal{O}\left(N_b^4\right)$.

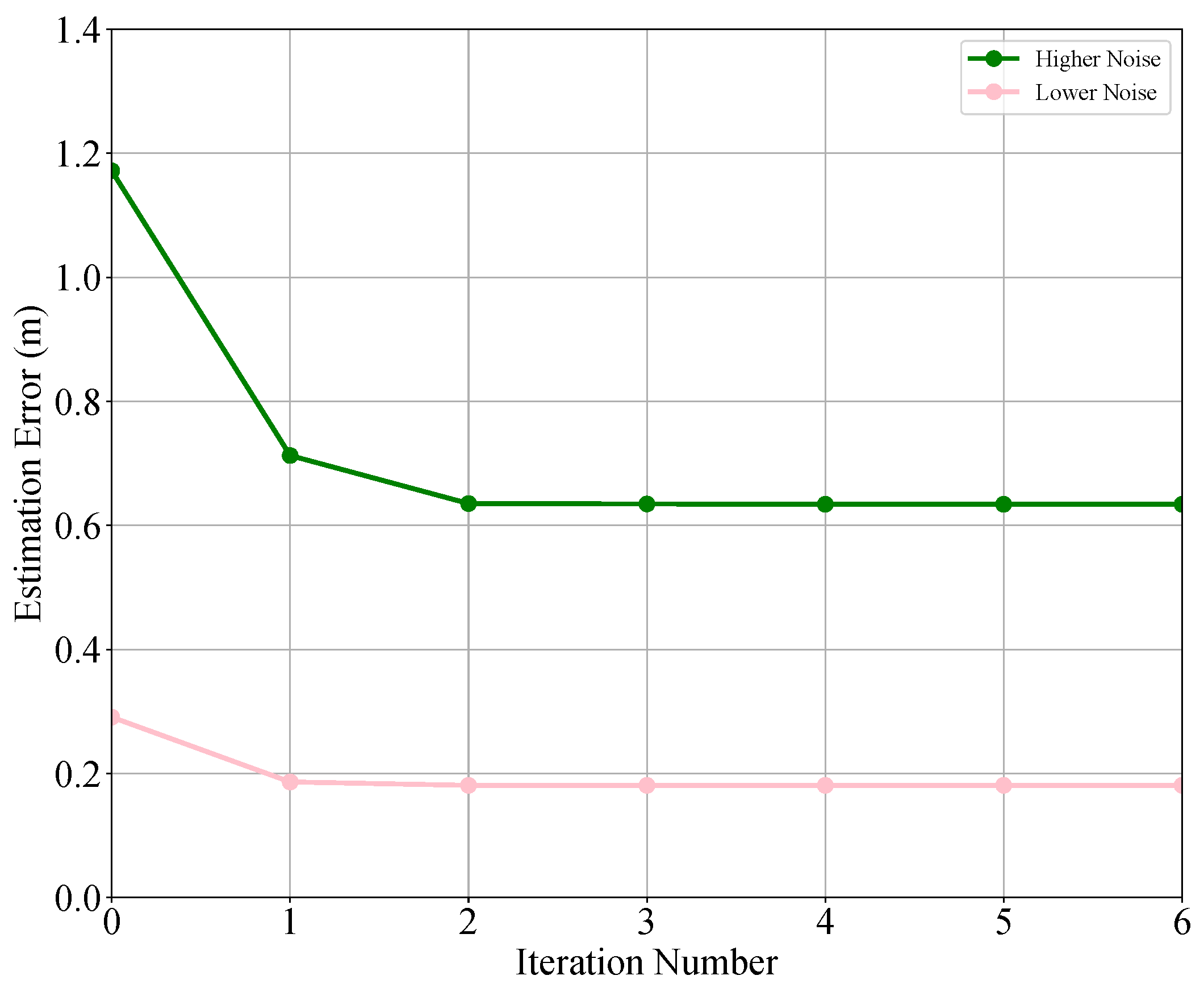
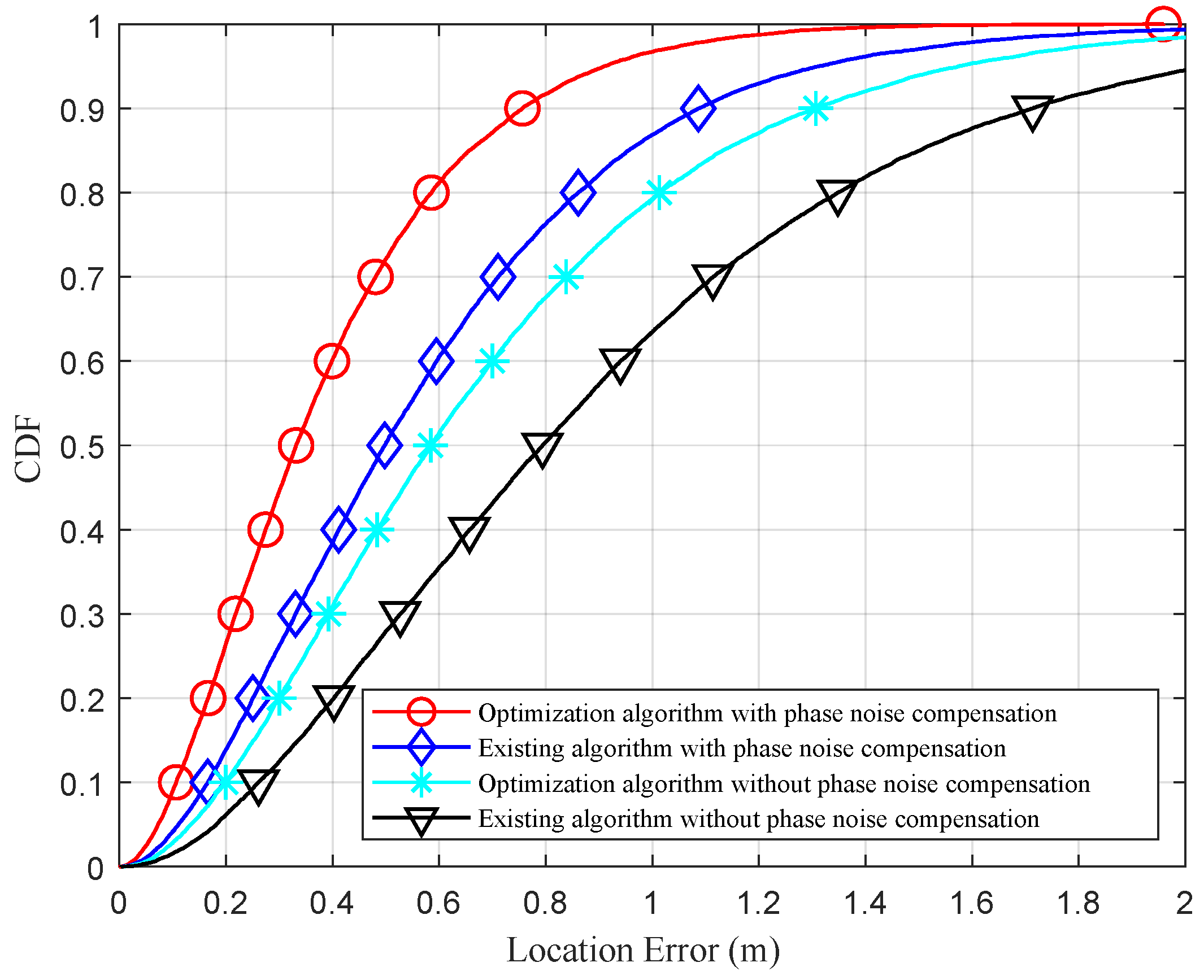
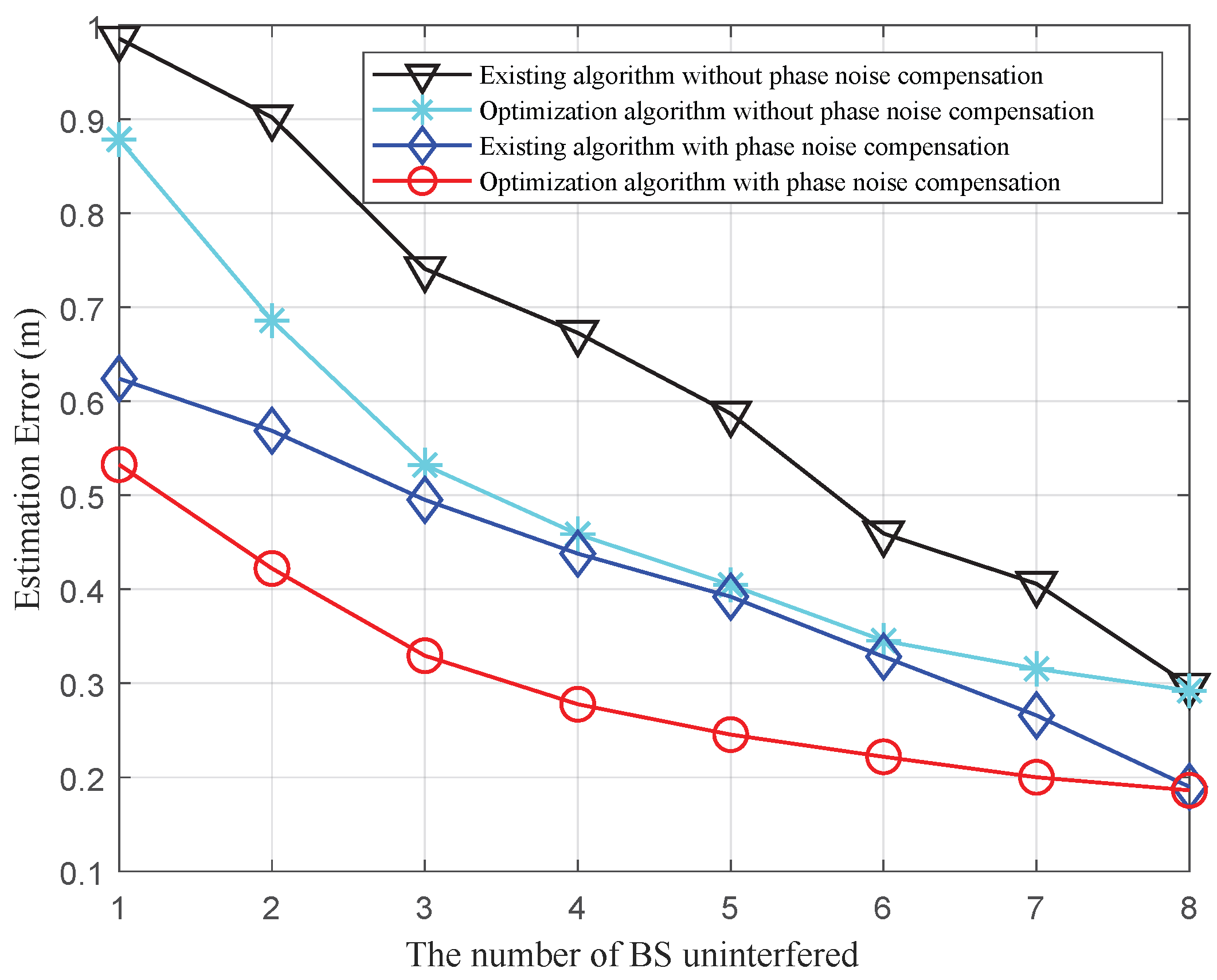
4. Simulation Results

This simulation system includes several devices whose locations need to be determined, as well as several base stations. Under typical circumstances, each base station has four antennas, and each antenna receives 32 digital signal samples per second, with a transmission symbol rate of 1 M. It is assumed that the signals received by the devices have already been synchronized and aligned with the communication signals in terms of timing and frequency.

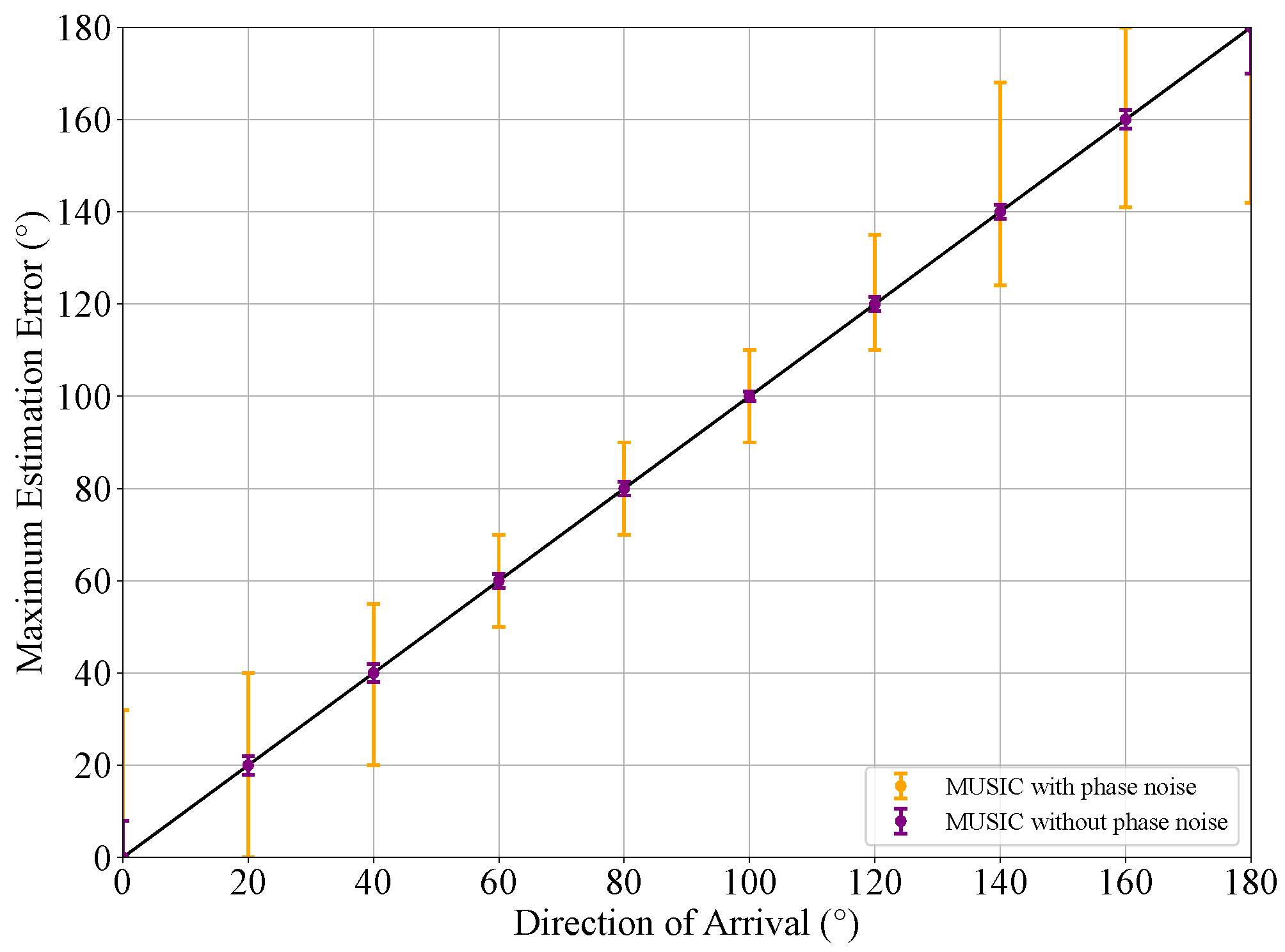
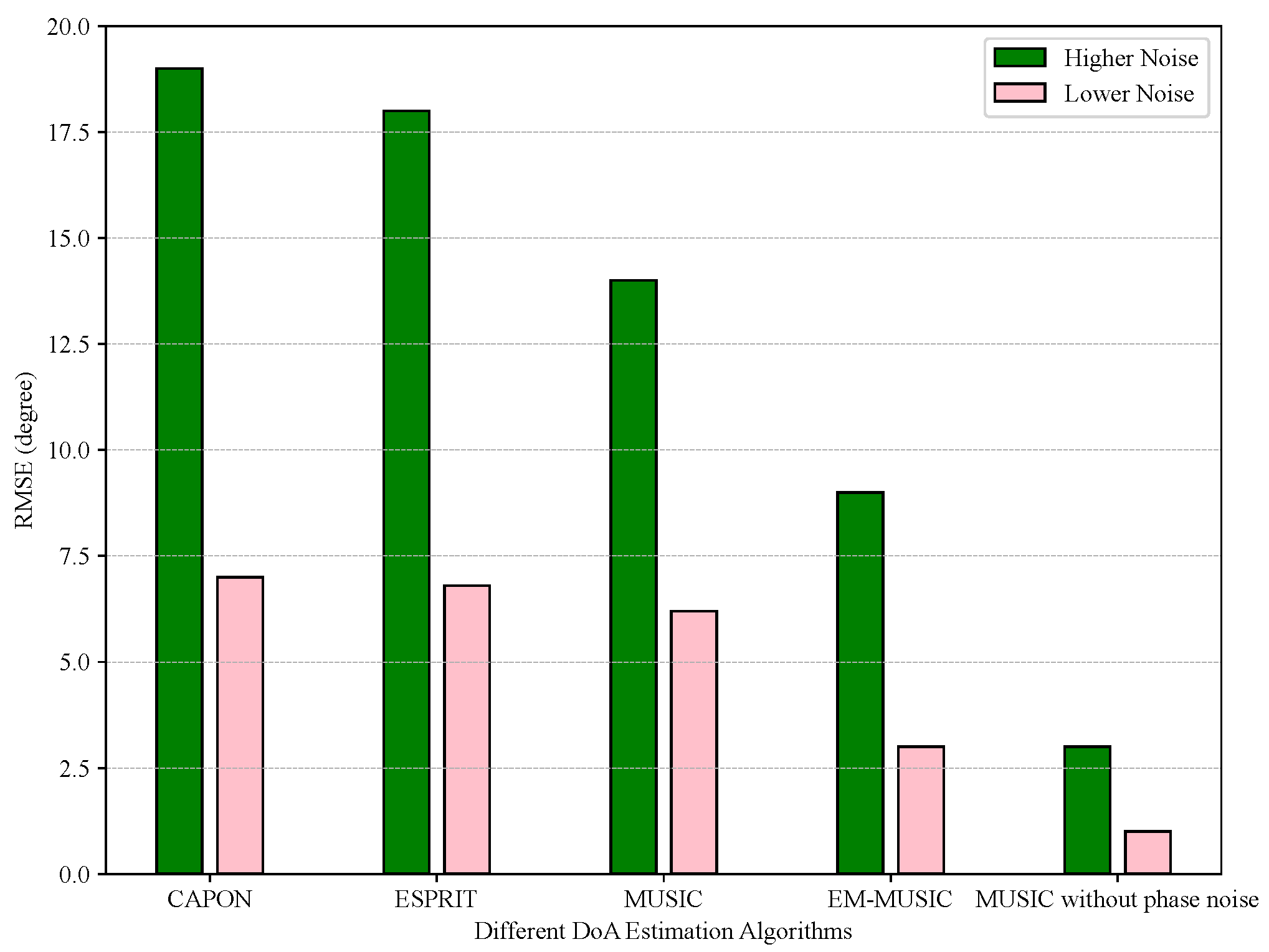
4.1. Performance of Angle Estimation

Using the MUSIC algorithm as an example, the first simulation experiment demonstrates the impact of phase noise on DoA estimation. Here, we consider the situation where the received signal arrives at the receiver from different DoAs (from $0^{\circ }$ to ${180}^{\circ }$), with additive Gaussian white noise at 20 dB SNR, and the magnitude of the phase noise is ${\sigma }_{\phi }^2={10}^{-4}$${\mathrm{rad}}^2$. The experimental results are shown in Figure 6, where error bars represent the maximum DoA estimation error of 10,000 Monte Carlo simulations. As seen from the figure, phase noise causes a significant increase in DoA estimation error in the MUSIC system. Furthermore, when the signals arrive from different angles, the RMSE of the DoA estimation differs. The reason is that the essence of DoA estimation is to calculate the phase difference between the baselines of the array. From Equation (2), it can be observed that their relationship is nonlinear. The actual layout of the base station leads to the inconsistency of the angle at which the signal reaches the receivers in the range of action, and different DoAs will lead to a large difference in the estimation error.

To further illustrate the impact of phase noise on DoA estimation, this paper calculates the RMSE of DoA estimation at the receiver for signals arriving from ${20}^{\circ }$ to ${160}^{\circ }$. Here, we consider two scenarios: (1) with relatively higher noise corresponding to an additive Gaussian white noise of SNR = 10 dB and phase noise magnitude of ${\sigma }_{\phi }^2={10}^{-3}$ ${\mathrm{rad}}^2$; (2) with relatively lower noise corresponding to an additive Gaussian white noise of SNR = 20 dB and phase noise magnitude of ${\sigma }_{\phi }^2={10}^{-4}$ ${\mathrm{rad}}^2$. In addition to the MUSIC algorithm, the CAPON [16], ESPRIT [15], and EM–MUSIC algorithms are also examined to understand the effect of phase noise. The results of the MUSIC algorithm under phase noise are shown in Figure 7. It can be observed that phase noise affects the DoA estimation performance of all algorithms in the communication system. The EM–MUSIC algorithm, by estimating and compensating for phase noise, can effectively reduce the RMSE of DoA estimation.

4.2. Performance of Localization Algorithm

The previous experiments demonstrate the performance of DoA estimation at a single base station. Now, we consider the localization of multiple base stations. The simulated scenario is shown in Figure 8: eight base stations receiving signals are uniformly distributed along the edges and corners of the room, while eight target points to be located are uniformly distributed within the room. In the experiment, each of the eight targets is located individually, without considering the mutual interference of signals transmitted by the targets.

Due to the solution of problem (13) involving assumptions and iterative substitutions, the first localization experiment studied the convergence of the proposed algorithm. This experiment calculates the mean absolute error of the localization results for all target points as the average error of the localization system. After 10,000 Monte Carlo simulations, where the noise level is consistent with that in Figure 7, the variation of the average error with the number of iterations is shown in Figure 9. The results in the figure indicate that when the noise is relatively lower, the proposed algorithm only requires one step to converge the average localization error to a very low level. When the noise is relatively higher, the algorithm can also converge the localization results to a stable value after two iterations. Summing up the above three experiments, the proposed algorithm exhibits good convergence under various noise levels, and the assumptions made in the solution derivation are reasonable.

The previous experimental results and analysis demonstrate the stability of the proposed algorithm. In the following text, the optimization experiment is used to study the improvement in localization accuracy achieved by the proposed algorithm. Existing algorithms do not consider phase noise and assign identical weights to the DoA estimation results of all base stations. Compared to existing algorithms, the proposed algorithm introduces two main improvements: phase noise compensation and optimization using different weights based on the RMSE of DoA estimation at each base station. The following sections will separately examine the effectiveness of these two improvements through experiments and explanations.

In actual communication systems, the interference levels of signals received by each base station are usually different. Considering the situation where six base stations have relatively high noise levels and two have relatively low noise levels, this experiment calculates the cumulative distribution function (CDF) of the localization results for eight targets using different algorithms. As shown in Figure 10, we can see that the optimization algorithm effectively reduces the error of localization results under different interference levels at each base station. Additionally, compensating for phase noise can yield more accurate DoA estimation results, thereby further improving localization accuracy.

In order to further study the performance of various algorithms under different levels of interference at each base station receiving a signal, the next experiment adjusts the number of base stations affected by interference. The average localization error of all target localization results is shown in Figure 11. From the results, it can be observed that when the interference levels at each base station are quite different, the average method, which assigns equal estimation weights for the DoA at each base station, has relatively large errors. The optimization algorithm can effectively improve the accuracy of localization results. When the levels of interference at each base station are similar (either all stations are affected by interference or none are), the performance of the optimization is not significantly different from the average method. Additionally, the compensation of phase noise can effectively reduce the error level of the localization results.

In the next experiment, we consider the scenario where each base station received signals under the same level of interference. The average localization error of the results is shown in Figure 12. In this scenario, the Gaussian white noise for the received signals at each base station is set to an SNR of 20 dB, and the phase noise variance is ${\sigma }_{\phi }^2={10}^{-4}$ ${\mathrm{rad}}^2$. From the results, it can be seen that the localization error of all algorithms decreases as the number of base stations used for localization increases. However, considering practical factors such as hardware limitations, the actual localization system needs to comprehensively account for system configuration. When the noise level of received signals at all base stations is the same, the advantage of the combined optimization algorithm is not apparent. Particularly under the influence of phase noise, the DoA estimation error is relatively large. In this case, if the assumptions made in the algorithm deviate from the actual situation, the performance of the algorithm may deteriorate. However, after processing the phase noise, the localization error of the combined optimization algorithm is smaller.

By comparing the results in Figure 11 and Figure 12, it can be observed that when the reception of some base stations is severely interfered with, the localization accuracy of the current average algorithm is significantly affected. For example, when the signals received by six base stations are severely interfered with, if only the signals from two better-quality base stations are used for localization, the error is around 1 m, as shown in Figure 12. In contrast, using signals from all base stations with the optimization algorithm yields a localization error of less than 1 m, as shown in Figure 11. This indicates that the proposed optimization algorithm can effectively utilize the estimated results from all base stations, providing better performance than traditional algorithms when the interference levels vary across the base stations.

The final experiment visually demonstrates the result of a cluster of single localization instances. The experimental parameters are set as follows: the AWGN of the received signal has an SNR of 20 dB, and the phase noise variance is ${\sigma }_{\phi }^2={10}^{-4}$ ${\mathrm{rad}}^2$. As shown in Figure 13, the black cross represents the true position of the target, and the orange points represent the localization results obtained through the existing algorithm, while the purple points indicate the results from the proposed algorithm in this paper. From the results in the figure, we observe that the localization points obtained through the proposed algorithm are more compact and concentrated compared to the existing algorithm.

5. Conclusions

Due to the influence of phase noise and other factors, the localization algorithm based on DoA estimation has significant errors. This paper proposes a multiple base station optimization localization algorithm with phase noise compensation. It utilizes the EM–MUSIC algorithm to optimize the DoA estimation results from each base station. Then, based on the estimation results, a non-convex optimization problem is constructed according to RMSE. Finally, a closed-form solution is obtained through reasonable assumptions and approximations. Simulation results show that this algorithm can effectively reduce the localization error, achieving sub-meter level localization accuracy.