A Spiking LSTM Accelerator for Automatic Speech Recognition Application Based on FPGA
Abstract
:1. Introduction
2. Spiking LSTM Network
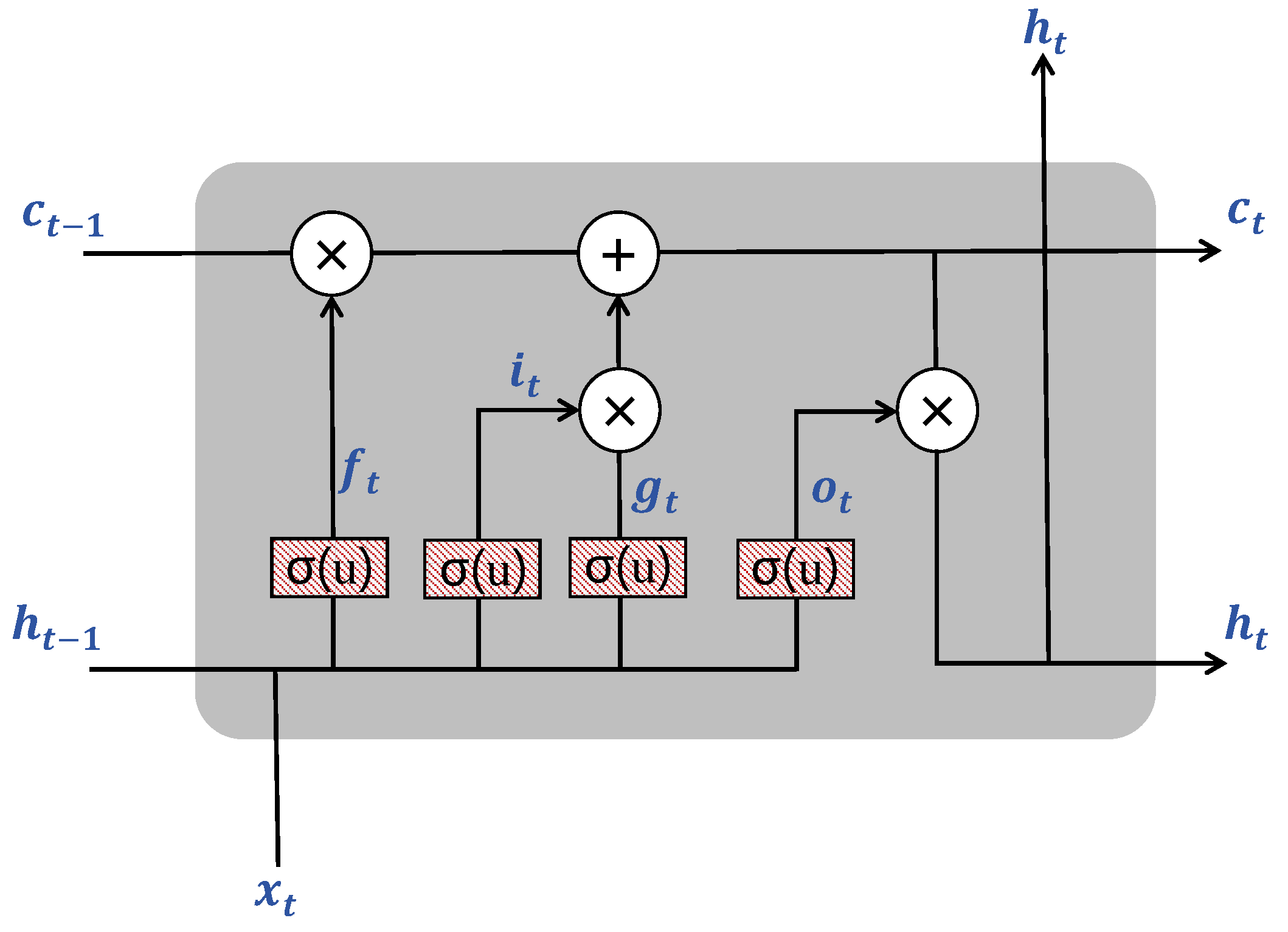
2.1. Traditional LSTM Network
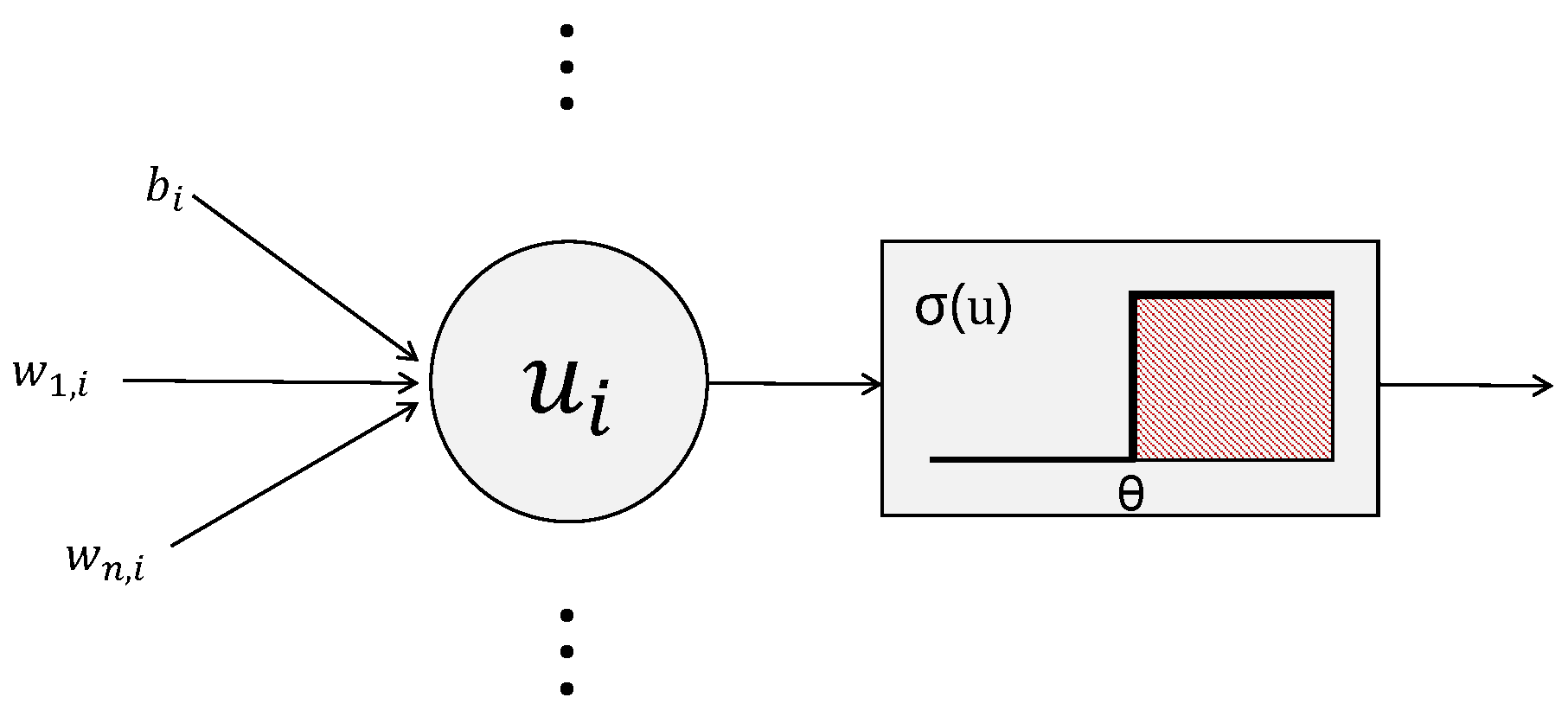
2.2. Spiking LSTM Network
2.3. Training Methodology for Spike LSTM
2.4. Spike Encoding
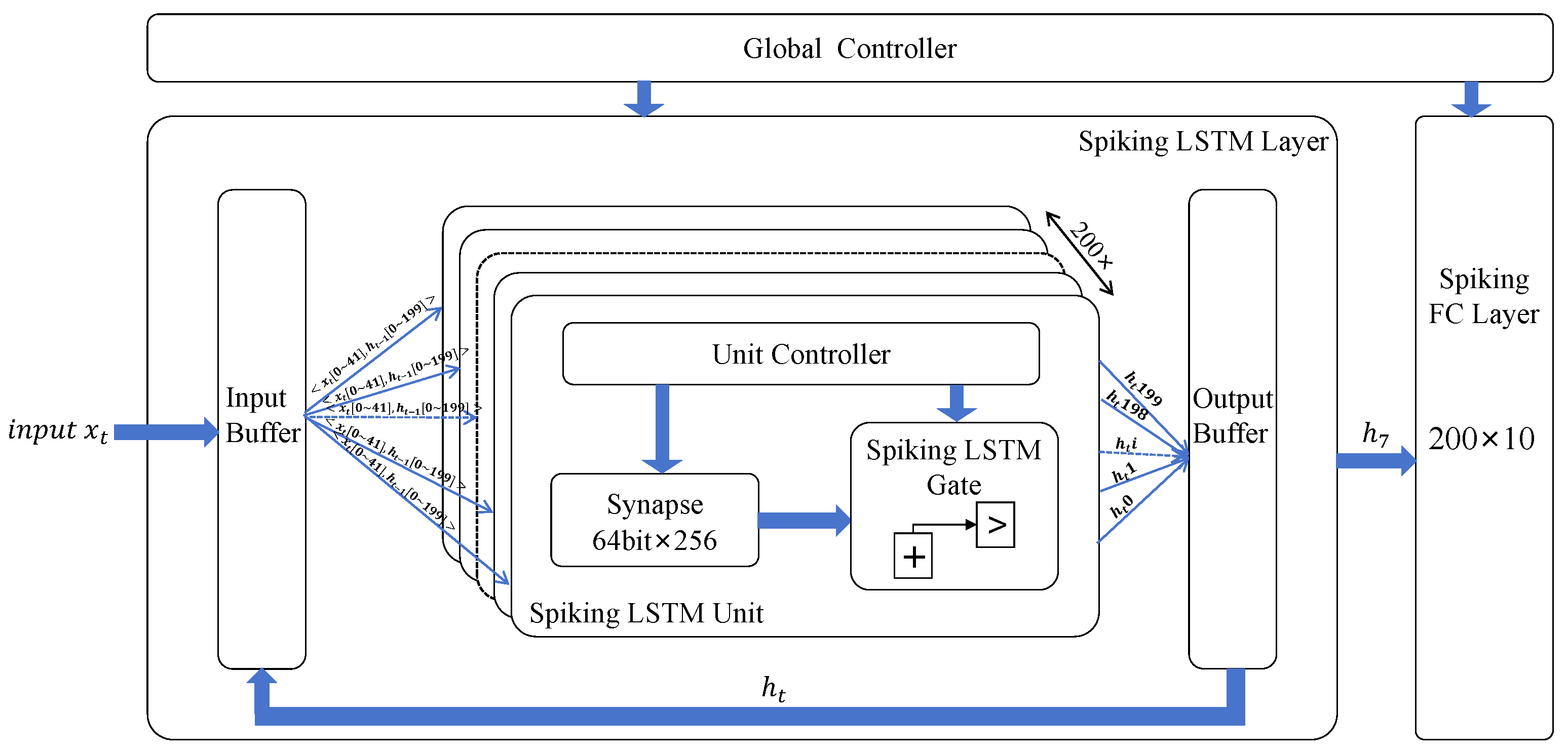
3. Proposed Spiking LSTM Accelerator
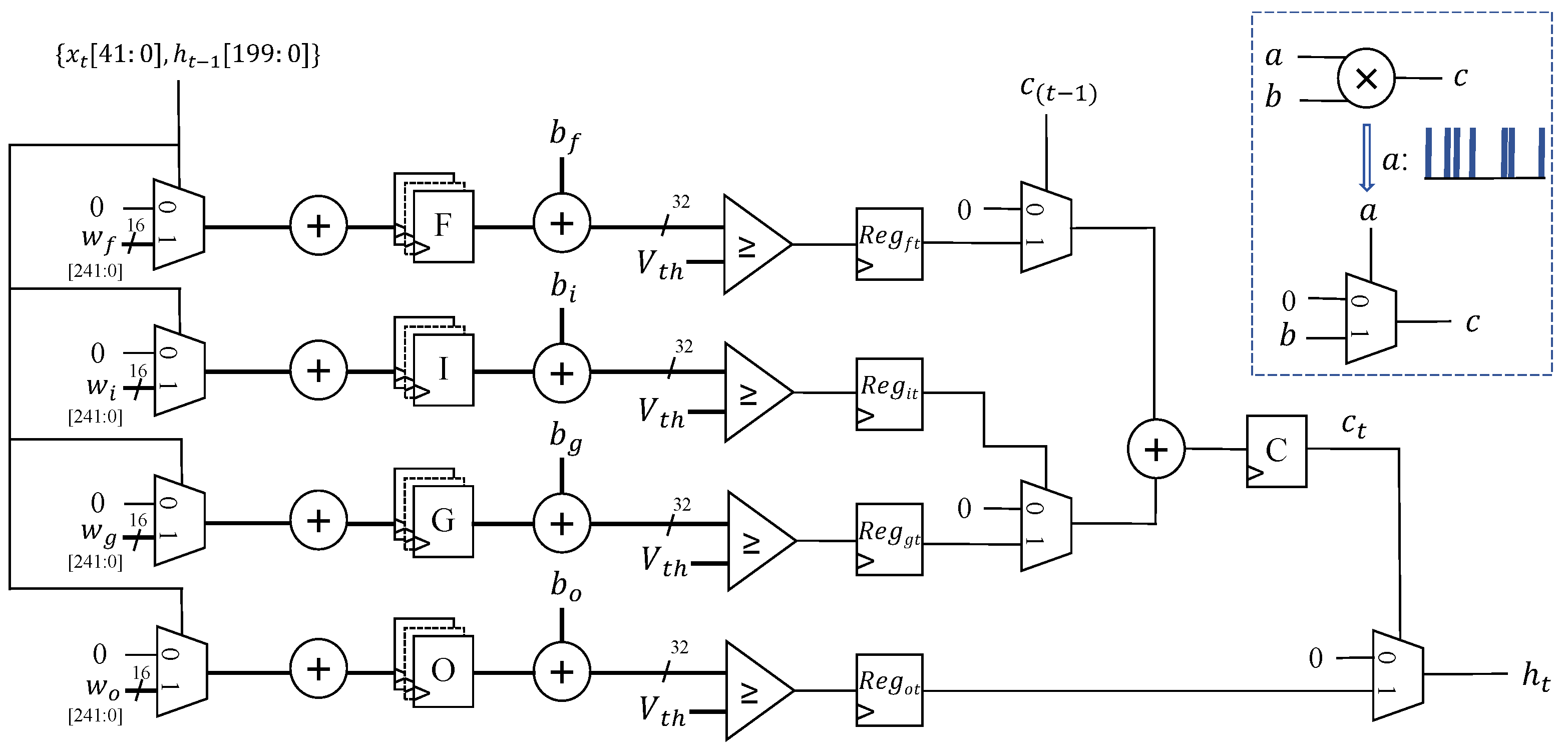
3.1. Circuit Implementation of the Spiking LSTM Layer
3.1.1. Low-Cost Spiking LSTM Gate
3.1.2. Serial–Parallel Processing
3.2. Circuit Implementation of the Spiking Fully Connected Layer
3.3. Hardware-Friendly Synapse Deployment
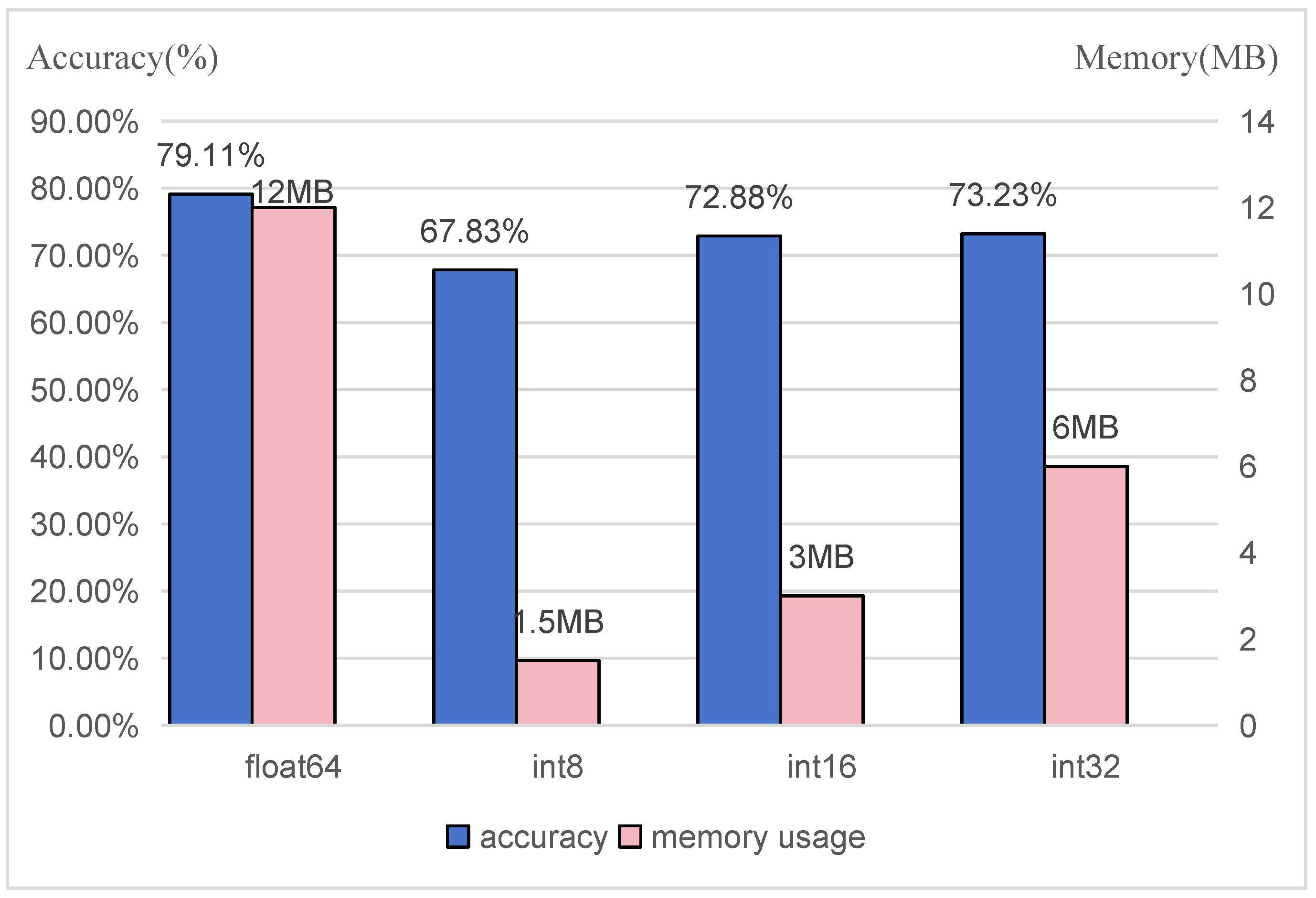
3.3.1. Weight Quantization
3.3.2. Memory Organization for Weight
4. Experiments and Results
4.1. Experimental Setup
4.2. Experimental Results
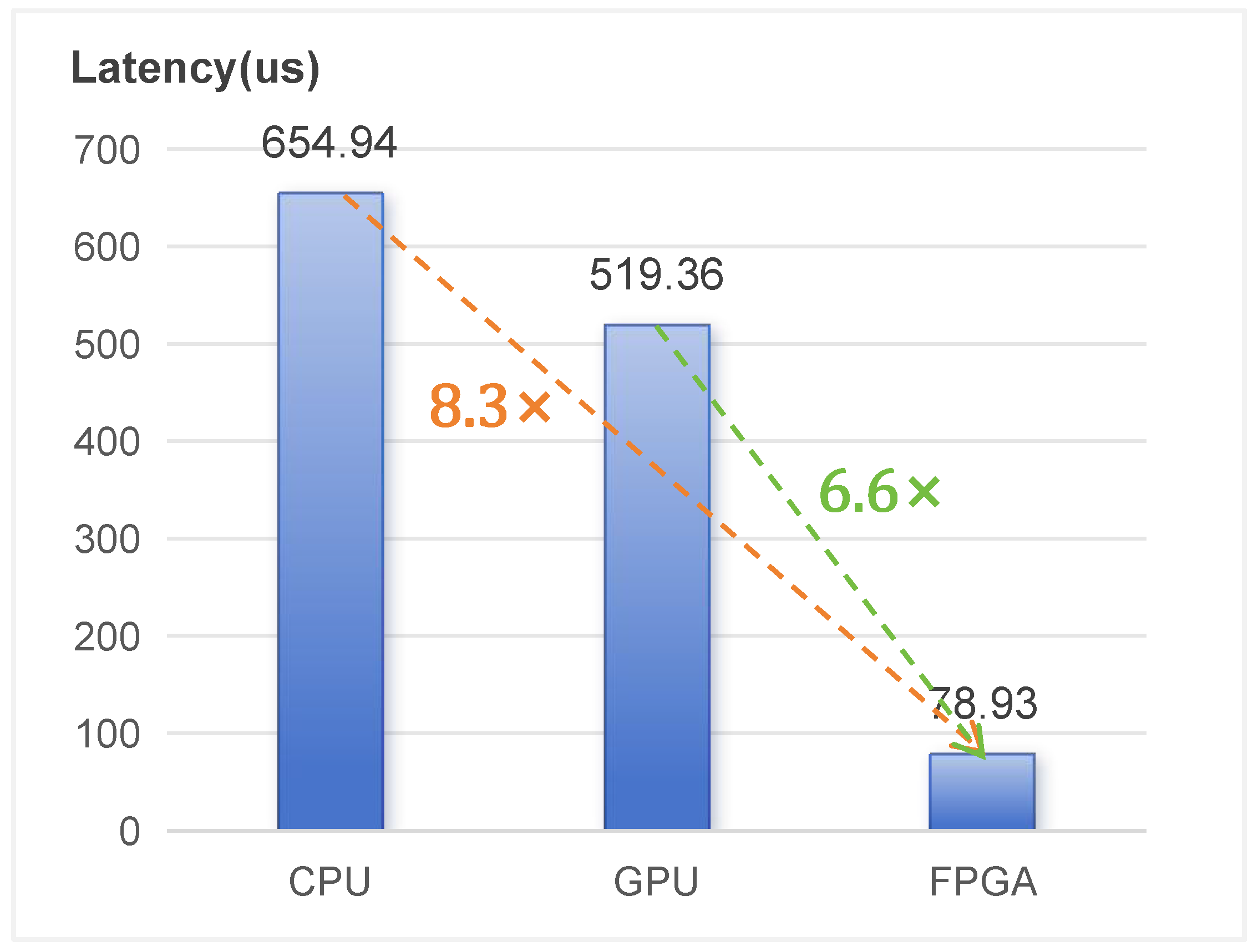
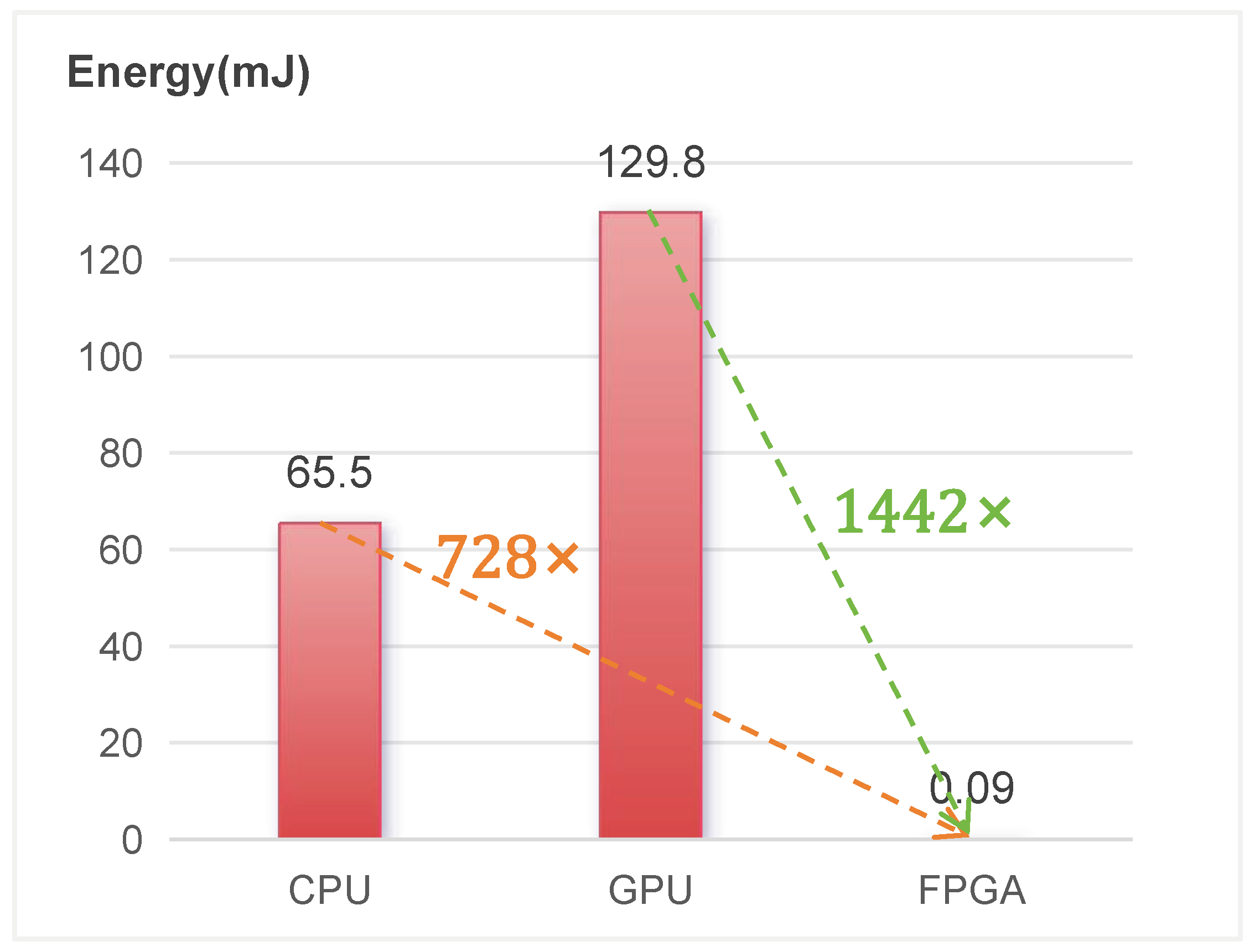
4.3. Comparison with Other Works
4.3.1. Comparison with CPU and GPU
4.3.2. Comparison with Traditional LSTM Accelerators Based on FPGA
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASR | Automatic Speech Recognition |
| LSTM | Long Short-Term Memory |
| SNN | Spiking Neural Network |
| RNN | Recurrent Neural Networks |
| FPGA | Field Programmable Gate Array |
References
- Yu, D.; Deng, L. Automatic Speech Recognition; Springer: Cham, Switzerland, 2015; Volume 1. [Google Scholar]
- Gondi, S.; Pratap, V. Performance and Efficiency Evaluation of ASR Inference on the Edge. Sustainability 2021, 13, 12392. [Google Scholar] [CrossRef]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E.; Mohamed, A.R.; Jaitly, N.; Senior, A.; Vanhoucke, V.; Nguyen, P.; Sainath, T.N.; et al. Deep Neural Networks for Acoustic Modeling in Speech Recognition: The Shared Views of Four Research Groups. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. Proc. Mach. Learn. Res. PMLR 2013, 28, 1310–1318. [Google Scholar]
- Sak, H.; Senior, A.W.; Beaufays, F. Long short-term memory recurrent neural network architectures for large scale acoustic modeling. In Proceedings of the INTERSPEECH, Singapore, 14–18 September 2014; pp. 338–342. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Cao, S.; Zhang, C.; Yao, Z.; Xiao, W.; Nie, L.; Zhan, D.; Liu, Y.; Wu, M.; Zhang, L. Efficient and effective sparse LSTM on FPGA with bank-balanced sparsity. In Proceedings of the 2019 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Seaside, CA, USA, 24–26 February 2019; pp. 63–72. [Google Scholar]
- Han, S.; Kang, J.; Mao, H.; Hu, Y.; Li, X.; Li, Y.; Xie, D.; Luo, H.; Yao, S.; Wang, Y.; et al. Ese: Efficient speech recognition engine with sparse lstm on fpga. In Proceedings of the 2017 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2017; pp. 75–84. [Google Scholar]
- Wang, M.; Wang, Z.; Lu, J.; Lin, J.; Wang, Z. E-LSTM: An Efficient Hardware Architecture for Long Short-Term Memory. IEEE J. Emerg. Sel. Top. Circuits Syst. 2019, 9, 280–291. [Google Scholar] [CrossRef]
- Wang, S.; Li, Z.; Ding, C.; Yuan, B.; Qiu, Q.; Wang, Y.; Liang, Y. C-LSTM: Enabling efficient LSTM using structured compression techniques on FPGAs. In Proceedings of the 2018 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 25–27 February 2018; pp. 11–20. [Google Scholar]
- Li, T.; Gu, S. FPGA Hardware Implementation of Efficient Long Short-Term Memory Network Based on Construction Vector Method. IEEE Access 2023, 11, 122357–122367. [Google Scholar] [CrossRef]
- Taherkhani, A.; Belatreche, A.; Li, Y.; Maguire, L.P. DL-ReSuMe: A Delay Learning-Based Remote Supervised Method for Spiking Neurons. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 3137–3149. [Google Scholar] [CrossRef] [PubMed]
- Hazan, H.; Saunders, D.; Sanghavi, D.T.; Siegelmann, H.; Kozma, R. Unsupervised Learning with Self-Organizing Spiking Neural Networks. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Rathi, N.; Panda, P.; Roy, K. STDP-Based Pruning of Connections and Weight Quantization in Spiking Neural Networks for Energy-Efficient Recognition. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2019, 38, 668–677. [Google Scholar] [CrossRef]
- Akopyan, F.; Sawada, J.; Cassidy, A.; Alvarez-Icaza, R.; Arthur, J.; Merolla, P.; Imam, N.; Nakamura, Y.; Datta, P.; Nam, G.J.; et al. TrueNorth: Design and Tool Flow of a 65 mW 1 Million Neuron Programmable Neurosynaptic Chip. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2015, 34, 1537–1557. [Google Scholar] [CrossRef]
- Davies, M.; Srinivasa, N.; Lin, T.H.; Chinya, G.; Cao, Y.; Choday, S.H.; Dimou, G.; Joshi, P.; Imam, N.; Jain, S.; et al. Loihi: A Neuromorphic Manycore Processor with On-Chip Learning. IEEE Micro 2018, 38, 82–99. [Google Scholar] [CrossRef]
- Frenkel, C.; Lefebvre, M.; Legat, J.D.; Bol, D. A 0.086-mm2 12.7-pJ/SOP 64k-Synapse 256-Neuron Online-Learning Digital Spiking Neuromorphic Processor in 28-nm CMOS. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 145–158. [Google Scholar] [CrossRef]
- Frenkel, C.; Legat, J.D.; Bol, D. MorphIC: A 65-nm 738k-Synapse/mm2 Quad-Core Binary-Weight Digital Neuromorphic Processor with Stochastic Spike-Driven Online Learning. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 999–1010. [Google Scholar] [CrossRef] [PubMed]
- Pu, J.; Goh, W.L.; Nambiar, V.P.; Wong, M.M.; Do, A.T. A 5.28-mm2 4.5-pJ/SOP Energy-Efficient Spiking Neural Network Hardware with Reconfigurable High Processing Speed Neuron Core and Congestion-Aware Router. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 5081–5094. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Z.; Mao, R.; Xiao, J.; Chang, L.; Zhou, J. A Fast and Energy-Efficient SNN Processor with Adaptive Clock/Event-Driven Computation Scheme and Online Learning. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 1543–1552. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, J.; Wong, W.F.; Peh, L.S. Shenjing: A low power reconfigurable neuromorphic accelerator with partial-sum and spike networks-on-chip. In Proceedings of the 2020 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 9–13 March 2020; pp. 240–245. [Google Scholar] [CrossRef]
- Lotfi Rezaabad, A.; Vishwanath, S. Long short-term memory spiking networks and their applications. In Proceedings of the International Conference on Neuromorphic Systems, Oak Ridge, TN, USA, 28–30 July 2020; pp. 1–9. [Google Scholar]
- Shrestha, A.; Ahmed, K.; Wang, Y.; Widemann, D.P.; Moody, A.T.; Van Essen, B.C.; Qiu, Q. A spike-based long short-term memory on a neurosynaptic processor. In Proceedings of the 2017 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), Irvine, CA, USA, 13–16 November 2017; pp. 631–637. [Google Scholar] [CrossRef]
- Rao, A.; Plank, P.; Wild, A.; Maass, W. A Long Short-Term Memory for AI Applications in Spike-based Neuromorphic Hardware. Nat. Mach. Intell. 2022, 4, 467–479. [Google Scholar] [CrossRef]
- Sengupta, A.; Ye, Y.; Wang, R.; Liu, C.; Roy, K. Going Deeper in Spiking Neural Networks: VGG and Residual Architectures. Front. Neurosci. 2019, 13, 95. [Google Scholar] [CrossRef]
- Jin, Y.; Zhang, W.; Li, P. Hybrid macro/micro level backpropagation for training deep spiking neural networks. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 3–8 December 2018; pp. 7005–7015. [Google Scholar]
- Roy, K.; Jaiswal, A.; Panda, P. Towards spike-based machine intelligence with neuromorphic computing. Nature 2019, 575, 607–617. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Jackson, Z. Free Spoken Digit Dataset (fsdd). Technical Report. 2016. Available online: https://zenodo.org/records/1342401 (accessed on 10 February 2023).
- Horowitz, M. Computing’s energy problem (and what we can do about it). In Proceedings of the 2014 IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC), San Francisco, CA, USA, 9–13 February 2014; pp. 10–14. [Google Scholar] [CrossRef]
- torch.quantize_per_tensor. Available online: https://pytorch.org/docs/stable/generated/torch.quantize_per_tensor.html (accessed on 11 May 2023).
- Que, Z.; Nakahara, H.; Nurvitadhi, E.; Fan, H.; Zeng, C.; Meng, J.; Niu, X.; Luk, W. Optimizing Reconfigurable Recurrent Neural Networks. In Proceedings of the 2020 IEEE 28th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Fayetteville, AR, USA, 3–6 May 2020; pp. 10–18. [Google Scholar] [CrossRef]
- Mao, N.; Yang, H.; Huang, Z. An Instruction-Driven Batch-Based High-Performance Resource-Efficient LSTM Accelerator on FPGA. Electronics 2023, 12, 1731. [Google Scholar] [CrossRef]






| Resource | Utilization | Available | Utilization% |
|---|---|---|---|
| LUT | 36,592 | 133,800 | 27.35 |
| FF | 24,521 | 269,200 | 9.11 |
| BRAM | 202 | 365 | 55.34 |
| BUFG | 12 | 32 | 37.50 |
| Resource | Utilization | Available | Utilization% |
|---|---|---|---|
| LUT | 34,578 | 53,200 | 65.00 |
| LUTRAM | 256 | 17,400 | 1.47 |
| FF | 22,911 | 106,400 | 21.53 |
| BRAM | 140 | 140 | 100.00 |
| BUFG | 12 | 32 | 37.50 |
| ESE [8] | C-LSTM [10] | E-LSTM [9] | [32] | [33] | [11] | Ours | Ours | |
|---|---|---|---|---|---|---|---|---|
| Year | 2017 | 2018 | 2019 | 2020 | 2023 | 2023 | - | - |
| Platform | XCKU060 | Virtex-7 | Arria10 | GX2800 | Alevo U50 | ZCU102 | XC7A200t | XC7Z020 |
| LUT | 293,920 | 621,201 | - | - | 122,935 | 187,084 | 36,592 | 34,578 |
| FF | 453,068 | 234,562 | - | - | 407,690 | 290,304 | 24,521 | 22,911 |
| BRAM | 947 | 942 | - | - | 282 | 610 | 202 | 140 |
| LUTRAM | 69,939 | 0 | - | - | 5536 | 0 | 0 | 256 |
| DSP | 1504 | 2347 | - | 4368 | 4224 | 1457 | 0 | 0 |
| Architecture | Google LSTM | Small LSTM | Vanilla LSTM | - | Google LSTM | 1024-1024 | 42-200-10 | 42-200-10 |
| Dataset | TIMIT | TIMIT | TIMIT | UCF101 | - | TIMIT | FSDD | FSDD |
| Accuracy | 79.30% | 75.43% | - | 70.10% | - | - | 72.88% | 72.88% |
| Quant. | int12 | int16 | int8 | int8 | int16 | int12 | int16 | int16 |
| Freq. (MHz) | 200 | 200 | 200 | 260 | 280 | 200 | 120 | 120 |
| Latency (µs) | 57 | 5.4 | 23.9 | 33 | 9786 | 12.4 | 78.93 | 78.93 |
| Power (W) | 41 | 22 | 15.9 | 125 | 32.3 | 15 | 1.1 | 0.84 |
| Energy/Inf. (µJ/I) | 2337 | 119 | 380 | 4125 | 316,088 | 186 | 87 | 66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, T.; Dong, F.; Chen, C.; Ouyang, C.; Wang, Z.; Yang, Y. A Spiking LSTM Accelerator for Automatic Speech Recognition Application Based on FPGA. Electronics 2024, 13, 827. https://doi.org/10.3390/electronics13050827
Yin T, Dong F, Chen C, Ouyang C, Wang Z, Yang Y. A Spiking LSTM Accelerator for Automatic Speech Recognition Application Based on FPGA. Electronics. 2024; 13(5):827. https://doi.org/10.3390/electronics13050827
Chicago/Turabian StyleYin, Tingting, Feihong Dong, Chao Chen, Chenghao Ouyang, Zheng Wang, and Yongkui Yang. 2024. "A Spiking LSTM Accelerator for Automatic Speech Recognition Application Based on FPGA" Electronics 13, no. 5: 827. https://doi.org/10.3390/electronics13050827
APA StyleYin, T., Dong, F., Chen, C., Ouyang, C., Wang, Z., & Yang, Y. (2024). A Spiking LSTM Accelerator for Automatic Speech Recognition Application Based on FPGA. Electronics, 13(5), 827. https://doi.org/10.3390/electronics13050827






