A Quadrature Oscillator with a Frequency-Tuned Distributed RC Network Analysis
Abstract
:1. Introduction
2. Design Strategies
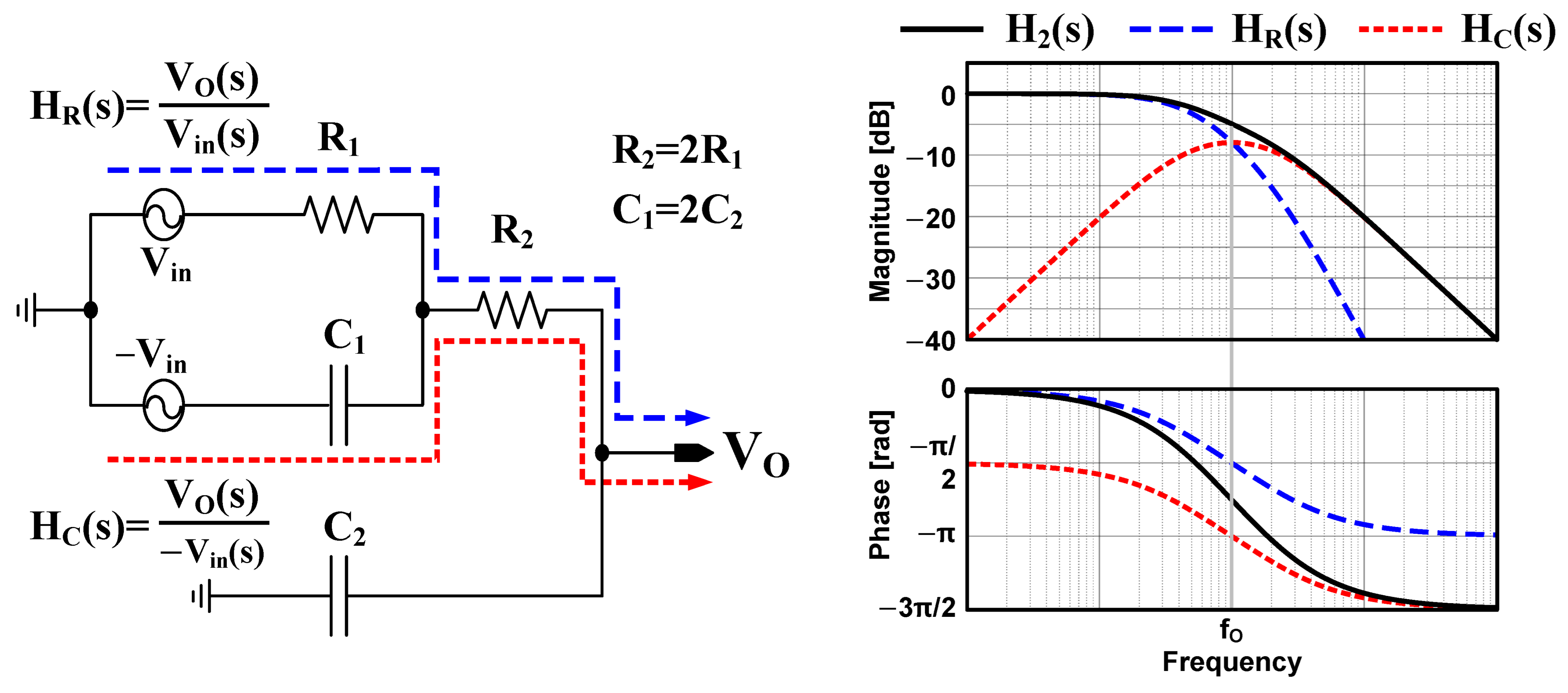
2.1. Proposed Two-Stage Distributed RC Network
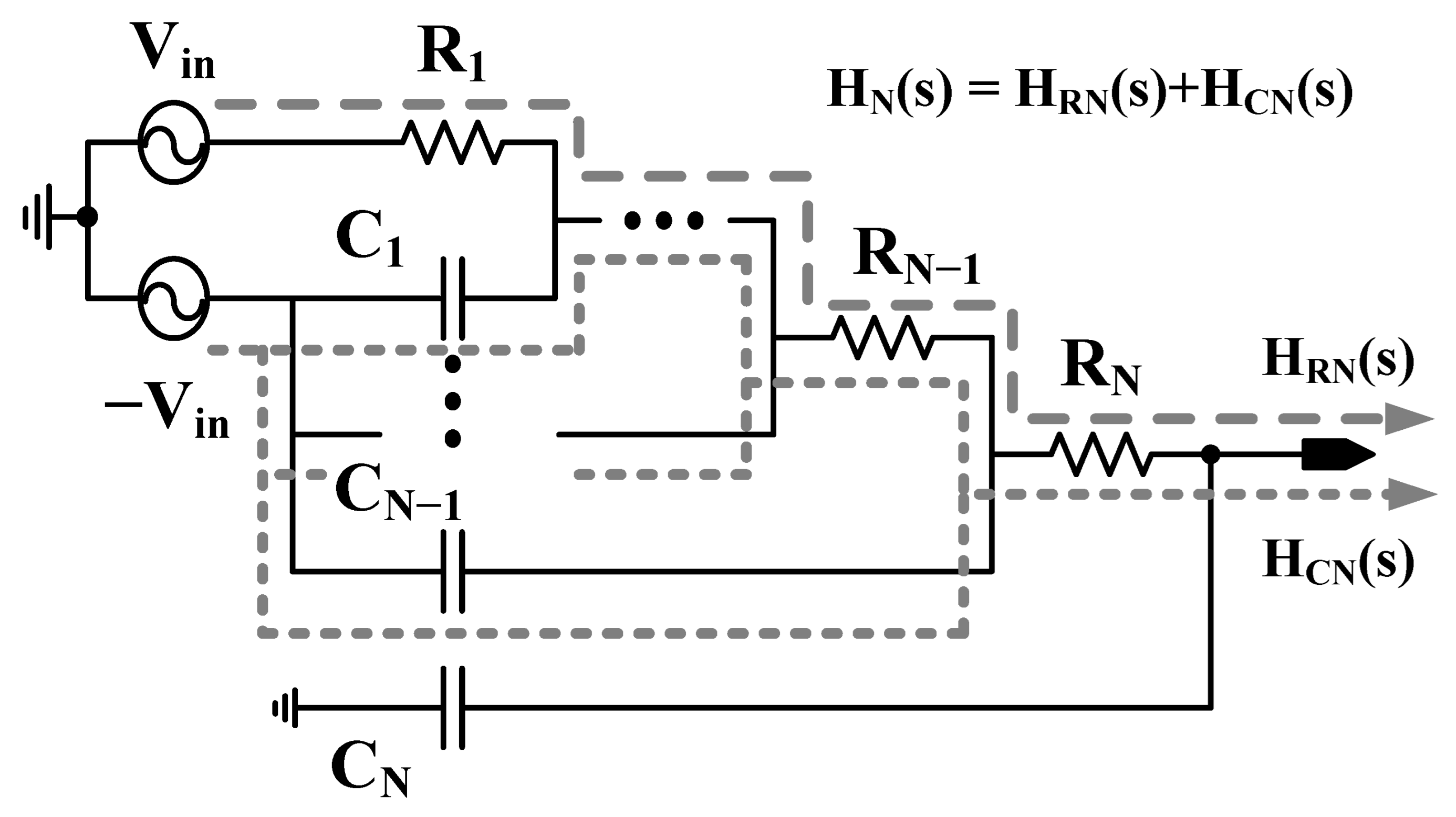
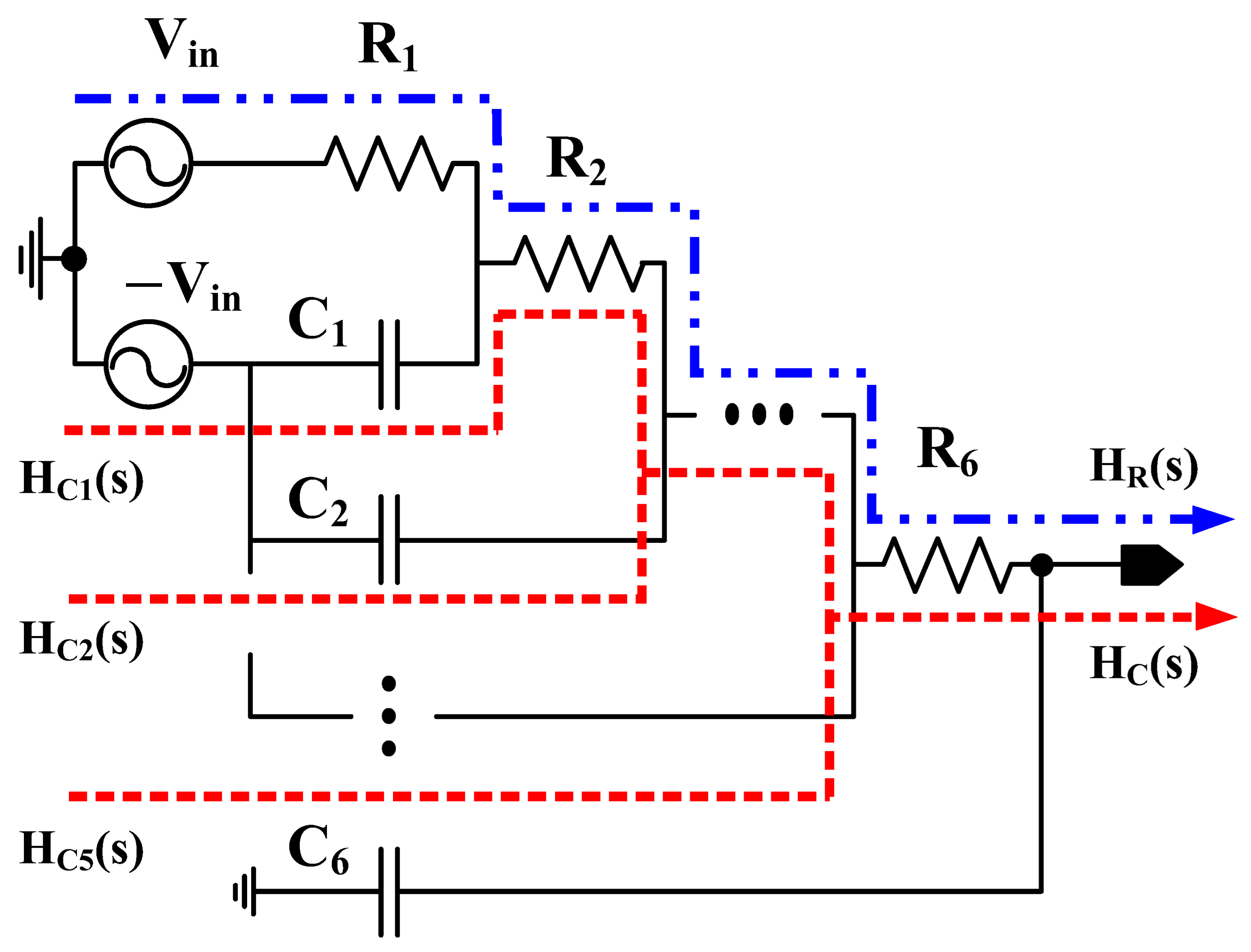
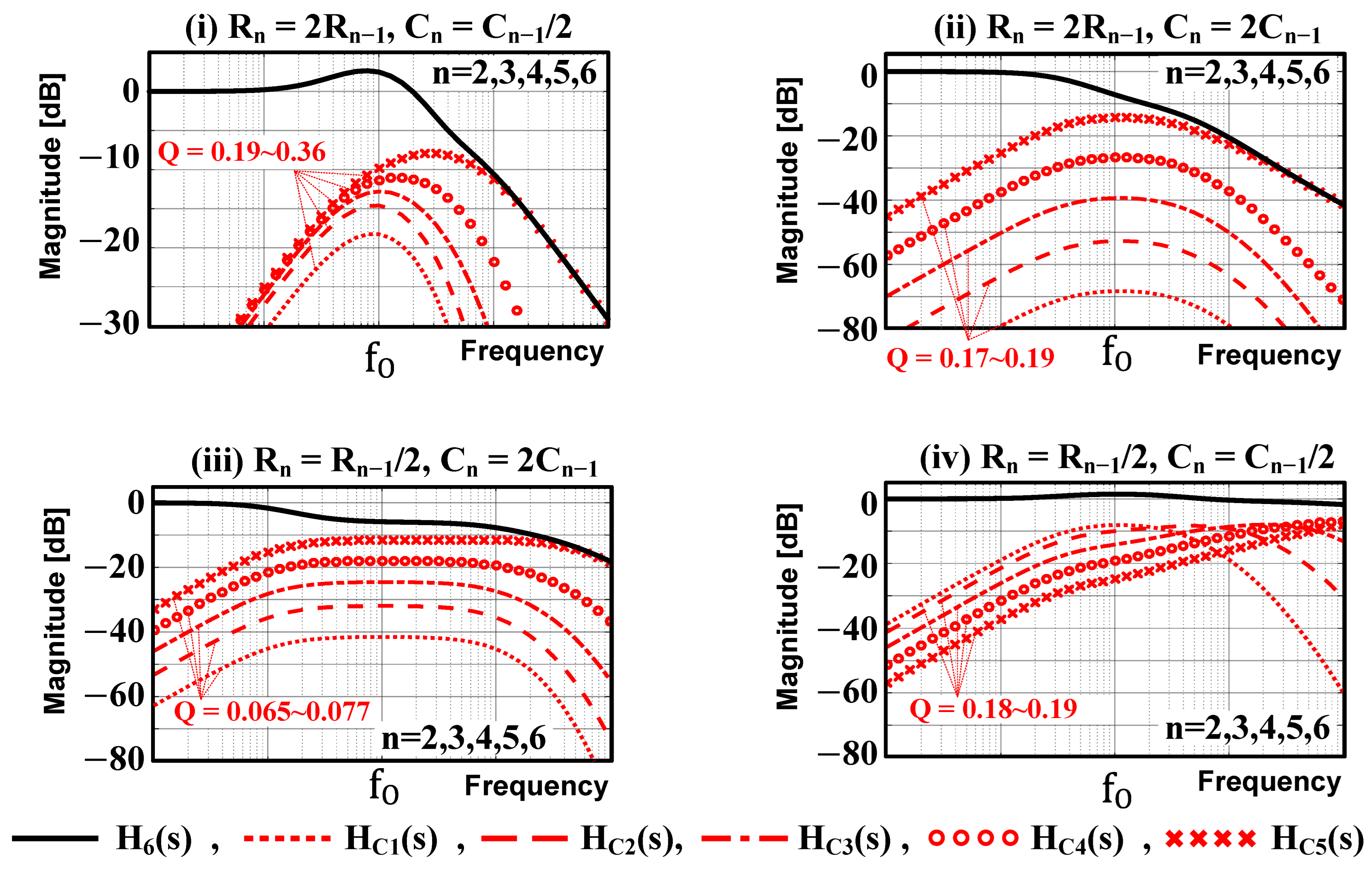
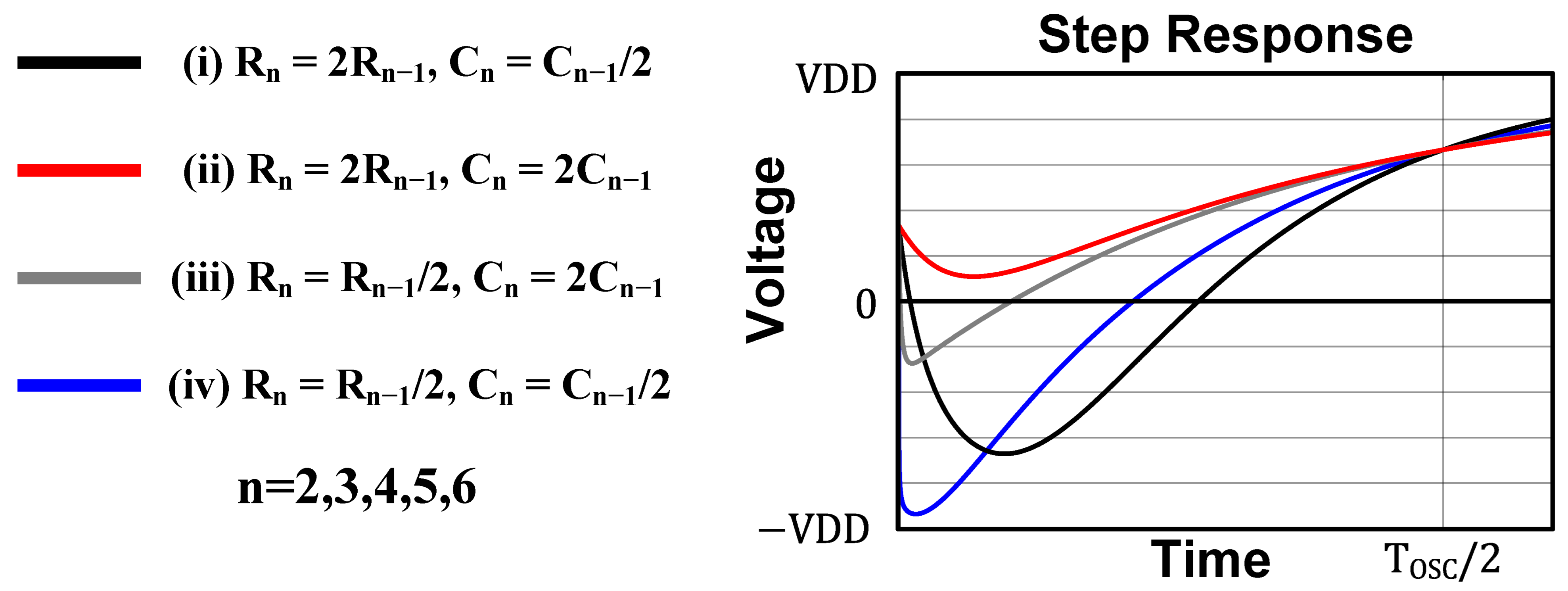
2.2. Multiple Stages of the Distributed RC Network
3. The Proposed Two-Stage Distributed RC Oscillator
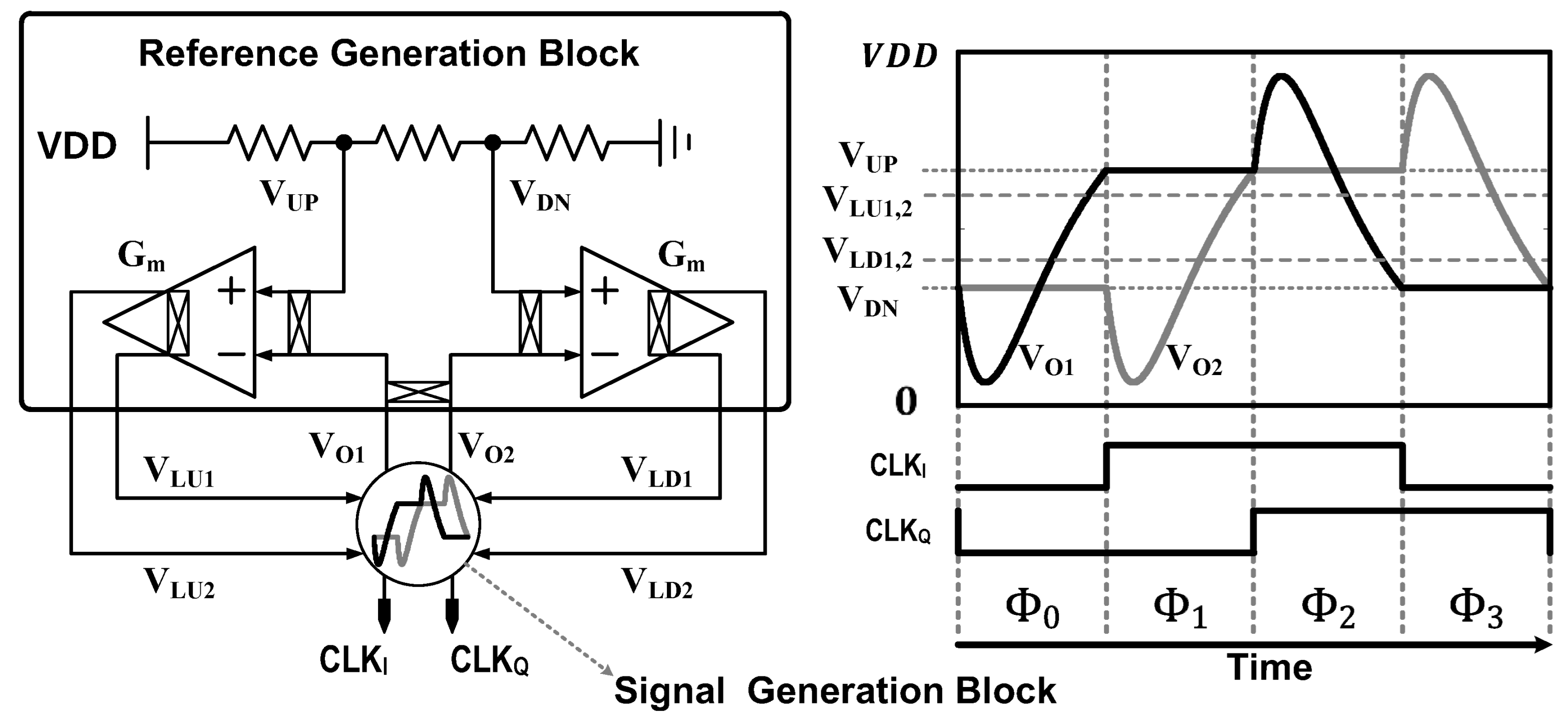
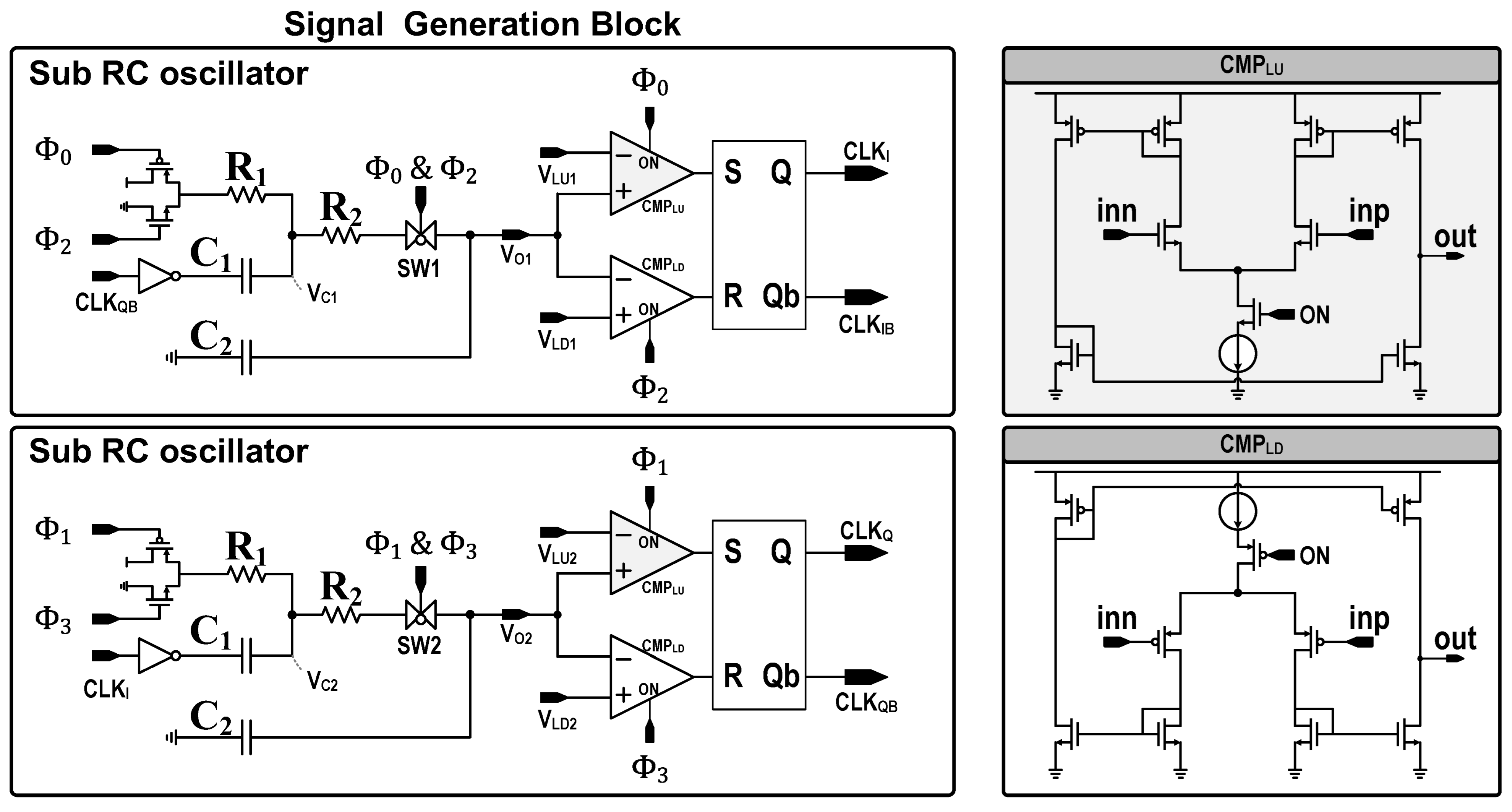
3.1. Quadrature Signal Generation
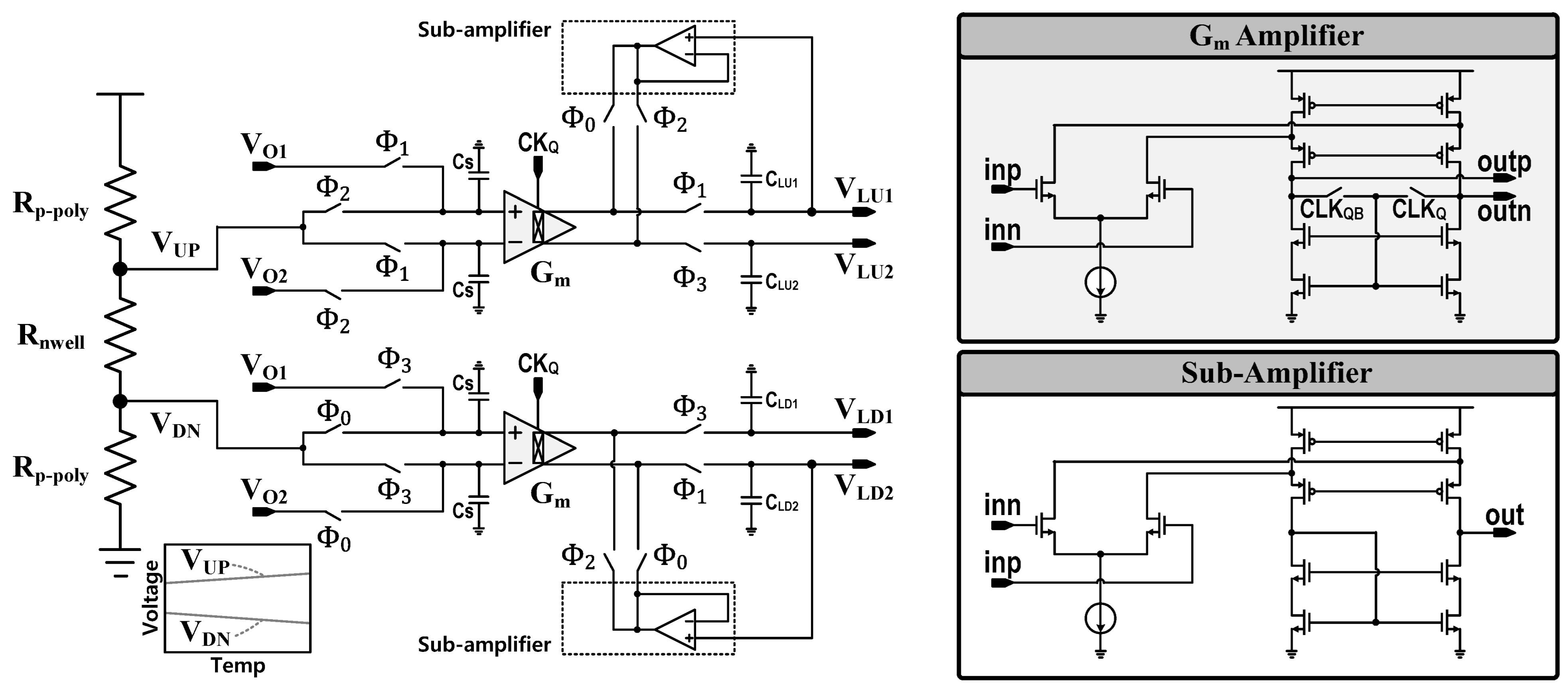
3.2. Reference Voltage Generation
4. Measurement
Noise Measurement
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Denier, U. Analysis and Design of an Ultralow-Power CMOS Relaxation Oscillator. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 57, 1973–1982. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhou, L.; Tian, F.; He, M.; Liao, H. A 51-nW 32.7-kHz CMOS relaxation oscillator with half-period pre-charge compensation scheme for ultra-low power systems. In Proceedings of the 2016 IEEE International Symposium on Circuits and Systems (ISCAS), Montreal, QC, Canada, 22–25 May 2016; pp. 830–833. [Google Scholar]
- Tokunaga, Y.; Sakiyama, S.; Matsumoto, A.; Dosho, S. An On-Chip CMOS Relaxation Oscillator with Voltage Averaging Feedback. IEEE J. Solid-State Circuits 2010, 45, 1150–1158. [Google Scholar] [CrossRef]
- Cao, Y.; Leroux, P.; De Cock, W.; Steyaert, M. A 63,000 Q-factor relaxation oscillator with switched-capacitor integrated error feedback. In Proceedings of the 2013 IEEE International Solid-State Circuits Conference Digest of Technical Papers, San Francisco, CA, USA, 17–21 February 2013; pp. 186–187. [Google Scholar]
- Tokunaga, Y.; Sakiyama, S.; Dosho, S. An over 20,000 quality factor on-chip relaxation oscillator using Power Averaging Feedback with a Chopped Amplifier. In Proceedings of the 2010 Symposium on VLSI Circuits, Honolulu, HI, USA, 16–18 June 2010; pp. 111–112. [Google Scholar]
- Hosseini Asl, S.A.; Rad, R.E.; Hejazi, A.; Pu, Y.; Lee, K.-Y. A 64-MHz 2.15-μW/MHz On-Chip Relaxation Oscillator with 130-ppm/°C Temperature Coefficient. Electronics 2023, 12, 1144. [Google Scholar] [CrossRef]
- Koo, J.; Kim, B.; Park, H.-J.; Sim, J.-Y. A Quadrature RC Oscillator with Noise Reduction by Voltage Swing Control. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 3077–3088. [Google Scholar] [CrossRef]
- Lei, K.-M.; Mak, P.-I.; Martins, R.P. A 0.35-V 5200-μm2 2.1-MHz Temperature Resilient Relaxation Oscillator With 667 fJ/Cycle Energy Efficiency Using an Asymmetric Swing-Boosted RC Network and a Dual-Path Comparator. IEEE J. Solid-State Circuits 2021, 56, 2701–2710. [Google Scholar] [CrossRef]
- Lee, J.; George, A.K.; Je, M. An Ultra-Low-Noise Swing-Boosted Differential Relaxation Oscillator in 0.18-μm CMOS. IEEE J. Solid-State Circuits 2020, 55, 2489–2497. [Google Scholar] [CrossRef]
- Lu, S.-Y.; Liao, Y.-T. A Low-Power, Differential Relaxation Oscillator with the Self-Threshold-Tracking and Swing-Boosting Techniques in 0.18-μm CMOS. IEEE J. Solid-State Circuits 2019, 54, 392–402. [Google Scholar] [CrossRef]
- Abidi, A.A.; Meyer, R.G. Noise in relaxation oscillators. IEEE J. Solid-State Circuits 1983, 18, 794–802. [Google Scholar] [CrossRef]
- Gierkink, S.L.; Van Tuij, E. A coupled sawtooth oscillator combining low jitter with high control linearity. IEEE J. Solid-State Circuits 2002, 37, 702–710. [Google Scholar] [CrossRef]
- Liao, F.-W.; Tsou, S.-C.; Chao, C.-S. A 6nW 30.8kHz Relaxation Oscillator with Sampling Bias-Free RC Circuit and Dynamic Power Scaling in a 12 nm FinFET. In Proceedings of the 2023 IEEE Symposium on VLSI Technology and Circuits (VLSI Technology and Circuits), Kyoto, Japan, 11–16 June 2023; pp. 1–2. [Google Scholar]
- Drakhlis, B. Calculate oscillator jitter by using phase-noise analysis: Part 2 of two parts. Microw. RF 2001, 40, 109–119. [Google Scholar]
- Sepke, T.; Holloway, P.; Sodini, C.G.; Lee, H.S. Noise Analysis for Comparator-Based Circuits. IEEE Trans. Circuits Syst. I 2009, 56, 541–553. [Google Scholar] [CrossRef]




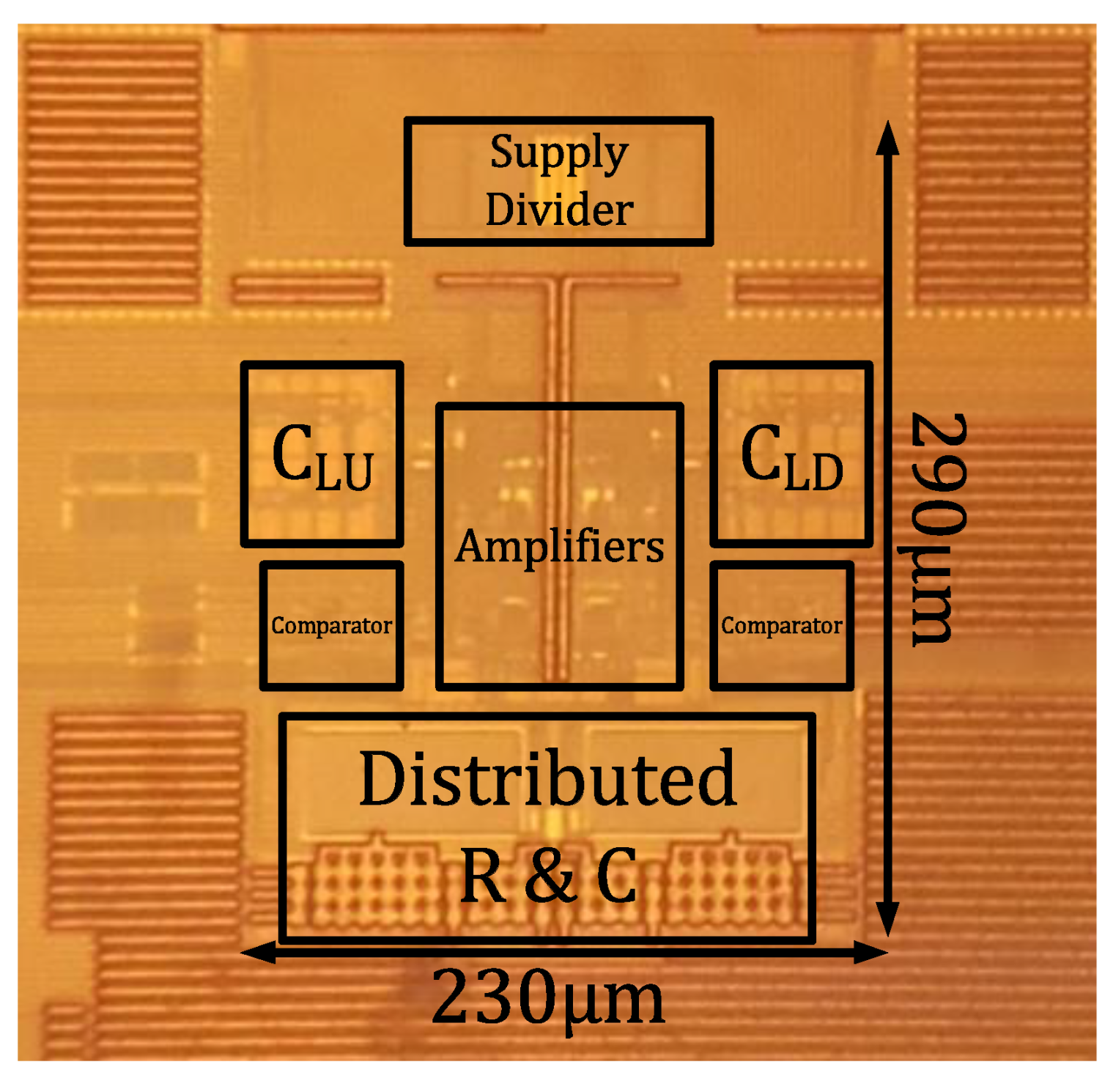

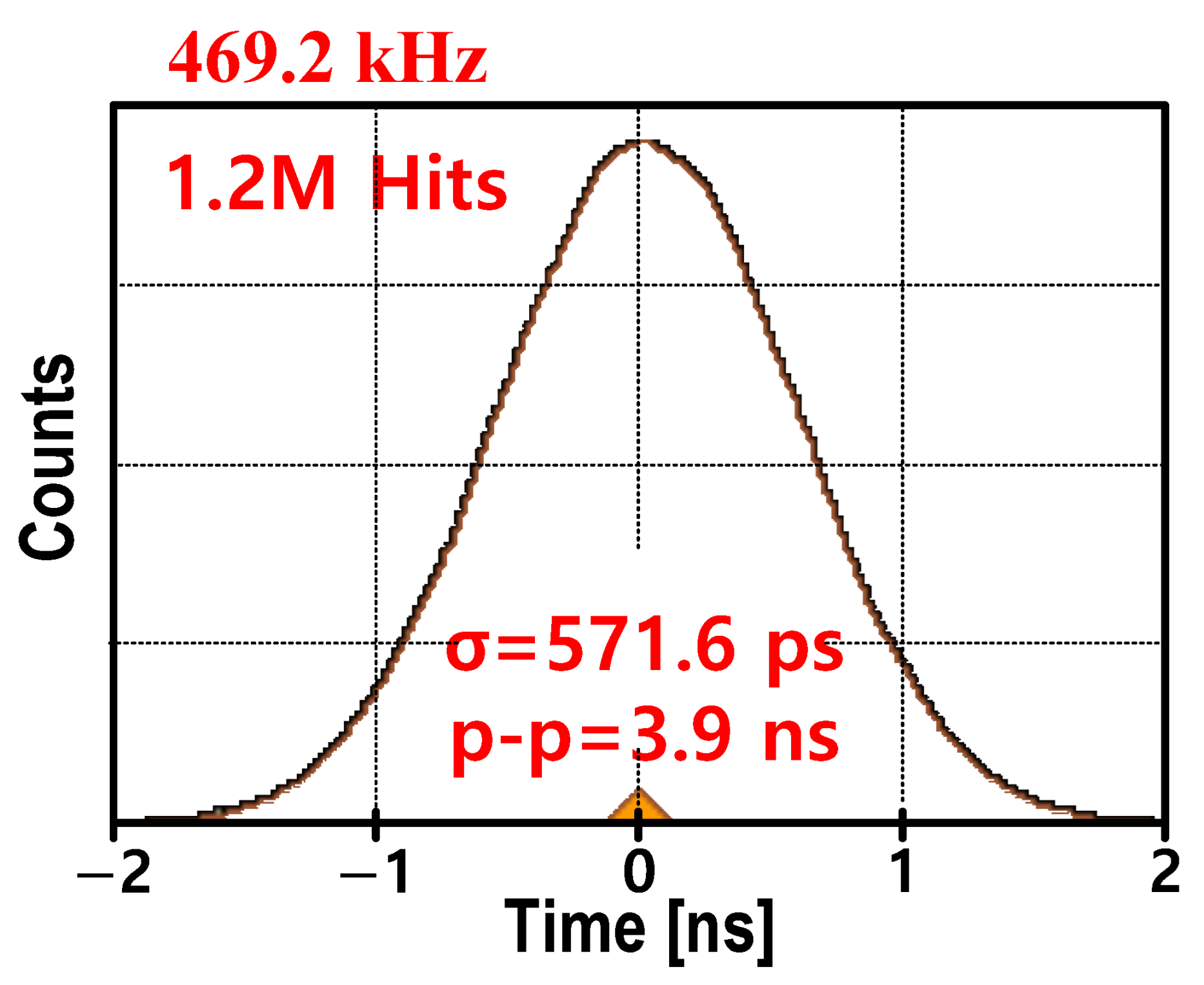

| JSSC 19 [10] | TCAS-I 19 [7] | JSSC 21 [8] | JSSC 20 [9] | This | |
|---|---|---|---|---|---|
| Technology [nm] | 180 | 180 | 28 | 180 | 180 |
| Area [mm2] | 0.028 | 0.058 | 0.0052 | 0.015 | 0.069 |
| Frequency | 8.2 MHz | 444.9 kHz | 2.1 MHz | 10.5 MHz | 469.2 kHz |
| Power [μW] | 46.3 | 21.3 | 1.4 | 219.8 | 23.4 |
| Period Jitter [ps] | 10.2 (0.0163%) | 1060 (0.047%) | 800 (0.112%) | 9.86 (0.01%) | 571.6 (0.0268%) |
| FoMPN | −150 @ 100 Hz −152.7 @ 10 kHz | −155 @ 100 Hz −152 @ 10 kHz | - −143.4 @ 10 kHz | −157.7 @ 1 kHz −162.1 @ 100 kHz | −160.34 @ 100 Hz −158.48 @ 10 kHz |
| Supply. Var. [%/V] | 0.91 @ 0.75~0.95 V | 0.07 @ 1.2~2.8 V | 2.3 @ 0.35~0.38 V | 0.44 @ 1.4~2 V | 1.15 @ 1.4~2 V |
| Temp. Var. [ppm/°C] | 123 @−20~100 °C | 224 @ −20~100 °C | 158 @ −20~120 °C | 137 @ −40~125 °C | 126 @ −14~120 °C |
| Allan Deviation Floor [ppm] | 1.56 | 1.1 | n/a | 2.8 | 0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koo, J.; Jeon, C. A Quadrature Oscillator with a Frequency-Tuned Distributed RC Network Analysis. Electronics 2024, 13, 878. https://doi.org/10.3390/electronics13050878
Koo J, Jeon C. A Quadrature Oscillator with a Frequency-Tuned Distributed RC Network Analysis. Electronics. 2024; 13(5):878. https://doi.org/10.3390/electronics13050878
Chicago/Turabian StyleKoo, Jahyun, and Cheonhoo Jeon. 2024. "A Quadrature Oscillator with a Frequency-Tuned Distributed RC Network Analysis" Electronics 13, no. 5: 878. https://doi.org/10.3390/electronics13050878
APA StyleKoo, J., & Jeon, C. (2024). A Quadrature Oscillator with a Frequency-Tuned Distributed RC Network Analysis. Electronics, 13(5), 878. https://doi.org/10.3390/electronics13050878






