Abstract
Neurons are crucial components of neural networks, but implementing biologically accurate neuron models in hardware is challenging due to their nonlinearity and time variance. This paper introduces the SC-IZ neuron model, a low-cost digital implementation of the Izhikevich neuron model designed for large-scale neuromorphic systems using stochastic computing (SC). Simulation results show that SC-IZ can reproduce the behaviors of the original Izhikevich neuron. The model is synthesized and implemented on an FPGA. Comparative analysis shows improved hardware efficiency; reduced resource utilization, which is a 56.25% reduction in slices, 57.61% reduction in Look-Up Table (LUT) usage, and a 58.80% reduction in Flip-Flop (FF) utilization; and a higher operating frequency compared to state-of-the-art Izhikevich implementation.
1. Introduction
The remarkable capabilities of the brain have inspired engineers to develop novel hardware and computational architectures that mimic or draw inspiration from the brain’s principles [1]. Spiking Neural Networks (SNNs) are unlike conventional Artificial Neural Networks (ANNs) that more closely resemble the structure and function of biological neural networks in the brain [2,3]. SNNs offer advantages such as energy efficiency on event-driven neuromorphic hardware and the ability to perform complex tasks like spike pattern recognition [4,5,6], image segmentation [7], optical flow estimation [8], and localization [9,10,11] due to their rich spatiotemporal dynamics and event-driven paradigm. The emergence of large-scale neuromorphic chips with a high number of neurons has indeed opened up new possibilities for the field of SNNs. These chips provide the computational power and resources required to simulate and implement complex SNNs at scale [3,12,13,14]. However, to fully harness the potential of these chips, it is essential to design neuronal models that strike a balance between computational efficiency and biological plausibility.
Neuromorphic research has developed various neuronal models that simulate real neurons at different levels of abstraction. These models range from highly detailed biophysical models to simplified abstract models. The choice of abstraction level depends on the balance between biological realism and computational efficiency required for a specific application [15,16]. Neuronal models can be expressed using ordinary differential equations (ODEs). The Hodgkin–Huxley model [17] is highly biologically accurate but computationally expensive due to its complexity, which consists of four equations and tens of biophysically meaningful parameters. The Leaky Integrate-and-Fire (LIF) model [16] consists of one equation that is the easiest to implement but lacks some fundamental properties of cortical spiking neurons. The Izhikevich model [18], consisting of two equations, can exhibit firing patterns of various cortical neurons and provides a good balance between computational efficiency and biological plausibility. It helps in understanding the temporal structure of cortical spike trains and how the neocortex processes information. Therefore, the Izhikevich neuron model is considered both computationally efficient and biologically plausible [16,19].
Researchers have explored various approaches for hardware implementation of the Izhikevich neuron model, aiming to replicate its behavior while leveraging specialized hardware for efficient computations. Ref. [20] involves replacing the quadratic polynomial of the Izhikevich model with a PieceWise Linear (PWL) model. However, the PWL model deviates significantly from the original quadratic polynomial and incurs high hardware costs. Another approach, proposed in [15], utilizes COordinate Rotation DIgital Computer (CORDIC) algorithms to calculate the quadratic polynomial. However, this method requires 12 iterations for accurate computation. In [21], researchers replaced the quadratic polynomial with an equation involving and functions, but this approach demands significant resources for achieving the desired performance. To simplify the scheme in [21], Ref. [22] used only the function to approximate the quadratic polynomial, yet this simplified scheme relies on the Deme GA search algorithm to find suitable parameters.
Graphics Processing Units (GPUs) have been widely used for executing neural network models due to their inherent parallel nature. However, cost and power constraints have driven the exploration of alternative computing architectures [23,24]. While Application-Specific Integrated Circuit (ASIC) design can be fast and efficient, it suffers from inflexibility and a long development time [25]. Over the past few years, Field-Programmable Gate Array (FPGA) platforms have become increasingly popular for addressing the needs of large-scale neuromorphic applications. FPGA implementation offers rapid, accurate, compact, and flexible alternatives compared to ASIC [26,27,28].
In contrast to previous approaches to hardware implementation of Izhikevich neurons, our proposal advocates for the utilization of stochastic computing (SC), an unconventional computing technique that has demonstrated effectiveness in specific applications [29,30,31,32,33,34,35,36]. It processes information using probabilities instead of conventional binary or real-valued representations [37]. SC encodes data as a sequence of random bits and performs computations using simple logic gates, often requiring fewer hardware resources compared to conventional binary computing [38]. SC enables efficient hardware utilization by leveraging parallel computations. Additionally, the probabilistic nature of SC allows for the mitigation of individual bit errors or transient disturbances through the statistical properties of the random sequences [39]. Stochastic integrator, a computation element often applied in SC, is utilized for solving Laplace’s equations, logarithm functions, and high-order polynomials [30,40].
In this paper, we introduce SC-IZ, a low-cost stochastic computing-based Izhikevich neuron model specifically designed for large-scale neuromorphic systems. The implementation of SC-IZ is performed on an FPGA platform, leveraging the flexibility, logic density, and rapid development cycle offered by FPGAs.
Our main contributions are as follows:
- We introduce SC-IZ, an Izhikevich neuron model based on stochastic computing (SC). In order to adapt the Izhikevich neuron model to the SC domain, we make mathematical modifications to accommodate the probabilistic nature of SC computations.
- We conduct a comprehensive investigation into the accuracy of the proposed SC-IZ model. This analysis includes error assessment and the study of its biologically plausible behavior. Simulation results indicate that our model can accurately represent various biologically plausible characteristics, similar to the original Izhikevich model.
- We validate the efficiency of the proposed SC-IZ model by synthesizing and implementing it on an FPGA platform. A comparative analysis is performed against state-of-the-art Izhikevich hardware implementations. The results demonstrate that SC-IZ exhibits improved hardware efficiency.
The remaining sections of the paper are organized as follows: Section 2 provides a review of stochastic computing and the original Izhikevich neuron model, and presents our SC-IZ neuron model. Section 3 evaluates the spiking patterns, conducts error analysis, and examines the network behaviors of SC-IZ. Section 4 describes the hardware architecture of SC-IZ and compares it with existing Izhikevich hardware implementations. Finally, Section 5 concludes the paper.
2. Methodology for SC-IZ Hardware Implementation
2.1. Stochastic Computing
Approximate computing is a promising approach that offers a trade-off between accuracy and performance. Stochastic computing (SC) is a prominent method within the realm of approximate computing [41]. It involves performing computations using randomized bitstreams and has shown promise for accelerating neural networks. One of the key benefits of SC is its ability to enable multiplication and addition using single gates, leading to significant improvements in computation density [42]. In contrast to the conventional base-2 format, SC is error-robust, with the bit represented in SC being free of the bit position [43]. SC utilizes two common representations: unipolar and bipolar. In the unipolar representation, values range from 0 to 1, where the probability of encountering a 1 in the bitstream, denoted as , encodes the actual value of a stochastic number X. For example, if a bitstream has the pattern 10110111, the value of is 6 divided by the length of the bitstream (8), which equals 6/8. In the bipolar representation, the range extends from −1 to 1. The probability is given by the formula and encodes the actual value X. The bitstream 10110111 in the bipolar representation represents a value of 4/8.
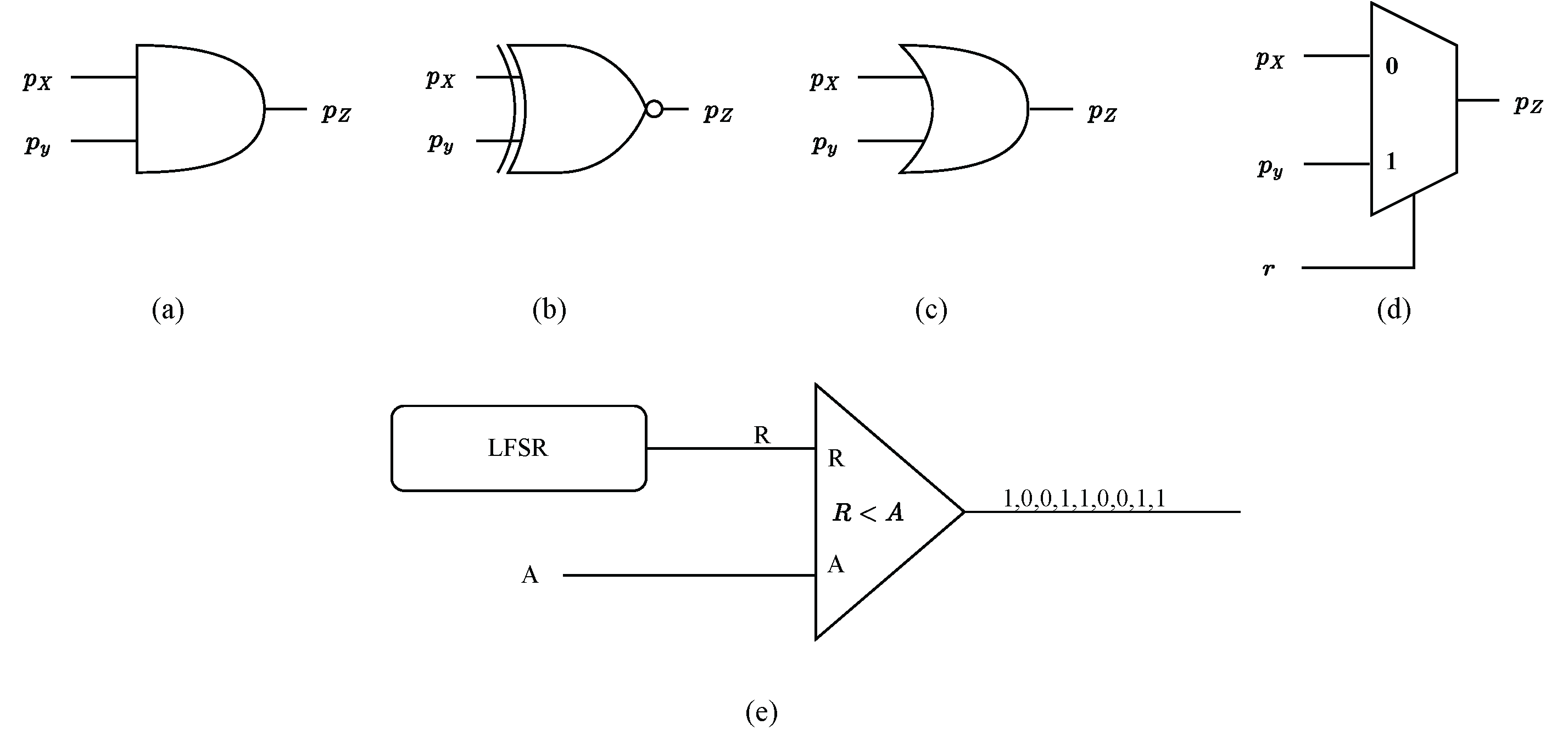
Arithmetic operations in SC can be implemented using basic logic gates and multiplexers. Unipolar multiplication can be achieved with an AND gate as depicted in Figure 1a, while bipolar multiplication can be realized using an XNOR gate as shown in Figure 1b. Unipolar addition can be implemented using an OR gate with negatively correlated bitstreams [44] as illustrated in Figure 1c. Additionally, both unipolar- and bipolar-scaled addition can be accomplished using a multiplexer as demonstrated in Figure 1d. To convert binary numbers to bitstreams, a Stochastic Number Generator (SNG) unit is commonly employed [45]. This unit consists of a Linear-Feedback Shift Register (LFSR)-based Random Number Generator (RNG) and a comparator as shown in Figure 1e. In each clock cycle, a 1 is generated if the binary number (A) is greater than the number (R) generated by the Linear Feedback Shift Register (LFSR).
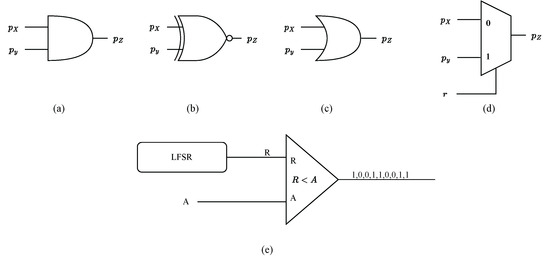
Figure 1.
Stochastic computing circuits. (a) Unipolar multiplication. (b) Bipolar multiplication. (c) Negatively correlated unipolar addition. (d) Scaled addition. (e) Stochastic number generator.
SC Finite-State Machines (FSMs) have been introduced as methods to perform various non-linear functions, such as exponential functions, Rectified Linear Unit (ReLU) functions, and hyperbolic tangent functions on stochastic bitstreams [46]. Furthermore, a stochastic integrator has been proposed to implement the accumulative function of the Euler method in an ODE solver [40]. Unlike conventional stochastic circuits that require long stochastic bitstreams for accurate results, the stochastic ODE solver offers estimates of the solution for each bit in the stochastic bitstream, resulting in notable reductions in latency and energy consumption [30,40]. The circuit diagram and symbol of the stochastic integrator are depicted in Figure 2a and Figure 2b, respectively.
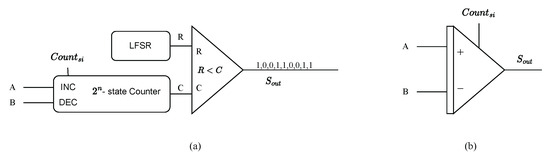
Figure 2.
The circuit diagram and symbol of a stochastic integrator. (a) The circuit diagram of a stochastic integrator. (b) A symbol of a stochastic integrator.
A crucial component of the stochastic integrator is a -state up/down counter. The counter’s value is encoded in a stochastic bitstream , generated by a RNG and a comparator acting as a SNG. The bitstream can serve as feedback or act as an input for subsequent stochastic integrators. If it is not necessary for the specific application, the RNG unit and the comparator can be omitted from the hardware design, leading to reduced hardware costs. The input signals A and B are stochastic bitstreams that dictate the operations to be executed on the counter. These operations include increasing (INC), decreasing (DEC), or maintaining the counter’s current value. We denote the integer value stored in the counter as I. In the unipolar representation, the probability encoded by the output stochastic bitstream is . At the i-th clock cycle, the two bits in the input streams A and B are denoted as and , respectively. The functionality of the up/down counter is as follows:
where input bit streams A and B only serve as the control signals for the counter.
For an ODE, , where and are probabilities encoded by the input sequences of the stochastic integrator at . The estimated value of the function at with a step size of can be obtained. The estimate is based on the normalized expected value of the up/down counter at the k-th clock cycle, assuming the same initial condition . The estimation is given by [30]:
In Equation (2), and represent the probabilities of and at the i-th clock cycle, respectively. The stochastic integrator provides estimates for the solution of the ODEs. By employing the stochastic integrator, we can approximate the dynamics of the two ODE equations that govern the behavior of the Izhikevich neuron model.
2.2. Izhikevich Neuron
The Izhikevich neuron model [18,47] is a quadratic excitation model with recovery variables, known for its simplicity, computational efficiency, and ability to replicate various firing patterns observed in real biological neurons. The model is defined by two ordinary differential equations, along with an auxiliary reset equation, as follows:
In these equations, v represents the membrane potential, u represents the recovery variable, and other parameters of the model are listed in Table 1. When the membrane potential v reaches or exceeds a threshold , the membrane potential resets to a value denoted as c and updates the recovery variable according to the increment specified by the parameter d. By adjusting the values of the parameters a, b, c, and d, different firing patterns observed in biological neurons (e.g., regular spiking (RS), intrinsically bursting (IB), chattering (CH), etc.) can be replicated [16,47].

Table 1.
Parametric description of the Izhikevich neuron model.
2.3. Proposed Izhikevich Neuron Model
In this section, we present SC-IZ, a stochastic computing-based implementation of the Izhikevich neuron model. SC-IZ leverages the principles of stochastic computing to simulate the behavior of Izhikevich neurons. Stochastic computing is a computational paradigm that represents and manipulates data using probabilistic bitstreams [30,48]. SC operates with a data range from 0 to 1, using unipolar representation. Therefore, to align with the SC computing paradigm, it becomes necessary to normalize the original Izhikevich neuron model. We suppose that v is in the range , and u is in the range , and , . The mapping procedure is as follows:
where and represent the mapped membrane potential and mapped recovery variable, respectively. From Equations (3) and (6), we have the following equation:
where parameters , , , and are
Then, the normalized spike reset equation is denoted as
The parameters , , and are denoted as
3. Dynamical Behaviors and Error Analysis
In this section, we perform evaluations on the spiking patterns and network behaviors of the proposed SC-IZ model. Furthermore, we analyze the accuracy of SC-IZ by comparing it to the original Izhikevich neuron model. To quantify the discrepancies between the two models, we calculate various error metrics, including (timing error between spike trains [15]), Root Mean Square Error () [49], Normalized Root Mean Square Error () [50], and correlation. Table 2 lists the parameters of the original Izhikevich neuron model [47].

Table 2.
Original Izhikevich neuron parameters used to generate different spike patterns.
3.1. Dynamical Behaviors
Leveraging shifting operations to implement coefficients based on 2 offers a valuable technique for reducing hardware complexity. In our model, if , where C and k are constants, the parameter in Equation (7) is set to 1. Furthermore, if is a coefficient based on 2, we can express as .
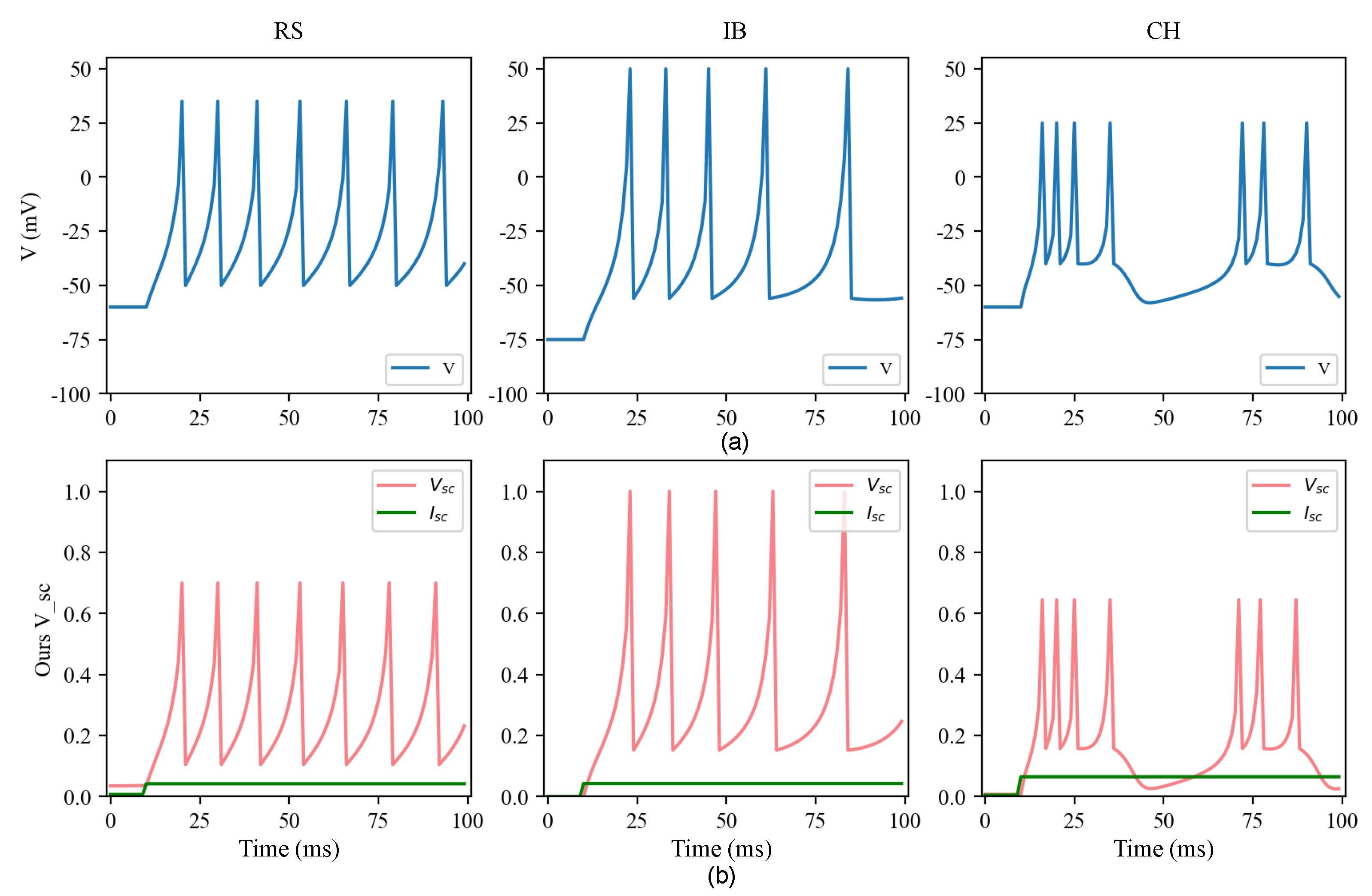
Table 3 provides the parameters for different firing patterns of the proposed model, allowing for the characterization and analysis of various neuron behaviors. The simulation results, as depicted in Figure 3, demonstrate that the SC-IZ model can successfully reproduce a range of biological neuron behaviors. Furthermore, the SC-IZ model closely follows the behavior exhibited by the original Izhikevich model.

Table 3.
SC-IZ neuron parameters used to generate different spike patterns.
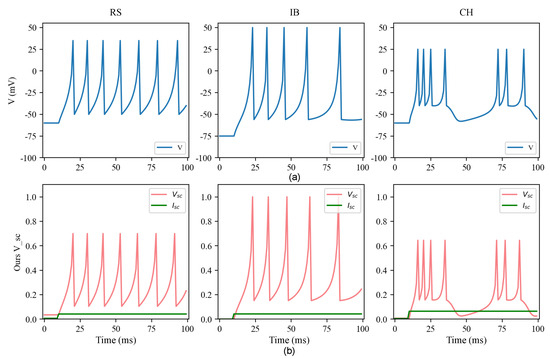
Figure 3.
Spiking patterns of the original Izhikevich model and the proposed SC-IZ model. (a) Spiking patterns of the original Izhikevich neurons. (b) Spiking patterns of our SC-IZ neurons. The spiking patterns from left to right are regular spiking (RS), intrinsically bursting (IB), and chattering (CH).
3.2. Network Behaviors
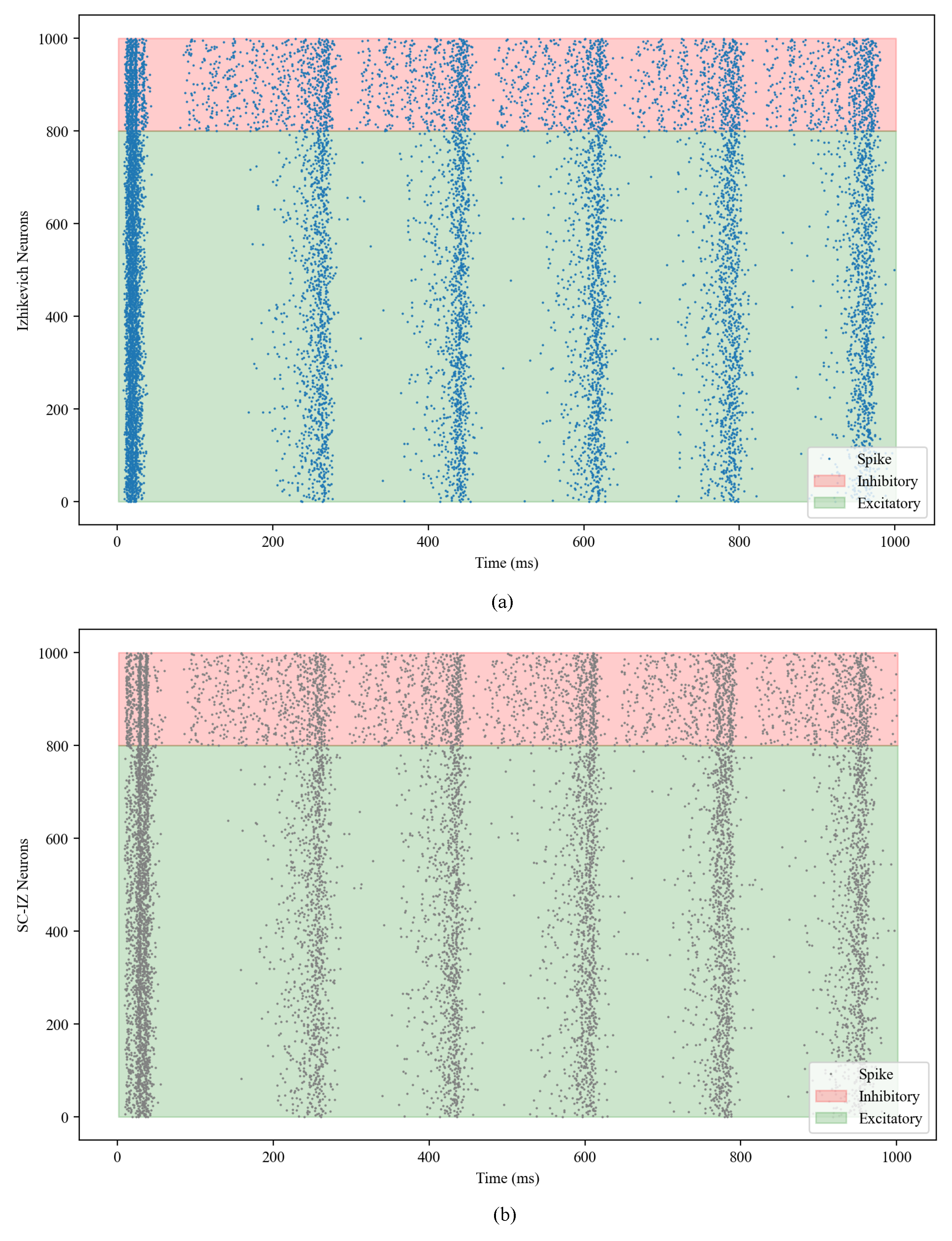
Raster plots, which are a common way to visualize the firing activity of neurons over time in network simulations, display the spikes generated by each neuron, providing insights into the temporal dynamics and synchrony within the network. Raster plots are crucial for understanding the emergent properties of neural networks [21,22]. In order to implement the SC-IZ model at the network scale, a simulation is conducted, using a network consisting of 1000 randomly connected neurons. The results of the simulation are illustrated in Figure 4, which displays raster plots representing the activity of the network. Upon examining the raster plots, it becomes apparent that the network behaviors of both the Izhikevich model and the SC-IZ model exhibit similar structures. The capacity of the neurons to organize themselves into assemblies is a crucial aspect in understanding the emergent behavior and information processing in neural networks [22]. The ability of the SC-IZ model to exhibit similar self-organizing capabilities as the original Izhikevich model further validates its effectiveness in capturing the essential dynamics of biological neurons, even within a network context.
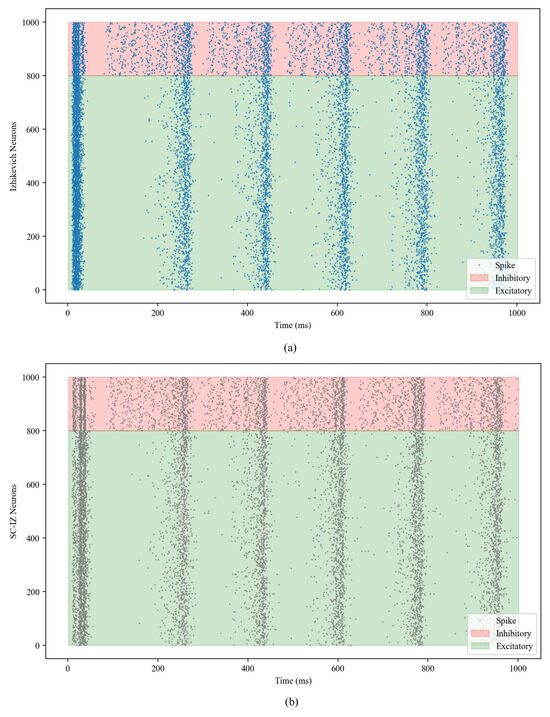
Figure 4.
Network behaviors of the Izhikevich model and proposed SC-IZ model. (a) Raster plot for the Izhikevich model. (b) Raster plot for the SC-IZ model.
3.3. Error Analysis
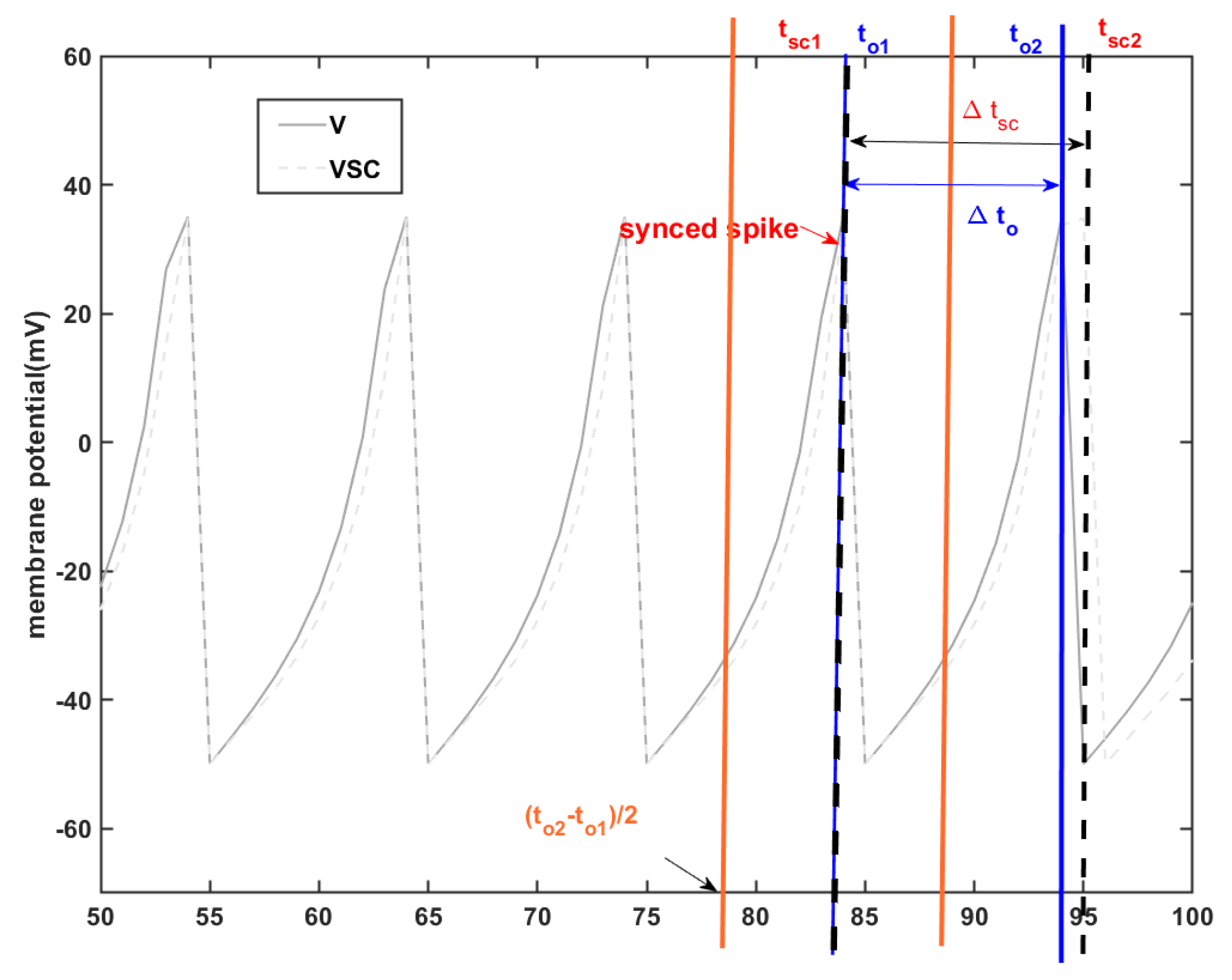
In accordance with [15], alterations made to the neuron model may lead to differences in spike timing, potentially causing a lag in the spike train of the modified model compared to the original. This timing variation between two spike trains, as defined in [15], is referred to as the timing error, denoted by . First, the two spike trains are synced, and the time to the next spike is used to compute the timing error for both the original Izhikevich model and the proposed model. This error can be given by
where is the time error between the second spike time and the first spike time .
In Equation (18), represents the SC-IZ model, while represents the original Izhikevich model as depicted in Figure 5.
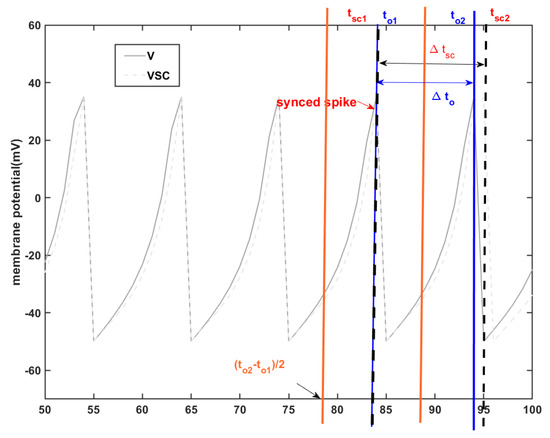
Figure 5.
: the time differences between the proposed SC-IZ and the original Izhikevich model.
The calculates the root mean square difference between the original Izhikevich model and our SC-IZ model, which is defined as
The is the normalized by the range of the spike train values. This error can be given by
represents the membrane potential of the SC-IZ model after denormalization, while represents the membrane potential of the original Izhikevich model. The domain of the membrane potential is bounded by its maximum value and its lowest value . Correlation measures the linear relationship between two neuron models. It provides insights into the similarity of spike patterns between the SC-IZ and original Izhikevich models. As shown in Table 4, the errors between the proposed SC-IZ model and the original Izhikevich model are found to be very small within a specific range of membrane potential values, specifically within the range of [−100 mV, 50 mV]. Additionally, a high average correlation of 99.581% is observed between the two models within this range.

Table 4.
The errors between the proposed SC-IZ model and the Izhikevich model.
4. Hardware Implementation and Evaluation
4.1. Square Unit
The SC ODE solver provides estimates for the solution of the ODEs [40]. For example, the ODE as
Equation (2) provides an estimation for the solution using a stochastic integrator at the k-th clock cycle, where . Here, represents the initial condition, and and represent the probabilities of v at the i-th clock cycle.
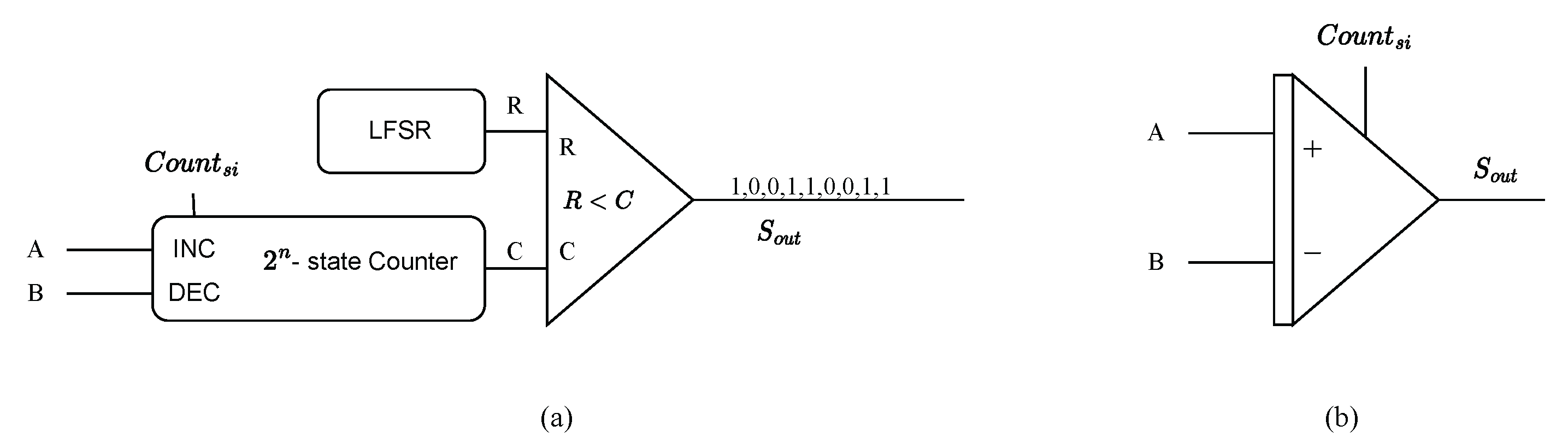
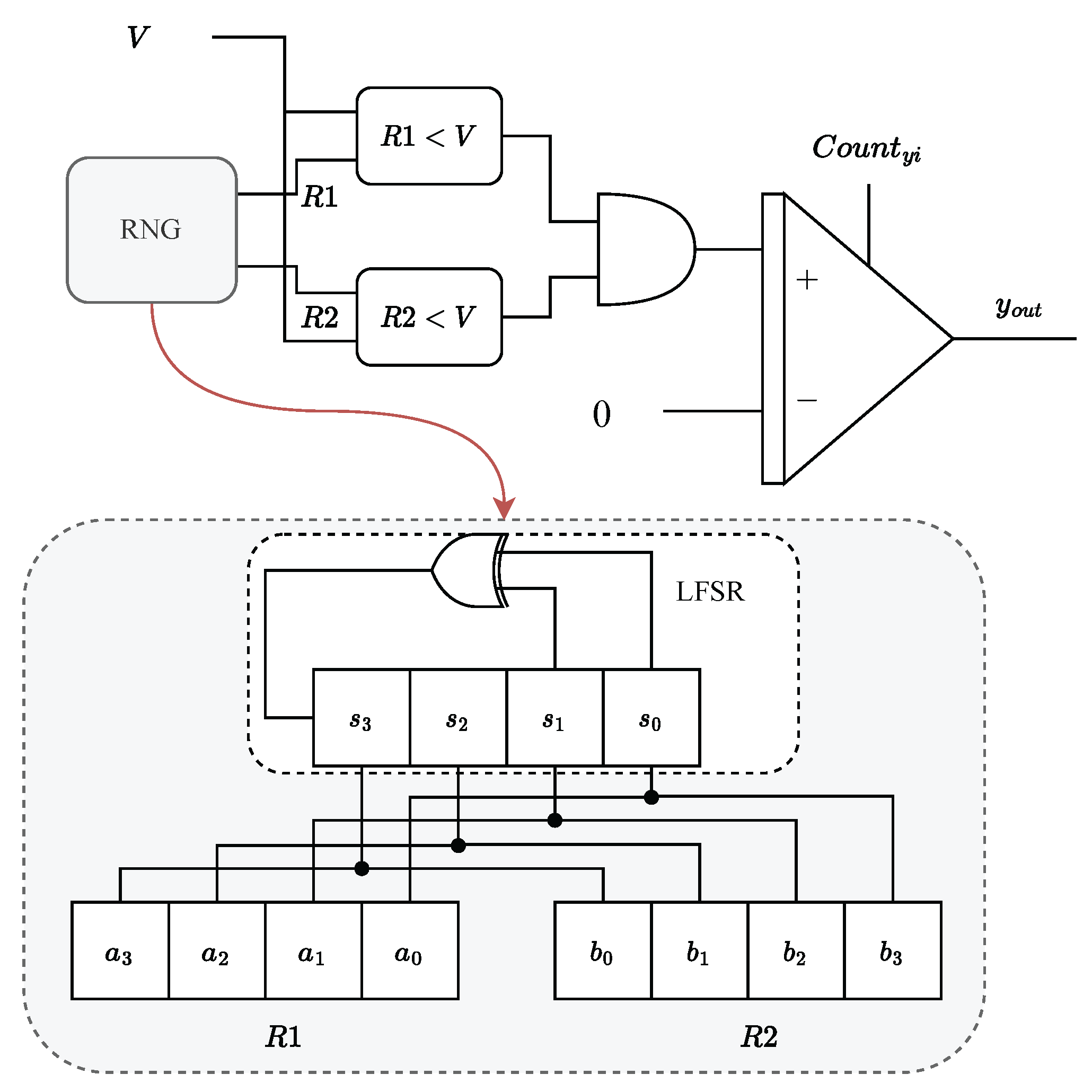
However, using correlated bitstreams in SC poses a significant design challenge and can lead to errors [51]. It is crucial to ensure that uncorrelated unipolar bitstreams achieve high accuracy in stochastic computation. This typically requires separate RNGs to generate independent random numbers for each bitstream. Unfortunately, this approach presents a significant challenge for large-scale SNNs. The necessity for numerous RNG units to maintain bitstream independence in these networks introduces substantial hardware demands, exacerbating both complexity and potential performance bottlenecks [38]. Considering the complexity of developing a true RNG, pseudo-random number generators like LFSR-based RNGs are frequently employed in SC. To reduce the size and energy consumption of the RNG circuitry, a proposed approach called LFSR sharing has been introduced. LFSR sharing involves utilizing an LFSR with multiple random number outputs. Ref. [52] recommends employing multiplexers to circularly shift the outputs of the LFSR. Ref. [53] proposes a hybrid RNG approach that combines an LFSR with a Halton sequence generator to diversify random number generation. While these methods utilize the LFSR module, they do require additional hardware resources to generate distinct random numbers. [30] suggests that rearranging the output of the LFSR can also yield different random numbers. Notably, permuting the LFSR outputs in reverse order can achieve lower cross-correlation without the need for extra hardware overhead. Consequently, we opt for the output rearrangement method to produce different random numbers. An LFSR with two random number outputs is employed in our SC-IZ model as depicted in Figure 6.
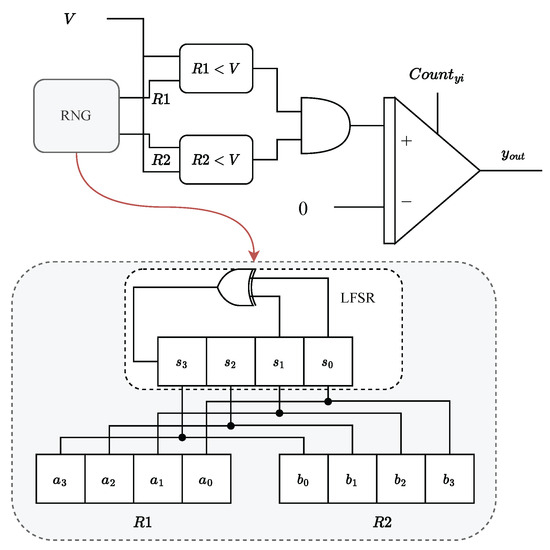
Figure 6.
The hardware architecture based on a stochastic integrator for Equation (22). The hardware architecture consists of an RNG unit that utilizes a single LFSR to generate two random numbers.
In our SC implementation, we have chosen a bit width of 8. However, for clarity purposes, we only display a 4-bit LFSR. Within our RNG unit, two variables are generated. The first variable corresponds to the LFSR outputs, denoted as , , , and , which are connected to , , , and , respectively. The second variable is generated by rearranging the LFSR outputs in reverse order, where , , , and are connected to , , , and , respectively. This rearrangement in reverse order is known to maximize the deviation distance, resulting in low-correlated random bitstreams [30]. The utilization of different LFSR outputs ensures statistical independence between the inputs of the AND gate. This independence allows the AND gate to effectively function as a multiplier as depicted in Figure 6. By comparing the value v with two random numbers and , different random bitstreams are generated for v. These random bitstreams serve as inputs to the AND gate, enabling the computation of .
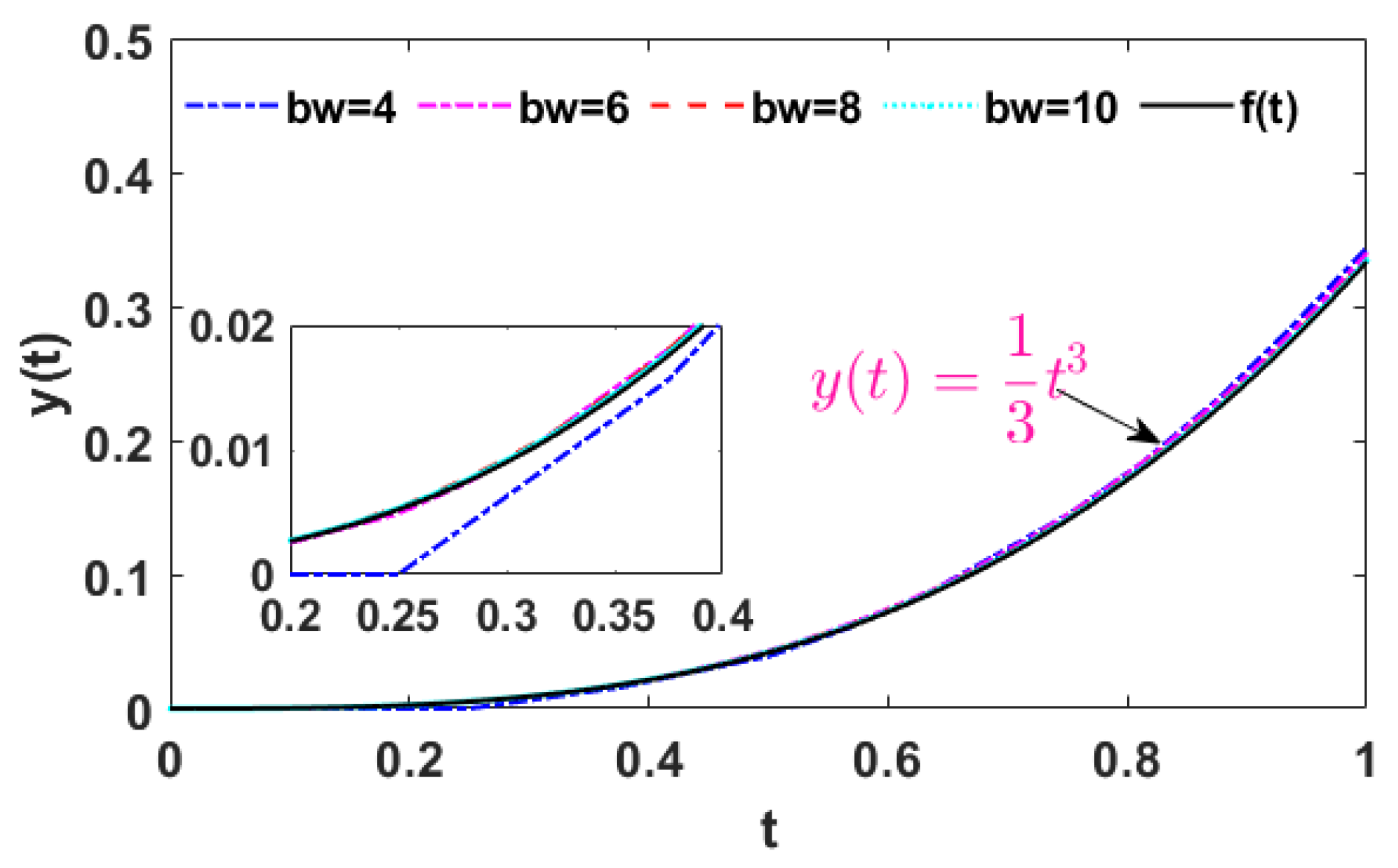
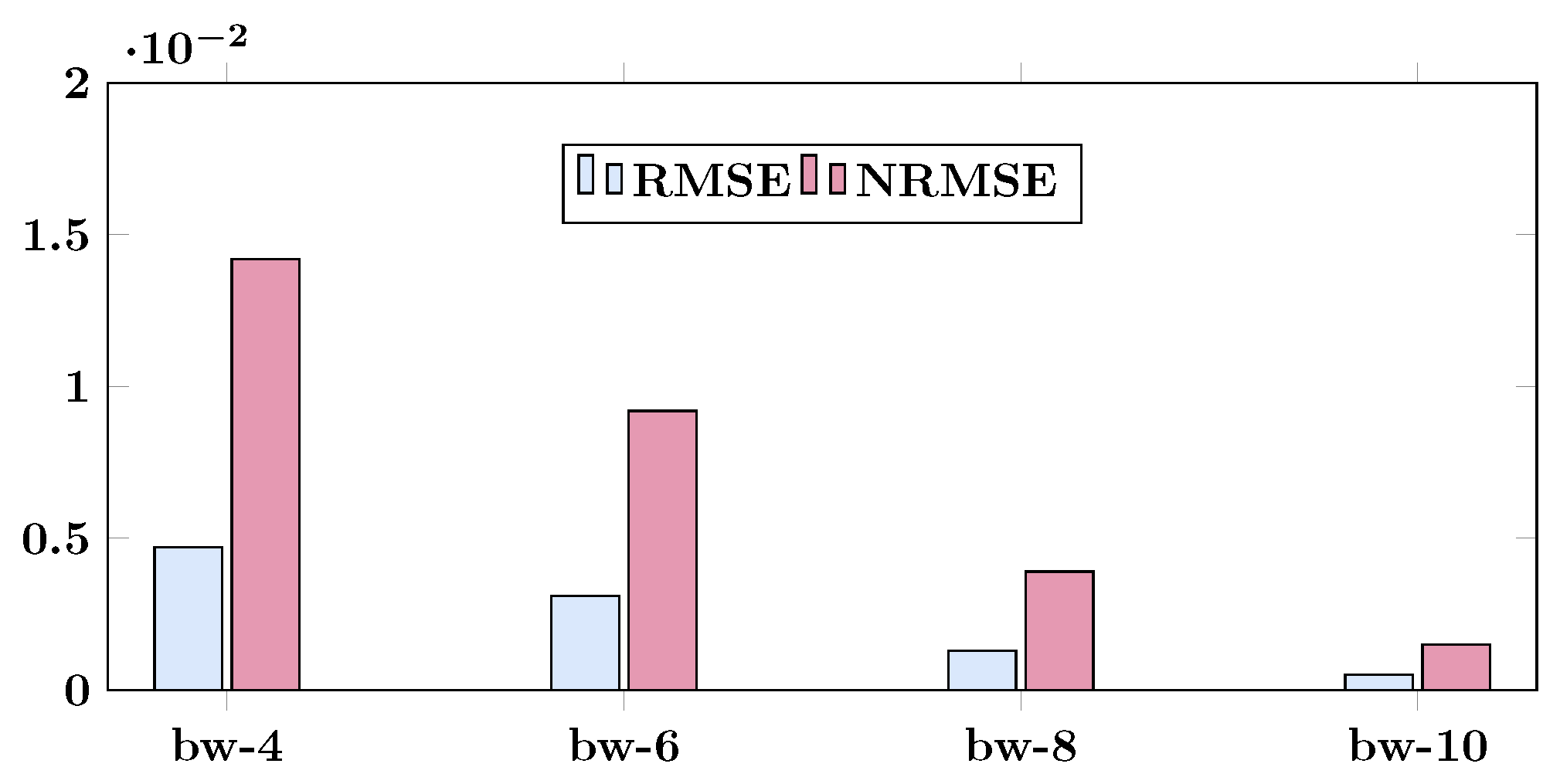
Figure 7 illustrates the comparison between the mathematical analysis results of Equation (22) and the results obtained from a SC implementation with different bit widths. When using 8-bit stochastic ODE solvers, the SC implementation provides relatively accurate solutions that closely match the analytical results. Zooming in on a narrow range reveals that the SC implementation with a bit width of 8 closely aligns with the analytical results, while the 4-bit implementation shows some differences. To evaluate the error between the SC implementation and the analytical results, the and are analyzed. Figure 8 displays the error analysis results. The value is lower than , indicating a very small error between the SC squaring operation and squaring using a normal multiplication operation.
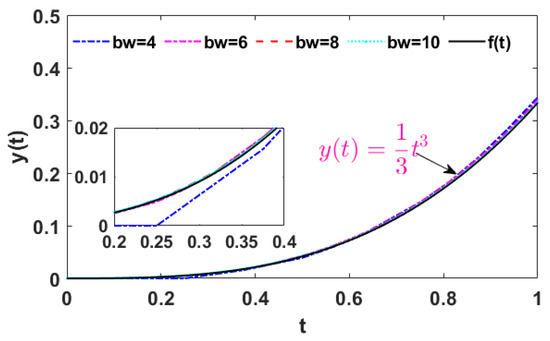
Figure 7.
Comparison between the mathematical analysis results of Equation (22) and the results obtained from a SC implementation with different bit widths.
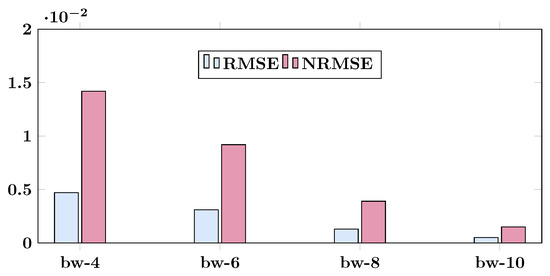
Figure 8.
and of mathematical analysis results vs. SC implementation results with different bit widths ( means bit width) for Equation (22).
4.2. The Overall Architecture of SC-IZ Model
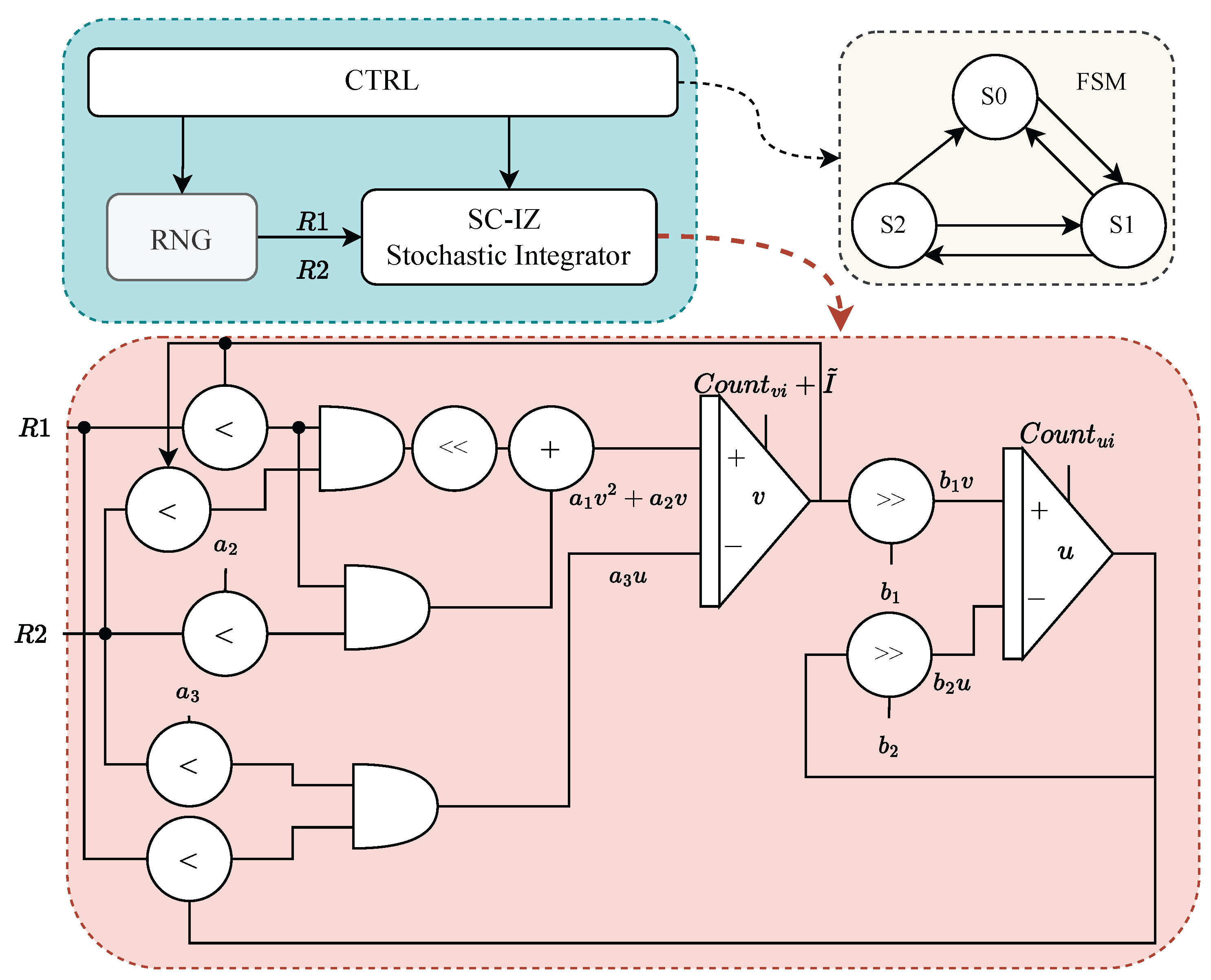
The overall architecture of our SC-IZ model is shown in Figure 9. To optimize hardware resources, the architecture utilizes shared RNG modules. Additionally, the hardware implementation focuses on simple operations such as simple addition, AND operations, and shift operations.
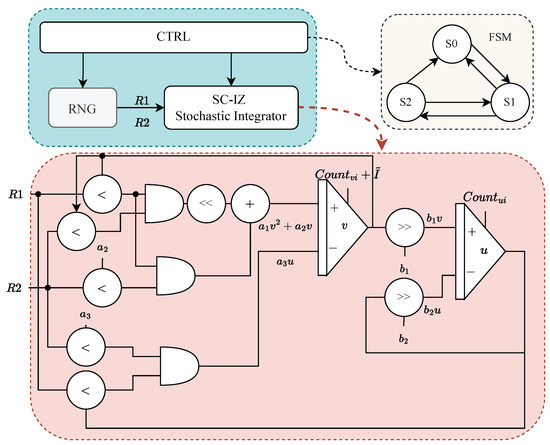
Figure 9.
The overall architecture of our SC-IZ model.
To improve implementation efficiency, fixed-point arithmetic was utilized in our design. The architecture consists of three main components: the control unit (CTRL), the SC-IZ stochastic integrators, and the RNG unit. A control Finite State Machine (FSM), depicted in Figure 9, governs the behavior of the model, featuring three states: idle (), integrate (), and fire (). These states correspond to the activities of integrate-and-fire neurons within the system.
Each neuron starts in the idle state () and transitions to the integrate state () upon triggering, where initial values are assigned to variables v and u. In the integrate state (), the neuron performs membrane potential accumulation and adaptation accumulation using SC-IZ stochastic integrators. The neuron remains in the integrate state until the reset condition, defined by Equation (16), is met. Once the reset condition is satisfied, the neuron switches from the integrate state () to the fire state (). The SC-IZ stochastic integrator within our architecture utilizes shared random numbers ( and ) generated by the RNG unit. The sign of parameters , , , , and determines whether the stochastic integral accumulator performs accumulation or decrement.
For multiplication operations, our hardware design avoids complex binary implementations and instead employs a simple AND gate. This approach, along with straightforward accumulation and shifting operations, significantly reduces complexity and resource requirements compared to traditional multiplication circuits. As a result, our design achieves a more compact and efficient hardware implementation. By minimizing hardware resource usage and simplifying circuitry, our architecture enables the realization of large-scale SNNs, opening up new possibilities for neural network applications.
4.3. Evaluation
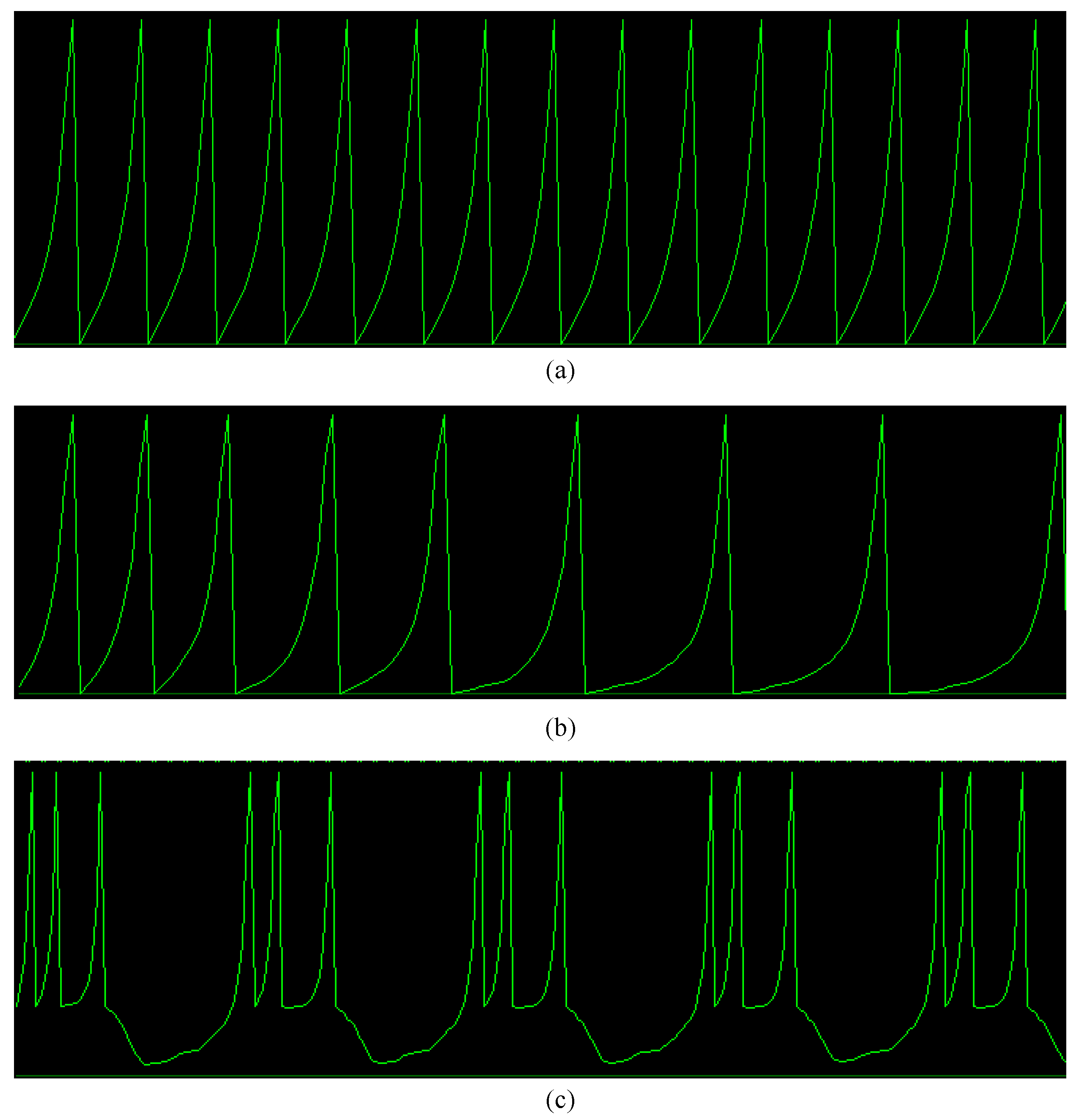
The SC-IZ neuron model was implemented on the Xilinx Zynq-7000 SoC ZC702 FPGA, and the simulation and analysis were performed using Vivado 2018.3. The FPGA implementation of the proposed SC-IZ design successfully reproduces various spiking patterns as demonstrated in Figure 10. Additionally, the resource utilization of the FPGA implementation was evaluated.
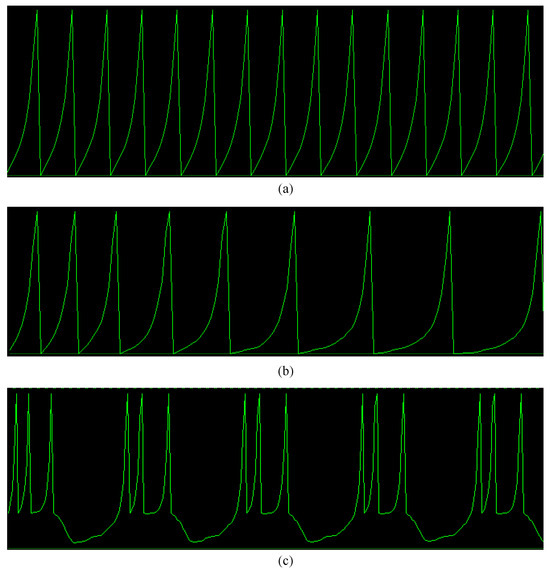
Figure 10.
Spiking patterns of the proposed SC-IZ model implemented on Xilinx Zynq-7000 SoC ZC702. (a) Regular spiking (RS). (b) Intrinsically bursting (IB). (c) Chattering (CH).
Table 5 presents a comprehensive comparison of hardware resources between the SC-IZ model and previously proposed Izhikevich neuron models. The SC-IZ model stands out with its remarkable achievements. It operates at a frequency of 260 MHz on the FPGA, demonstrating its high-speed processing capabilities. In terms of power consumption, the total on-chip power usage for the SC-IZ model is 117 mW, with dynamic power accounting for 12 mW and device static power for 105 mW. These power levels highlight the model’s energy efficiency and its suitability for low-power applications.

Table 5.
Comparison of FPGA resource utilization of the implemented SC-IZ model with the previously proposed Izhikevich model.
One of the significant advantages of the SC-IZ model is its minimal hardware resource requirements compared to previous works. Notably, when compared to the state-of-the-art work [22], the SC-IZ model showcases impressive advancements. It achieves substantial reductions in the utilization of hardware resources, specifically reducing the utilization of Slices, Look-Up Tables (LUTs), and Flip-Flops (FFs) by 56.25%, 57.61%, and 58.80%, respectively. Additionally, the SC-IZ model is able to operate at a higher frequency. The constrained hardware resources of FPGA platforms necessitate efficient utilization to realize large-scale SNN implementations. For instance, on the Xilinx Zynq-7000 SoC ZC702 platform, which provides 13,300 Slices, 53,200 LUTs, and 106,400 FFs, the efficient utilization of these resources is paramount. In the state-of-the-art work [22], each neuron commands a substantial portion of these resources, consuming 96 Slices, 309 LUTs, and 274 FFs. As a consequence, the platform can accommodate up to 138 neurons. In contrast, our proposed SC-IZ endeavors to optimize resource utilization, significantly diminishing the resource footprint required per neuron. Specifically, our approach achieves a marked reduction to 42 slices, 131 LUTs, and 113 FFs per neuron. This optimization facilitates our implementation’s ability to accommodate up to 316 neurons on the same Xilinx Zynq-7000 SoC ZC702 platform. This substantial reduction in resource consumption underscores the superior efficiency of our approach in enabling large-scale SNN deployments.
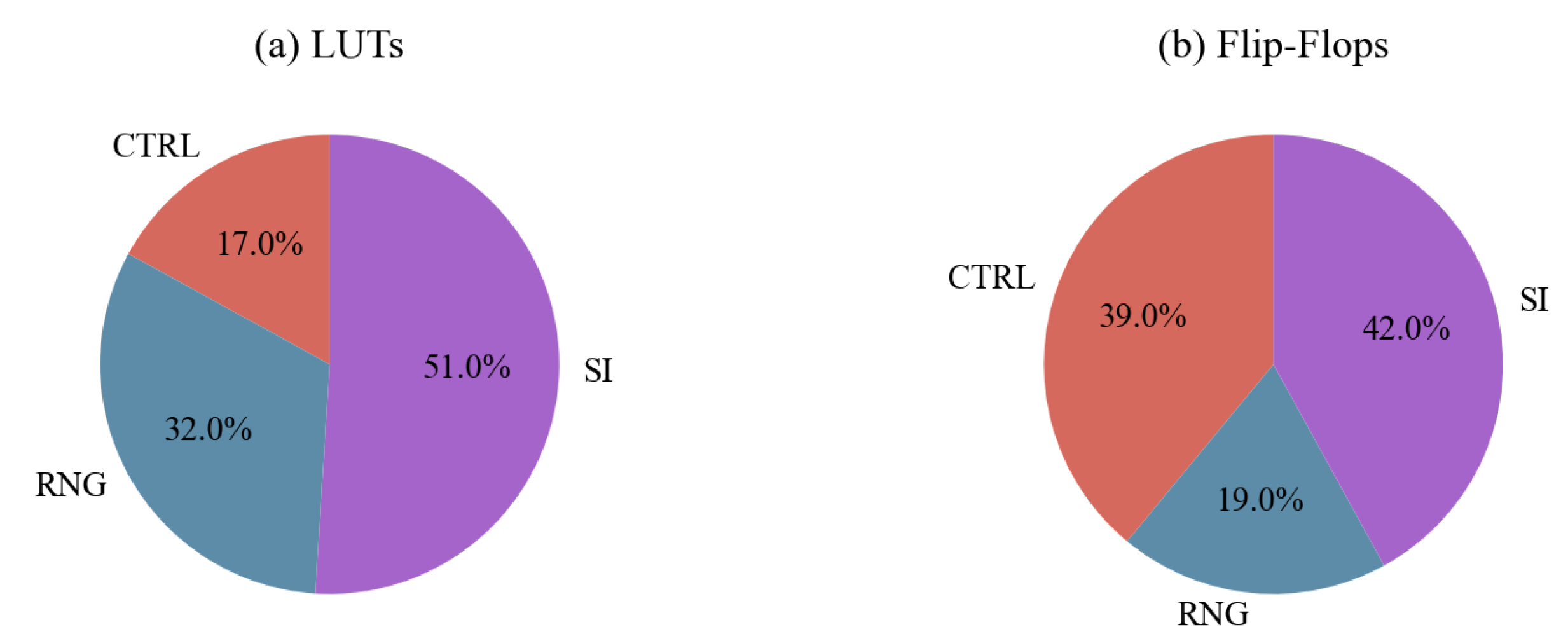
Figure 11 provides a breakdown of the hardware resources, revealing that a significant portion is consumed by the RNG unit. Therefore, optimizing the RNG unit becomes crucial. If each random bit stream is generated using independent LFSR-based RNG units, it would lead to higher hardware resource consumption. However, our approach employs the LFSR sharing technique, which reduces the number of independent LFSRs from five to just one. This reduction in the number of RNG units amounts to an 80% decrease. By utilizing simple operations such as addition, AND operations, and shift operations, along with the LFSR sharing approach, we successfully minimize the FPGA resources required.
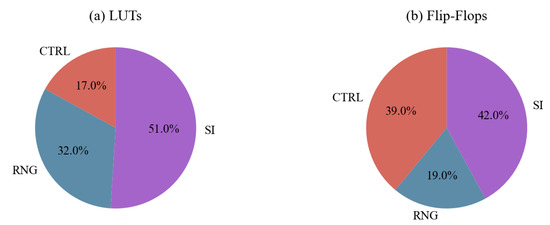
Figure 11.
The breakdown of hardware resources. (a) Hardware resource breakdown of LUTs. (b) Hardware resource breakdown of FFs.
5. Conclusions
SNNs built on simplistic LIF models exhibit shortcomings in both biological plausibility and performance. The Izhikevich model can exhibit firing patterns of various cortical neurons. Recent studies have demonstrated that SNNs developed using Izhikevich neuron models outperform SNNs based on LIF models, especially for image classification tasks [55,56]. In this work, we propose SC-IZ, a hardware-efficient and biologically plausible Izhikevich neuron model based on stochastic computing. The SC-IZ model accurately reproduces a wide range of biological neural behaviors and is well suited for large-scale SNN implementations. Simulation results have demonstrated that the SC-IZ model achieves high accuracy while maintaining efficiency. Compared to the state-of-the-art Izhikevich neuron model, SC-IZ offers lower hardware cost and higher operating frequency. While the SC-IZ model presents a compelling solution for efficient and scalable SNN implementations, continued research efforts are necessary to address its limitations and further optimize its performance for a broader range of applications. Investigating strategies for seamlessly integrating SC-IZ into real-world applications and platforms would be invaluable for its practical adoption and deployment.
Author Contributions
Conceptualization, W.L. and S.X.; methodology, W.L. and S.X.; software, W.L.; validation, W.L. and B.L.; writing—original draft preparation, W.L.; writing—review and editing, W.L., S.X., B.L. and Z.Y.; funding acquisition, S.X. and Z.Y.; All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (NSFC) under Grant 62334014, and in part by the Key-Area Research and Development Program of Guangdong Province under Grant 2021B0101410004.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lin, C.K.; Wild, A.; Chinya, G.N.; Cao, Y.; Davies, M.; Lavery, D.M.; Wang, H. Programming spiking neural networks on Intel’s Loihi. Computer 2018, 51, 52–61. [Google Scholar] [CrossRef]
- Yang, J.Q.; Wang, R.; Ren, Y.; Mao, J.Y.; Wang, Z.P.; Zhou, Y.; Han, S.T. Neuromorphic engineering: From biological to spike-based hardware nervous systems. Adv. Mater. 2020, 32, 2003610. [Google Scholar] [CrossRef] [PubMed]
- Akopyan, F.; Sawada, J.; Cassidy, A.; Alvarez-Icaza, R.; Arthur, J.; Merolla, P.; Imam, N.; Nakamura, Y.; Datta, P.; Nam, G.J.; et al. Truenorth: Design and tool flow of a 65 mw 1 million neuron programmable neurosynaptic chip. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. 2015, 34, 1537–1557. [Google Scholar] [CrossRef]
- Tavanaei, A.; Ghodrati, M.; Kheradpisheh, S.R.; Masquelier, T.; Maida, A. Deep learning in spiking neural networks. Neural Netw. 2019, 111, 47–63. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Deng, L.; Li, G.; Zhu, J.; Xie, Y.; Shi, L. Direct training for spiking neural networks: Faster, larger, better. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 1311–1318. [Google Scholar]
- Wu, Y.; Deng, L.; Li, G.; Zhu, J.; Shi, L. Spatio-temporal backpropagation for training high-performance spiking neural networks. Front. Neurosci. 2018, 12, 331. [Google Scholar] [CrossRef]
- Patel, K.; Hunsberger, E.; Batir, S.; Eliasmith, C. A spiking neural network for image segmentation. arXiv 2021, arXiv:2106.08921. [Google Scholar]
- Haessig, G.; Cassidy, A.; Alvarez, R.; Benosman, R.; Orchard, G. Spiking optical flow for event-based sensors using ibm’s truenorth neurosynaptic system. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 860–870. [Google Scholar] [CrossRef]
- Vidal, A.R.; Rebecq, H.; Horstschaefer, T.; Scaramuzza, D. Ultimate SLAM? Combining events, images, and IMU for robust visual SLAM in HDR and high-speed scenarios. IEEE Robot. Autom. Lett. 2018, 3, 994–1001. [Google Scholar] [CrossRef]
- Barchid, S.; Mennesson, J.; Eshraghian, J.; Djéraba, C.; Bennamoun, M. Spiking neural networks for frame-based and event-based single object localization. Neurocomputing 2023, 559, 126805. [Google Scholar] [CrossRef]
- Moro, F.; Hardy, E.; Fain, B.; Dalgaty, T.; Clémençon, P.; De Prà, A.; Esmanhotto, E.; Castellani, N.; Blard, F.; Gardien, F.; et al. Neuromorphic object localization using resistive memories and ultrasonic transducers. Nat. Commun. 2022, 13, 3506. [Google Scholar] [CrossRef]
- Davies, M.; Srinivasa, N.; Lin, T.H.; Chinya, G.N.; Cao, Y.; Choday, S.H.; Dimou, G.D.; Joshi, P.; Imam, N.; Jain, S.; et al. Loihi: A Neuromorphic Manycore Processor with On-Chip Learning. IEEE Micro 2018, 38, 82–99. [Google Scholar] [CrossRef]
- Benjamin, B.V.; Gao, P.; McQuinn, E.; Choudhary, S.; Chandrasekaran, A.; Bussat, J.M.; Alvarez-Icaza, R.; Arthur, J.V.; Merolla, P.; Boahen, K.A. Neurogrid: A Mixed-Analog-Digital Multichip System for Large-Scale Neural Simulations. Proc. IEEE 2014, 102, 699–716. [Google Scholar] [CrossRef]
- Painkras, E.; Plana, L.A.; Garside, J.D.; Temple, S.; Galluppi, F.; Patterson, C.; Lester, D.R.; Brown, A.D.; Furber, S.B. SpiNNaker: A 1-W 18-Core System-on-Chip for Massively-Parallel Neural Network Simulation. IEEE J.-Solid-State Circuits 2013, 48, 1943–1953. [Google Scholar] [CrossRef]
- Heidarpur, M.; Ahmadi, A.; Ahmadi, M.; Azghadi, M.R. CORDIC-SNN: On-FPGA STDP learning with izhikevich neurons. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 2651–2661. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Which model to use for cortical spiking neurons? IEEE Trans. Neural Netw. 2004, 15, 1063–1070. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500. [Google Scholar] [CrossRef] [PubMed]
- Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Hybrid spiking models. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 5061–5070. [Google Scholar] [CrossRef]
- Soleimani, H.; Ahmadi, A.; Bavandpour, M. Biologically Inspired Spiking Neurons: Piecewise Linear Models and Digital Implementation. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 2991–3004. [Google Scholar] [CrossRef]
- Haghiri, S.; Zahedi, A.; Naderi, A.; Ahmadi, A. Multiplierless Implementation of Noisy Izhikevich Neuron with Low-Cost Digital Design. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 1422–1430. [Google Scholar] [CrossRef]
- Pu, J.; Goh, W.L.; Nambiar, V.P.; Chong, Y.S.; Do, A.T. A Low-Cost High-Throughput Digital Design of Biorealistic Spiking Neuron. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 1398–1402. [Google Scholar] [CrossRef]
- Arthur, J.V.; Merolla, P.; Akopyan, F.; Alvarez-Icaza, R.; Cassidy, A.S.; Chandra, S.; Esser, S.K.; Imam, N.; Risk, W.P.; Rubin, D.B.D.; et al. Building block of a programmable neuromorphic substrate: A digital neurosynaptic core. In Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar]
- Smithson, S.C.; Boga, K.; Ardakani, A.; Meyer, B.H.; Gross, W.J. Stochastic Computing Can Improve Upon Digital Spiking Neural Networks. In Proceedings of the 2016 IEEE International Workshop on Signal Processing Systems (SiPS), Dallas, TX, USA, 26–28 October 2016; pp. 309–314. [Google Scholar]
- Soleimani, H.; Ahmadi, A.; Bavandpour, M.; Sharifipoor, O. A generalized analog implementation of piecewise linear neuron models using CCII building blocks. Neural Netw. Off. J. Int. Neural Netw. Soc. 2014, 51, 26–38. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.; Kim, S.; Park, W.; Jo, W.; Yoo, H.J. A Resource-Efficient Super-Resolution FPGA Processor with Heterogeneous CNN and SNN Core Architecture. In Proceedings of the 2023 IEEE Asian Solid-State Circuits Conference (A-SSCC), Haikou, China, 5–8 November 2023; pp. 1–3. [Google Scholar]
- Plagwitz, P.; Hannig, F.; Teich, J.; Keszocze, O. To Spike or Not to Spike? A Quantitative Comparison of SNN and CNN FPGA Implementations. arXiv 2023, arXiv:abs/2306.12742. [Google Scholar]
- Pham, Q.T.; Nguyen, T.Q.; Hoang-Phuong, C.; Dang, Q.H.; Nguyen, D.M.; Nguyen-Huy, H. A review of SNN implementation on FPGA. In Proceedings of the 2021 International Conference on Multimedia Analysis and Pattern Recognition (MAPR), Hanoi, Vietnam, 15–16 October 2021; pp. 1–6. [Google Scholar]
- Liu, Y.; Liu, L.; Lombardi, F.; Han, J. An Energy-Efficient and Noise-Tolerant Recurrent Neural Network Using Stochastic Computing. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2019, 27, 2213–2221. [Google Scholar] [CrossRef]
- Xiao, S.; Liu, W.; Guo, Y.; Yu, Z. Low-cost adaptive exponential integrate-and-fire neuron using stochastic computing. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 942–950. [Google Scholar] [CrossRef] [PubMed]
- Lunglmayr, M.; Wiesinger, D.; Haselmayr, W. Design and analysis of efficient maximum/minimum circuits for stochastic computing. IEEE Trans. Comput. 2019, 69, 402–409. [Google Scholar] [CrossRef]
- Abdellatef, H.; Khalil-Hani, M.; Shaikh-Husin, N.; Ayat, S.O. Accurate and compact convolutional neural network based on stochastic computing. Neurocomputing 2022, 471, 31–47. [Google Scholar] [CrossRef]
- Abdellatef, H.; Khalil-Hani, M.; Shaikh-Husin, N.; Ayat, S.O. Low-area and accurate inner product and digital filters based on stochastic computing. Signal Process. 2021, 183, 108040. [Google Scholar] [CrossRef]
- Aygun, S.; Gunes, E.O.; De Vleeschouwer, C. Efficient and robust bitstream processing in binarised neural networks. Electron. Lett. 2021, 57, 219–222. [Google Scholar] [CrossRef]
- Schober, P. Stochastic Computing and Its Application to Sound Source Localization. Ph.D. Thesis, Technische Universität Wien, Wien, Austria, 2022. [Google Scholar]
- Onizawa, N.; Katagiri, D.; Matsumiya, K.; Gross, W.J.; Hanyu, T. An accuracy/energy-flexible configurable Gabor-filter chip based on stochastic computation with dynamic voltage–frequency–length scaling. IEEE J. Emerg. Sel. Top. Circuits Syst. 2018, 8, 444–453. [Google Scholar] [CrossRef]
- Najafi, M.H.; Salehi, M.E. A fast fault-tolerant architecture for sauvola local image thresholding algorithm using stochastic computing. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2015, 24, 808–812. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Wang, Y.; Lombardi, F.; Han, J. A Survey of Stochastic Computing Neural Networks for Machine Learning Applications. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 2809–2824. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Xie, G.; Xu, W.; Han, J.; Zhang, Y. Accelerating Stochastic Computing Using Deterministic Halton Sequences. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3351–3355. [Google Scholar] [CrossRef]
- Liu, S.; Han, J. Hardware ODE solvers using stochastic circuits. In Proceedings of the 2017 54th ACM/EDAC/IEEE Design Automation Conference (DAC), Austin, TX, USA, 18–22 June 2017; pp. 1–6. [Google Scholar]
- Gaines, B.R. Stochastic Computing Systems. In Advances in Information Systems Science; Springer: Berlin/Heidelberg, Germany, 1969; pp. 37–172. [Google Scholar]
- Joe, H.; Kim, Y. Novel Stochastic Computing for Energy-Efficient Image Processors. Electronics 2019, 8, 720. [Google Scholar] [CrossRef]
- Qian, W.; Li, X.; Riedel, M.D.; Bazargan, K.; Lilja, D.J. An Architecture for Fault-Tolerant Computation with Stochastic Logic. IEEE Trans. Comput. 2011, 60, 93–105. [Google Scholar] [CrossRef]
- Li, B.; Najafi, M.H.; Lilja, D.J. Using Stochastic Computing to Reduce the Hardware Requirements for a Restricted Boltzmann Machine Classifier. In Proceedings of the 2016 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 21–23 February 2016. [Google Scholar]
- Winstead, C. Tutorial on stochastic computing. In Stochastic Computing: Techniques and Applications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 39–76. [Google Scholar]
- Lee, Y.Y.; Halim, Z.A. Stochastic computing in convolutional neural network implementation: A review. PeerJ Comput. Sci. 2020, 6, e309. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Dynamical Systems in Neuroscience; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Sim, H.; Nguyen, D.; Lee, J.; Choi, K. Scalable stochastic-computing accelerator for convolutional neural networks. In Proceedings of the 2017 22nd Asia and South Pacific Design Automation Conference (ASP-DAC), Chiba, Japan, 16–19 January 2017; pp. 696–701. [Google Scholar]
- Ribeiro, M.H.D.M.; Stefenon, S.F.; de Lima, J.D.; Nied, A.; Mariani, V.C.; Coelho, L.d.S. Electricity price forecasting based on self-adaptive decomposition and heterogeneous ensemble learning. Energies 2020, 13, 5190. [Google Scholar] [CrossRef]
- da Silva, R.G.; Moreno, S.R.; Ribeiro, M.H.D.M.; Larcher, J.H.K.; Mariani, V.C.; dos Santos Coelho, L. Multi-step short-term wind speed forecasting based on multi-stage decomposition coupled with stacking-ensemble learning approach. Int. J. Electr. Power Energy Syst. 2022, 143, 108504. [Google Scholar] [CrossRef]
- Lee, V.T.; Alaghi, A.; Ceze, L. Correlation manipulating circuits for stochastic computing. In Proceedings of the 2018 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 19–23 March 2018; pp. 1417–1422. [Google Scholar]
- Ichihara, H.; Sugino, T.; Ishii, S.; Iwagaki, T.; Inoue, T. Compact and accurate digital filters based on stochastic computing. IEEE Trans. Emerg. Top. Comput. 2016, 7, 31–43. [Google Scholar] [CrossRef]
- Lee, D.; Baik, J.; Kim, Y. Enhancing Stochastic Computing using a Novel Hybrid Random Number Generator Integrating LFSR and Halton Sequence. In Proceedings of the 2023 20th International SoC Design Conference (ISOCC), Jeju, Republic of Korea, 25–28 October 2023; pp. 7–8. [Google Scholar]
- Leigh, A.J.; Mirhassani, M.; Muscedere, R. An Efficient Spiking Neuron Hardware System Based on the Hardware-Oriented Modified Izhikevich Neuron (HOMIN) Model. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3377–3381. [Google Scholar]
- Jin, C.; Zhu, R.J.; Wu, X.; Deng, L.J. Sit: A bionic and non-linear neuron for spiking neural network. arXiv 2022, arXiv:2203.16117. [Google Scholar]
- Caruso, A. Izhikevich Neural Model and STDP Learning Algorithm Mapping on Spiking Neural Network Hardware Emulator. Master’s Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2020. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).