Transformer Core Fault Diagnosis via Current Signal Analysis with Pearson Correlation Feature Selection
Abstract
:1. Introduction
- We have designed an experimental setup with the aim of collecting current signals, which should serve as a baseline for other researchers in analyzing transformer core fault analysis.
- We applied the Hilbert transform, a time-domain signal processing technique, to extract the magnitude envelope. This step is critical in improving the interpretation of signal analysis.
- We have established a comprehensive framework for robust feature engineering, focusing on extracting time-domain statistical features and filter-based Pearson correlation feature selection.
- We have conducted a comparative analysis in terms of performance evaluation to validate the efficiency of the proposed framework.
2. Motivation and Review of the Related Literature
2.1. Analysis Concerning Time Domain and Frequency Domain
2.2. Overview of Selected Machine Learning Algorithms
3. Theoretical Background
3.1. Fast Fourier Transform
3.2. Hilbert Transform
- Complex representation: The analytic signal is complex, with both real and imaginary components. The actual component signifies the original signal, while the imaginary component represents the Hilbert transform of the signal.
- A 90-degree phase shift: The positive frequency shifts to a negative 90-degree angle, and the negative frequency shifts to a positive 90-degree angle in the context of HT. This introduces a phase shift of 90 degrees between the original signal and its HT, which is crucial in applications such as demodulation and phase-sensitive analysis. Additionally, the analytic signal, derived through the HT, provides a representation of the original signal that separates positive and negative frequency components. This property is valuable for analyzing the frequency content of a signal.
- Enveloping: The envelope of the original signal can be extracted from the magnitude of the analytic signal. The envelope represents the slowly varying magnitude of the signal and is useful in applications such as amplitude modulation.
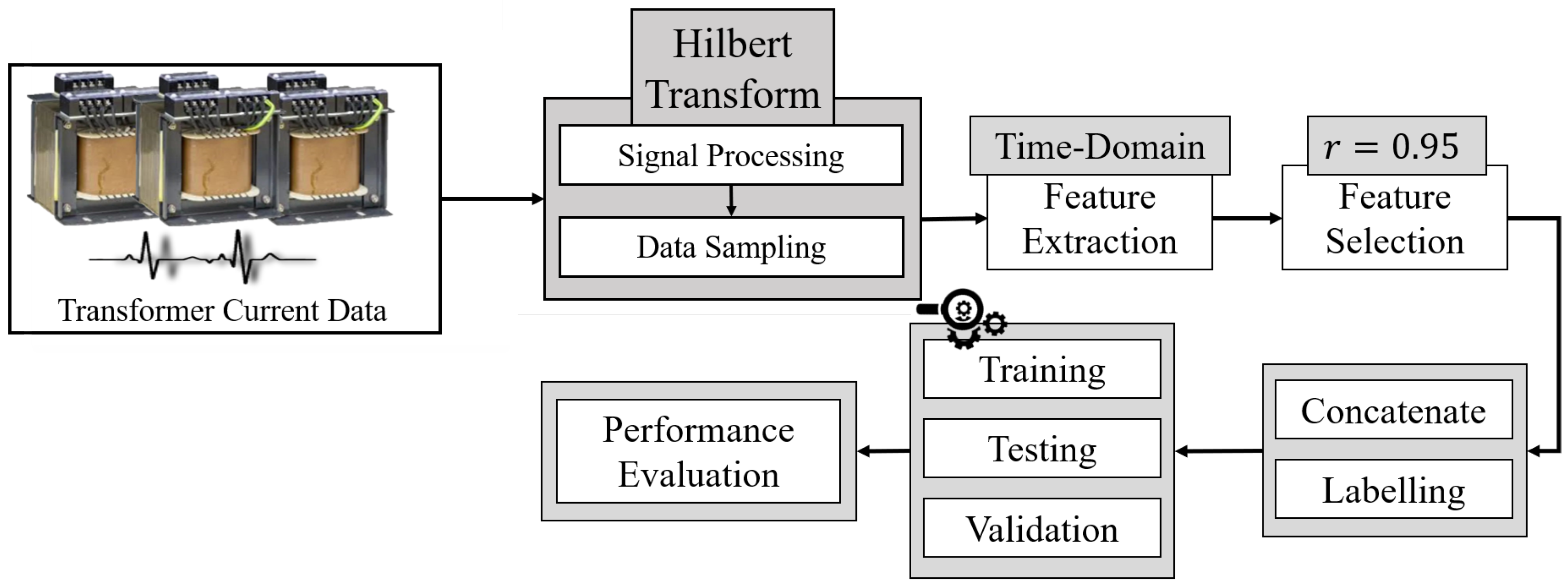
4. Proposed Diagnostic Framework
| Domain | Features | Formulas |
|---|---|---|
| Time-based | Crest Factor | |
| Form Factor | ||
| Interquartile Range | ||
| Margin | ||
| Max | ||
| Mean | ||
| Median Absolute Deviation | ||
| nth Percentile (5, 25, 75) | 100 | |
| Peak-to-peak | ||
| Root Mean Square (RMS) | ||
| Standard Deviation | ||
| Variance |
| Domain | Features | Formulas |
|---|---|---|
| Frequency-based | Mean Frequency | |
| Median Frequency | , where is the cumulative power spectral density | |
| Spectral Entropy | ||
| Spectral Centroid | ||
| Spectral Spread | ||
| Spectral Skewness | ||
| Spectral Kurtosis | ||
| Total Power | ||
| Spectral Flatness | ||
| Peak Frequency and Frequency | ||
| Peak Amplitude | ||
| Dominant Frequency and Frequency | ||
| Spectral Roll-Off (n = 80%, 90%) | Frequency , where is the cumulative power spectral density. |
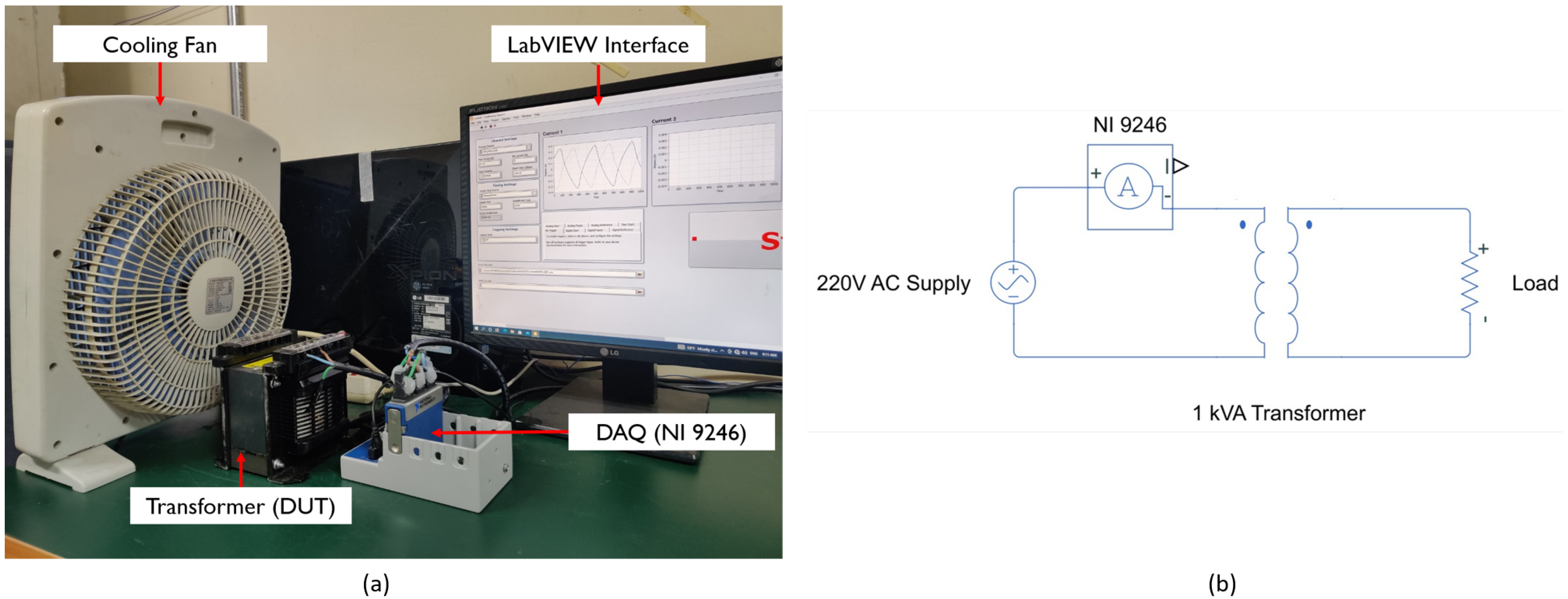
5. Experimental Setup and Data Collection
- Three isolated analog input channels were employed, each operating at a simultaneous sample rate of 50 kS/s, ensuring comprehensive data collection.
- The system offers a broad input range of 22 continuous arms, with a ±30 A peak input range and 24-bit resolution, exclusively for AC signals.
- Specifically designed to accommodate 1 A/5 A nominal CTs, ensuring compatibility and accuracy during measurements.
- Channel-to-earth isolation of up to 300 Vrms and channel-to-channel CAT III isolation of 480 Vrms guarantees safety and accuracy during experimentation.
- It has ring lug connectors tailored for up to 10 AWG cables, ensuring secure and reliable connections.
- It operates within a wide temperature range, from −40 °C to 70 °C, and is engineered to withstand 5 g vibrations and 50 g shocks, ensuring stability and functionality across varying environmental conditions.
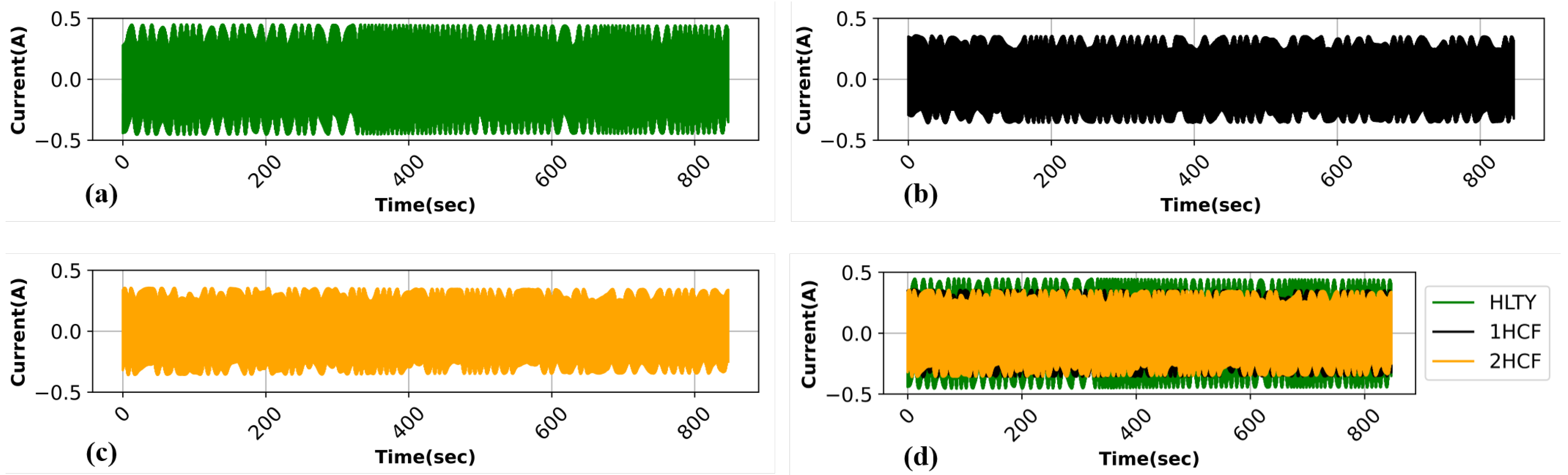
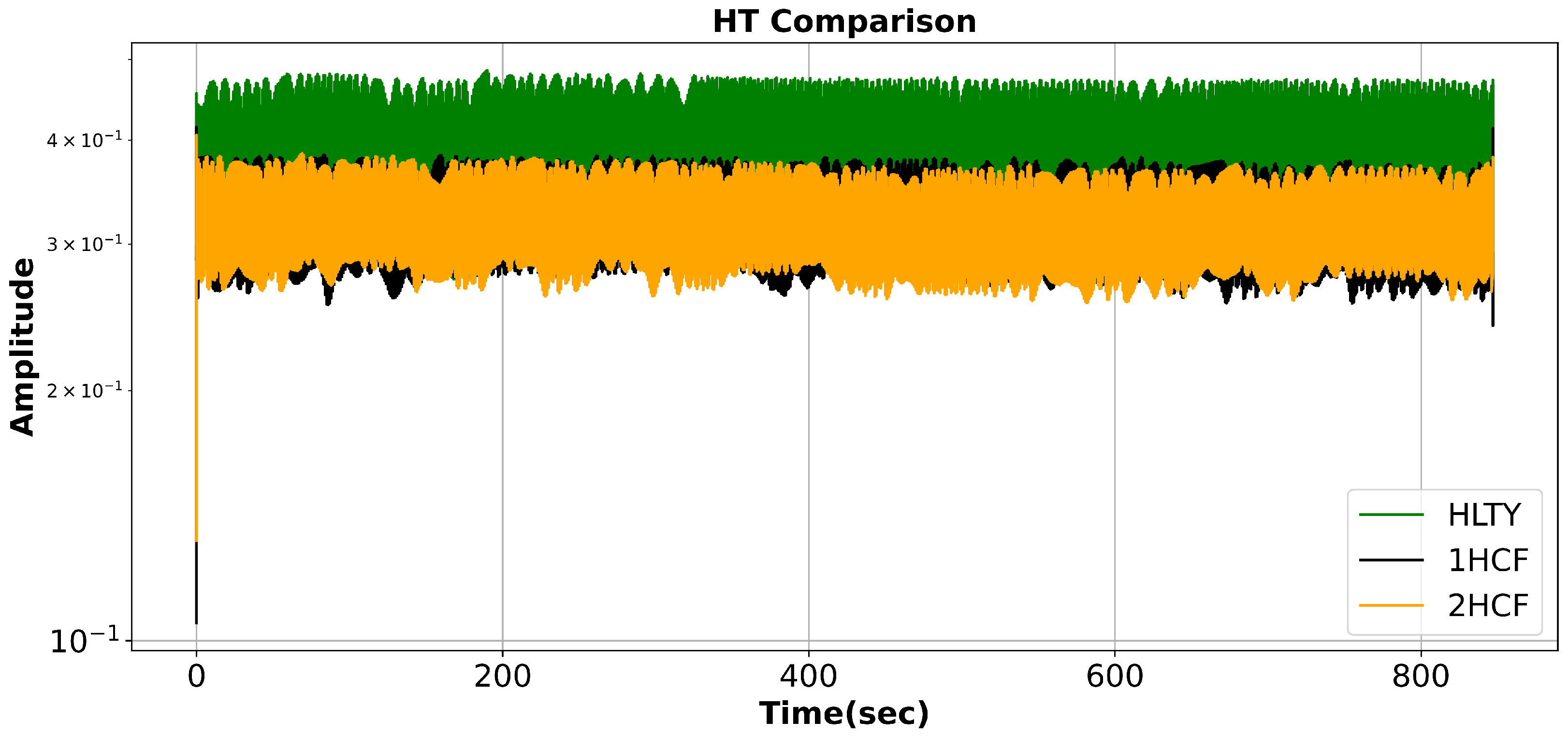
5.1. Applying Signal Processing Technique
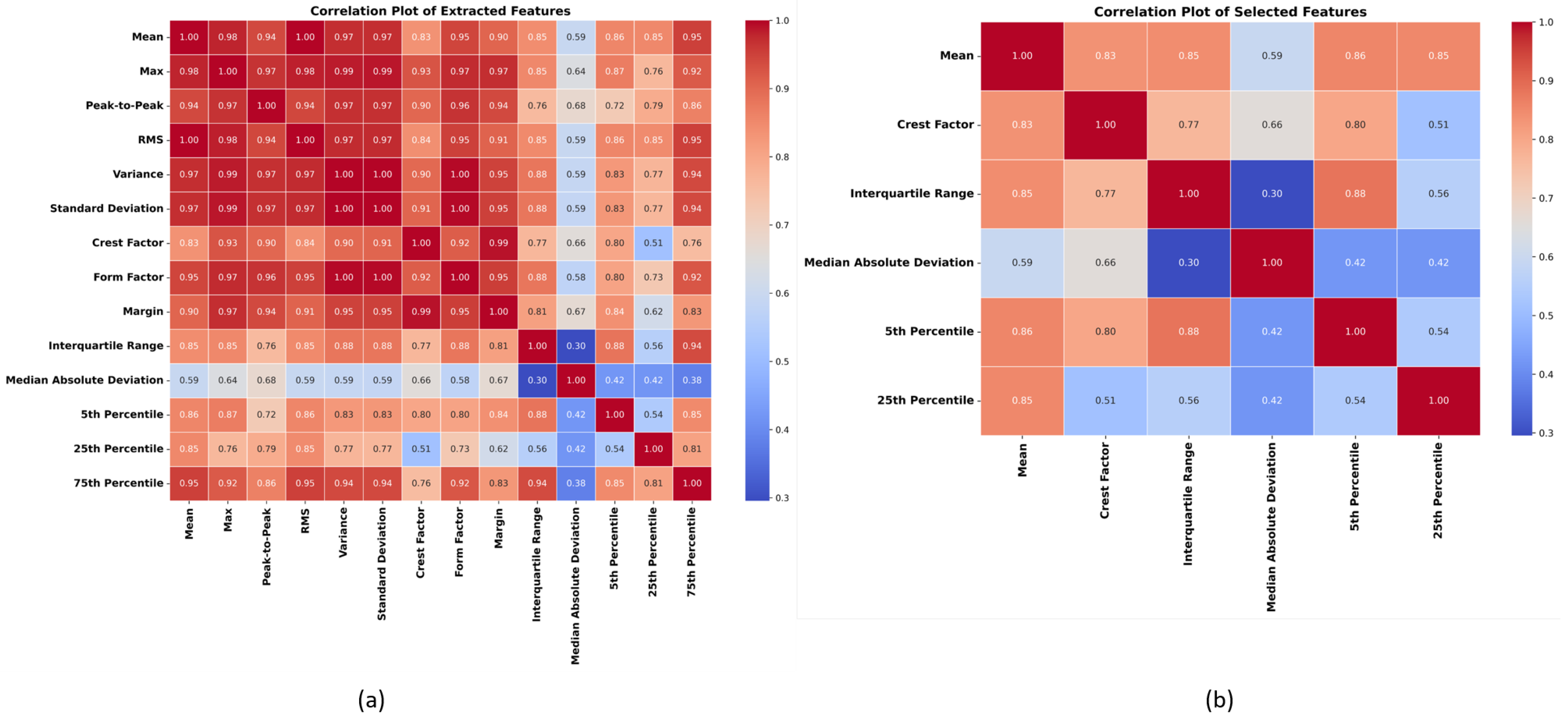
5.2. Correlation Matrix of Extracted and Selected Time-Domain Statistical Features
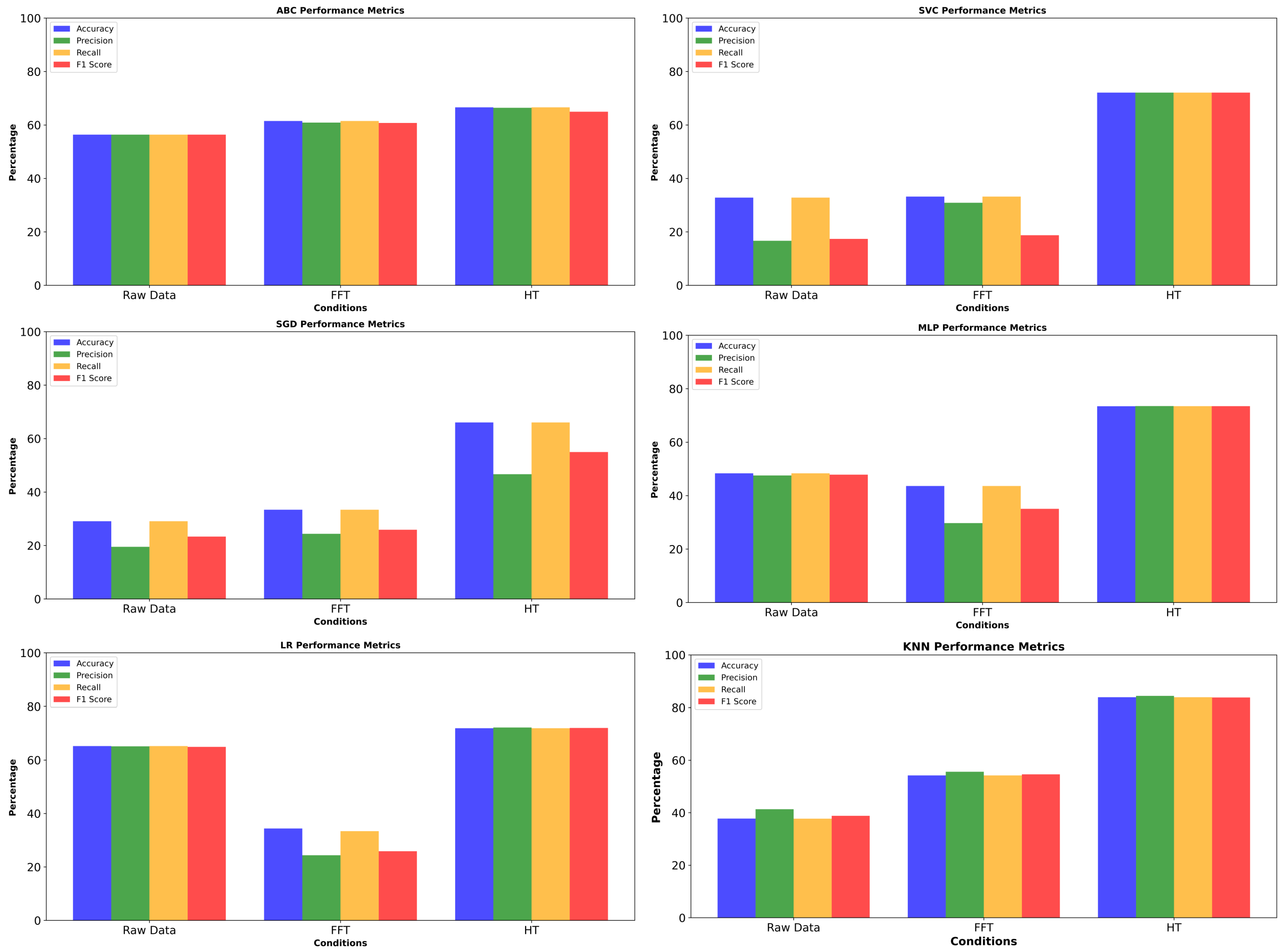
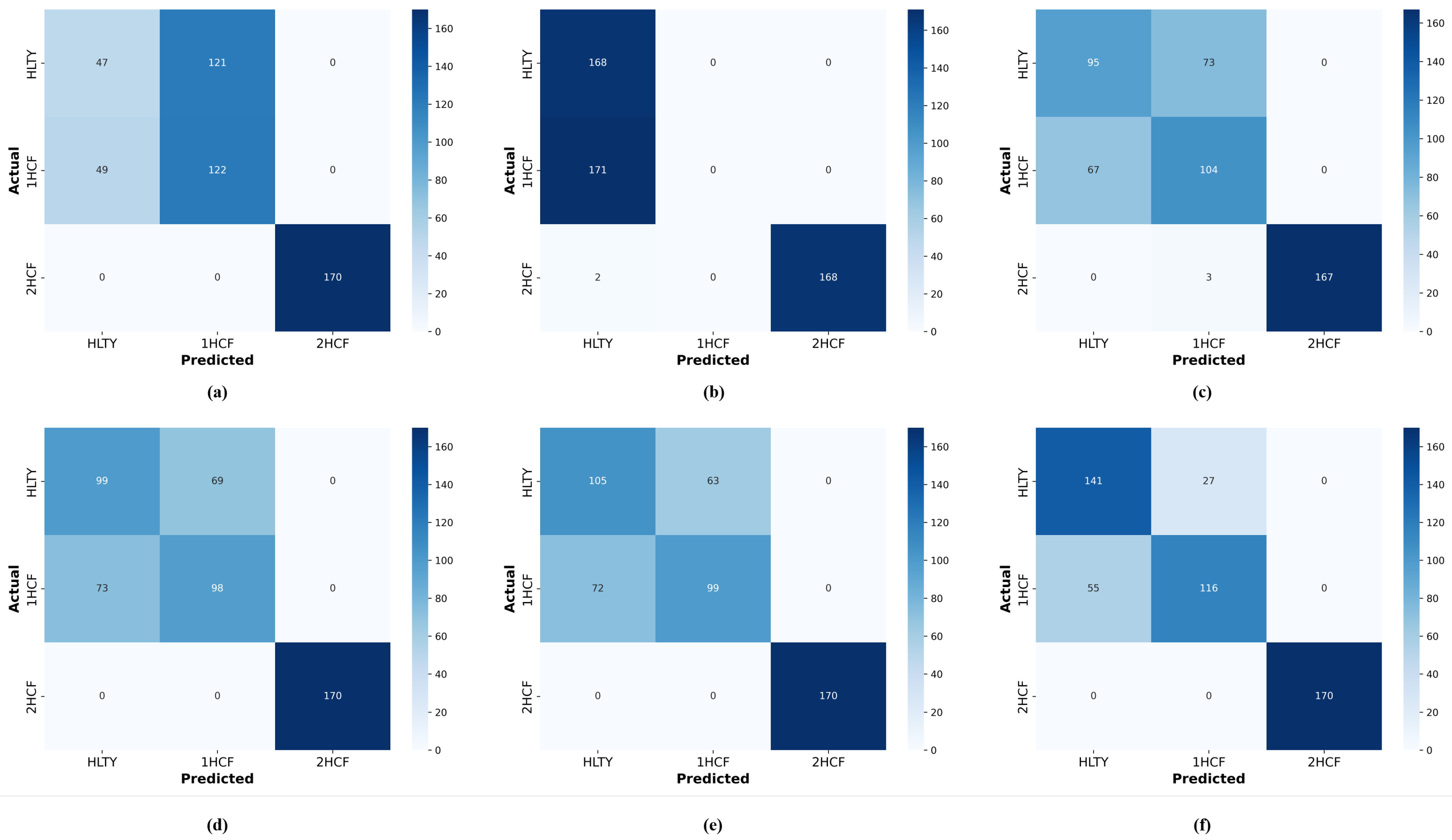
6. ML Diagnostic Results and Discussion
Limitations, Open Issues, and Future Directions
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, N.H.; An, D.; Choi, J.H. Prognostics and Health Management of Engineering Systems: An Introduction; Springer: Cham, Switzerland, 2017; pp. 127–241. [Google Scholar]
- Do, J.S.; Kareem, A.B.; Hur, J.-W. LSTM-Autoencoder for Vibration Anomaly Detection in Vertical Carousel Storage and Retrieval System (VCSRS). Sensors 2023, 23, 1009. [Google Scholar] [CrossRef]
- Fink, O.; Wang, Q.; Svensén, M.; Dersin, P.; Lee, W.-J.; Ducoffe, M. Potential, challenges and future directions for deep learning in prognostics and health management applications. Eng. Appl. Artif. Intell. 2020, 92, 103678. [Google Scholar] [CrossRef]
- Jia, Z.; Wang, S.; Zhao, K.; Li, Z.; Yang, Q.; Liu, Z. An efficient diagnostic strategy for intermittent faults in electronic circuit systems by enhancing and locating local features of faults. Meas. Sci. Technol. 2024, 35, 036107. [Google Scholar] [CrossRef]
- Aciu, A.-M.; Nițu, M.-C.; Nicola, C.-I.; Nicola, M. Determining the Remaining Functional Life of Power Transformers Using Multiple Methods of Diagnosing the Operating Condition Based on SVM Classification Algorithms. Machines 2024, 12, 37. [Google Scholar] [CrossRef]
- Yu, Q.; Bangalore, P.; Fogelström, S.; Sagitov, S. Optimal Preventive Maintenance Scheduling for Wind Turbines under Condition Monitoring. Energies 2024, 17, 280. [Google Scholar] [CrossRef]
- Zhuang, L.; Johnson, B.K.; Chen, X.; William, E. A topology-based model for two-winding, shell-type, single-phase transformer inter-turn faults. In Proceedings of the 2016 IEEE/PES Trans. and Dist. Conference and Exposition (T&D), Dallas, TX, USA, 3–5 May 2016; pp. 1–5. [Google Scholar]
- Manohar, S.S.; Subramaniam, A.; Bagheri, M.; Nadarajan, S.; Gupta, A.K.; Panda, S.K. Transformer Winding Fault Diagnosis by Vibration Monitoring. In Proceedings of the 2018 Condition Monitoring and Diagnosis (CMD), Perth, WA, Australia, 23–26 September 2018; pp. 1–6. [Google Scholar]
- Olayiwola, T.N.; Hyun, S.-H.; Choi, S.-J. Photovoltaic Modeling: A Comprehensive Analysis of the I–V Characteristic Curve. Sustainability 2024, 16, 432. [Google Scholar] [CrossRef]
- Islam, M.M.; Lee, G.; Hettiwatte, S.N. A nearest neighbor clustering approach for incipient fault diagnosis of power transformers. Electr. Eng. 2017, 99, 1109–1119. [Google Scholar] [CrossRef]
- Wang, M.; Vandermaar, A.J.; Srivastava, K.D. Review of condition assessment of power transformers in service. IEEE Electr. Insul. Mag. 2002, 18, 12–25. [Google Scholar] [CrossRef]
- Okwuosa, C.N.; Hur, J.W. A Filter-Based Feature-Engineering-Assisted SVC Fault Classification for SCIM at Minor-Load Conditions. Energies 2022, 15, 7597. [Google Scholar] [CrossRef]
- Kareem, A.B.; Hur, J.-W. Towards Data-Driven Fault Diagnostics Framework for SMPS-AEC Using Supervised Learning Algorithms. Electronics 2022, 11, 2492. [Google Scholar] [CrossRef]
- Shifat, T.A.; Hur, J.W. ANN Assisted Multi-Sensor Information Fusion for BLDC Motor Fault Diagnosis. IEEE Access 2021, 9, 9429–9441. [Google Scholar] [CrossRef]
- Lee, J.-H.; Okwuosa, C.N.; Hur, J.-W. Extruder Machine Gear Fault Detection Using Autoencoder LSTM via Sensor Fusion Approach. Inventions 2023, 8, 140. [Google Scholar] [CrossRef]
- Kareem, A.B.; Hur, J.-W. A Feature Engineering-Assisted CM Technology for SMPS Output Aluminium Electrolytic Capacitors (AEC) Considering D-ESR-Q-Z Parameters. Processes 2022, 10, 1091. [Google Scholar] [CrossRef]
- Gao, B.; Yu, R.; Hu, G.; Liu, C.; Zhuang, X.; Zhou, P. Development Processes of Surface Trucking and Partial Discharge of Pressboards Immersed in Mineral Oil: Effect of Tip Curvatures. Energies 2019, 12, 554. [Google Scholar] [CrossRef]
- Liu, J.; Cao, Z.; Fan, X.; Zhang, H.; Geng, C.; Zhang, Y. Influence of Oil–Pressboard Mass Ratio on the Equilibrium Characteristics of Furfural under Oil Replacement Conditions. Polymers 2020, 12, 2760. [Google Scholar] [CrossRef]
- Fritsch, M.; Wolter, M. Saturation of High-Frequency Current Transformers: Challenges and Solutions. IEEE Trans. Instrum. Meas. 2023, 72, 9004110. [Google Scholar] [CrossRef]
- Altayef, E.; Anayi, F.; Packianather, M.; Benmahamed, Y.; Kherif, O. Detection and Classification of Lamination Faults in a 15 kVA Three-Phase Transformer Core Using SVM, KNN and DT Algorithms. IEEE Access 2022, 10, 50925–50932. [Google Scholar] [CrossRef]
- Yuan, F.; Shang, Y.; Yang, D.; Gao, J.; Han, Y.; Wu, J. Comparison on multiple signal analysis method in transformer core looseness fault. In Proceedings of the IEEE Asia-Pacific Conference on Image Processing, Electronics and Computers, Dalian, China, 14–16 April 2021. [Google Scholar]
- Tian, H.; Peng, W.; Hu, M.; Yuan, G.; Chen, Y. Feature extraction of the transformer core loosening based on variational mode decomposition. In Proceedings of the 2017 1st International Conference on Electrical Materials and Power Equipment (ICEMPE), Xi’an, China, 14–17 May 2017. [Google Scholar]
- Yao, D.; Li, L.; Zhang, S.; Zhang, D.; Chen, D. The Vibroacoustic Characteristics Analysis of Transformer Core Faults Based on Multi-Physical Field Coupling. Symmetry 2022, 14, 544. [Google Scholar] [CrossRef]
- Bagheri, M.; Zollanvari, A.; Nezhivenko, S. Transformer Fault Condition Prognosis Using Vibration Signals Over Cloud Environment. IEEE Access 2018, 6, 9862–9874. [Google Scholar] [CrossRef]
- Shengchang, J.; Yongfen, L.; Yanming, L. Research on extraction technique of transformer core fundamental frequency vibration based on OLCM. IEEE Trans. Power Deliv. 2006, 21, 1981–1988. [Google Scholar] [CrossRef]
- Okwuosa, C.N.; Hur, J.W. An Intelligent Hybrid Feature Selection Approach for SCIM Inter-Turn Fault Classification at Minor Load Conditions Using Supervised Learning. IEEE Access 2023, 11, 89907–89920. [Google Scholar] [CrossRef]
- Pietrzak, P.; Wolkiewicz, M. Demagnetization Fault Diagnosis of Permanent Magnet Synchronous Motors Based on Stator Current Signal Processing and Machine Learning Algorithms. Sensors 2023, 23, 1757. [Google Scholar] [CrossRef]
- Merizalde, Y.; Hernández-Callejo, L.; Duque-Perez, O.; López-Meraz, R.A. Fault Detection of Wind Turbine Induction Generators through Current Signals and Various Signal Processing Techniques. Appl. Sci. 2020, 10, 7389. [Google Scholar] [CrossRef]
- Dehina, W.; Boumehraz, M.; Kratz, F. Detectability of rotor failure for induction motors through stator current based on advanced signal processing approaches. Int. J. Dynam. Control 2021, 9, 1381–1395. [Google Scholar] [CrossRef]
- Pradhan, P.K.; Roy, S.K.; Mohanty, A.R. Detection of Broken Impeller in Submersible Pump by Estimation Rotational Frequency from Motor Current Signal. J. Vib. Eng. Technol. 2020, 8, 613–620. [Google Scholar] [CrossRef]
- Zhao, K.; Liu, Z.; Zhao, B.; Shao, H. Class-Aware Adversarial Multiwavelet Convolutional Neural Network for Cross-Domain Fault Diagnosis. IEEE Trans. Ind. Inform. 2023, 1–12. [Google Scholar] [CrossRef]
- Altaf, M.; Akram, T.; Khan, M.A.; Iqbal, M.; Ch, M.M.I.; Hsu, C.-H. A New Statistical Features Based Approach for Bearing Fault Diagnosis Using Vibration Signals. Sensors 2022, 22, 2012. [Google Scholar] [CrossRef] [PubMed]
- Akpudo, U.E.; Hur, J.-W. A Cost-Efficient MFCC-Based Fault Detection and Isolation Technology for Electromagnetic Pumps. Electronics 2021, 10, 439. [Google Scholar] [CrossRef]
- Badihi, H.; Zhang, Y.; Jiang, B.; Pillay, P.; Rakheja, S. A Comprehensive Review on Signal-Based and Model-Based Condition Monitoring of Wind Turbines: Fault Diagnosis and Lifetime Prognosis. Proc. IEEE 2022, 110, 754–806. [Google Scholar] [CrossRef]
- Ismail, A.; Saidi, L.; Sayadi, M.; Benbouzid, M. A New Data-Driven Approach for Power IGBT Remaining Useful Life Estimation Based On Feature Reduction Technique and Neural Network. Electronics 2018, 9, 1571. [Google Scholar] [CrossRef]
- Stavropoulos, G.; van Vorstenbosch, R.; van Schooten, F.; Smolinska, A. Random Forest and Ensemble Methods. Chemom. Chem. Biochem. Data Anal. 2020, 2, 661–672. [Google Scholar]
- Yang, J.; Sun, Z.; Chen, Y. Fault Detection Using the Clustering-kNN Rule for Gas Sensor Arrays. Sensors 2016, 16, 2069. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Jiang, Z.; Yu, D. An Improved KNN Algorithm Based on Kernel Methods and Attribute Reduction. In Proceedings of the 5th International Conference on Instrumentation and Measurement, Computer, Communication and Control (IMCCC), Qinhuangdao, China, 18–20 September 2015; pp. 567–570. [Google Scholar]
- Saadatfar, H.; Khosravi, S.; Joloudari, J.H.; Mosavi, A.; Shamshirband, S. A New K-Nearest Neighbors Classifier for Big Data Based on Efficient Data Pruning. Mathematics 2020, 8, 286. [Google Scholar] [CrossRef]
- Couronné, R.; Probst, P.; Boulesteix, A.-L. Random forest versus logistic regression: A large-scale benchmark experiment. BMC Bioinform. 2018, 19, 270. [Google Scholar] [CrossRef] [PubMed]
- Carreras, J.; Kikuti, Y.Y.; Miyaoka, M.; Hiraiwa, S.; Tomita, S.; Ikoma, H.; Kondo, Y.; Ito, A.; Nakamura, N.; Hamoudi, R. A Combination of Multilayer Perceptron, Radial Basis Function Artificial Neural Networks and Machine Learning Image Segmentation for the Dimension Reduction and the Prognosis Assessment of Diffuse Large B-Cell Lymphoma. AI 2021, 2, 106–134. [Google Scholar] [CrossRef]
- Huang, J.; Ling, S.; Wu, X.; Deng, R. GIS-Based Comparative Study of the Bayesian Network, Decision Table, Radial Basis Function Network and Stochastic Gradient Descent for the Spatial Prediction of Landslide Susceptibility. Land 2022, 11, 436. [Google Scholar] [CrossRef]
- Han, T.; Jiang, D.; Zhao, Q.; Wang, L.; Yin, K. Comparison of random forest, artificial neural networks and support vector machine for intelligent diagnosis of rotating machinery. Trans. Inst. Meas. Control 2018, 40, 2681–2693. [Google Scholar] [CrossRef]
- Riza Alvy Syafi’i, M.H.; Prasetyono, E.; Khafidli, M.K.; Anggriawan, D.O.; Tjahjono, A. Real Time Series DC Arc Fault Detection Based on Fast Fourier Transform. In Proceedings of the 2018 International Electronics Symposium on Engineering Technology and Applications (IES-ETA), Bali, Indonesia, 29–30 October 2018; pp. 25–30. [Google Scholar]
- Misra, S.; Kumar, S.; Sayyad, S.; Bongale, A.; Jadhav, P.; Kotecha, K.; Abraham, A.; Gabralla, L.A. Fault Detection in Induction Motor Using Time Domain and Spectral Imaging-Based Transfer Learning Approach on Vibration Data. Sensors 2022, 22, 8210. [Google Scholar] [CrossRef]
- Ewert, P.; Kowalski, C.T.; Jaworski, M. Comparison of the Effectiveness of Selected Vibration Signal Analysis Methods in the Rotor Unbalance Detection of PMSM Drive System. Electronics 2022, 11, 1748. [Google Scholar] [CrossRef]
- El Idrissi, A.; Derouich, A.; Mahfoud, S.; El Ouanjli, N.; Chantoufi, A.; Al-Sumaiti, A.S.; Mossa, M.A. Bearing fault diagnosis for an induction motor controlled by an artificial neural network—Direct torque control using the Hilbert transform. Mathematics 2022, 10, 4258. [Google Scholar] [CrossRef]
- Dias, C.G.; Silva, L.C. Induction Motor Speed Estimation based on Airgap flux measurement using Hilbert transform and fast Fourier transform. IEEE Sens. J. 2022, 22, 12690–12699. [Google Scholar] [CrossRef]
- Metsämuuronen, J. Artificial systematic attenuation in eta squared and some related consequences: Attenuation-corrected eta and eta squared, negative values of eta, and their relation to Pearson correlation. Behaviormetrika 2023, 50, 27–61. [Google Scholar] [CrossRef]
- Denuit, M.; Trufin, J. Model selection with Pearson’s correlation, concentration and Lorenz curves under autocalibration. Eur. Actuar. J. 2023, 13, 871–878. [Google Scholar] [CrossRef]
- Kareem, A.B.; Ejike Akpudo, U.; Hur, J.-W. An Integrated Cost-Aware Dual Monitoring Framework for SMPS Switching Device Diagnosis. Electronics 2021, 10, 2487. [Google Scholar] [CrossRef]
- Jeong, S.; Kareem, A.B.; Song, S.; Hur, J.-W. ANN-Based Reliability Enhancement of SMPS Aluminum Electrolytic Capacitors in Cold Environments. Energies 2023, 16, 6096. [Google Scholar] [CrossRef]
- Satija, U.; Ramkumar, B.; Manikandan, M.S. A Review of Signal Processing Techniques for Electrocardiogram Signal Quality Assessment. IEEE Rev. Biomed. Eng. 2018, 11, 36–52. [Google Scholar] [CrossRef] [PubMed]
- Qiu, S.; Cui, X.; Ping, Z.; Shan, N.; Li, Z.; Bao, X.; Xu, X. Deep Learning Techniques in Intelligent Fault Diagnosis and Prognosis for Industrial Systems: A Review. Sensors 2023, 23, 1305. [Google Scholar] [CrossRef] [PubMed]
- Hakim, M.; Omran, A.; Ahmed, A.; Al-Waily, M.; Abdellatif, A. A systematic review of rolling bearing fault diagnoses based on deep learning and transfer learning: Taxonomy, overview, application, open challenges, weaknesses and recommendations. Ain Shams Eng. J. 2023, 14, 101945. [Google Scholar] [CrossRef]
- Ying, X. An Overview of Overfitting and its Solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef] [PubMed]
- Rahman, K.; Ghani, A.; Misra, S.; Rahman, A.U. A deep learning framework for non-functional requirement classification. Sci. Rep. 2024, 14, 3216. [Google Scholar] [CrossRef] [PubMed]
- Taye, M.M. Understanding of Machine Learning with Deep Learning: Architectures, Workflow, Applications and Future Directions. Computers 2023, 12, 91. [Google Scholar] [CrossRef]
- Sarker, I.H. Deep Learning: A Comprehensive Overview on Techniques, Taxonomy, Applications and Research Directions. SN Comput. Sci. 2021, 2, 420. [Google Scholar] [CrossRef] [PubMed]


| Type | Description | Cause | Effect |
|---|---|---|---|
| Saturation | Occurs when the magnetic flux reaches its limit | Overloading, sudden changes in load, or system faults | Overheating, and distorted output waveform |
| Lamination fault | Deterioration of insulation between laminations | Aging, excessive moisture, or manufacturing defects | Potential short circuit and reduced insulation resistance |
| Mechanical damage | Physical damage to the core, such as bending or cracking | Mechanical stress, operational stress, or overloading | Altered magnetic properties, increased core losses |
| ML Model | Parameter | Value |
|---|---|---|
| AdaBoost (ABC) | n estimators | 50 |
| k-Nearest Neighbor (KNN) | k | 9 |
| Logistic Regression (LR) | Regularization | L2 |
| Multilayer Perceptron (MLP) | Learning rate, n layers | Constant, 100 |
| Stochastic Gradient Descent (SGD) | Loss function | Perceptron |
| Support Vector Machine (SVC) | C, gamma | 90, scale |
| ML Model | Accuracy (%) | Precision (%) | Recall (%) | F1 Score (%) | Time Cost (s) |
|---|---|---|---|---|---|
| ABC | 59.39 | 56.38 | 56.39 | 56.37 | 0.3425 |
| KNN | 37.72 | 41.35 | 37.72 | 38.84 | 0.1421 |
| LR | 65.23 | 65.13 | 65.23 | 64.94 | 0.0427 |
| MLP | 48.33 | 47.53 | 48.33 | 47.85 | 0.1745 |
| SGD | 29.08 | 19.51 | 29.08 | 23.34 | 0.0170 |
| SVC | 32.81 | 16.68 | 32.81 | 17.36 | 0.2040 |
| ML Model | Accuracy (%) | Precision (%) | Recall (%) | F1 Score (%) | Time Cost (s) |
|---|---|---|---|---|---|
| ABC | 61.49 | 60.88 | 61.49 | 60.74 | 0.2545 |
| KNN | 54.22 | 55.63 | 54.22 | 54.63 | 0.0138 |
| LR | 33.40 | 24.37 | 33.40 | 25.88 | 0.0168 |
| MLP | 43.61 | 29.73 | 43.61 | 35.06 | 0.1381 |
| SGD | 33.40 | 24.37 | 33.40 | 25.88 | 0.0156 |
| SVC | 33.20 | 30.89 | 33.20 | 18.74 | 0.1980 |
| ML Model | Accuracy (%) | Precision (%) | Recall (%) | F1 Score (%) | Time Cost (s) |
|---|---|---|---|---|---|
| ABC | 66.60 | 66.42 | 66.60 | 64.95 | 0.2963 |
| KNN | 83.89 | 84.39 | 83.89 | 83.79 | 0.0156 |
| LR | 71.91 | 72.16 | 71.91 | 72.01 | 0.0251 |
| MLP | 73.45 | 73.51 | 73.48 | 73.47 | 1.3454 |
| SGD | 66.01 | 46.66 | 66.01 | 54.99 | 0.0253 |
| SVC | 72.10 | 72.11 | 72.10 | 72.10 | 0.0732 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domingo, D.; Kareem, A.B.; Okwuosa, C.N.; Custodio, P.M.; Hur, J.-W. Transformer Core Fault Diagnosis via Current Signal Analysis with Pearson Correlation Feature Selection. Electronics 2024, 13, 926. https://doi.org/10.3390/electronics13050926
Domingo D, Kareem AB, Okwuosa CN, Custodio PM, Hur J-W. Transformer Core Fault Diagnosis via Current Signal Analysis with Pearson Correlation Feature Selection. Electronics. 2024; 13(5):926. https://doi.org/10.3390/electronics13050926
Chicago/Turabian StyleDomingo, Daryl, Akeem Bayo Kareem, Chibuzo Nwabufo Okwuosa, Paul Michael Custodio, and Jang-Wook Hur. 2024. "Transformer Core Fault Diagnosis via Current Signal Analysis with Pearson Correlation Feature Selection" Electronics 13, no. 5: 926. https://doi.org/10.3390/electronics13050926
APA StyleDomingo, D., Kareem, A. B., Okwuosa, C. N., Custodio, P. M., & Hur, J.-W. (2024). Transformer Core Fault Diagnosis via Current Signal Analysis with Pearson Correlation Feature Selection. Electronics, 13(5), 926. https://doi.org/10.3390/electronics13050926











