Analysis of Phase-Locked Loop Filter Delay on Transient Stability of Grid-Following Converters
Abstract
:1. Introduction
1.1. Novelty and Contribution
1.2. Chapter Organization
2. Modeling of Synchronization Stability
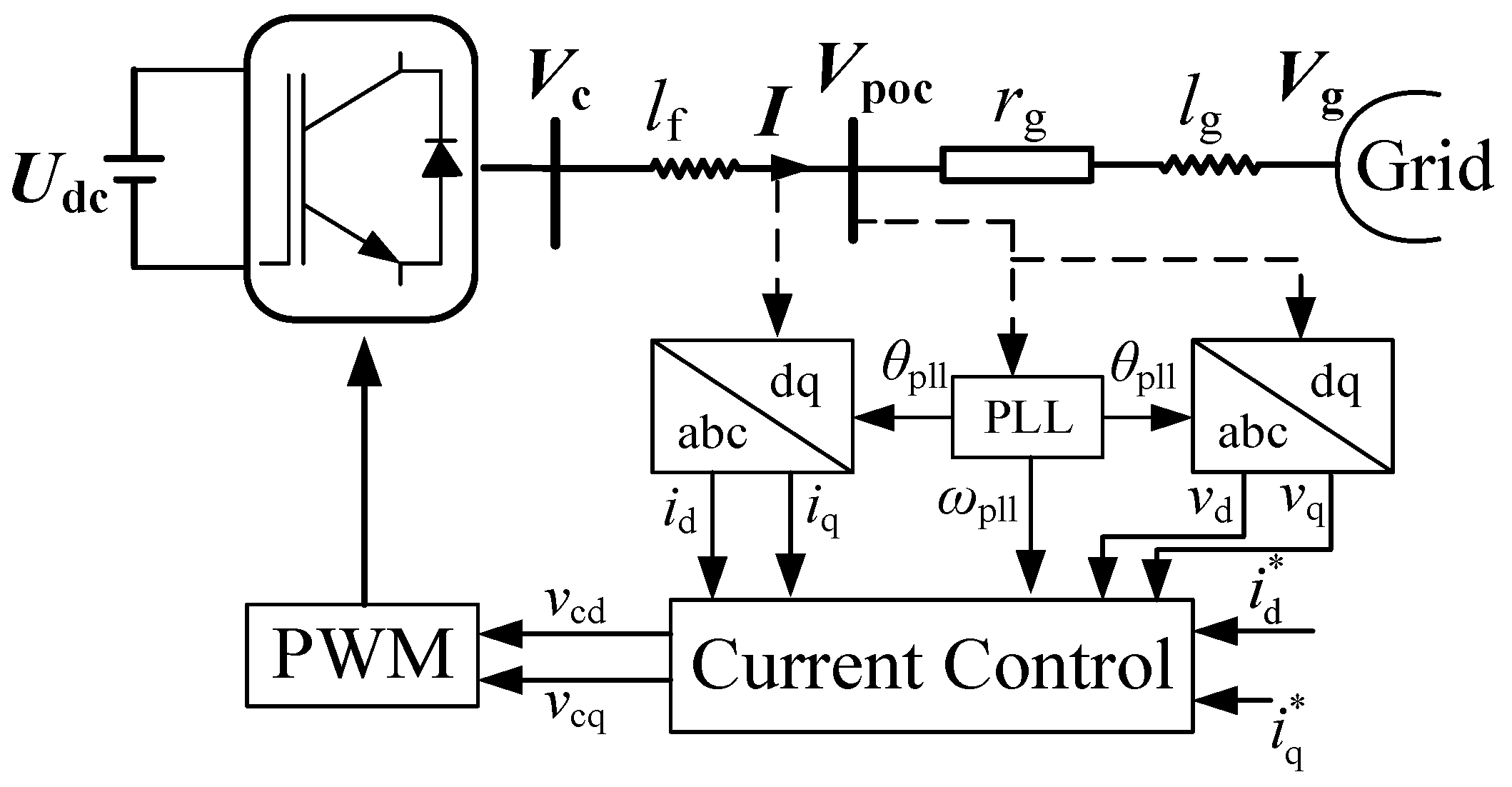
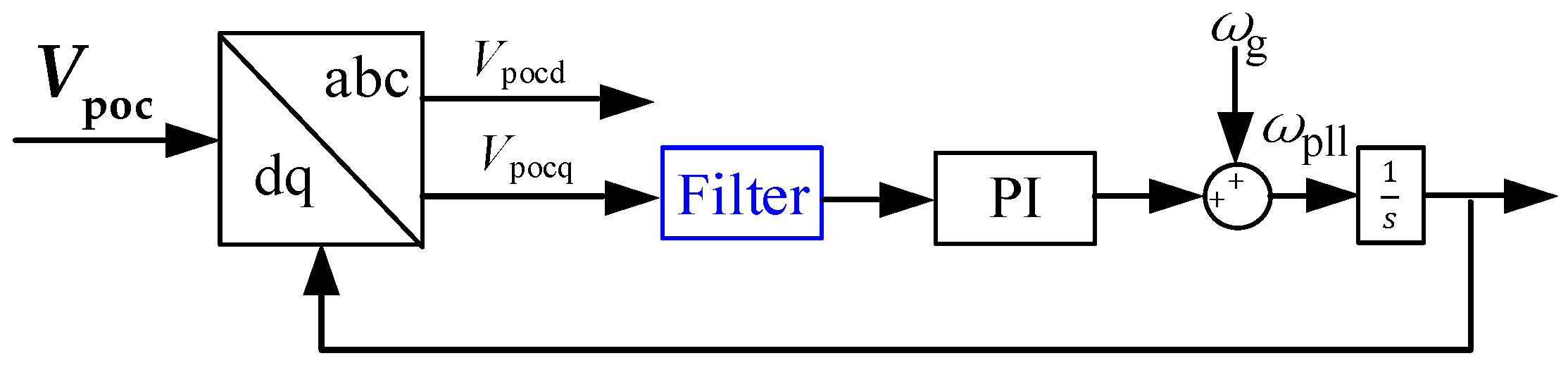
2.1. GFL Modeling
2.2. Filter Modeling
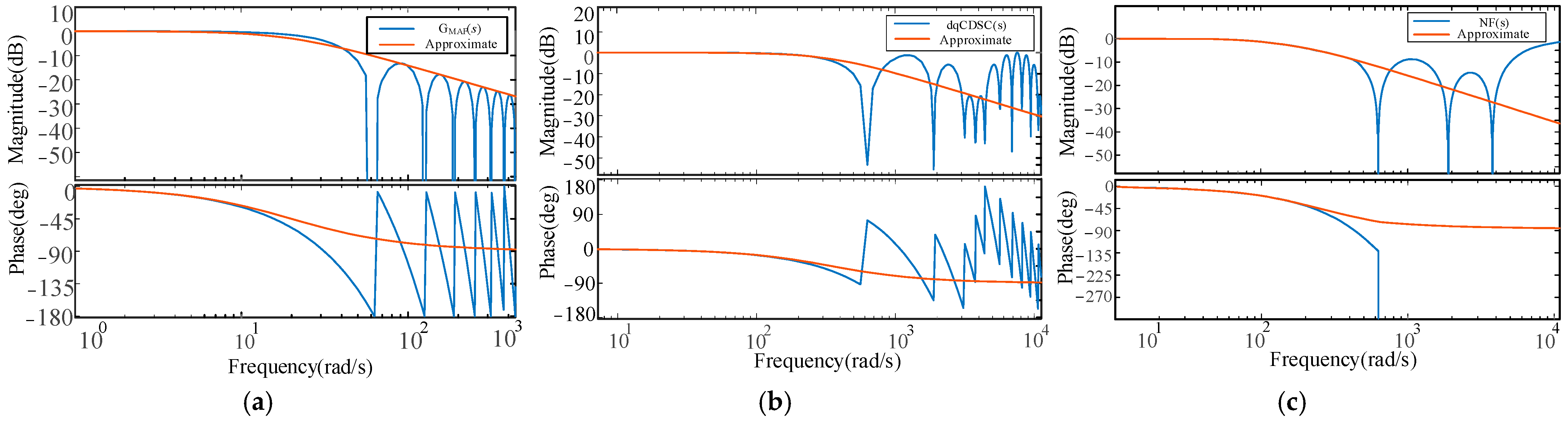
2.2.1. MAF
2.2.2. dqCDSC
2.2.3. NF
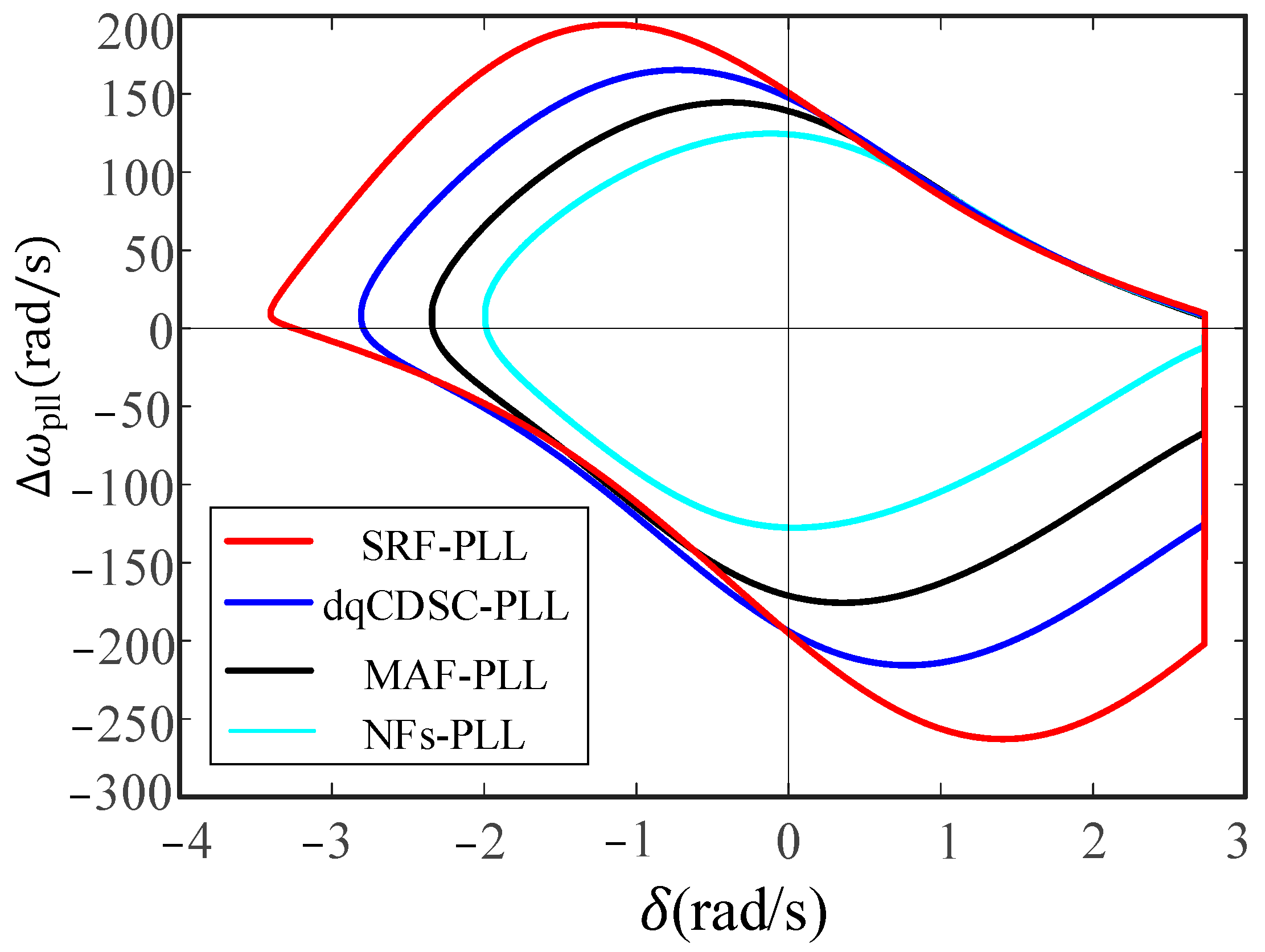
3. Synchronization Stability Analysis
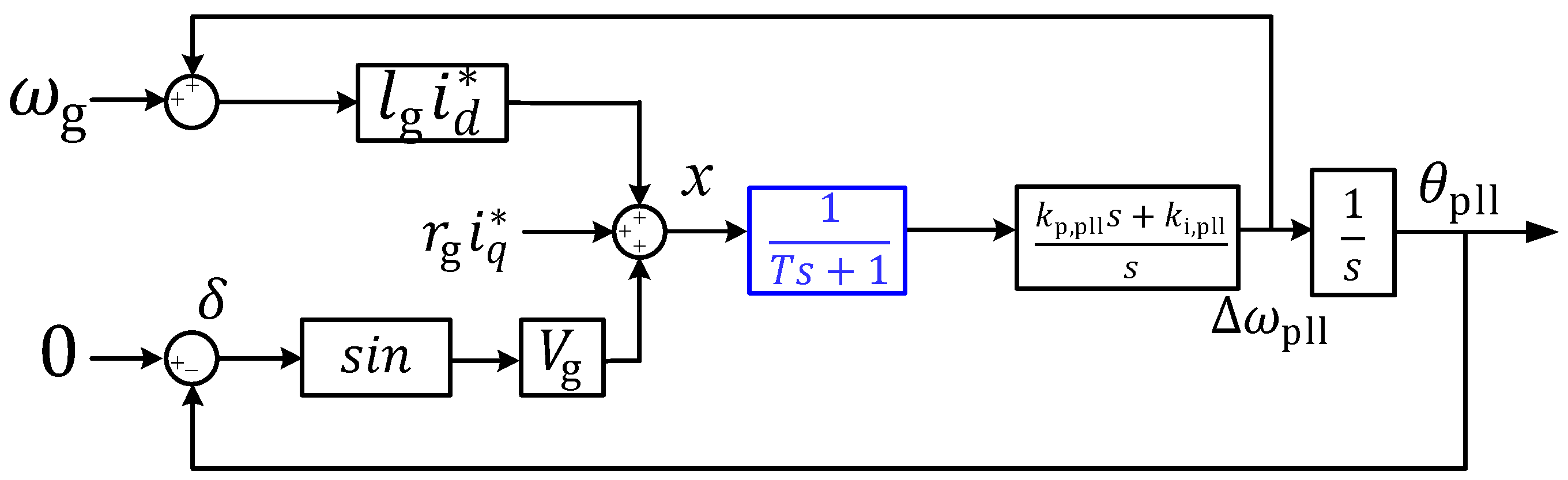
3.1. 3rd PLL QSLS Model
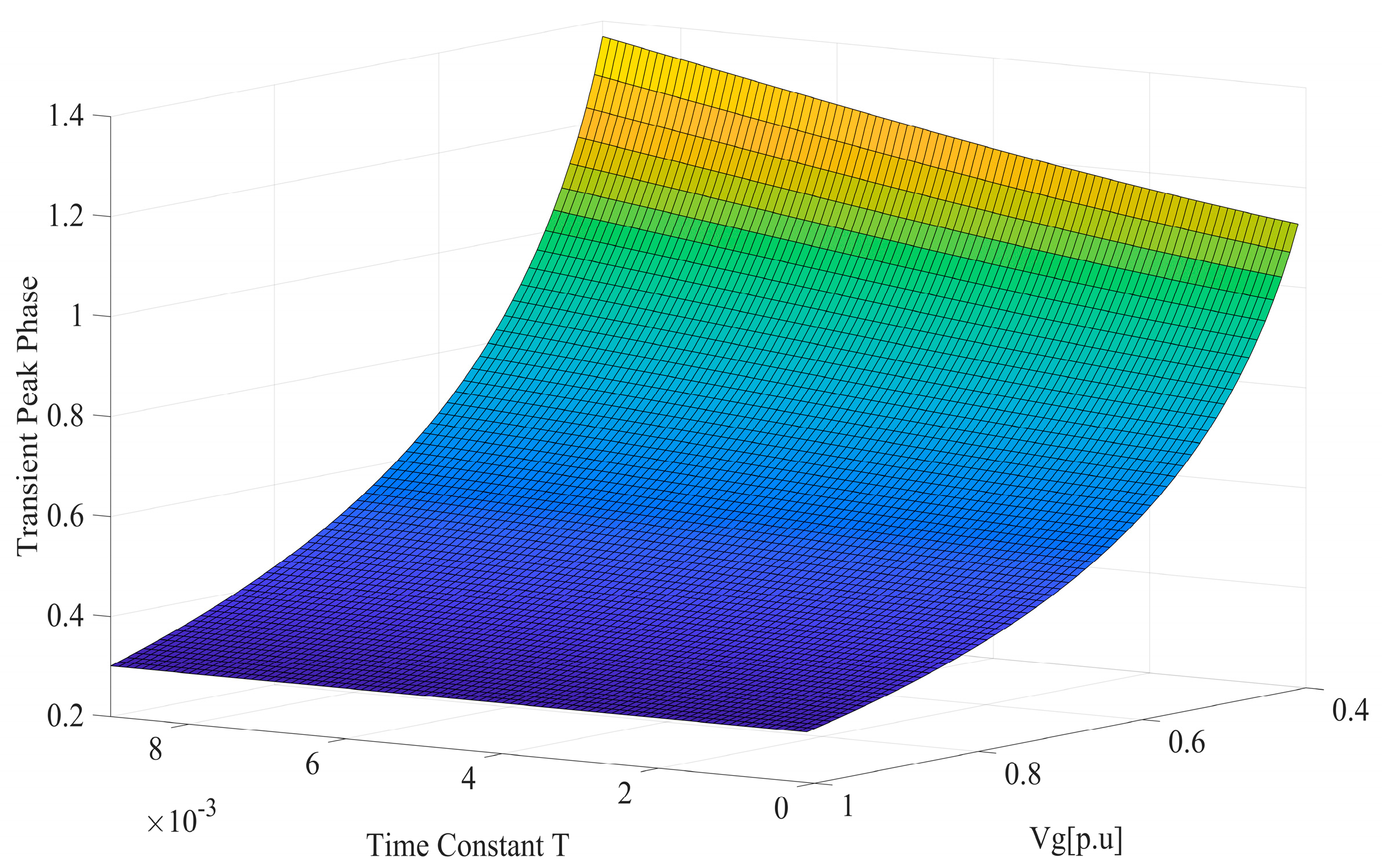
3.2. Transient Stability Analysis Due to Time Constant of the Inertial Element
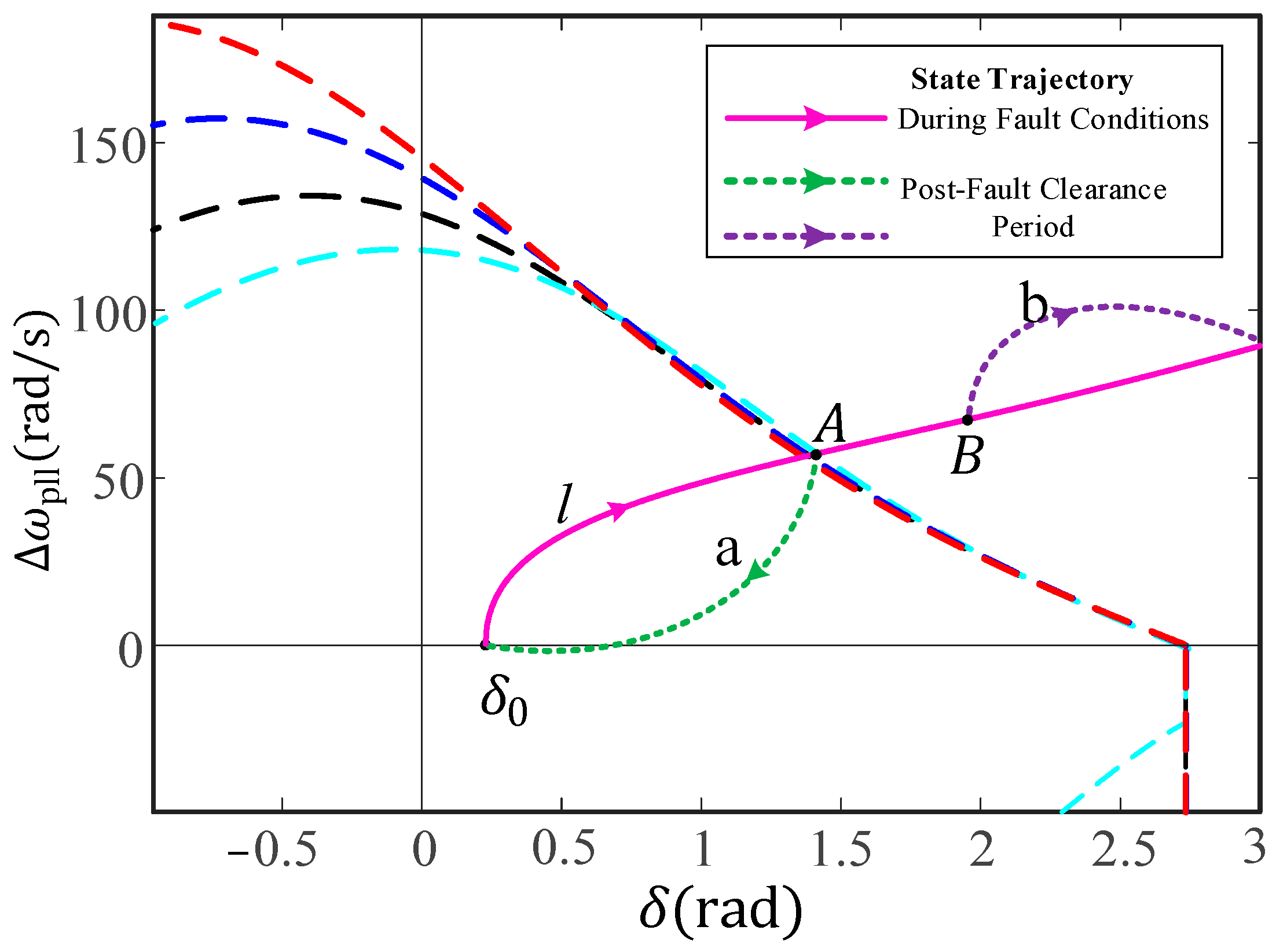
3.3. Estimation of Attraction Domains
4. Simulation Validation
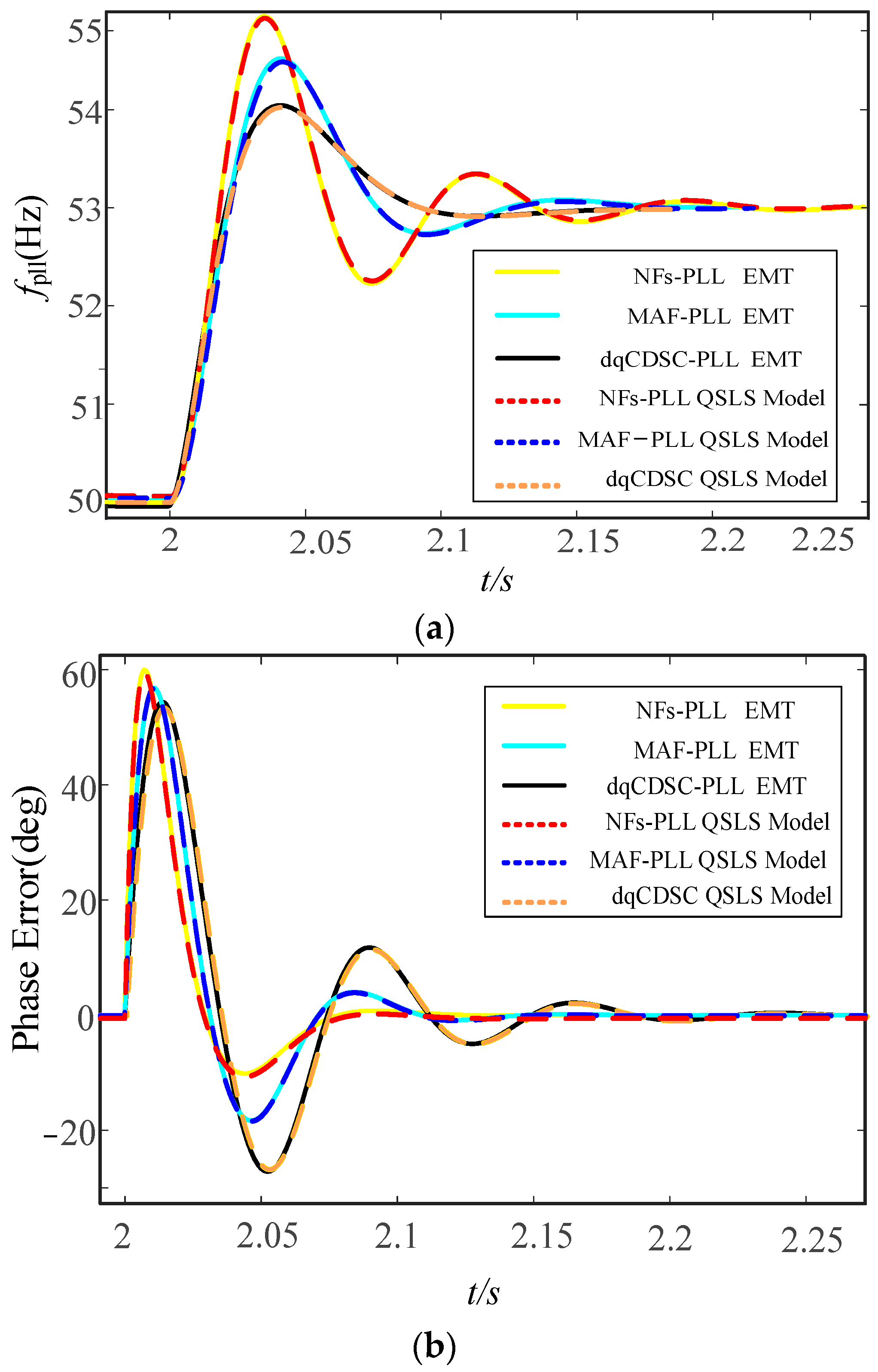
4.1. Validity Assessment of the 3rd-PLL QSLS Model
4.2. Impact of Inertial Element on Transient Synchronization Stability of GFL
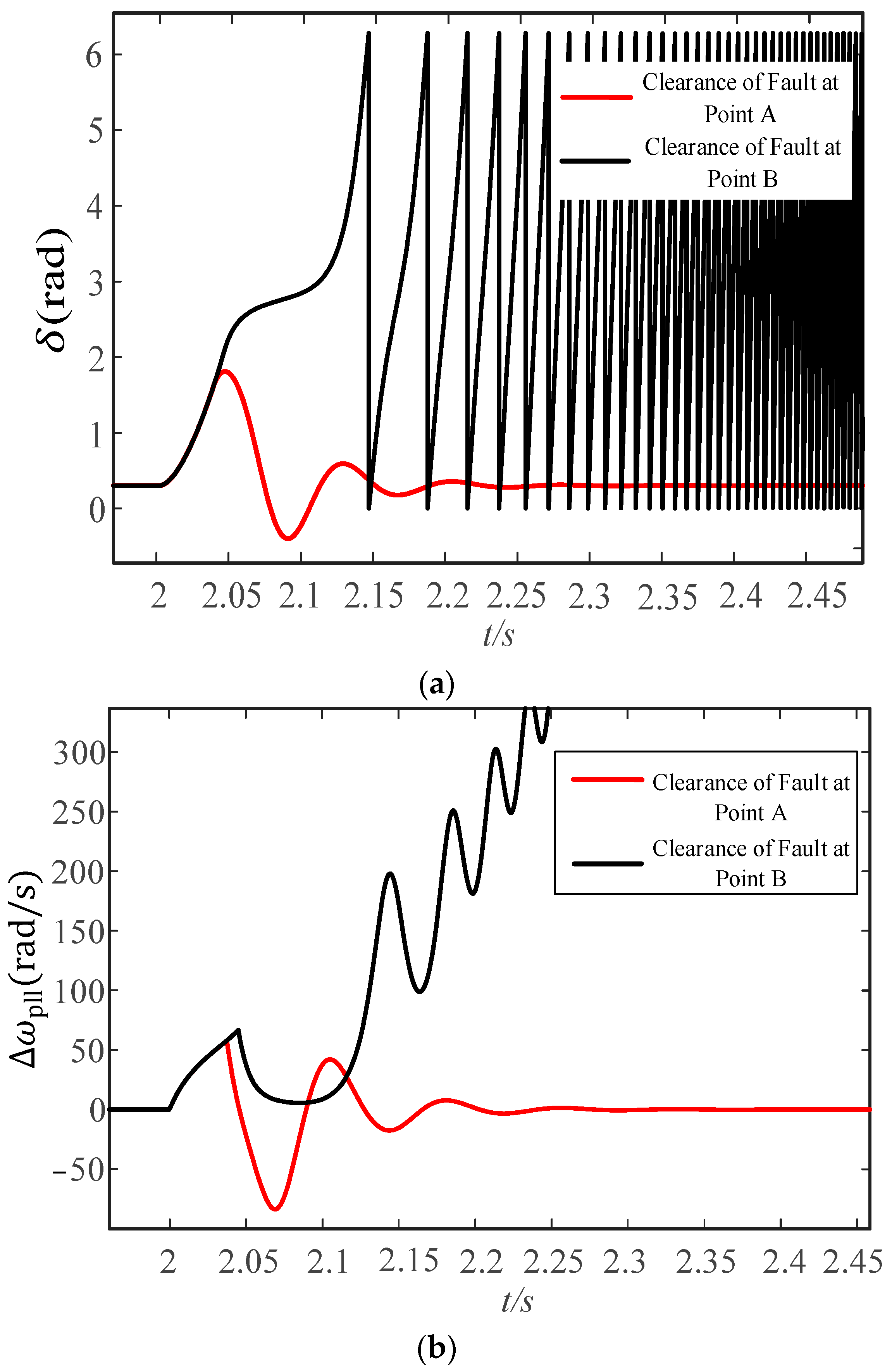
4.3. Validation of the Effectiveness of the Attraction Domain
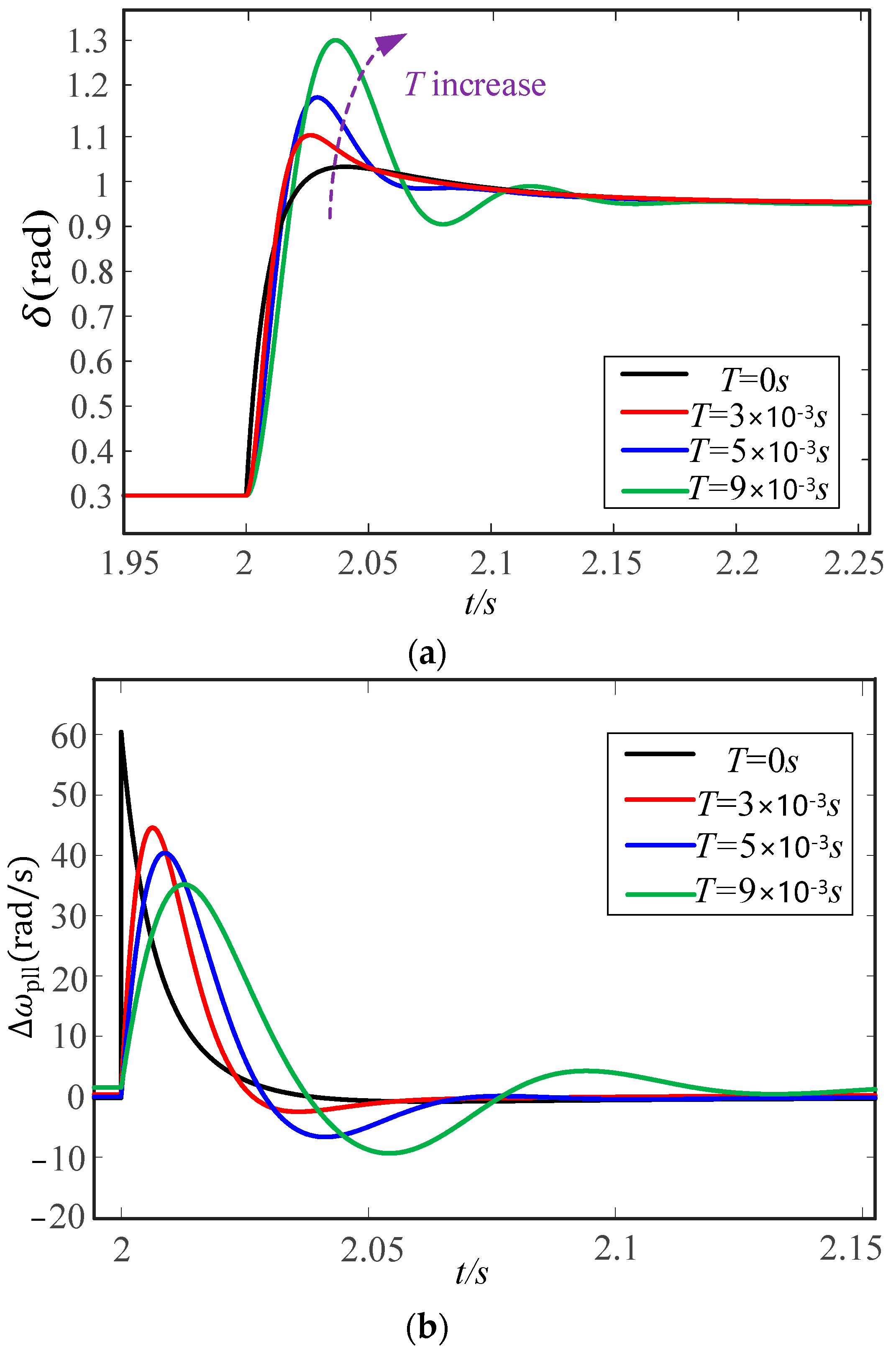
4.4. Verification of the Impact of Filter Time Constants on Transient Synchronization Stability
5. Conclusions
- (1)
- In juxtaposition with the traditional SRF-PLL, integrating a filter within the q-axis control loop of the PLL has been observed to compromise the transient stability of GFL. This phenomenon is characterized by amplified peak phase deviations during transient episodes and protracted durations for the GFL to re-establish a stable equilibrium state in the aftermath of substantial grid perturbations. Notably, the severity of these impacts escalates concomitantly with the increment in the filter’s delay time constant.
- (2)
- In power grids containing a significant amount of odd-order harmonics, to improve the accuracy of phase locking in the PLL while avoiding transient instability of the GFL, it is recommended to use the dqCDSC-PLL with smaller delay time constants in practice.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kroposki, B.; Johnson, B.; Zhang, Y.; Gevorgian, V.; Denholm, P.; Hodge, B.-M.; Hannegan, B. Achieving a 100% renewable grid: Operating electric Power systems with extremely high levels of variable renewable energy. IEEE Power Energy Mag. 2017, 15, 61–73. [Google Scholar] [CrossRef]
- Paul, S.; Dey, T.; Saha, P.; Dey, S.; Sen, R. Review on the development scenario of renewable energy in different country. In Proceedings of the 2021 Innovations in Energy Management and Renewable Resources (52042), Kolkata, India, 5–7 February 2021; pp. 1–2. [Google Scholar]
- Zhao, J.T.; Huang, M.; Yan, H.; Tse, C.K.; Zha, X.M. Nonlinear and Transient Stability Analysis of Phase-Locked Loops in Grid-Connected Converters. IEEE Trans. Power Electron. 2021, 36, 1018–1029. [Google Scholar] [CrossRef]
- He, X.Q.; Geng, H. PLL Synchronization Stability of Grid-Connected Multiconverter Systems. IEEE Trans. Ind. Appl. 2022, 58, 830–842. [Google Scholar] [CrossRef]
- North American Electric Reliability Corporation. 1200 MW Fault Induced Solar Photovoltaic Resource Interruption Disturbance Report; North American Electric Reliability Corporation: Atlanta, GA, USA, 2016. [Google Scholar]
- Bialek, J. What does the GB power outage on 9 August 2019 tell us about the current state of decarbonised power systems? Energy Policy 2020, 146, 111821. [Google Scholar] [CrossRef]
- Haro-Larrode, M.; Bergna-Diaz, G.; Eguia, P.; Santos-Mugica, M. On the Tuning of Fractional Order Resonant Controllers for a Voltage Source Converter in a Weak AC Grid Context. IEEE Access 2021, 9, 52741–52758. [Google Scholar] [CrossRef]
- de Bosio, F.; Pastorelli, M.; Ribeiro, L.A.; Lima, M.S.; Freijedo, F.; Guerrero, J.M. Current control loop design and analysis based on resonant regulators for microgrid applications. In Proceedings of the 41st Annual Conference of the IEEE Industrial Electronics Society (IECON), Yokohama, Japan, 9–12 November 2015; pp. 5322–5327. [Google Scholar]
- Heredero-Peris, D.; Chillón-Antón, C.; Sanchez-Sanchez, E.; MontesinosMiracle, D. Fractional proportional-resonant current controllers for voltage source converters. Electr. Power Syst. Res. 2019, 168, 20–45. [Google Scholar] [CrossRef]
- Wang, X.F.; Taul, M.G.; Wu, H.; Liao, Y.C.; Blaabjerg, F.; Harnefors, L. Grid-synchronization stability of converter-based resources—An overview. IEEE Trans. Ind. Appl. 2020, 1, 115–134. [Google Scholar] [CrossRef]
- Zhang, Y.; Cai, X.; Zhang, C.; Lv, J.; Li, Y. Transient synchronization stability analysis of voltage source converters: A review. Proc. CSEE 2021, 41, 1687–1702. [Google Scholar]
- Chen, Q.; Lyu, J.; Li, R.; Cai, X. Impedance modeling of modular multilevel converter based on harmonic state space. In Proceedings of the 2016 IEEE 17th Workshop on Control and Modeling for Power Electronics (COMPEL), Trondheim, Norway, 27–30 June 2016; pp. 1–5. [Google Scholar]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C. Three-Phase PLL: A review of recent advances. IEEE Trans. Power Electron. 2017, 32, 1894–1907. [Google Scholar] [CrossRef]
- Zhu, X.L.; Wen, C. Notch Filter Design based on Linear Quadratic Regulation Method. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 1779–1784. [Google Scholar]
- Mellouli, M.; Hamouda, M.; Slama, J.B.H.; Al-Haddad, K. A Third-Order MAF Based QT1-PLL That is Robust Against Harmonically Distorted Grid Voltage with Frequency Deviation. IEEE Trans. Energy Convers. 2021, 36, 1600–1613. [Google Scholar] [CrossRef]
- Wang, L.P.; Freeman, C.T.; Rogers, E.; Young, P.C. Disturbance Observer-Based Repetitive Control System with Nonminimal State-Space Realization and Experimental Evaluation. IEEE Trans. Control Syst. Technol. 2023, 31, 961–968. [Google Scholar] [CrossRef]
- Gude, S.; Chu, C.-C. Three-Phase PLLs by Using Frequency Adaptive Multiple Delayed Signal Cancellation Prefilters under Adverse Grid Conditions. IEEE Trans. Ind. Appl. 2018, 54, 3832–3844. [Google Scholar] [CrossRef]
- Golestan, S.; Ramezani, M.; Guerrero, J.M.; Monfared, M. dq-frame cascaded delayed signal cancellation-based PLL: Analysis, design, and comparison with moving average filter-based PLL. IEEE Trans. Power Electron. 2014, 30, 1618–1632. [Google Scholar] [CrossRef]
- Çelik, Ö.; Teke, A. A Hybrid MPPT method for grid connected photovoltaic systems under rapidly changing atmospheric conditions. Electr. Power Syst. Res. 2017, 152, 194–210. [Google Scholar] [CrossRef]
- Haro-Larrode, M.; Bayod-Rújula, A. A coordinated control hybrid MPPT algorithm for a grid-tied PV system considering a VDCIQ control structure. Electr. Power Syst. Res. 2023, 221, 109426. [Google Scholar] [CrossRef]
- Geng, H.; He, C.J.; Liu, Y.S.; He, X.Q.; Li, M. Overview on Transient Synchronization Stability of Renewable-rich Power Systems. High Volt. Eng. 2022, 48, 3367–3383. [Google Scholar]
- Dong, D.; Wen, B.; Boroyevich, D.; Mattavelli, P.; Xue, Y.S. Analysis of phase-locked loop low-frequency stability in three-phase grid-connected power converters considering impedance interactions. IEEE Trans. Ind. Electron. 2015, 62, 310–321. [Google Scholar] [CrossRef]
- Taul, M.G.; Wang, X.F.; Davari, P.; Blaabjerg, F. An Overview of Assessment Methods for Synchronization Stability of Grid-Connected Converters Under Severe Symmetrical Grid Faults. IEEE Trans. Power Electron. 2019, 34, 9655–9670. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X.F. Design-oriented transient stability analysis of PLL-synchronized voltage-source converters. IEEE Trans. Power Electron. 2019, 35, 3573–3589. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, C.; Cai, X.; Qiu, W.; Zhao, X.B. Transient Grid-synchronization Stability Analysis of Grid-tied Voltage Source Converters: Stability Region Estimation and Stabilization Control. Proc. CSEE 2022, 42, 7871–7884. [Google Scholar]
- Chen, J.R.; Liu, M.Y.; O’Donnell, T.; Milano, F. Impact of current transients on the synchronization stability assessment of grid-feeding converters. IEEE Trans. Power Syst. 2020, 35, 4131–4134. [Google Scholar] [CrossRef]
- Zhu, D.H.; Zhou, S.Y.; Zou, X.D.; Kang, Y. Improved design of PLL controller for LCL-type grid connected converter in weak grid. IEEE Trans. Power Electron. 2020, 35, 4715–4727. [Google Scholar] [CrossRef]
- Haro-Larrode, M.; Eguia, P.; Santos-Mugica, M. Analysis of voltage dynamics within current control time-scale in a VSC connected to a weak AC grid via series compensated AC line. Electr. Power Syst. Res. 2024, 229, 110189. [Google Scholar] [CrossRef]
- Zhou, D.H.; Zhou, S.Y.; Zou, X.D.; Kang, Y. An improved design of current controller for LCL -type grid connected converter to reduce negative effect of PLL in weak grid. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 648–663. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Gharehpetian, G.B. Five approaches to deal with problem of DC offset in phase-locked loop algorithms: Design considerations and performance evaluations. IEEE Trans. Power Electron. 2015, 31, 648–661. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, J.; Pei, J.X.; Zhao, Y.; Sun, P.; Zeng, D.Y.; Chen, S.Y. Transient stability enhancement control strategy based on improved PLL for grid connected VSC during severe grid fault. IEEE Trans. Energy Convers. 2020, 36, 218–229. [Google Scholar] [CrossRef]
- Zou, Z.-X.; Liserre, M. Modeling phase-locked loop-based synchronization in grid-interfaced converters. IEEE Trans. Energy Convers. 2019, 35, 394–404. [Google Scholar] [CrossRef]
- Dai, Z.Y.; Li, G.Q.; Fan, M.D.; Huang, J.; Yang, Y.; Hang, W. Global stability analysis for synchronous reference frame phase-locked loops. IEEE Trans. Ind. Electron. 2021, 69, 10182–10191. [Google Scholar] [CrossRef]
- Wu, C.; Xiong, X.L.; Taul, M.G.; Blaabjerg, F.J. Enhancing transient stability of PLL-synchronized converters by introducing voltage normalization control. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 11, 69–78. [Google Scholar] [CrossRef]
- Fu, X.K.; Sun, J.J.; Huang, M.; Tian, Z.; Yan, H.; Iu, H.H.-C.; Hu, P.; Zha, X.M. Large-signal stability of grid-forming and grid-following controls in voltage source converter: A comparative study. IEEE Trans. Power Electron. 2020, 36, 7832–7840. [Google Scholar] [CrossRef]
- Geng, H.; Liu, L.; Li, R.Q. Synchronization and reactive current support of PMSG-based wind farm during severe grid fault. IEEE Trans. Sustain. Energy 2018, 9, 1596–1604. [Google Scholar] [CrossRef]
- Wu, Q.H.; Lin, Y.Q.; Hong, C.; Su, Y.S.; Wen, T.H.; Liu, Y. Transient stability analysis of large-scale power systems: A survey. CSEE J. Power Energy Syst. 2023, 9, 1284–1300. [Google Scholar]
- Hu, P.F.; Chen, Z.; Yu, Y.X.; Jiang, D.Z. On Transient Instability Mechanism of PLL-Based VSC Connected to a Weak Grid. IEEE Trans. Ind. Electron. 2022, 70, 3836–3846. [Google Scholar] [CrossRef]



| PLL | MAF-PLL | dqCDSC-PLL | NFs-PLL |
|---|---|---|---|
| Time constant | 5 × 10−3 s | 2.9 × 10−3 s | 8 × 10−3 s |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Grid voltage Vg | 220 V | Converter capacity | 5000 W |
| Grid inductance lg | 0.025 H | Grid resistance rg | 0.1 Ω |
| Active current reference value | 11.72 A | Reactive current reference value | 0 A |
| Proportional coefficients of PLL kp,pll | 0.3 | Integral coefficients of PLL ki,pll | 14 |
| Converter DC side voltage Udc | 1200 V | Proportional gain of current loop kpc | 214.5 |
| Integral gain of current loop kic | 1347.7 | Inductance of converter output inductor lf | 0.032 H |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Chen, J.; Si, W. Analysis of Phase-Locked Loop Filter Delay on Transient Stability of Grid-Following Converters. Electronics 2024, 13, 986. https://doi.org/10.3390/electronics13050986
Zhang C, Chen J, Si W. Analysis of Phase-Locked Loop Filter Delay on Transient Stability of Grid-Following Converters. Electronics. 2024; 13(5):986. https://doi.org/10.3390/electronics13050986
Chicago/Turabian StyleZhang, Chenglin, Junru Chen, and Wenjia Si. 2024. "Analysis of Phase-Locked Loop Filter Delay on Transient Stability of Grid-Following Converters" Electronics 13, no. 5: 986. https://doi.org/10.3390/electronics13050986





