High-Power Terahertz Free Electron Laser via Tapering-Enhanced Superradiance
Abstract
:1. Introduction
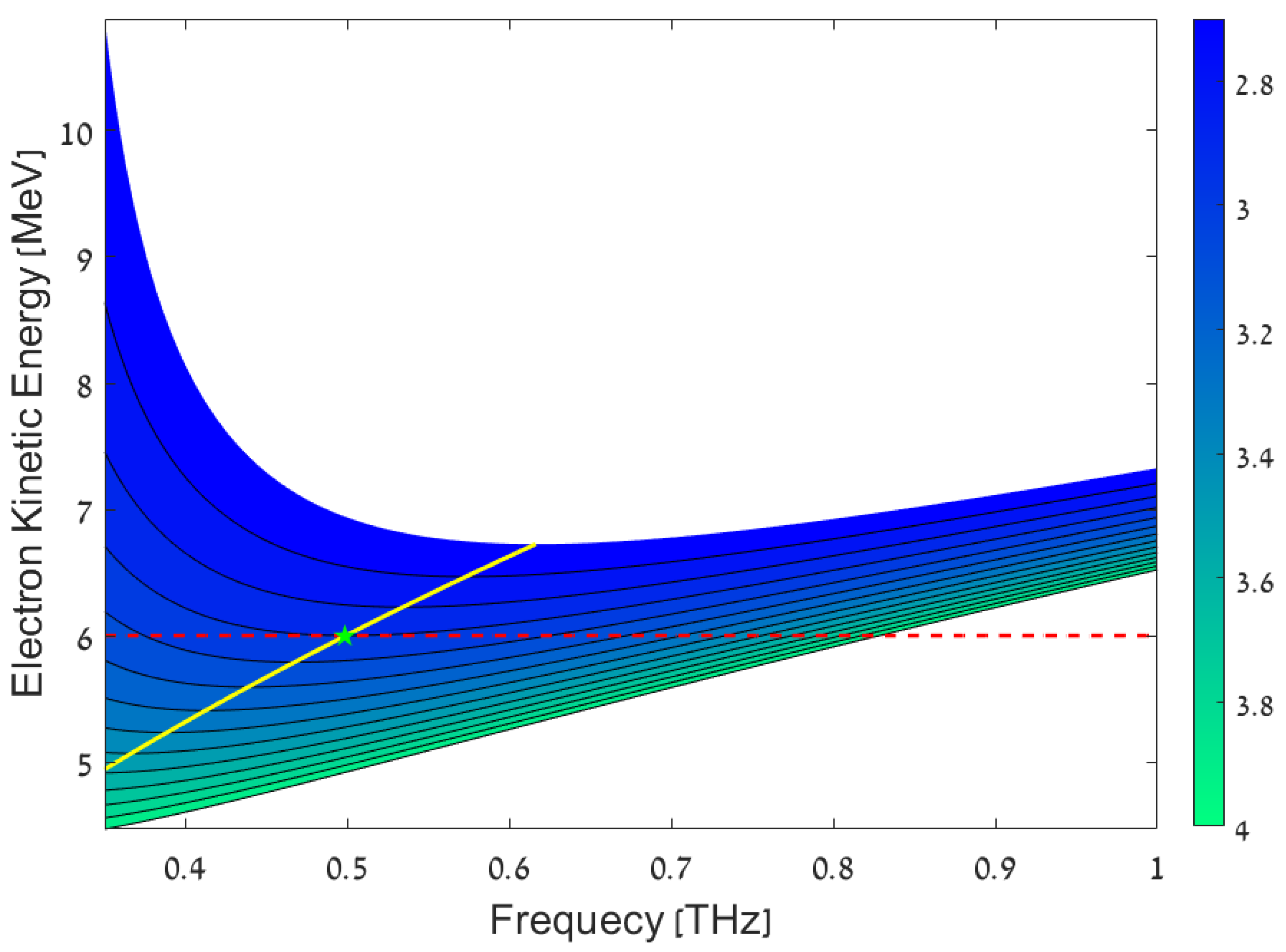
2. Zero-Slippage Condition
3. Tapering-Enhanced Superradiance
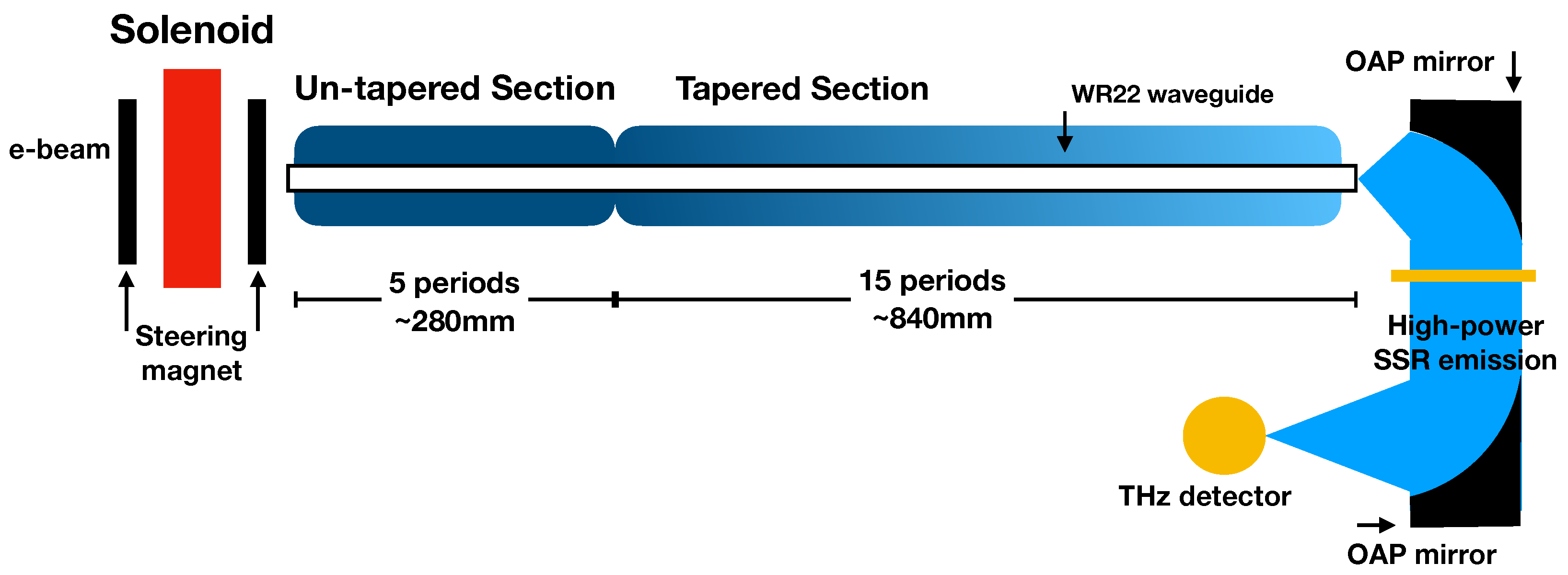
4. Hamiltonian of a Waveguided Planar Undulator
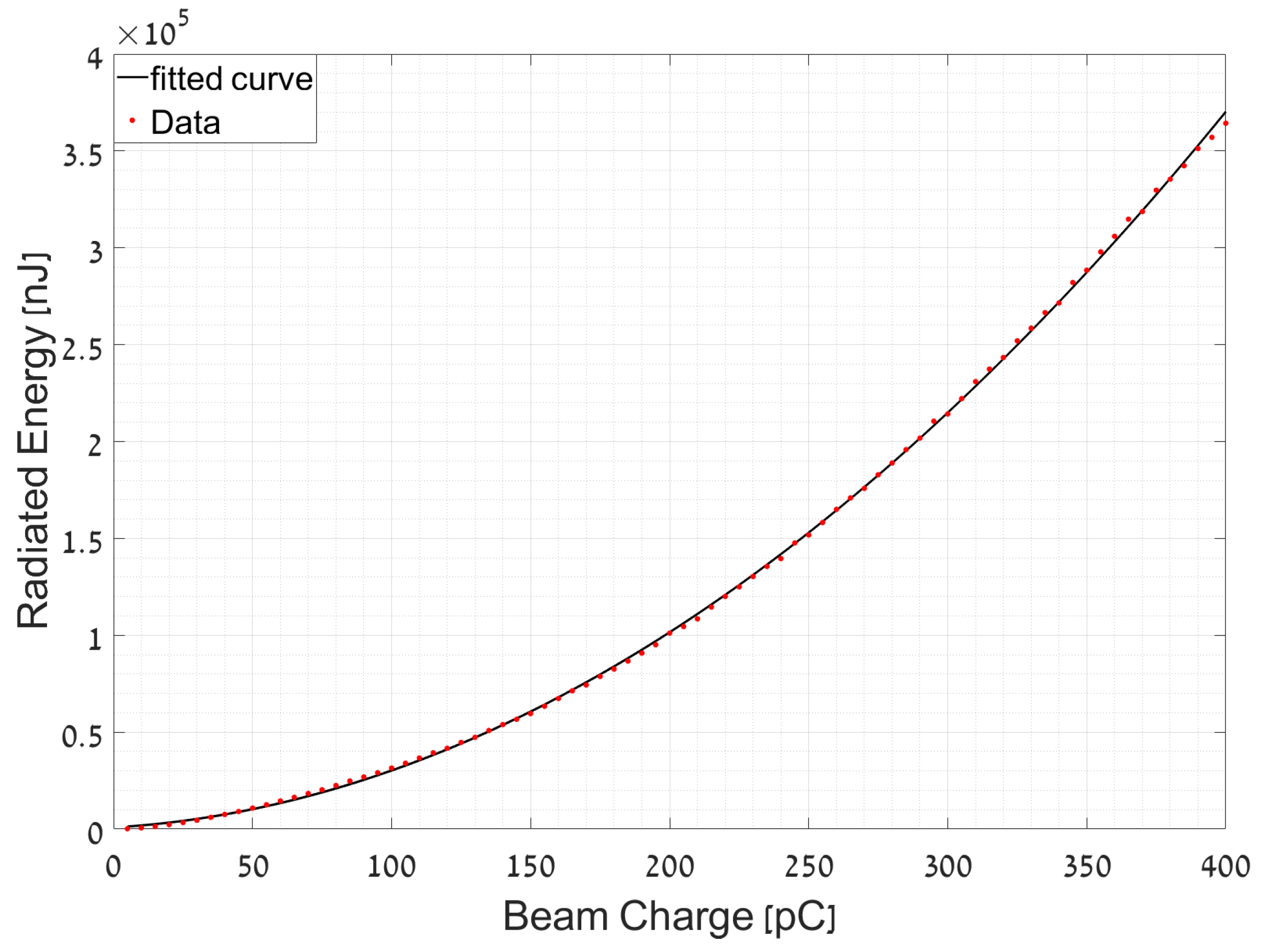
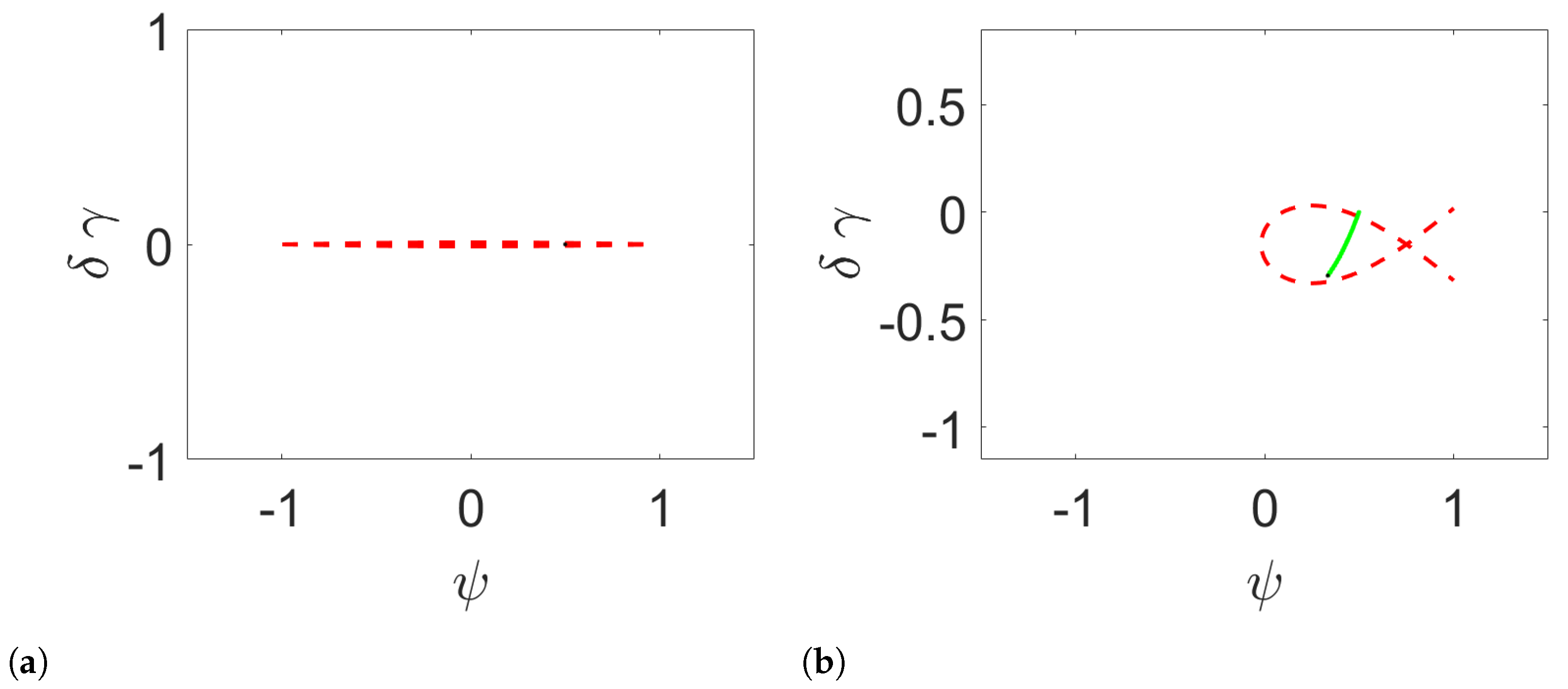
5. Simulations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Hamiltonian of a Waveguided Undulator Derivation
References
- Nause, A.; Friedman, A.; Fukasawa, A.; Rosenzweig, J.; Roussel, R.; Spataro, B. First Operation of a Hybrid e-Gun at the Schlesinger Center for Compact Accelerators in Ariel University. In Proceedings of the 10th International Particle Accelerator Conference, Melbourne, Australia, 19–24 May 2019. [Google Scholar] [CrossRef]
- Feigin, L.; Weinberg, A.; Nause, A. Algorithm Verification of Single-Shot Relativistic Emittance Proposed Measuring Method. Electronics 2022, 11, 2092. [Google Scholar] [CrossRef]
- Feigin, L.; Nause, A. Single-shot emittance measurement and optimization of a hybrid photo-cathode gun beam. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2023, 1055, 168539. [Google Scholar] [CrossRef]
- Nause, A.; Friedman, A.; Weinberg, A.; Borodin, D.; Feigin, L.; Fukasawa, A.; Rosenzweig, J.; Roussel, R.; Spataro, B. 6 MeV novel hybrid (standing wave-traveling wave) photo-cathode electron gun for a THz superradiant FEL. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2021, 1010, 165547. [Google Scholar] [CrossRef]
- Gover, A. Superradiant and stimulated-superradiant emission in prebunched electron-beam radiators. I. Formulation. Phys. Rev. ST Accel. Beams 2005, 8, 030701. [Google Scholar] [CrossRef]
- Kitaeva, G. Terahertz generation by means of optical lasers. Laser Phys. Lett. 2008, 5, 559–576. [Google Scholar] [CrossRef]
- Piyathilaka, H.P.; Sooriyagoda, R.; Dewasurendra, V.; Johnson, M.B.; Zawilski, K.T.; Schunemann, P.G.; Bristow, A.D. Terahertz generation by optical rectification in chalcopyrite crystals ZnGeP2, CdGeP2 and CdSiP2. Opt. Express 2019, 27, 16958–16965. [Google Scholar] [CrossRef]
- Kroh, T.; Matlis, N.; Kärtner, F. High-energy Single-cycle Terahertz Sources for Compact Particle Accelerators and Manipulators. In Proceedings of the 14th International Particle Accelerator Conference, Venice, Italy, 7–12 May 2023. [Google Scholar] [CrossRef]
- Pacey, T.H.; Saveliev, Y.; Healy, A.; Huggard, P.G.; Alderman, B.; Karataev, P.; Fedorov, K.; Xia, G. Continuously tunable narrow-band terahertz generation with a dielectric lined waveguide driven by short electron bunches. Phys. Rev. Accel. Beams 2019, 22, 091302. [Google Scholar] [CrossRef]
- Ciocci, F.; Doria, A.; Gallerano, G.P.; Giabbai, I.; Kimmitt, M.F.; Messina, G.; Renieri, A.; Walsh, J.E. Observation of coherent millimeter and submillimeter emission from a microtron-driven Cherenkov free-electron laser. Phys. Rev. Lett. 1991, 66, 699–702. [Google Scholar] [CrossRef]
- Sideris, S.; Ellenbogen, T. Terahertz generation in parallel plate waveguides activated by nonlinear metasurfaces. Opt. Lett. 2019, 44, 3590. [Google Scholar] [CrossRef]
- Vicario, C.; Ovchinnikov, A.V.; Ashitkov, S.I.; Agranat, M.B.; Fortov, V.E.; Hauri, C.P. Generation of 0.9-mJ THz pulses in DSTMS pumped by a Cr:Mg2SiO4 laser. Opt. Lett. 2014, 39, 6632–6635. [Google Scholar] [CrossRef]
- Liao, G.; Li, Y.; Liu, H.; Scott, G.G.; Neely, D.; Zhang, Y.; Zhu, B.; Zhang, Z.; Armstrong, C.; Zemaityte, E.; et al. Multimillijoule coherent terahertz bursts from picosecond laser-irradiated metal foils. Proc. Natl. Acad. Sci. USA 2019, 116, 3994–3999. [Google Scholar] [CrossRef]
- Balal, N.; Magori, E.; Yahalom, A. Design of a Permanent Magnet Wiggler for a THz Free Electron Laser. Acta Phys. Pol. A 2015, 128, 259–264. [Google Scholar] [CrossRef]
- Dicke, R.H. Coherence in Spontaneous Radiation Processes. Phys. Rev. 1954, 93, 99–110. [Google Scholar] [CrossRef]
- Gross, M.; Haroche, S. Superradiance: An essay on the theory of collective spontaneous emission. Phys. Rep. 1982, 93, 301–396. [Google Scholar] [CrossRef]
- Fisher, A.; Park, Y.; Lenz, M.; Ody, A.; Agustsson, R.; Hodgetts, T.; Murokh, A.; Musumeci, P. Single-pass high-efficiency terahertz free-electron laser. Nat. Photonics 2022, 16, 1–7. [Google Scholar] [CrossRef]
- Gover, A.; Ianconescu, R.; Friedman, A.; Emma, C.; Sudar, N.; Musumeci, P.; Pellegrini, C. Superradiant and stimulated-superradiant emission of bunched electron beams. Rev. Mod. Phys. 2019, 91, 035003. [Google Scholar] [CrossRef]
- Duris, J.; Murokh, A.; Musumeci, P. Tapering Enhanced Stimulated Superradiant Amplification. New J. Phys. 2015, 17, 063036. [Google Scholar] [CrossRef]
- Sudar, N.; Musumeci, P.; Duris, J.; Gadjev, I.; Polyanskiy, M.; Pogorelsky, I.; Fedurin, M.; Swinson, C.; Kusche, K.; Babzien, M.; et al. High Efficiency Energy Extraction from a Relativistic Electron Beam in a Strongly Tapered Undulator. Phys. Rev. Lett. 2016, 117, 174801. [Google Scholar] [CrossRef]
- Zhao, Z.; Xu, Y.; Jia, Q.; Li, H. High efficiency tapered free-electron lasers with a prebunched electron beam from echo-enabled harmonic generation. Phys. Rev. Accel. Beams 2023, 26, 070701. [Google Scholar] [CrossRef]
- Emma, C.; Sudar, N.; Musumeci, P.; Urbanowicz, A.; Pellegrini, C. High efficiency tapered free-electron lasers with a prebunched electron beam. Phys. Rev. Accel. Beams 2017, 20, 110701. [Google Scholar] [CrossRef]
- Slater, J. Tapered-wiggler free-electron laser optimization. IEEE J. Quantum Electron. 1981, 17, 1476–1479. [Google Scholar] [CrossRef]
- Snively, E. Electron-THz Wave Interactions in a Guided Inverse Free Electron Laser; University of California: Los Angeles, CA, USA, 2018. [Google Scholar]
- Schmüser, P.; Dohlus, M.; Rossbach, J.; Behrens, C. Free-Electron Lasers in the Ultraviolet and X-ray Regime; Springer International Publishing: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Clarke, J. The Science and Technology of Undulators and Wigglers; Oxford University Press: Oxford, UK, 2004. [Google Scholar] [CrossRef]
- Jeong, Y.U.; Kawamura, Y.; Toyoda, K.; Nam, C.H.; Lee, S.S. Observation of coherent effect in undulator radiation. Phys. Rev. Lett. 1992, 68, 1140–1143. [Google Scholar] [CrossRef]
- Krinsky, S. Undulators as Sources of Synchrotron Radiation. IEEE Trans. Nucl. Sci. 1983, 30, 3078–3082. [Google Scholar] [CrossRef]
- Andersson, A.; Johnson, M.S.; Nelander, B. Coherent synchrotron radiation in the far-infrared from a 1 mm electron bunch. Opt. Eng. 2000, 39, 3099–3105. [Google Scholar] [CrossRef]
- Hirschmugl, C.J.; Sagurton, M.; Williams, G.P. Multiparticle coherence calculations for synchrotron-radiation emission. Phys. Rev. A 1991, 44, 1316–1320. [Google Scholar] [CrossRef]
- Green, G.K. Spectra and Optics of Synchrotron Radiation; Brookhaven National Lab. (BNL): Upton, NY, USA, 1976. [CrossRef]
- Asakawa, M.; Sakamoto, N.; Inoue, N.; Yamamoto, T.; Mima, K.; Nakai, S.; Chen, J.; Fujita, M.; Imasaki, K.; Yamanaka, C.; et al. A millimeter-range FEL experiment using coherent synchrotron radiation emitted from electron bunches. Nucl. Instrum. Methods Phys. Res. Sect. A: Accel. Spectrometers, Detect. Assoc. Equip. 1994, 341, 72–75. [Google Scholar] [CrossRef]
- Curry, E.; Fabbri, S.; Musumeci, P.; Gover, A. THz-driven zero-slippage IFEL scheme for phase space manipulation. New J. Phys. 2016, 18, 113045. [Google Scholar] [CrossRef]
- Gover, A.; Hartemann, F.V.; Le Sage, G.P.; Luhmann, N.C.; Zhang, R.S.; Pellegrini, C. Time and frequency domain analysis of superradiant coherent synchrotron radiation in a waveguide free-electron laser. Phys. Rev. Lett. 1994, 72, 1192–1195. [Google Scholar] [CrossRef]
- Gallerano, G.; Doria, A.; Giovenale, E.; Renieri, A. Compact free electron lasers: From Cerenkov to waveguide free electron lasers. Infrared Phys. Technol. 1999, 40, 161–174. [Google Scholar] [CrossRef]
- Marcuvitz, N. Waveguide Handbook; Institution of Electrical Engineers, McGraw-Hill: New York, NY, USA, 1986. [Google Scholar]
- Wiedemann, H. Particle accelerator physics; Springer Nature: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Minty, M.; Zimmermann, F. Measurement and Control of Charged Particle Beams; Springer Nature: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Snively, E.C.; Xiong, J.; Musumeci, P.; Gover, A. Broadband THz amplification and superradiant spontaneous emission in a guided FEL. Opt. Express 2019, 27, 20221–20230. [Google Scholar] [CrossRef]
- Pozar, D. Microwave Engineering, 4th ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Xu, K. Silicon electro-optic micro-modulator fabricated in standard CMOS technology as components for all silicon monolithic integrated optoelectronic systems. J. Micromech. Microeng. 2021, 31, 054001. [Google Scholar] [CrossRef]
- Collin, R. Foundations for Microwave Engineering, 2nd ed.; McGraw-Hill Series in Electrical Engineering: Radar and Antennas; IEEE Press: New York, NY, USA, 2007. [Google Scholar]
- Rosenzweig, J.B. Fundamentals of Beam Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Jackson, J. Classical Electrodynamics; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Jerby, E.; Gover, A. Investigation of the gain regimes and gain parameters of the free electron laser dispersion equation. IEEE J. Quantum Electron. 1985, 21, 1041–1058. [Google Scholar] [CrossRef]
- Bartolini, R.; Doria, A.; Gallerano, G.; Renieri, A. Theoretical and experimental aspects of a waveguide FEL. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1991, 304, 417–420. [Google Scholar] [CrossRef]
- Bratman, V.; Lurie, Y.; Oparina, Y.; Savilov, A. Capabilities of Terahertz Cyclotron and Undulator Radiation from Short Ultrarelativistic Electron Bunches. Instruments 2019, 3, 55. [Google Scholar] [CrossRef]
- Neuman, C.P.; Graves, W.S.; O’Shea, P.G. Coherent off-axis undulator radiation from short electron bunches. Phys. Rev. ST Accel. Beams 2000, 3, 030701. [Google Scholar] [CrossRef]
- Doria, A.; Bartolini, R.; Feinstein, J.; Gallerano, G.; Pantell, R. Coherent emission and gain from a bunched electron beam. IEEE J. Quantum Electron. 1993, 29, 1428–1436. [Google Scholar] [CrossRef]
- Bonifacio, R.; Pellegrini, C.; Narducci, L. Collective instabilities and high-gain regime in a free electron laser. Opt. Commun. 1984, 50, 373–378. [Google Scholar] [CrossRef]
- Ratner, D.; Hemsing, E.; Gover, A.; Marinelli, A.; Nause, A. Subradiant spontaneous undulator emission through collective suppression of shot noise. Phys. Rev. Spec. Top.-Accel. Beams 2015, 18, 050703. [Google Scholar] [CrossRef]
- Gover, A.; Dyunin, E.; Duchovni, T.; Nause, A. Collective microdynamics and noise suppression in dispersive electron beam transport. Phys. Plasmas 2011, 18, 123102. [Google Scholar] [CrossRef]
- Pinhasi, Y.; Lurie, Y. Generalized theory and simulation of spontaneous and super-radiant emissions in electron devices and free-electron lasers. Phys. Rev. E 2002, 65, 026501. [Google Scholar] [CrossRef]
- Lurie, Y.; Pinhasi, Y. Enhanced super-radiance from energy-modulated short electron bunch free-electron lasers. Phys. Rev. ST Accel. Beams 2007, 10, 080703. [Google Scholar] [CrossRef]
- Kroll, N.; Morton, P.; Rosenbluth, M. Free-electron lasers with variable parameter wigglers. IEEE J. Quantum Electron. 1981, 17, 1436–1468. [Google Scholar] [CrossRef]
- Musumeci, P.; Tochitsky, S.Y.; Boucher, S.; Clayton, C.E.; Doyuran, A.; England, R.J.; Joshi, C.; Pellegrini, C.; Ralph, J.E.; Rosenzweig, J.B.; et al. High Energy Gain of Trapped Electrons in a Tapered, Diffraction-Dominated Inverse-Free-Electron Laser. Phys. Rev. Lett. 2005, 94, 154801. [Google Scholar] [CrossRef]
- Park, Y. Tapering Enhanced Stimulated Superradiant Amplification; University of California: Los Angeles, CA, USA, 2022. [Google Scholar]
- Fisher, A.; Musumeci, P.; Van der Geer, S.B. Self-consistent numerical approach to track particles in free electron laser interaction with electromagnetic field modes. Phys. Rev. Accel. Beams 2020, 23, 110702. [Google Scholar] [CrossRef]
- Musumeci, P.; Fisher, A.; Gover, A.; Nanni, E.; Snively, E.; van der Geer, B. A Waveguide-Based High Efficiency Super-Radiant FEL Operating in the THz Regime. In Proceedings of the 39th International Free Electron Laser Conference, Hamburg, Germany, 26–30 August 2019; p. TUP036. [Google Scholar] [CrossRef]
- van der Geer, S.; Setija, I.; Smorenburg, P.; Williams, P.; de Loos, M. GPT-CSR: A New Simulation Code for CSR Effects. In Proceedings of the 60th ICFA Advanced Beam Dynamics Workshop (FLS’18), Shanghai, China, 5–9 March 2018; Springer: Geneva, Switzerland, 2018. Number 60 in ICFA Advanced Beam Dynamics Workshop. pp. 157–159. [Google Scholar] [CrossRef]
- Geer, S.; de Loos, M.; Bongerd, D.; Soest, X. General Particle Tracer: A New 3D Code for Accelerator and Beamline Design. In Proceedings of the 5th European Particle Accelerator Conference, Sitges, Spain, 10–14 June 1996. [Google Scholar]
- van der Geer, B.; De Loos, M. Applications of the General Particle Tracer code. In Proceedings of the 1997 Particle Accelerator Conference (Cat. No.97CH36167), Vancouver, BC, Canada, 16 May 1997; Volume 2, pp. 2577–2579. [Google Scholar] [CrossRef]
- van der Geer, B.; De Loos, M. The general particle tracer code:design, implementation and application. J. Bus. Commun. 2001. [Google Scholar] [CrossRef]
- Kim, K.J. Rf and space-charge effects in laser-driven rf electron guns. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1989, 275, 201–218. [Google Scholar] [CrossRef]
- Rosenzweig, J.; Colby, E. Charge and wavelength scaling of RF photoinjectors: A design tool. In Proceedings of the Particle Accelerator Conference, Dallas, TX, USA, 1–5 May 1995; Volume 2, pp. 957–960. [Google Scholar] [CrossRef]


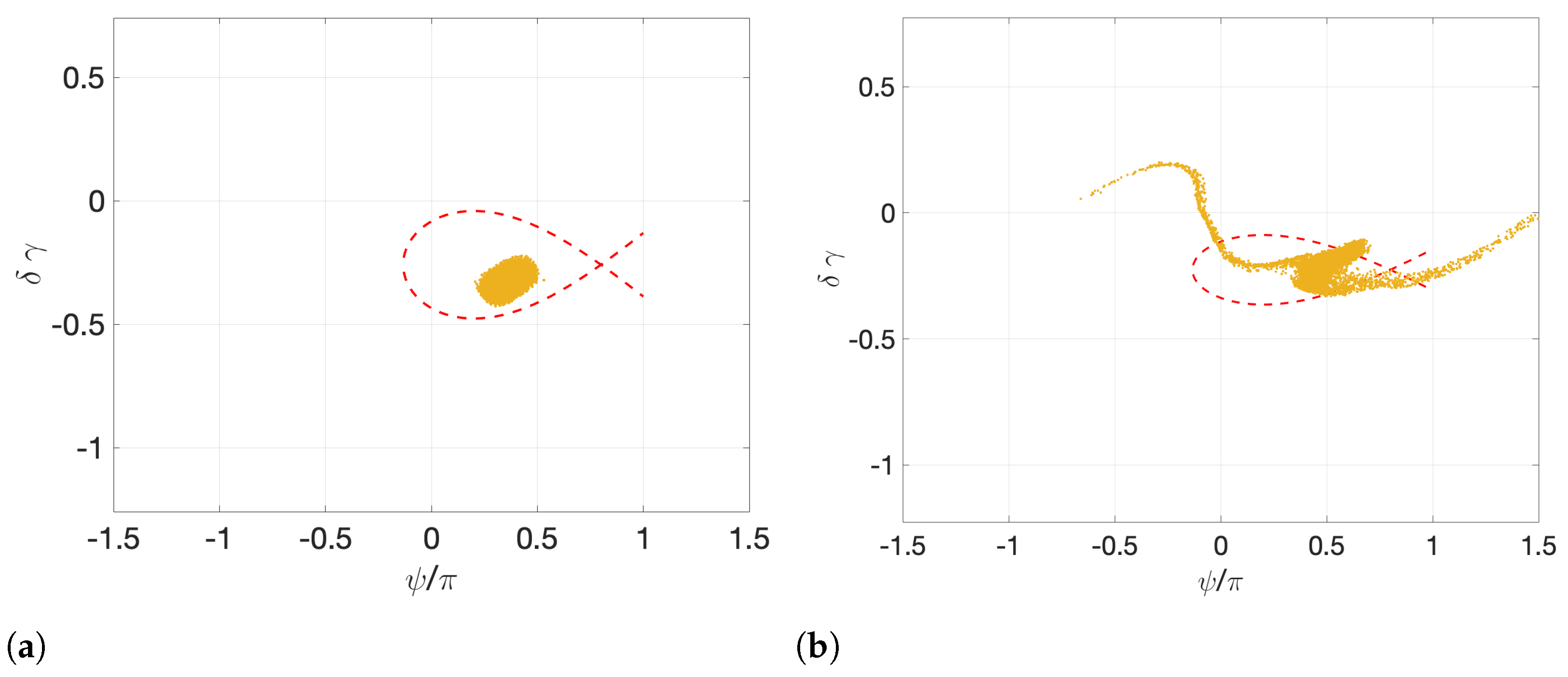
| Bunch Energy | 6 MeV |
| Energy Spread [RMS] | 1% |
| Bunch Length [RMS] | 150 fs |
| Beam Charge | 20 pC |
| Undulator Wavelength, | 56 mm |
| Undulator Magnetic Field, (K) | T () |
| Number of Uniform Undulator Periods | 5 |
| Number of Tapered Undulator Periods | 15 |
| Nominal Resonant Electron Pondermotive Phase, | rad |
| Nominal Undulator Tapering Rate, () | ( ) |
| Radiation Mode | |
| Rectangular Waveguide (WR22) | 5.6896 mm × 2.8448 mm |
| Mode Cut-off Frequency () | GHz |
| Peak THz (Zero-Slippage) Frequency () | THz |
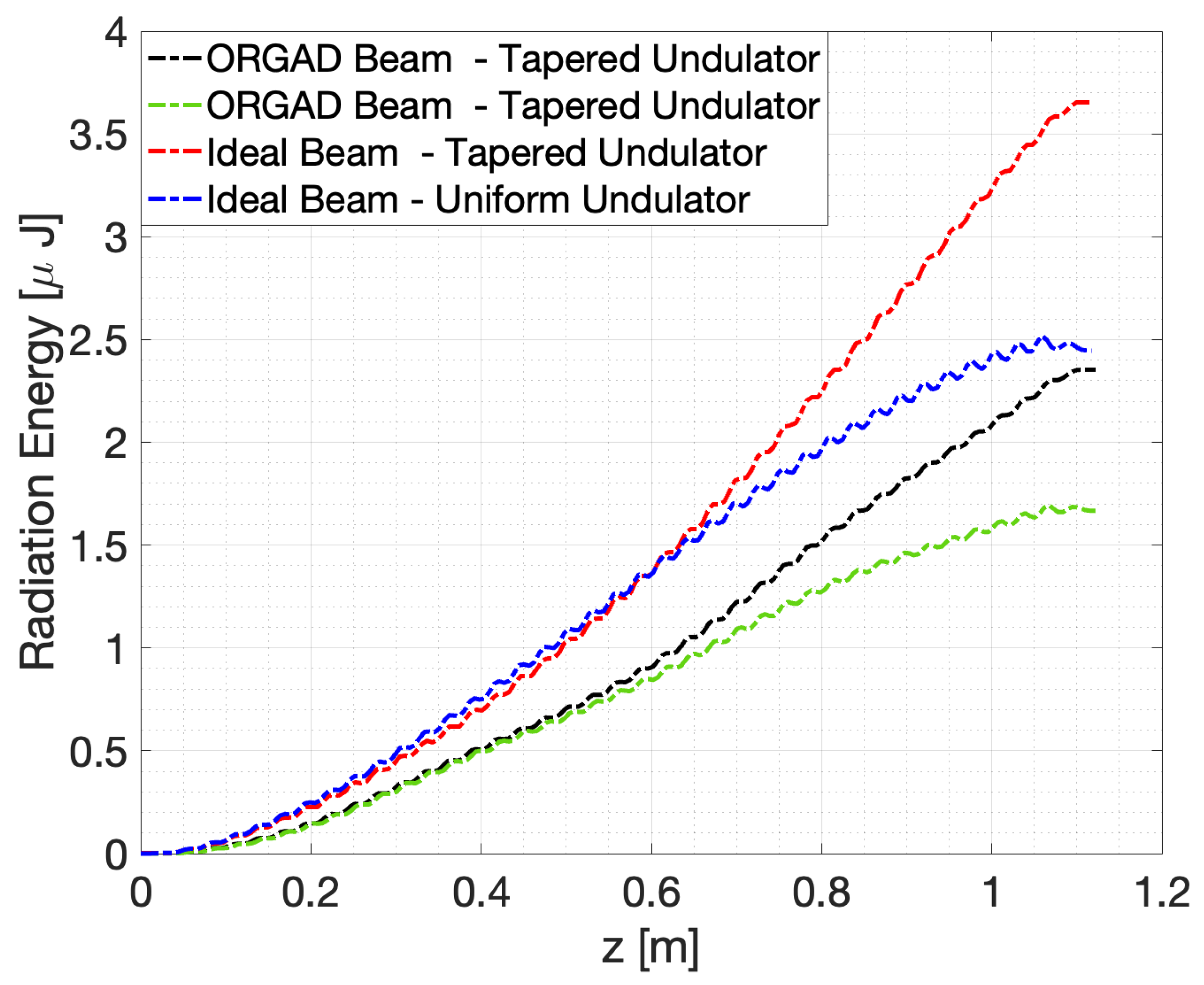
| Superradiant Emission Energy | ||
|---|---|---|
| Beam | Uniform Undulator [J] | Tapered Undulator (TES) [J] |
| Ideal | 2.43 | 3.66 |
| ORGAD | 1.66 | 2.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feigin, L.; Gover, A.; Friedman, A.; Weinberg, A.; Azar, D.; Nause, A. High-Power Terahertz Free Electron Laser via Tapering-Enhanced Superradiance. Electronics 2024, 13, 1171. https://doi.org/10.3390/electronics13071171
Feigin L, Gover A, Friedman A, Weinberg A, Azar D, Nause A. High-Power Terahertz Free Electron Laser via Tapering-Enhanced Superradiance. Electronics. 2024; 13(7):1171. https://doi.org/10.3390/electronics13071171
Chicago/Turabian StyleFeigin, Leon, Avraham Gover, Aharon Friedman, Amir Weinberg, Dekel Azar, and Ariel Nause. 2024. "High-Power Terahertz Free Electron Laser via Tapering-Enhanced Superradiance" Electronics 13, no. 7: 1171. https://doi.org/10.3390/electronics13071171






