Reliability Research on Quantum Neural Networks

Abstract

Quantum neural networks (QNNs) leverage the strengths of both quantum computing and neural networks, offering solutions to challenges that are often beyond the reach of traditional neural networks. QNNs are being used in areas such as computer games, function approximation, and big data processing. Moreover, quantum neural network algorithms are finding utility in social network modeling, associative memory systems, and automatic control mechanisms. Nevertheless, ensuring the reliability of quantum neural networks is crucial as it directly influences network performance and stability. To investigate the reliability of quantum neural networks, this paper proposes a methodology wherein operator measurements are performed on the final states of the output quantum states of a quantum neural network. The proximity of these measurements to the target value is compared, and the fidelity value, combined with a quantum gate operation, is utilized to assess the reliability of the quantum neural network. Through network training, the results demonstrate that, under optimal parameters, both the fidelity of the final state measurement value and the target value of the model approach are approximately equal to 1. It indicates that training mitigates the errors stemming from encoding into the initial quantum state, thereby resulting in enhanced system reliability and accuracy.

1. Introduction

An artificial neural network (ANN) is a computational model that mimics the functioning of the human nervous system, wherein it comprises numerous interconnected neurons. Each neuron receives input signals, computes an output signal using a specific activation function, and transmits this signal to the next layer of neurons. Through training and learning, ANNs can discern and forecast various patterns and trends. ANNs constitute a pivotal branch in the realm of artificial intelligence, facilitating the processing and recognition of intricate data and patterns by emulating the structure and functionality of the human nervous system. With ongoing technological advancements and the broadening of application domains, ANNs are poised to assume an increasingly significant role in future developments.

A quantum neural network (QNN) is a computational neural network model founded on the principles of quantum mechanics with the aim of harnessing the properties of qubits to facilitate more efficient computation and learning. Its inception dates back to 1995 when Subhash Kak and Ron Chrisley independently proposed the idea, whereby they suggested that quantum effects might influence cognitive functions [1]. QNNs leverage the superposition and entangled states of qubits for information processing, emulating, and learning the behavior of intricate quantum systems through the definition of qubits and their interactions. This network model holds promise for practical applications in domains such as quantum simulation, quantum chemical computations, and quantum optimization, thus offering potent tools for the future of quantum computing.

By integrating the strengths of classical neural networks with quantum information processing, quantum neural networks are poised to tackle complex problems that have proved challenging for classical neural networks. Li and Xiao [2] introduced a quantum neural network model and algorithm based on controlled revolving door sequence inputs to predict the interest in purchasing RV insurance and the incidence of breast cancer. Li and Li [3] proposed a quantum neuron model with sequential inputs, leveraging the properties of quantum rotating gates and CNOT gates to enhance neural network capabilities. Xuan et al. [4] outlined the fundamental model and learning algorithm of quantum neurons, as well as introduced the model and learning algorithm of the quantum adaptive resonance theory neural network. Then, it was applied to the field of pattern recognition by incorporating quantum computing into adaptive resonance theory. Verification results have demonstrated the superiority of the quantum adaptive resonance theory neural network over its classical counterpart. Liu and Chen et al. [5] proposed a novel single hidden layer feedforward quantum neural network model that combines quantum principles with feedforward neural networks. Quantum hidden neurons, which are defined and interconnected with quantum weights, serve as the fundamental information processing units of single hidden layer feedforward neural networks. The model utilizes Grover’s algorithm for network training and assesses quantum network performance through simulation. Results have demonstrated the quantum network’s capability for accurate learning. Behrman et al. [6] leveraged the foundational concepts of interference and entanglement in quantum computing to enhance the computational power of QNNs. They posited that a two-qubit quantum system constitutes a trainable quantum neural network, and that it provides relative phase outputs. Purushothaman and Karayiannis [7] observed that QNNs excel in solving pattern classification problems. Experiments have revealed that QNNs exhibit a network of S-shaped hidden units capable of identifying data structures, a feature that is absent in traditional feedforward neural networks. Zhong and Yuan [8] conducted a thorough analysis of quantum neural network performance through simulation, thereby demonstrating the potent learning capabilities of quantum neurons. Additionally, various other pertinent issues concerning quantum neural computation were addressed. Ventura and Martinez [9] presented a concise overview of advanced quantum theory and quantum neuron modeling. Quantum computation harnesses microscopic quantum-level effects to execute computational tasks, resulting in expedited outcomes when compared to classical computation in certain scenarios. Zhao et al. [10] introduced a quantum neural network model where all the weights between neurons are quantum states. They devised quantum circuits to implement the model and proposed a learning algorithm. The efficacy of the learning algorithm was not only theoretically substantiated but also numerically validated, thus highlighting the potential of quantum neural networks.

QNNs have seen applications in different fields. In 2021, to design an effective COVID-19 prediction method and accurately identify the virus and its variants, Essam H. Houssein et al. [11] proposed a hybrid quantum–classical convolutional layer, whereby they merged quantum convolutional layers with convolutional neural networks (CNNs). Accumulated neural networks can effectively help in the early diagnosis of COVID-19 with high accuracy through the image recognition of chest X-rays. Ge et al. [12] proposed a method inspired by Elman neural networks and quantum mechanics to address the high volatility of stock market behavior. They introduced internal, self-connected signals akin to Elman networks and employed a double-chain quantum genetic algorithm to adjust the learning rate. The model’s effectiveness was demonstrated through the prediction of closing prices across six stock markets. Yan et al. [13] explored the potential of combining quantum probability with graph neural networks and proposed a quantum probability-inspired graph neural network model to capture the global structural information of the interactions between documents for document representation and classification. The network model builds a document interaction graph for a given corpus based on document word relationships and frequency information, and it then learns a graph neural network driven by quantum probability on the defined graph.

QNNs have also been applied to image processing [14]. Kouda et al. [15] investigated the performance of QNNs in large-size image compression problems. Their simulation results showcased the superior image compression capabilities of QNNs compared to classical neural networks. Silva et al. [16] proposed a quantum neural network model that is a direct extension of the classical perceptron model and solves some of the shortcomings of the existing quantum perceptron models. QNNs can also be used in pattern recognition. Fard et al. [17] proposed a quantum neural network with multi-neuron interaction and used it for pattern recognition tasks. Additionally, QNNs have been utilized for iris flower identification through a model based on exchange testing and phase estimation [18], as well as for constructing a quantum parallel neural network capable of recognizing MNIST handwriting, among others. To further investigate the application of QNNs to real data and obfuscated images synthesized by deformation, the aforementioned authors tested their model on synthetic data and examined the fuzzy decision boundary of QNNs, thereby illustrating its mechanism and characteristics.

The essence of quantum neural network training is the learning problem of variational quantum circuits. Similar to classical neural network training, training quantum neural networks necessitates employing algorithms to compute the gradient vector of the loss function with respect to network parameters, which is followed by iterative optimization using gradient descent methods. However, once the intermediate quantum state of the quantum circuit is measured during operation, it will inevitably affect the output results of the entire circuit, and its stability and reliability will also be affected to a certain extent.

Therefore, while developing quantum neural networks, we must recognize the importance of research on the safety and reliability of quantum neural networks themselves, thus providing increased possibilities for achieving more efficient and powerful quantum computing.

This thesis innovatively presents a unique methodology at the quantum bit level. The proposed method comprehensively assesses the reliability of a quantum neural network by performing operator measurements on the end state of the quantum neural network outputs and comparing the proximity between the measured values and the target values. We employ fidelity as an evaluation metric to ensure the accuracy and comprehensiveness of the assessment. By training the quantum neural network model, we found that, under the optimal parameters, the fidelity between the end state measurements of the model and the target value was nearly perfect, i.e., close to 1. This result not only proves the success of the training process, but also demonstrates the outstanding ability of the model to eliminate initial quantum state encoding errors, thus highlighting the excellent reliability of the quantum neural network.

The rest of the paper is organized as follows: Section 2 introduces the Qubit neural network model, which serves as the foundation model for the method proposed in this paper. This section includes the basic principles of the model and its parameters. Section 3 analyzes the reliability of quantum neural networks, including factors influencing their reliability. Section 4 presents the experimental design, results, and analysis of reliability verification. Section 5 provides the conclusion of this paper and discusses future research directions.

2. Qubit Neural Network

A qubit neural network is a method of implementing neural network models utilizing the principles of quantum computing. It employs qubits as computing units to perform efficient calculations and information transmission through properties such as quantum entanglement and quantum superposition.

This model was proposed by Japanese scholars in 2000 [19]. It is a network model that uses qubits to represent the state of neurons. While the network topology resembles traditional neural networks, the methods for representing neuron information, weights, and activation functions differ significantly. Neuron models employ quantum states for information representation, with computing being achieved by modifying these quantum states. The rotation transformation of the quantum state phase is governed by the action of the weights, and the role of the activation function is to perform a controllable NOT gate operation on the phase. However, a limitation arises as its input can only be in the form of 0 and 1 values, and the output is one of probability amplitude, which greatly limits its application. Current experiments are limited to logic gate operations, parity checks [19,20,21], etc. Kouda et al. [22] proposed a qubit neural network, in which the interaction between the states of neurons and other neurons is based on the laws of quantum mechanics. The qubit neuron model produces a new multi-layer quantum feedforward neural network that realizes the quantum phenomena previously given by Kouda et al. [23]. To improve the computing power of neural networks, several works and studies, specifically those regarding a multi-layer neural network composed of qubit neurons, have been carried out in the field of quantum neural networks.

Qubit Neuron Model

In quantum computers, ‘‘qubits’’ correspond to ‘‘bits’’ in classical computers [24], and they are used to store the states of circuits used for quantum computations. Labeled $\left|0\right.〉$ and $\left|1\right.〉$, each of these two quantum states represents one bit of information: $\left|0\right.〉$ corresponds to the 0 bit of classical computers, and $\left|1\right.〉$ corresponds to the 1 bit. The qubit state $\left|\psi \right.〉$ maintains a coherent superposition of states, which are $\left|0\right.〉$ and $\left|1\right.〉$ according to the following expression:

$$\left|\psi \right.〉=\alpha \left|0\right.〉+\beta \left|1\right.〉,$$

(1)

where $\alpha$ and $\beta$ are complex numbers called probability amplitudes. These satisfy the following equation:

$${\left|\alpha \right|}^2+{\left|\beta \right|}^2=1.$$

(2)

We can rewrite the neuron state in (1) as [22]:

$$f(\phi )=e^{i\phi }=\cos \phi +i\sin \phi .$$

(3)

The qubit neuron model definition is illustrated in Figure 1:

The neuron state $Z$ represents the total inputs from different neurons $K$ as follows:

$$u={\displaystyle \sum _k^{K}f({\theta }_k)}\cdot x_k-f(\lambda )={\displaystyle \sum _k^{K}f({\theta }_k)}\cdot f(y_k)-f(\lambda ),$$

(4)

$$\begin{array}{l}y=\frac{\pi }{2}\cdot g(\delta )-\arg (u)\\ z=f(y)\end{array}.$$

(5)

Here, the neuron model has the following two parameters: the phase parameter in the form of weighted connections ${\theta }_k$ and the thresholds $\lambda$. $f(\phi )$ is another way through which to express the quantum state, and $\phi$ is the phase that describes the quantum state. $f({\theta }_k)$ represents the weight corresponding to the neuron state $x_k$, and $f(\phi )$ converts the input value $x_k$ into a quantum state whose phase value is ${\theta }_k$. $x_k$ is the state of the k-th neuron. After multiplying the weight $f({\theta }_k)$ with the input $x_k$, the neuron state undergoes rotation based on the rotation gates. Equation (4) expresses the state $u$ of a neuron in the usual way, i.e., as the weighted sum of the states of the inputs minus a threshold. Equation (5) adjusts the output qubit phase $y$ more roughly than Equation (4). In Equation (5), $\arg (u)$ represents the argument of the complex number $u$, and is implemented by $\arctan (\mathrm{Im}(u)/\mathrm{Re}(u))$. The neuron state $Z$ is the output state of the model, and it is obtained by a weighted computation of k different neuron states.

The activation function $g(\delta )$ is used in Equation (5) with the aim of obtaining a generalized inverse representation of a quantum logic gate that operates like a controlled NOT gate in quantum computing. In addition, it can compensate for the effect of small changes in the weights on the output of the network. Here, $\mathrm{g}$ is defined as the sigmoid function in the following:

$$\mathrm{g}(\delta )=\frac{1}{1+e^{-\delta }}.$$

(6)

Building upon quantum computing principles, Matsui et al. [14] proposed a multi-layer qubit neural network with qubit neurons. They explored its performance in two additional application scenarios, i.e., image compression and pattern recognition. Qubit neural networks exhibit superior computing power and parallel processing capabilities compared to traditional neural networks, thereby enabling a more effective handling of high-dimensional data and complex models. Furthermore, qubit neural networks offer enhanced privacy protection and heightened security, thus rendering them suitable for applications in secure communication and data encryption.

3. Reliability Analysis of Quantum Neural Networks

3.1. Factors Affecting the Reliability of Quantum Neural Networks

As an emerging technology, the reliability of quantum neural networks is influenced by various factors. These include qubits, quantum algorithms, quantum hardware, and quantum data, all of which serve as significant limiting factors. Overcoming these challenges, enhancing basic research, and further advancing quantum computing technology are essential steps for improving the reliability of quantum neural networks.

Qubit noise and errors represent the significant factors affecting the reliability of quantum neural networks. Given that the coherence and entanglement states of qubits are highly sensitive to environmental noise and interference, they are susceptible to environmental noise, interference, and decoherence factors; for example, changes in temperature and the presence of electromagnetic radiation can adversely affect the stability of quantum bits, leading to errors in the results of quantum computation. In practical applications, the noise and errors of qubits may have a negative impact on the performance and stability of the network. Bit-flip errors and phase-flip errors may occur when manipulating logic gates in a quantum neural network model. These errors can affect the interaction between quantum bits and the transmission of information in the quantum neural network. Secondly, the topology of the network also has an important impact on the reliability of quantum neural networks. Different network topologies may exhibit varying degrees of robustness and stability. For example, the design of network connections and weights may affect its robustness to noise and perturbations. Different training methods may have different effects on the reliability of the network. Some training methods may make the network more susceptible to noise, whereas others may enhance robustness. Therefore, choosing appropriate training methods and optimization strategies is crucial for improving the reliability of quantum neural networks. Moreover, there are hardware limitations inherent to quantum computers. The implementation of quantum neural networks relies on specific quantum hardware, and hardware limitations and defects may affect the reliability of the network. Factors such as hardware noise, errors, and the finite number of qubits can influence network performance. The quality and quantity of data fed into a quantum neural network also affect its reliability. If the data are noisy or biased, it may affect the network’s training and inference results.

To enhance the reliability of quantum neural networks, researchers are exploring various technologies and methods, such as the use of quantum error-correcting codes, the optimization of training methods, and weight design. With the continuous development of quantum technology, it is anticipated that the reliability of quantum neural networks will be continuously optimized and improved.

3.2. Reliability Analysis

The reliability analysis of quantum neural networks mainly refers to how one should ensure the correctness and stability of the output of quantum neural networks in practical applications. As quantum neural networks operate based on the principles of quantum mechanics, their computation processes and results are influenced by the uncertainty and coherence of qubits, thereby necessitating reliability analysis.

Firstly, when investigating the reliability of quantum neural networks, one needs to consider the noise and errors of qubits. In actual quantum computing, the coherence and fidelity of qubits are affected by environmental noise and other factors, thus leading to calculation errors and unreliability. Hence, methods are required to mitigate noise and errors, such as employing quantum error correction codes and correcting quantum gate operations. Secondly, the reliability of quantum neural networks should consider the robustness and generalization capabilities of the network. Robustness refers to the stability and correctness of the network’s output when faced with some changes and disturbances in the input data; the generalization ability refers to the performance of the network on unknown data other than the training data. To ensure the reliability of quantum neural networks, it is necessary to design appropriate network structures and training methods to improve their robustness and generalization capabilities.

In addition, when determining the reliability of quantum neural networks, one also needs to consider their interpretability and security. Interpretability refers to the understandability and interpretability of the network so that reliable results can be obtained in practical applications; security refers to the network’s resistance to malicious attacks and interference. To ensure the security and reliability of quantum neural networks, some defense technologies need to be adopted, such as quantum encryption, quantum signatures, etc.

In general, reliability analyses of quantum neural networks constitute a crucial research avenue, which require in-depth research and analysis by combining the theoretical and practical knowledge of quantum computing and neural networks. With the continuous development and maturity of quantum computing technology, quantum neural networks will play an increasingly important role in future applications; thus, at the same time, it is necessary to strengthen research and guarantee their reliability.

4. Reliability Verification of Quantum Neural Networks

4.1. Design of an Experimental Scheme for Reliability Verification

To investigate the reliability of the quantum neural network model, we constructed a quantum circuit based on the qubit neural network model, which is depicted in Figure 2. Among them, Figure 2a is a framework diagram of a basic quantum neural network. Figure 2b illustrates the quantum neural network model designed to verify the reliability of the network. The coding part of the neural network consists of different quantum gates, including parameter-containing quantum gates and non-parametric quantum gates. The training part of the circuit consists of two parameter-containing quantum gates, and the measurement is the Pauli $Z$ operator acting on the 0-th qubit. The objective is to train the parameters in the quantum circuit with the aim of ensuring that the measured value closely aligns with the target expected value. Specifically, we seek to achieve a measured value that closely matches the expected value corresponding to the Pauli $Z$ operator of the $\left|0\right.〉$ state, $\left|1\right.〉$ state, or a superposition of both. Then, the state at this time is a $\left|0\right.〉$ state, $\left|1\right.〉$ state, or a superposition thereof. This can also be interpreted as training to compensate for the errors stemming from the encoding process when it is applied to the initial quantum state.

When considering the coding circuit as the system’s error impact on the initial quantum state (the parameters ${\alpha }_0$, ${\alpha }_1$, and ${\alpha }_2$ are fixed values that are obtained after preprocessing the original classical data, and they were set to 0.2, 0.3, and 0.4, respectively, in this study, but they can be other values), we need to train a quantum circuit to offset this error so that the final quantum state is still in the $\left|0\right.〉$ state, $\left|1\right.〉$ state, or a superposition of both.

Another crucial aspect to mention is the feature importance of attributes. Feature importance analysis is utilized to understand the usefulness or value of each feature (variable or input) in making predictions. The goal is to identify the most important features that have the greatest impact on the output of the model, and it is a commonly used technique in machine learning. Majumder et al. [25] evaluated the predictive skill of machine learning algorithms for each queue using ten pairs of predefined training and testing datasets to study the classification problem of inter-individual variability. They compared the performance of various machine learning algorithms using six key performance metrics. These performance metrics reflect the attributes learned under given conditions that best improve the accuracy of the model.

Feature importance analysis is a crucial technique that accurately identifies and focuses on the most informative features. This analytical process brings several significant advantages. Firstly, it helps enhance the performance of the model, making predictions more accurate. Secondly, by focusing on key features, we can effectively reduce the risk of overfitting and improve the model’s generalization ability. Additionally, feature importance analysis can accelerate the training and inference speed of the model, thus enhancing overall efficiency. Finally, it also enhances the interpretability of the model, making it easier to understand the working principle and decision-making process of the model.

In the model construction, various attributes of quantum states can be taken into consideration. These attributes include the normalization characteristics of states, the application of superposition principles (i.e., that two quantum states can generate a brand-new quantum state through linear superposition), the determination of observables and eigenstates, the presence of potential entangled states, etc. In particular, different eigenstates correspond to their unique eigenvalues, as shown in Equation (7). In this paper, we designed the model parameters based on this attribute to achieve optimal predictive performance. This means that, at the output of the model, the measured end-state values should be as close as possible to the target values we set, thereby ensuring the model achieves the best performance in predicting and simulating quantum states.

When performing the Pauli $Z$ operator measurement on the final state, and the measured value at this time is the expected value of the current quantum state concerning the Pauli $Z$ operator. Since $\left|0\right.〉$ and $\left|1\right.〉$ are the eigenstates of the $Z$ operator and the eigenvalue are 1 and −1, then it is easy to know that the following applies:

$$〈0\left|Z\right|0〉=1, 〈1\left|Z\right|1〉=-1.$$

(7)

By training the parameters in the quantum circuit, our aim is to ensure that the measured value closely approximates the target expected value. Essentially, our goal is to achieve a measured value that closely aligns with the expected value corresponding to the Pauli $Z$ operator of the $\left|0\right.〉$ state, $\left|1\right.〉$ state, or a superposition of both. Consequently, the state at this stage will be the $\left|0\right.〉$ state, $\left|1\right.〉$ state, or a superposition state. In essence, the quantum training circuit works to counteract errors introduced by the encoding circuit on the initial quantum state.

The quantum coding circuit comprises four quantum gates, as depicted in Figure 3. Three of them contain parameterized quantum gates with parameters denoted as ${\alpha }_0$, ${\alpha }_1$, and ${\alpha }_2$. The number of qubits controlled by this quantum circuit is 1, that is, a single-bit quantum neural network.

The evolved quantum circuit, once the quantum gates within the quantum circuit are parameterized (which requires an assignment of parameter values), yields the evolved final state, which is a superposition state composed of $\left|0\right.〉$ and $\left|1\right.〉$.

The training circuit in the quantum circuit consists of two quantum gates, as shown in Figure 4. Both of these quantum gates contain parameterized quantum gates and the parameters labeled as ${\theta }_0$ and ${\theta }_1$. Similar to the coding circuit, the number of qubits controlled by this quantum circuit is also 1.

Assigning values to the parameters in the training circuit involves setting values for the parameters ${\theta }_0$ and ${\theta }_1$. As the training circuit is a quantum circuit that requires training, these parameters can be initialized randomly. Typically, the initial default value is set to 0.

A complete quantum neural network model is formed by combining the two circuits described above, as depicted in Figure 2b. The quantum circuit comprises six quantum gates, with five of them containing parametric quantum gates. The parameters for these gates are denoted as ${\alpha }_0$, ${\alpha }_1$, ${\alpha }_2$, ${\theta }_0$, and ${\theta }_1$. Similar to the individual circuits, the number of qubits controlled by the quantum circuit remains 1.

When conducting a Pauli $Z$ operator measurement on the 0th qubit and calculating the expected value of the Hamiltonian quantity, we have the following:

$$E(\theta )=\left.〈\phi \right|U_l^{†}(\theta )H{U}_r(\theta )\left|\psi \right.〉.$$

(8)

This denotes the expected value of the Hamiltonian quantity of the quantum circuit in the initial state, i.e., the default case. It plays a crucial role in the training process for obtaining information about the gradient of the circuit parameters and thus optimizing the performance of the quantum circuit, where $H$ denotes the Hamiltonian quantity in the circuit, $U_l(\theta )$ represents the left part of the circuit, $U_r(\theta )$ represents the right part of the circuit, $\left|\psi \right.〉$ represents the current quantum state of the simulator, and $\left|\phi \right.〉$ represents the quantum state of the left part of the simulator. By default, $U_r(\theta )\left|\psi \right.〉={\left(\left.〈\phi \right|U_l^{†}(\theta )\right)}^{†}$.

The constructed Hamiltonian is aimed at performing a Pauli $Z$ operator measurement on the 0th qubit with a coefficient of −1. This coefficient is set to −1 because, during the training of quantum neural networks, the gradients of the parameters in the training circuit typically decrease, thus also leading to a decrease in the measured values. If it eventually converges to −1, it indicates that the corresponding quantum state is the $\left|1\right.〉$ state instead the $\left|0\right.〉$ state, as shown in the below:

$$〈1\left|Z\right|1〉=-1.$$

(9)

If we aim to obtain the $\left|0\right.〉$ state, we set the coefficient to negative 1. Then, when the measured value is −1, the corresponding quantum state is the $\left|0\right.〉$ state, as shown in the below:

$$〈0|(-Z)|0〉=-1.$$

(10)

The next step is to generate variable component subcircuit simulation operators and gradient-solving operators. The calculation model is as follows:

$$E(\theta )=\left.〈0\right|U_l^{†}(\theta )H{U}_r(\theta )\left|0\right.〉.$$

(11)

As depicted in Figure 5, the loss of the network is observed when the input is, respectively, the $\left|0\right.〉$ state and $\left|1\right.〉$ state. The derivative of the parameter decreases and approaches 0, thus causing the measured value to approach −1.

The aforementioned cases represent the outcomes obtained when the input state is, respectively, $\left|0\right.〉$ and $\left|1\right.〉$. To comprehensively consider the input states of the quantum neural network, i.e., when the input is the superposition state $\left|\psi \right.〉=\alpha \left|0\right.〉+\beta \left|1\right.〉$, it is essential to include an $H$ gate to flip the superposition state before conducting the Pauli $Z$ operator measurement at the end of the quantum neural network, as depicted in Figure 2b. This is illustrated in Figure 6 to facilitate a comparison of the measurement results with the target state.

A Hadamard gate is a quantum logic gate that changes the ground state into a superposition state, which is sometimes referred to simply as the $H$ gate. The Hadamard gate matrix is of the following form: $H=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]$. The Hadamard gate operates on a single bit, which changes the ground state $\left|0\right.〉$ to $(\left|0\right.〉+\left|1\right.〉)/\sqrt{2}$, and the ground state $\left|1\right.〉$ to $(\left|0\right.〉-\left|1\right.〉)/\sqrt{2}$.

Suppose that the $H$ gate acts on any quantum state $\psi =\alpha \left|0\right.〉+\beta \left|1\right.〉$, then the new quantum state is as follows:

$${\left|\psi \right.〉}^{\prime }=H\left|\psi \right.〉=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]\left[\begin{array}{c}\alpha \\ \beta \end{array}\right]=\frac{\alpha +\beta }{\sqrt{2}}\left|0\right.〉+\frac{\alpha -\beta }{\sqrt{2}}\left|1\right.〉.$$

(12)

After the evolution of the quantum circuit, the final state of the newly obtained quantum state becomes a superposition of the $\left|0\right.〉$ state and $\left|1\right.〉$ state. Subsequently, it undergoes learning in the training circuit, which involves the function of the $H$ gate. Finally, the Pauli $Z$ operator is performed at the end to, respectively, measure the measured values of the $\left|0\right.〉$ state and $\left|1\right.〉$ state, which are then compared with the target values.

4.2. Analysis of the Experimental Results of the Reliability Verification

Finally, we performed the training of the quantum neural network model. During this process, the primary adjustment involves fine tuning the parameters within the quantum circuits, with the objective of continuously reducing the derivatives of these parameters toward zero. When this criterion is met, the results obtained through measurements from the quantum circuits will tend toward −1, thus signifying the successful training of the model and achieving optimal predictive performance. This ensures the optimization of the model performance and enhancement of accuracy.

The validation scheme devised in this paper aims to comprehensively test and evaluate the accuracy and reliability of the quantum neural network model. Specifically, this scheme employs various quantum states as inputs and conducts a meticulous analysis of the model’s performance under diverse scenarios, thereby accurately assessing the model’s accuracy and reliability. We conducted model training to obtain the quantum state of the quantum circuit at the optimal parameters and to calculate the fidelity of this quantum state to the target state. The fidelity is used as a measure of the reliability of the quantum neural network, where the larger the value, the higher the accuracy and the more reliable the model.

The result pairs are presented in

Table 1. A comparison of the output measured value and the target value of the quantum neural network under different input states.

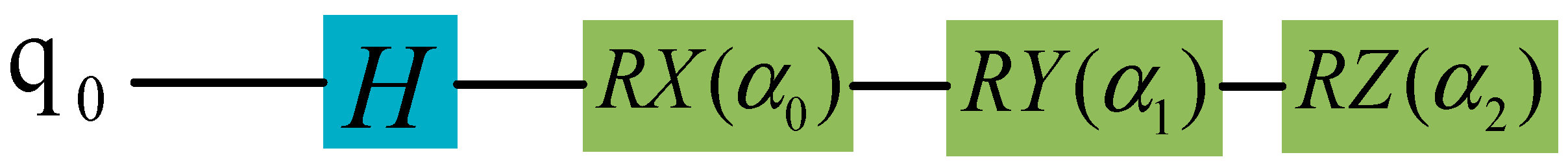
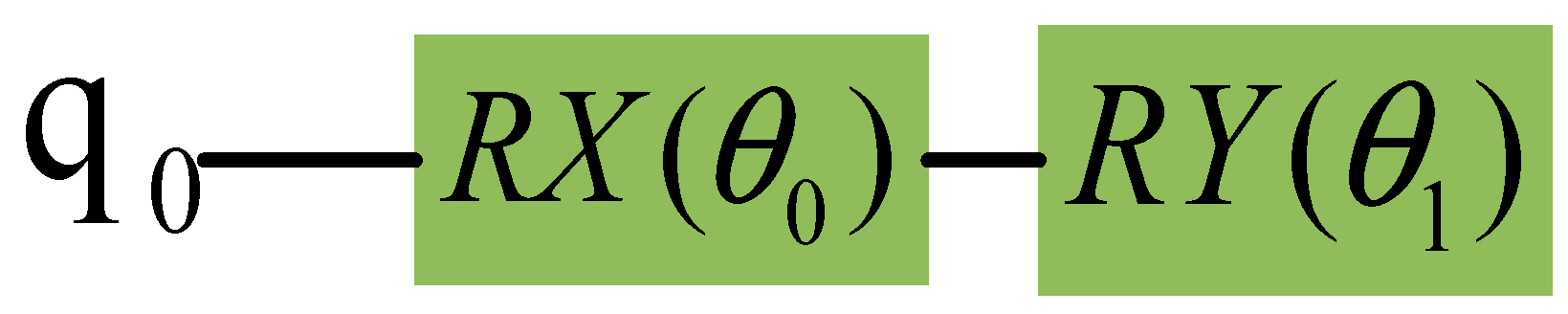
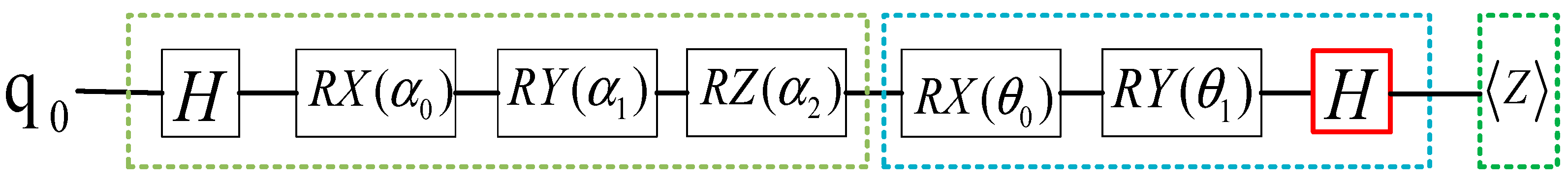
Input State	Output State	Fidelity
$\left|0\right.〉$	(0.37130919062752576 − 0.9285092807985207j) $\left|0\right.〉$ (1.995967198215043 × 10−5 + 5.306337058308408 × 10−6j) $\left|1\right.〉$	Approximately equal to 1
$\left|1\right.〉$	(6.778891857961433 × 10−6 + 2.684974533762041 × 10−6j) $\left|0\right.〉$ (−0.37128647139550186 + 0.9285183660571905j) $\left|1\right.〉$	Approximately equal to 1
$\left|\psi \right.〉=\alpha \left|0\right.〉+\beta \left|1\right.〉$	In particular, when $\alpha =\beta =\frac{1}{\sqrt{2}}$, the corresponding final state measurement value is $\frac{1}{\sqrt{2}}\left|0\right.〉,\frac{1}{\sqrt{2}}\left|1\right.〉$; When $\alpha =\frac{1}{\sqrt{2}},\beta =-\frac{1}{\sqrt{2}}$, the corresponding final state measurement value is $\frac{1}{\sqrt{2}}\left|0\right.〉,-\frac{1}{\sqrt{2}}\left|1\right.〉$.	The amplitude of the final state measurements $\left|0\right.〉$ and $\left|1\right.〉$ is consistent with the amplitude of the input state

. Upon calculation, the fidelity of the measured output quantum state and the target state were 0.999999 and 0.999997 (when keeping 6 digits after the decimal point), respectively, which are approximately equal to 1. When the input is a superposition state, it transforms into a new quantum state after the evolution of the quantum circuit, thus potentially resulting in a new superposition state or a pure state. Following the input into the training circuit, the training process remains consistent with the previous case. The data in the table show that when different quantum states are used as inputs, high fidelity is demonstrated between the measured and target values for the same quantum neural network model. This fully demonstrates the high accuracy of the model in processing the training data, thus further reflecting its excellent reliability.

5. Conclusions

To investigate the reliability of quantum neural networks, we designed a single-bit quantum neural network based on the qubit neural network model and then conducted the training process. Operator measurements were executed at the output terminal of the network, and the obtained results were juxtaposed with the anticipated values. The fidelity between the two was computed as one of the metrics to measure the reliability of the quantum neural network. Following measurement and computation, the outcomes demonstrated that the fidelity between the final state measurement and the target value of the system was approximately equal to 1 under optimal parameters. This signifies that the training compensates for the errors induced by encoding the initial quantum state, thereby indicating the system’s robust reliability.

Research on the reliability of quantum neural networks may extend to multiple domains in the future. With the continuous increase in model complexity, there is an urgent need to update and improve methods for evaluating the reliability of quantum neural networks. Therefore, we will devote ourselves to developing more precise and comprehensive reliability assessment metrics and methods to more accurately reflect the performance of quantum neural networks in practical applications. When dealing with sensitive information, the security and privacy protection issues of quantum neural networks are equally important. In the future, we will focus on the security challenges of quantum neural networks and explore the application of encryption technology and privacy protection algorithms to ensure that the models have high reliability when handling sensitive data. Furthermore, research on the reliability of quantum neural networks also needs to draw on and integrate knowledge and techniques from various fields such as physics, materials science, and information security. We look forward to strengthening cooperation and communication within these fields in the future to jointly promote the in-depth development of quantum neural network reliability research.

In summary, the future expansion of research on the reliability of quantum neural networks has broad prospects and significant practical value. Through the continuous deepening of research, optimization of techniques, and enhanced cooperation, we have reason to believe that quantum neural networks will demonstrate higher reliability and stability in addressing practical problems.