Analysis and Mitigating Methods for Jamming in the Optical Reconfigurable Intelligent Surfaces-Assisted Dual-Hop FSO Communication Systems
Abstract
:1. Introduction
- (1)
- Mitigation of Atmospheric Transmission Losses: By leveraging RIS, we can manipulate the propagation path of signals, thereby reducing losses incurred due to atmospheric transmission [19]. RIS facilitates directing signals towards the intended receiver, effectively minimizing transmission distances and associated losses within the atmosphere [12].
- (2)
- Compensation for Pointing Errors: RIS provides the capability to adjust phase and amplitude during signal propagation, offering compensation for pointing errors. Through the intelligent modulation capabilities of RIS, we can achieve more precise signal alignment, thus enhancing system stability and performance [18,20].
- The closed-form expression of the PDF of the legitimate channel in the RIS-assisted dual-hop FSO system is derived. Additionally, The PDF of the UAV jamming receiver and the RIS channel is derived. Novel closed-form expressions for the end-to-end ABER in both jamming scenarios have been derived based on the obtained link statistics. These expressions are derived considering the impact of non-Gaussian additive noise, which varies depending on the jammer’s location.
- The closed-form PDF of the legitimate channel in a 1 × N SIMO-FSO system and the channels under various jamming scenarios were derived using Mellin transforms to mitigate the impact of jamming. Analytical expressions for the end-to-end ABER in the two jamming scenarios were subsequently provided.
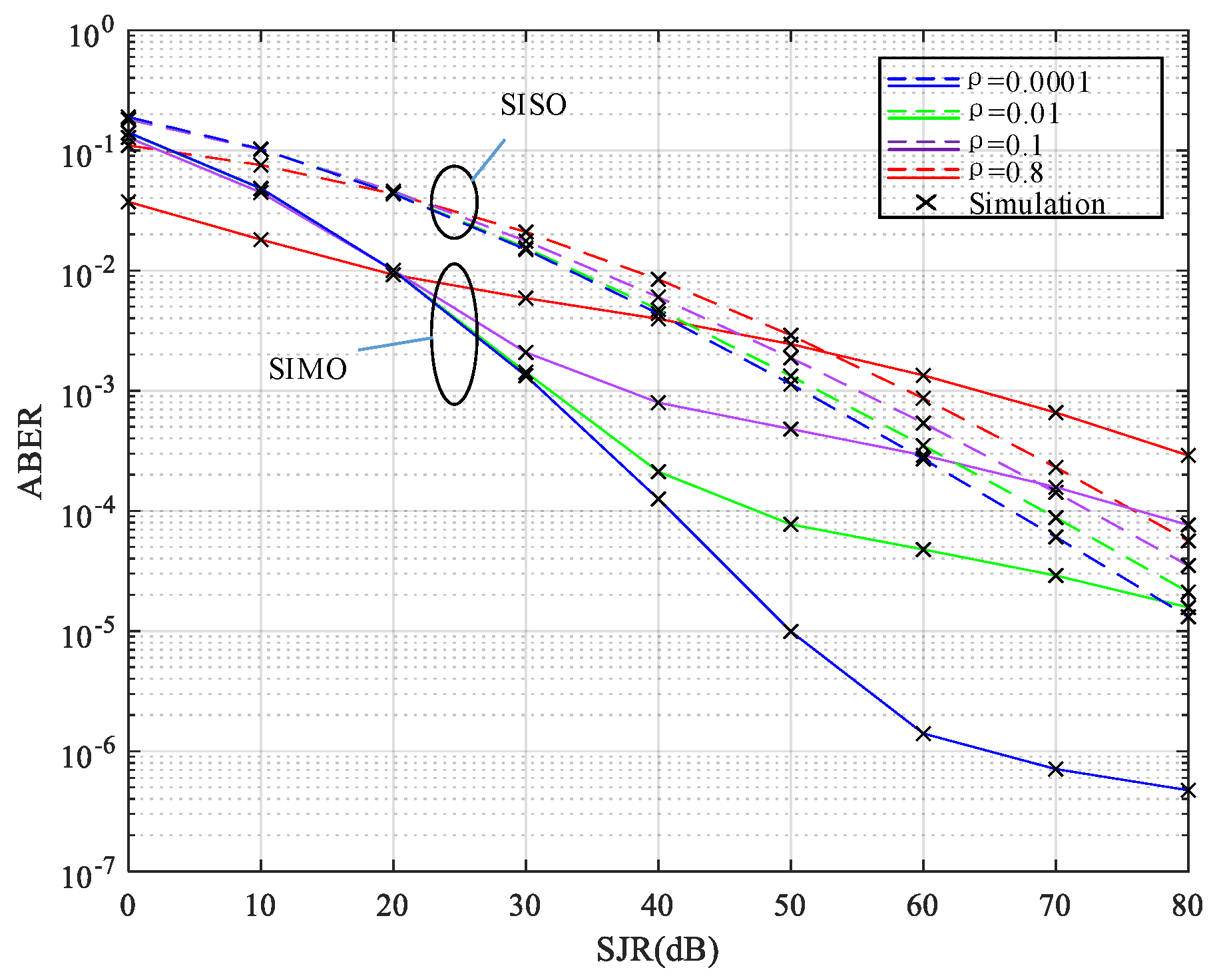
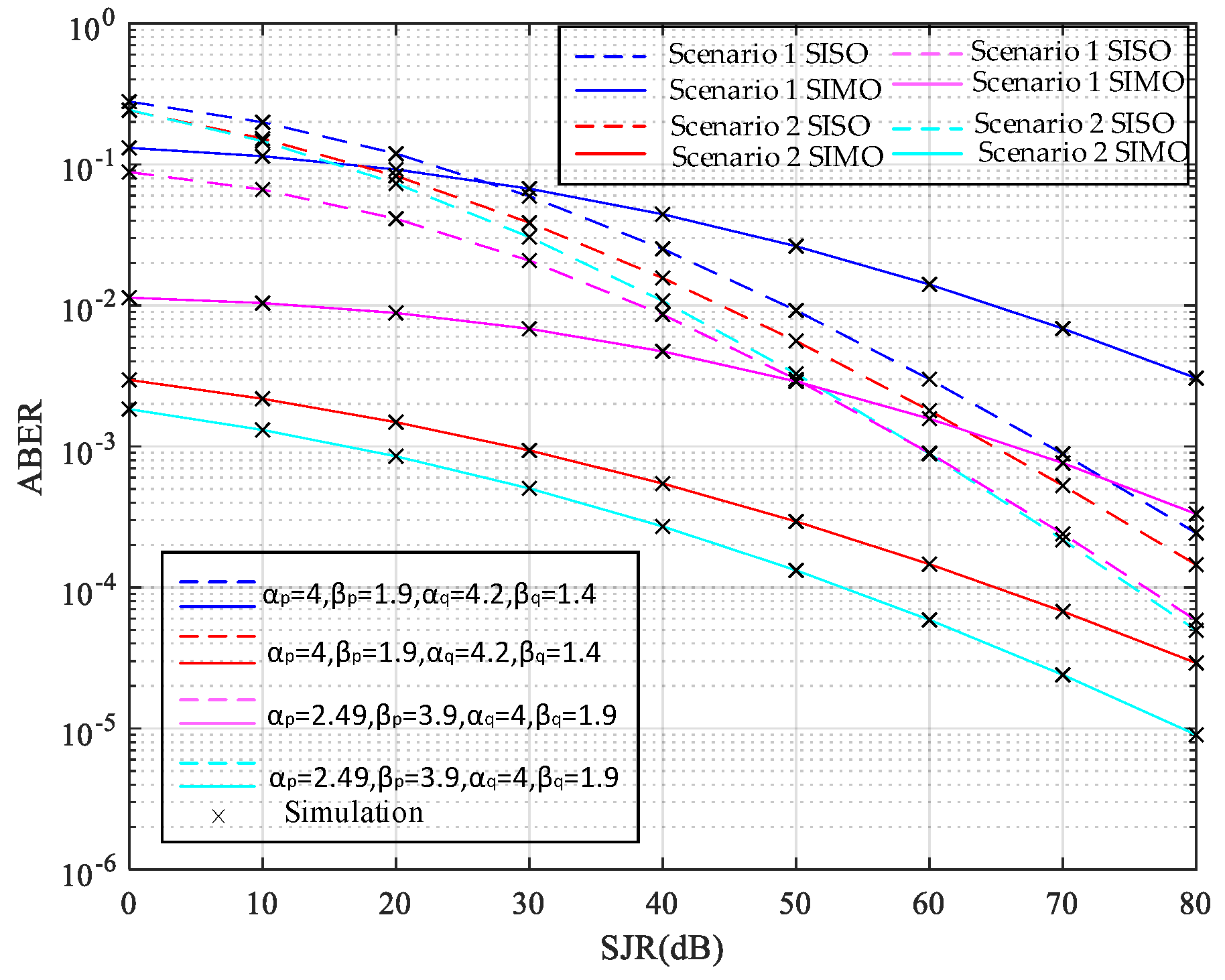
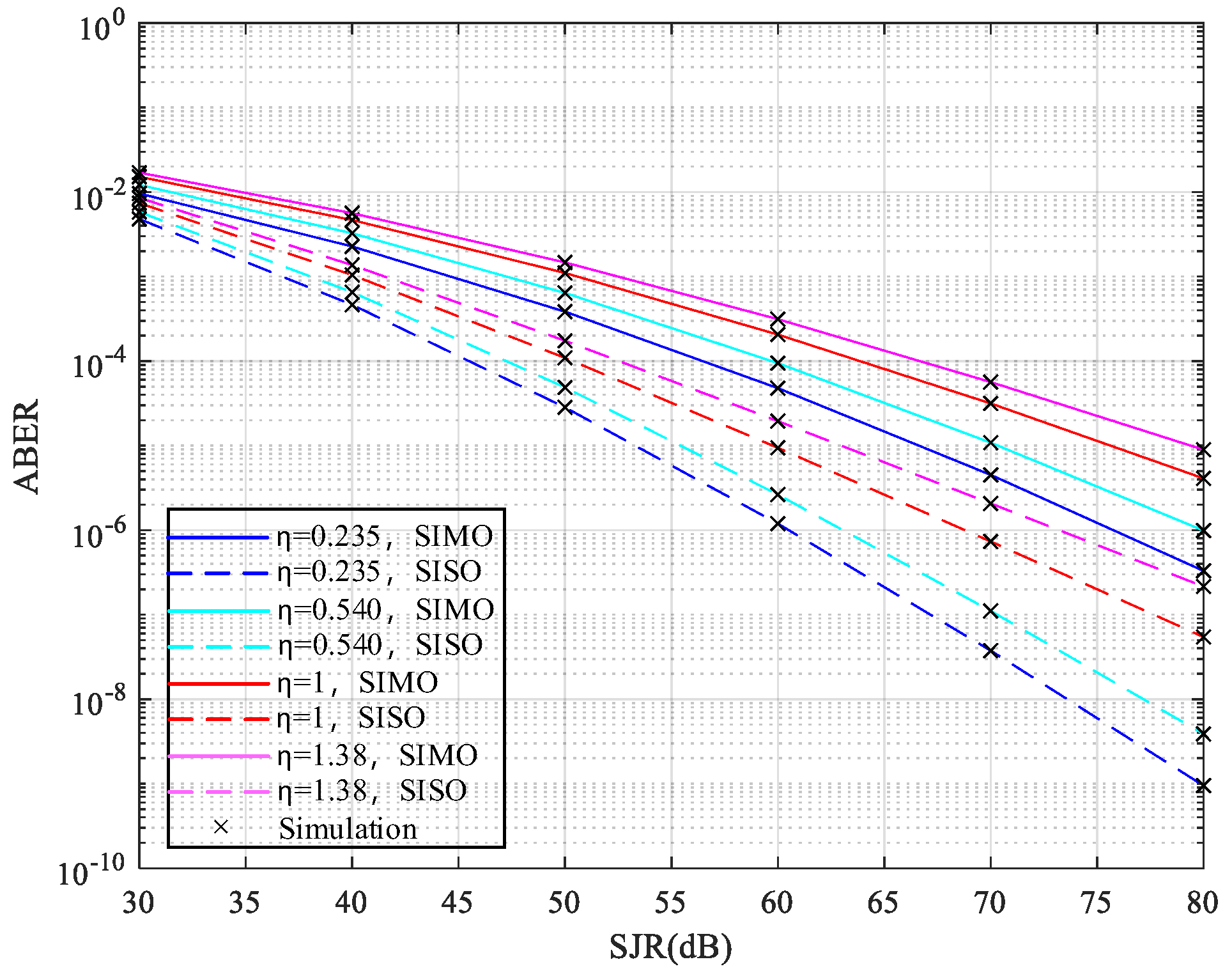
- A comprehensive system ABER analysis is conducted in terms of atmospheric turbulence strength, N (the number of receiving apertures), the probability of jamming and different RIS positions. Moreover, some useful insights are obtained.
2. System and Channel Model
2.1. System Model
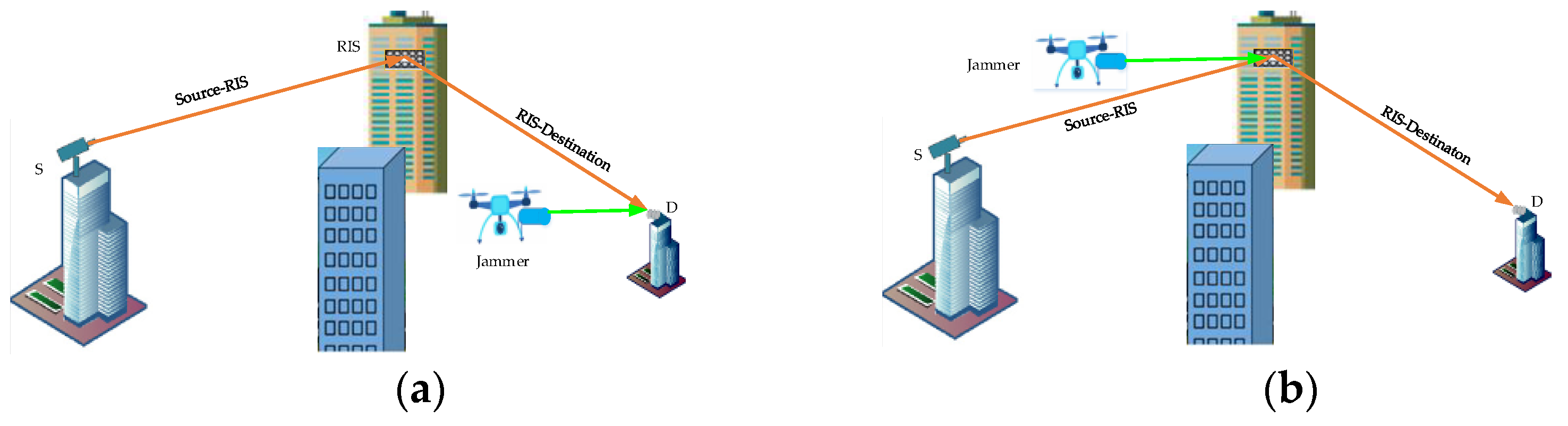
2.1.1. System Model for Scenario 1
2.1.2. System Model for Scenario 2
2.2. Channel Model
3. Analysis of BER for SISO System
3.1. Scenario 1
3.1.1. BER during Jamming Active
3.1.2. BER during Jamming Idle
3.2. Scenario 2
4. Methods for Mitigating Jamming
4.1. Scenario 1
4.2. Scenario 2
4.3. ABER Calculation
4.3.1. Analysis of the ABER for SIMO in Scenario 1
4.3.2. Analysis of the ABER for SIMO in Scenario 2
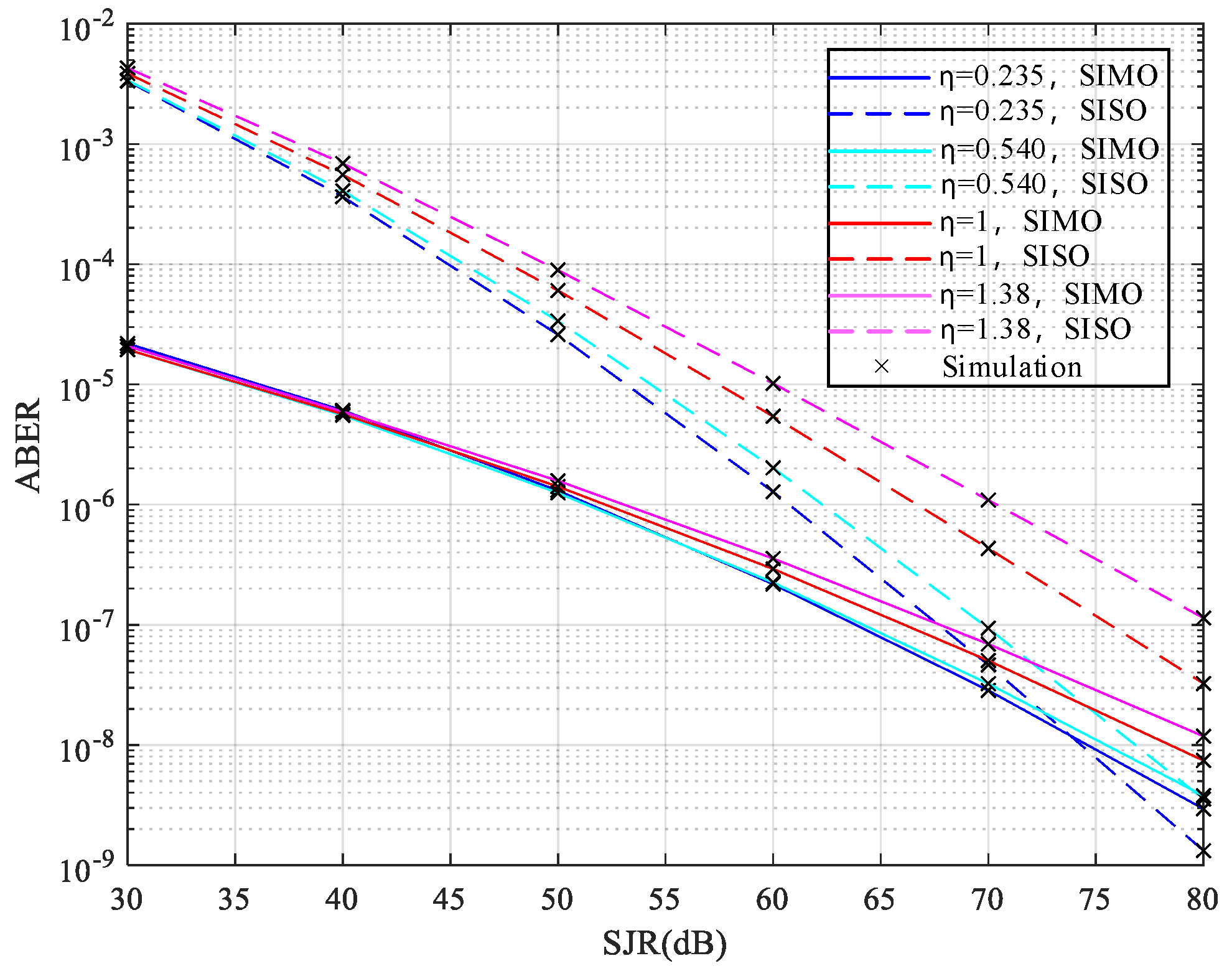
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Mishra, P.; Singh, G. Energy management systems in sustainable smart cities based on the internet of energy: A technical review. Energies 2023, 16, 6903. [Google Scholar] [CrossRef]
- Huang, Y.; Jin, J.; Lou, M.; Dong, J.; Wu, D.; Xia, L.; Wang, S.; Zhang, X. 6G mobile network requirements and technical feasibility study. China Commun. 2022, 19, 123–136. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Chen, D.; Dong, Y.; Ding, H.; Gao, D. Performance analysis and verification of FSO based inter-ship communication systems on sea. Opt. Commun. 2024, 557, 130271. [Google Scholar] [CrossRef]
- Elamassie, M.; Uysal, M. Free space optical communication: An enabling backhaul technology for 6G non-terrestrial networks. Photonics 2023, 10, 1210. [Google Scholar] [CrossRef]
- Raj, A.A.B.; Krishnan, P.; Darusalam, U.; Kaddoum, G.; Ghassemlooy, Z.; Abadi, M.M.; Majumdar, A.K.; Ijaz, M. A review–unguided optical communications: Developments, technology evolution, and challenges. Electronics 2023, 12, 1922. [Google Scholar] [CrossRef]
- Yücel, M.; Açikgöz, M. Optical communication infrastructure in new generation mobile networks. Fiber Integr. Opt. 2023, 42, 53–92. [Google Scholar] [CrossRef]
- Hayal, M.R.; Yousif, B.B.; Azim, M.A. Performance enhancement of DWDM-FSO optical fiber communication systems based on hybrid modulation techniques under atmospheric turbulence channel. Photonics 2021, 8, 464. [Google Scholar] [CrossRef]
- Al-Nahhal, M.; Ismail, T. Enhancing spectral efficiency of FSO system using adaptive SIM/M-PSK and SIMO in the presence of atmospheric turbulence and pointing errors. Int. J. Commun. Syst. 2019, 32, e3942. [Google Scholar] [CrossRef]
- Ismail, T.; Leitgeb, E.; Ghassemlooy, Z.; Al-Nahhal, M. Performance improvement of FSO system using multi-pulse pulse position modulation and SIMO under atmospheric turbulence conditions and with pointing errors. IET Netw. 2018, 7, 165–172. [Google Scholar] [CrossRef]
- Xu, M.; Xu, G.; Dong, Y.; Wang, W.; Zhang, Q.; Song, Z. UAV-assisted FSO communication system with amplify-and-forward protocol under AOA fluctuations: A performance analysis. China Commun. 2023, 20, 111–130. [Google Scholar] [CrossRef]
- Chapala, V.K.; Zafaruddin, S.M. Unified performance analysis of reconfigurable intelligent surface empowered free-space optical communications. IEEE Trans. Commun. 2021, 70, 2575–2592. [Google Scholar] [CrossRef]
- Najafi, M.; Schmauss, B.; Schober, R. Intelligent reflecting surfaces for free space optical communication systems. IEEE Trans. Commun. 2021, 69, 6134–6151. [Google Scholar] [CrossRef]
- Basar, E.; Poor, H.V. Present and future of reconfigurable intelligent surface-empowered communications [perspectives]. IEEE Signal Process. Mag. 2021, 38, 146–152. [Google Scholar] [CrossRef]
- Aboagye, S.; Ndjiongue, A.R.; Ngatched, T.M.; Dobre, O.A.; Poor, H.V. RIS-assisted visible light communication systems: A tutorial. IEEE Commun. Surv. Tutor. 2022, 25, 251–288. [Google Scholar] [CrossRef]
- Basar, E.; Di Renzo, M.; De Rosny, J.; Debbah, M.; Alouini, M.-S.; Zhang, R. Wireless communications through reconfigurable intelligent surfaces. IEEE Access 2019, 7, 116753–116773. [Google Scholar] [CrossRef]
- Ali, M.F.; Jayakody, D.N.K.; Garg, S.; Kaddoum, G.; Hossain, M.S. Dual-hop mixed FSO-VLC underwater wireless communication link. IEEE Trans. Netw. Serv. Manag. 2022, 19, 3105–3120. [Google Scholar] [CrossRef]
- Zhang, S.; Zhu, D.; Liu, Y. Artificial intelligence empowered physical layer security for 6G: State-of-the-art, challenges, and opportunities. Comput. Netw. 2024, 242, 110255. [Google Scholar] [CrossRef]
- Ndjiongue, A.R.; Ngatched, T.M.; Dobre, O.A.; Armada, A.G.; Haas, H. Analysis of RIS-based terrestrial-FSO link over GG turbulence with distance and jitter ratios. J. Light. Technol. 2021, 39, 6746–6758. [Google Scholar] [CrossRef]
- Huang, J.; Wang, C.-X.; Sun, Y.; Feng, R.; Huang, J.; Guo, B.; Zhong, Z.; Cui, T.J. Reconfigurable intelligent surfaces: Channel characterization and modeling. Proc. IEEE 2022, 110, 1290–1311. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Song, X.; Shao, L.; Li, H. RIS assisted UAV for weather-dependent satellite terrestrial integrated network with hybrid FSO/RF systems. IEEE Photonics J. 2023, 15, 7304217. [Google Scholar] [CrossRef]
- Paul, P.; Bhatnagar, M.R. Jamming Threats in Free-Space Optics. IEEE Commun. Mag. 2022, 60, 104–108. [Google Scholar] [CrossRef]
- Jahid, A.; Alsharif, M.H.; Hall, T.J. A contemporary survey on free space optical communication: Potentials, technical challenges, recent advances and research direction. J. Netw. Comput. Appl. 2022, 200, 103311. [Google Scholar] [CrossRef]
- Dong, Y.; Sadegh Aminian, M. Routing in Terrestrial Free Space Optical Ad-Hoc Networks. Master’s Thesis, Linköping University Electronic Press: Linköping, Sweden, 21 November 2014. [Google Scholar]
- Paul, P.; Bhatnagar, M.R.; Jaiswal, A. Alleviation of jamming in free space optical communication over Gamma-Gamma channel with pointing errors. IEEE Photonics J. 2019, 11, 7906418. [Google Scholar] [CrossRef]
- Paul, P.; Bhatnagar, M.R.; Nebhen, J. Pulse jamming in aperture-averaged fso receiver over exponentiated weibull fading channel. IEEE Trans. Wirel. Commun. 2021, 21, 4242–4254. [Google Scholar] [CrossRef]
- Shukla, A.K.; Bhatnagar, M.R. Mitigating Jamming in FSO Cooperative Networks: A Buffer-Aided Relaying Approach. IEEE Commun. Lett. 2023, 27, 2078–2082. [Google Scholar] [CrossRef]
- Saxena, P.; Chung, Y.H. Analysis of jamming effects in IRS assisted UAV dual-hop FSO communication systems. IEEE Trans. Veh. Technol. 2023, 72, 8956–8971. [Google Scholar] [CrossRef]
- Chauhan, I.; Bhatnagar, M.R. UAV-Based FSO Communication Under Jamming. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference:(VTC2022-Spring), Helsinki, Finland, 19–22 June 2022; pp. 1–5. [Google Scholar]
- Wolfram Research. Available online: http://functions.wolfram.com/06.27.21.0133.01 (accessed on 27 April 2018).
- Dabiri, M.T.; Sadough, S.M.S.; Khalighi, M.A. Channel modeling and parameter optimization for hovering UAV-based free-space optical links. IEEE J. Sel. Areas Commun. 2018, 36, 2104–2113. [Google Scholar] [CrossRef]
- Saxena, P.; Bhatnagar, M.R. A simplified form of beam spread function in underwater wireless optical communication and its applications. IEEE Access 2019, 7, 105298–105313. [Google Scholar] [CrossRef]
- Roach, K. Meijer G function representations. In Proceedings of the 1997 International Symposium On symbolic and Algebraic Computation, Kihei, HI, USA, 21–23 July 1997. [Google Scholar]
- Pang, W.; Wang, P.; Li, S.; Li, H.; Song, X. Reliability analysis of optical IRS-enabled FSO system with multiple detectors and PCB under composite turbulence fading channels considering the impact of GML. Opt. Commun. 2023, 537, 129465. [Google Scholar] [CrossRef]
- Tsiftsis, T.A.; Sandalidis, H.G.; Karagiannidis, G.K.; Uysal, M. Optical wireless links with spatial diversity over strong atmospheric turbulence channels. IEEE Trans. Wirel. Commun. 2009, 8, 951–957. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Gao, D.; Li, J.; Huang, L.; Ding, H.; Zhou, S. Analysis and Mitigating Methods for Jamming in the Optical Reconfigurable Intelligent Surfaces-Assisted Dual-Hop FSO Communication Systems. Electronics 2024, 13, 1730. https://doi.org/10.3390/electronics13091730
Wang J, Gao D, Li J, Huang L, Ding H, Zhou S. Analysis and Mitigating Methods for Jamming in the Optical Reconfigurable Intelligent Surfaces-Assisted Dual-Hop FSO Communication Systems. Electronics. 2024; 13(9):1730. https://doi.org/10.3390/electronics13091730
Chicago/Turabian StyleWang, Jingyu, Dingshan Gao, Juan Li, Linhe Huang, Haiyang Ding, and Shaohua Zhou. 2024. "Analysis and Mitigating Methods for Jamming in the Optical Reconfigurable Intelligent Surfaces-Assisted Dual-Hop FSO Communication Systems" Electronics 13, no. 9: 1730. https://doi.org/10.3390/electronics13091730
APA StyleWang, J., Gao, D., Li, J., Huang, L., Ding, H., & Zhou, S. (2024). Analysis and Mitigating Methods for Jamming in the Optical Reconfigurable Intelligent Surfaces-Assisted Dual-Hop FSO Communication Systems. Electronics, 13(9), 1730. https://doi.org/10.3390/electronics13091730





