Multi-Electrode EMG Spatial-Filter Implementation Based on Current Conveyors
Abstract
1. Introduction
2. Methodology and Design
2.1. NDD Electrode Modes
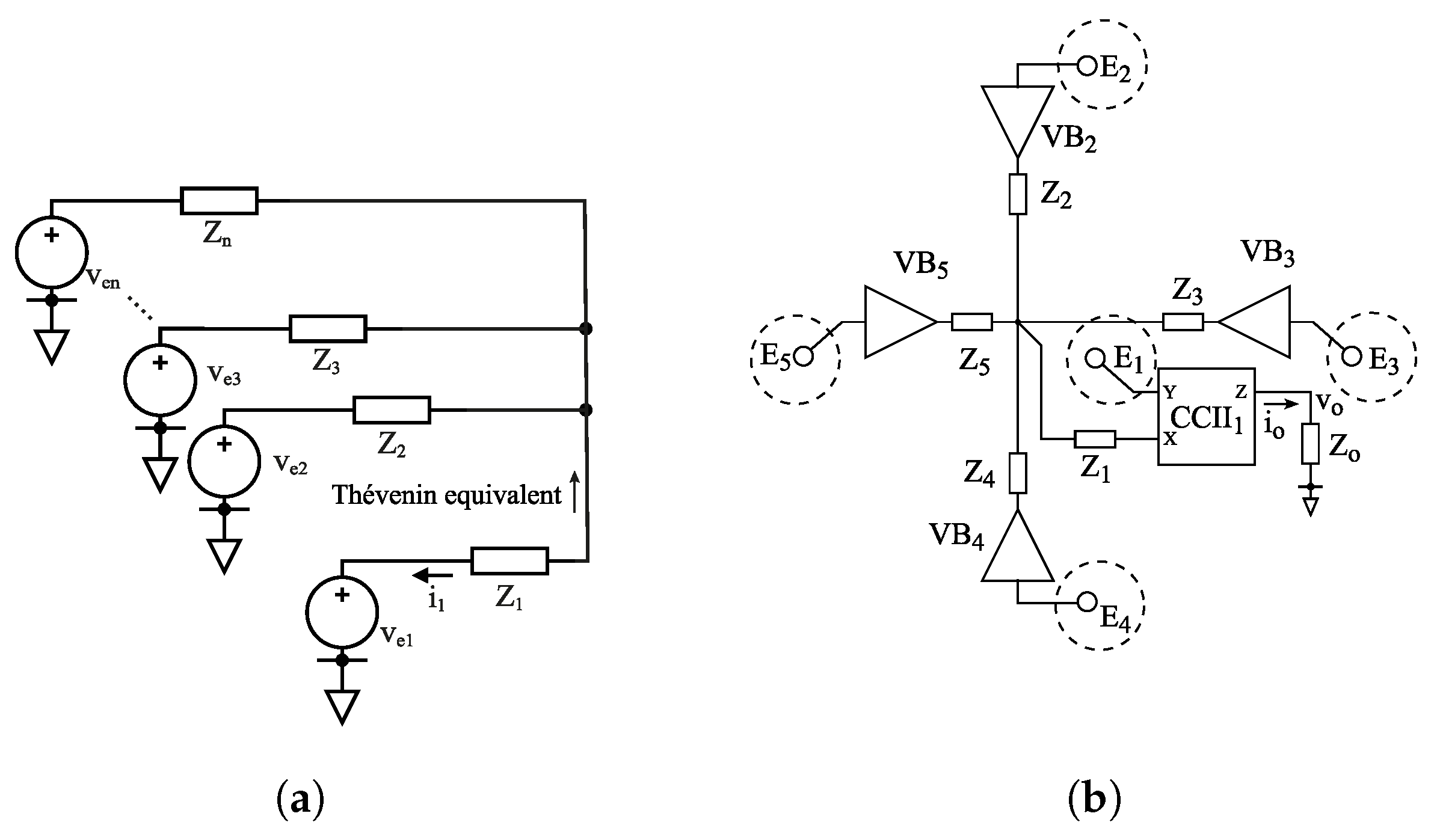
2.2. Circuit Topology
2.3. Rejection Ratios
2.4. CCII and Proof-of-Concept Implementation
2.5. Noise Analysis
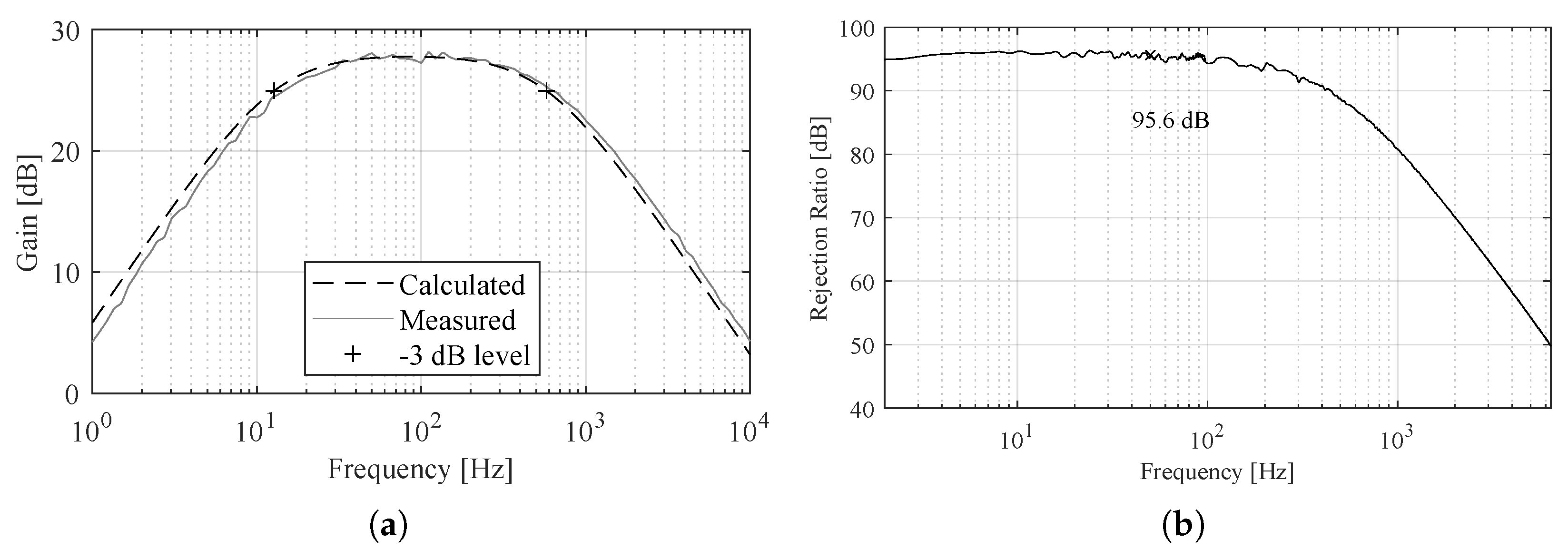
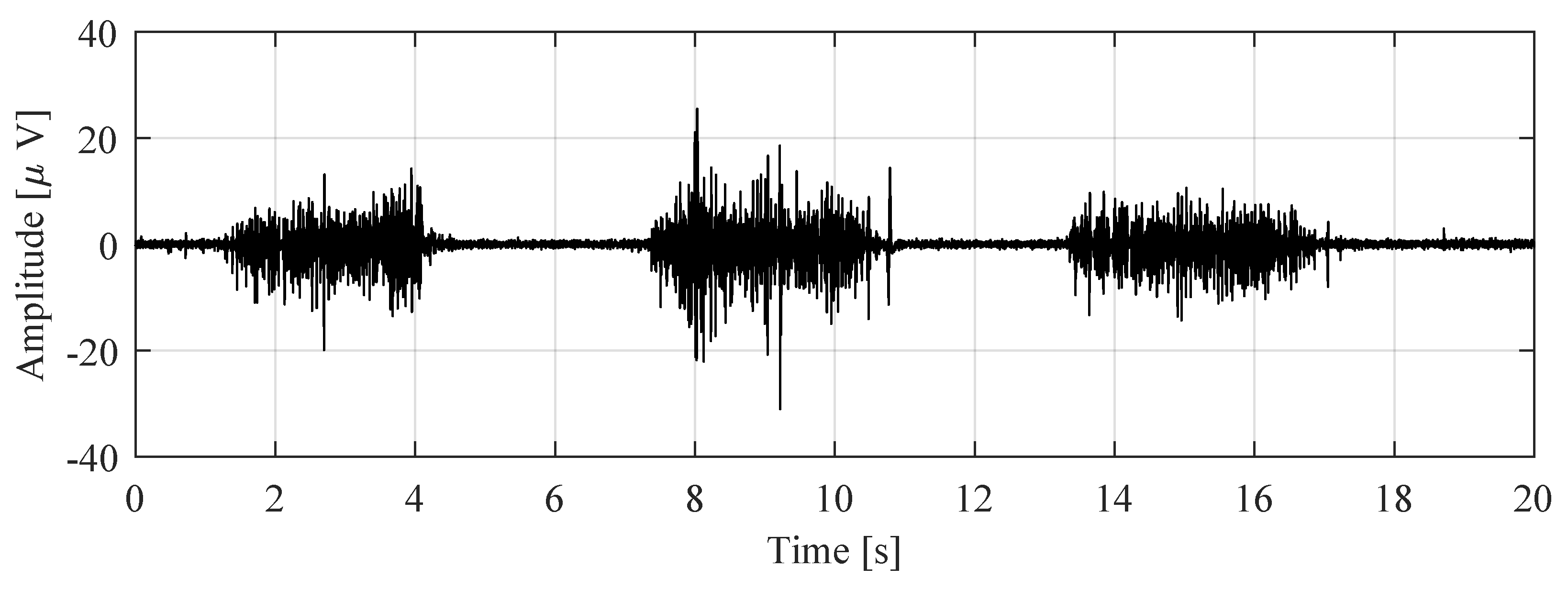
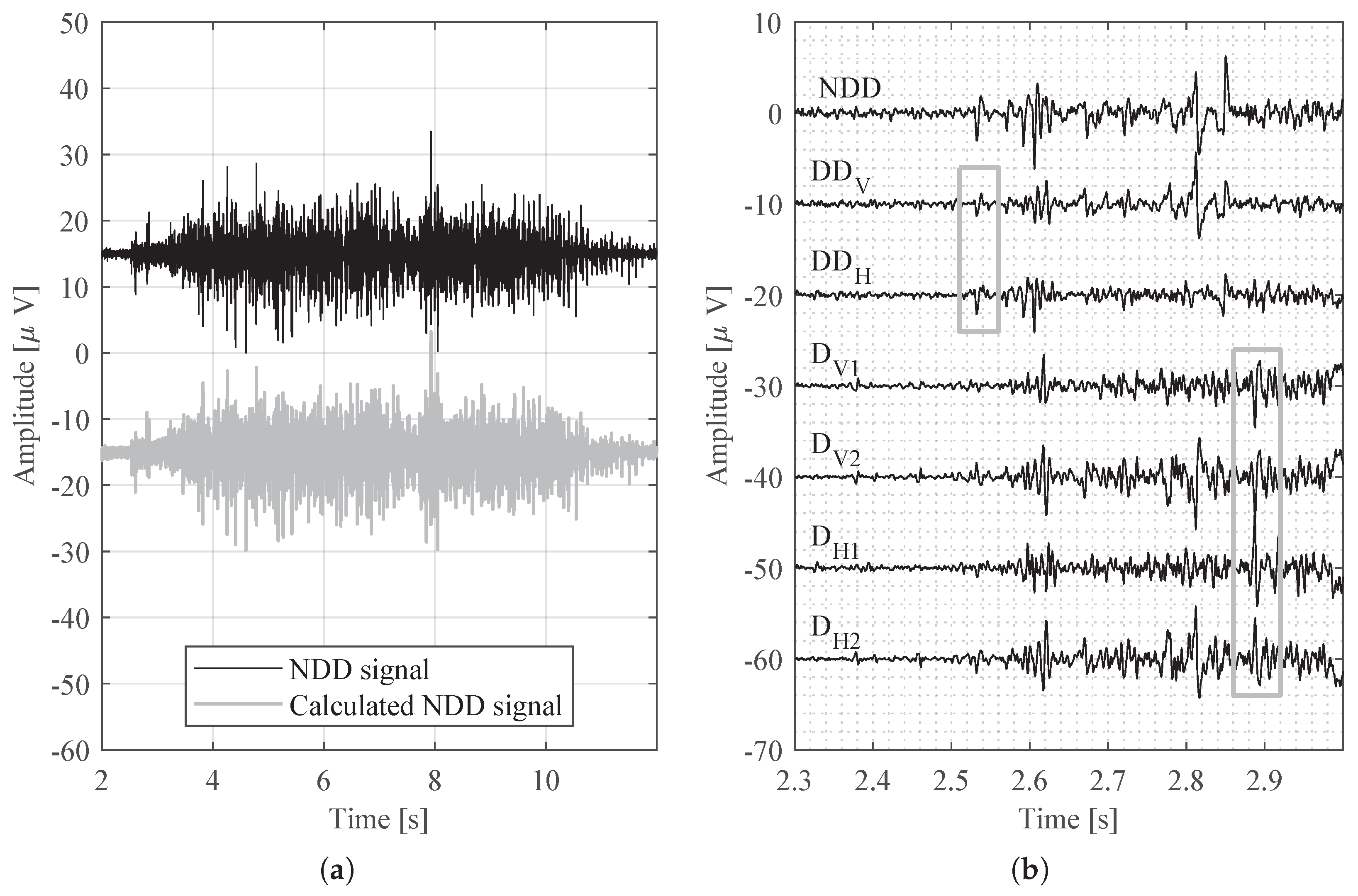
3. Measurement Results
4. Final Remarks and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Casale, R.; Rainoldi, A. Fatigue and fibromyalgia syndrome: Clinical and neurophysiologic pattern. Best Pract. Res. Clin. Rheumatol. 2011, 25, 241–247. [Google Scholar] [CrossRef] [PubMed]
- Jarque-Bou, N.J.; Sancho-Bru, J.L.; Vergara, M. A Systematic Review of EMG Applications for the Characterization of Forearm and Hand Muscle Activity during Activities of Daily Living: Results, Challenges, and Open Issues. Sensors 2021, 21, 3035. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Wu, Z.; Zhao, R.; Ni, Y.; Jing, X.; Gao, S. A Review of EMG-, FMG-, and EIT-Based Biosensors and Relevant Human–Machine Interactivities and Biomedical Applications. Biosensors 2022, 12, 516. [Google Scholar] [CrossRef] [PubMed]
- Zhao, N.; Zhao, B.; Shen, G.; Jiang, C.; Wang, Z.; Lin, Z.; Zhou, L.; Liu, J. A robust HD-sEMG sensor suitable for convenient acquisition of muscle activity in clinical post-stroke dysphagia. J. Neural Eng. 2022, 20, 016018. [Google Scholar] [CrossRef] [PubMed]
- Lara, J.E.; Cheng, L.K.; Röhrle, O.; Paskaranandavadivel, N. Muscle-specific high-density electromyography arrays for hand gesture classification. IEEE Trans. Biomed. Eng. 2021, 69, 1758–1766. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, J.; Boyd, W.J.; Martinez-Luna, C.; Dai, C.; Wang, H.; Wang, H.; Huang, X.; Farrell, T.R.; Clancy, E.A. Myoelectric Control Performance of Two Degree of Freedom Hand-Wrist Prosthesis by Able-Bodied and Limb-Absent Subjects. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 893–904. [Google Scholar] [CrossRef]
- Wang, H.; Zuo, S.; Cerezo-Sanchez, M.; Arekhloo, N.G.; Nazarpour, K.; Heidari, H. Wearable super-resolution muscle–machine interfacing. Front. Neurosci. 2022, 16, 1020546. [Google Scholar] [CrossRef]
- Campanini, I.; Merlo, A.; Disselhorst-Klug, C.; Mesin, L.; Muceli, S.; Merletti, R. Fundamental Concepts of Bipolar and High-Density Surface EMG Understanding and Teaching for Clinical, Occupational, and Sport Applications: Origin, Detection, and Main Errors. Sensors 2022, 22, 4150. [Google Scholar] [CrossRef]
- Farina, D.; Arendt-Nielsen, L.; Merletti, R.; Indino, B.; Graven-Nielsen, T. Selectivity of spatial filters for surface EMG detection from the tibialis anterior muscle. IEEE Trans. Biomed. Eng. 2003, 50, 354–364. [Google Scholar] [CrossRef]
- Dimitrov, G.V.; Disselhorst-Klug, C.; Dimitrova, N.a.; Schulte, E.; Rau, G. Simulation analysis of the ability of different types of multi-electrodes to increase selectivity of detection and to reduce cross-talk. J. Electromyogr. Kinesiol. 2003, 13, 125–138. [Google Scholar] [CrossRef]
- Germer, C.M.; Farina, D.; Elias, L.A.; Nuccio, S.; Hug, F.; Del Vecchio, A. Surface EMG cross talk quantified at the motor unit population level for muscles of the hand, thigh, and calf. J. Appl. Physiol. 2021, 131, 808–820. [Google Scholar] [CrossRef] [PubMed]
- Prasad, S.; Paulin, M.; Cannon, R.D.; Palla, S.; Farella, M. Smartphone-assisted monitoring of masticatory muscle activity in freely moving individuals. Clin. Oral Investig. 2019, 23, 3601–3611. [Google Scholar] [CrossRef]
- Zadeh, S.M.; MacDermid, J.; Johnson, J.; Birmingham, T.B.; Shafiee, E. Applications of wearable sensors in upper extremity MSK conditions: A scoping review. J. NeuroEng. Rehabil. 2023, 20, 158. [Google Scholar] [CrossRef]
- Alizadeh-Meghrazi, M.; Sidhu, G.; Jain, S.; Stone, M.; Eskandarian, L.; Toossi, A.; Popovic, M.R. A Mass-Producible Washable Smart Garment with Embedded Textile EMG Electrodes for Control of Myoelectric Prostheses: A Pilot Study. Sensors 2022, 22, 666. [Google Scholar] [CrossRef]
- Kinugasa, R.; Kubo, S. Development of Consumer-Friendly surface electromyography system for muscle fatigue detection. IEEE Access 2023, 11, 6394–6403. [Google Scholar] [CrossRef]
- Tam, S.; Bilodeau, G.; Brown, J.; Gagnon-Turcotte, G.; Campeau-Lecours, A.; Gosselin, B. A Wearable Wireless Armband Sensor for High-Density Surface Electromyography Recording. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 6040–6044. [Google Scholar] [CrossRef]
- Reis Carneiro, M.; Majidi, C.; Tavakoli, M. Multi-Electrode Printed Bioelectronic Patches for Long-Term Electrophysiological Monitoring. Adv. Funct. Mater. 2022, 32, 2205956. [Google Scholar] [CrossRef]
- Al-Ayyad, M.; Owida, H.A.; De Fazio, R.; Al-Naami, B.; Visconti, P. Electromyography Monitoring Systems in Rehabilitation: A Review of Clinical Applications, Wearable Devices and Signal Acquisition Methodologies. Electronics 2023, 12, 1520. [Google Scholar] [CrossRef]
- Lee, S.; Yoon, J.; Lee, D.; Seong, D.; Lee, S.; Jang, M.; Choi, J.; Yu, K.J.; Kim, J.; Lee, S.; et al. Wireless Epidermal Electromyogram Sensing System. Electronics 2020, 9, 269. [Google Scholar] [CrossRef]
- Kawano, T.; Koganezawa, K. A method of discriminating fingers and wrist action from surface EMG signals for controlling robotic or prosthetic forearm hand. In Proceedings of the 2016 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Banff, AB, Canada, 12–15 July 2016; IEEE: Banff, AB, Canada, 2016; pp. 13–18. [Google Scholar] [CrossRef]
- Pizzolato, S.; Tagliapietra, L.; Cognolato, M.; Reggiani, M.; Müller, H.; Atzori, M. Comparison of six electromyography acquisition setups on hand movement classification tasks. PLoS ONE 2017, 12, e0186132. [Google Scholar] [CrossRef]
- Garcia-Casado, J.; Ye-Lin, Y.; Prats-Boluda, G.; Makeyev, O. Evaluation of Bipolar, Tripolar, and Quadripolar Laplacian Estimates of Electrocardiogram via Concentric Ring Electrodes. Sensors 2019, 19, 3780. [Google Scholar] [CrossRef]
- Catacora, V.A.; Guerrero, F.N.; Spinelli, E.M. Three-Electrode Double-Differential Biopotential Amplifier for Surface EMG Measurements. IEEE Trans. Instrum. Meas. 2023, 72, 2003508. [Google Scholar] [CrossRef]
- Samani, A.; Srinivasan, D.; Mathiassen, S.E.; Madeleine, P. Variability in spatio-temporal pattern of trapezius activity and coordination of hand-arm muscles during a sustained repetitive dynamic task. Exp. Brain Res. 2017, 235, 389–400. [Google Scholar] [CrossRef] [PubMed]
- Messaoudi, N.; Bekka, R.E.; Belkacem, S. Classification of the Systems Used in Surface Electromyographic Signal Detection according to the Degree of Isotropy. Adv. Biomed. Eng. 2018, 7, 107–116. [Google Scholar] [CrossRef]
- Guerrero, F.N.; Spinelli, E.M.; Grasso, A.D.; Palumbo, G. Double-Differential Amplifier for sEMG Measurement by Means of a Current-Mode Approach. IEEE Access 2022, 10, 45870–45880. [Google Scholar] [CrossRef]
- Smith, K.C.; Sedra, A. The Current Conveyor*—A New Circuit Building Block. Proc. IEEE 1968, 56, 1368–1369. [Google Scholar] [CrossRef]
- Sedra, A.; Smith, K.C. A Second-Generation Current Conveyor and Its Applications. IEEE Trans. Circuit Theory 1970, 17, 132–134. [Google Scholar] [CrossRef]
- Huhta, J.C.; Webster, J.G. 60-HZ interference in electrocardiography. IEEE Trans. Bio-Med Eng. 1973, 20, 91–101. [Google Scholar] [CrossRef]
- Guerrero, F.N.; Spinelli, E.M.; Haberman, M.A. Analysis and simple circuit design of double differential EMG active electrode. IEEE Trans. Biomed. Circuits Syst. 2015, 10, 787–795. [Google Scholar] [CrossRef] [PubMed]
- Koli, K.; Halonen, K.A. CMRR enhancement techniques for current-mode instrumentation amplifiers. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 622–632. [Google Scholar] [CrossRef]
- Pu, J.; Ma, K.; Luo, Y.; Tang, S.; Liu, T.; Liu, J.; Leung, M.; Yang, J.; Hui, R.; Xiong, Y.; et al. Textile electronics for wearable applications. Int. J. Extrem. Manuf. 2023, 5, 042007. [Google Scholar] [CrossRef]
- Kim, J.; Ouh, H.; Johnston, M.L. A 43.8 μW per Channel Biopotential Readout System using Frequency Division Multiplexing with Cable Motion Artifact Suppression. In Proceedings of the 2020 IEEE Custom Integrated Circuits Conference (CICC), Boston, MA, USA, 22–25 March 2020; IEEE: Piscateville, NJ, USA, 2020; Volume 2020-March, pp. 1–4. [Google Scholar]
- Hsu, Y.P.; Liu, Z.; Hella, M.M. A -68 dB THD, 0.6 mm2 Active Area Biosignal Acquisition System with a 40-320 Hz Duty-Cycle Controlled Filter. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 48–59. [Google Scholar] [CrossRef]
- Fath, P.; Pretl, H. A 370-nW Quad-Channel Multi-Mode Bio-Signal Acquisition AFE with 2.9-μVrms Input Noise. In Proceedings of the 2023 IEEE Nordic Circuits and Systems Conference (NorCAS), Aalborg, Denmark, 31 October–1 November 2023; IEEE: Piscateville, NJ, USA, 2023; pp. 1–5. [Google Scholar]
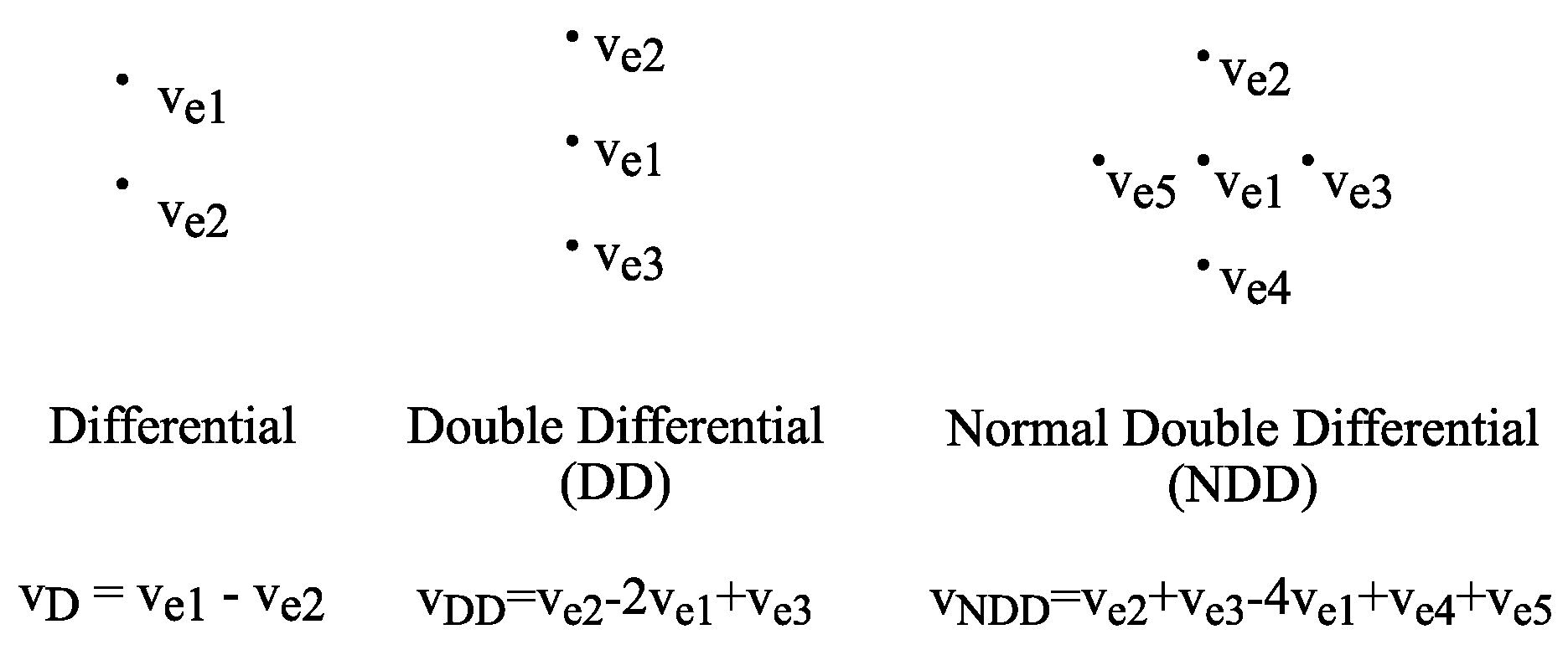



| Component Selection | Parameters | ||
|---|---|---|---|
| 2 × OPA4243 | DD Gain | 27.9 dB | |
| , | 1 , 10 | Bandwidth | 12–578 Hz |
| 1 | RTI noise 30–450 | rms | |
| , | 125 , | CMRR @ 50 Hz | 95.6 dB |
| DC Input range | Rail-to-Rail | ||
| Supply | 326 , 5 or | ||
| Key | CICC’20 [33] | TCAS-I’20 [34] | NorCAS’23 [35] | This Work |
|---|---|---|---|---|
| Type * | D EMG/ECG | D EMG | 4 ch. ExG | NDD EMG |
| Implementation | ASIC | ASIC | ASIC | Discrete |
| Noise [] | 3.52 | 3.45 | 4.2 | 3.7 |
| CMRR [dB] | N/A | 112 | 81.6 | 95.6 |
| Bandwidth [Hz] | 1–150 | 40–320 | 0.2–512 | 12–578 |
| Gain [dB] | 35 | 43–55 | 19.9–53.1 | 27.9 |
| Supply | V | 2 V | 1 V | V |
| 326 | ||||
| Input impedance | N/A | N/A | 216 @ 10 Hz | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerrero, F.N.; Catacora, V.A.; Grasso, A.D.; Palumbo, G. Multi-Electrode EMG Spatial-Filter Implementation Based on Current Conveyors. Electronics 2024, 13, 1735. https://doi.org/10.3390/electronics13091735
Guerrero FN, Catacora VA, Grasso AD, Palumbo G. Multi-Electrode EMG Spatial-Filter Implementation Based on Current Conveyors. Electronics. 2024; 13(9):1735. https://doi.org/10.3390/electronics13091735
Chicago/Turabian StyleGuerrero, Federico N., Valentín A. Catacora, Alfio Dario Grasso, and Gaetano Palumbo. 2024. "Multi-Electrode EMG Spatial-Filter Implementation Based on Current Conveyors" Electronics 13, no. 9: 1735. https://doi.org/10.3390/electronics13091735
APA StyleGuerrero, F. N., Catacora, V. A., Grasso, A. D., & Palumbo, G. (2024). Multi-Electrode EMG Spatial-Filter Implementation Based on Current Conveyors. Electronics, 13(9), 1735. https://doi.org/10.3390/electronics13091735









