Research on Frequency Discrimination Method Using Multiplicative-Integral and Linear Transformation Network
Abstract
:1. Introduction
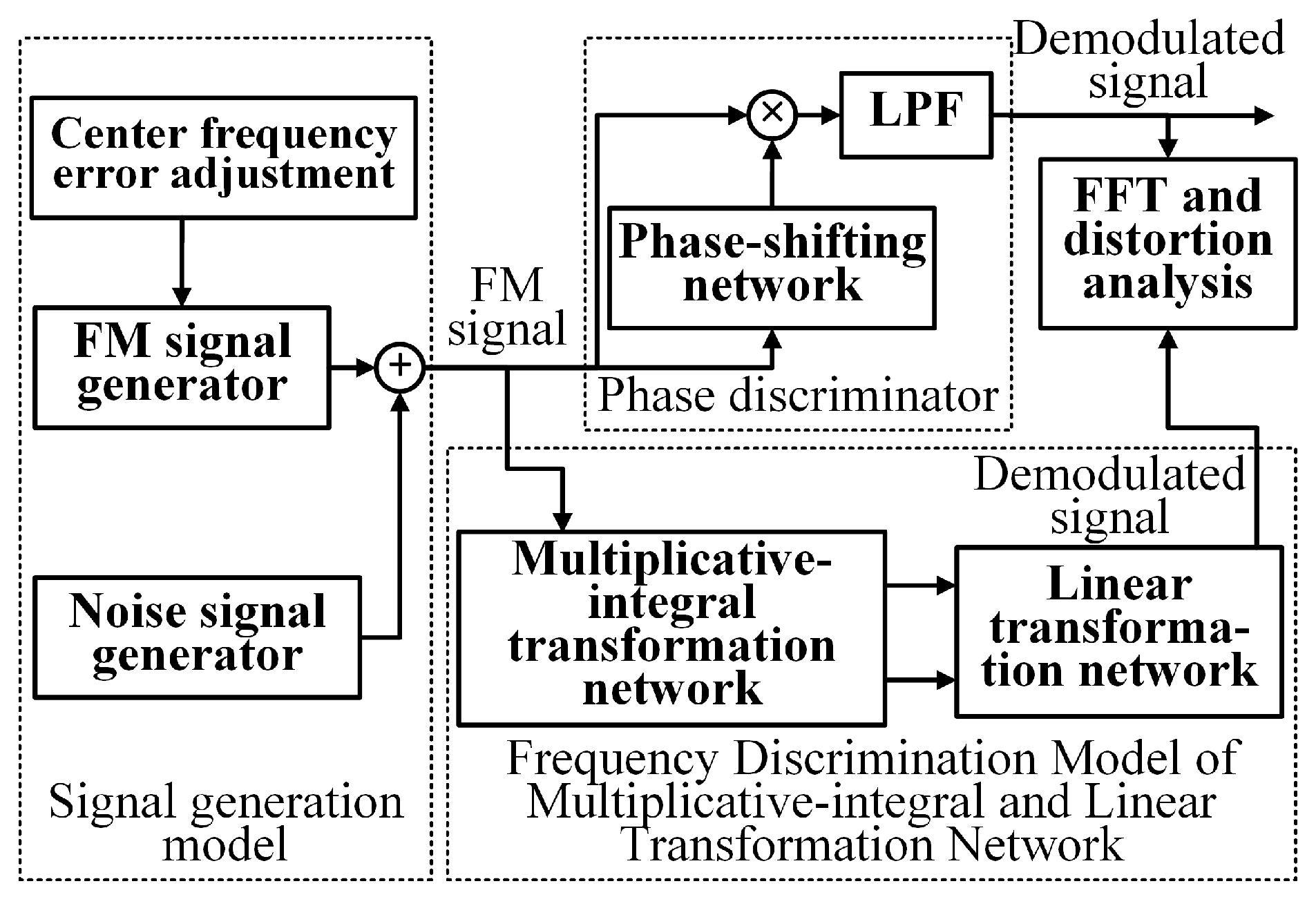
2. Theory
2.1. Multiplicative-Integral Transformation Network
2.2. Linear Transformation Network
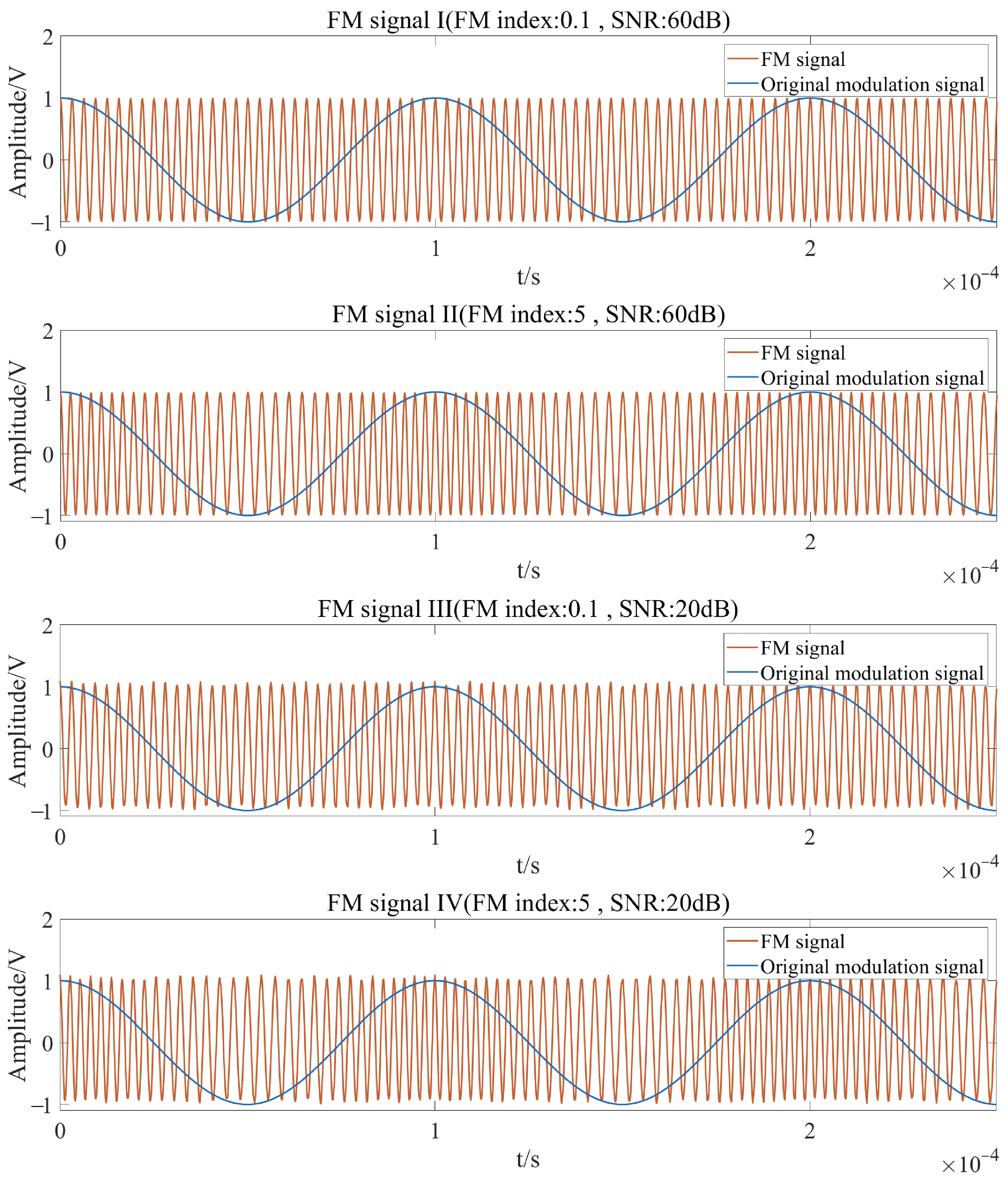
3. Design of Simulation
4. Simulation and Discussion
4.1. Discussion on Frequency Discrimination Bandwidth
4.2. Influence of Carrier Center Frequency Error
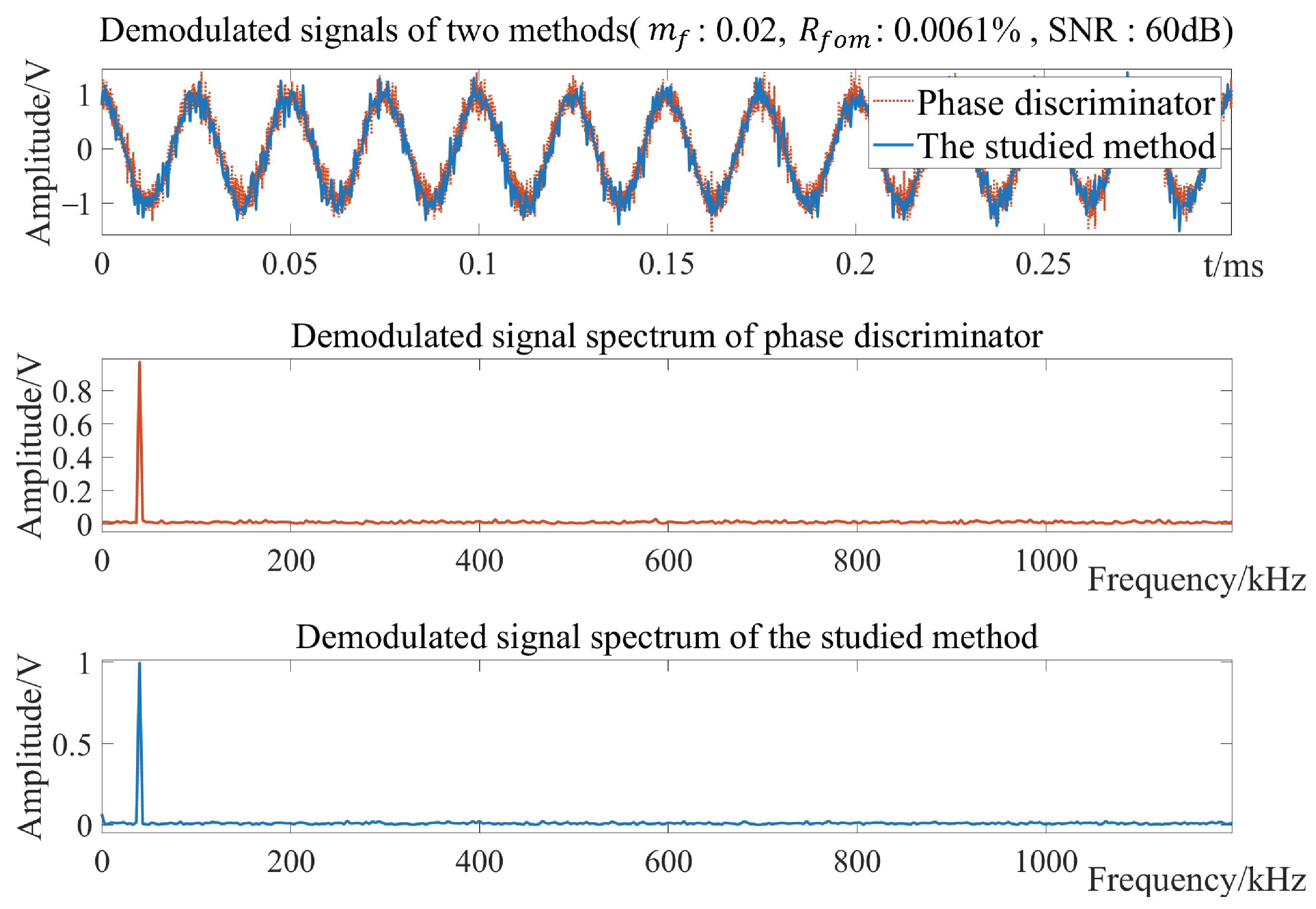
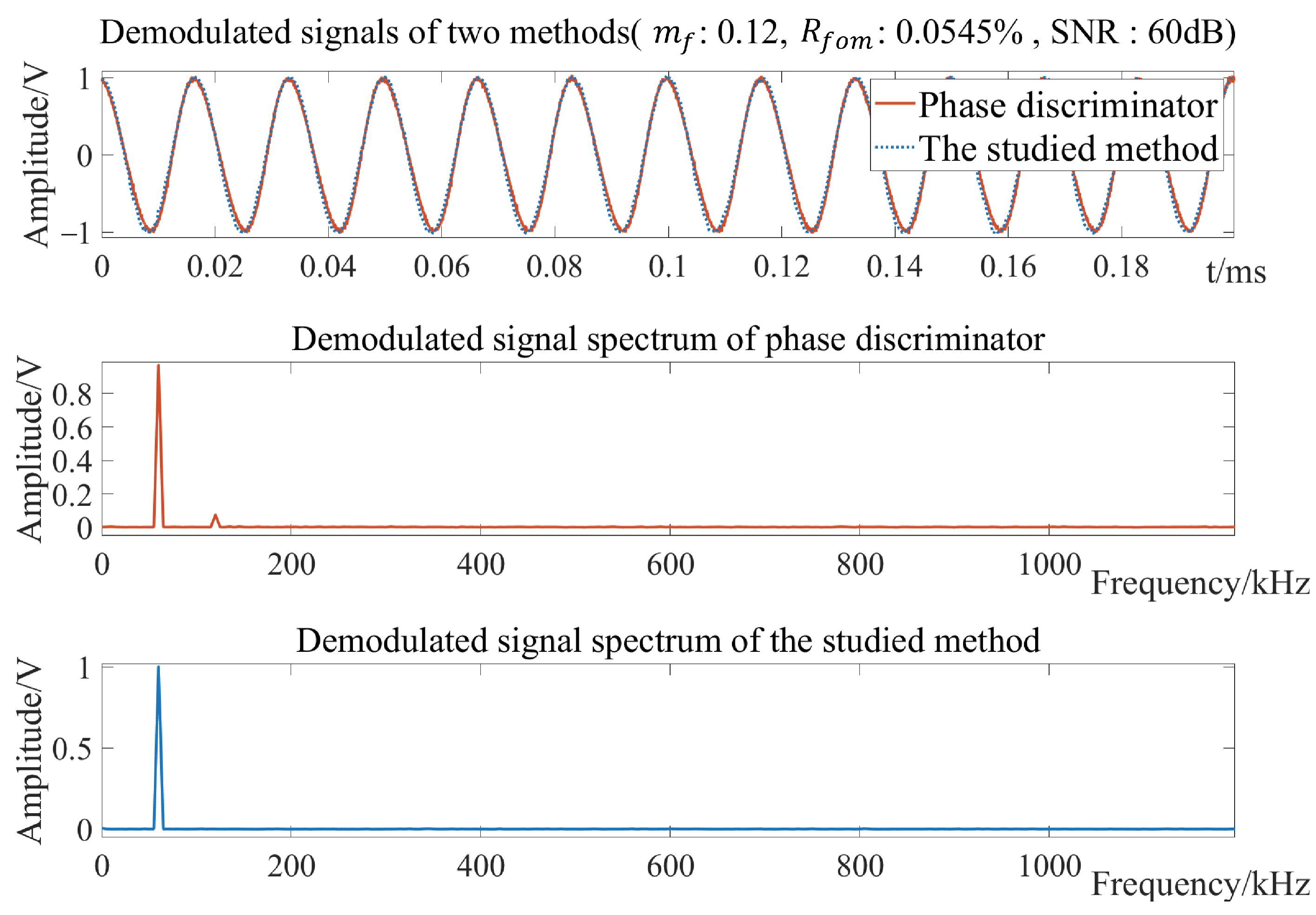
4.3. Anti-Noise Performance Analysis
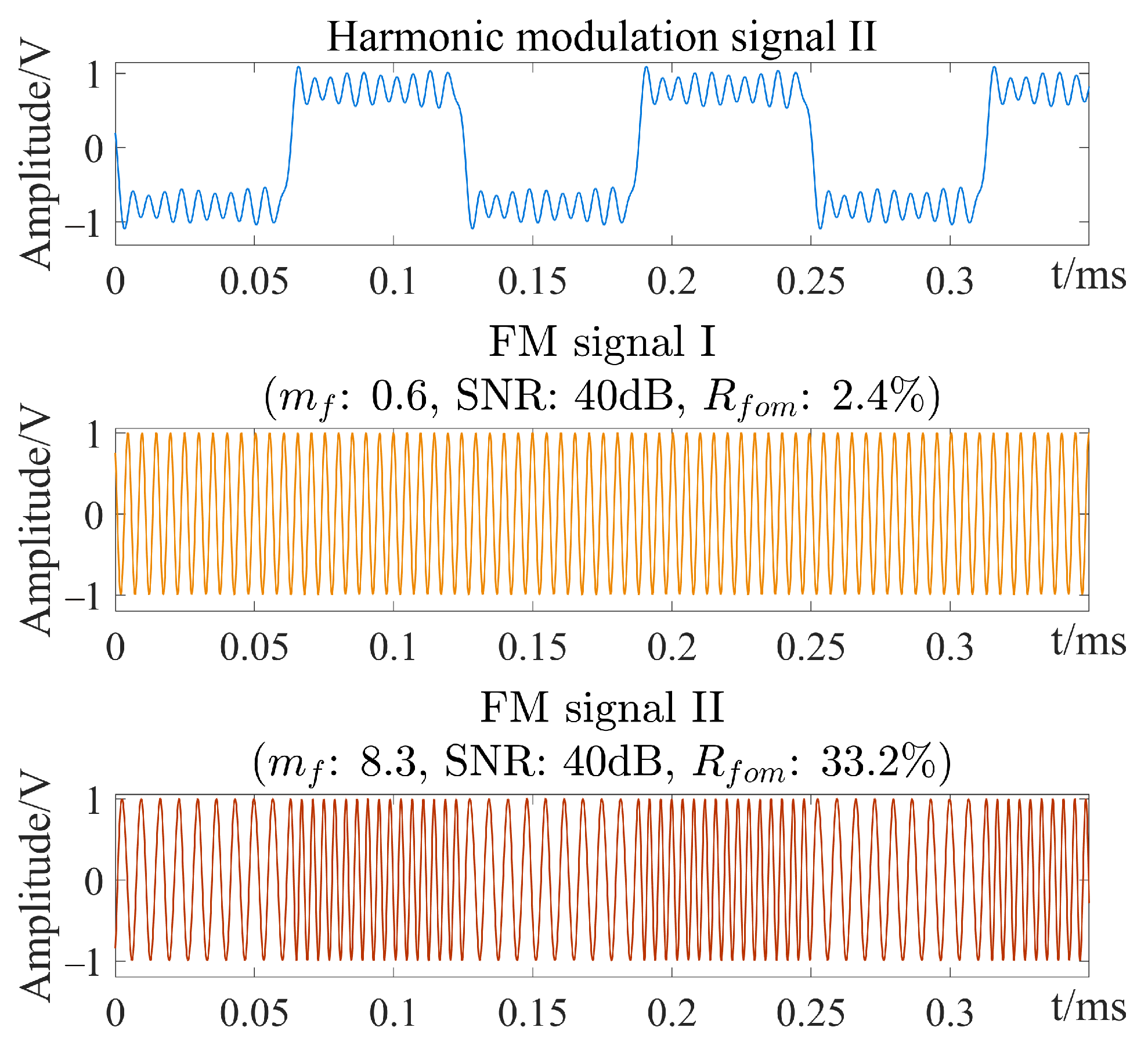
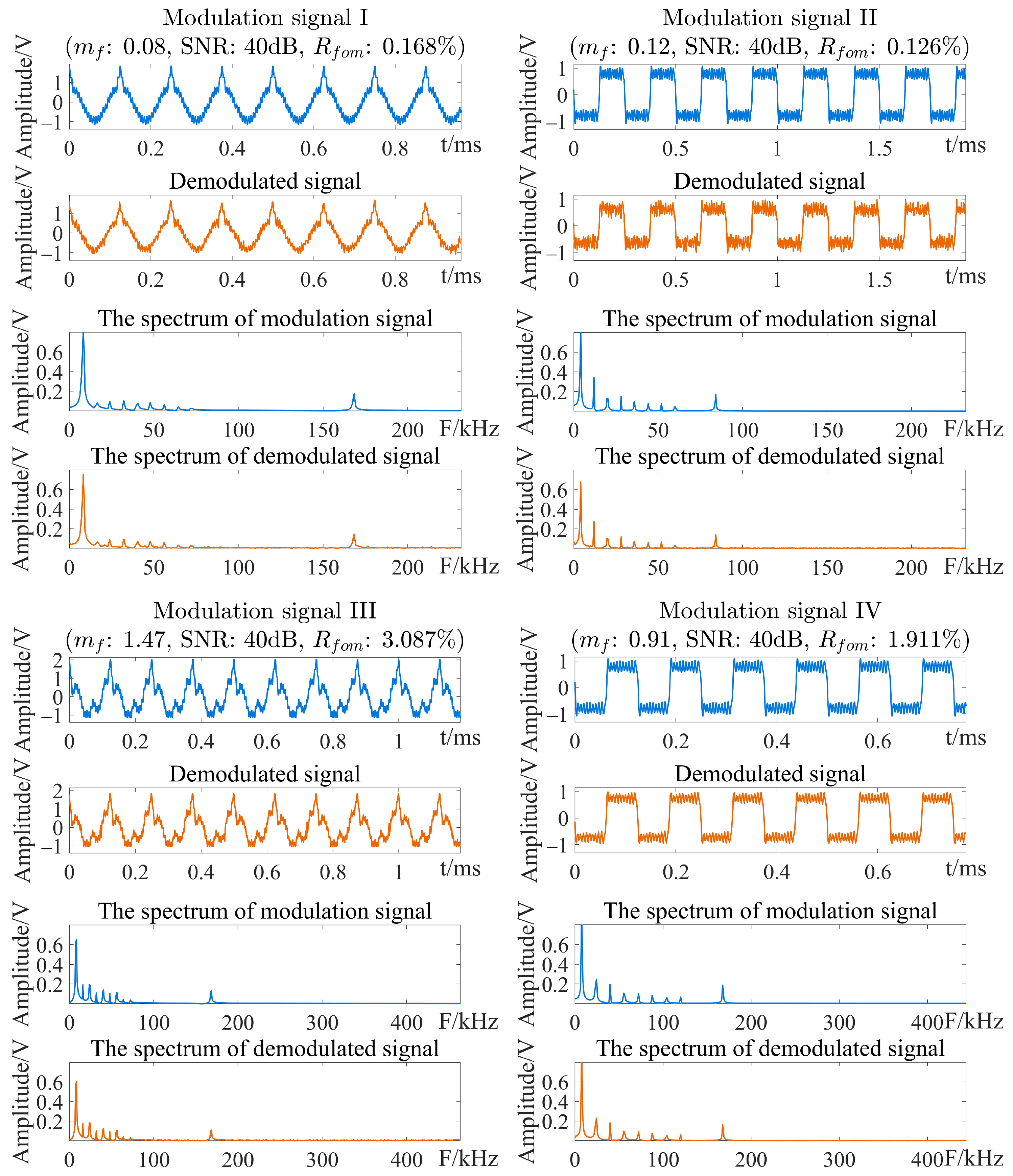
4.4. Frequency Discrimination Performance of FM Signal Modulated with Harmonic Signal
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FM | Frequency Modulation |
| SNR | Signal-to-Noise Ratio |
| AM | Amplitude Modulation |
| AC | Alternating Current |
| LPF | Low Pass Filter |
| FFT | Fast Fourier Transform |
| FDD | Frequency Discrimination Distortion |
| PD | Phase Discriminator |
References
- Hu, Z.; Li, S.; Xiang, Y. Time Information Transmission Based on FM Broadcast Signal. IEEE Access 2021, 9, 16360–16364. [Google Scholar] [CrossRef]
- Pound, R.V. Electronic Frequency Stabilization of Microwave Oscillators. Rev. Sci. Instrum. 2004, 17, 490. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Chen, X.; Men, A.; Zhang, L.; Wu, S. Carrier Frequency Offset Estimation for FM and Symbiotic FM Radio Data System Hybrid Signal. China Commun. 2020, 17, 129–139. [Google Scholar] [CrossRef]
- Foster, D.E.; Seeley, S.W. Automatic Tuning, Simplified Circuits, and Design Practice. Proc. IEEE 1937, 25, 289–313. [Google Scholar] [CrossRef]
- Sotner, R.; Polak, L.; Jerabek, J.; Petrzela, J.; Kledrowetz, V. Analog Multipliers-Based Double Output Voltage Phase Detector for Low-Frequency Demodulation of Frequency Modulated Signals. IEEE Access 2021, 9, 93062–93078. [Google Scholar] [CrossRef]
- Salzenstein, P.; Wu, T.Y. Uncertainty analysis for a phase-detector based phase noise measurement system. Measurement 2016, 85, 118–123. [Google Scholar] [CrossRef]
- Carr, J.; Frank, B. Static Phase Offset in a Multiplying Phase Detector. IEEE Microw. Wirel. Components Lett. 2009, 19, 518–520. [Google Scholar] [CrossRef]
- Andersson, S. Frequency-discriminator-stabilized oscillators with common resonators. Microw. Opt. Technol. Lett. 1999, 21, 417–423. [Google Scholar] [CrossRef]
- Hamdan, A.; Ros, L.; Hijazi, H.; Siclet, C.; Al-Ghouwayel, A. On multi-carrier systems robustness to Doppler in fast varying flat fading wireless channel. Digit. Signal Process. 2021, 117, 103189. [Google Scholar] [CrossRef]
- Robson, S.; Tan, G.; Haddad, A. Low-Cost Monitoring of Synchrophasors Using Frequency Modulation. Energies 2019, 12, 611. [Google Scholar] [CrossRef]
- Nakhostin, M. Digital discrimination of neutrons and γ-rays in liquid scintillation detectors by using low sampling frequency ADCs. Nuclear Instrum. Methods Phys. Res. Sect. A 2018, 916, 66–70. [Google Scholar] [CrossRef]


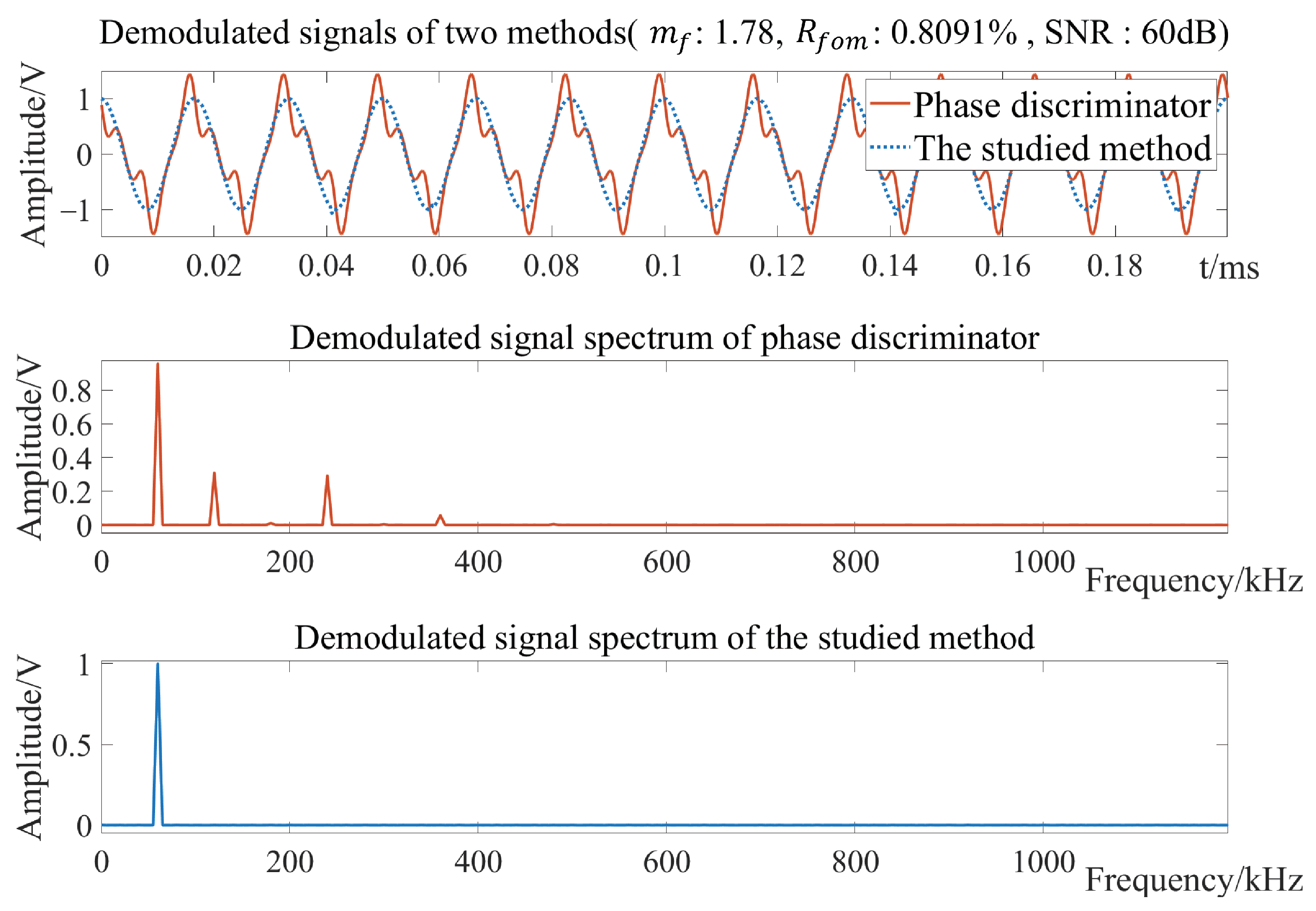

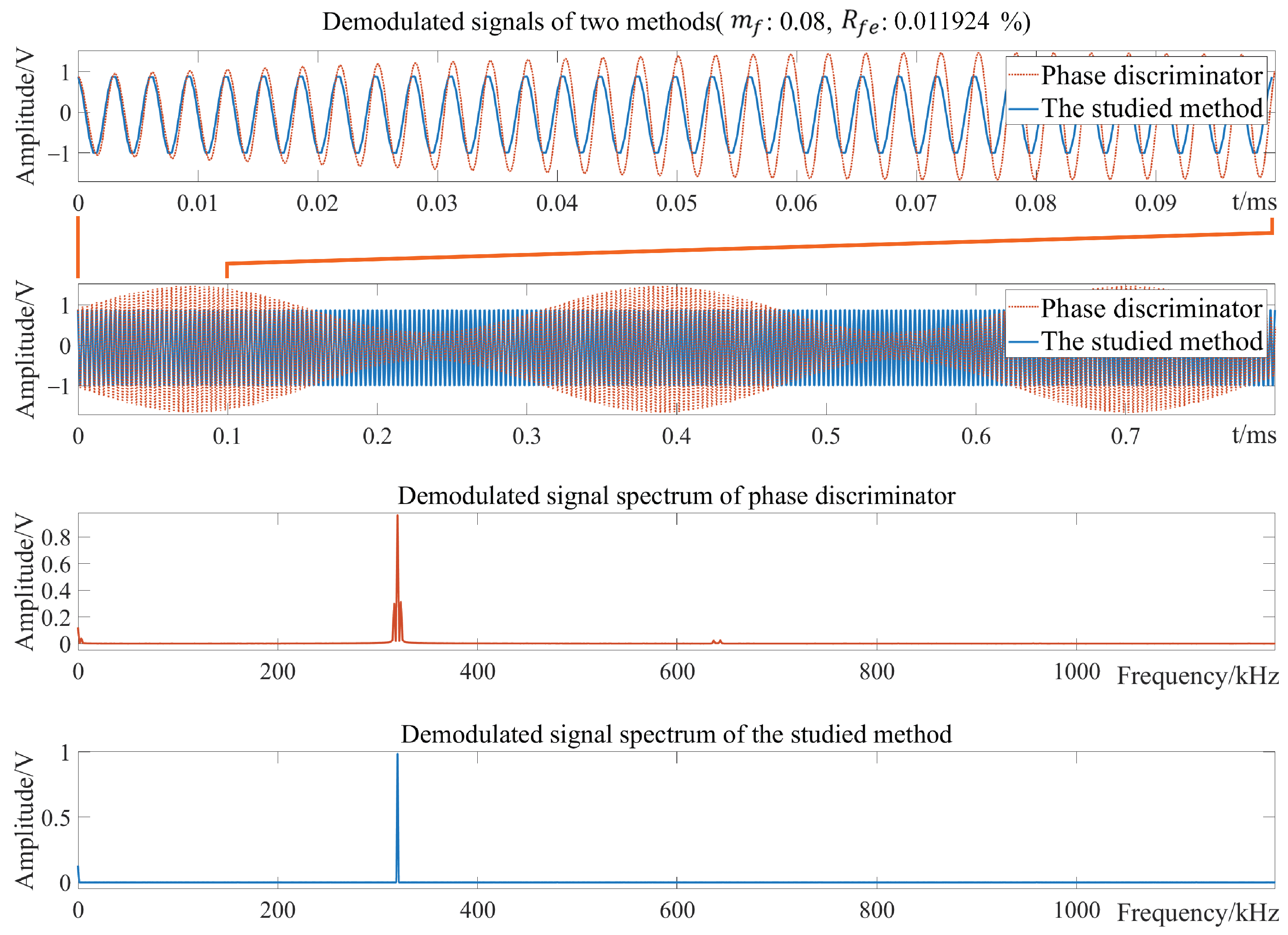
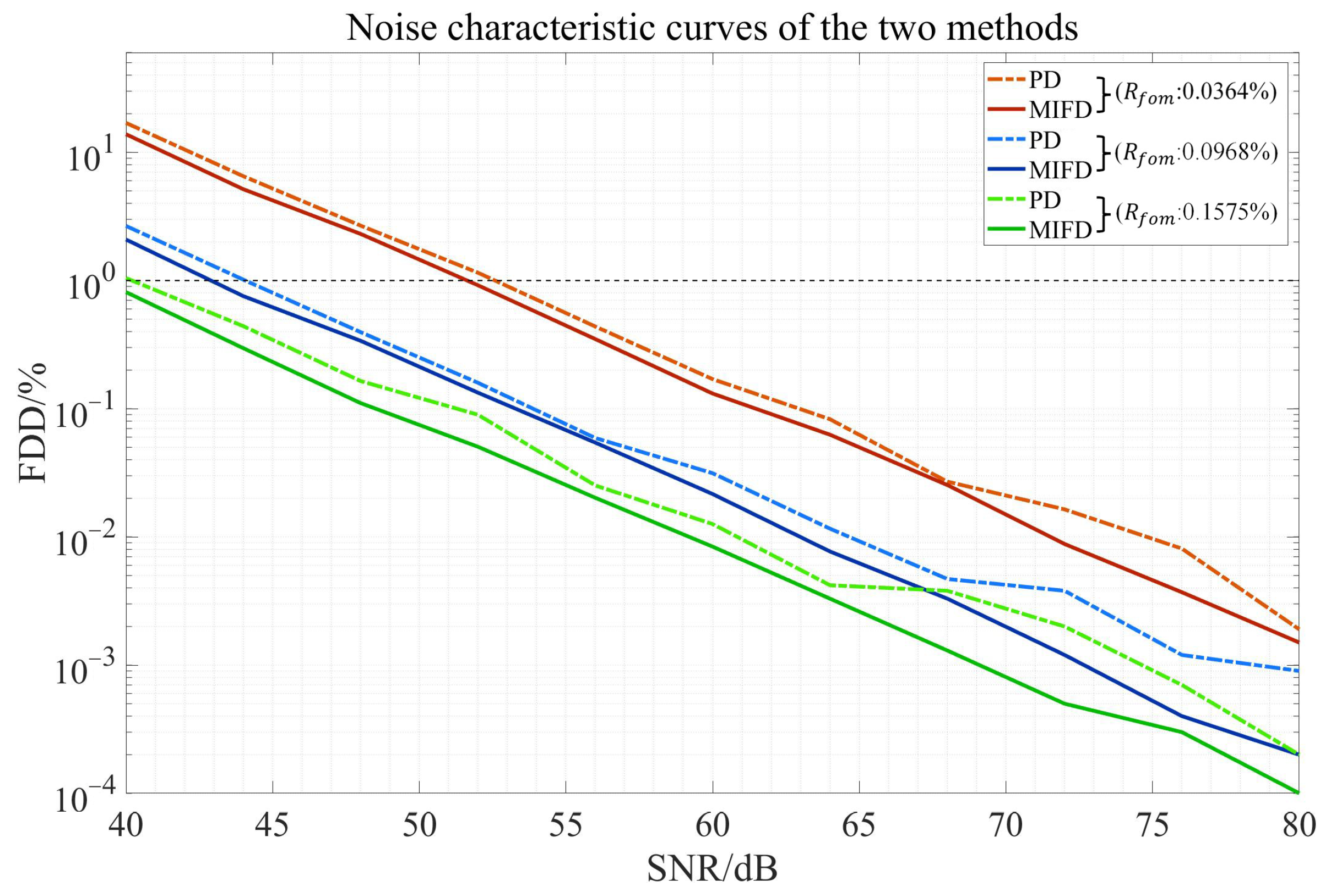
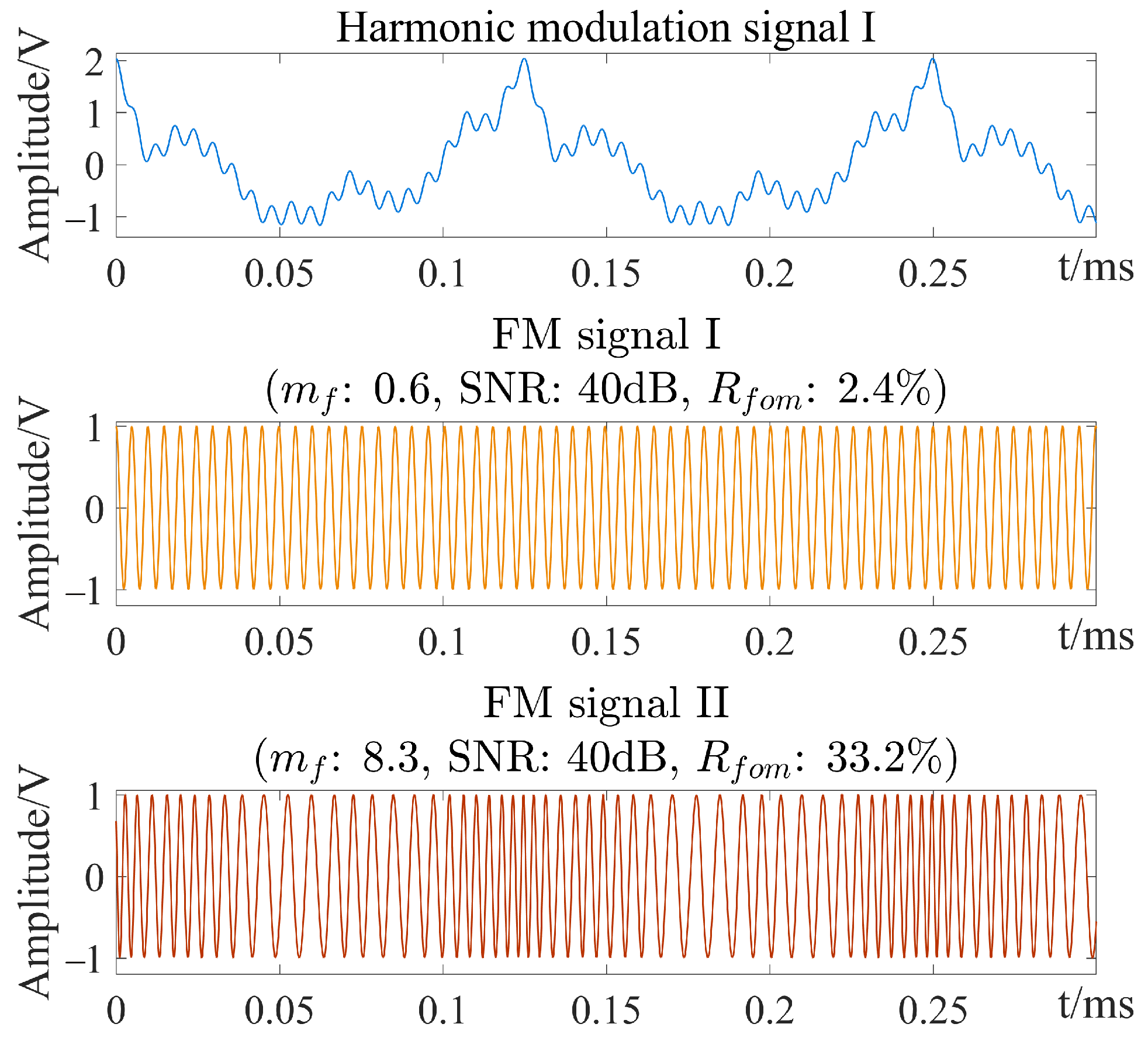
| Simulation Conditions | Value |
|---|---|
| (MHz) | 13.20 |
| Center frequency error rate (%) | 0.00 |
| (V) | 1.00 |
| (V) | 1.00 |
| SNR (dB) | 60.00 |
| (MHz) | 3.20 |
| (MHz) | 12.80 |
| 4 | |
| (MHz) | 19.20 |
| 6 |
| FDD (%) When : (kHz) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 60 | 100 | 140 | 180 | 220 | 260 | 300 | 340 | 380 | |
| 0.01 | 81.3420 | 12.1644 | 4.1555 | 2.1753 | 1.2260 | 0.8721 | 0.6449 | 0.4163 | 0.3610 | 0.2968 |
| 0.02 | 22.0443 | 3.1011 | 1.0379 | 0.5601 | 0.3197 | 0.2389 | 0.1174 | 0.1274 | 0.1015 | 0.0836 |
| 0.04 | 6.5478 | 0.7884 | 0.3101 | 0.1947 | 0.1382 | 0.1069 | 0.1037 | 0.0885 | 0.0858 | 0.0822 |
| 0.06 | 3.2004 | 0.4515 | 0.2585 | 0.2077 | 0.1779 | 0.1646 | 0.1620 | 0.1556 | 0.1470 | 0.1478 |
| 0.08 | 1.8429 | 0.4476 | 0.3182 | 0.2792 | 0.2761 | 0.2769 | 0.2646 | 0.2613 | 0.2615 | 0.2480 |
| 0.10 | 1.4381 | 0.5256 | 0.4382 | 0.4234 | 0.3938 | 0.3937 | 0.3974 | 0.3969 | 0.3911 | 0.3898 |
| 0.12 | 1.1220 | 0.6643 | 0.6082 | 0.5729 | 0.5714 | 0.5556 | 0.5634 | 0.5572 | 0.5629 | 0.5600 |
| 0.14 | 1.3030 | 0.8244 | 0.7623 | 0.7655 | 0.7581 | 0.7614 | 0.7661 | 0.7572 | 0.7587 | 0.7549 |
| 0.16 | 1.2671 | 1.0099 | 0.9828 | 0.9927 | 1.0021 | 0.9808 | 0.9811 | 0.9892 | 0.9849 | 0.9809 |
| 0.18 | 1.5830 | 1.2902 | 1.2573 | 1.2487 | 1.2429 | 1.2414 | 1.2319 | 1.2389 | 1.2350 | 1.2351 |
| 0.20 | 1.8795 | 1.5234 | 1.5385 | 1.5362 | 1.5252 | 1.5192 | 1.5211 | 1.5221 | 1.5172 | 1.5182 |
| 0.22 | 2.0561 | 1.8592 | 1.8511 | 1.8261 | 1.8256 | 1.8263 | 1.8263 | 1.8225 | 1.8221 | 1.8215 |
| 0.24 | 2.3010 | 2.2072 | 2.1740 | 2.1615 | 2.1591 | 2.1610 | 2.1605 | 2.1526 | 2.1479 | 2.1470 |
| 0.26 | 2.6320 | 2.5396 | 2.5279 | 2.5153 | 2.5126 | 2.5063 | 2.5079 | 2.5090 | 2.5028 | 2.4994 |
| 0.28 | 2.9929 | 2.9035 | 2.9050 | 2.8988 | 2.8933 | 2.8803 | 2.8790 | 2.8837 | 2.8803 | 2.8777 |
| 0.30 | 3.4357 | 3.3039 | 3.2824 | 3.2888 | 3.2797 | 3.2753 | 3.2797 | 3.2746 | 3.2757 | 3.2667 |
| 0.32 | 3.8156 | 3.7242 | 3.6952 | 3.7007 | 3.7004 | 3.6992 | 3.6940 | 3.6876 | 3.6834 | 3.6800 |
| 0.34 | 4.2917 | 4.1400 | 4.1623 | 4.1325 | 4.1428 | 4.1250 | 4.1311 | 4.1181 | 4.1174 | 4.1129 |
| 0.36 | 4.6026 | 4.6002 | 4.5885 | 4.5870 | 4.5917 | 4.5796 | 4.5738 | 4.5667 | 4.5554 | 4.5617 |
| FDD (%) When : (kHz) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 60 | 100 | 140 | 180 | 220 | 260 | 300 | 340 | 380 | |
| 0.01 | 63.8998 | 8.2775 | 3.1443 | 1.5245 | 0.9214 | 0.5704 | 0.4607 | 0.3094 | 0.2858 | 0.2216 |
| 0.02 | 18.3046 | 2.0716 | 0.8632 | 0.3889 | 0.2507 | 0.1600 | 0.1759 | 0.0864 | 0.0668 | 0.0576 |
| 0.04 | 4.9758 | 0.5482 | 0.1861 | 0.1030 | 0.0549 | 0.0414 | 0.0278 | 0.0227 | 0.0178 | 0.0156 |
| 0.06 | 2.0844 | 0.2649 | 0.0768 | 0.0465 | 0.0288 | 0.0193 | 0.0134 | 0.0117 | 0.0087 | 0.0083 |
| 0.08 | 1.3574 | 0.1388 | 0.0510 | 0.0234 | 0.0177 | 0.0107 | 0.0082 | 0.0062 | 0.0061 | 0.0056 |
| 0.10 | 0.8117 | 0.0994 | 0.0343 | 0.0183 | 0.0106 | 0.0083 | 0.0058 | 0.0050 | 0.0053 | 0.0056 |
| 0.12 | 0.5512 | 0.0686 | 0.0227 | 0.0132 | 0.0073 | 0.0063 | 0.0048 | 0.0043 | 0.0046 | 0.0045 |
| 0.14 | 0.5003 | 0.0492 | 0.0200 | 0.0122 | 0.0062 | 0.0048 | 0.0039 | 0.0044 | 0.0045 | 0.0062 |
| 0.16 | 0.4026 | 0.0378 | 0.0142 | 0.0081 | 0.0061 | 0.0046 | 0.0040 | 0.0044 | 0.0051 | 0.0073 |
| 0.18 | 0.3182 | 0.0342 | 0.0141 | 0.0062 | 0.0048 | 0.0032 | 0.0050 | 0.0064 | 0.0087 | 0.0077 |
| 0.20 | 0.2394 | 0.0265 | 0.0116 | 0.0065 | 0.0041 | 0.0042 | 0.0046 | 0.0053 | 0.0073 | 0.0105 |
| 0.22 | 0.3063 | 0.0287 | 0.0096 | 0.0053 | 0.0036 | 0.0043 | 0.0054 | 0.0065 | 0.0096 | 0.0133 |
| 0.24 | 0.2748 | 0.0257 | 0.0095 | 0.0062 | 0.0042 | 0.0047 | 0.0061 | 0.0089 | 0.0118 | 0.0183 |
| 0.26 | 0.1908 | 0.0251 | 0.0100 | 0.0074 | 0.0043 | 0.0050 | 0.0085 | 0.0105 | 0.0155 | 0.0220 |
| 0.28 | 0.2413 | 0.0251 | 0.0109 | 0.0052 | 0.0064 | 0.0061 | 0.0098 | 0.0146 | 0.0197 | 0.0299 |
| 0.30 | 0.2716 | 0.0284 | 0.0128 | 0.0076 | 0.0072 | 0.0083 | 0.0122 | 0.0199 | 0.0266 | 0.0418 |
| 0.32 | 0.3409 | 0.0361 | 0.0120 | 0.0090 | 0.0074 | 0.0114 | 0.0175 | 0.0287 | 0.0393 | 0.0583 |
| 0.34 | 0.5393 | 0.0424 | 0.0216 | 0.0131 | 0.0108 | 0.0180 | 0.0256 | 0.0421 | 0.0594 | 0.0855 |
| 0.36 | 0.8031 | 0.0844 | 0.0517 | 0.0254 | 0.0230 | 0.0284 | 0.0449 | 0.0690 | 0.0970 | 0.1403 |
| Simulation Conditions | Value |
|---|---|
| (MHz) | 13.20 |
| (V) | 1.00 |
| 0.08 | |
| Maximum frequency offset ratio | 0.1939% |
| (V) | 1.00 |
| SNR (dB) | 60.00 |
| (MHz) | 3.2 |
| (MHz) | 12.8 |
| 4 | |
| 19.2 | |
| 6 |
| (%) | FDD of PD (%) | Relative Error (%) | FDD of MIFD (%) | Relative Error (%) | () (%) | FDD of PD (%) | Relative Error (%) | FDD of MIFD (%) | Relative Error (%) |
|---|---|---|---|---|---|---|---|---|---|
| 0.000000 | 0.2570 | 0.00 | 0.0061 | 0.00 | 0.007492 | 1.4790 | 476.20 | 0.0062 | 1.64 |
| 0.000379 | 0.2960 | 15.40 | 0.0068 | 11.48 | 0.007727 | 1.5480 | 503.20 | 0.0062 | 1.64 |
| 0.000568 | 0.3540 | 37.80 | 0.0065 | 6.56 | 0.007962 | 1.6730 | 551.70 | 0.0067 | 9.84 |
| 0.000780 | 0.4380 | 70.60 | 0.0063 | 3.28 | 0.008197 | 1.8190 | 608.60 | 0.0064 | 4.92 |
| 0.000902 | 0.5030 | 95.90 | 0.0063 | 3.28 | 0.008432 | 2.0270 | 689.70 | 0.0059 | −3.28 |
| 0.001023 | 0.5580 | 117.50 | 0.0069 | 13.11 | 0.008667 | 2.2880 | 791.20 | 0.0062 | 1.64 |
| 0.001144 | 0.6230 | 142.50 | 0.0061 | 0.00 | 0.008902 | 2.5780 | 904.40 | 0.0068 | 11.48 |
| 0.001265 | 0.7010 | 173.10 | 0.0064 | 4.92 | 0.009136 | 2.9500 | 1049.00 | 0.0063 | 3.28 |
| 0.001386 | 0.7740 | 201.50 | 0.0057 | −6.56 | 0.009371 | 3.3750 | 1214.80 | 0.0063 | 3.28 |
| 0.001508 | 0.8530 | 232.30 | 0.0058 | −4.92 | 0.009606 | 3.8510 | 1400.40 | 0.0070 | 14.75 |
| 0.001629 | 0.9190 | 258.10 | 0.0064 | 4.92 | 0.009841 | 4.3830 | 1607.50 | 0.0073 | 19.67 |
| 0.001750 | 1.0020 | 290.30 | 0.0062 | 1.64 | 0.010076 | 4.9740 | 1837.70 | 0.0059 | −3.28 |
| 0.001871 | 1.0750 | 318.60 | 0.0071 | 16.39 | 0.010689 | 6.7600 | 2533.60 | 0.0063 | 3.28 |
| 0.001992 | 1.1520 | 348.90 | 0.0056 | −8.20 | 0.011311 | 8.9050 | 3368.90 | 0.0060 | −1.64 |
| 0.002114 | 1.2280 | 378.30 | 0.0064 | 4.92 | 0.011924 | 11.1530 | 4244.70 | 0.0061 | 0.00 |
| 0.002341 | 1.3610 | 430.10 | 0.0073 | 19.67 | 0.012545 | 13.4900 | 5155.00 | 0.0065 | 6.56 |
| 0.003902 | 1.8810 | 632.70 | 0.0063 | 3.28 | 0.013159 | 15.6030 | 5978.20 | 0.0061 | 0.00 |
| 0.005462 | 1.7010 | 562.60 | 0.0065 | 6.56 | 0.013780 | 17.3550 | 6660.70 | 0.0066 | 8.20 |
| 0.007023 | 1.4100 | 449.20 | 0.0061 | 0.00 | 0.014402 | 18.6480 | 7164.50 | 0.0069 | 13.11 |
| 0.007258 | 1.4330 | 458.30 | 0.0061 | 0.00 | 0.015015 | 19.3550 | 7439.90 | 0.0064 | 4.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Yan, S.; Li, X. Research on Frequency Discrimination Method Using Multiplicative-Integral and Linear Transformation Network. Electronics 2024, 13, 1742. https://doi.org/10.3390/electronics13091742
Wang P, Yan S, Li X. Research on Frequency Discrimination Method Using Multiplicative-Integral and Linear Transformation Network. Electronics. 2024; 13(9):1742. https://doi.org/10.3390/electronics13091742
Chicago/Turabian StyleWang, Pengcheng, Sen Yan, and Xiuhua Li. 2024. "Research on Frequency Discrimination Method Using Multiplicative-Integral and Linear Transformation Network" Electronics 13, no. 9: 1742. https://doi.org/10.3390/electronics13091742
APA StyleWang, P., Yan, S., & Li, X. (2024). Research on Frequency Discrimination Method Using Multiplicative-Integral and Linear Transformation Network. Electronics, 13(9), 1742. https://doi.org/10.3390/electronics13091742






