SpikeExplorer: Hardware-Oriented Design Space Exploration for Spiking Neural Networks on FPGA
Abstract
1. Introduction
2. Background
2.1. Network Architecture
2.2. Neuron Models
2.3. Training
2.4. Automatic Design Space Exploration
3. Related Works
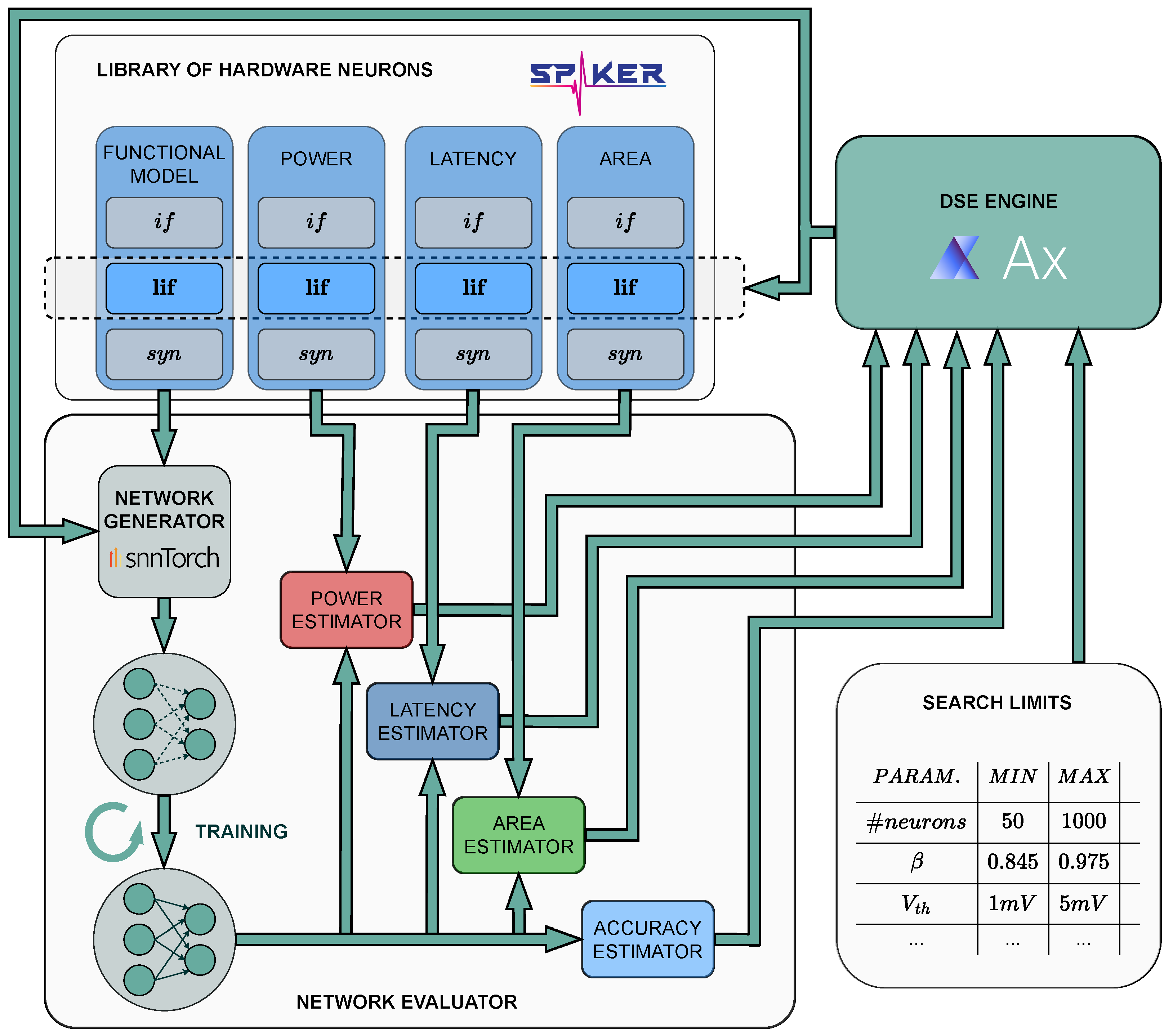
4. Materials and Methods
4.1. Network Generator and Hardware Neurons
4.2. Area
4.3. Accuracy and Latency
4.4. Power
4.5. DSE Engine
| Listing 1. Summarized code of SpikeExplorer. |
 |
5. Experimental Results
5.1. Experimental Setup
- MNIST [43]: Grayscale images of handwritten digits, converted into sequences of spikes using rate encoding. The corresponding number of inputs is .
- SHD [44]: Audio recordings of numbers pronounced in English and German, converted to spikes through a faithful emulation of the human cochlea. Recordings were performed with 700 channels, corresponding to the number of inputs of the network.
- DVS128 [45]: Video recordings of 11 gestures through a DVS converting images into spikes. The sensor’s resolution is pixels, accounting for 16,384 inputs.
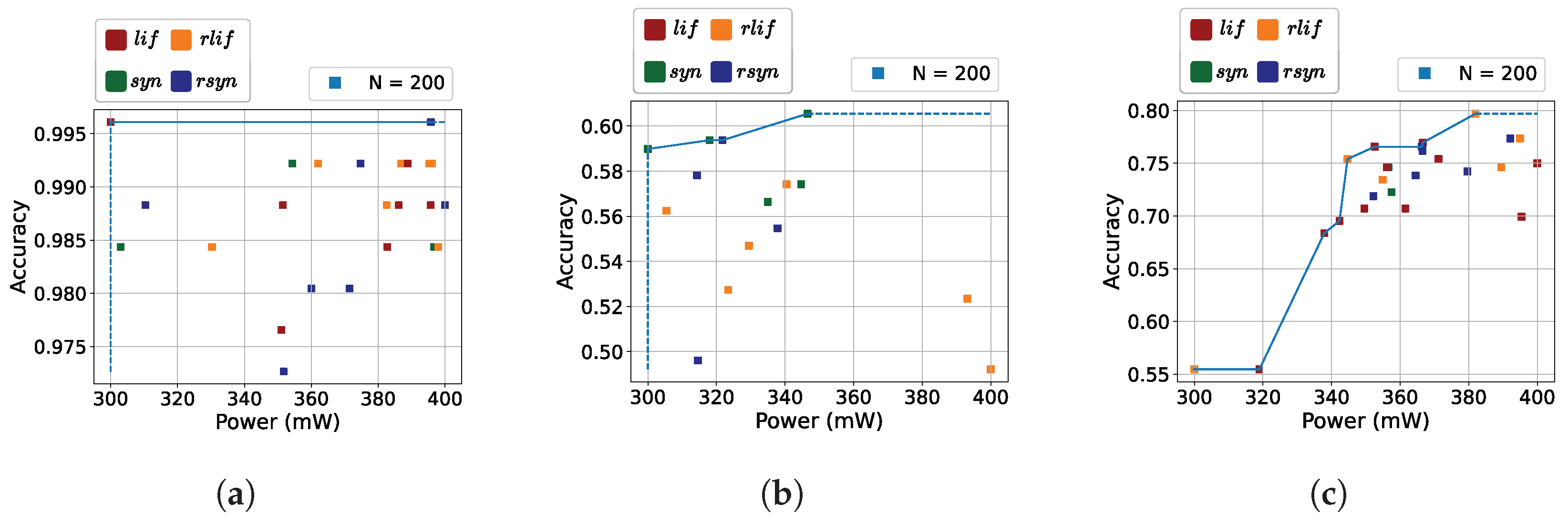
5.2. Global Exploration
5.3. Fixed Neuron Models and Network Size
5.4. Synthesis and Comparison with State of Art
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kasabov, N.K. Time-Space, Spiking Neural Networks and Brain-Inspired Artificial Intelligence; Springer Series on Bio- and Neurosystems; Springer: Berlin/Heidelberg, Germany, 2019; Volume 7. [Google Scholar] [CrossRef]
- Maass, W. Networks of spiking neurons: The third generation of neural network models. Neural Netw. 1997, 10, 1659–1671. [Google Scholar] [CrossRef]
- Narayanan, S.; Taht, K.; Balasubramonian, R.; Giacomin, E.; Gaillardon, P.E. SpinalFlow: An Architecture and Dataflow Tailored for Spiking Neural Networks. In Proceedings of the 2020 ACM/IEEE 47th Annual International Symposium on Computer Architecture (ISCA), Valencia, Spain, 30 May–3 June 2020; pp. 349–362. [Google Scholar] [CrossRef]
- Basu, A.; Frenkel, C.; Deng, L.; Zhang, X. Spiking Neural Network Integrated Circuits: A Review of Trends and Future Directions. arXiv 2022, arXiv:2203.07006. [Google Scholar] [CrossRef]
- Isik, M. A Survey of Spiking Neural Network Accelerator on FPGA. arXiv 2023, arXiv:2307.03910. [Google Scholar] [CrossRef]
- Musisi-Nkambwe, M.; Afshari, S.; Barnaby, H.; Kozicki, M.; Esqueda, I.S. The viability of analog-based accelerators for neuromorphic computing: A survey. Neuromorphic Comput. Eng. 2021, 1, 012001. [Google Scholar] [CrossRef]
- Wang, T.T.; Chu, S.C.; Hu, C.C.; Jia, H.D.; Pan, J.S. Efficient Network Architecture Search Using Hybrid Optimizer. Entropy 2022, 24, 656. [Google Scholar] [CrossRef] [PubMed]
- Ghaffari, A.; Savaria, Y. CNN2Gate: An Implementation of Convolutional Neural Networks Inference on FPGAs with Automated Design Space Exploration. Electronics 2020, 9, 2200. [Google Scholar] [CrossRef]
- Czako, Z.; Sebestyen, G.; Hangan, A. AutomaticAI–A hybrid approach for automatic artificial intelligence algorithm selection and hyperparameter tuning. Expert Syst. Appl. 2021, 182, 115225. [Google Scholar] [CrossRef]
- Balaji, A.; Song, S.; Titirsha, T.; Das, A.; Krichmar, J.; Dutt, N.; Shackleford, J.; Kandasamy, N.; Catthoor, F. NeuroXplorer 1.0: An Extensible Framework for Architectural Exploration with Spiking Neural Networks. In Proceedings of the International Conference on Neuromorphic Systems 2021, ICONS 2021, Knoxville, TN, USA, 27–29 July 2021; pp. 1–9. [Google Scholar] [CrossRef]
- Abderrahmane, N.; Lemaire, E.; Miramond, B. Design Space Exploration of Hardware Spiking Neurons for Embedded Artificial Intelligence. Neural Netw. 2020, 121, 366–386. [Google Scholar] [CrossRef] [PubMed]
- Xue, J.; Xie, L.; Chen, F.; Wu, L.; Tian, Q.; Zhou, Y.; Ying, R.; Liu, P. EdgeMap: An Optimized Mapping Toolchain for Spiking Neural Network in Edge Computing. Sensors 2023, 23, 6548. [Google Scholar] [CrossRef]
- Samsi, S.; Zhao, D.; McDonald, J.; Li, B.; Michaleas, A.; Jones, M.; Bergeron, W.; Kepner, J.; Tiwari, D.; Gadepally, V. From Words to Watts: Benchmarking the Energy Costs of Large Language Model Inference. arXiv 2023, arXiv:2310.03003. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef] [PubMed]
- Izhikevich, E. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef] [PubMed]
- Brunel, N.; van Rossum, M.C.W. Quantitative investigations of electrical nerve excitation treated as polarization. Biol. Cybern. 2007, 97, 341–349. [Google Scholar] [CrossRef] [PubMed]
- Eshraghian, J.K.; Ward, M.; Neftci, E.; Wang, X.; Lenz, G.; Dwivedi, G.; Bennamoun, M.; Jeong, D.S.; Lu, W.D. Training Spiking Neural Networks Using Lessons From Deep Learning. arXiv 2021, arXiv:2109.12894. [Google Scholar]
- Markram, H.; Gerstner, W.; Sjöström, P.J. Spike-Timing-Dependent Plasticity: A Comprehensive Overview. Front. Synaptic Neurosci. 2012, 4, 2. [Google Scholar] [CrossRef] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Neftci, E.O.; Mostafa, H.; Zenke, F. Surrogate Gradient Learning in Spiking Neural Networks: Bringing the Power of Gradient-Based Optimization to Spiking Neural Networks. IEEE Signal Process. Mag. 2019, 36, 51–63. [Google Scholar] [CrossRef]
- Marti, K. Optimization under Stochastic Uncertainty: Methods, Control and Random Search Methods; International Series in Operations Research & Management Science; Springer International Publishing: Cham, Switzerland, 2020; Volume 296. [Google Scholar] [CrossRef]
- Ferrandi, F.; Lanzi, P.L.; Loiacono, D.; Pilato, C.; Sciuto, D. A Multi-objective Genetic Algorithm for Design Space Exploration in High-Level Synthesis. In Proceedings of the 2008 IEEE Computer Society Annual Symposium on VLSI, Montpellier, France, 7–9 April 2008; pp. 417–422, ISSN 2159-3477. [Google Scholar] [CrossRef]
- Savino, A.; Vallero, A.; Di Carlo, S. ReDO: Cross-Layer Multi-Objective Design-Exploration Framework for Efficient Soft Error Resilient Systems. IEEE Trans. Comput. 2018, 67, 1462–1477. [Google Scholar] [CrossRef]
- Saeedi, S.; Savino, A.; Di Carlo, S. Design Space Exploration of Approximate Computing Techniques with a Reinforcement Learning Approach. In Proceedings of the 2023 53rd Annual IEEE/IFIP International Conference on Dependable Systems and Networks Workshops (DSN-W), Porto, Portugal, 27–30 June 2023; pp. 167–170, ISSN 2325-6664. [Google Scholar] [CrossRef]
- Reagen, B.; Hernández-Lobato, J.M.; Adolf, R.; Gelbart, M.; Whatmough, P.; Wei, G.Y.; Brooks, D. A case for efficient accelerator design space exploration via Bayesian optimization. In Proceedings of the 2017 IEEE/ACM International Symposium on Low Power Electronics and Design (ISLPED), Taipei, Taiwan, 24–26 July 2017; pp. 1–6. [Google Scholar] [CrossRef]
- March, J.G. Exploration and Exploitation in Organizational Learning. Organ. Sci. 1991, 2, 71–87. [Google Scholar] [CrossRef]
- Candelieri, A. A Gentle Introduction to Bayesian Optimization. In Proceedings of the 2021 Winter Simulation Conference (WSC), Phoenix, AZ, USA, 12–15 December 2021; pp. 1–16. [Google Scholar] [CrossRef]
- Bouvier, M.; Valentian, A.; Mesquida, T.; Rummens, F.; Reyboz, M.; Vianello, E.; Beigne, E. Spiking Neural Networks Hardware Implementations and Challenges: A Survey. J. Emerg. Technol. Comput. Syst. 2019, 15, 1–35. [Google Scholar] [CrossRef]
- Han, J.; Li, Z.; Zheng, W.; Zhang, Y. Hardware implementation of spiking neural networks on FPGA. Tsinghua Sci. Technol. 2020, 25, 479–486. [Google Scholar] [CrossRef]
- Gupta, S.; Vyas, A.; Trivedi, G. FPGA Implementation of Simplified Spiking Neural Network. In Proceedings of the 2020 27th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Glasgow, UK, 23–25 November 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Z.; Mao, R.; Xiao, J.; Chang, L.; Zhou, J. A Fast and Energy-Efficient SNN Processor With Adaptive Clock/Event-Driven Computation Scheme and Online Learning. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 1543–1552. [Google Scholar] [CrossRef]
- Carpegna, A.; Savino, A.; Di Carlo, S. Spiker: An FPGA-optimized Hardware accelerator for Spiking Neural Networks. In Proceedings of the 2022 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Nicosia, Cyprus, 4–6 July 2022; pp. 14–19, ISSN 2159-3477. [Google Scholar] [CrossRef]
- Carpegna, A.; Savino, A.; Di Carlo, S. Spiker+: A framework for the generation of efficient Spiking Neural Networks FPGA accelerators for inference at the edge. arXiv 2024, arXiv:2401.01141. [Google Scholar] [CrossRef]
- Gerlinghoff, D.; Wang, Z.; Gu, X.; Goh, R.S.M.; Luo, T. E3NE: An End-to-End Framework for Accelerating Spiking Neural Networks With Emerging Neural Encoding on FPGAs. IEEE Trans. Parallel Distrib. Syst. 2022, 33, 3207–3219. [Google Scholar] [CrossRef]
- Kim, Y.; Li, Y.; Park, H.; Venkatesha, Y.; Panda, P. Neural Architecture Search for Spiking Neural Networks. In Proceedings of the Computer Vision—ECCV 2022, Tel Aviv, Israel, 23–27 October 2022; Lecture Notes in Computer Science. Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Springer: Cham, Switzerland, 2022; pp. 36–56. [Google Scholar] [CrossRef]
- Moradi, S.; Qiao, N.; Stefanini, F.; Indiveri, G. A Scalable Multicore Architecture With Heterogeneous Memory Structures for Dynamic Neuromorphic Asynchronous Processors (DYNAPs). IEEE Trans. Biomed. Circuits Syst. 2018, 12, 106–122. [Google Scholar] [CrossRef] [PubMed]
- Putra, R.V.W.; Shafique, M. Q-SpiNN: A Framework for Quantizing Spiking Neural Networks. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–8, ISBN 9781665439008. [Google Scholar] [CrossRef]
- Li, C.; Ma, L.; Furber, S. Quantization Framework for Fast Spiking Neural Networks. Front. Neurosci. 2022, 16, 918793. [Google Scholar] [CrossRef] [PubMed]
- Castagnetti, A.; Pegatoquet, A.; Miramond, B. Trainable quantization for Speedy Spiking Neural Networks. Front. Neurosci. 2023, 17, 1154241. [Google Scholar] [CrossRef]
- Meta. Ax · Adaptive Experimentation Platform—ax.dev. Available online: https://ax.dev (accessed on 3 April 2024).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ng, A.Y. Feature selection, L1 vs. L2 regularization, and rotational invariance. In Proceedings of the Twenty-First International Conference on Machine Learning, ICML ’04, Banff, AB, Canada, 4–8 July 2004; p. 78. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Cramer, B.; Stradmann, Y.; Schemmel, J.; Zenke, F. The Heidelberg Spiking Data Sets for the Systematic Evaluation of Spiking Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 2744–2757. [Google Scholar] [CrossRef]
- Amir, A.; Taba, B.; Berg, D.; Melano, T.; McKinstry, J.; Di Nolfo, C.; Nayak, T.; Andreopoulos, A.; Garreau, G.; Mendoza, M.; et al. A Low Power, Fully Event-Based Gesture Recognition System. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 7388–7397. [Google Scholar] [CrossRef]
- Iakymchuk, T.; Rosado-Muñoz, A.; Guerrero-Martínez, J.F.; Bataller-Mompeán, M.; Francés-Víllora, J.V. Simplified spiking neural network architecture and STDP learning algorithm applied to image classification. EURASIP J. Image Video Process. 2015, 2015, 4. [Google Scholar] [CrossRef]




| Parameter | Values | ||
|---|---|---|---|
| Net | # layers | Discrete | |
| # neurons/layer | Set | ||
| Architecture | Feed
Forward | Recurrent | |
| Neuron | Model | if lif syn | rif rlif rsyn |
| Reset | Hard | ||
| Subtractive | |||
| , | Continuous | ||
| Continuous | |||
| Time-steps | Set | ||
| Training | Learning rate | Continuous | |
| Optimizer | |||
| Regularizer | |||
| Surrogate slope | |||
| Surrogate |
Sigmoid, Fast Sigmoid, ATan, Straight Through Estimator, Triangular, SpikeRateEscape, Custom [17] | ||
| MNIST | SHD | DVS128 | ||||
|---|---|---|---|---|---|---|
| Min | Max | Min | Max | Min | Max | |
| Learning rate | ||||||
| Adam | 0.9 | 0.999 | 0.9 | 0.999 | 0.9 | 0.999 |
| # layers | 1 | 3 | 1 | 3 | 1 | 3 |
| Model | lif, syn, rlif, rsyn | lif, syn, rlif, rsyn | lif, syn, rlif, rsyn | |||
| Reset | subtractive | subtractive | subtractive | |||
| Time steps | 10, 25, 50 | 10, 25, 50 | 10, 25, 50 | |||
| # neurons/layers | 200, 100, 50 | 200, 100, 50 | 200, 100, 50 | |||
| Search iterations | 25 | 15 | 25 | |||
| Training epochs | 50 | 100 | 50 | |||
| Model | Arch. | TS | Acc. | Power (mW) |
|---|---|---|---|---|
| LIF | 200-10 | 10 | 99.61% | 310 |
| RLIF | 200-100-200-10 | 10 | 99.22% | 860 |
| SYN | 200-200-10 | 25 | 99.22% | 680 |
| RSYN | 100-10 | 25 | 99.22% | 140 |
| Model | Arch. | TS | Acc. | Power (mW) |
|---|---|---|---|---|
| LIF | 200-20 | 50 | 59.41% | 360 |
| RLIF | 200-200-20 | 50 | 61.70% | 760 |
| SYN | 100-100-200-20 | 10 | 58.98% | 720 |
| RSYN | 100-20 | 50 | 58.59% | 140 |
| Model | Arch. | TS | Acc. | Power (mW) |
|---|---|---|---|---|
| LIF | 200-200-50-11 | 50 | 72.27% | 500 |
| RLIF | 200-200-50-11 | 25 | 76.17% | 760 |
| SYN | 200-100-11 | 50 | 75.78% | 500 |
| RSYN | 100-200-50-10 | 50 | 73.83% | 590 |
| Design | Han et al. [29] | Gupta et al. [30] | Li et al. [31] | Spiker [32] | Spiker+ [33] | This Work |
|---|---|---|---|---|---|---|
| Year | 2020 | 2020 | 2021 | 2022 | 2024 | |
| [MHz] | 200 | 100 | 100 | 100 | ||
| Neuron bw | 16 | 24 | 16 | 16 | 6 | |
| Weights bw | 16 | 24 | 16 | 16 | 4 | |
| Update | Event | Event | Hybrid | Clock | ||
| Model | LIF | LIF [46] | LIF | LIF | ||
| FPGA | XC7Z045 | XC6VLX240T | XC7VX485 | XC7Z020 | ||
| Avail. BRAM | 545 | 416 | 2060 | 140 | ||
| Used BRAM | 40.5 | 162 | N/R | 45 | 18 | |
| Avail. DSP | 900 | 768 | 2800 | 220 | ||
| Used DSP | 0 | 64 | N/R | 0 | ||
| Avail. logic cells | 655,800 | 452,160 | 485,760 | 159,600 | ||
| Used logic cells | 12,690 | 79,468 | N/R | 55,998 | 7612 | |
| Arch | 1024-1024-10 | 784-16 | 200-100-10 | 400 | 128-10 | |
| #syn | 1,861,632 | 12,544 | 177,800 | 313,600 | 101,632 | |
| /img [ms] | 6.21 | 0.50 | 3.15 | 0.22 | 0.78 | 0.12 |
| Power [W] | 0.477 | N/R | 1.6 | 59.09 | 0.18 | |
| E/img [mJ] | 2.96 | N/R | 5.04 | 13 | 0.14 | 0.02 |
| E/syn [nJ] | 1.59 | N/R | 28 | 41 | 1.37 | 0.22 |
| Accuracy | 97.06% | N/R | 92.93% | 73.96% | 93.85% | 95.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Padovano, D.; Carpegna, A.; Savino, A.; Di Carlo, S. SpikeExplorer: Hardware-Oriented Design Space Exploration for Spiking Neural Networks on FPGA. Electronics 2024, 13, 1744. https://doi.org/10.3390/electronics13091744
Padovano D, Carpegna A, Savino A, Di Carlo S. SpikeExplorer: Hardware-Oriented Design Space Exploration for Spiking Neural Networks on FPGA. Electronics. 2024; 13(9):1744. https://doi.org/10.3390/electronics13091744
Chicago/Turabian StylePadovano, Dario, Alessio Carpegna, Alessandro Savino, and Stefano Di Carlo. 2024. "SpikeExplorer: Hardware-Oriented Design Space Exploration for Spiking Neural Networks on FPGA" Electronics 13, no. 9: 1744. https://doi.org/10.3390/electronics13091744
APA StylePadovano, D., Carpegna, A., Savino, A., & Di Carlo, S. (2024). SpikeExplorer: Hardware-Oriented Design Space Exploration for Spiking Neural Networks on FPGA. Electronics, 13(9), 1744. https://doi.org/10.3390/electronics13091744








