Cosine Distance Loss for Open-Set Image Recognition

Abstract

Traditional image classification often misclassifies unknown samples as known classes during testing, degrading recognition accuracy. Open-set image recognition can simultaneously detect known classes (KCs) and unknown classes (UCs) but still struggles to improve recognition performance caused by open space risk. Therefore, we introduce a cosine distance loss function (CDLoss), which exploits the orthogonality of one-hot encoding vectors to align known samples with their corresponding one-hot encoder directions. This reduces the overlap between the feature spaces of KCs and UCs, mitigating open space risk. CDLoss was incorporated into both Softmax-based and prototype-learning-based frameworks to evaluate its effectiveness. Experimental results show that CDLoss improves AUROC, OSCR, and accuracy across both frameworks and different datasets. Furthermore, various weight combinations of the ARPL and CDLoss were explored, revealing optimal performance with a 1:2 ratio. T-SNE analysis confirms that CDLoss reduces the overlap between the feature spaces of KCs and UCs. These results demonstrate that CDLoss helps mitigate open space risk, enhancing recognition performance in open-set image classification tasks.

1. Introduction

Deep neural networks have achieved significant advancements in computer vision, particularly in image classification tasks [1]. These algorithms typically operate under the closed-set assumption, where the classes in the training set match those in the test set. However, in real-world scenarios, test samples often include unknown classes (UCs) absent from the training set. Traditional deep neural networks misclassify these UCs into one of the known classes (KCs), resulting in errors that can have serious consequences. For instance, in medical diagnosis, a new disease might be misidentified as an existing one, delaying appropriate treatment. Similarly, in autonomous driving, an unknown obstacle might be classified as a familiar object, leading to unsafe decisions or actions.

To address these challenges, open-set recognition (OSR) aims to perform two tasks during testing: (1) accurately classifying KCs and (2) correctly identifying UCs [2]. The primary difficulty arises from the overlap between KCs and UCs in the feature space. During training, the model learns features only for KCs, as UCs are absent. This limitation often causes UCs to be misclassified as KCs during testing, particularly when they share similar intrinsic features. Without effective strategies to separate these feature spaces, the model faces high open space risk, where UCs are incorrectly classified as KCs. Reducing this risk requires learning effective latent feature representations or designing robust thresholding strategies to differentiate between open- and closed-set spaces [3].

Threshold selection strategies provide one approach to mitigating open space risk. For example, an intuitive method involves identifying UCs by setting a threshold based on the model’s output probability during testing [4]. More sophisticated approaches include calibrated scores, which model the distribution of mean activation distances for KCs and define thresholds using extreme value theory (EVT) [5] or estimating class distributions in the latent space by adjusting the model after calculating average class activation values [6,7]. While these methods improve UC detection, they often depend on high-quality feature representations to work effectively.

Closed-set classifiers, however, focus solely on learning decision boundaries between KCs, which can lead to all available feature space being occupied by KCs, leaving no space for UCs. Designing an effective feature space ensures that features of the same class are tightly clustered while features of different classes are well separated. This reduces overlap between KCs and UCs and minimizes open space risk. Prototype learning, which clusters features around class centers and measures distances to prototypes, has emerged as a key technique for learning feature spaces that separate KCs and UCs [8,9,10,11].

For OSR methods based on convolutional neural networks, UCs often have feature values near the origin of the feature space, while KCs occupy regions with larger responses. Reducing the overlap between these regions is essential for improving recognition performance. In this study, we propose the cosine distance loss (CDLoss) function to address this issue. CDLoss minimizes the cosine distance between sample embeddings and their corresponding category labels, aligning KCs with their respective one-hot encoding vectors. By leveraging the orthogonality of one-hot vectors, this approach reserves more space for UCs, reducing overlap and mitigating open space risk.

Our contributions are as follows: (1) Novel loss function: We introduce CDLoss as a plug-and-play loss function that measures the similarity between one-hot encoding vectors and logit outputs, aligning KCs with their corresponding one-hot vectors and freeing up feature space for UCs. (2) Improved OSR performance: CDLoss integrates seamlessly with existing loss functions, enhancing open-set classification by reducing inter-class overlap and increasing intra-class compactness. (3) Extensive evaluation: Experimental results demonstrate significant improvements across multiple metrics, including AUROC, OSCR, and accuracy, on various benchmark datasets. Specifically, on the TinyImageNet dataset, CDLoss achieves up to a 3.93% improvement in AUROC and a 7.58% improvement in OSCR compared to baseline algorithms. By minimizing overlap in the feature space and enhancing separation between KCs and UCs, CDLoss demonstrates its effectiveness in addressing the challenges of open-set recognition.

2. Related Work

The OSR problem was first defined by Scheirer et al. in 2014 [12]. Early OSR methods predominantly relied on traditional machine learning approaches, including OSR with extreme value theory [13,14], open-set nearest neighbor methods [15], sparse representation-based OSR methods [16], and three-way clustering methods [17]. With advancements in computational power, deep neural networks have been increasingly applied to OSR. Bendale et al. introduced the Openmax method, which detects UCs by modeling the distances between activated vectors using a Weibull distribution [5]. Shu et al. proposed an end-to-end framework with K-sigmoid activation, eliminating the need for external outlier detectors [18]. Yoshihashi et al. incorporated reconstructed representations into OSR [19]. Jang et al. developed a method based on multiple one-to-many networks to establish strict decision boundaries between KCs and UCs [20]. Chen et al. introduced a framework combining an OSR module with a new category discovery module, using K-contrast loss to achieve accurate differentiation of UCs while transferring knowledge from KCs through deep clustering [21]. Vareto et al. proposed a compact adapter network incorporating loss functions such as maximal entropy loss, achieving improved results in open-set face recognition tasks using additional negative samples [22]. However, these discriminative methods primarily focus on partitioning feature space for KCs, often neglecting the need to reserve space for UCs.

To address this limitation, generative models have been introduced to consider the spatial distribution of UCs. These models can be categorized into two main types: (1) those that generate synthetic UCs to obtain feature distributions for both KCs and UCs, with their performance relying heavily on the quality and diversity of generated samples [6,20]; and (2) those that learn latent feature representations for KCs using autoencoders [21] or stream-based models [22]. Wang et al. proposed JCGAN, a generative framework that transforms OSR into a closed-set problem by generating synthetic interference patterns and using a ternary loss to reduce feature overlap, demonstrating its effectiveness in open-set interference pattern recognition [23]. Guo et al. introduced a capsule network combined with a variational self-encoder, matching capsule features of KCs to predefined Gaussian distributions during training, which improved feature compactness and achieved state-of-the-art results [24]. Cao et al. proposed a Gaussian hybrid variational self-encoder, jointly optimizing reconstruction and category-based clustering in the latent space to enhance robustness and accuracy [25]. Sun et al. introduced a mixture of exponential power distributions within a self-encoder framework to represent latent feature distributions, achieving superior performance in both open-set and closed-set recognition tasks [26]. Despite their strengths, generative models often struggle to impose discriminative constraints on KCs, limiting their ability to reduce overlap effectively.

To combine the strengths of discriminative and generative methods, hybrid approaches have emerged. OpenHybrid [22] and convolutional prototype networks [27] leverage both paradigms to improve OSR performance. Huang et al. proposed class-specific semantic reconstruction, integrating autoencoders and prototype learning to model KCs and reject UCs through thresholding. This method combines DNNs and AEs in an end-to-end manner to learn discriminative and representative information [28]. PROSER assigns placeholders to UCs within the classifier to maintain KC classification performance in open-set settings [29].

Prototype learning has also been extensively explored for OSR tasks, clustering feature space points to represent categories. Centreloss was initially introduced to encourage discriminative feature learning [30]. Generalized convolutional prototype learning (GCPL) allocates feature space for UCs by setting thresholds and assigning multiple prototypes per category, with prototype loss serving as regularization [8]. Reciprocal point learning (RPL) introduced reciprocal points to construct bounded spaces that incorporate UC information, enabling models to learn more compact representations [9]. ARPL, a variant of RPL, imposes adversarial marginal constraints to estimate UC distributions in regions indistinguishable from KCs and applies adversarial augmentation to generate confounded training samples [10]. SLCPL identified open space risk as stemming from low activation values for UCs and high values for KCs, introducing a spatial location constraint prototype loss to confine KC features to the feature space periphery, thereby reducing overlap and improving robustness [11].

Existing OSR methods, however, often fail to effectively separate KCs and UCs in feature space. KCs tend to dominate the feature space, leaving insufficient room for UCs. This issue becomes more pronounced when handling complex datasets, leading to increased open space risk and degraded recognition performance. These challenges highlight the need for innovative approaches to address feature space overlap and improve OSR performance.

3. Open-Set Image Classification by Incorporating CDLoss

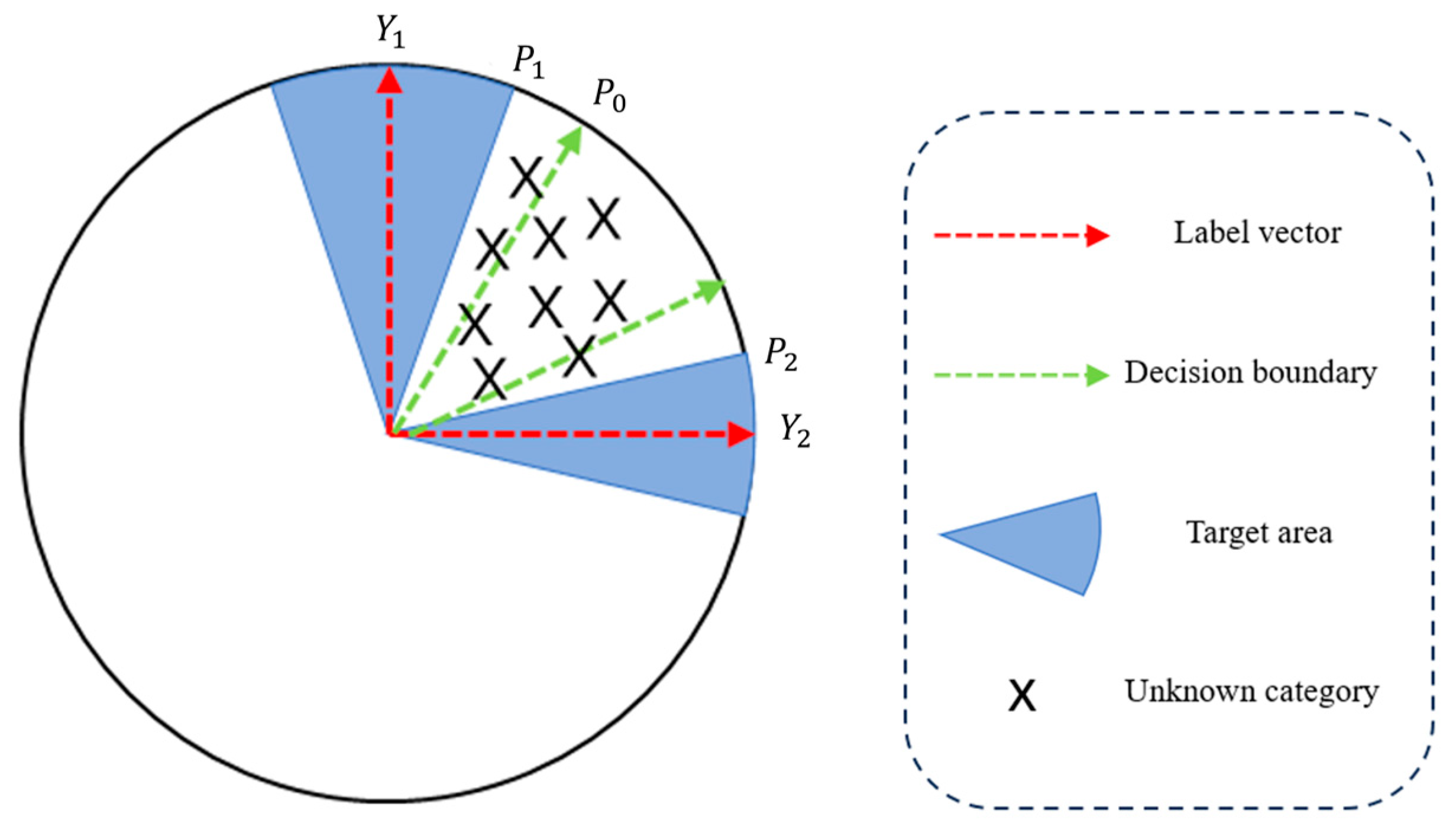
3.1. Motivation for Incorporation of CDLoss

Convolutional kernels are designed to extract specific features or patterns from images. In OSR, these kernels are optimized during training to represent known classes (KCs). During testing, test samples matching KCs produce high activation values, while unknown classes (UCs) typically yield lower activation values. In the feature space, UCs are often clustered near the center, leading to significant overlap with KCs. To address this, we leverage one-hot encoding vectors as an orthogonal basis and introduce CDLoss to align sample feature vectors closer to their corresponding encoding vectors. This alignment reduces overlap, minimizes open space risk, and enhances recognition performance.

3.2. Proposed Framework

The proposed framework for OSR operates in two stages (Figure 1): (1) Training phase: Backbone networks (e.g., ResNet50) extract features from KCs, which are pooled, flattened, and passed through a fully connected layer to generate logit prediction scores. CDLoss is added to the original loss to be used in calculating the total loss. Through the backpropagation algorithm, the model computes the gradients of the model parameters based on this total loss. These gradients reflect how the loss function changes with respect to each parameter, guiding the direction in which the model parameters should be updated. Subsequently, the optimizer leverages this gradient information to adjust the model parameters in order to minimize the total loss. (2) Testing phase: A prediction score is computed for each test sample, either through Softmax normalization or by calculating the distance between the sample’s feature vector and the class prototype centroid. This score is compared to a threshold to classify the sample as belonging to a KC or UC.

3.3. CDLoss and Its Spatial Characteristics

CDLoss calculates the cosine value of the angle between the feature vector of a sample and its corresponding class label vector. This encourages better alignment of KCs along their designated directions, reducing inter-class overlap and creating space for UCs. The penalty imposed by CDLoss strengthens decision boundaries and improves the robustness of the model in open-set scenarios. By treating class label vectors as basis vectors, CDLoss enhances the dispersion of prediction vectors, further improving classification performance.

Given the logit value for each sample x_i and its label y_i, their similarity can be expressed by the cosine distance:

$$CDLoss=1-{\displaystyle \frac{x_i·y_i}{\parallel x_i\parallel \parallel y_i\parallel }},$$

(1)

By incorporating CDLoss between the predicted vectors and their true label vectors, a penalty is imposed for deviations from the directional alignment of the labeled vectors. This penalty mechanism strengthens the model’s prediction accuracy along the direction of the KCs’ vectors, thus enhancing its performance. Furthermore, CDLoss refines the decision boundary, creating larger margins for UCs, thereby improving robustness in OSR. Additionally, as class label vectors serve as basis vectors, CDLoss encourages greater dispersion of the prediction vectors in their respective directions, reducing inter-class similarity and improving the model’s ability to differentiate between classes.

Figure 2 illustrates the role of CDLoss in optimizing decision boundaries. By aligning feature vectors closer to one-hot encoding directions, CDLoss reduces the angle of the decision boundary, shifting it from P₀ to P₁. This adjustment minimizes overlap between KCs and UCs, ensuring better separation in the feature space.

3.4. Loss Function for Model

Without adjusting the original loss, the CDLoss function is a plug-and-play module that is directly added to the existing loss to form the overall model loss function. If the original model loss is denoted as L_ori and the CDLoss is represented as L_CD, then the total model loss after adding the CDLoss can be expressed as:

$$L_{total}=L_{ori}+L_{CD}.$$

(2)

3.5. Unknown Class Detection

For the Softmax method, the probability of a test sample x belonging to a particular known class can be expressed mathematically through the following equation:

$$p(\widehat{y}=k|x)\propto \mathrm{e}\mathrm{x}\mathrm{p}(\Theta \left(x\right)),$$

(3)

where $\Theta \left(x\right)$ is the raw score or activation value associated with the input sample x. The Softmax function calculates the probability of each category by exponentiating and normalizing the scores across all categories.

For the prototype approach, the probability of a test sample x belonging to a particular known class is calculated with the following equation:

$$p(\widehat{y}=k|x)\propto \mathrm{e}\mathrm{x}\mathrm{p}(-{min}_{k\in \left\{1,...,N\right\}}d(\Theta \left(x\right),O^k)),$$

(4)

where $\Theta \left(x\right)$ is the feature vector of the input sample $x$, similar to the score in the Softmax method, $O^k$ is the prototype of category k, and $d(\Theta \left(x\right),O^k)$ is a distance metric that measures the difference between the feature vector Θ(x) of the test sample $x$ and the prototype $O^k$ of the category k. This part of $min$ indicates that for all known prototypes $O^k$ of category k, the distance from sample $x$ to each prototype is computed and the smallest distance is chosen; in other words, this means that the category prototype closest to the test sample is chosen among all the categories. $\mathrm{e}\mathrm{x}\mathrm{p}\left(\right)$ is the value of the smallest distance that is converted into a probability using an exponential function. Here, the smaller the distance, the larger the value of $\mathrm{e}\mathrm{x}\mathrm{p}(-{min}_{k\in \left\{1,...,N\right\}}d(\Theta \left(x\right),O^k\left)\right)$, indicating that the sample $x$ is more likely to belong to the category. Thus, the intuitive interpretation of this formula is that the closer the test sample $x$ is to the prototype $O^k$ of category k, the higher the probability that it belongs to that category.

The threshold τ is employed to ascertain whether a test sample x belongs to a known class or not.

$$\widehat{y}=\left\{\begin{array}{c}k+1,ifp\left(\widehat{y}=k|x\right)<\tau \\ otherwise\end{array}\right.,$$

(5)

where τ is determined by ensuring that 95% of the images in the validation set are correctly identified as known [22,31].

4. Experimental Platform and Settings

4.1. Experimental Platform

The experiments were conducted on an Ubuntu 18.04 operating system. The deep learning framework employed was PyTorch, 1.10.2, with CUDA 11.1 and cuDNN 10.2 for GPU acceleration, and with Python 3.8.12 serving as the programming language. The hardware utilized in this study comprises an Intel Core i7-10700K CPU operating at 3.80 GHz (Intel Corporation in Santa Clara, CA, USA) and an GeForce RTX 3090 GPU with 24 GB of memory (NVIDIA Corporation in Santa Clara, CA, USA).

4.2. Parameter Settings

The proposed CDLoss is a plug-and-play loss function, integrated into the original loss function for open-set classification. CDLoss is integrated into the original loss function without requiring adjustments to other parameters. The hyperparameters were set as follows: batch size = 128, initial learning rate = 0.1, 100 epochs, and SGD with momentum = 0.9 and weight decay = 10⁻⁴.

4.3. Dataset Partitioning

To verify the ability of our method to detect the UCs and classify the KCs, five public datasets are selected, and the division of the KCs and the UCs follows the settings of the published papers about OSR tasks. The detailed settings in this study are as follows:

• MNIST, SVHN, CIFAR10. These datasets consist of a total of 10 categories, 6 of which are selected as the KCs and the remaining 4 categories are the UCs, i.e., |K| = 6, |U| = 4.
• CIFAR+50. Derived from CIFAR10 and CIFAR100, 4 classes are taken from CIFAR10 as the KCs and 50 classes are taken from CIFAR100 as the UCs, i.e., |K| = 4 and |U| = 50.
• TinyImagenet. The dataset has a total of 200 classes, 20 of which are selected as the KCs and the remaining180 as the UCs, i.e., |K| = 20, |U| = 180.

MNIST is a widely used dataset for handwritten digit recognition, featuring white digits on a black background. SVHN is a real-world digit dataset derived from Google Street View images, where each image may contain multiple digits. CIFAR-10 is a color image dataset with ten categories, including objects like aircraft, cars, and animals, set against varied but distinct backgrounds. CIFAR-50 expands on CIFAR-10 with a broader range of categories. TinyImageNet is a larger classification dataset, containing rich content across diverse real-world scenes and objects.

4.4. Evaluation Metrics

Since the distribution of UCs in real-world scenarios is unknown, OSR methods relying on arbitrary thresholds or sensitivities lack objectivity. To address this, threshold-independent metrics, such as the area under the ROC curve (AUROC) [32], are commonly used. AUROC plots the true positive rate (TPR) versus the false positive rate (FPR) across varying thresholds, reflecting the probability that a predicted positive example receives a higher detection score than a predicted negative one [33]. A higher detection score suggests a greater likelihood that the sample belongs to KCs, while a lower score indicates a higher probability of being an UC. Thus, AUROC assesses the model’s ability to differentiate between KCs and UCs, with higher values indicating better performance.

However, AUROC evaluates only the distinction between KCs and UCs, without considering the accuracy of KCs in OSR. To address this limitation, the open-set categorization rate (OSCR) is introduced as a novel metric [34]. If δ is the threshold value, the correct classification rate (CCR) is defined as the fraction of correctly classified samples from the KCs where the correct class has a probability greater than δ:

$$CCR\left(\delta \right)={\displaystyle \frac{\left|\right\{x\in D_{\tau }^k\bigwedge argma{x}_{k}P\left(k|x\right)=\widehat{k}\bigwedge P\left(\widehat{k}\right|x)\ge \delta \}|}{\left|D_{\tau }^k\right|}},$$

(6)

The FPR is defined as the fraction of samples from the UCs that are classified as any known class with a probability greater than δ:

$$FPR\left(\delta \right)={\displaystyle \frac{\left|\right\{x|x\in D_U\wedge {max}_{k}P(k\left|x\right)\ge \delta \left\}\right|}{\left|D_U\right|}},$$

(7)

Finally, by varying δ, the CCR versus FPR curve was plotted, and the OSCR value was then calculated by iteratively multiplying the increment in FPR (representing changes in false positives) with the average CCR (representing correct classifications of KCs) between neighboring points on the curve and accumulating these values to obtain the overall OSCR score. Specifically, for each interval on the FPR axis (X axis), the difference between successive FPR values (ΔFPR) is multiplied by the average CCR value over that interval, and the result is added to the previous accumulated total. This process is repeated for all intervals on the curve. By capturing both CCR and FPR, this method provides a comprehensive evaluation of the model’s performance in OSR. The larger the OSCR value, the better the detection performance, as it indicates a higher CCR while minimizing false positives across the range of thresholds δ. Recognition accuracy is defined as the percentage of samples that are correctly predicted out of the total number of samples tested. The formula for calculating recognition accuracy is provided as follows:

$$Accuracy={\displaystyle \frac{P_{Corr}}{P_{Corr}+P_{Error}}}\times 100\%,$$

(8)

where P_Corr represents the number of samples that are correctly categorized, while P_Error denotes the number of misclassified samples. The sum of P_Corr and P_Error gives the total number of samples.

5. Results and Analyses

5.1. Performance Comparison

To assess the efficacy of CDLoss for OSR, two types of frameworks, MSP (maximum Softmax probability) [35], a Softmax framework, and GCPL [8], RPL [9], ARPL [10], and SLCPL [11], prototype-based derived approaches, are taken as baseline algorithms. The performance was assessed using AUROC, OSCR, and accuracy.

Table 1. Unknown class recognition performance evaluation with AUROC.

Method	MNIST	SVHN	CIFAR10	CIFAR+50	TinyImagenet
MSP [28]	99.42	94.46	86.08	90.04	74.02
MSP + CDLoss	99.58	95.18	86.96	91.31	74.70
GCPL [7]	99.40	94.71	84.29	88.40	69.89
GCPL + CDLoss	99.48	94.88	85.57	89.57	73.23
RPL [8]	99.46	94.69	85.6	88.97	68.82
RPL + CDLoss	99.52	94.87	85.96	89.30	72.79
ARPL [9]	99.57	95.68	89.39	93.91	75.77
ARPL + CDLoss	99.62	95.77	89.67	93.86	76.11
SLCPL [10]	99.40	94.86	85.11	88.22	70.15
SLCPL + CDLoss	99.42	95.10	85.65	89.04	74.08

shows that integrating CDLoss significantly enhances the detection capabilities for both KCs and UCs. For MSP, AUROC improved across all datasets, increasing by 0.88% on CIFAR10 (from 86.08 to 86.96), by 1.27% on CIFAR+50 (from 90.04 to 91.31), and by 0.68% on TinyImageNet (from 74.02 to 74.70). These results suggest that CDLoss optimizes feature representation by reducing overlap between KCs and UCs, leading to better separation.

For prototype-based methods, CDLoss consistently improved AUROC. In GCPL, AUROC increased by 1.28% on CIFAR10 (from 84.29 to 85.57), by 1.17% on CIFAR+50 (from 88.40 to 89.57), and by 3.34% on TinyImageNet (from 69.89 to 73.23). Similarly, SLCPL showed improvements of 0.54% on CIFAR10, 0.82% on CIFAR+50, and 3.93% on TinyImageNet. These gains highlight CDLoss’s ability to refine decision boundaries in high-dimensional feature spaces.

For RPL and ARPL, which incorporate reciprocal points to separate KCs from UCs, CDLoss also showed notable improvements. RPL achieved AUROC increases of 0.36% on CIFAR10, 0.33% on CIFAR+50, and 3.97% on TinyImageNet. Similarly, ARPL improved AUROC by 0.28% on CIFAR10 and 0.34% on TinyImageNet.

Overall, the results demonstrate that CDLoss improves AUROC across all datasets and methods, with particularly significant gains in more challenging datasets like TinyImageNet.

The OSCR metric, which accounts for both CCR and FPR, provides a more comprehensive evaluation than AUROC by balancing UC detection with KC classification. As shown in

Table 2. Open-set classification rate (OSCR) results.

Method	MNIST	SVHN	CIFAR10	CIFAR+50	TinyImagenet
MSP	99.24	92.63	83.75	88.21	60.50
MSP + CDLoss	99.41	93.45	84.62	89.49	61.36
GCPL	99.24	93.05	81.69	86.47	48.83
GCPL + CDLoss	99.30	93.33	83.14	87.73	55.70
RPL	99.31	93.18	83.29	87.51	48.92
RPL + CDLoss	99.37	93.41	83.78	87.86	56.50
ARPL	99.36	93.51	86.04	91.36	61.87
ARPL + CDLoss	99.39	93.85	86.46	91.48	62.39
SLCPL	99.23	93.24	82.51	86.33	50.69
SLCPL + CDLoss	99.27	93.53	83.10	87.37	57.12

, the inclusion of CDLoss improves OSCR across all datasets for every method.

For MSP, CDLoss increased OSCR by 0.87% on CIFAR10 (from 83.75 to 84.62), by 1.28% on CIFAR+50 (from 88.21 to 89.49), and by 0.86% on TinyImageNet. For GCPL, CDLoss yielded larger gains, with OSCR improvements of 1.45% on CIFAR10 (from 81.69 to 83.14), 1.26% on CIFAR+50 (from 86.47 to 87.73), and 6.87% on TinyImageNet (from 48.83 to 55.70). SLCPL also benefited from CDLoss, with OSCR increasing by 0.59% on CIFAR10, 1.04% on CIFAR+50, and 6.43% on TinyImageNet.

For RPL, CDLoss improved OSCR by 0.49% on CIFAR10 (from 83.29 to 83.78), 0.35% on CIFAR+50 (from 87.51 to 87.86), and 7.58% on TinyImageNet (from 48.92 to 56.50). ARPL exhibited smaller but consistent improvements, with OSCR increasing by 0.42% on CIFAR10, 0.12% on CIFAR+50, and 0.52% on TinyImageNet.

These results confirm that CDLoss reduces inter-class overlap while enhancing intra-class cohesion, leading to improved OSCR performance, particularly in complex datasets.

As presented in

Table 3. Accuracy results for known classes.

Method	MNIST	SVHN	CIFAR10	CIFAR+50	TinyImagenet
MSP	99.74	96.59	94.31	96.10	73.66
MSP + CDLoss	99.78	96.89	94.49	96.34	74.06
GCPL	99.80	97.00	93.90	95.91	60.50
GCPL + CDLoss	99.80	97.15	94.50	96.31	67.68
RPL	99.76	97.05	94.35	96.48	61.56
RPL + CDLoss	99.79	93.15	94.63	96.53	68.98
ARPL	99.73	93.61	94.41	96.29	74.98
ARPL + CDLoss	99.70	93.91	94.61	96.47	75.36
SLCPL	99.79	97.06	94.22	96.09	63.30
SLCPL + CDLoss	99.82	97.20	94.45	96.44	69.06

, CDLoss enhances classification accuracy for KCs across all datasets and methods. For MSP, CDLoss resulted in modest improvements, increasing accuracy by 0.04% on MNIST (from 99.74 to 99.78), 0.30% on SVHN (from 96.59 to 96.89), and 0.18% on CIFAR10 (from 94.31 to 94.49).

Prototype-based methods exhibited more substantial gains. For GCPL, accuracy improved by 0.60% on CIFAR10 (from 93.90 to 94.50), 0.40% on CIFAR+50 (from 95.91 to 96.31), and a notable 7.18% on TinyImageNet (from 60.50 to 67.68). RPL also saw noticeable improvements, with increases of 0.28% on CIFAR10, 0.05% on CIFAR+50, and 7.42% on TinyImageNet. ARPL and SLCPL showed consistent gains, with accuracy improvements of 0.20% and 0.23% on CIFAR10, respectively, and notable gains on TinyImageNet (e.g., 0.38% for ARPL and 5.76% for SLCPL).

These findings demonstrate that CDLoss enhances the discriminative power of feature representations, leading to improved KC classification accuracy.

Despite these improvements, performance on TinyImageNet remains lower compared to other datasets. This discrepancy is attributed to the dataset’s inherent complexity, including diverse backgrounds, rich content, and high variability. Additionally, the large number of UCs in TinyImageNet increases the overlap with KCs in feature space, posing greater challenges for accurate recognition.

5.2. The Influence of Different Weights of Loss on Performance

The weight of the loss function can significantly affect recognition performance. To examine this influence, we tested different weight combinations between the ARPL loss and CDLoss on the TinyImageNet dataset, with ratios of 1:1, 2:1, and 1:2.

Table 4. Performance under different weight combinations.

ARPL	CDLoss	AUROC	OSCR	Accuracy
1	1	76.11	62.39	75.36
2	1	75.82	61.99	74.72
1	2	76.57	62.53	78.76

shows that the best performance in terms of AUROC, OSCR, and accuracy occurs when the weight ratio is 1:2, with AUROC, OSCR, and accuracy reaching 76.57%, 62.53%, and 78.56%, respectively. In contrast, the worst performance is observed with a 2:1 ratio. The differences between the best and worst performance are 0.75% for AUROC, 0.54% for OSCR, and 4.04% for accuracy. These results highlight the significant impact of CDLoss on open-set recognition and suggest that an appropriate weight for CDLoss further enhances the algorithm’s performance.

5.3. Visualization of the Impact of CDLoss on Feature Response

To investigate the impact of CDLoss on feature separation, T-SNE was used to visualize feature responses with and without CDLoss on the MNIST dataset. Digits 0, 1, 5, and 7 were designated as UCs, while the remaining digits served as KCs.

Figure 3 demonstrates the feature distributions for original methods and those improved with CDLoss. UCs are shown in blue, while other colors represent KCs. Without CDLoss, UCs tend to cluster near the center of the feature space, leading to significant overlap with KCs. This overlap complicates the model’s ability to distinguish between UCs and KCs, especially when their features are intrinsically similar.

The introduction of CDLoss reduces overlap by aligning samples more closely with their one-hot encoding vectors. For example, in the MSP method, the incorporation of CDLoss pushes UCs (e.g., category 6) towards the periphery of the feature space, minimizing their overlap with KCs. Similarly, in GCPL, CDLoss reduces overlap between UCs and classes 1 and 4. In the SLCPL framework, overlap between UCs and class 2 is effectively minimized.

However, certain limitations remain. In the RPL method, CDLoss reduces overlap between UCs and classes 2 and 4, but overlap with classes 3 and 5 persists. Similarly, ARPL exhibits reduced overlap for some categories (e.g., classes 2 and 4), but overlap with others remains near the feature space center. These observations suggest that while CDLoss significantly enhances feature separation, further optimization is needed for certain complex categories.

5.4. Stability Analysis of the Proposed Method

To evaluate the stability of CDLoss in OSR tasks, experiments were conducted on five datasets, with each dataset randomly divided into KCs and UCs following the settings described in Section 4.3. The process was repeated five times, and the mean and standard deviation of AUROC were calculated.

Figure 4 compares the stability of original methods (panel a) and CDLoss-enhanced methods (panel b). Across most datasets, the inclusion of CDLoss results in higher mean AUROC values and lower standard deviations, indicating improved stability. For example, ARPL and SLCPL exhibit more consistent performance after incorporating CDLoss, demonstrating its robustness in handling diverse data distributions.

However, on the TinyImageNet dataset, the stability of both ARPL and SLCPL decreases slightly, likely due to the dataset’s inherent complexity. TinyImageNet’s rich content and high variability make it challenging to optimize feature representations, potentially requiring further tuning of CDLoss parameters.

In conclusion, CDLoss enhances stability across most datasets and frameworks. Nonetheless, datasets like TinyImageNet highlight the need for additional optimization to address challenges posed by increased complexity and variability.

6. Conclusions

Open-set recognition (OSR) faces two key challenges: empirical space risk, where KCs are misclassified, and open space risk, where UCs are mistaken for KCs. Minimizing feature space overlap between KCs and UCs is essential to reducing open space risk and achieving better class separability.

This study introduces CDLoss, a lightweight and efficient loss function that minimizes the cosine distance between a sample’s one-hot encoding vector and its corresponding logit vector. By aligning logits with one-hot encoding vectors, CDLoss leverages their orthogonality to allocate more feature space for UCs, reducing overlap with KCs. Combined with Softmax or prototype loss, CDLoss further enhances feature representation, improving both the discriminative and generalization capabilities of the model.

Experimental results validate the effectiveness of CDLoss: (1) AUROC: CDLoss enhances AUROC across all baseline methods and datasets, indicating improved UC detection. (2) OSCR: By reducing inter-class overlap and improving intra-class aggregation, CDLoss increases OSCR across diverse datasets. (3) Accuracy: CDLoss improves the discriminative power of KC features, resulting in higher classification accuracy.

Despite its advantages, CDLoss has certain limitations. Its sensitivity to hyperparameter settings, especially across different datasets and model architectures, necessitates further research into robust hyperparameter optimization techniques. Additionally, CDLoss’s computational impact, while minimal, could be further reduced by integrating lightweight network designs, making it more practical for resource-constrained environments.

Future work could explore the integration of CDLoss into advanced frameworks, such as self-supervised learning and domain adaptation, to address OSR challenges more comprehensively. Beyond OSR, CDLoss holds promise for other computer vision tasks. For object detection, it can reduce feature space overlap between KCs and UCs, improving the identification and localization of unknown objects. In semantic segmentation, it can optimize pixel-level feature representations, reducing spatial overlap among categories and enhancing segmentation accuracy.

In high-stakes applications like medical diagnostics and autonomous driving, CDLoss can provide substantial benefits. For medical diagnosis, tailored one-hot encoding vectors for specific diseases can enhance the model’s ability to distinguish between various unknown conditions, enabling timely and accurate treatment. In autonomous driving, CDLoss can optimize feature spaces for different obstacles and traffic signs, reducing overlap with KCs and improving recognition accuracy and safety. These applications demonstrate the potential of CDLoss to address critical challenges in both research and real-world scenarios. This work highlights CDLoss as a versatile and effective tool for OSR, paving the way for further advancements in tackling open-set challenges.