Sales Forecasting for New Products Using Homogeneity-Based Clustering and Ensemble Method
Abstract
1. Introduction
2. Literature Review
3. Methodology
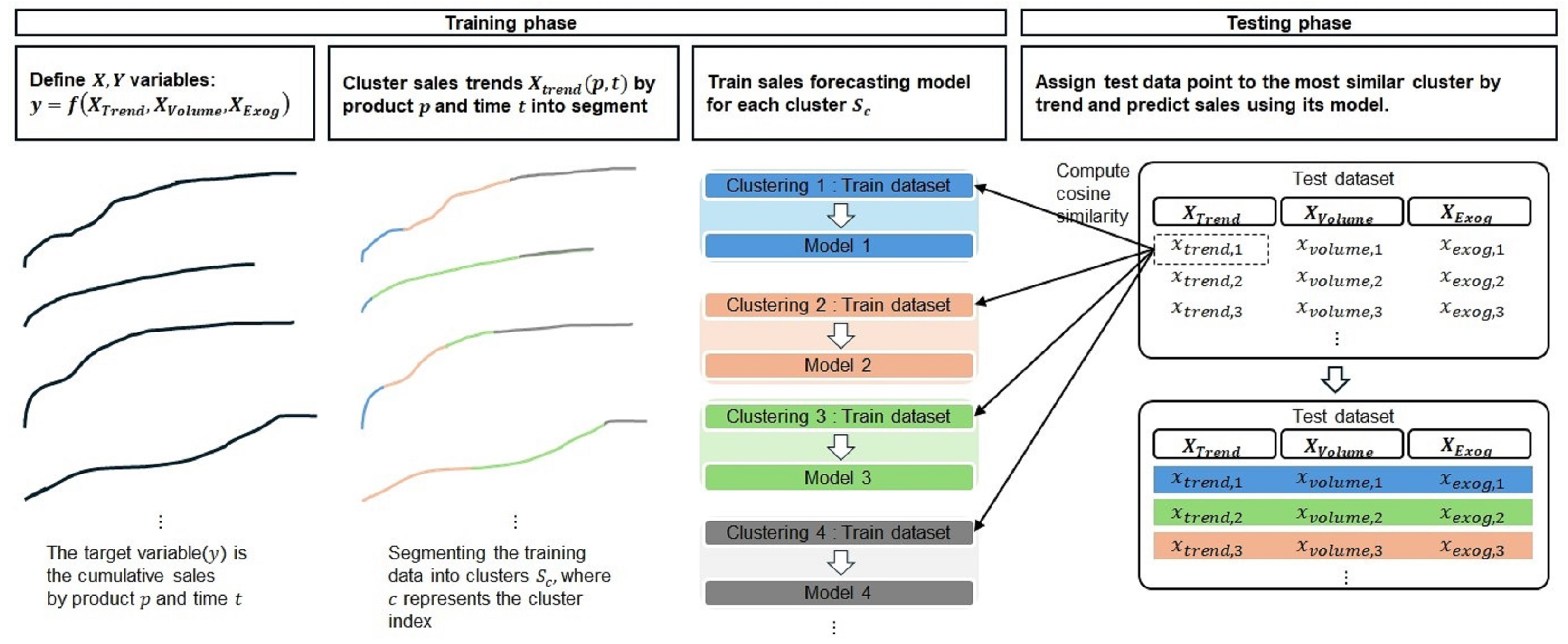
3.1. Proposed Framework
| Algorithm 1: New product sales forecasting with data homogeneity clustering. |
 |
3.2. Predictor Variables
3.2.1. Sales Volume-Related Variables ( to )
- : Cumulative sales for the previous week ();
- : Cumulative sales for the week before last ();
- : Cumulative sales for three weeks ago ();
- : Moving average of cumulative sales over the last two weeks ( and );
- : Moving average of cumulative sales over the last three weeks (, , and ).
3.2.2. Sales Trend-Related Variables ( to )
- : Number of weeks since product launch;
- : Change rate between cumulative sales for the previous week () and the week before last ();
- : Change rate between cumulative sales for the previous week () and three weeks prior ();
- : Moving average of the change rate between cumulative sales for the previous week () and the week before last ();
- : Moving average of the change rate between cumulative sales for the previous week () and three weeks prior ().
3.2.3. Exogenous Variables ( to )
- : Google Trends score for the previous week ();
- : Google Trends score for the week before last ();
- : Google Trends score for three weeks ago ().
3.3. K-Means Clustering Algorithm and Ensemble Method
3.3.1. K-Means Clustering
3.3.2. Ensemble Method
4. Experiments and Results
4.1. Data Collection and Preprocessing
4.2. Evaluation Procedures and Metrics
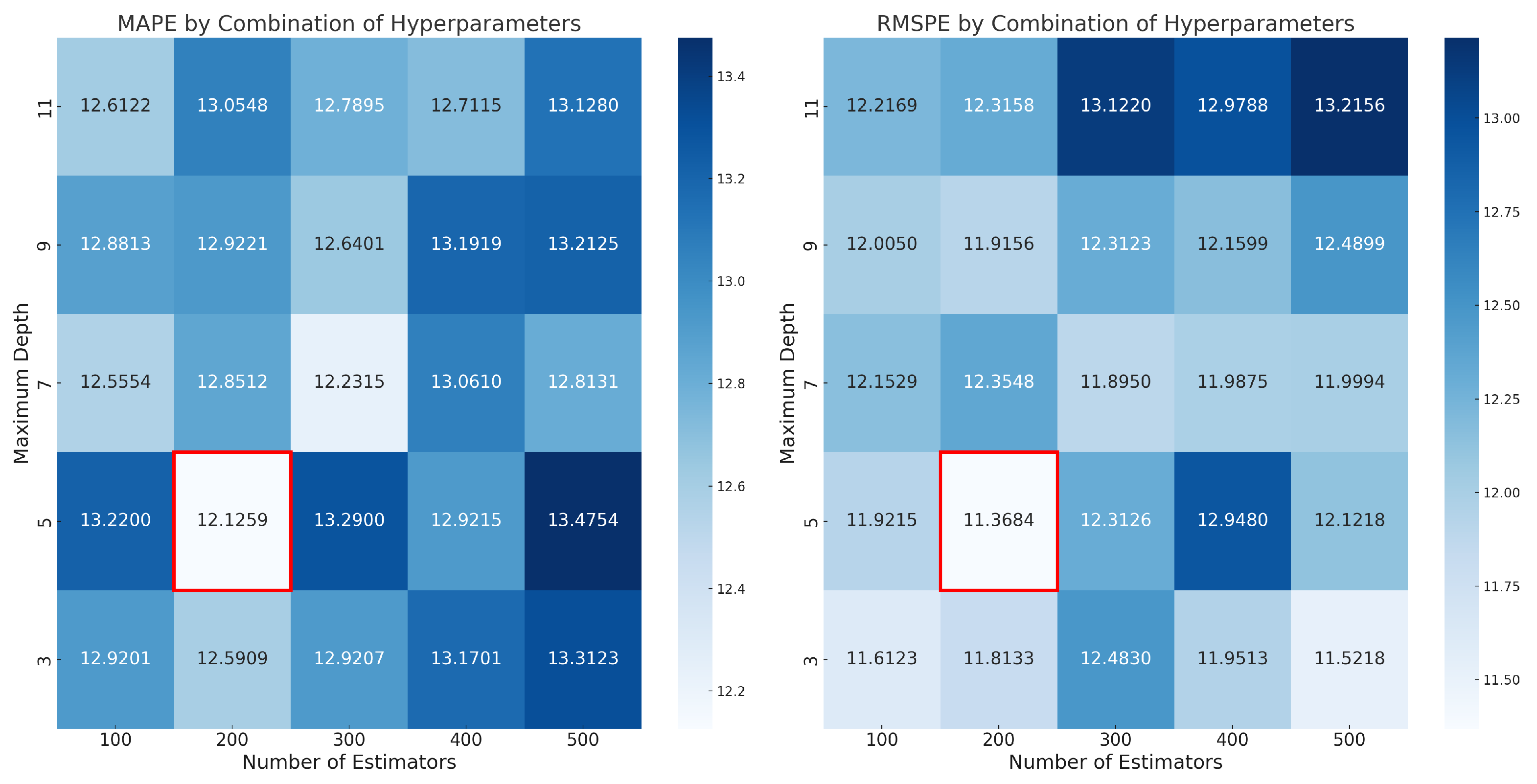
4.3. Model Development and Optimization
- Number of Estimators: This indicates the number of trees built in the model, with candidate values of 100, 200, 300, 400, and 500.
- Maximum Depth: This sets the maximum depth each tree can achieve, tested with values of 3, 5, 7, 9, and 11.
- Maximum Epochs: This defines the upper limit of training cycles, tested with values of 40, 60, 80, 100, and 200.
- Batch Size: This is the number of examples processed in each batch, with options of 128, 256, 512, 1024, and 2048.
- Virtual Batch Size: This size is used for “Ghost Batch Normalization”, with tested sizes of 32, 64, 128, 256, and 512.
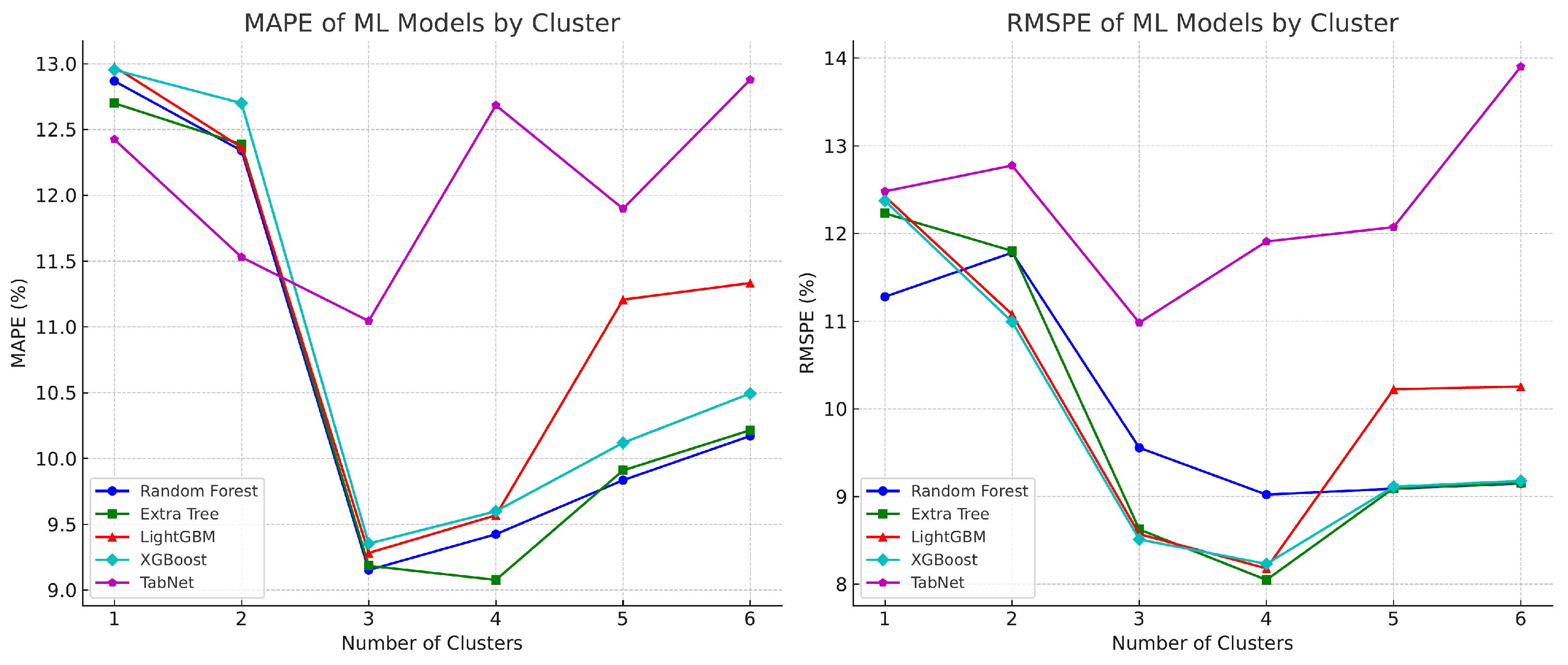
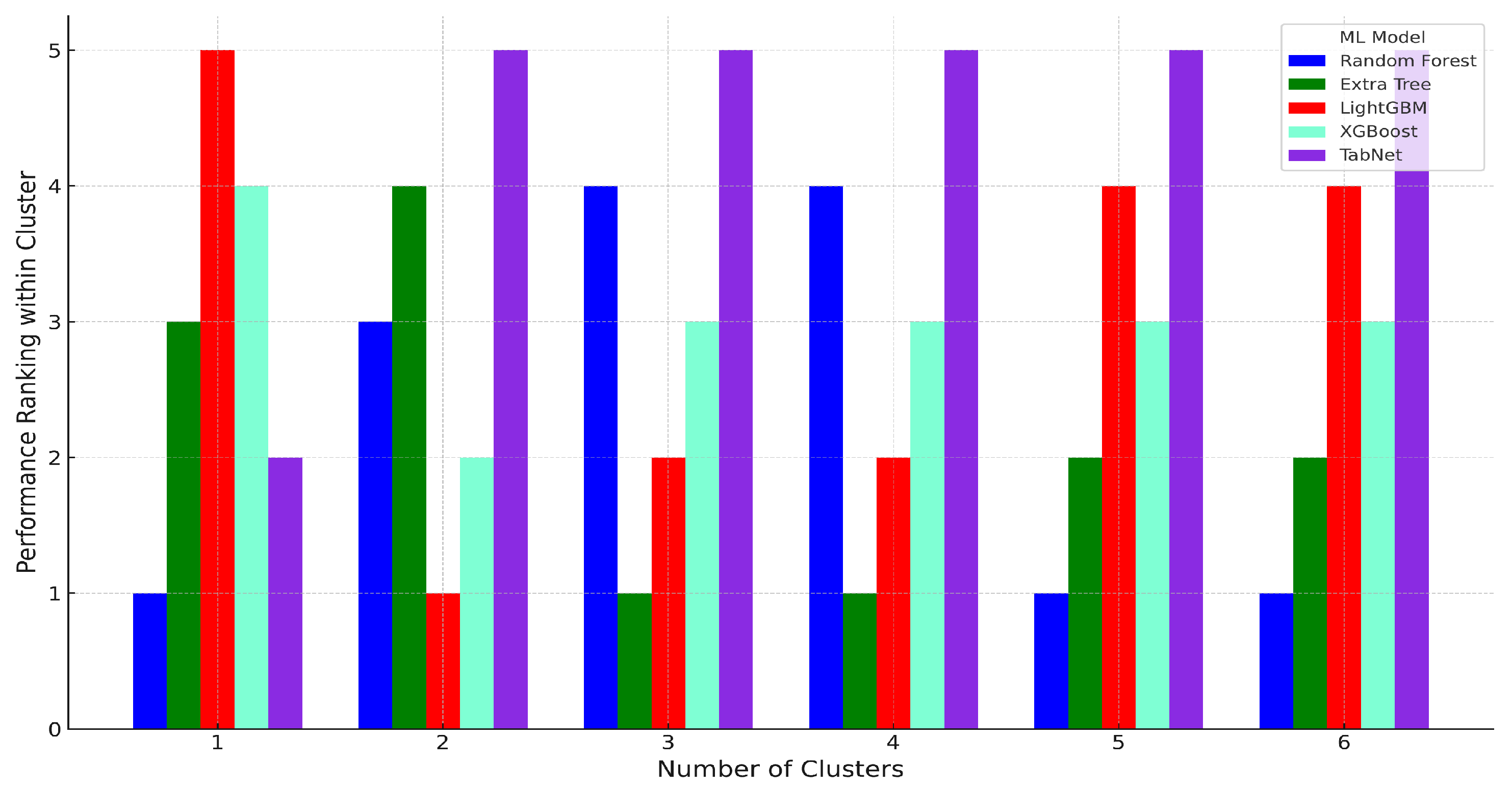
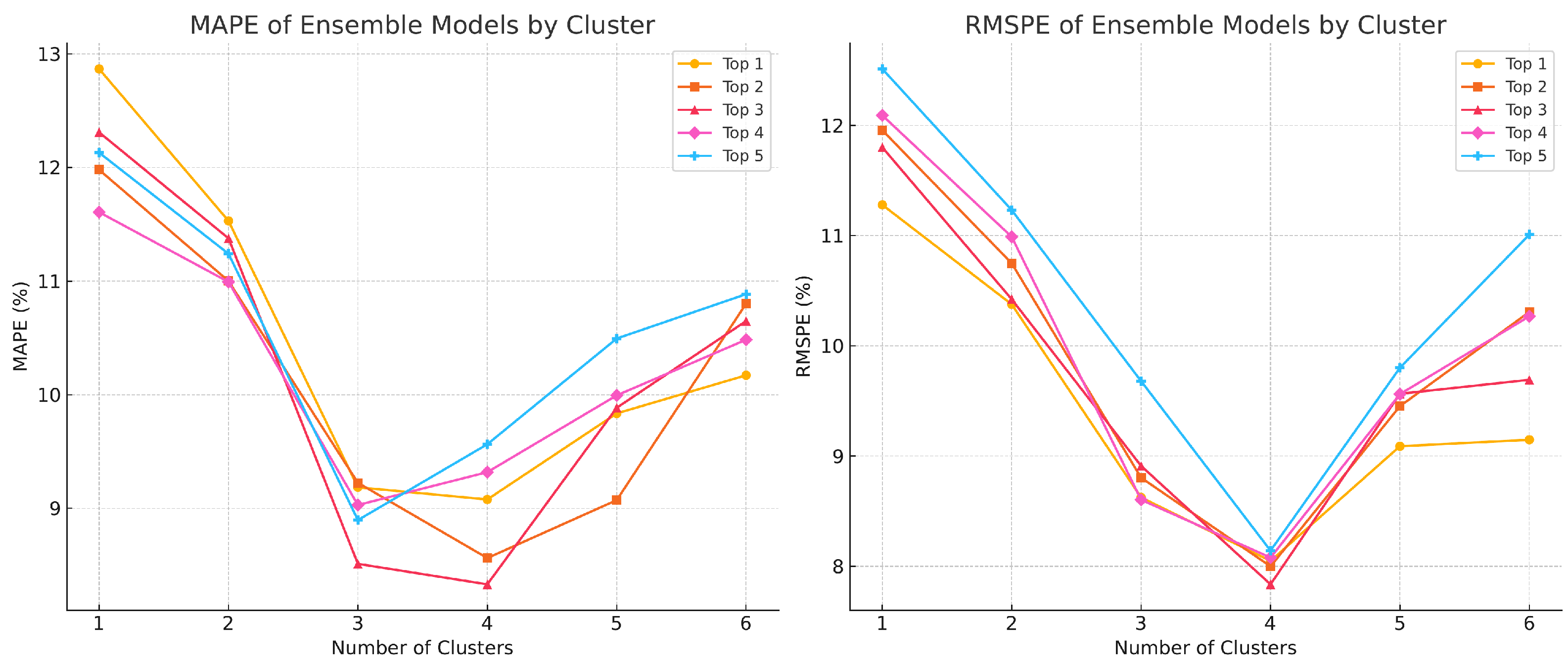
4.4. Model Results for Test Dataset
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cucculelli, M.; Peruzzi, V. Innovation over the Industry Life-Cycle. Does Ownership Matter? Res. Policy 2020, 49, 103878. [Google Scholar] [CrossRef]
- Baardman, L.; Levin, I.; Perakis, G.; Singhvi, D. Leveraging Comparables for New Product Sales Forecasting. Prod. Oper. Manag. 2018, 27, 2340–2343. [Google Scholar] [CrossRef]
- Kourentzes, N.; Trapero, J.R.; Barrow, D.K. Optimising Forecasting Models for Inventory Planning. Int. J. Prod. Econ. 2020, 225, 107597. [Google Scholar] [CrossRef]
- Huang, T.; Fildes, R.; Soopramanien, D. Forecasting retailer product sales in the presence of structural change. Eur. J. Oper. Res. 2019, 279, 459–470. [Google Scholar] [CrossRef]
- Feiler, D.; Tong, J.D. From Noise to Bias: Overconfidence in New Product Forecasting. Manag. Sci. 2021, 68, 4685–4702. [Google Scholar] [CrossRef]
- Hwang, S.; Yoon, G.; Baek, E.; Jeon, B.K. A Sales Forecasting Model for New-Released and Short-Term Product: A Case Study of Mobile Phones. Electronics 2023, 12, 3256. [Google Scholar] [CrossRef]
- Chen, I.F.; Lu, C.J. Sales forecasting by combining clustering and machine-learning techniques for computer retailing. Neural Comput. Appl. 2016, 28, 2633–2647. [Google Scholar] [CrossRef]
- Lo, J.E.; Kang, E.Y.C.; Chen, Y.N.; Hsieh, Y.T.; Wang, N.K.; Chen, T.C.; Chen, K.J.; Wu, W.C.; Hwang, Y.S.; Lo, F.S.; et al. Data Homogeneity Effect in Deep Learning-Based Prediction of Type 1 Diabetic Retinopathy. J. Diabetes Res. 2021, 2021, 1–9. [Google Scholar] [CrossRef]
- Fenza, G.; Gallo, M.; Loia, V.; Orciuoli, F.; Herrera-Viedma, E. Data set quality in Machine Learning: Consistency measure based on Group Decision Making. Appl. Soft Comput. 2021, 106, 107366. [Google Scholar] [CrossRef]
- Abuassba, A.O.M.; Zhang, D.; Luo, X.; Shaheryar, A.; Ali, H. Improving Classification Performance through an Advanced Ensemble Based Heterogeneous Extreme Learning Machines. Comput. Intell. Neurosci. 2017, 2017, 3405463. [Google Scholar] [CrossRef] [PubMed]
- Van Belle, J.; Guns, T.; Verbeke, W. Using shared sell-through data to forecast wholesaler demand in multi-echelon supply chains. Eur. J. Oper. Res. 2021, 288, 466–479. [Google Scholar] [CrossRef]
- Shwartz-Ziv, R.; Armon, A. Tabular Data: Deep Learning Is Not All You Need. Inf. Fusion 2022, 81, 84–90. [Google Scholar] [CrossRef]
- Grinsztajn, L.; Oyallon, E.; Varoquaux, G. Why Do Tree-Based Models Still Outperform Deep Learning on Typical Tabular Data? In Advances in Neural Information Processing Systems; Koyejo, S., Mohamed, S., Agarwal, A., Belgrave, D., Cho, K., Oh, A., Eds.; Curran Associates, Inc.: Nice, France, 2022; Volume 35, pp. 507–520. [Google Scholar]
- Matloob, F.; Ghazal, T.M.; Taleb, N.; Aftab, S.; Ahmad, M.; Khan, M.A. Software Defect Prediction Using Ensemble Learning: A Systematic Literature Review. IEEE Access 2021, 9, 98754–98771. [Google Scholar] [CrossRef]
- Uddin, S.; Lu, H. Confirming the statistically significant superiority of tree-based machine learning algorithms over their counterparts for tabular data. PLoS ONE 2024, 19, e0301541. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Kwong, S.; Wang, R.; Li, X.; Li, K.; Kong, X. Class-specific soft voting based multiple extreme learning machines ensemble. Neurocomputing 2015, 149, 275–284. [Google Scholar] [CrossRef]
- Khamparia, A.; Singh, A.; Anand, D.; Gupta, D.; Khanna, A.; Arun Kumar, N.; Tan, J. A novel deep learning-based multi-model ensemble method for the prediction of neuromuscular disorders. Neural Comput. Appl. 2018, 32, 11083–11095. [Google Scholar] [CrossRef]
- Lee, H.; Kim, S.G.; Park, H.w.; Kang, P. Pre-launch new product demand forecasting using the Bass model: A statistical and machine learning-based approach. Technol. Forecast. Soc. Change 2014, 86, 49–64. [Google Scholar] [CrossRef]
- Tanaka, K. A sales forecasting model for new-released and nonlinear sales trend products. Expert Syst. Appl. 2010, 37, 7387–7393. [Google Scholar] [CrossRef]
- Elalem, Y.K.; Maier, S.; Seifert, R.W. A machine learning-based framework for forecasting sales of new products with short life cycles using deep neural networks. Int. J. Forecast. 2022, 39, 1874–1894. [Google Scholar] [CrossRef]
- van Steenbergen, R.; Mes, M. Forecasting demand profiles of new products. Decis. Support Syst. 2020, 139, 113401. [Google Scholar] [CrossRef]
- Yin, P.; Dou, G.; Lin, X.; Liu, L. A hybrid method for forecasting new product sales based on fuzzy clustering and deep learning. Kybernetes 2020, 49, 3099–3118. [Google Scholar] [CrossRef]
- Ekambaram, V.; Manglik, K.; Mukherjee, S.; Sajja, S.S.K.; Dwivedi, S.; Raykar, V. Attention Based Multi-Modal New Product Sales Time-series Forecasting. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual, 23–27 August 2020; pp. 3110–3118. [Google Scholar] [CrossRef]
- Abubaker, F.; Ala’Khalifeh. Sales’ Forecasting Based on Big Data and Machine Learning Analysis. In Proceedings of the 2023 9th International Conference on Control, Decision and Information Technologies (CoDIT), Rome, Italy, 3–6 July 2023; pp. 804–808. [Google Scholar] [CrossRef]
- Smirnov, P.S.; Sudakov, V.A. Forecasting New Product Demand Using Machine Learning. J. Phys. Conf. Ser. 2021, 1925, 012033. [Google Scholar] [CrossRef]
- Afrin, K.; Nepal, B.; Monplaisir, L. A Data-Driven Framework to New Product Demand Prediction: Integrating Product Differentiation and Transfer Learning Approach. Expert Syst. Appl. 2018, 108, 246–257. [Google Scholar] [CrossRef]
- Anitha, S.; Neelakandan, R. A Demand Forecasting Model Leveraging Machine Learning to Decode Customer Preferences for New Fashion Products. Complexity 2024, 2024, 8425058. [Google Scholar] [CrossRef]
- Xu, Q.; Sharma, V. Ensemble Sales Forecasting Study in Semiconductor Industry. In Advances in Data Mining. Applications and Theoretical Aspects, Proceedings of the 17th Industrial Conference (ICDM 2017), New York, NY, USA, 12–13 July 2017; Lecture Notes in Computer Science; Perner, P., Ed.; Springer: Cham, Switzerland, 2017; Volume 10357, pp. 31–44. [Google Scholar] [CrossRef]
- Yuan, F.C.; Lee, C.H. Intelligent Sales Volume Forecasting Using Google Search Engine Data. Soft Comput. 2020, 24, 2033–2047. [Google Scholar] [CrossRef]
- Wolters, J.; Huchzermeier, A. Joint In-Season and Out-of-Season Promotion Demand Forecasting in a Retail Environment. J. Retail. 2021, 97, 73–87. [Google Scholar] [CrossRef]
- Van Donselaar, K.H.; Peters, J.; de Jong, A.; Broekmeulen, R.A.C.M. Analysis and Forecasting of Demand During Promotions for Perishable Items. Int. J. Prod. Econ. 2016, 172, 65–75. [Google Scholar] [CrossRef]
- Huber, J.; Gossmann, A.; Stuckenschmidt, H. Cluster-Based Hierarchical Demand Forecasting for Perishable Goods. Expert Syst. Appl. 2017, 77, 138–150. [Google Scholar] [CrossRef]
- Sohrabpour, V.; Oghazi, P.; Toorajipour, R.; Nazarpour, A. Export sales forecasting using artificial intelligence. Technol. Forecast. Soc. Change 2020, 163, 120480. [Google Scholar] [CrossRef]
- Chen, T.; Yin, H.; Chen, H.; Wang, H.; Zhou, X.; Li, X. Online sales prediction via trend alignment-based multitask recurrent neural networks. Knowl. Inf. Syst. 2019, 62, 2139–2167. [Google Scholar] [CrossRef]
- Bi, X.; Adomavicius, G.; Li, W.; Qu, A. Improving Sales Forecasting Accuracy: A Tensor Factorization Approach with Demand Awareness. INFORMS J. Comput. 2020, 34, 1644–1660. [Google Scholar] [CrossRef]
- Boone, T.; Ganeshan, R.; Hicks, R.L.; Sanders, N.R. Can Google Trends Improve Your Sales Forecast? Prod. Oper. Manag. 2018, 27, 1770–1774. [Google Scholar] [CrossRef]
- Skenderi, G.; Joppi, C.; Denitto, M.; Cristani, M. Well Googled Is Half Done: Multimodal Forecasting of New Fashion Product Sales with Image-Based Google Trends. J. Forecast. 2024, 43, 1982–1997. [Google Scholar] [CrossRef]
- Xiao-ping, X. More effective algorithm for K-means clustering. Comput. Eng. Des. 2008, 29, 378–380. [Google Scholar]
- Kao, Y.; Zahara, E.; Kao, I. A hybridized approach to data clustering. Expert Syst. Appl. 2008, 34, 1754–1762. [Google Scholar] [CrossRef]
- Xie, Y.; Peng, M. Forest fire forecasting using ensemble learning approaches. Neural Comput. Appl. 2019, 31, 4541–4550. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Strobl, C.; Boulesteix, A.L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Nice, France, 2017; Volume 30. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Arik, S.Ö.; Pfister, T. TabNet: Attentive Interpretable Tabular Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021. [Google Scholar] [CrossRef]
- Ambarwari, A.; Jafar Adrian, Q.; Herdiyeni, Y. Analysis of the Effect of Data Scaling on the Performance of the Machine Learning Algorithm for Plant Identification. J. Resti (Rekayasa Sist. Dan Teknol. Inf.) 2020, 4, 117–122. [Google Scholar] [CrossRef]
- de Amorim, L.B.V.; Cavalcanti, G.D.C.; Cruz, R.M.O. Meta-Scaler: A Meta-Learning Framework for the Selection of Scaling Techniques. IEEE Trans. Neural Netw. Learn. Syst. 2024, Early Access. [Google Scholar] [CrossRef]
- Varma, S.; Simon, R. Nested cross-validation when selecting classifiers is overzealous for most practical applications. Expert Syst. Appl. 2021, 184, 115664. [Google Scholar] [CrossRef]
- Wong, T.T. Performance evaluation of classification algorithms by k-fold and leave-one-out cross validation. Pattern Recognit. 2015, 48, 2839–2846. [Google Scholar] [CrossRef]
- Shao, Z.; Er, M.J. Efficient Leave-One-Out Cross-Validation-based Regularized Extreme Learning Machine. Neurocomputing 2016, 194, 260–270. [Google Scholar] [CrossRef]
- Hadavandi, E.; Shavandi, H.; Ghanbari, A. An improved sales forecasting approach by the integration of genetic fuzzy systems and data clustering: Case study of printed circuit board. Expert Syst. Appl. 2011, 38, 9392–9399. [Google Scholar] [CrossRef]
- Panarese, A.; Settanni, G.; Vitti, V.; Galiano, A. Developing and Preliminary Testing of a Machine Learning-Based Platform for Sales Forecasting Using a Gradient Boosting Approach. Appl. Sci. 2022, 12, 11054. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)? – Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Bashir, N.; Mir, A.A.; Daud, A.; Rafique, M.; Bukhari, A. Time Series Reconstruction With Feature-Driven Imputation: A Comparison of Base Learning Algorithms. IEEE Access 2024, 12, 85511–85530. [Google Scholar] [CrossRef]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Abbas, F.; Zhang, F.; Ismail, M.; Khan, G.; Iqbal, J.; Alrefaei, A.; Albeshr, M. Optimizing Machine Learning Algorithms for Landslide Susceptibility Mapping Along the Karakoram Highway, Gilgit Baltistan, Pakistan: A Comparative Study of Baseline, Bayesian, and Metaheuristic Hyperparameter Optimization Techniques. Sensors 2023, 23, 6843. [Google Scholar] [CrossRef] [PubMed]
- Probst, P.; Wright, M.N.; Boulesteix, A. Hyperparameters and tuning strategies for random forest. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 9, e1301. [Google Scholar] [CrossRef]
- Hancock, J.T.; Khoshgoftaar, T. Optimizing Ensemble Trees for Big Data Healthcare Fraud Detection. In Proceedings of the 2022 IEEE 23rd International Conference on Information Reuse and Integration for Data Science (IRI), San Diego, CA, USA, 9–11 August 2022; pp. 243–249. [Google Scholar] [CrossRef]
- Ryu, S.E.; Shin, D.H.; Chung, K. Prediction Model of Dementia Risk Based on XGBoost Using Derived Variable Extraction and Hyper Parameter Optimization. IEEE Access 2020, 8, 177708–177720. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgo, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2020, 54, 1937–1967. [Google Scholar] [CrossRef]
- Zhang, L.; Suganthan, P. Visual Tracking With Convolutional Random Vector Functional Link Network. IEEE Trans. Cybern. 2017, 47, 3243–3253. [Google Scholar] [CrossRef] [PubMed]
- Osawa, K.; Tsuji, Y.; Ueno, Y.; Naruse, A.; Foo, C.S.; Yokota, R. Scalable and Practical Natural Gradient for Large-Scale Deep Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 404–415. [Google Scholar] [CrossRef] [PubMed]
- Thietart, R.; Vivas, R. An Empirical Investigation of Success Strategies for Businesses Along the Product Life Cycle. Manag. Sci. 1984, 30, 1405–1423. [Google Scholar] [CrossRef]
- Zhu, X.; Jiao, C.; Yuan, T. Optimal decisions on product reliability, sales and promotion under nonrenewable warranties. Reliab. Eng. Syst. Saf. 2019, 192, 106268. [Google Scholar] [CrossRef]
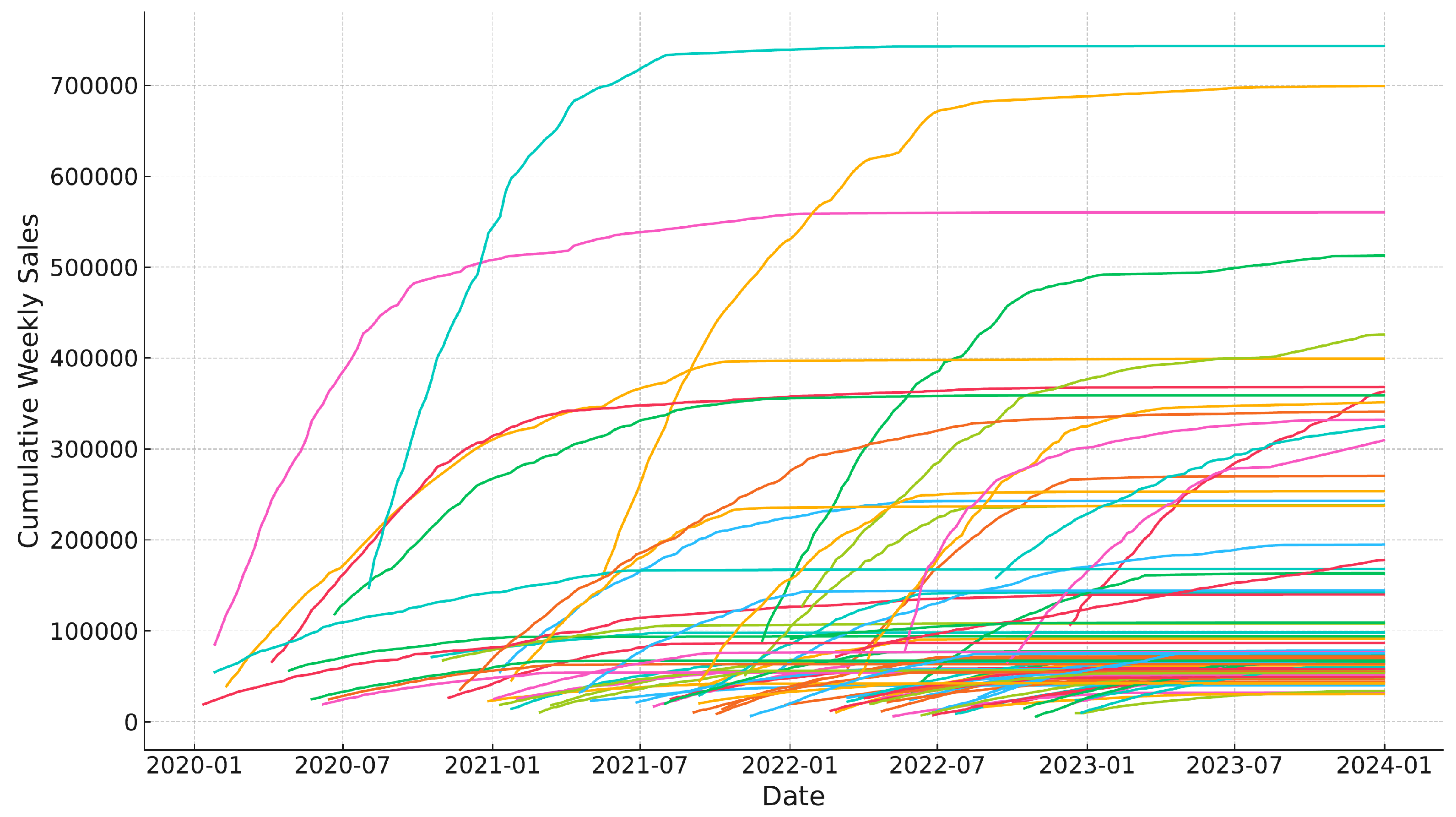
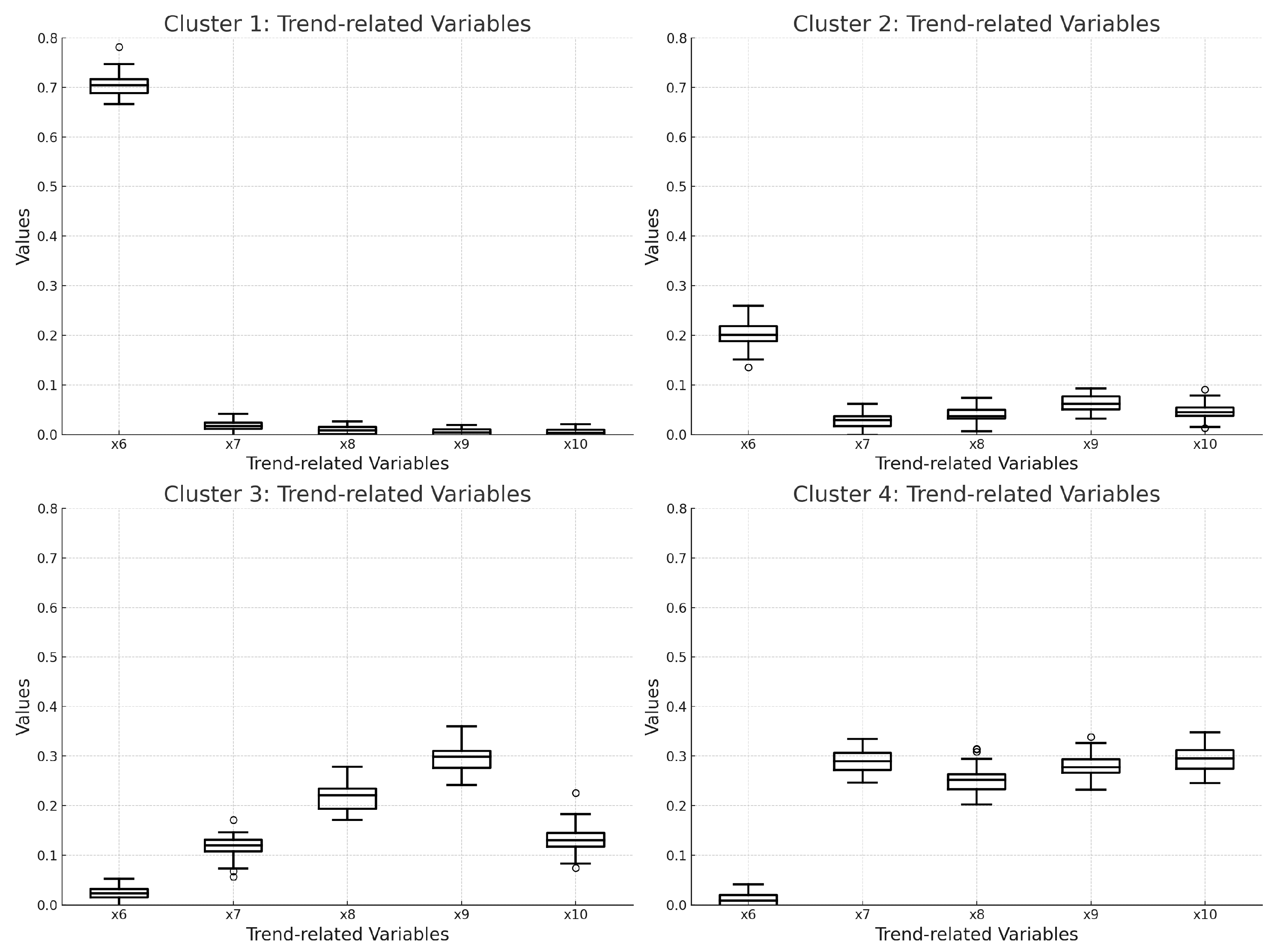
| Data Count | Mean | Median | Min | Max |
|---|---|---|---|---|
| 10,012 | 92,281.12 | 55,698 | 44 | 73,813 |
| Number of Products | Mean | Median | Min | Max |
|---|---|---|---|---|
| 79 | 107.57 | 109 | 50 | 190 |
| Dataset | Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 |
|---|---|---|---|---|
| Training | 3380 | 3700 | 1194 | 1669 |
| Test | 30 | 17 | 14 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, S.; Lee, Y.; Jeon, B.-K.; Oh, S.H. Sales Forecasting for New Products Using Homogeneity-Based Clustering and Ensemble Method. Electronics 2025, 14, 520. https://doi.org/10.3390/electronics14030520
Hwang S, Lee Y, Jeon B-K, Oh SH. Sales Forecasting for New Products Using Homogeneity-Based Clustering and Ensemble Method. Electronics. 2025; 14(3):520. https://doi.org/10.3390/electronics14030520
Chicago/Turabian StyleHwang, Seongbeom, Yuna Lee, Byoung-Ki Jeon, and Sang Ho Oh. 2025. "Sales Forecasting for New Products Using Homogeneity-Based Clustering and Ensemble Method" Electronics 14, no. 3: 520. https://doi.org/10.3390/electronics14030520
APA StyleHwang, S., Lee, Y., Jeon, B.-K., & Oh, S. H. (2025). Sales Forecasting for New Products Using Homogeneity-Based Clustering and Ensemble Method. Electronics, 14(3), 520. https://doi.org/10.3390/electronics14030520






