The Intrinsic Mechanism and Suppression Strategy of Transient Current Imbalance Among Parallel Converters
Abstract
:1. Introduction
2. State–Space Model of Parallel Interleaved Phase-Shift Full-Bridge Converters
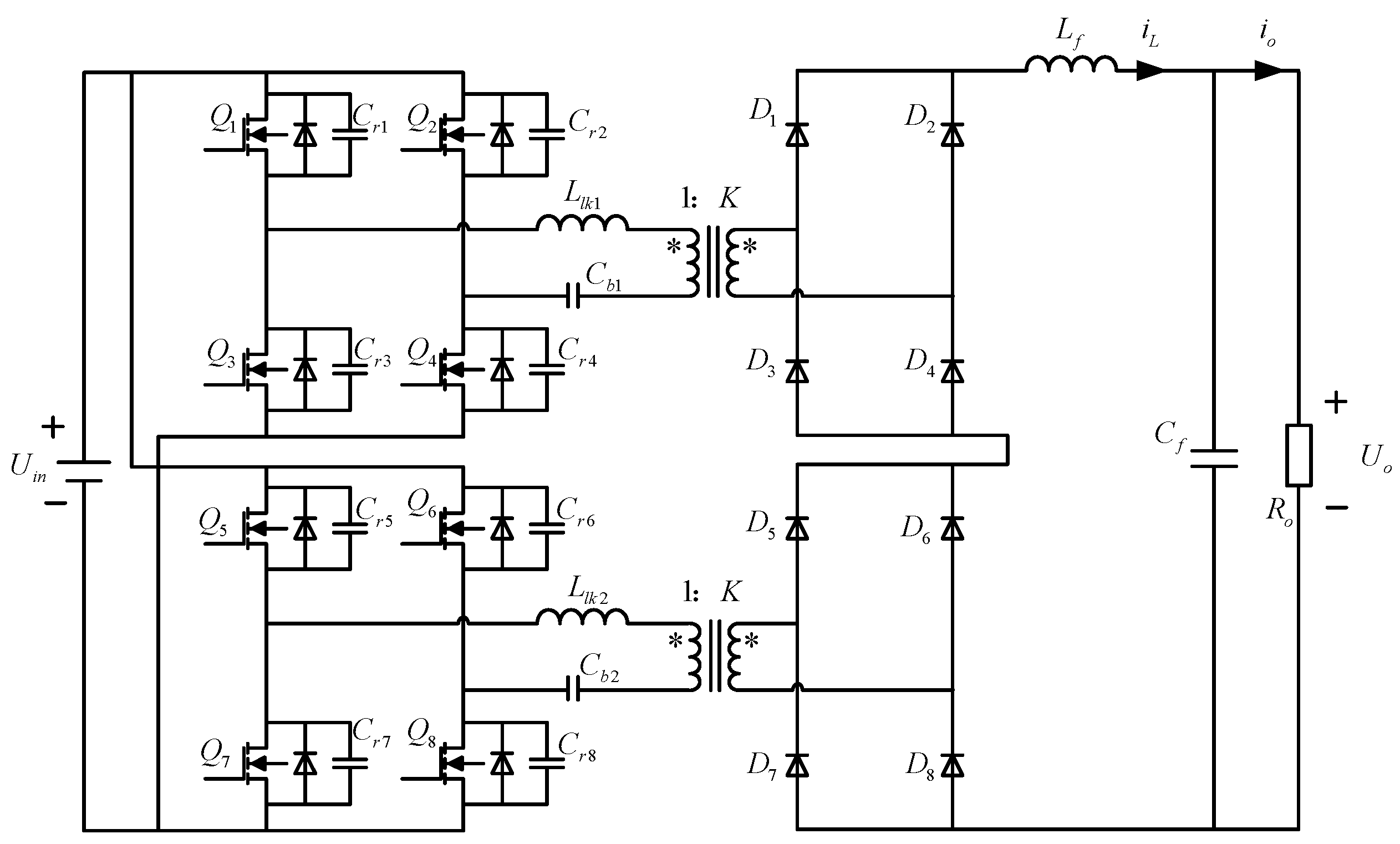
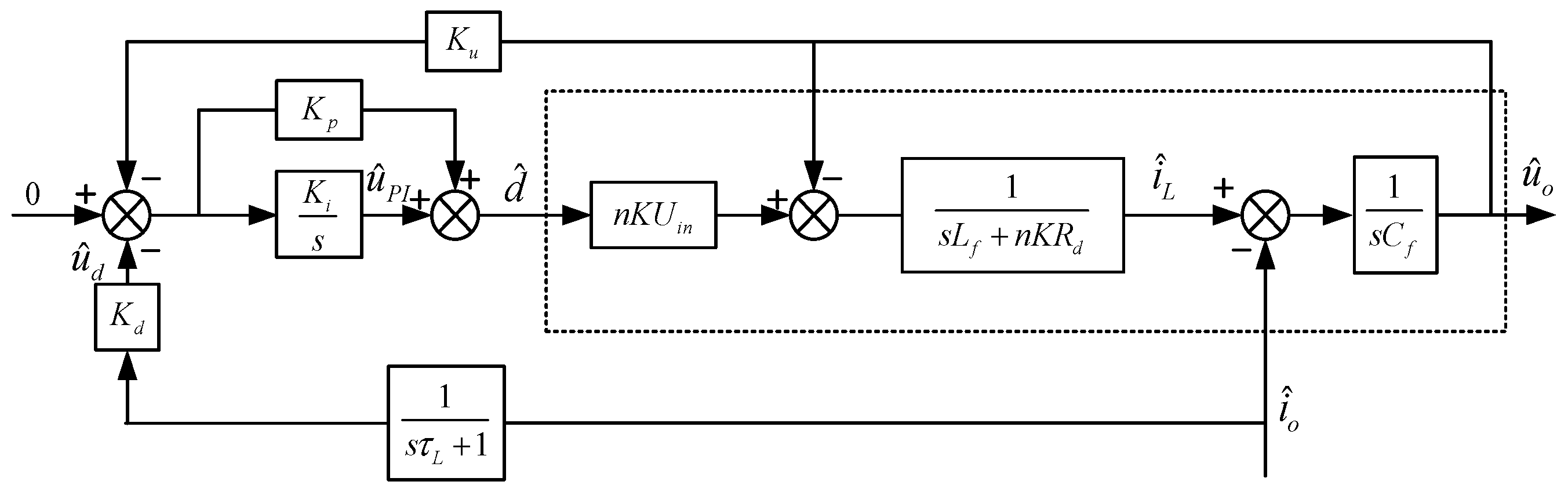
2.1. Modeling of Single-Module IPOS Phase-Shifted Full-Bridge System
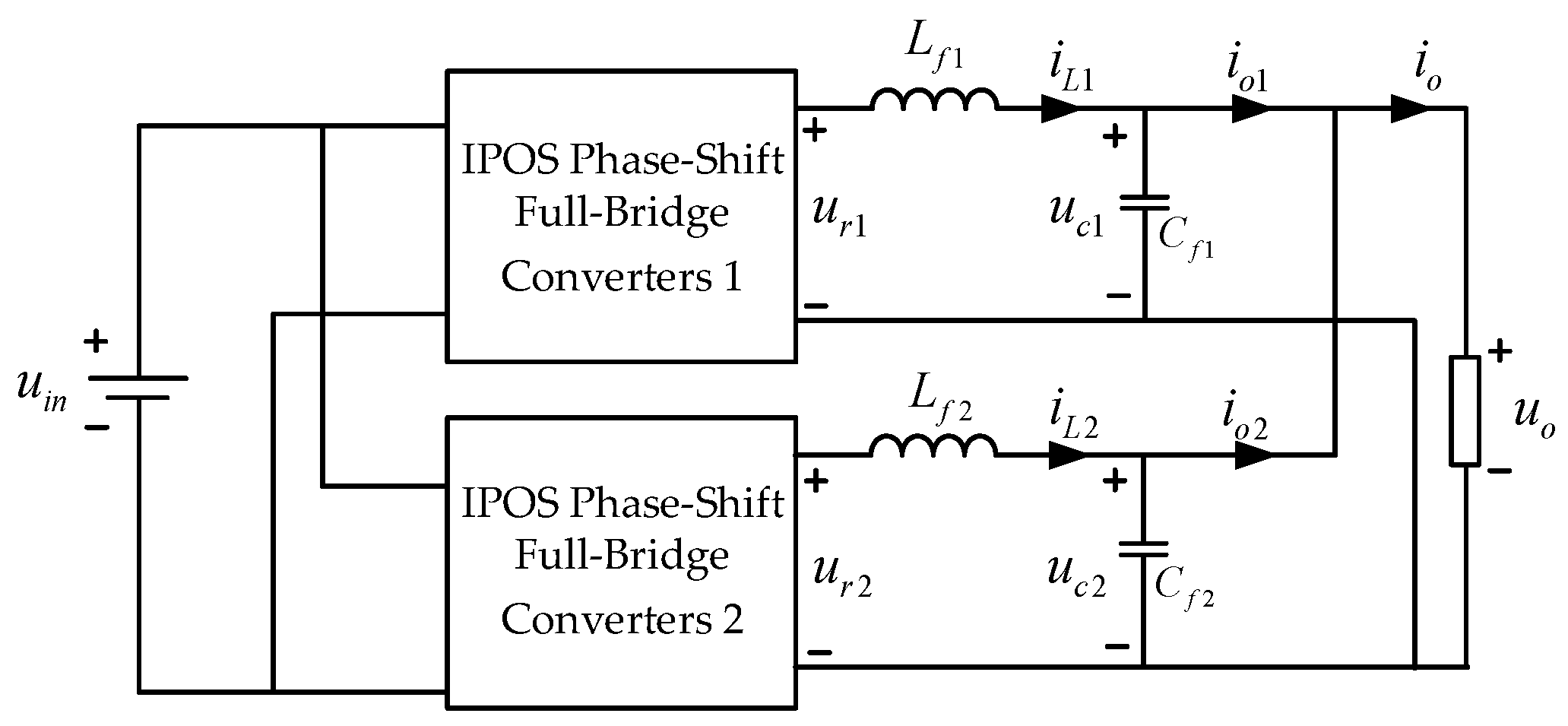
2.2. Model of a Parallel System with Two IPOS Phase-Shift Full-Bridge Converters
3. Impact of Inconsistency of the Output Voltage Feedback Coefficients on the Transient Currents of the Parallel System
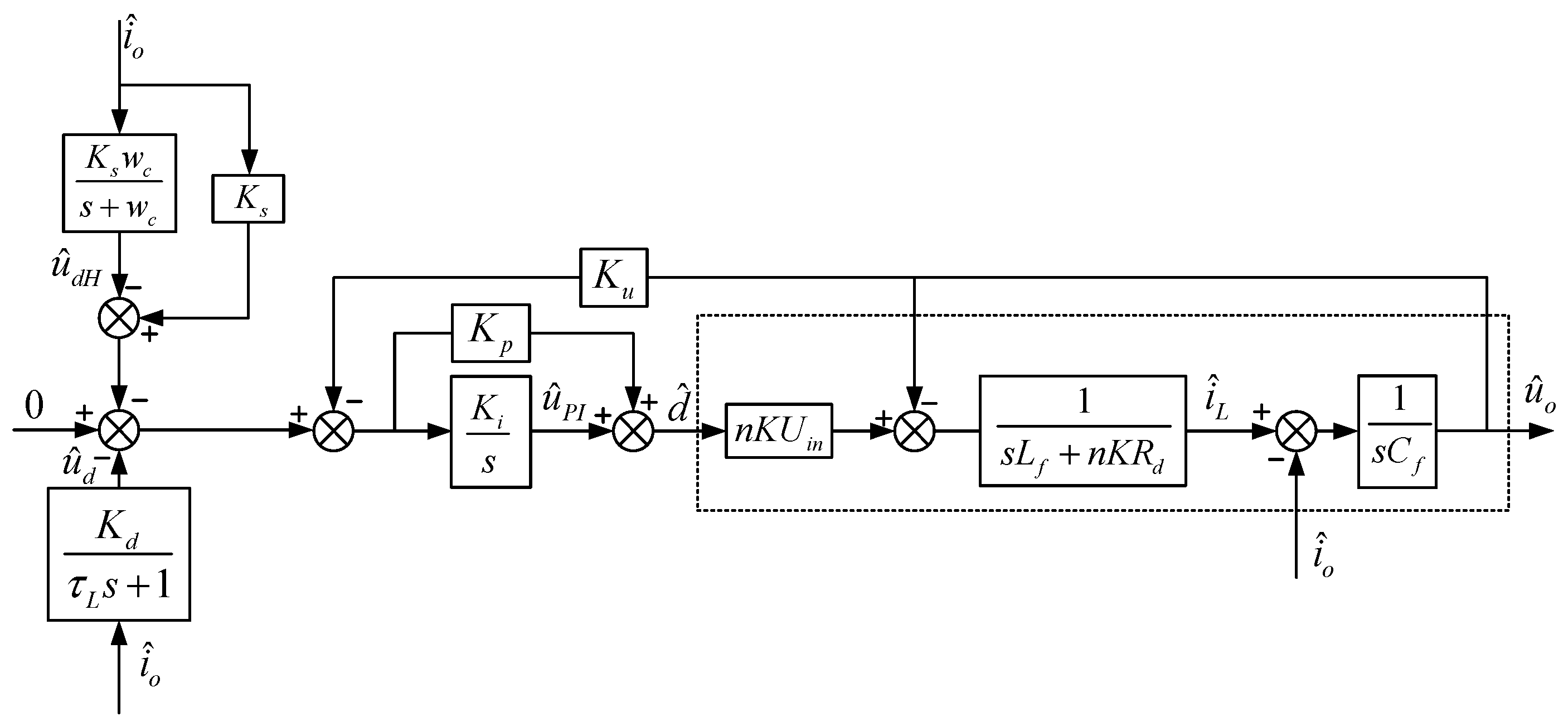
4. Improved Virtual Impedance Droop Control and Stability
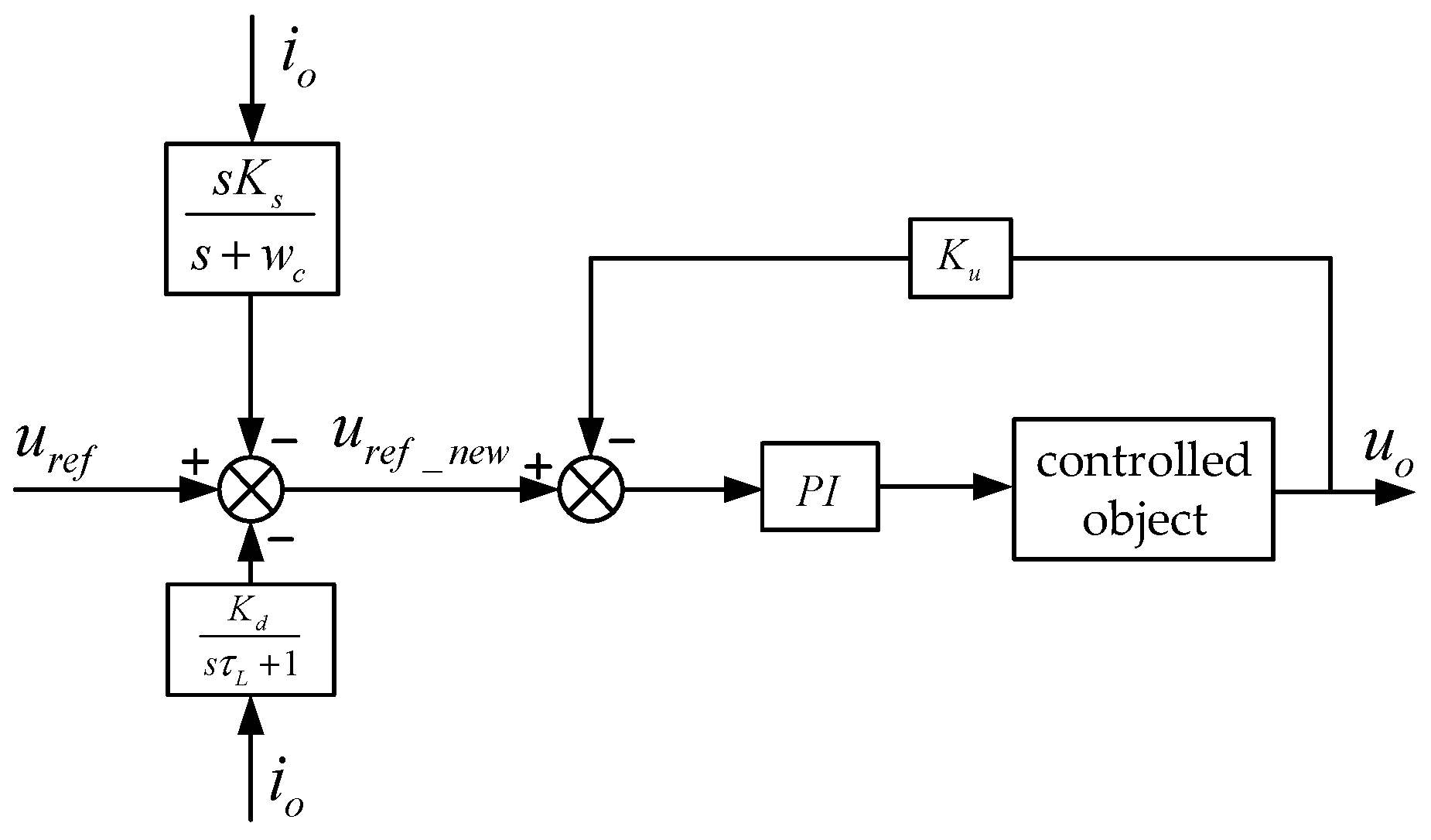
4.1. Improved Virtual Impedance Droop Control
4.2. Improved Virtual Impedance Control Stability Analysis
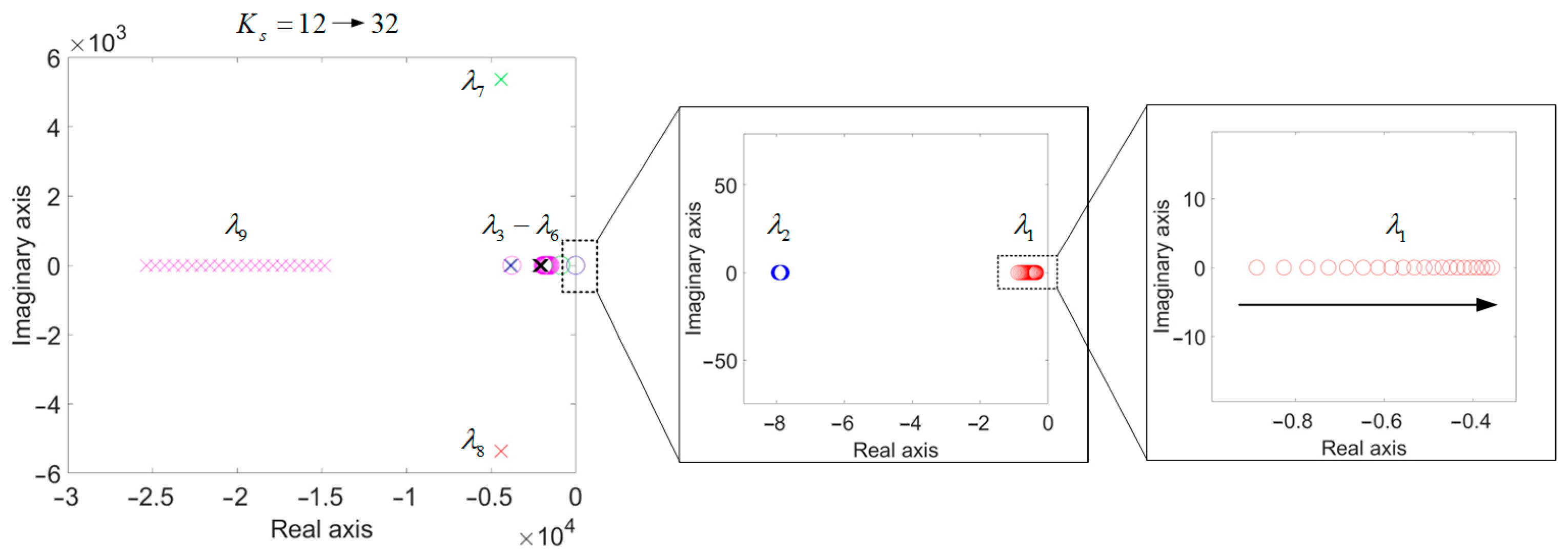
4.2.1. Impact of Gain on System Stability and Dynamic Performance
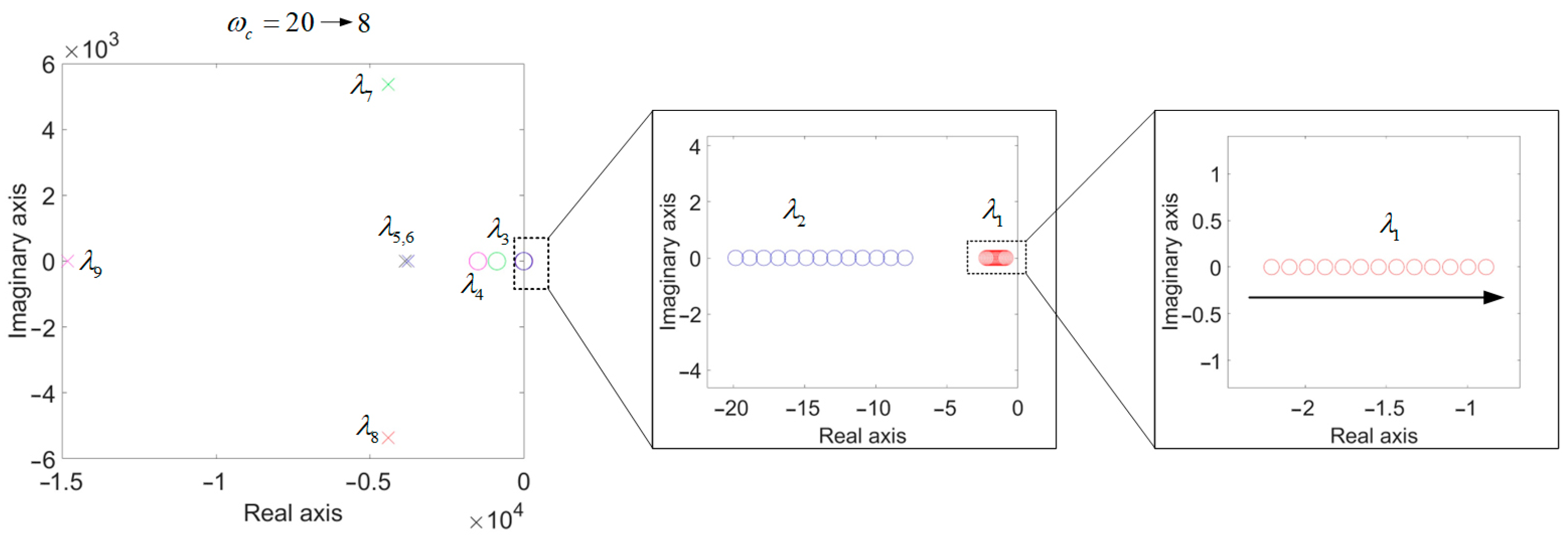
4.2.2. Impact of Cutoff Frequency on System Stability and Dynamic Performance
5. Simulation and Experimental Verification
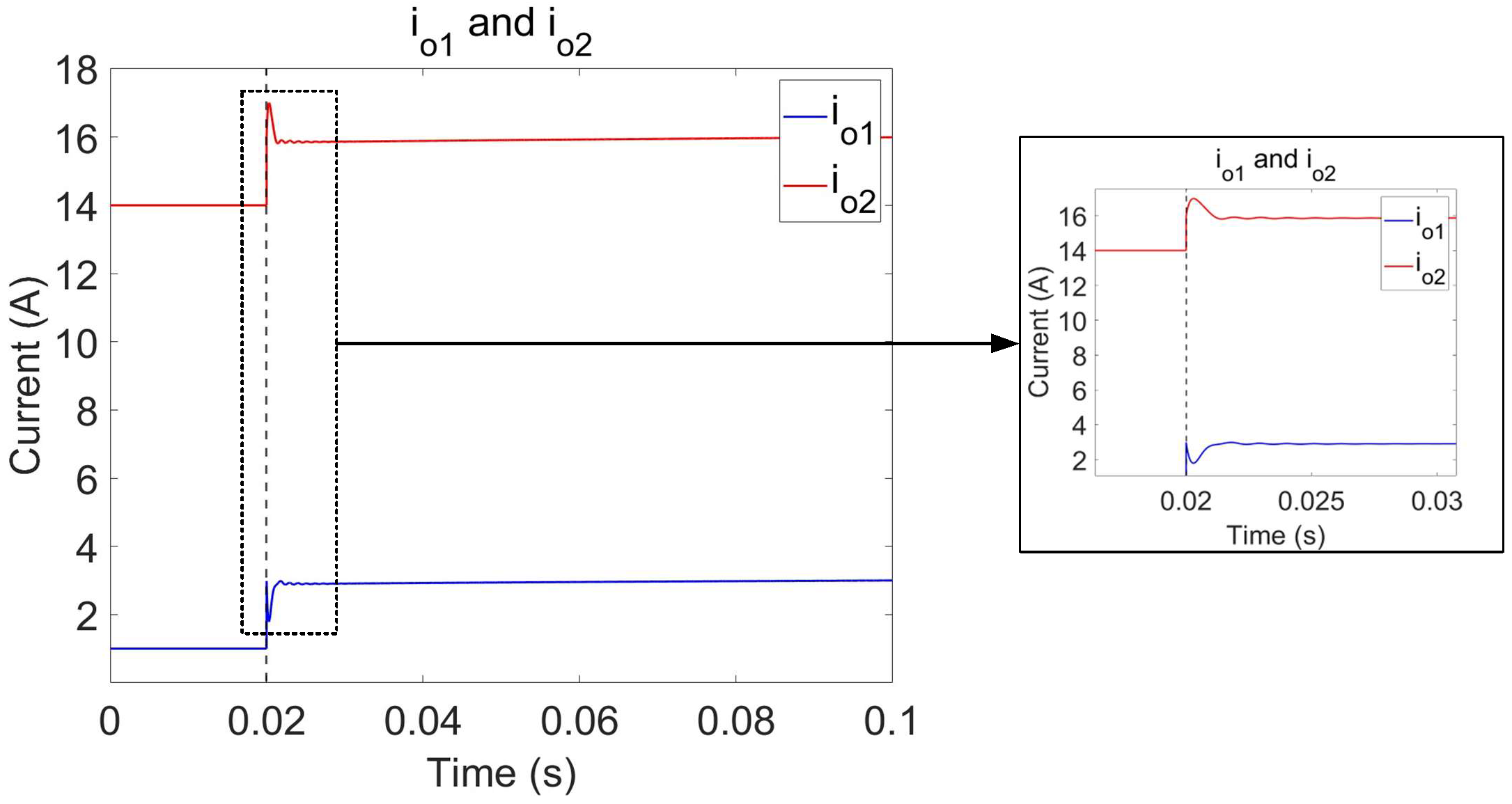
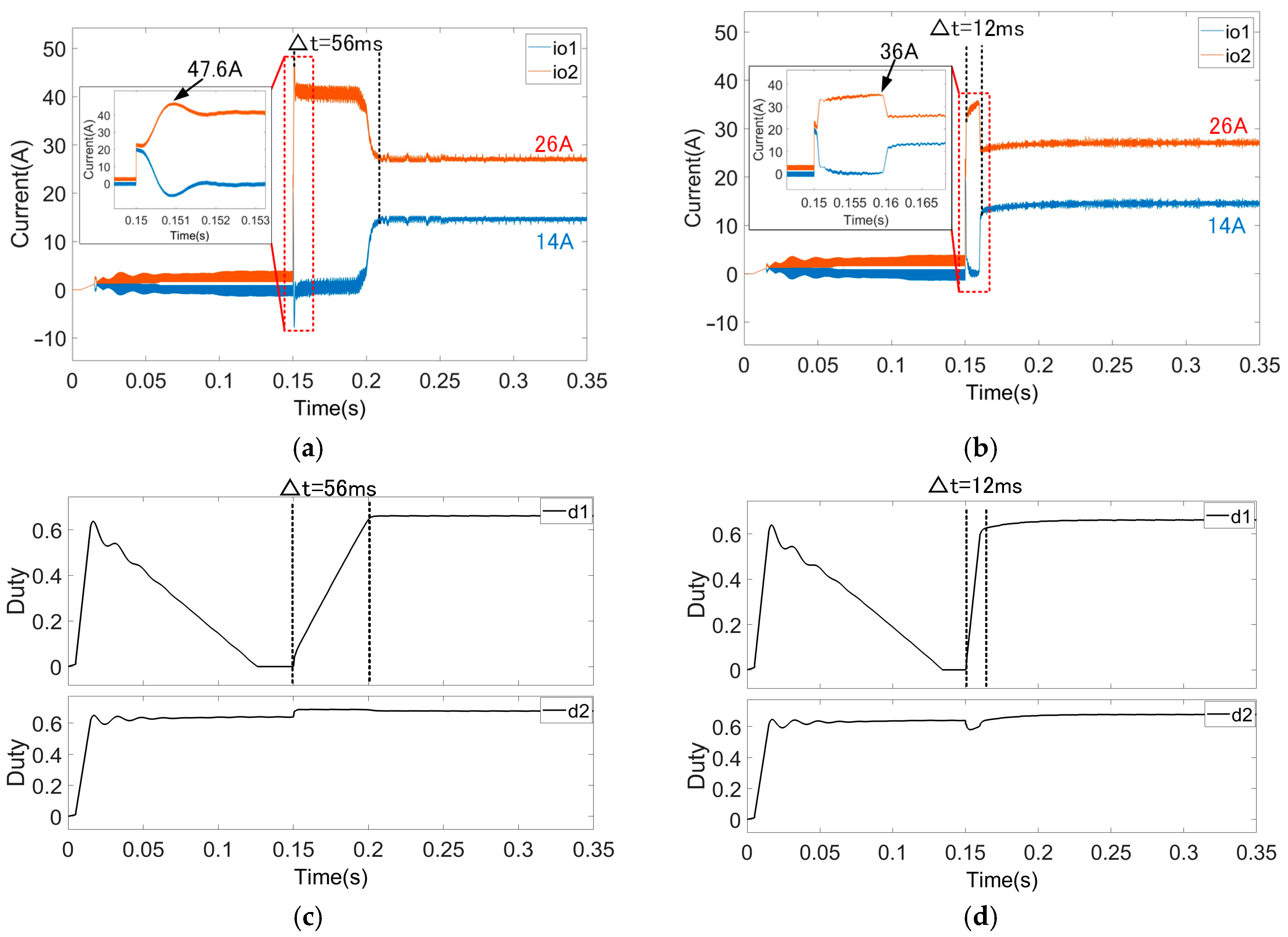
5.1. Simulation
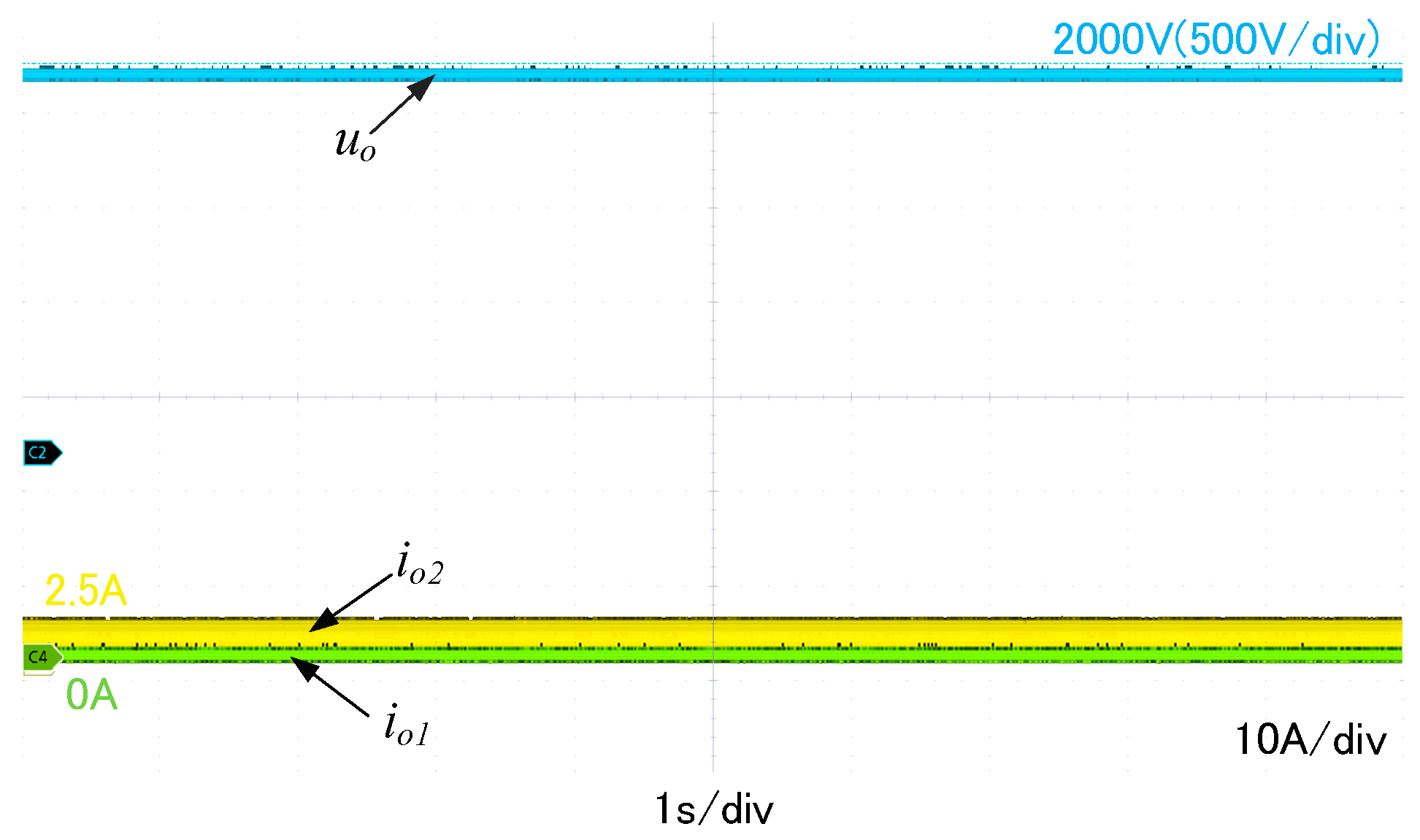
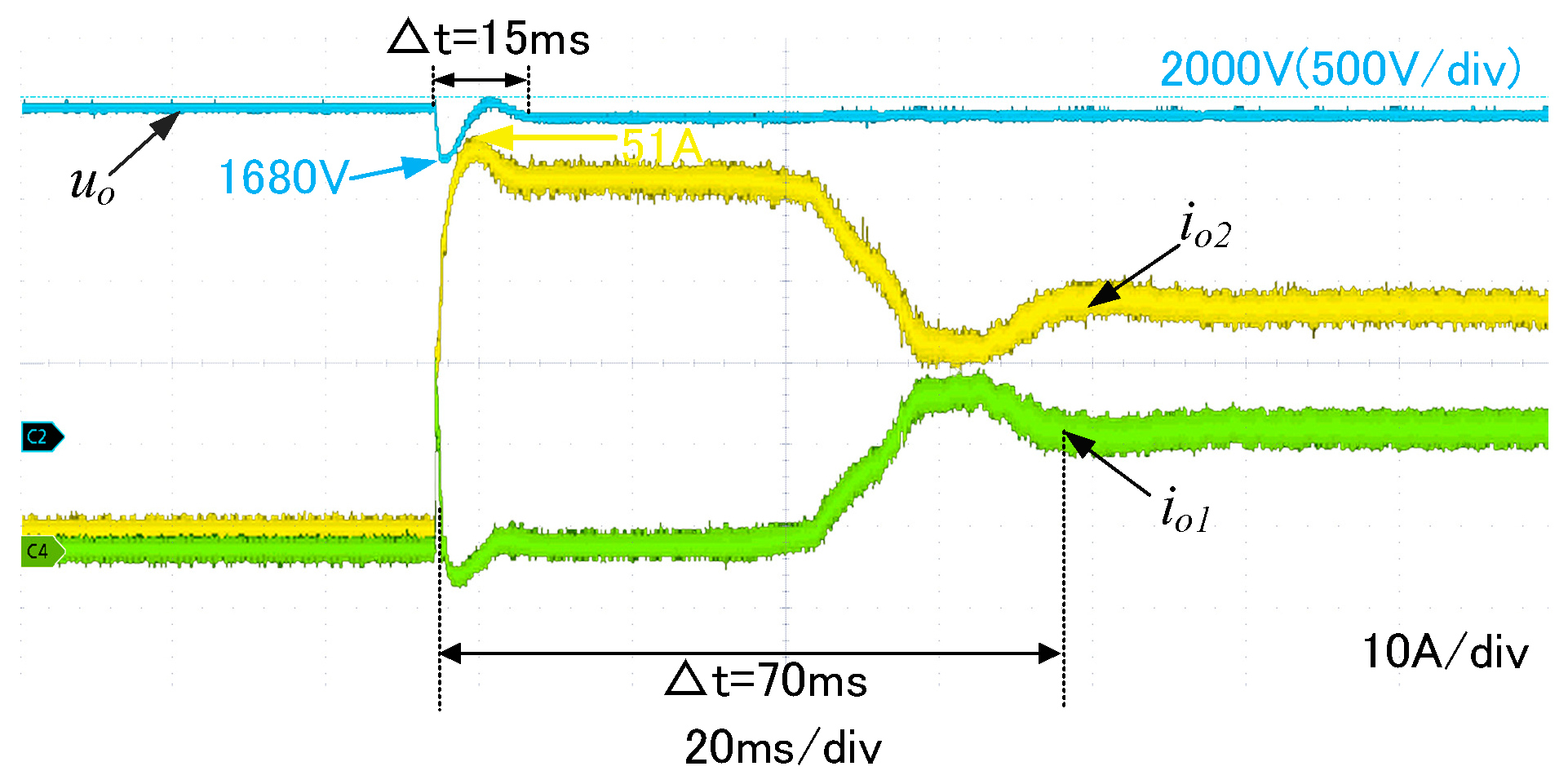
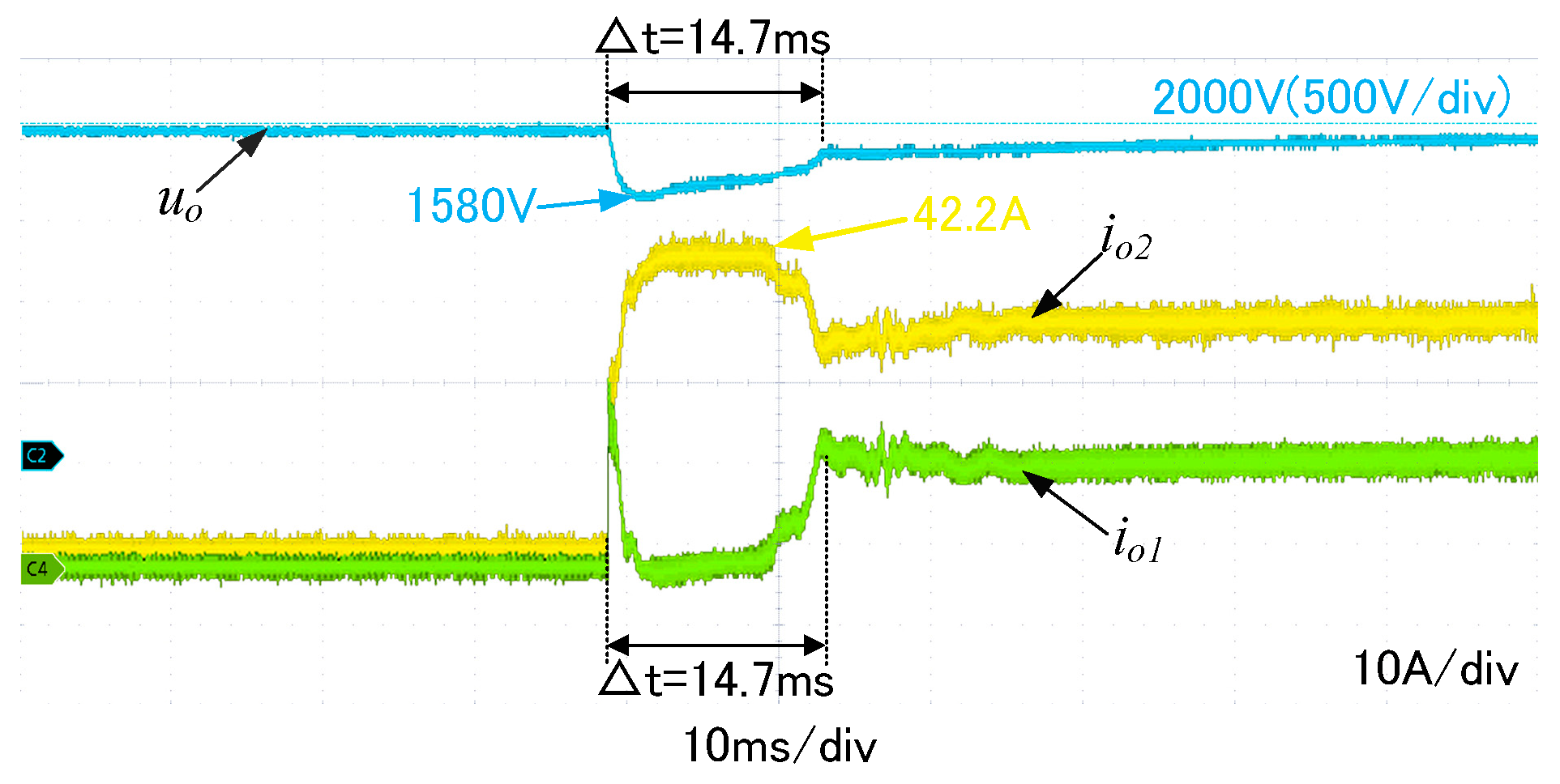
5.2. Experimental Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Tu, C.; Xiao, F.; Liu, B.; Li, P. Intrinsic Regularity Analysis and Optimization Control of Current Stress and RMS for Dual-Active Bridge Converter. Electronics 2024, 13, 4802. [Google Scholar] [CrossRef]
- Darwish, A. A Modular Step-Up DC/DC Converter for Electric Vehicles. Energies 2024, 17, 6305. [Google Scholar] [CrossRef]
- Ren, C.; He, Y.; Qin, Y.; Hui, Y.; Li, X.; Han, X.; He, X. A Novel Modular Sigma DC/DC Converter with a Wide Input Voltage Range. Electronics 2024, 13, 995. [Google Scholar] [CrossRef]
- Kroičs, K.; Gaspersons, K.; Elkhateb, A. Response Time Reduction of DC–DC Converter in Voltage Mode with Application of GaN Transistors and Digital Control. Electronics 2024, 13, 901. [Google Scholar] [CrossRef]
- Kok, C.L.; Tang, H.; Teo, T.H.; Koh, Y.Y. A DC-DC Converter with Switched-Capacitor Delay Deadtime Controller and Enhanced Unbalanced-Input Pair Zero-Current Detector to Boost Power Efficiency. Electronics 2024, 13, 1237. [Google Scholar] [CrossRef]
- Shinde, N.; Sankad, S.; Patil, S.L. Design and Study Voltage Characteristics of Buck Converter by Matlab Simulink. In Proceedings of the 2018 2nd International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 11–12 May 2018; pp. 680–683. [Google Scholar]
- Reyes-Malanche, J.A.; Vázquez, N.; Leyva-Ramos, J. Switched-capacitor quadratic buck converter for wider conversion ratios. IET Power Electron. 2015, 8, 2370–2376. [Google Scholar] [CrossRef]
- Fan, S.; Sun, L.; Duan, J.; Zhang, K. Improved active clamped ZVS buck converter with freewheeling current transfer circuit. IET Power Electron. 2019, 12, 1341–1348. [Google Scholar] [CrossRef]
- Botao, Z.; Qi, W.; Min, Z.; Huan, H. Analytical solution for the inductor current of BOOST converter. IET Power Electron. 2019, 12, 2424–2432. [Google Scholar] [CrossRef]
- Muhammad, M.; Armstrong, M.; Elgendy, M.A. A Nonisolated Interleaved Boost Converter for High-Voltage Gain Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 4, 352–362. [Google Scholar] [CrossRef]
- Atmaca, Ö.; Erol, E.; Kamal, T.; Karabacak, M. Design of an H-Bridge Bidirectional DC-DC Converter with LCL Filter for High Power Battery Applications. In Proceedings of the 2019 1st Global Power, Energy and Communication Conference (GPECOM), Nevsehir, Turkey, 12–15 June 2019; pp. 238–241. [Google Scholar]
- Gummi, K.; Ferdowsi, M. Derivation of new double-input DC-DC converters using H-Bridge cells as building blocks. In Proceedings of the 2008 34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 10–13 November 2008; pp. 2806–2811. [Google Scholar]
- Lazar, J.F.; Martinelli, R. Steady-state analysis of the LLC series resonant converter. In Proceedings of the APEC 2001. Sixteenth Annual IEEE Applied Power Electronics Conference and Exposition (Cat. No. 01CH37181), Anaheim, CA, USA, 4–8 March 2001. [Google Scholar]
- Tang, W.; Wang, H.; Zhu, X.; Gao, W.; Zheng, Z.; Yue, X. A Passive Current Sharing Method for Two-Phase Common Inductor LLC Resonant Converters and Mathematical Analysis of Current Sharing Effect. IEEE Trans. Power Electron. 2022, 37, 12316–12326. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Jeong, Y.-S.; Han, B. An Isolated DC/DC Converter Using High-Frequency Unregulated Resonant Converter for Fuel Cell Applications. IEEE Trans. Ind. Electron. 2011, 58, 2926–2934. [Google Scholar] [CrossRef]
- García Pérez, R.A.; Muñoz-Cruzado-Alba, J.; Galván Díez, E.; Carrasco Solís, J.M. Classification of Design Methodologies of Dual Active Bridge-Based Resonant Converters for Battery Energy Storage Systems. Electronics 2024, 13, 4748. [Google Scholar] [CrossRef]
- Jia, D.; Wang, D. Current Stress Minimization Based on Particle Swarm Optimization for Dual Active Bridge DC–DC Converter. Actuators 2024, 13, 421. [Google Scholar] [CrossRef]
- Kang, Z.; Li, L.; Zhang, H. Feedforward Control Strategy of a DC-DC Converter for an Off-Grid Hydrogen Production System Based on a Linear Extended State Observer and Super-Twisting Sliding Mode Control. Electronics 2024, 13, 3934. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, X.; Guo, B.; Bian, Y. The simulation and design of PSFB ZVS DC-DC converter based on Saber. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–4. [Google Scholar]
- Benites Quispe, J.B.; Mezaroba, M.; Batschauer, A.L.; de Souza Ribeiro, J.M. A Reconfigurable Phase-Shifted Full-Bridge DC–DC Converter with Wide Range Output Voltage. Energies 2024, 17, 3483. [Google Scholar] [CrossRef]
- Liu, J.; Gong, C.; Zhang, Y. A Novel Second Harmonic Voltage Suppression Control for PSFB Converter in Dual-Stage Single-Phase Rectifier. Electronics 2024, 13, 1830. [Google Scholar] [CrossRef]
- Wang, H.; Yang, G.; Kang, W.; Zhang, X.; Fan, X.; Xiao, F. Minimum-Output-Current-Ripple Control of Current-Fed Three-Level Phase-Shift Full-Bridge Converter. Energies 2022, 15, 6444. [Google Scholar] [CrossRef]
- Sun, X.; Zhou, Y.; Chen, G.; Ren, B. Model Predictive Control of a Phase-Shifted Full-Bridge DC-DC Converter. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020; pp. 2710–2714. [Google Scholar]
- Bakan, A.F.; Altintaş, N.; Aksoy, İ. An Improved PSFB PWM DC–DC Converter for High-Power and Frequency Applications. IEEE Trans. Power Electron. 2013, 28, 64–74. [Google Scholar] [CrossRef]
- Wang, J.B. Parallel DC/DC converters system with a novel primary droop current sharing control. IET Power Electron. 2012, 5, 1569–1576. [Google Scholar] [CrossRef]
- Jin, Z.; Savaghebi, M.; Vasquez, J.C.; Meng, L.; Guerrero, J.M. Maritime DC microgrids–a combination of microgrid technologies and maritime onboard power system for future ships. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 179–184. [Google Scholar]
- Liu, W.-S.; Chen, J.-F.; Liang, T.-J.; Lai, T.-L. Implementation and design of hybrid power module for DC power grid in paralleled applications. In Proceedings of the 2013 IEEE 10th International Conference on Power Electronics and Drive Systems (PEDS), Kitakyushu, Japan, 22–25 April 2013; pp. 323–329. [Google Scholar]
- Liu, J.; Gong, C.; Zhang, Y. Global Efficiency Optimal Control Strategy for Parallel Phase Shift Full-bridge Converter. In Proceedings of the 2023 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Wuhan, China, 16–19 June 2023; pp. 1–6. [Google Scholar]
- Shi, J.; Zhou, L.; He, X. Common-Duty-Ratio Control of Input-Parallel Output-Parallel (IPOP) Connected DC–DC Converter Modules With Automatic Sharing of Currents. IEEE Trans. Power Electron. 2012, 27, 3277–3291. [Google Scholar] [CrossRef]
- Panov, Y.; Rajagopalan, J.; Lee, F.C. Analysis and design of N paralleled DC-DC converters with master-slave current-sharing control. In Proceedings of the APEC 97–Applied Power Electronics Conference, Atlanta, GA, USA, 23–27 February 1997; Volume 1, pp. 436–442. [Google Scholar]
- Ghanbari, N.; Bhattacharya, S. Adaptive Droop Control Method for Suppressing Circulating Currents in DC Microgrids. IEEE Open Access J. Power Energy 2020, 7, 100–110. [Google Scholar] [CrossRef]
- Li, C.; Wu, J.; Zhang, K.; Dai, X.; Xu, S. Improved droop control based voltage compensation and variable droop coefficient in DC microgrids. In Proceedings of the 2016 UKACC 11th International Conference on Control (CONTROL), Belfast, UK, 31 August–2 September 2016; pp. 1–6. [Google Scholar]
- Cousineau, M.; Xiao, Z. Fully decentralized modular approach for parallel converter control. In Proceedings of the 2013 28th Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 237–243. [Google Scholar]
- Hernandez, B.; Giraldo, E.; Ospina, S.; Garces, A. Master-Slave Operation of DC Microgrids: An Adaptive Control Approach with Estimation. In Proceedings of the 2019 IEEE 4th Colombian Conference on Automatic Control (CCAC), Medellin, Colombia, 15–18 October 2019; pp. 1–6. [Google Scholar]
- Anand, S.; Fernandes, B.G.; Guerrero, J. Distributed Control to Ensure Proportional Load Sharing and Improve Voltage Regulation in Low-Voltage DC Microgrids. IEEE Trans. Power Electron. 2013, 28, 1900–1913. [Google Scholar] [CrossRef]
- Vivek, K. Design and Analysis of Voltage Droop Control Technique for DC Microgrids. In Proceedings of the 2019 3rd International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 12–14 June 2019; pp. 795–799. [Google Scholar]
- Hassan, M.A.; Li, E.; Chi, S.; Li, T.; Cheng, L.; Duan, C. Sliding Mode Control of Parallel-Connected DC-DC Buck Power Converters in DC Microgrid Systems. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–6. [Google Scholar]
- Prabhakaran, P.; Goyal, Y.; Agarwal, V. Novel Nonlinear Droop Control Techniques to Overcome the Load Sharing and Voltage Regulation Issues in DC Microgrid. IEEE Trans. Power Electron. 2018, 33, 4477–4487. [Google Scholar] [CrossRef]
- Gong, B.; Liu, K.; Luan, H.; Wu, J.; Zhou, J.; Tan, S.; Huang, C.; Wu, H. Design of a Dynamic Hybrid Compensator for Current Sharing Control of Parallel Phase-Shifted Full-Bridge Converter. Energies 2023, 16, 2204. [Google Scholar] [CrossRef]
- You, J.; Cheng, L.; Fu, B.; Deng, M. Analysis and Control of Input-Parallel Output-Series Based Combined DC/DC Converter With Modified Connection in Output Filter Circuit. IEEE Access 2019, 7, 58264–58276. [Google Scholar] [CrossRef]
- Qin, Z.; Cai, H.; Lin, X. Stability Analysis and Control Strategy Optimization of a Paralleled IPOS Phase-Shifted Full-Bridge Converters System Based on Droop Control. Electronics 2023, 12, 3685. [Google Scholar] [CrossRef]
- Augustine, S.; Mishra, M.K.; Lakshminarasamma, N. Circulating current minimization and current sharing control of parallel boost converters based on Droop Index. In Proceedings of the 2013 9th IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives (SDEMPED), Valencia, Spain, 27–30 August 2013; pp. 454–460. [Google Scholar]
- Dadi, R.; Meenakshy, K.; Damodaran, S.K. A Modified Droop Control Method for DC Microgrid with Improved Voltage Regulation and Current Sharing. In Proceedings of the 2020 International Conference on Power, Instrumentation, Control and Computing (PICC), Thrissur, India, 17–19 December 2020; pp. 1–6. [Google Scholar]
- Lin, X.; Zamora, R.; Baguley, C. Droop Control Based on Improved Virtual Impedance in a Stand-Alone Microgrid. In Proceedings of the 2019 IEEE PES GTD Grand International Conference and Exposition Asia (GTD Asia), Bangkok, Thailand, 19–23 March 2019; pp. 883–888. [Google Scholar]
- Liu, H.; Chen, Y.; Li, S.; Hou, Y. Improved droop control of isolated microgrid with virtual impedance. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Thomas, V.; Kumaravel, S.; Ashok, S. Control of parallel DC-DC converters in a DC microgrid using virtual output impedance method. In Proceedings of the 2016 2nd International Conference on Advances in Electrical, Electronics, Information, Communication and Bio-Informatics (AEEICB), Chennai, India, 27–28 February 2016; pp. 587–591. [Google Scholar]
- Yogithanjali Saimadhuri, K.N.; Janaki, M. Advanced control strategies for microgrids: A review of droop control and virtual impedance techniques. Results Eng. 2025, 25, 103799. [Google Scholar] [CrossRef]
- Dorf, R.C.; Bishop, R.H. Modern Control Systems; Pearson: Upper Saddle River, NJ, USA, 2015. [Google Scholar]
- Deraz, S.A.; Zaky, M.S.; Tawfiq, K.B.; Mansour, A.S. State Space Average Modeling, Small Signal Analysis, and Control Implementation of an Efficient Single-Switch High-Gain Multicell Boost DC-DC Converter with Low Voltage Stress. Electronics 2024, 13, 3264. [Google Scholar] [CrossRef]
- Vlatkovic, V.; Sabate, J.A.; Ridley, R.B.; Lee, F.C.; Cho, B.H. Small-signal analysis of the phase-shifted PWM converter. IEEE Trans. Power Electron. 1992, 7, 128–135. [Google Scholar] [CrossRef]
- Lv, Z.; Zhou, M.; Wang, Q.; Hu, W. Small-Signal Stability Analysis for Multi-Terminal LVDC Distribution Network Based on Distributed Secondary Control Strategy. Electronics 2021, 10, 1575. [Google Scholar] [CrossRef]



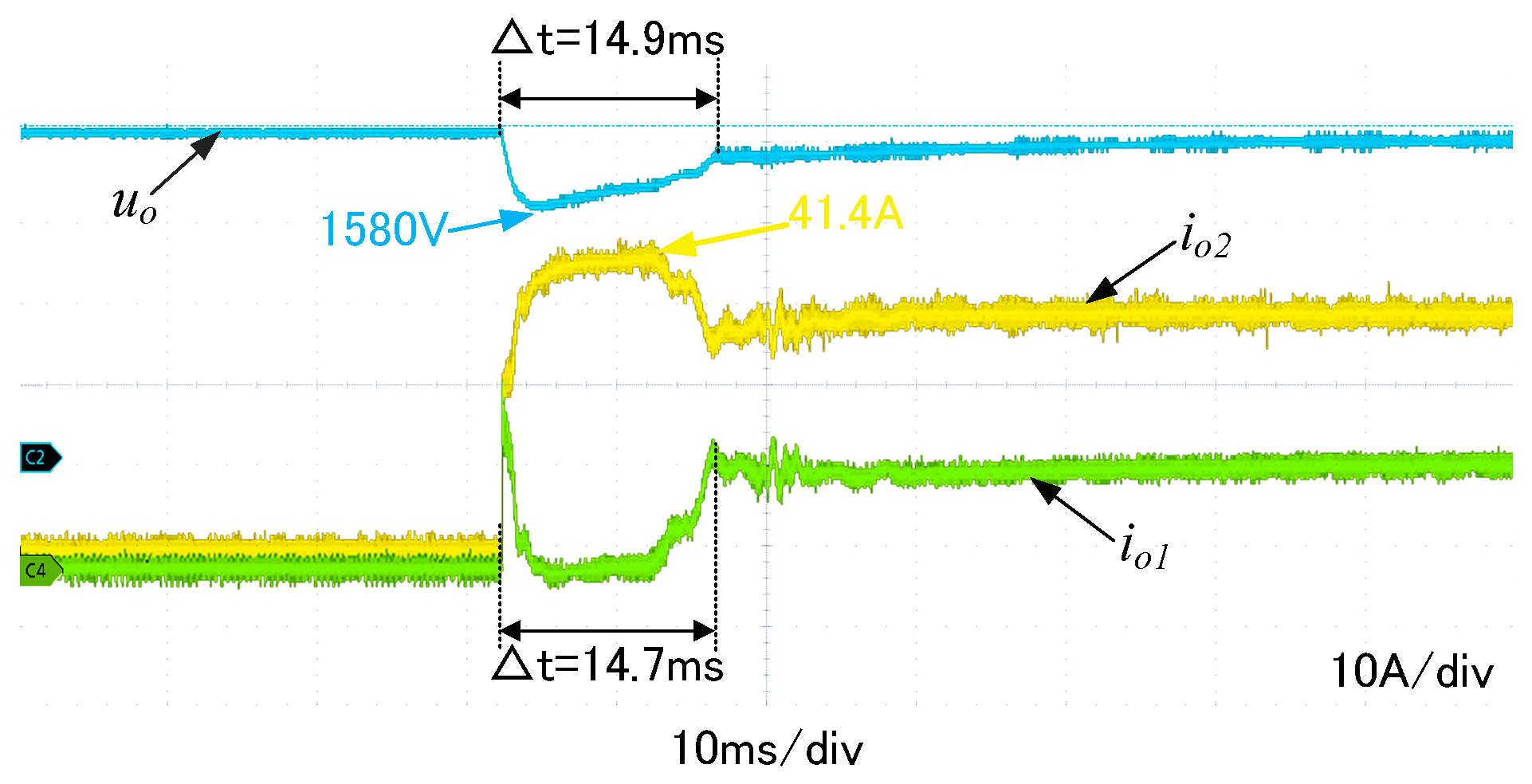
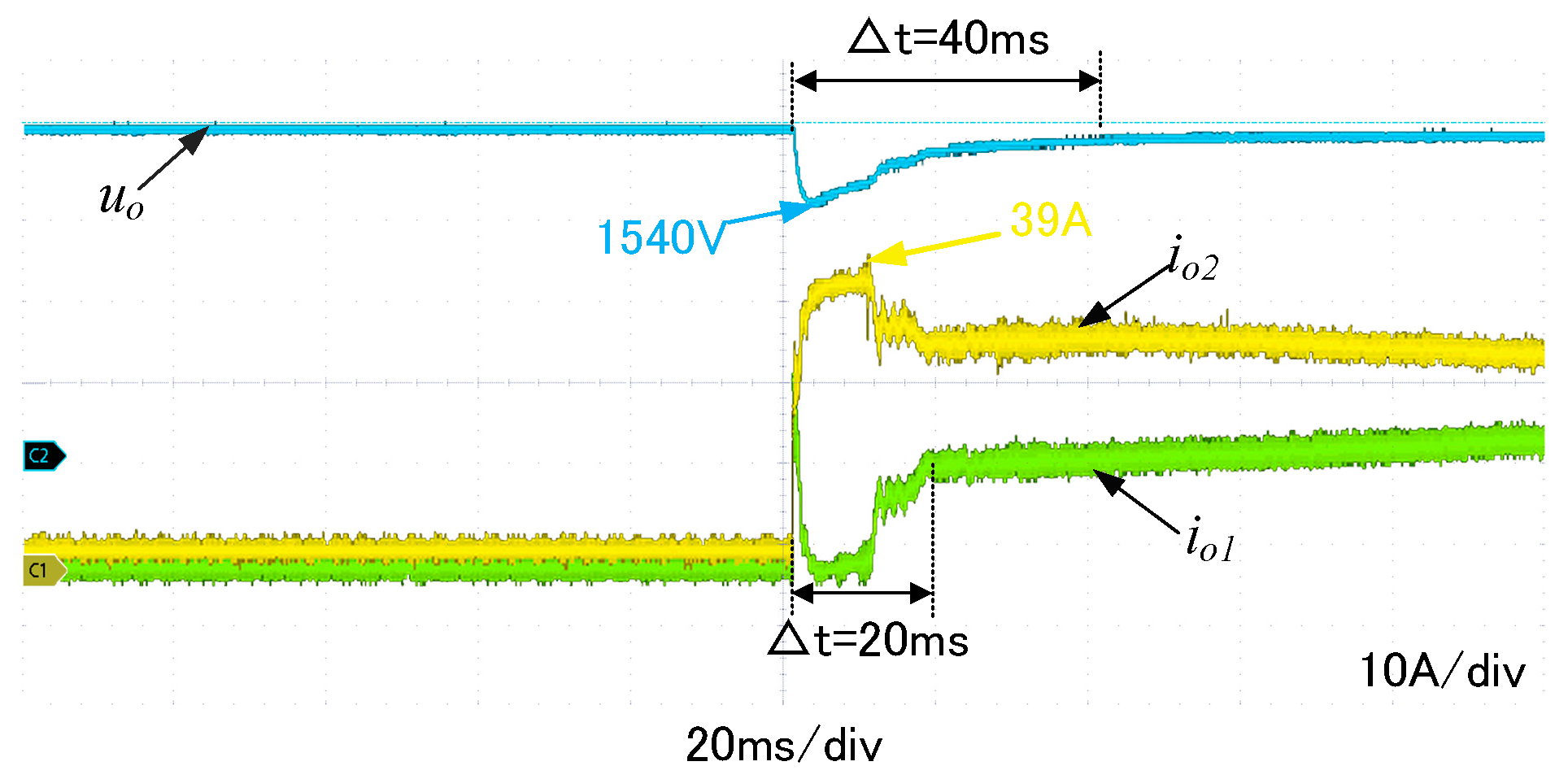
| Parameter Name | Sign | Value |
|---|---|---|
| Input voltage | 280 V | |
| Output voltage | 2000 V | |
| Ratio of transformer | 1:6 | |
| Switching frequency | 15 kHz | |
| Transformer leakage inductance | 0.3 μH | |
| Switching tube parasitic capacitance | 3 nF | |
| Output filtering inductance | 0.6 mH | |
| Output filtering capacitance | 40 μF | |
| Rated power | 100 kW | |
| Droop coefficient | 1.5 | |
| Proportional coefficient | 0.0001 | |
| Integral coefficient | 0.3 | |
| Cutoff frequency of low-pass filter | 600 Hz | |
| Feedback coefficient of output voltage of Converter 1 | 1.01 | |
| Feedback coefficient of output voltage of Converter 2 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, M.; Cai, H.; Lin, X. The Intrinsic Mechanism and Suppression Strategy of Transient Current Imbalance Among Parallel Converters. Electronics 2025, 14, 714. https://doi.org/10.3390/electronics14040714
Fu M, Cai H, Lin X. The Intrinsic Mechanism and Suppression Strategy of Transient Current Imbalance Among Parallel Converters. Electronics. 2025; 14(4):714. https://doi.org/10.3390/electronics14040714
Chicago/Turabian StyleFu, Mingjie, Huafeng Cai, and Xinchun Lin. 2025. "The Intrinsic Mechanism and Suppression Strategy of Transient Current Imbalance Among Parallel Converters" Electronics 14, no. 4: 714. https://doi.org/10.3390/electronics14040714
APA StyleFu, M., Cai, H., & Lin, X. (2025). The Intrinsic Mechanism and Suppression Strategy of Transient Current Imbalance Among Parallel Converters. Electronics, 14(4), 714. https://doi.org/10.3390/electronics14040714






