Channel Estimation in 5G-and-Beyond Wireless Communication: A Comprehensive Survey
Abstract
1. Introduction
Contribution and Uniqueness of Our Survey
- Comprehensive classification framework: Unlike previous surveys that often have presented a broad overview of massive MIMO challenges, this paper introduces a distinct classification framework that organizes channel estimation techniques based on their approach to addressing pilot contamination and feedback overhead. This framework provides researchers with a clear roadmap for understanding state-of-the-art solutions and their applicability in different scenarios.
- Focus on emerging technologies: While many existing surveys focus on traditional channel estimation methods, this work extensively covers emerging technologies such as reconfigurable intelligent surfaces (RISs) and machine learning (ML)-assisted channel estimation. These technologies are critical for beyond-5G networks, and their inclusion in this survey provides a forward-looking perspective that is often missing in related works.
- Comparative analysis and future directions: This survey not only reviews existing techniques, but also provides a detailed comparative analysis of their advantages, limitations, and application scenarios (see Table 1). Additionally, it identifies specific open research challenges and future directions, such as scalability in ultra-dense networks, energy-efficient estimation, and integration with artificial intelligence (AI)/ML for real-time adaptation. These insights are particularly valuable for guiding future research efforts.
- Integration of practical considerations: Many existing surveys focus on theoretical aspects of channel estimation. In contrast, this paper emphasizes practical considerations, such as computational complexity, implementation challenges, and standardization issues. This practical focus makes the survey more relevant for engineers and practitioners working on real-world deployments of massive MIMO systems.
2. Challenges and Approaches of Channel Estimation on MIMO
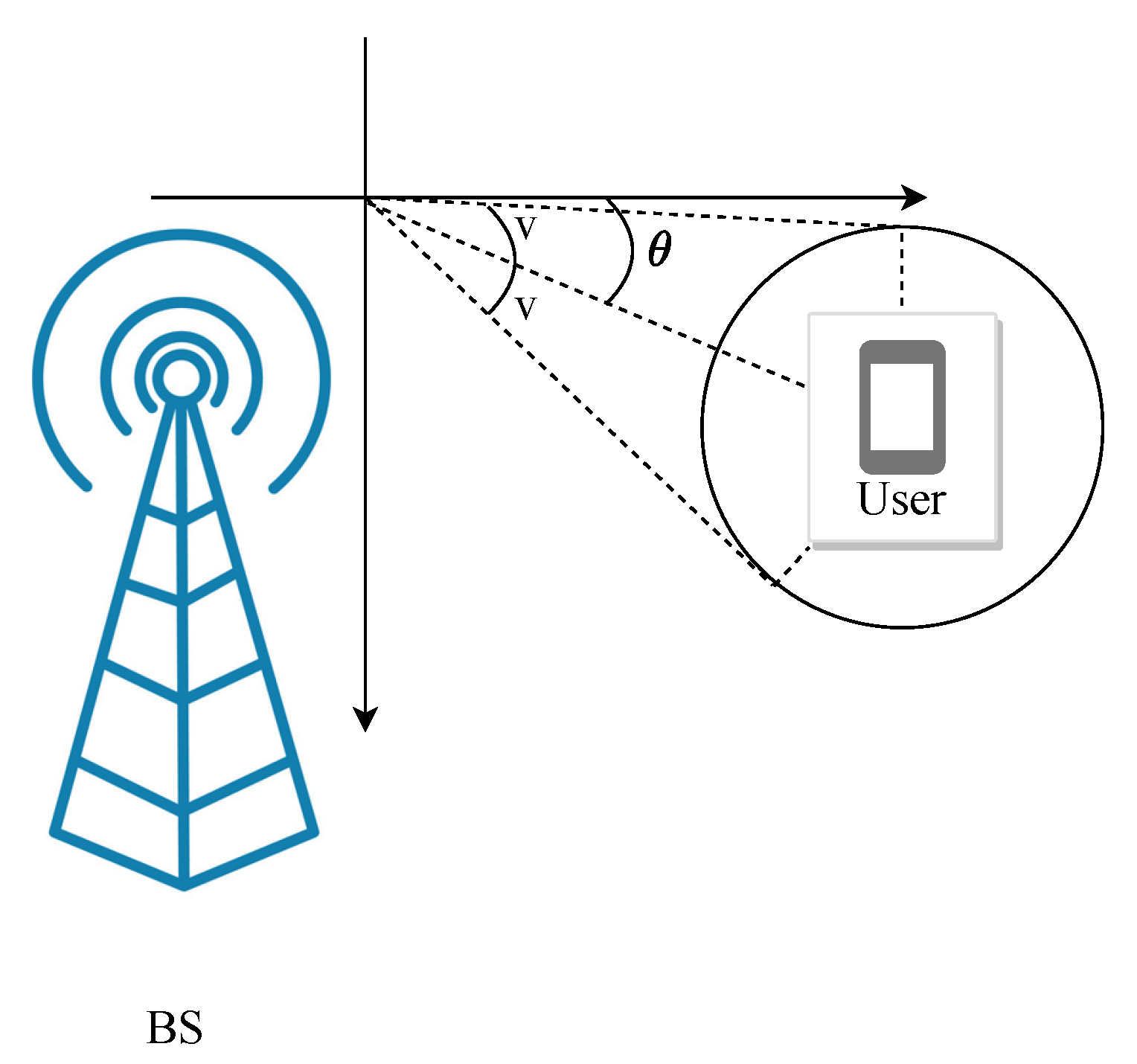
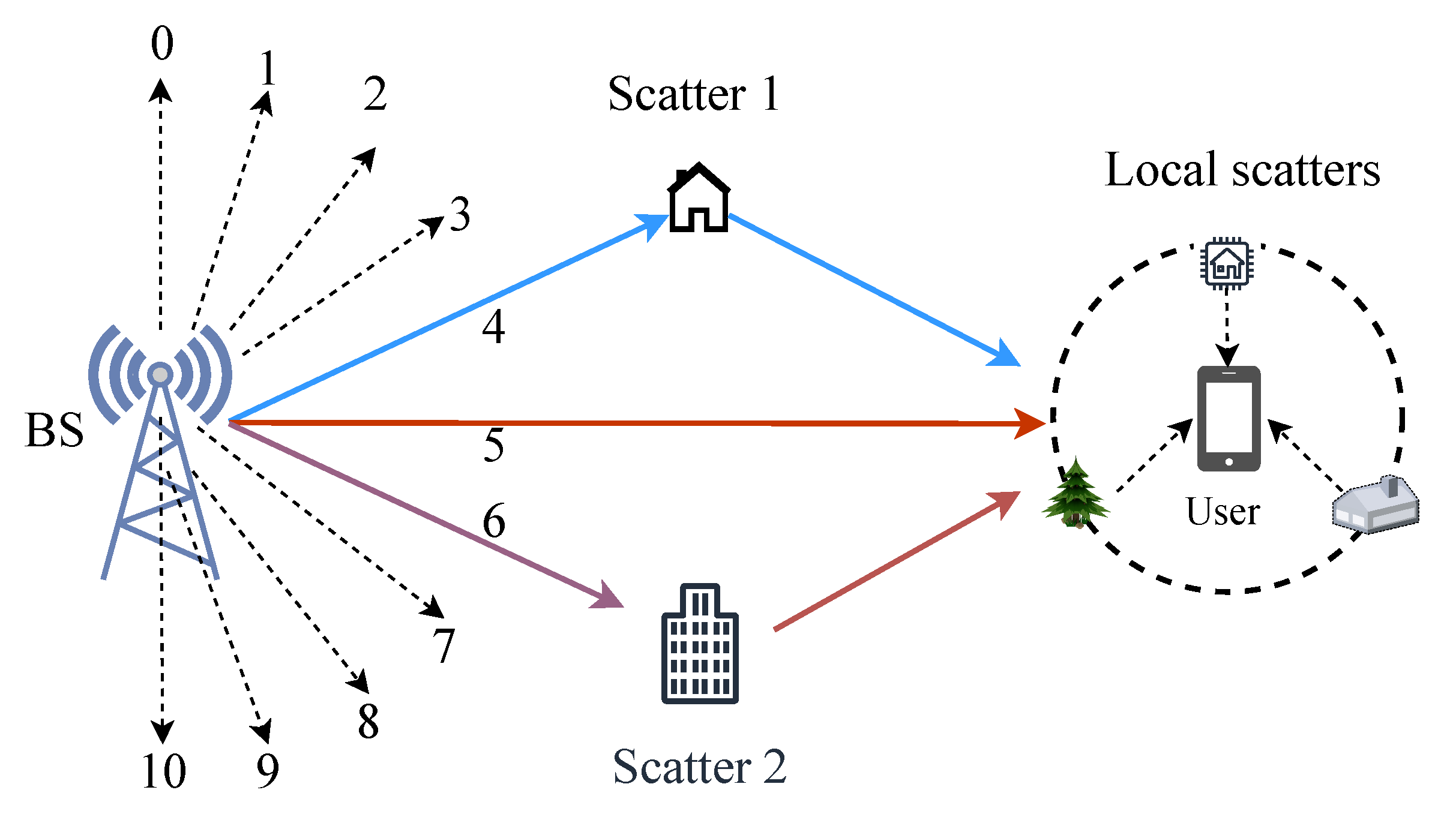
2.1. Approaches for Channel Estimation
2.2. Overhead Issues in Channel Estimation
3. Channel Estimation Methodologies
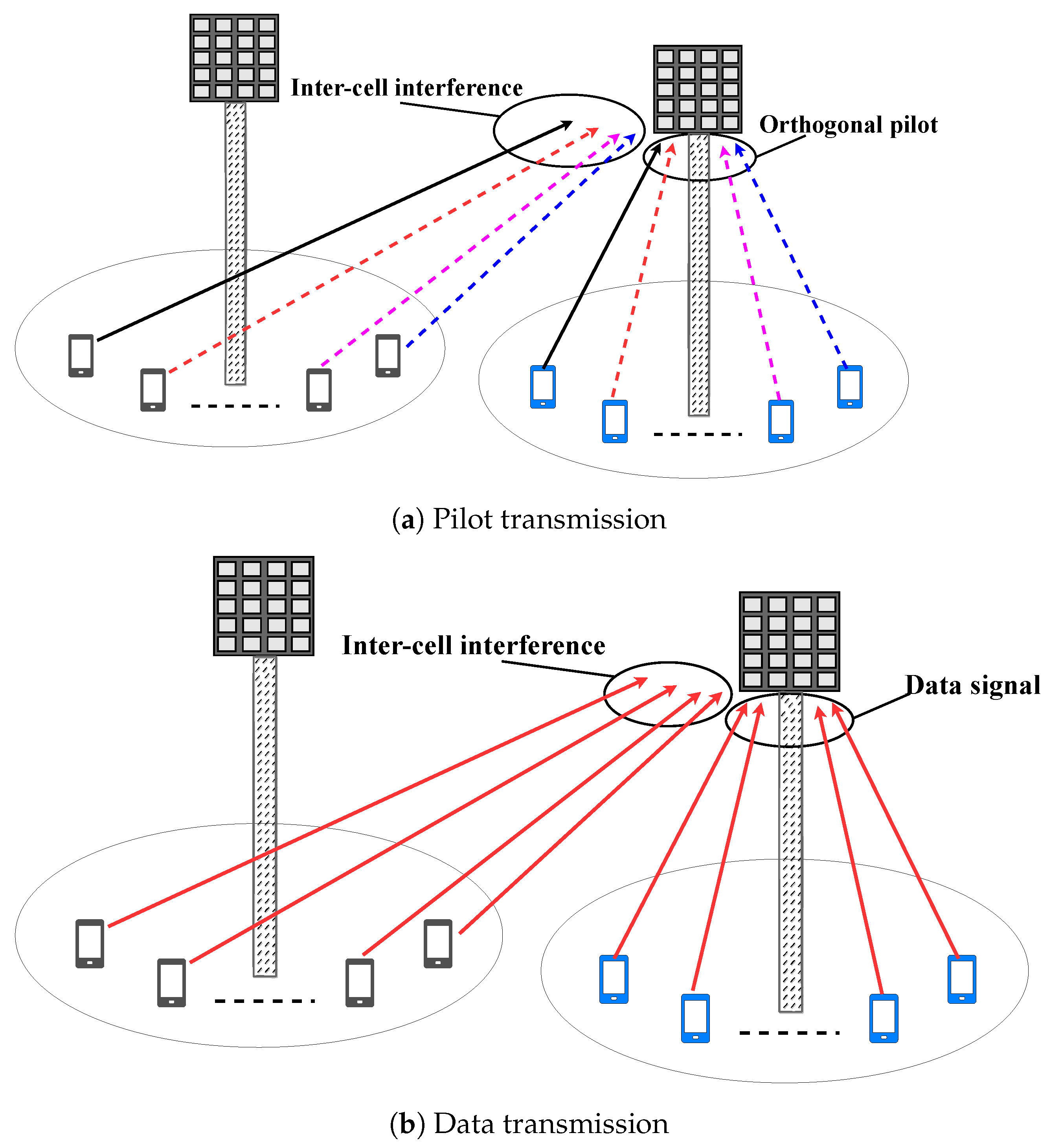
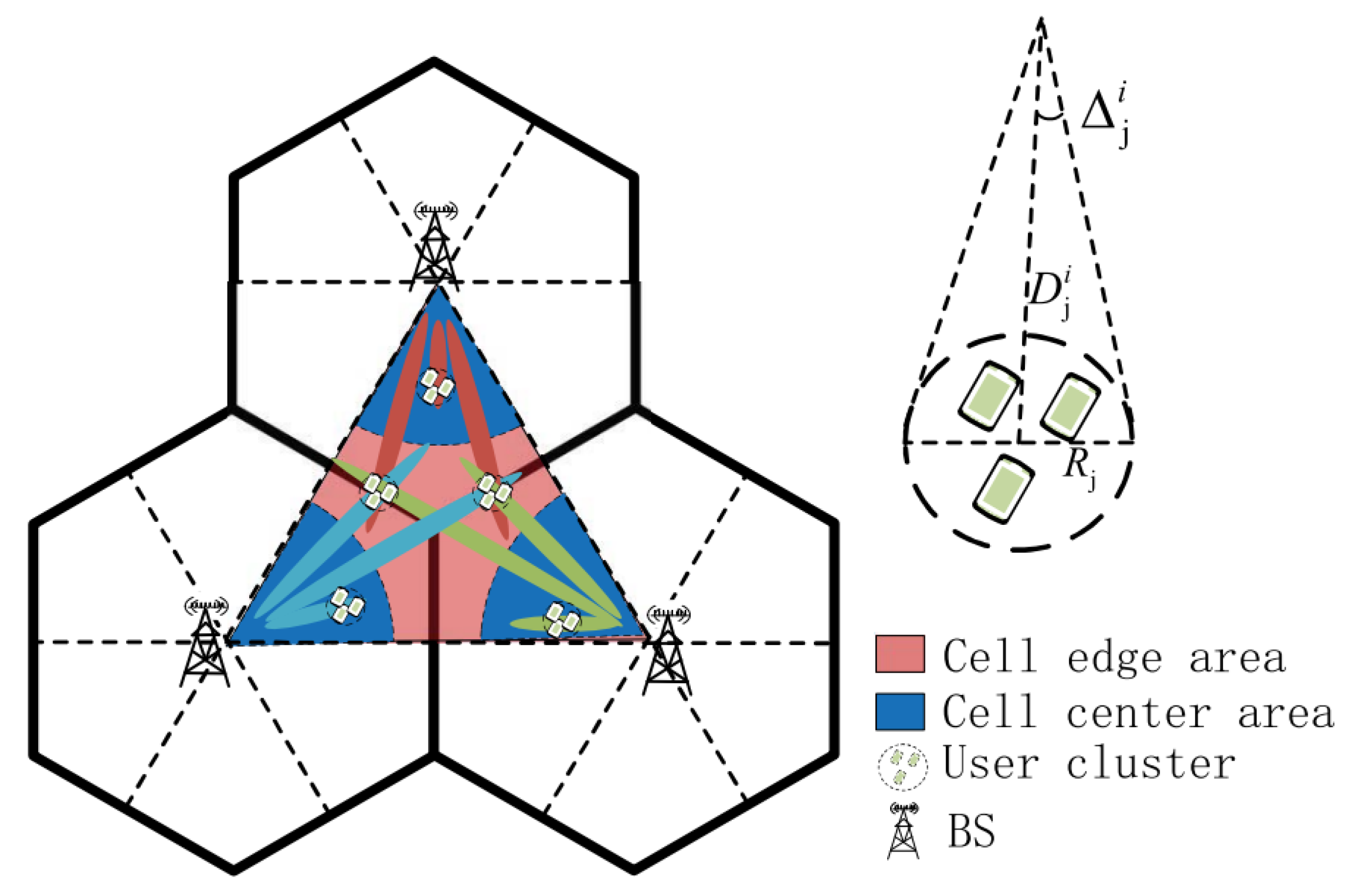
3.1. Pilot Contamination-Related Estimation Methodologies
3.2. CSI Feedback Overhead-Related Methodologies
4. Learning-Based Channel Estimation and Usage Scenarios in Beyond-5G Communications
4.1. Deep Learning-Aided Channel Estimation
4.2. Channel Estimation for RIS
5. Comparative Analysis and Future Directions
5.1. Comparative Analysis of Channel Estimation Techniques
5.2. Future Directions and Open Research Challenges
- Scalability in ultra-dense networks: As the number of connected devices continues to grow, especially in IoT and smart city applications, scalable channel estimation techniques that can handle ultra-dense networks with minimal overhead are needed. Future research could explore distributed and federated learning approaches, to address this challenge.
- Integration with RIS: RIS technology offers promising opportunities for enhancing channel estimation by dynamically controlling the propagation environment. However, the cascaded channel estimation in RIS-assisted systems remains a complex problem. Future work could focus on developing low-complexity algorithms that exploit the unique properties of RIS, such as two-timescale channel estimation.
- Robustness in dynamic environments: Current channel estimation techniques often assume quasi-static channel conditions, which may not hold in highly dynamic environments such as vehicular networks or drone-assisted communications. Future research should aim to develop adaptive algorithms that can quickly respond to rapid channel variations.
- Energy-efficient estimation: With the increasing emphasis on green communication, energy-efficient channel estimation techniques are crucial. Future studies could explore the use of low-power hardware and energy-aware algorithms to reduce the computational and feedback overhead associated with channel estimation.
- Integration with AI/ML for real-time adaptation: While DL has shown promise in channel estimation, its real-time implementation remains challenging, due to the high computational requirements. Future research could focus on lightweight AI/ML models that can be deployed in real-time systems, possibly leveraging edge computing and federated learning frameworks.
- Standardization and interoperability: As 5G-and-beyond networks evolve, standardization of channel estimation techniques across different network architectures and devices will be critical. Future work could explore the development of standardized frameworks that ensure interoperability between different massive MIMO deployments.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Larsson, E.; Edfors, O.; Tufvesson, F.; Marzetta, T. Massive MIMO for next generation wireless systems. IEEE Commun. Mag. 2014, 52, 186–195. [Google Scholar] [CrossRef]
- Guo, F.; Yu, F.; Zhang, H.; Li, X.; Ji, H.; Leung, V. Enabling massive IoT toward 6G: A comprehensive survey. IEEE Internet Things J. 2021, 8, 11891–11915. [Google Scholar] [CrossRef]
- Spantideas, S.; Giannopoulos, A.; Trakadas, P. Smart Mission Critical Service Management: Architecture, Deployment Options, and Experimental Results. IEEE Trans. Netw. Serv. Manag. 2024; early access. [Google Scholar] [CrossRef]
- Alwakeel, A.; Mehana, A. Multicell MMSE data detection for massive MIMO: New simplified bounds. IET Commun. 2019, 13, 2386–2394. [Google Scholar] [CrossRef]
- Qi, C.; Yue, G.; Wu, L.; Nallanathan, A. Pilot Design for Sparse Channel Estimation in OFDM-Based Cognitive Radio Systems. IEEE Trans. Veh. Technol. 2014, 63, 982–987. [Google Scholar] [CrossRef]
- Marzetta, T. Noncooperative Cellular Wireless with Unlimited Numbers of Base Station Antennas. IEEE Trans. Wirel. Commun. 2010, 9, 3590–3600. [Google Scholar] [CrossRef]
- Maruta, K.; Ahn, C. Uplink Interference Suppression by Semi-Blind Adaptive Array with Decision Feedback Channel Estimation on Multicell Massive MIMO Systems. IEEE Trans. Commun. 2018, 66, 6123–6134. [Google Scholar] [CrossRef]
- Albataineh, Z.; Hayajneh, K.; Salameh, H.; Dang, C.; Dagmseh, A. Robust massive MIMO channel estimation for 5G networks using compressive sensing technique. Aeu-Int. J. Electron. Commun. 2020, 120, 153197. [Google Scholar] [CrossRef]
- Rusek, F.; Persson, D.; Lau, B.; Larsson, E.; Marzetta, T.; Edfors, O.; Tufvesson, F. Scaling Up MIMO: Opportunities and Challenges with Very Large Arrays. IEEE Signal Process. Mag. 2013, 30, 40–60. [Google Scholar] [CrossRef]
- Shen, W.; Dai, L.; Shi, Y.; Gao, Z.; Wang, Z. Massive MIMO channel estimation based on block iterative support detection. In Proceedings of the 2016 IEEE Wireless Communications and Networking Conference, Doha, Qatar, 3–6 April 2016; pp. 1–6. [Google Scholar]
- Ozdemir, M.; Arslan, H. Channel estimation for wireless OFDM systems. IEEE Commun. Surv. Tutor. 2007, 9, 18–48. [Google Scholar] [CrossRef]
- Albataineh, Z. Robust blind channel estimation algorithm for linear STBC systems using fourth order cumulant matrices. Telecommun. Syst. 2018, 68, 573–582. [Google Scholar] [CrossRef]
- Xie, H.; Wang, Y.; Andrieux, G.; Ren, X. Efficient Compressed Sensing Based Non-Sample Spaced Sparse Channel Estimation in OFDM System. IEEE Access 2019, 7, 133362–133370. [Google Scholar] [CrossRef]
- Han, B.; Jiang, Z.; Liang, L.; Chen, P.; Yang, F.; Bi, Q. Joint Precoding and Scheduling Algorithm for Massive MIMO in FDD Multi-Cell Network. Wirel. Netw. 2019, 25, 75–85. [Google Scholar] [CrossRef]
- Gao, Z.; Dai, L.; Wang, Z.; Chen, S. Spatially Common Sparsity Based Adaptive Channel Estimation and Feedback for FDD Massive MIMO. IEEE Trans. Signal Process. 2015, 63, 6169–6183. [Google Scholar] [CrossRef]
- Lee, B.; Choi, J.; Seol, J.; Love, D.; Shim, B. Antenna Grouping Based Feedback Compression for FDD-Based Massive MIMO Systems. IEEE Trans. Commun. 2015, 63, 3261–3274. [Google Scholar] [CrossRef]
- Cheng, P.; Chen, Z. Multidimensional Compressive Sensing Based Analog CSI Feedback for Massive MIMO-OFDM Systems. In Proceedings of the 2014 IEEE 80th Vehicular Technology Conference (VTC2014-Fall), Vancouver, BC, Canada, 14–17 September 2014; pp. 1–6. [Google Scholar]
- Duarte, M.; Eldar, Y. Structured Compressed Sensing: From Theory to Applications. IEEE Trans. Signal Process. 2011, 59, 4053–4085. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, L.; Zhang, J. FD-MIMO via Pilot-Data Superposition: Tensor-Based DOA Estimation and System Performance. IEEE J. Sel. Top. Signal Process. 2019, 13, 931–946. [Google Scholar] [CrossRef]
- Cheng, X.; Yang, Y.; Xia, B.; Wei, N.; Li, S. Sparse Channel Estimation for Millimeter Wave Massive MIMO Systems with Lens Antenna Array. IEEE Trans. Veh. Technol. 2019, 68, 11348–11352. [Google Scholar] [CrossRef]
- Do, T.; Gan, L.; Nguyen, N.; Tran, T. Sparsity adaptive matching pursuit algorithm for practical compressed sensing. In Proceedings of the 2008 42nd Asilomar Conference on Signals, Systems And Computers, Grove, CA, USA, 26–29 October 2008; pp. 581–587. [Google Scholar]
- Gao, Z.; Dai, L.; Yuen, C.; Wang, Z. Asymptotic Orthogonality Analysis of Time-Domain Sparse Massive MIMO Channels. IEEE Commun. Lett. 2015, 19, 1826–1829. [Google Scholar] [CrossRef]
- De Figueiredo, F.; Cardoso, F.; Moerman, I.; Fraidenraich, G. Channel Estimation for Massive MIMO TDD Systems Assuming Pilot Contamination and Frequency Selective Fading. IEEE Access 2017, 5, 17733–17741. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, Z.; Dang, J.; Wang, J.; Liu, H.; Wu, Y. Channel Estimation for Multicell Multiuser Massive MIMO Uplink over Rician Fading Channels. IEEE Trans. Veh. Technol. 2017, 66, 8872–8882. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, D.; Wang, J.; You, X. Channel Estimation for Massive MIMO-OFDM Systems by Tracking the Joint Angle-Delay Subspace. IEEE Access 2016, 4, 10166–10179. [Google Scholar] [CrossRef]
- Wu, C.; Huang, W.; Chung, W. Low-Complexity Semiblind Channel Estimation in Massive MU-MIMO Systems. IEEE Trans. Wirel. Commun. 2017, 16, 6279–6290. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, Z.; Dang, J.; Liu, H. Enhanced time-shifted pilot based channel estimation in massive MIMO systems with finite number of antennas. In Proceedings of the 2017 IEEE International Conference on Communications Workshops (ICC Workshops), Paris, France, 21–25 May 2017; pp. 222–227. [Google Scholar]
- Wei, X.; Peng, W.; Chen, D.; Schober, R.; Jiang, T. Uplink Channel Estimation in Massive MIMO Systems Using Factor Analysis. IEEE Commun. Lett. 2018, 22, 1620–1623. [Google Scholar] [CrossRef]
- Dao, H.; Kim, S. Vertex Graph-Coloring-Based Pilot Assignment with Location-Based Channel Estimation for Massive MIMO Systems. IEEE Access 2018, 6, 4599–4607. [Google Scholar] [CrossRef]
- Jing, X.; Li, M.; Liu, H.; Li, S.; Pan, G. Superimposed Pilot Optimization Design and Channel Estimation for Multiuser Massive MIMO Systems. IEEE Trans. Veh. Technol. 2018, 67, 11818–11832. [Google Scholar] [CrossRef]
- Ioushua, S.; Eldar, Y. Pilot contamination mitigation with reduced RF chains. In Proceedings of the 2017 IEEE 18th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Sapporo, Japan, 3–6 July 2017; pp. 1–5. [Google Scholar]
- Upadhya, K.; Vorobyov, S.; Vehkapera, M. Superimposed Pilots are Superior for Mitigating Pilot Contamination in Massive MIMO. IEEE Trans. Signal Process. 2017, 65, 2917–2932. [Google Scholar] [CrossRef]
- Li, J.; Yuen, C.; Li, D.; Wu, X.; Zhang, H. On Hybrid Pilot for Channel Estimation in Massive MIMO Uplink. IEEE Trans. Veh. Technol. 2019, 68, 6670–6685. [Google Scholar] [CrossRef]
- Mawatwal, K.; Sen, D.; Roy, R. Performance Analysis of a SAGE-Based Semi-Blind Channel Estimator for Pilot Contaminated MU Massive MIMO Systems. IEEE Access 2020, 8, 46682–46700. [Google Scholar] [CrossRef]
- Choi, J.; Chance, Z.; Love, D.; Madhow, U. Noncoherent Trellis Coded Quantization: A Practical Limited Feedback Technique for Massive MIMO Systems. IEEE Trans. Commun. 2013, 61, 5016–5029. [Google Scholar] [CrossRef]
- Fang, J.; Li, X.; Li, H.; Gao, F. Low-rank covariance-assisted downlink training and channel estimation for FDD massive MIMO systems. IEEE Trans. Wirel. Commun. 2017, 16, 1935–1947. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, Z.; Sun, C. Angular domain pilot design and channel estimation for FDD massive MIMO networks. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Zhao, L.; Ng, D.; Yuan, J. Multi-User Precoding and Channel Estimation for Hybrid Millimeter Wave Sys-tems. IEEE J. Sel. Areas Commun. 2017, 35, 1576–1590. [Google Scholar] [CrossRef]
- Alevizos, P.; Fu, X.; Sidiropoulos, N.; Yang, Y.; Bletsas, A. Limited Feedback Channel Estimation in Massive MIMO with Non-Uniform Directional Dictionaries. IEEE Trans. Signal Process. 2018, 66, 5127–5141. [Google Scholar] [CrossRef]
- Heath, R.; González-Prelcic, N.; Rangan, S.; Roh, W.; Sayeed, A. An Overview of Signal Processing Techniques for Millimeter Wave MIMO Systems. IEEE J. Sel. Top. Signal Process. 2016, 10, 436–453. [Google Scholar] [CrossRef]
- Bajwa, W.; Haupt, J.; Sayeed, A.; Nowak, R. Compressed Channel Sensing: A New Approach to Estimating Sparse Multipath Channels. Proc. IEEE 2010, 98, 1058–1076. [Google Scholar] [CrossRef]
- Abdallah, A.; Mansour, M. Efficient Angle-Domain Processing for FDD-Based Cell-Free Massive MIMO Systems. IEEE Trans. Commun. 2020, 68, 2188–2203. [Google Scholar] [CrossRef]
- Huang, W.; Huang, Y.; Xu, W.; Yang, L. Beam-Blocked Channel Estimation for FDD Massive MIMO with Compressed Feedback. IEEE Access 2017, 5, 11791–11804. [Google Scholar] [CrossRef]
- Kulsoom, F.; Vizziello, A.; Chaudhry, H.; Savazzi, P. Joint Sparse Channel Recovery with Quantized Feedback for Multi-User Massive MIMO Systems. IEEE Access 2020, 8, 11046–11060. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, J.; Gao, Y.; Zhao, H. Block Bayesian matching pursuit based channel estimation for FDD massive MIMO system. AEU-Int. J. Electron. Commun. 2018, 93, 296–304. [Google Scholar] [CrossRef]
- Khan, I.; Zafar, M.; Jan, M.; Lloret, J.; Basheri, M.; Singh, D. Spectral and Energy Efficient Low-Overhead Uplink and Downlink Channel Estimation for 5G Massive MIMO Systems. Entropy 2018, 20, 92. [Google Scholar] [CrossRef]
- Saraereh, O.; Khan, I.; Alsafasfeh, Q.; Alemaishat, S.; Kim, S. Low-Complexity Channel Estimation in 5G Massive MIMO-OFDM Systems. Symmetry 2019, 11, 713. [Google Scholar] [CrossRef]
- Nguyen, S.; Ghrayeb, A. Compressive sensing-based channel estimation for massive multiuser MIMO systems. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 2890–2895. [Google Scholar]
- Xiong, X.; Wang, X.; Gao, X.; You, X. Beam-Domain Channel Estimation for FDD Massive MIMO Systems with Optimal Thresholds. IEEE Trans. Wirel. Commun. 2017, 16, 4669–4682. [Google Scholar] [CrossRef]
- Zhang, F.; Sun, S.; Gao, Q.; Tang, W. Enhanced CSI Acquisition for FDD Multi-User Massive MIMO Systems. IEEE Access 2018, 6, 23034–23042. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, S.; Li, H.; Zhao, N.; Leung, V. Interference-Alignment and Soft-Space-Reuse Based Cooperative Transmission for Multi-cell Massive MIMO Networks. IEEE Trans. Wirel. Commun. 2018, 17, 1907–1922. [Google Scholar] [CrossRef]
- Barzegar Khalilsarai, M.; Haghighatshoar, S.; Yi, X.; Caire, G. FDD Massive MIMO via UL/DL Channel Covariance Extrapolation and Active Channel Sparsification. IEEE Trans. Wirel. Commun. 2019, 18, 121–135. [Google Scholar] [CrossRef]
- Han, Y.; Liu, Q.; Wen, C.; Jin, S.; Wong, K. FDD Massive MIMO Based on Efficient Downlink Channel Reconstruction. IEEE Trans. Commun. 2019, 67, 4020–4034. [Google Scholar] [CrossRef]
- Jiang, Z.; Chen, S.; Molisch, A.; Vannithamby, R.; Zhou, S.; Niu, Z. Exploiting Wireless Channel State Information Structures Beyond Linear Correlations: A Deep Learning Approach. IEEE Commun. Mag. 2019, 57, 28–34. [Google Scholar] [CrossRef]
- Qing, C.; Cai, B.; Yang, Q.; Wang, J.; Huang, C. Deep Learning for CSI Feedback Based on Superimposed Coding. IEEE Access 2019, 7, 93723–93733. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Zhang, Y.; Zhang, T. Blind Denoiser-based Beamspace Channel Estimation with GAN in Millimeter-Wave Systems. In Proceedings of the IEEE Vehicular Technology Conference (VTC2021-Fall), Norman, OK, USA, 27–30 September 2021; pp. 1–5. [Google Scholar]
- Doshi, A.; Gupta, M.; Andrews, J. Over-the-Air Design of GAN Training for mmWave MIMO Channel Estimation. IEEE J. Sel. Areas Inf. Theory 2022, 3, 557–573. [Google Scholar] [CrossRef]
- Zhang, B.; Hu, D.; Wu, J.; Xu, Y. An effective generative model based channel estimation method with reduced overhead. IEEE Trans. Veh. Technol. 2022, 71, 8414–8423. [Google Scholar] [CrossRef]
- Mishra, D.; Johansson, H. Channel Estimation and Low-complexity Beamforming Design for Passive Intelligent Surface Assisted MISO Wireless Energy Transfer. In Proceeding of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 4659–4663. [Google Scholar]
- Ye, M.; Zhang, H.; Wang, J. Channel estimation for intelligent reflecting surface aided wireless communi-cations using conditional GAN. IEEE Commun. Lett. 2022, 26, 2340–2344. [Google Scholar] [CrossRef]
- Shen, W.; Qin, Z.; Nallanathan, A. Deep learning enabled channel estimation for RIS-aided wireless systems. In Proceedings of the GLOBECOM 2022–2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 4–8 December 2022; pp. 4226–4231. [Google Scholar]
- Nadeem, Q.; Alwazani, H.; Kammoun, A.; Chaaban, A.; Debbah, M.; Alouini, M. Intelligent Reflecting Sur-face-Assisted Multi-User MISO Communication: Channel Estimation and Beamforming Design. IEEE Open J. Commun. Soc. 2020, 1, 661–680. [Google Scholar] [CrossRef]
- Hu, C.; Dai, L.; Han, S.; Wang, X. Two-Timescale Channel Estimation for Reconfigurable Intelligent Surface Aided Wireless Communications. IEEE Trans. Commun. 2021, 69, 7736–7747. [Google Scholar] [CrossRef]
- Guan, X.; Wu, Q.; Zhang, R. Anchor-Assisted Intelligent Reflecting Surface Channel Estimation for Multiuser Communications. In Proceedings of the GLOBECOM 2020—2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar]
- Liu, H.; Yuan, X.; Zhang, Y. Matrix-Calibration-Based Cascaded Channel Estimation for Reconfigurable Intelligent Surface Assisted Multiuser MIMO. IEEE J. Sel. Areas Commun. 2020, 38, 2621–2636. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, L.; Cui, S. Channel Estimation for Intelligent Reflecting Surface Assisted Multiuser Communications. In Proceedings of the 2020 IEEE Wireless Communications And Networking Conference (WCNC), Seoul, Republic of Korea, 25–28 May 2020; pp. 1–6. [Google Scholar]
- Wang, P.; Fang, J.; Duan, H.; Li, H. Compressed Channel Estimation for Intelligent Reflecting Sur-face-Assisted Millimeter Wave Systems. IEEE Signal Process. Lett. 2020, 27, 905–909. [Google Scholar] [CrossRef]
- Zhang, J.; Qi, C.; Li, P.; Lu, P. Channel Estimation for Reconfigurable Intelligent Surface Aided Massive MIMO System. In Proceedings of the 2020 IEEE 21st International Workshop On Signal Processing Advances In Wireless Communications (SPAWC), Atlanta, GA, USA, 26–29 May 2020; pp. 1–5. [Google Scholar]

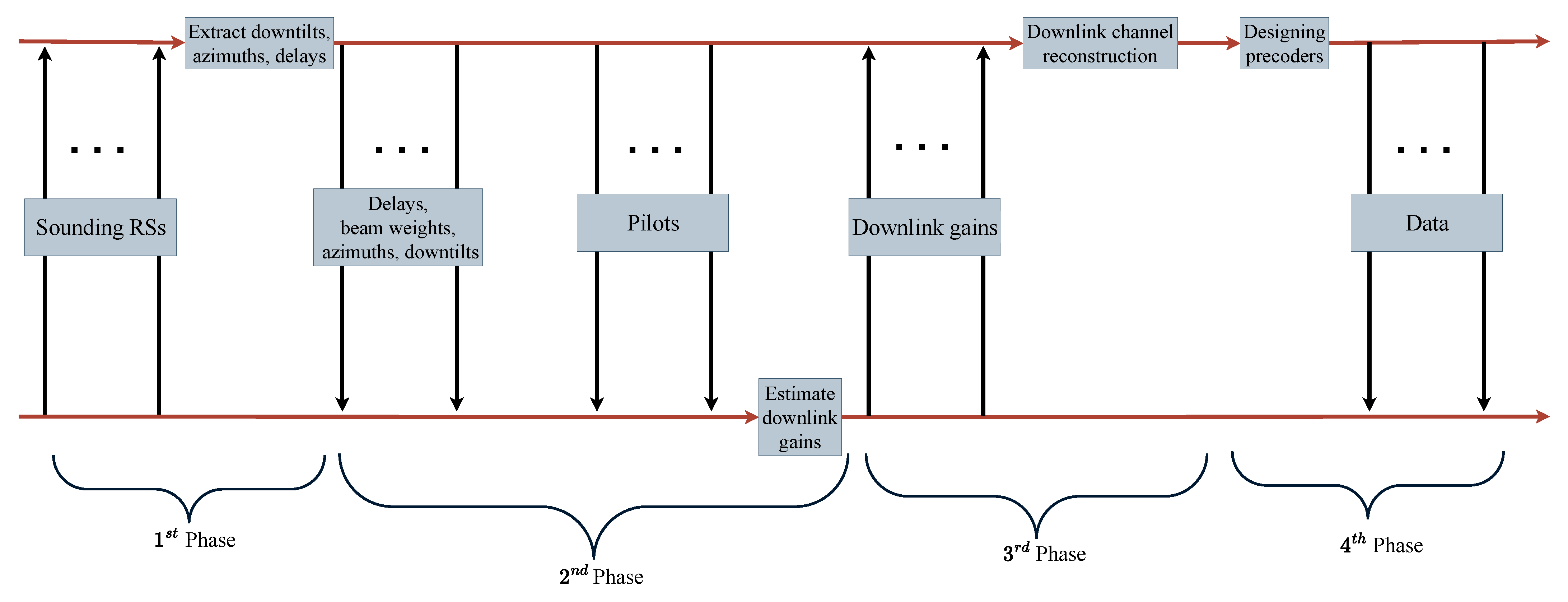
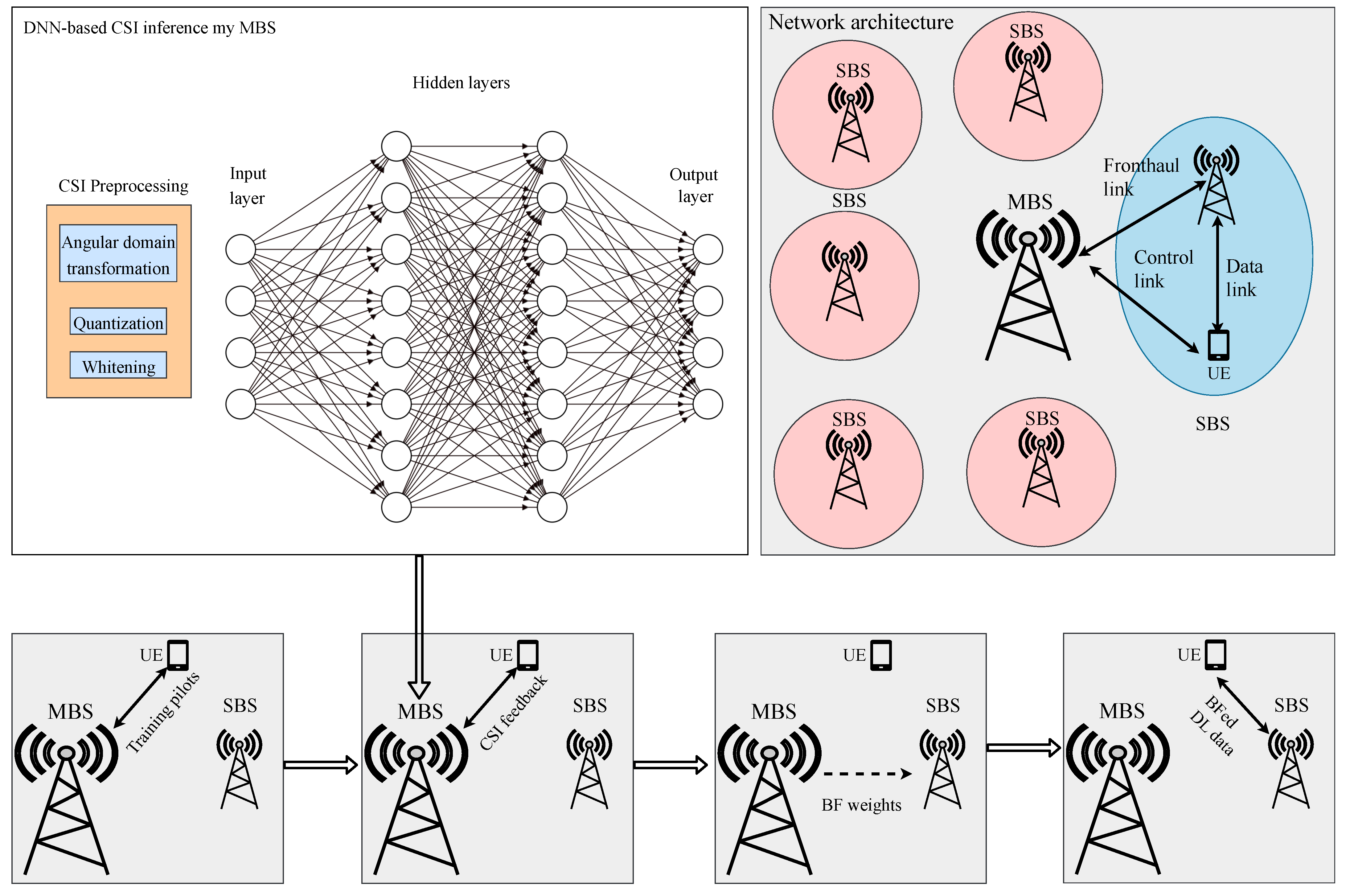
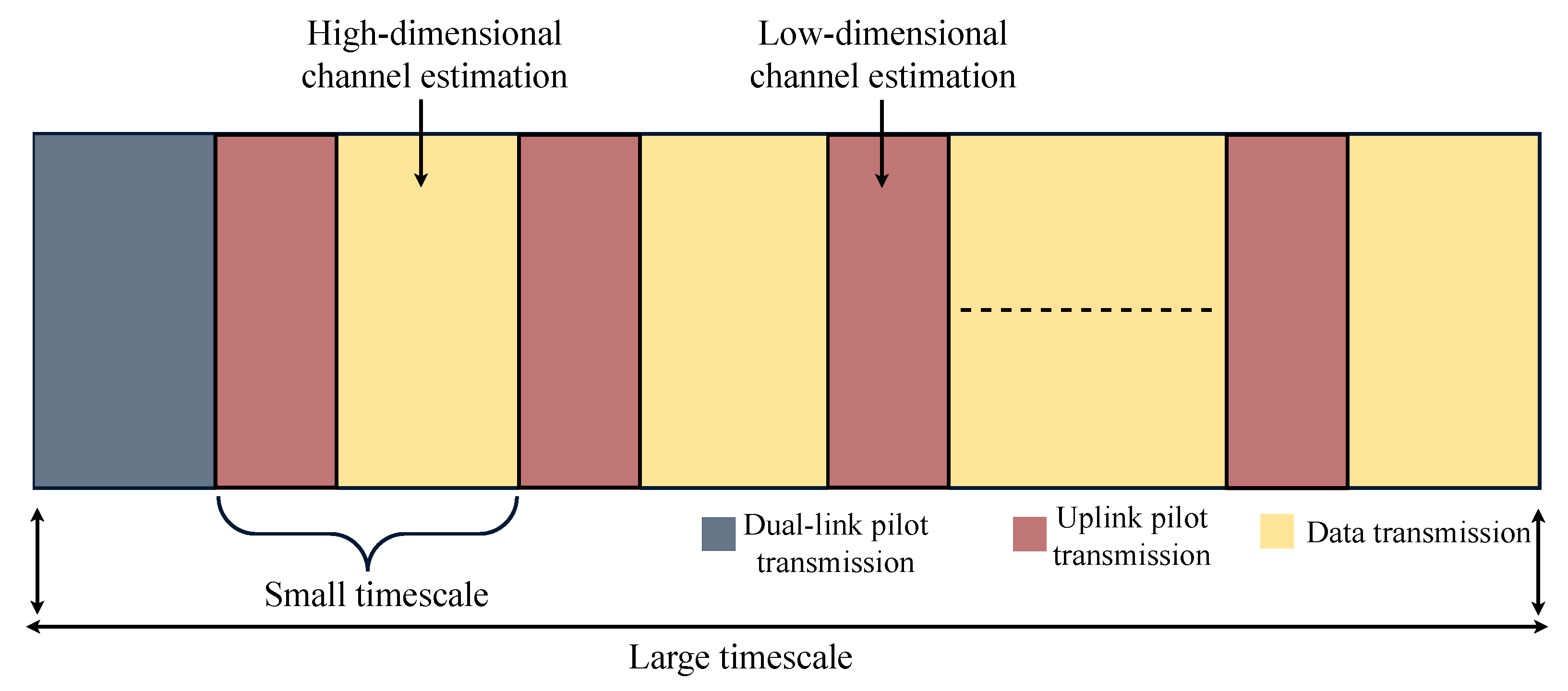
| Technique | Advantages | Limitations | Application Scenarios |
|---|---|---|---|
| Pilot-assisted estimation | High accuracy in low-noise environments; well-suited for TDD systems. | High pilot overhead; susceptible to pilot contamination. | Single-cell environments with limited user mobility. |
| Compressive sensing | Reduces pilot overhead; leverages channel sparsity. | Requires prior knowledge of sparsity; performance degrades in low SNR. | Sparse channel environments; FDD systems with limited feedback resources. |
| Deep learning | Adapts to complex channel conditions; reduces feedback overhead. | High computational cost; requires extensive training data. | Dynamic environments with varying channel conditions; RIS-assisted systems. |
| RIS-assisted estimation | Enhances signal propagation; reduces interference. | High pilot overhead; complex cascaded channel estimation. | Urban environments with high user density; mmWave communication systems. |
| Hybrid pilot schemes | Balances pilot overhead and estimation accuracy. | Increased complexity in pilot design and scheduling. | Multi-user scenarios with varying channel coherence times. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarafder, P.; Chun, C.; Ullah, A.; Kim, Y.; Choi, W. Channel Estimation in 5G-and-Beyond Wireless Communication: A Comprehensive Survey. Electronics 2025, 14, 750. https://doi.org/10.3390/electronics14040750
Tarafder P, Chun C, Ullah A, Kim Y, Choi W. Channel Estimation in 5G-and-Beyond Wireless Communication: A Comprehensive Survey. Electronics. 2025; 14(4):750. https://doi.org/10.3390/electronics14040750
Chicago/Turabian StyleTarafder, Pulok, Chanjun Chun, Arif Ullah, Yonggang Kim, and Wooyeol Choi. 2025. "Channel Estimation in 5G-and-Beyond Wireless Communication: A Comprehensive Survey" Electronics 14, no. 4: 750. https://doi.org/10.3390/electronics14040750
APA StyleTarafder, P., Chun, C., Ullah, A., Kim, Y., & Choi, W. (2025). Channel Estimation in 5G-and-Beyond Wireless Communication: A Comprehensive Survey. Electronics, 14(4), 750. https://doi.org/10.3390/electronics14040750







