Optimization of Active Disturbance Rejection Control System for Vehicle Servo Platform Based on Artificial Intelligence Algorithm
Abstract
:1. Introduction
2. Methods and Materials
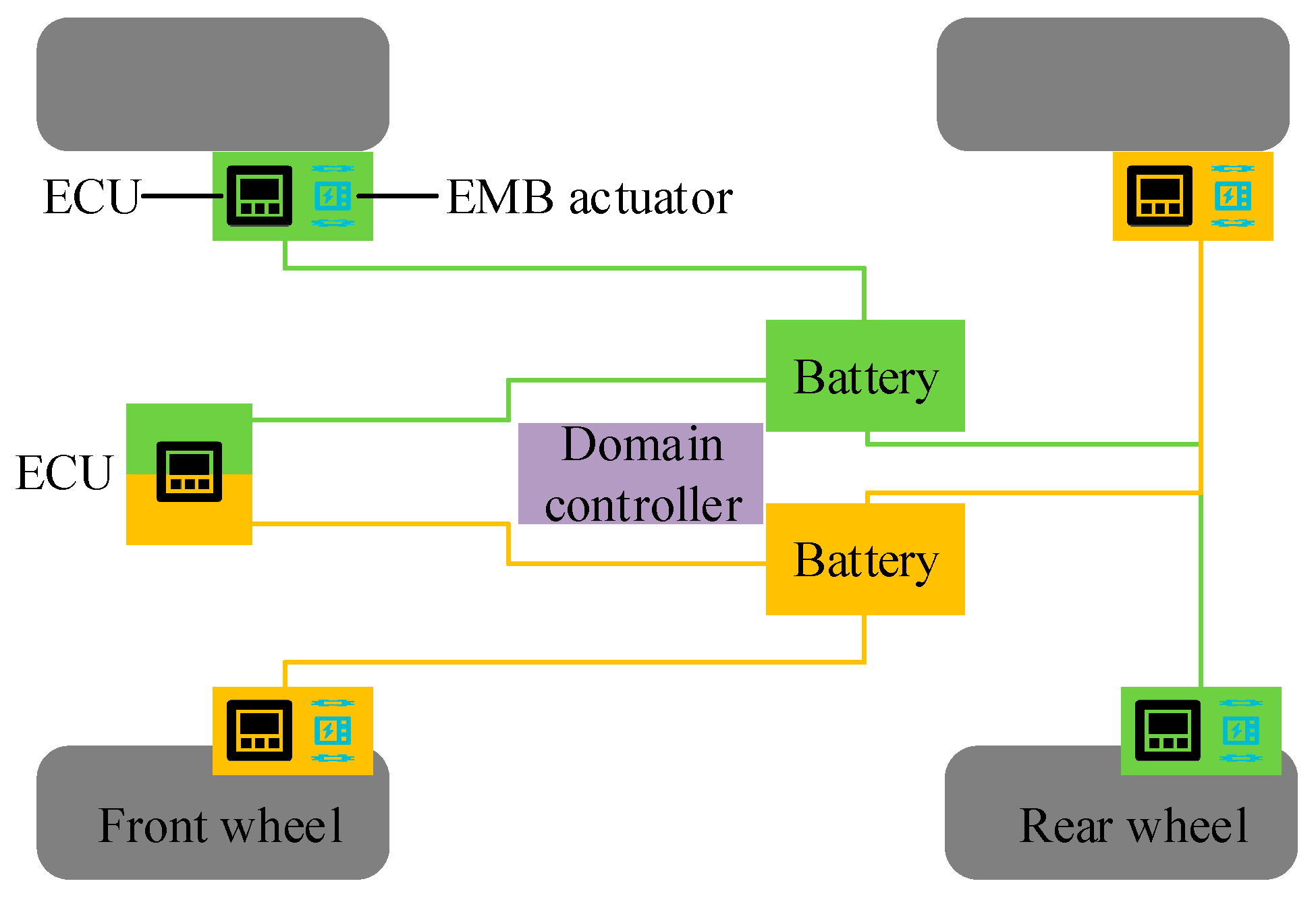
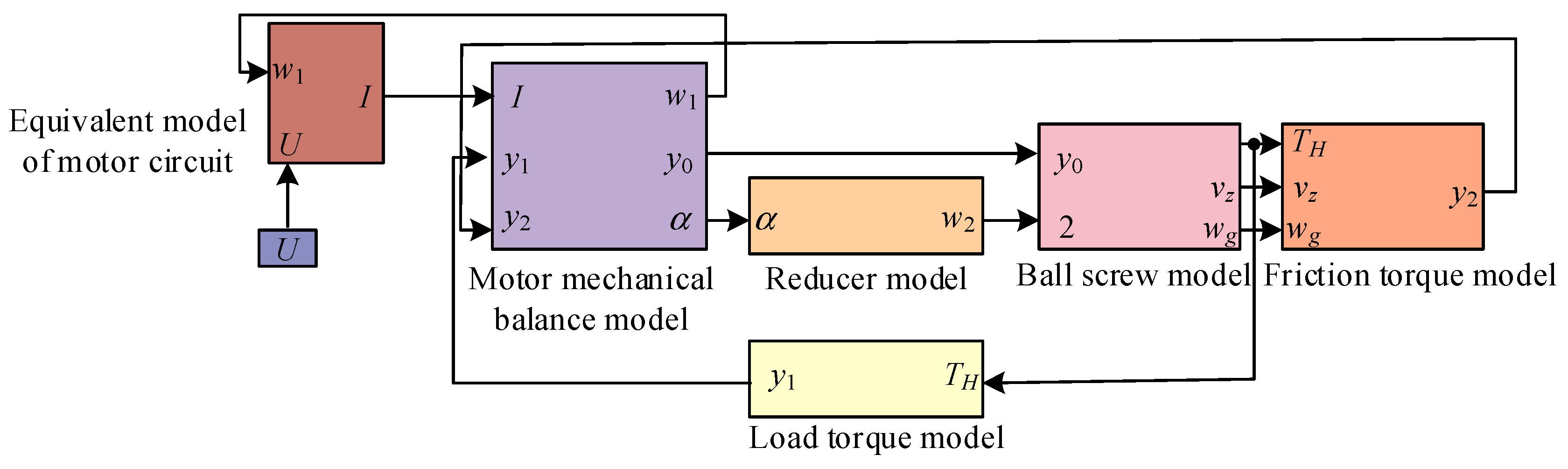
2.1. EMB Actuator Modeling
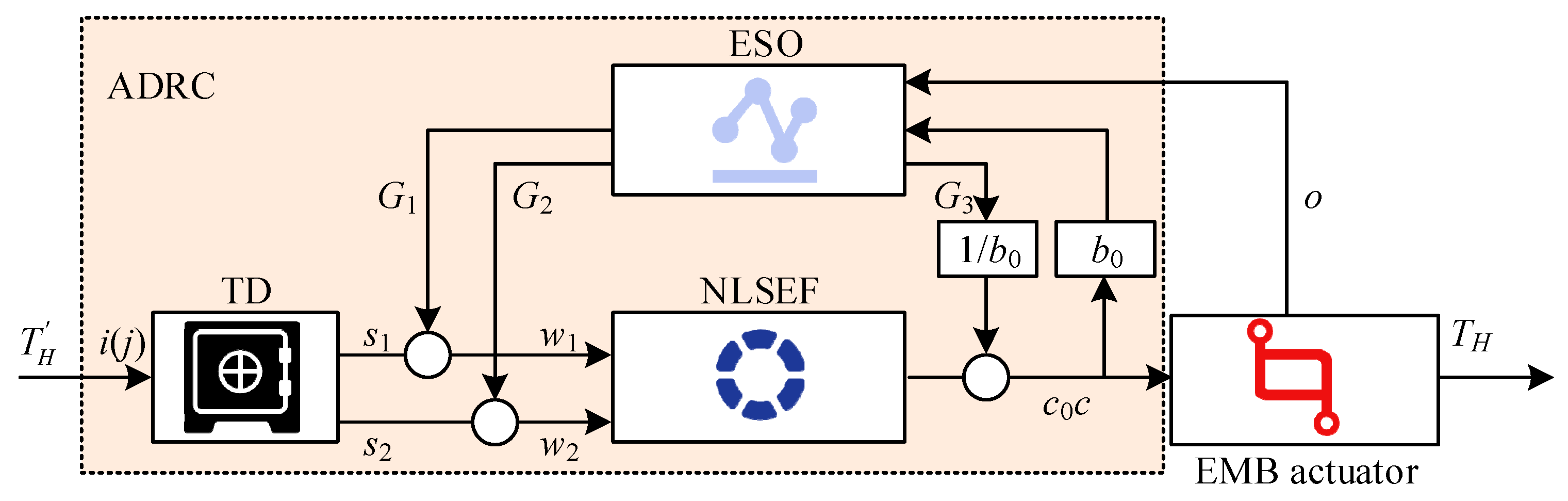
2.2. Optimization Method for ADRC Clamping Force Control Introducing PSO Algorithm
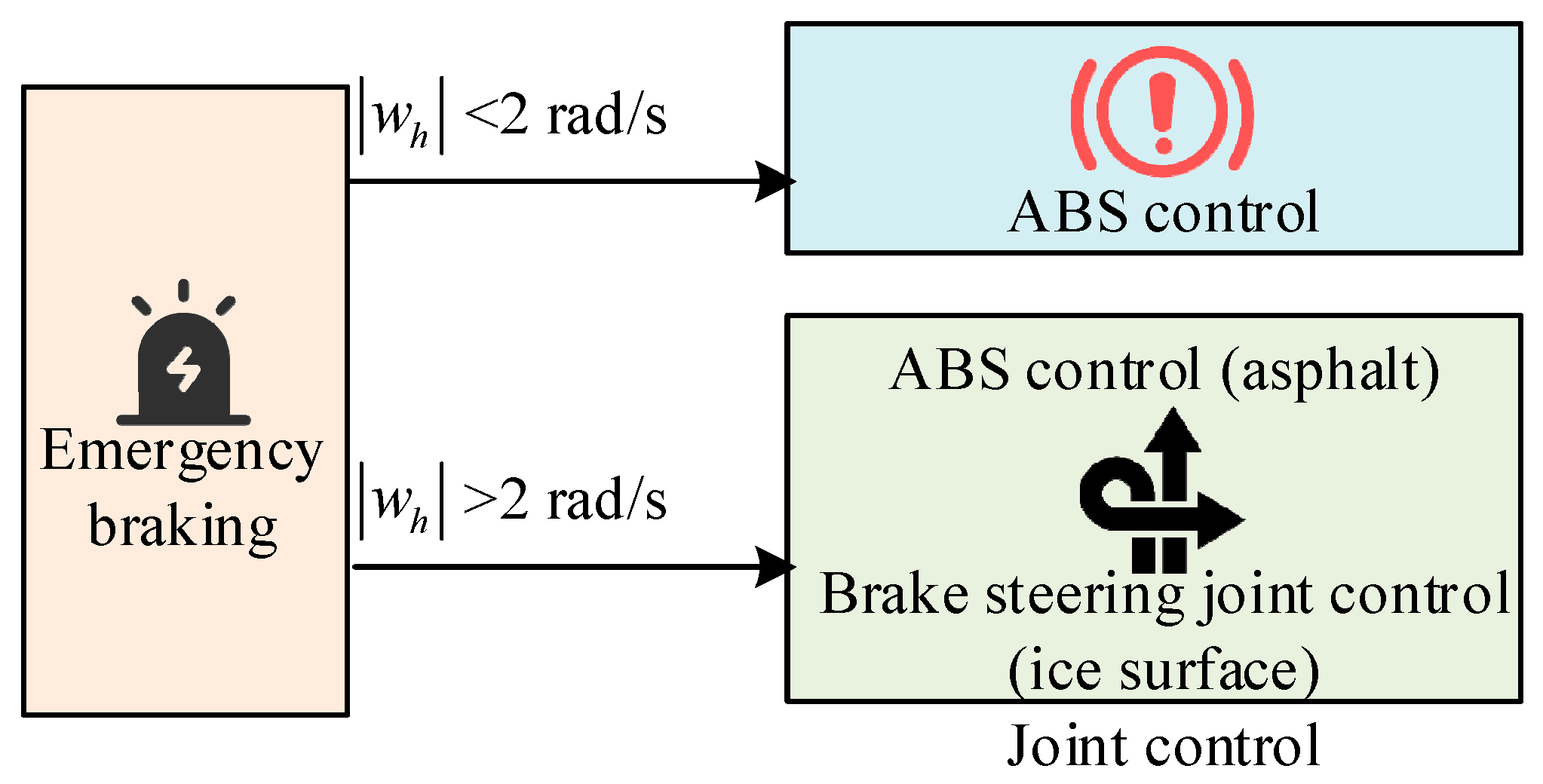
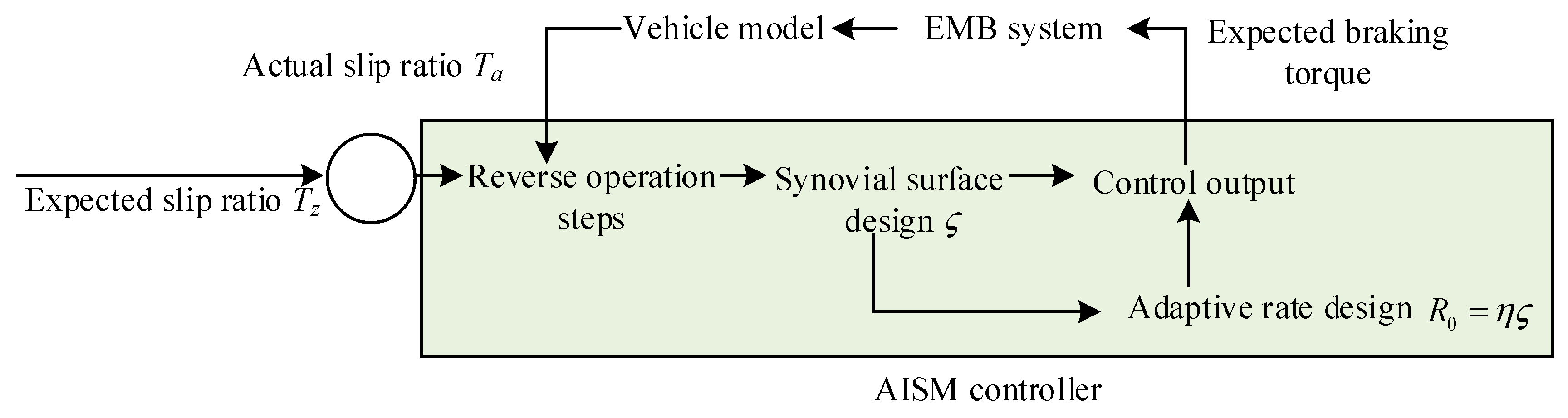
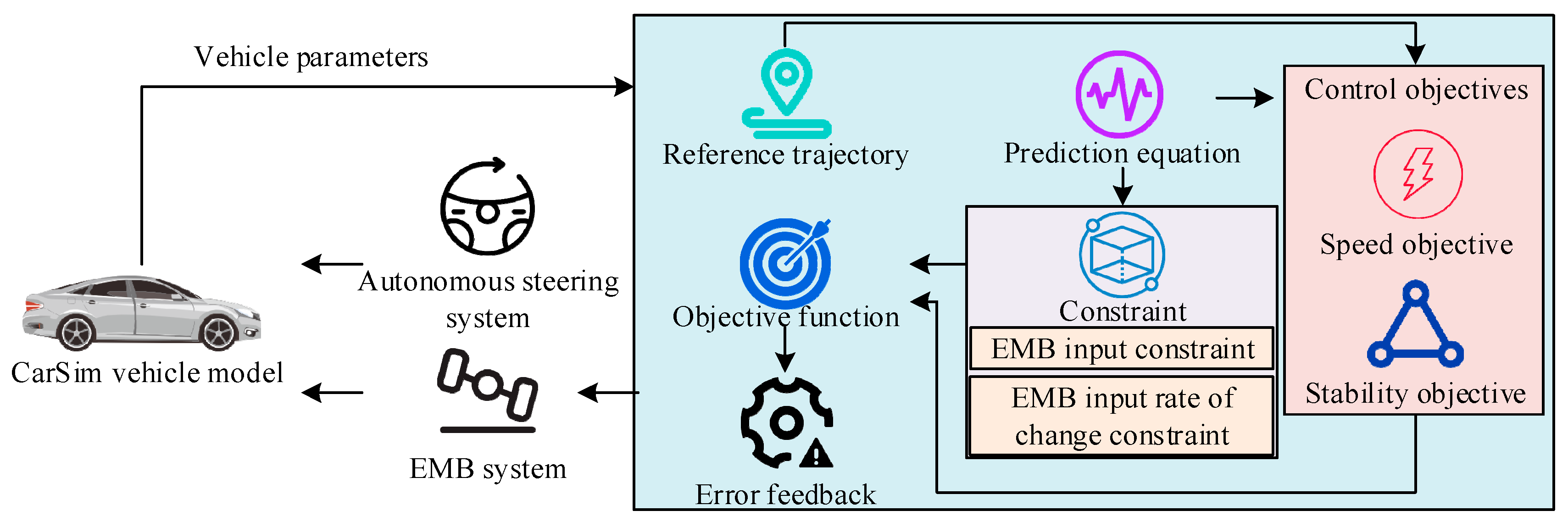
2.3. Joint Control Method for Steering and Braking
3. Results
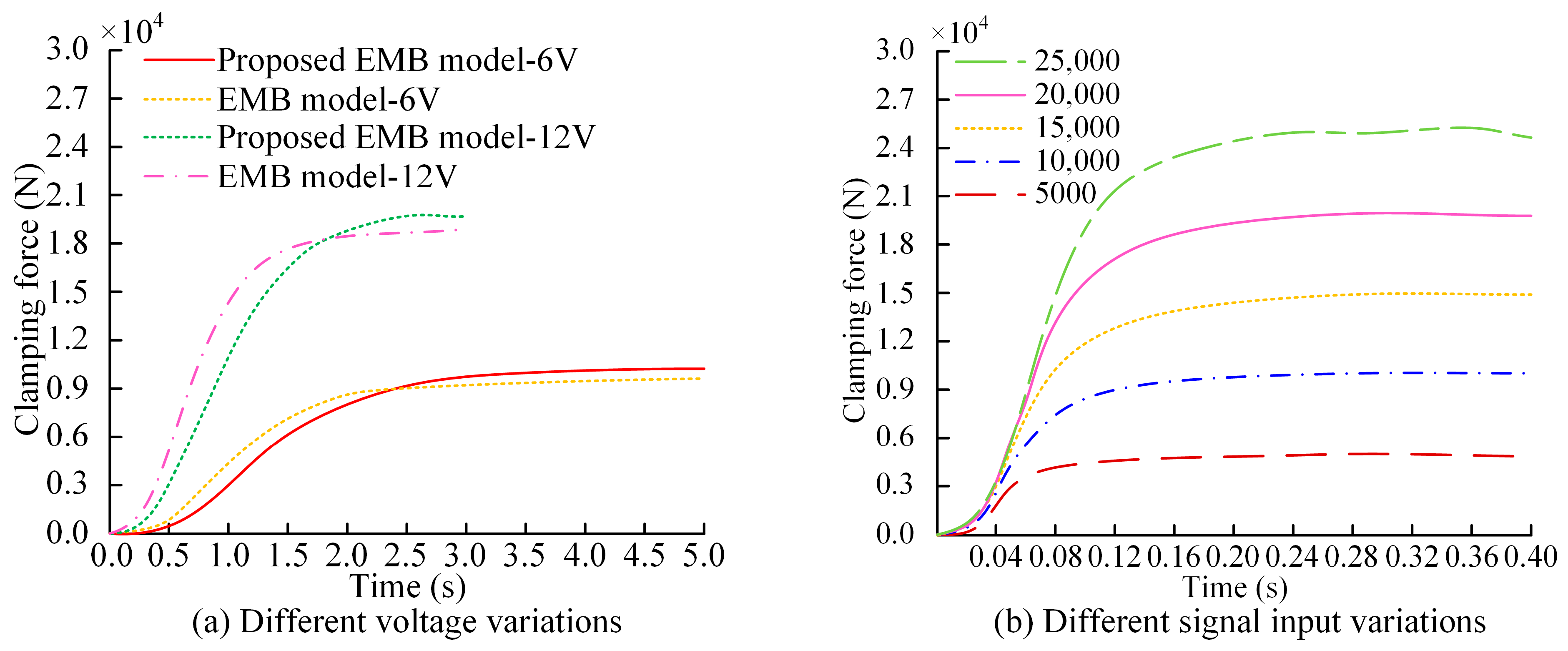
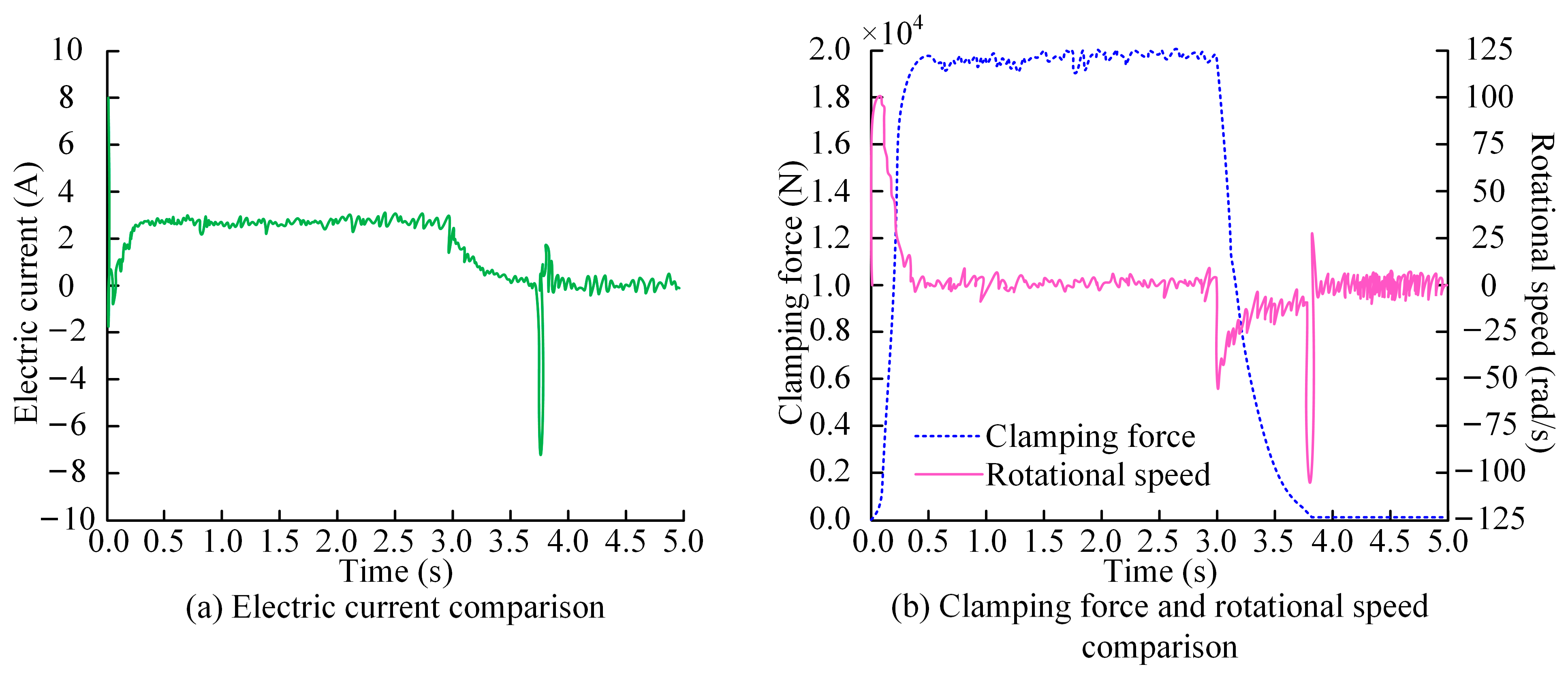
3.1. EMB Control Test Results
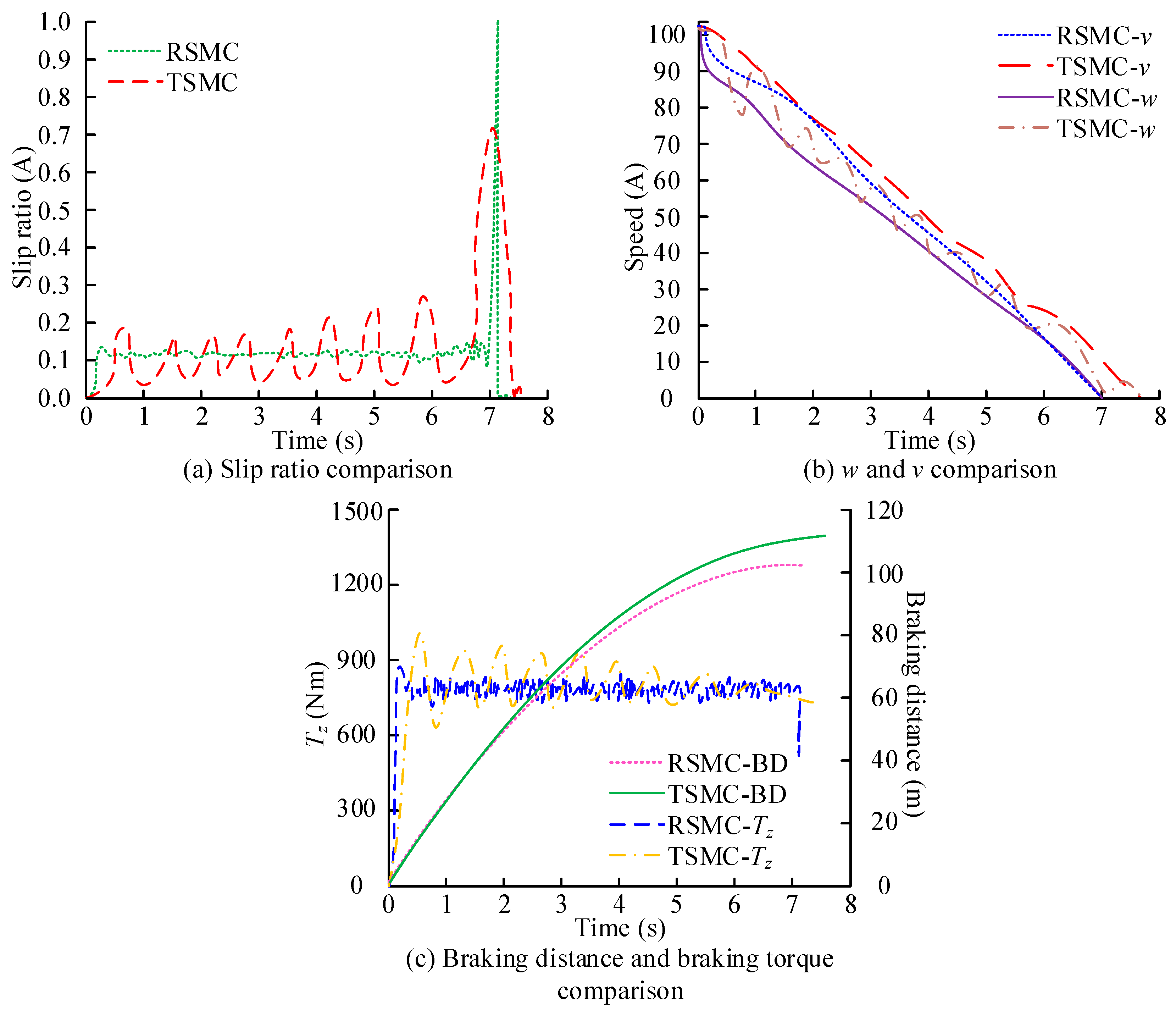
3.2. Analysis of ABS Control Effect
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shaojun, L.; Yingjie, L.; Wei, L.; Zhe, X.; Guoyou, W.; Yan, X.; Fansheng, J. Resonance Suppression Method of Vehicle Mounted Lifting Photoelectric Platform. Infrared Technol. 2024, 46, 406–412. [Google Scholar]
- Duan, S.C.; Sun, J.; ‘Frank’Bai, X.X.; Nguyen, Q.H.; Si, Z.Y.; Li, W.H.; Liu, Y. Principle design and control of a brake-by-wire actuator featuring magnetorheological clutch. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 237, 793–802. [Google Scholar] [CrossRef]
- Chen, G.; Zhao, X.; Gao, Z.; Hua, M. Dynamic drifting control for general path tracking of autonomous vehicles. IEEE Trans. Intell. Veh. 2023, 8, 2527–2537. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Iqbal, J. Improving stability and adaptability of automotive electric steering systems based on a novel optimal integrated algorithm. Eng. Comput. 2024, 41, 991–1034. [Google Scholar] [CrossRef]
- Gao, B.; Zheng, L.; Shen, W.; Zhang, W. A summary of parameter tuning of active disturbance rejection controller. Recent Adv. Electr. Electron. Eng. (Former. Recent Pat. Electr. Electron. Eng.) 2023, 16, 180–196. [Google Scholar] [CrossRef]
- Wng, Y.; Hu, Z.; Li, Y.; Zhang, X.; Cui, Y. Current Predictive Control of Electro-Mechanical Braking System for Unmanned Tracked Vehicles. Trans. Beijing Inst. Technol. 2024, 44, 792–800. [Google Scholar]
- Song, B.K.; Kim, J.H.; Hwang, K.Y.; Lim, M.S. Electro-mechanical characteristics of dual-winding motor according to winding arrangement for brake systems in highly automated driving vehicles. IEEE Trans. Veh. Technol. 2023, 72, 12524–12539. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, J.; Wng, Z.; Sun, S. Research on Design Optimization and Simulation of Regenerative Braking Control Strategy for Pure Electric Vehicle Based on EMB Systems. Trans. FAMENA 2023, 47, 33–49. [Google Scholar] [CrossRef]
- Xu, Z.; Gerada, C. Enhanced estimation of clamping-force for automotive EMB actuators using a switching extended state observer. IEEE Trans. Ind. Electron. 2023, 71, 2220–2230. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, H.; Elahi, H.; Miao, F.; Riaz, S. Clamping force sensor fault analysis and fault-tolerant control of the electromechanical brake system. Arab. J. Sci. Eng. 2023, 48, 6011–6023. [Google Scholar] [CrossRef]
- Wng, J.; Wang, X.; Luo, Z.; Assadian, F. Active Disturbance Rejection Control of Differential Drive Assist Steering for Electric Vehicles. Energies 2020, 13, 2647. [Google Scholar] [CrossRef]
- Zhao, L.; Wng, N.; Xia, G.; Mei, X.; Wng, H.; Zhang, D. Regenerative braking torque compensation control based on improved ADRC. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 238, 1315–1329. [Google Scholar] [CrossRef]
- Jin, H.; Gao, Z. On the notions of normality, locality, and operational stability in ADRC. Control Theory Technol. 2023, 21, 97–109. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Y.; Zhou, L.; Wng, B.; Cheng, Z.; Fan, H. Cascade ADRC with neural network-based ESO for hypersonic vehicle. J. Frankl. Inst. 2023, 360, 9115–9138. [Google Scholar] [CrossRef]
- Safiullah, S.; Rahman, A.; Lone, S.A. A second-order ADRC for synchronized frequency-voltage mitigation of EV integrated power system. IETE J. Res. 2024, 70, 515–530. [Google Scholar] [CrossRef]
- Madonski, R.; Herbst, G.; Stankovic, M. ADRC in output and error form: Connection, equivalence, performance. Control Theory Technol. 2023, 21, 56–71. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, H.; Miao, F. An adaptive backstepping nonsingular fast terminal sliding-mode control for the electromechanical brake system with backlash nonlinearity compensation. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2023, 237, 858–870. [Google Scholar] [CrossRef]
- Chen, Q.; Lv, Z.; Tong, H.; Zeng, D.; Ouyang, L.; Liu, Q. Study on multi-closed loop control of electro-mechanical braking for electric vehicles based on clamping force. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 238, 4245–4254. [Google Scholar] [CrossRef]
- Anderson, E.; Fan, F.R.; Cai, J.; Holtzmann, W.; Taniguchi, T.; Watanabe, K.; Xiao, D.; Yao, W.; Xu, X. Programming correlated magnetic states with gate-controlled moire geometry. Science 2023, 381, 325–330. [Google Scholar] [CrossRef]
- Shen, Q.; Huang, S.; Sun, B.; Chen, X.; Tao, D.; Wan, H.; Bao, E. PVII: A pedestrian-vehicle interactive and iterative prediction framework for pedestrian’s trajectory. Appl. Intell. 2024, 54, 9881–9891. [Google Scholar] [CrossRef]
- Son, S.J.; Meetei, T.S.; Park, D.K. Wide Optical Beam Steering LCOS Device for Solid-State LiDAR Applications. IEEE Photonics Technol. Lett. 2024, 36, 35–38. [Google Scholar] [CrossRef]
- Lee, D.H. Efficient perception, planning, and control algorithm for vision-based automated vehicles. Appl. Intell. 2024, 54, 8278–8295. [Google Scholar] [CrossRef]
- Lancaster, P.; Mavrogiannis, C.; Srinivasa, S.; Smith, J.R. Electrostatic brakes enable individual joint control of underactuated, highly articulated robots. Int. J. Robot. Res. 2024, 43, 2204–2220. [Google Scholar] [CrossRef]
- Zhu, S.; Fan, X.; Qi, G.; Wng, P. Review of control algorithms of vehicle anti-lock braking system. Recent Pat. Eng. 2023, 17, 30–45. [Google Scholar] [CrossRef]
- Kong, X.; Deng, Z.; Zhao, Y.; Gao, W. Stability control of distributed drive electric vehicle based on adaptive fuzzy sliding mode. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 238, 2741–2752. [Google Scholar] [CrossRef]
- Yin, C.; Mei, Z.; Feng, Y.; Tang, L. A novel traction control strategy for an electric bus. Int. J. Veh. Perform. 2024, 10, 215–237. [Google Scholar] [CrossRef]
- Yang, T.; Li, P.; Li, Q.; Li, Z. Vehicle stability control strategy for high-speed curves based on mode switching. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 238, 3825–3842. [Google Scholar] [CrossRef]
- Gao, L.; Gao, Q.H.; Cheng, H.J.; Liu, Z.; He, X. Multi-body modeling and dynamic analysis of the heavy-load multi-axle vehicle Based on 6S/6M ABS control. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 238, 491–508. [Google Scholar] [CrossRef]
- Zeng, X.; Gao, H.; Song, D.; Li, L. Coordinated control algorithm of lateral stability of hybrid electric commercial vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 238, 2767–2785. [Google Scholar] [CrossRef]
- Nagarkar, M.; Bhalerao, Y.; Sashikumar, S.; Sashikumar, S.; Hase, V.; Navthar, R.; Zaware, R.; Surner, N. Multi-objective optimization and experimental investigation of quarter car suspension system. Int. J. Dyn. Control 2024, 12, 1222–1238. [Google Scholar] [CrossRef]



| Parameters | Numerical Value |
|---|---|
| Integral step size | 1.0 × 10−4 |
| Speed factor | 2.0 × 106 |
| Correction factor | 7.4 × 105 |
| Scale factor | 4.5 × 10−4 |
| Differential coefficient | 1.6 × 10−4 |
| Control parameter | 1067 |
| Control parameter | 101,525 |
| Control parameter | 651.7 × 106 |
| Road Surface Type | Asphalt Pavement | Ice Road Surface | Docking with the Road Surface | |||
|---|---|---|---|---|---|---|
| Control Method | Optimized Control | Original Control | Optimized Control | Original Control | Optimized Control | Original Control |
| RMSE of slip ratio | 0.0498 | 0.0522 | 0.0149 | 0.0172 | 0.0173 | 0.00178 |
| Maximum slip rate error | 0.0428 | 0.0492 | 0.0632 | 0.1266 | 0.0233 | 0.0947 |
| RMSE of current | 2.3522 | 3.6477 | 1.4137 | 3.4686 | 1.6143 | 2.0705 |
| Road Surface Type | 0.4 | 0.6 |
|---|---|---|
| Maximum lateral braking deviation (m) | 0.148 | 0.243 |
| Longitudinal braking distance (m) | 153.4 | 113.2 |
| Maximum center of mass lateral deviation angle (°) | 1.802 | 4.193 |
| Maximum lateral angular velocity (°/s) | 3.880 | 4.343 |
| Maximum yaw angle (°) | 2.327 | 3.654 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Su, X.; Ren, X. Optimization of Active Disturbance Rejection Control System for Vehicle Servo Platform Based on Artificial Intelligence Algorithm. Electronics 2025, 14, 752. https://doi.org/10.3390/electronics14040752
Yang F, Su X, Ren X. Optimization of Active Disturbance Rejection Control System for Vehicle Servo Platform Based on Artificial Intelligence Algorithm. Electronics. 2025; 14(4):752. https://doi.org/10.3390/electronics14040752
Chicago/Turabian StyleYang, Fei, Xiaopeng Su, and Xuemei Ren. 2025. "Optimization of Active Disturbance Rejection Control System for Vehicle Servo Platform Based on Artificial Intelligence Algorithm" Electronics 14, no. 4: 752. https://doi.org/10.3390/electronics14040752
APA StyleYang, F., Su, X., & Ren, X. (2025). Optimization of Active Disturbance Rejection Control System for Vehicle Servo Platform Based on Artificial Intelligence Algorithm. Electronics, 14(4), 752. https://doi.org/10.3390/electronics14040752





