An Approach to Control Multilevel Flying-Capacitor Converters Using Optimal Dynamic Programming Benchmark
Abstract
:1. Introduction
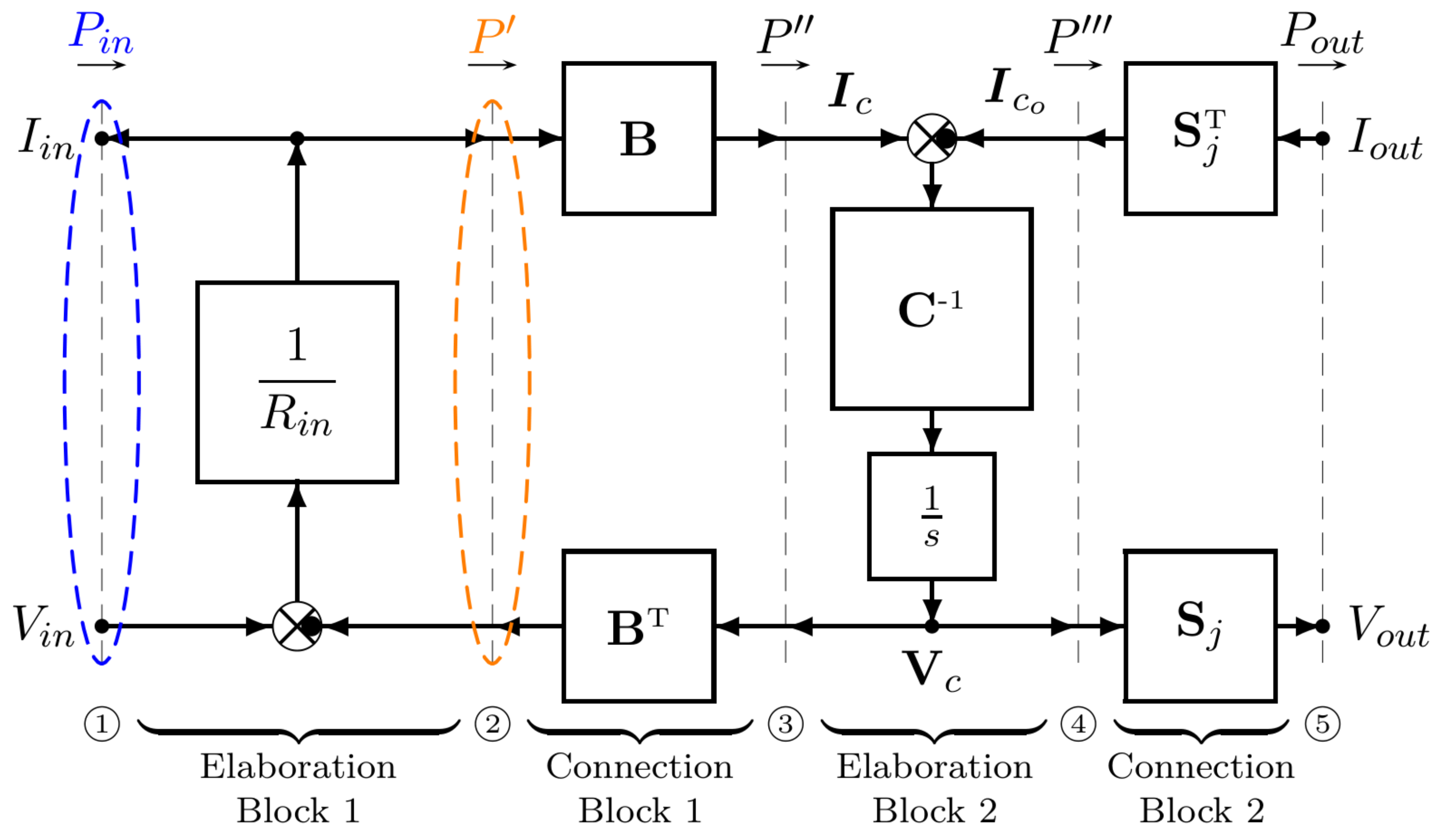
2. Converter Modeling
Discrete-Time Model
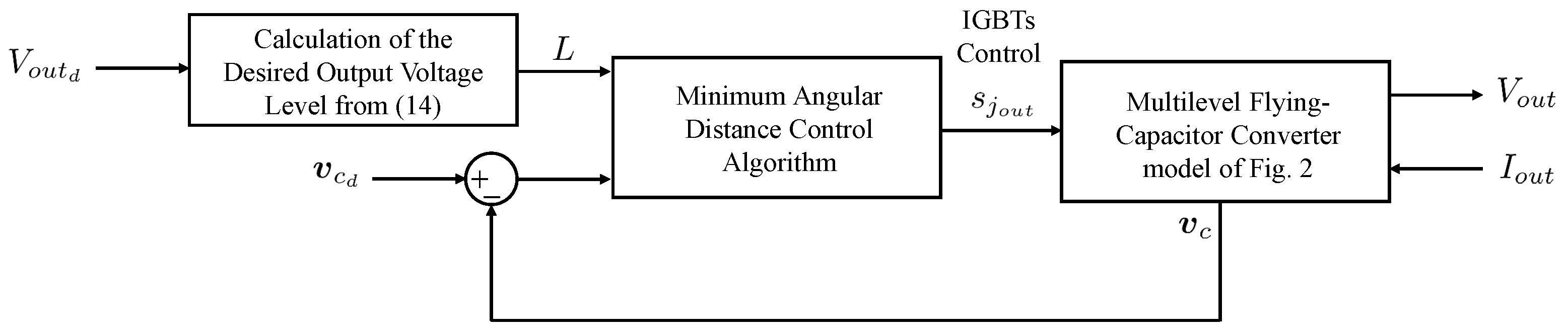
3. Converter Control
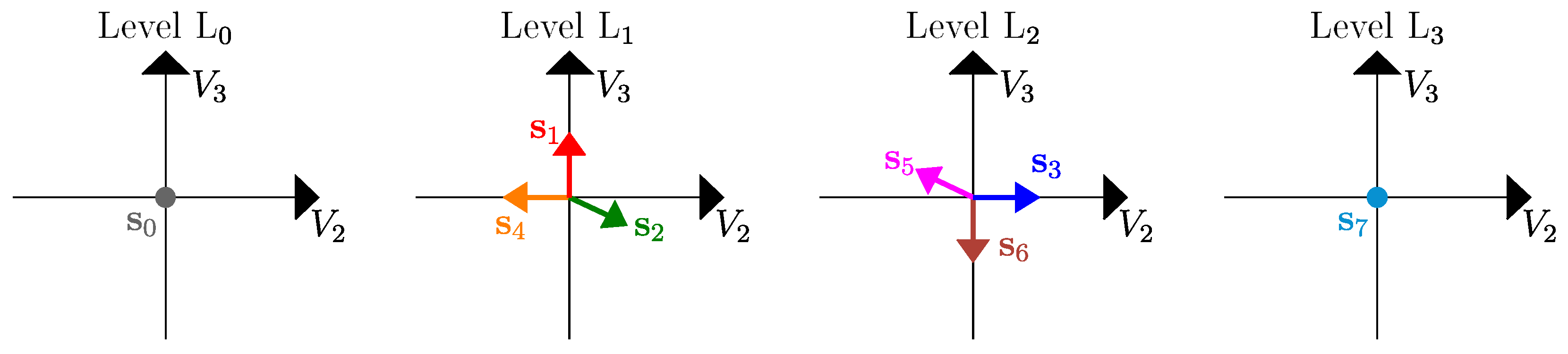
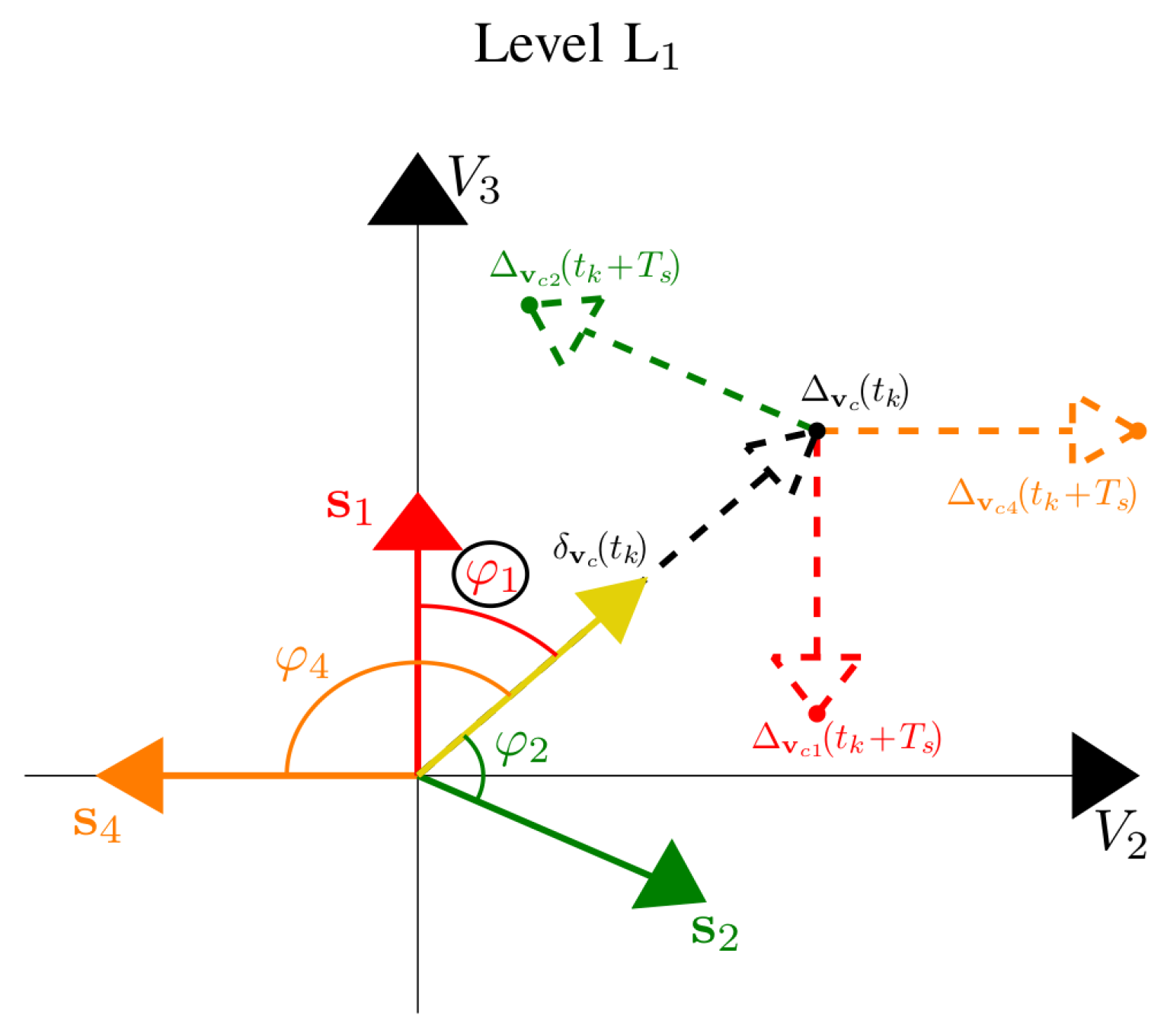
3.1. Proposed Minimum Angular Distance (MAD) Control
| Algorithm 1 Matlab-like form of the minimum angular distance algorithm. |
|
3.2. Optimal Solution Using Dynamic Programming
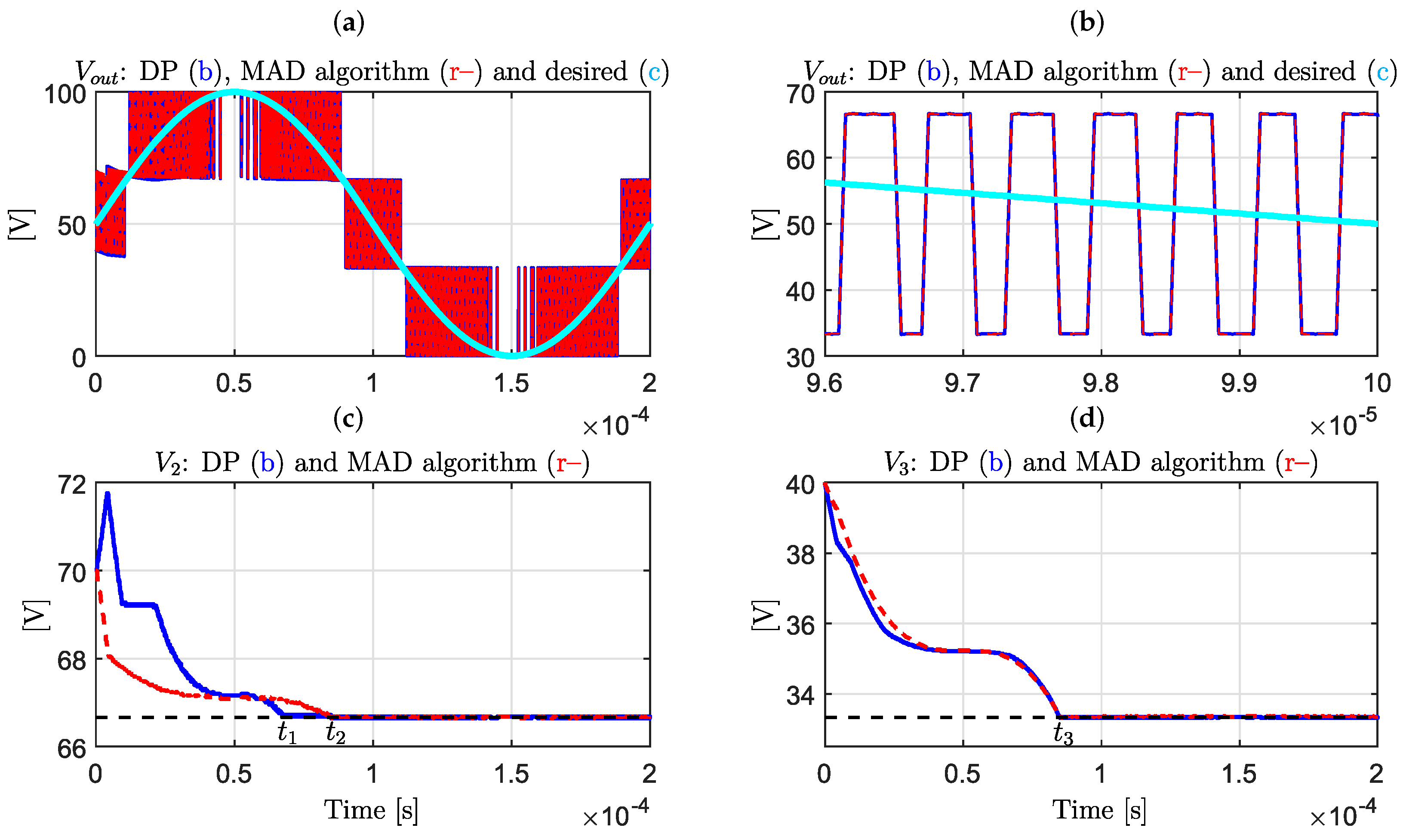
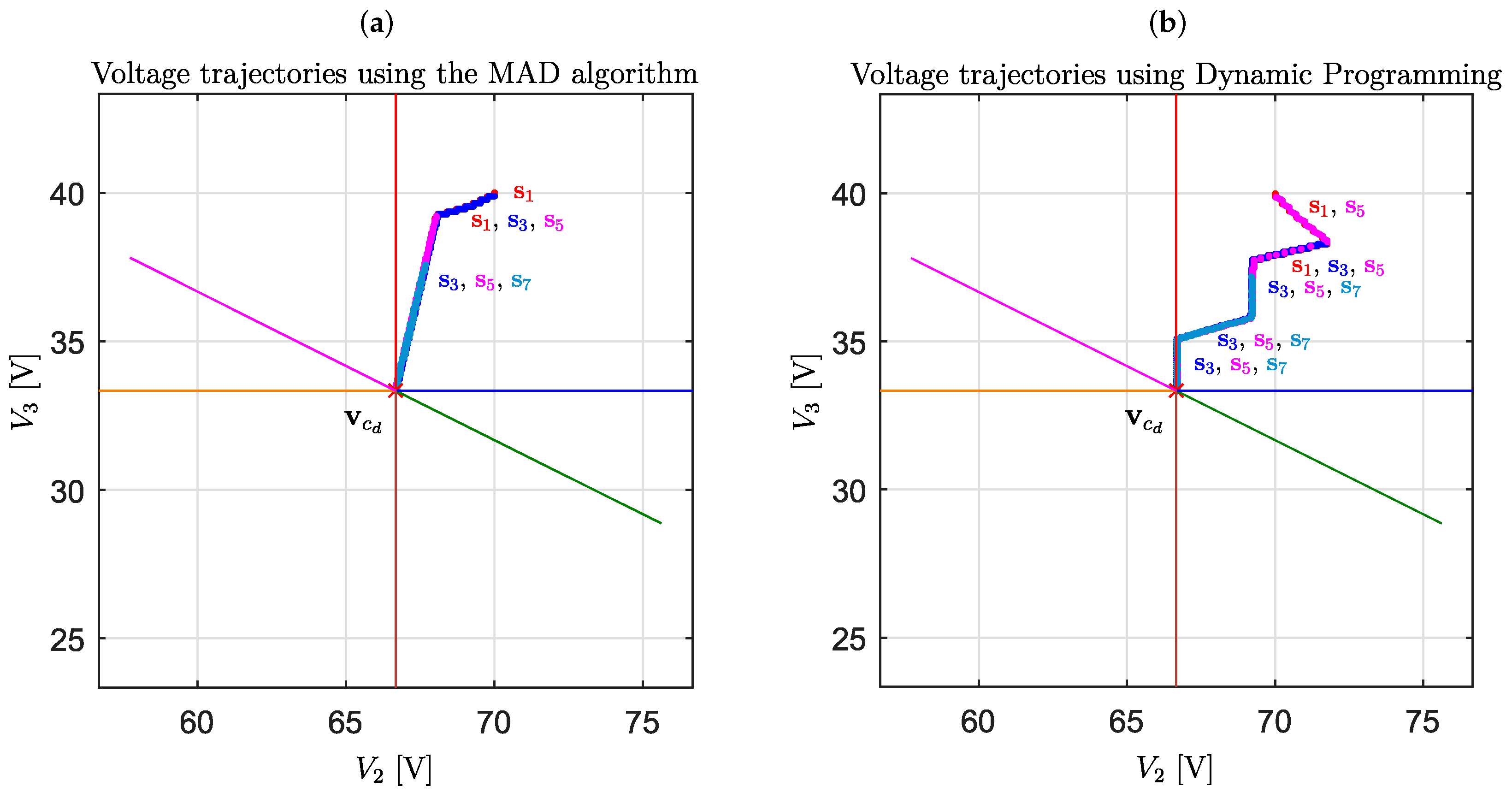
4. Results
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chang, H.; Vanfretti, L. Power Hardware-in-the-Loop Smart Inverter Testing with Distributed Energy Resource Management Systems. Electronics 2024, 13, 1866. [Google Scholar] [CrossRef]
- Cai, J.; Zhang, X.; Zhang, W.; Zeng, Y. An Integrated Power Converter-Based Brushless DC Motor Drive System. IEEE Trans. Power Electron. 2022, 37, 8322–8332. [Google Scholar] [CrossRef]
- Zanasi, R.; Tebaldi, D. Study of the Bidirectional Efficiency of Linear and Nonlinear Physical Systems. In Proceedings of the Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 545–552. [Google Scholar]
- Muniandi, B.; Wan, S.; El-Yabroudi, M. Bi-Directional Charging with V2L Integration for Optimal Energy Management in Electric Vehicles. Electronics 2024, 13, 4221. [Google Scholar] [CrossRef]
- Gómez-Ruiz, G.; Sánchez-Herrera, R.; Clavijo-Camacho, J.; Cano, J.M.; Ruiz-Rodríguez, F.J.; Andújar, J.M. A Versatile Platform for PV System Integration into Microgrids. Electronics 2024, 13, 3995. [Google Scholar] [CrossRef]
- Alaql, F.; Alfraidi, W.; Alhatlani, A.; Al-Shamma’a, A.A.; Farh, H.M.H.; Allehyani, A. A Detailed Analysis and Gain Derivation of Reconfigurable Voltage Rectifier-Based LLC Converter. Electronics 2024, 13, 3788. [Google Scholar] [CrossRef]
- Alouache, H.E.; Sayah, S.; Bosisio, A.; Hamouda, A.; Kouadri, R.; Shirvani, R. Optimal Placement of HVDC-VSC in AC System Using Self-Adaptive Bonobo Optimizer to Solve Optimal Power Flows: A Case Study of the Algerian Electrical Network. Electronics 2024, 13, 3848. [Google Scholar] [CrossRef]
- Zanasi, R.; Tebaldi, D. Modeling control and robustness assessment of multilevel flying-capacitor converters. Energies 2021, 14, 1903. [Google Scholar] [CrossRef]
- Agheb, E.; Holtsmark, N.; Høidalen, H.K.; Molinas, M. High frequency wind energy conversion system for offshore DC collection grid—Part I: Comparative loss evaluation. Sustain. Energy Grids Netw. 2016, 5, 167–176. [Google Scholar] [CrossRef]
- Holtsmark, N.; Agheb, E.; Molinas, M.; Høidalen, H.K. High frequency wind energy conversion system for offshore DC collection grid—Part II: Efficiency improvements. Sustain. Energy Grids Netw. 2016, 5, 177–185. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Lee, H.-H. Development of a three-to-five-phase indirect matrix converter with carrier-based PWM based on space-vector modulation analysis. IEEE Trans. Ind. Electron. 2016, 63, 13–24. [Google Scholar] [CrossRef]
- Rodrìguez, J.; Lai, J.-S.; Peng, F.Z. Multilevel inverters: A survey of topologies, controls, and applications. IEEE Trans. Ind. Electron. 2002, 49, 724–738. [Google Scholar] [CrossRef]
- Rodrìguez, J.; Bernet, S.; Wu, B.; Pontt, J.O.; Kouro, S. Multilevel voltage-source-converter topologies for industrial medium-voltage drives. IEEE Trans. Ind. Electron. 2007, 54, 2930–2945. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y.; Liu, Y.; Jiang, S. Model Assisted Extended State Observer-Based Deadbeat Predictive Current Control for Modular Multilevel Converter. Electronics 2024, 13, 3789. [Google Scholar] [CrossRef]
- Katir, H.; Abouloifa, A.; Noussi, K.; Lachkar, I.; Aroudi, A.E.; Aourir, M.; Otmani, F.E.; Giri, F. Fault tolerant backstepping control for double-stage grid-connected photovoltaic systems using cascaded H-Bridge multilevel inverters. IEEE Control Syst. Lett. 2021, 6, 1406–1411. [Google Scholar] [CrossRef]
- Lopez, A.; Patino, D.; Diez, R.; Perilla, G. An equivalent continuous model for switched systems. Syst. Control Lett. 2013, 62, 124–131. [Google Scholar] [CrossRef]
- Liu, M.; Li, Z.; Yang, X. A universal mathematical model of modular multilevel converter with half-bridge. Energies 2020, 13, 4464. [Google Scholar] [CrossRef]
- Trip, S.; Cucuzzella, M.; Cheng, X.; Scherpen, J. Distributed averaging control for voltage regulation and current sharing in DC microgrids. IEEE Control Syst. Lett. 2019, 3, 174–179. [Google Scholar] [CrossRef]
- Tebaldi, D.; Zanasi, R. Modeling Control and Simulation of a Series Hybrid Propulsion System. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Gijon, Spain, 18 November–16 December 2020; pp. 1–7. [Google Scholar]
- Tebaldi, D.; Zanasi, R. Systematic modeling of complex time-variant gear systems using a Power-Oriented approach. Control Eng. Pract. 2023, 132, 105420. [Google Scholar] [CrossRef]
- Michos, G.; Baldivieso-Monasterios, P.R.; Konstantopoulos, G.C. Distributed economic nonlinear MPC for DC Micro-Grids with inherent bounded dynamics and coupled constraints. Syst. Control Lett. 2022, 167, 105327. [Google Scholar] [CrossRef]
- Komaee, A. Optimal control with maximum cost performance measure. IEEE Control Syst. Lett. 2021, 6, 127–132. [Google Scholar] [CrossRef]
- Ben-Brahim, L.; Gastli, A.; Trabelsi, M.; Ghazi, K.A.; Houchati, M.; Abu-Rub, H. Modular multilevel converter circulating current reduction using model predictive control. IEEE Trans. Ind. Electron. 2016, 63, 3857–3866. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, C.; Chen, C.; Xiong, J.; Zhang, K. Ripple analysis and capacitor voltage balancing of five-level hybrid clamped inverter (5L-HC) for medium-voltage applications. IEEE Access 2019, 7, 86077–86089. [Google Scholar] [CrossRef]
- Tian, H.; Li, Y.W. Carrier-based stair edge PWM (SEPWM) for capacitor balancing in multilevel converters with floating capacitors. IEEE Trans. Ind. Appl. 2018, 54, 3440–3452. [Google Scholar] [CrossRef]
- McGrath, B.P.; Holmes, D.G. Enhanced voltage balancing of a flying capacitor multilevel converter using phase disposition (PD) modulation. IEEE Trans. Power Electron. 2011, 26, 1933–1942. [Google Scholar] [CrossRef]
- Kang, D.-W.; Lee, B.-K.; Jeon, J.-H.; Kim, T.-J.; Hyun, D.-S. A symmetric carrier technique of CRPWM for voltage balance method of flying-capacitor multilevel inverter. IEEE Trans. Ind. Electron. 2005, 52, 879–888. [Google Scholar] [CrossRef]
- Moritz, R.M.B.; Batschauer, A.L. Capacitor voltage balancing in a 5-L full-bridge flying capacitor inverter. In Proceedings of the Brazilian Power Electronics Conference (COBEP), Juiz de Fora, Brazil, 19–22 November 2017. [Google Scholar]
- Amini, J.; Abedini, A. A straightforward close-loop control strategy for a single-phase asymmetrical flying capacitor multilevel inverter. In Proceedings of the Annual International Power Electronics, Drive Systems and Technologies Conference, Tehran, Iran, 13–14 February 2013. [Google Scholar]
- Saleh, S.A. Maximum resolution based method for balancing capacitor voltages in 7-level single phase flying-capacitor wavelet modulated inverters. IEEE Trans. Ind. Appl. 2023, 59, 5019–5031. [Google Scholar] [CrossRef]
- Choi, S.; Saeedifard, M. Capacitor voltage balancing of flying capacitor multilevel converters by space vector PWM. IEEE Trans. Power Deliv. 2012, 27, 1154–1161. [Google Scholar] [CrossRef]
- Borrelli, F.; Bemporad, A.; Morari, M. Predictive Control for Linear and Hybrid Systems; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
- Ebrahimian, A.; Khan, W.A.; Weise, N. Enhanced Model Predictive Nearest Level Control for 5-Level Flying Capacitor Multilevel Converter, Hardware Implementation and Comparison. In Proceedings of the 2023 IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 19–23 March 2023; pp. 2728–2734. [Google Scholar]
- Garcia, C.; Mohammadinodoushan, M.; Yaramasu, V.; Norambuena, M.; Davari, S.A.; Zhang, Z.; Khaburi, D.A.; Rodriguez, J. FCS-MPC Based Pre-Filtering Stage for Computational Efficiency in a Flying Capacitor Converter. IEEE Access 2021, 9, 111039–111049. [Google Scholar] [CrossRef]
- Ma, W.; Zhang, B.; Qiu, D. Robust Single-Loop Control Strategy for Four-Level Flying-Capacitor Converter Based on Switched System Theory. IEEE Trans. Ind. Electron. 2023, 70, 7832–7844. [Google Scholar] [CrossRef]
- Bakeer, A.; Mohamed, I.S.; Malidarreh, P.B.; Hattabi, I.; Liu, L. An Artificial Neural Network-Based Model Predictive Control for Three-Phase Flying Capacitor Multilevel Inverter. IEEE Access 2022, 10, 70305–70316. [Google Scholar] [CrossRef]
- Wang, D.; Shen, Z.J.; Yin, X.; Tang, S.; Liu, X.; Zhang, C.; Wang, J.; Rodriguez, J.; Norambuena, M. Model Predictive Control Using Artificial Neural Network for Power Converters. IEEE Trans. Ind. Electron. 2022, 69, 3689–3699. [Google Scholar] [CrossRef]
- Ren, K.; Wang, J.; Wang, D.; He, M. Sensorless Model Predictive Control Using Artificial Neural Network for Multilevel Flying Capacitor Boost Converters. In Proceedings of the 2022 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Guangzhou, China, 4–7 November 2022; pp. 1093–1097. [Google Scholar]
- Wang, D.; Yin, X.; Tang, S.; Zhang, C.; Shen, Z.J.; Wang, J.; Shuai, Z. A Deep Neural Network Based Predictive Control Strategy for High Frequency Multilevel Converters. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 2988–2992. [Google Scholar]
- Bellman, R.E. The Theory of Dynamic Programming; The RAND Corporation: Santa Monica, CA, USA, 1954. [Google Scholar]
- Sundstrom, O.; Guzzella, L. A generic dynamic programming Matlab function. In Proceedings of the 2009 IEEE Control Applications, (CCA) & Intelligent Control, (ISIC), St. Petersburg, Russia, 8–10 July 2009. [Google Scholar]


| (if (4) holds) | Level | ||||
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 1 | |||
| 0 | 1 | 0 | |||
| 0 | 1 | 1 | |||
| 1 | 0 | 0 | |||
| 1 | 0 | 1 | |||
| 1 | 1 | 0 | |||
| 1 | 1 | 1 |
| = 100 V, = 0.1 Ω, = 5 μF, , = 1 A |
| = 50 ns, = 0.6 μs, |
| Average Efficiency | Average Power Loss | THD | |
|---|---|---|---|
| MAD | % | 0.164 [W] | [dBc] |
| DP | % | 0.159 [W] | [dBc] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tebaldi, D. An Approach to Control Multilevel Flying-Capacitor Converters Using Optimal Dynamic Programming Benchmark. Electronics 2025, 14, 948. https://doi.org/10.3390/electronics14050948
Tebaldi D. An Approach to Control Multilevel Flying-Capacitor Converters Using Optimal Dynamic Programming Benchmark. Electronics. 2025; 14(5):948. https://doi.org/10.3390/electronics14050948
Chicago/Turabian StyleTebaldi, Davide. 2025. "An Approach to Control Multilevel Flying-Capacitor Converters Using Optimal Dynamic Programming Benchmark" Electronics 14, no. 5: 948. https://doi.org/10.3390/electronics14050948
APA StyleTebaldi, D. (2025). An Approach to Control Multilevel Flying-Capacitor Converters Using Optimal Dynamic Programming Benchmark. Electronics, 14(5), 948. https://doi.org/10.3390/electronics14050948







