Method for Network-Wide Characteristics in Multi-Terminal DC Distribution Networks During Asymmetric Short-Circuit Faults
Abstract
1. Introduction
2. Materials and Methods
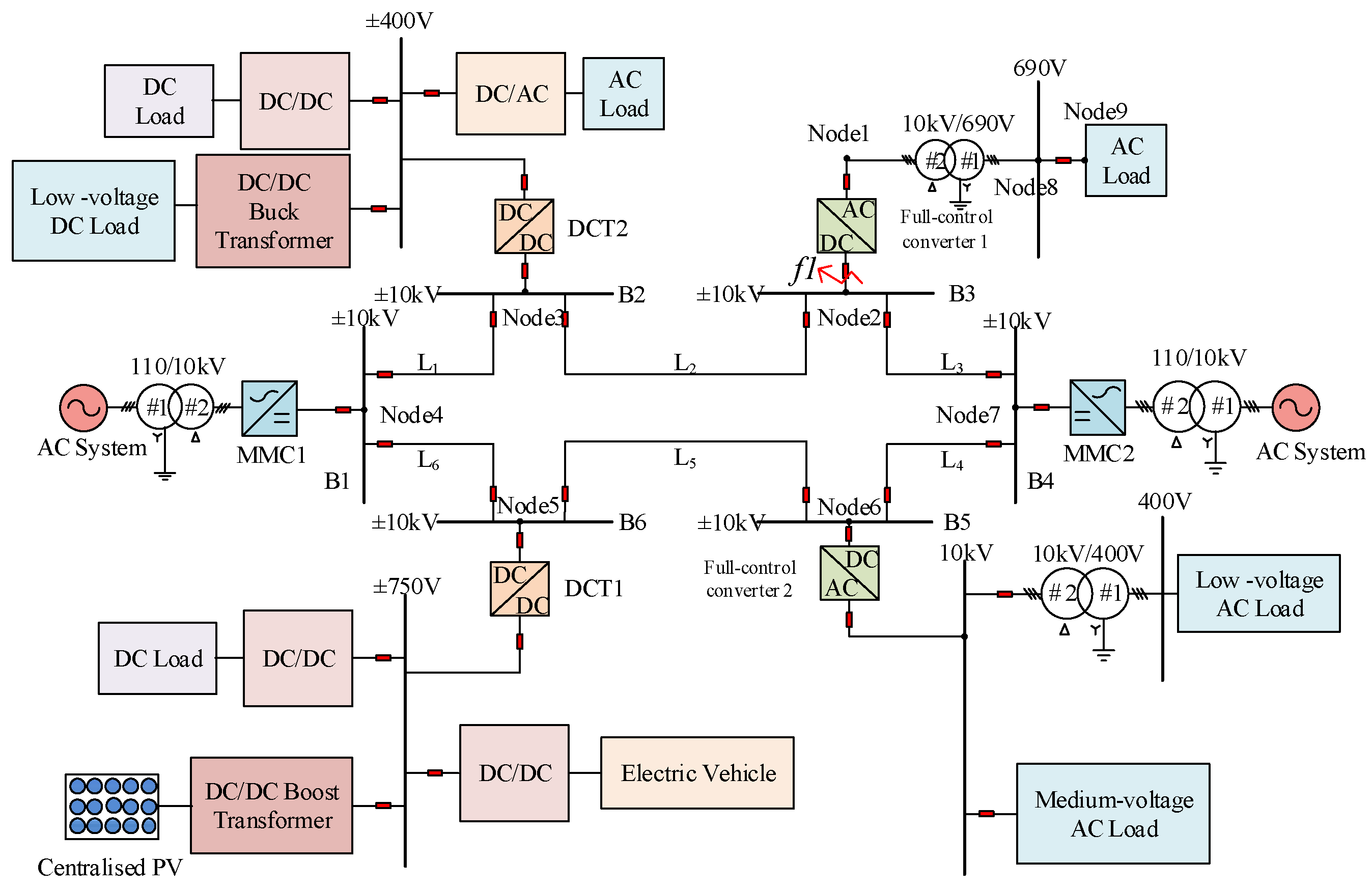
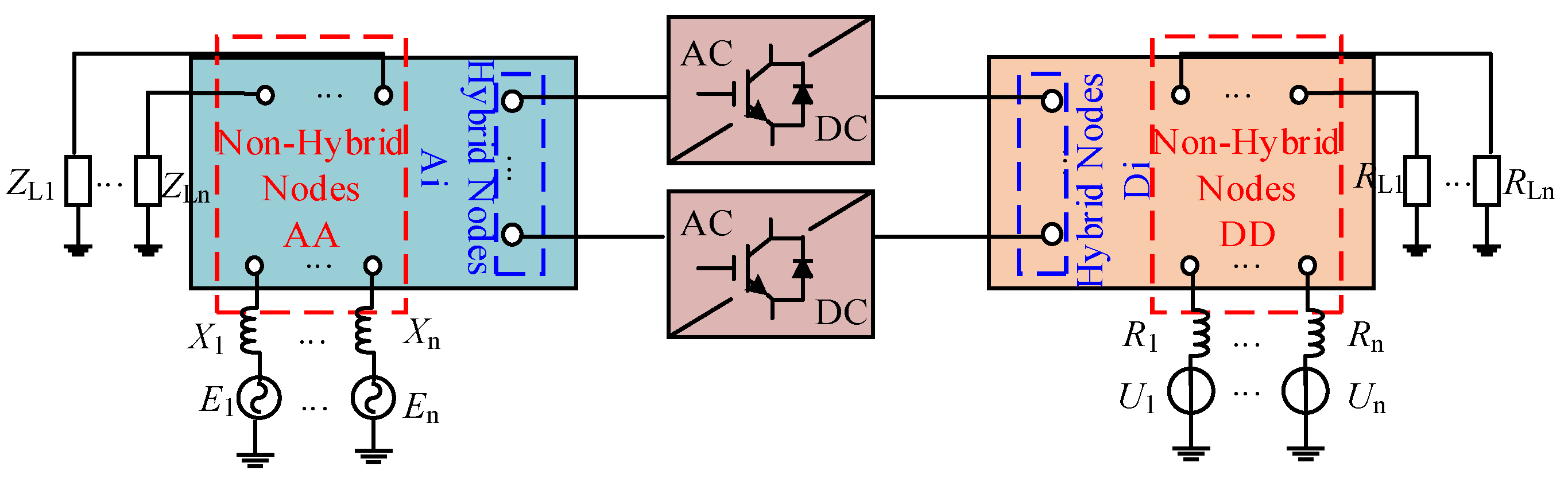
2.1. Equivalent Model During Capacitor Discharge Stage
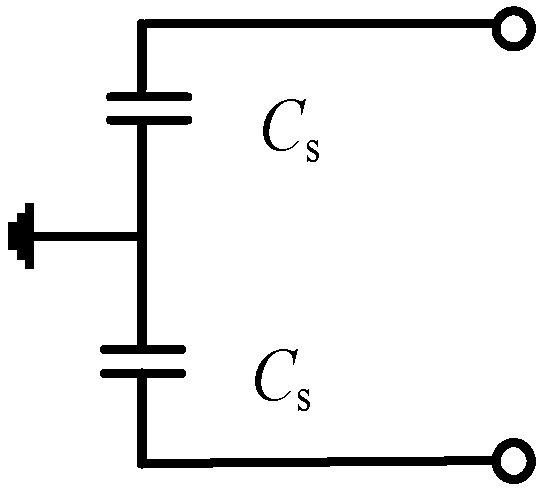
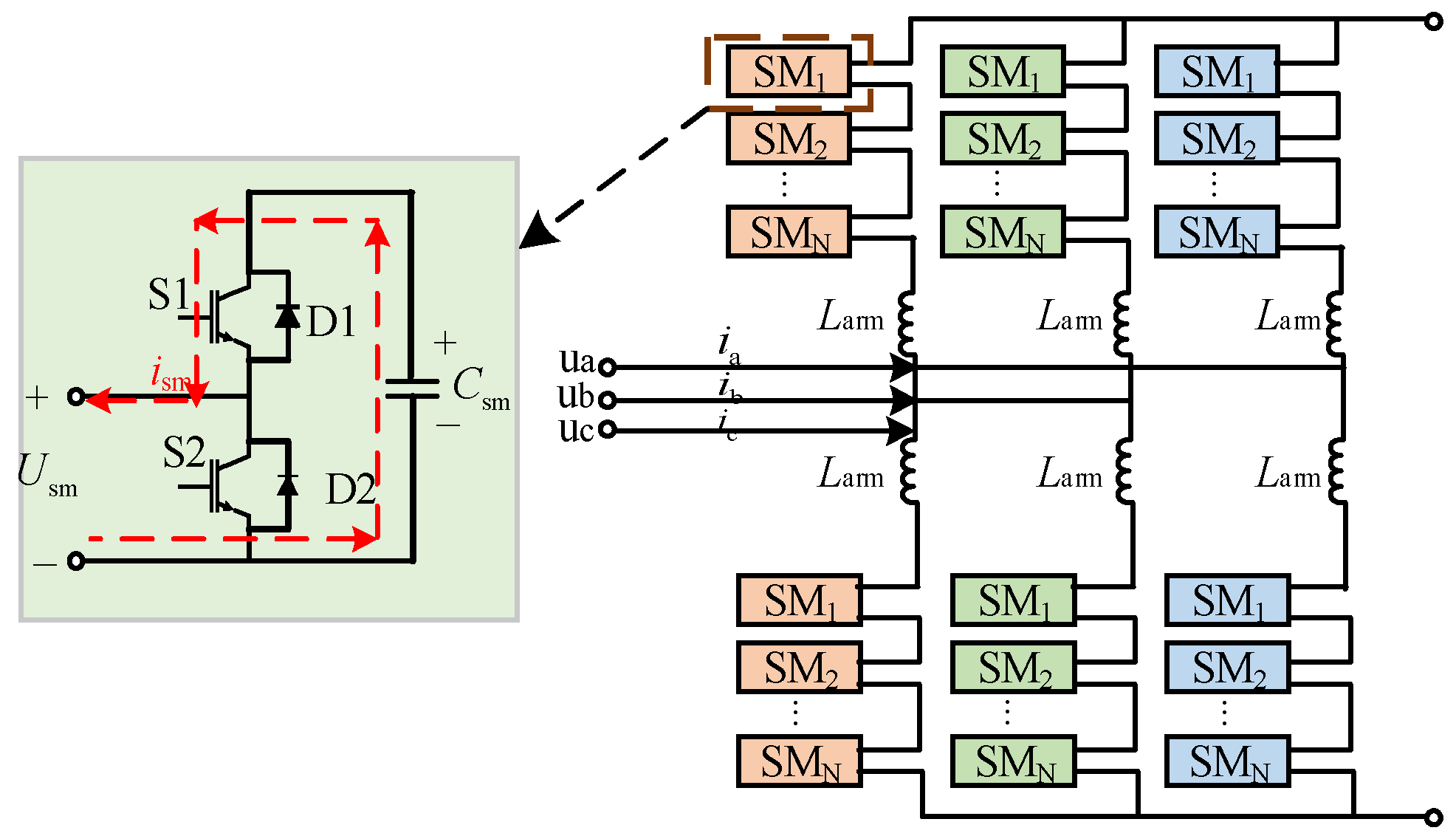
2.1.1. Equivalent Models of Converters
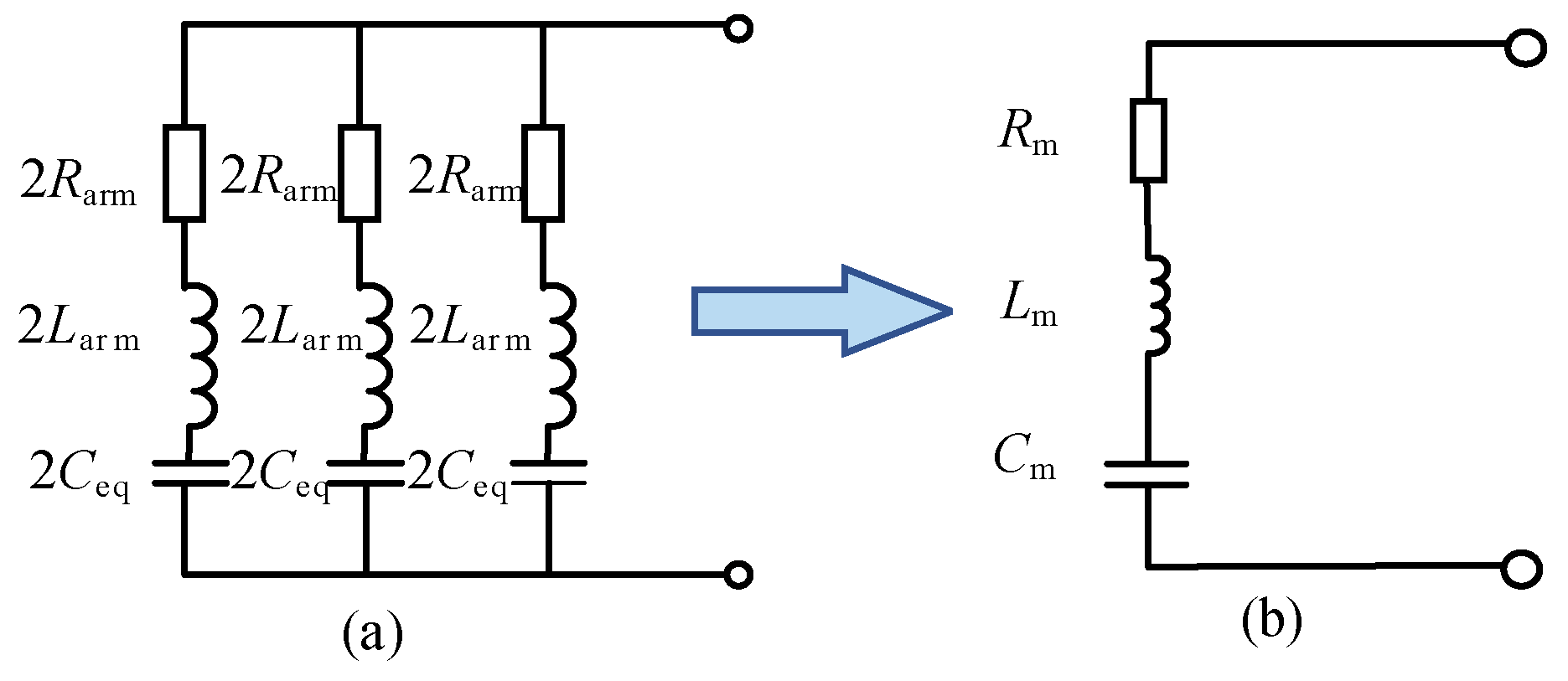
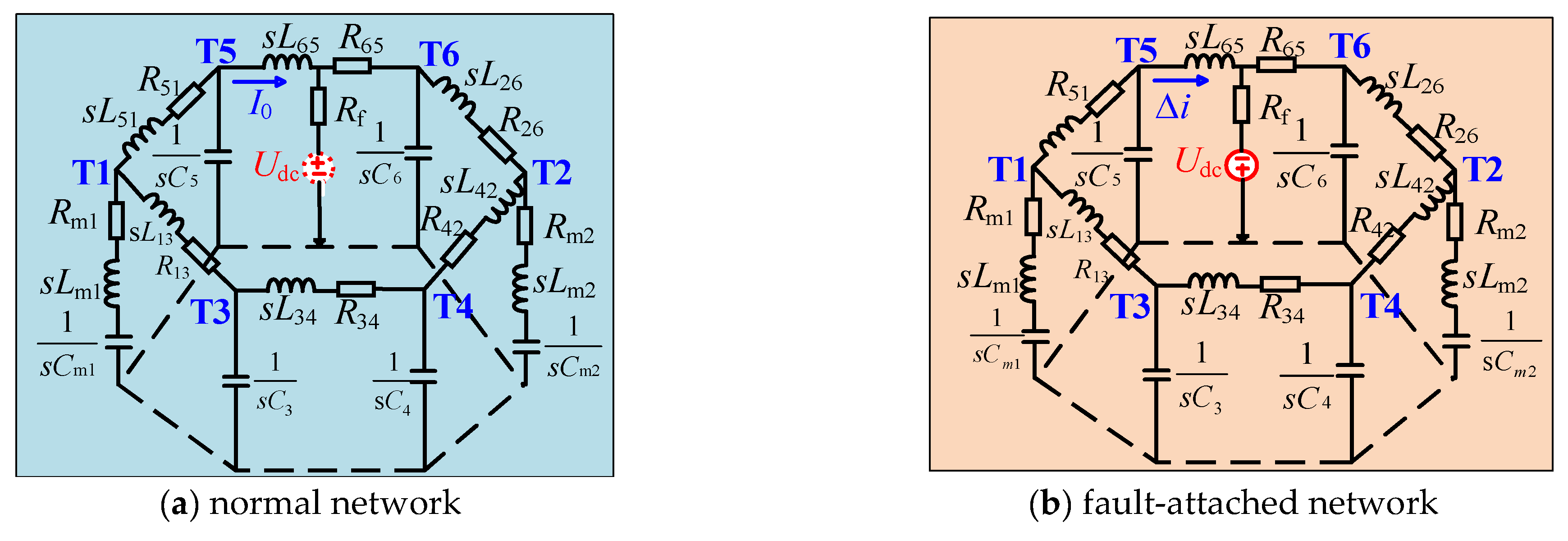
2.1.2. Equivalent Model of DC Lines
- (1)
- Due to the short transmission distance in a medium-voltage DC distribution network and its low sensitivity to frequency-varying parameters, this paper uses the lumped parameter model for the line, which can not only accurately describe the change of fault current but also simplify the process of solving.
- (2)
- During the initial fault stage, short-circuit current is primarily supplied by the discharge current of converter stations. Due to the symmetrical configuration of the three-phase system on the AC side, it merely provides current continuity through the bridge arm and does not directly supply power to the fault point. Therefore, the influence of the AC side current can be approximately ignored during the capacitor discharge stage [25].
- (3)
- In the early capacitor discharge stage (within 2 ms), the short-circuit current can be regarded as the superposition of high-frequency signals. The impedance of the capacitor in the high-frequency band approaches zero. Considering the high-frequency characteristics of the impedance, the equivalent fault model in this phase can be simplified to a resistance–inductance network [14].
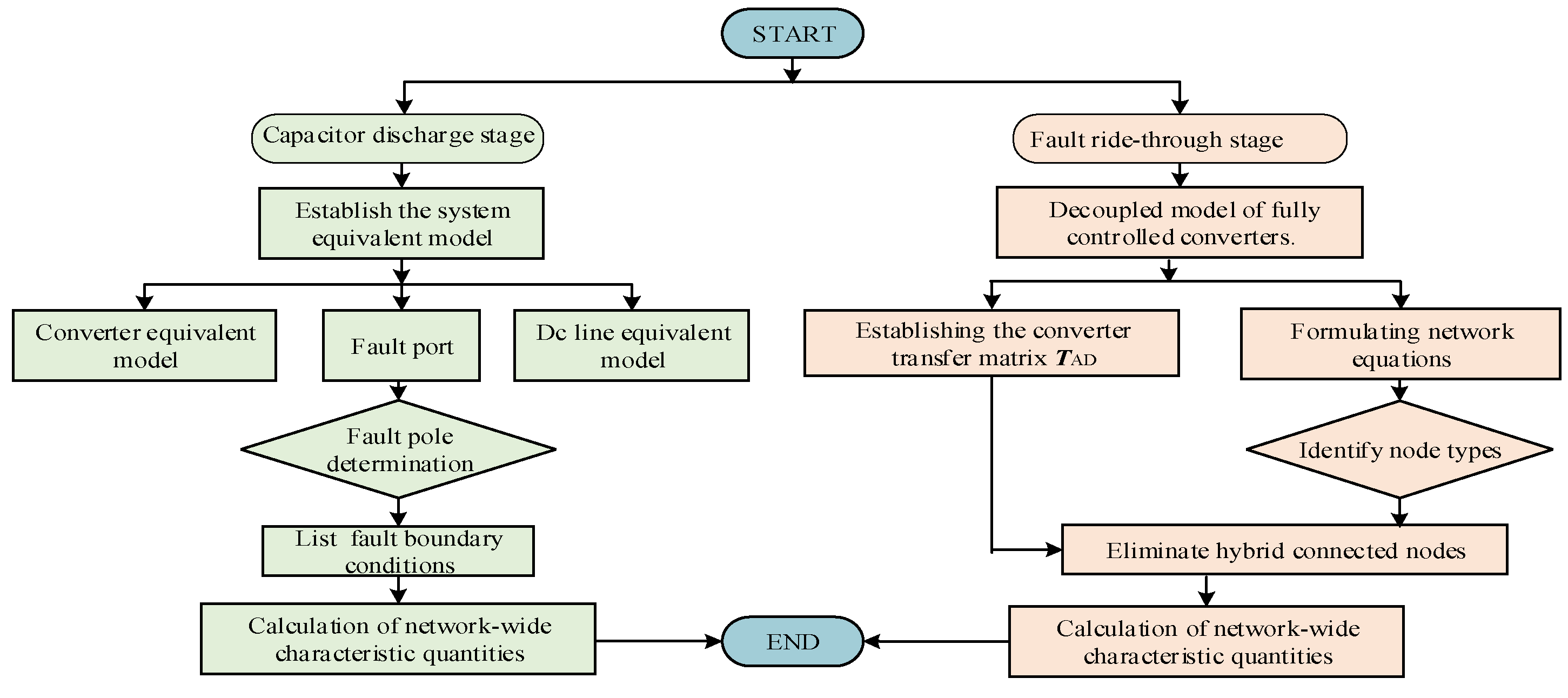
2.2. Short-Circuit Calculation Method During Capacitor Discharge Stage
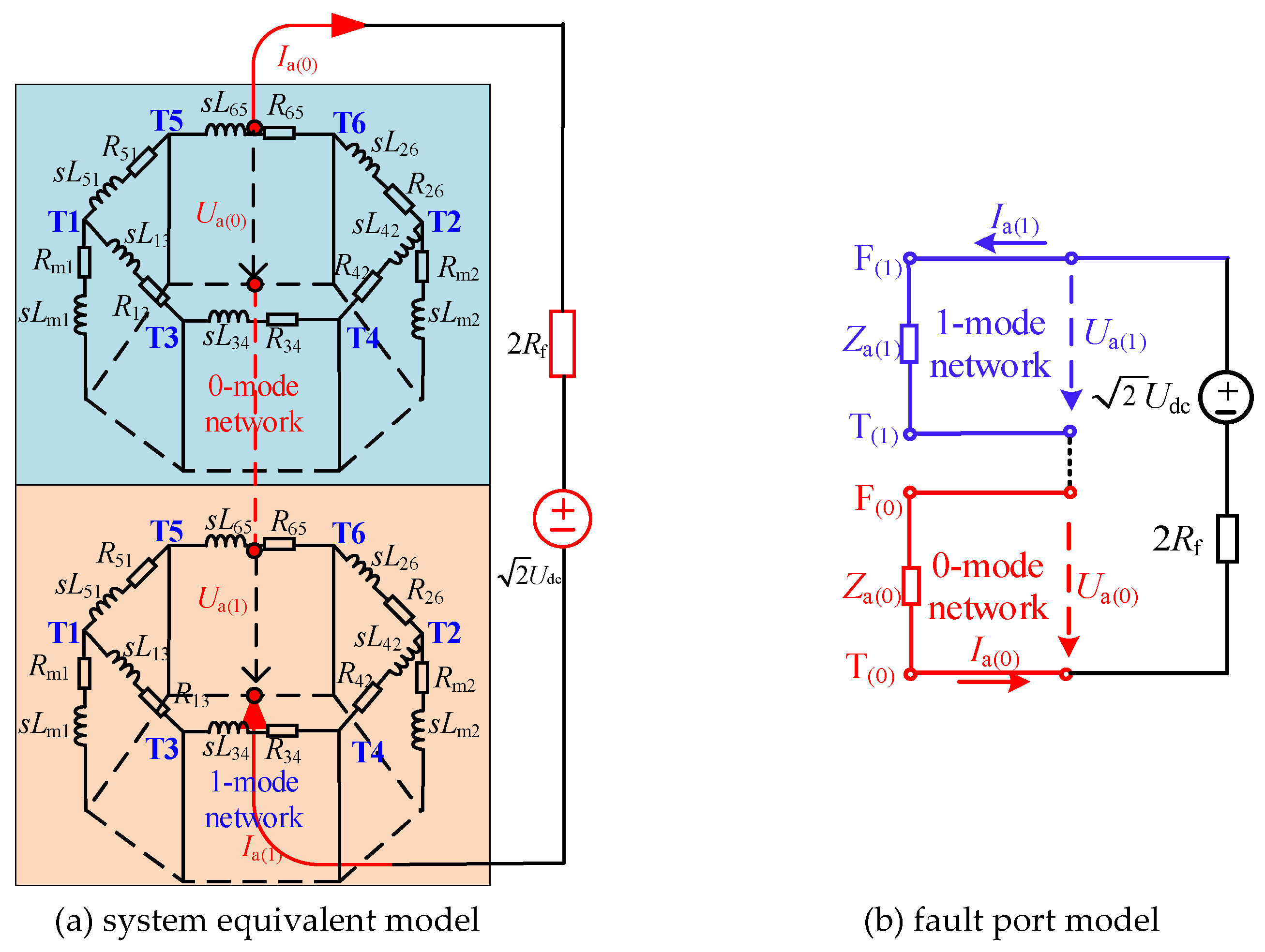
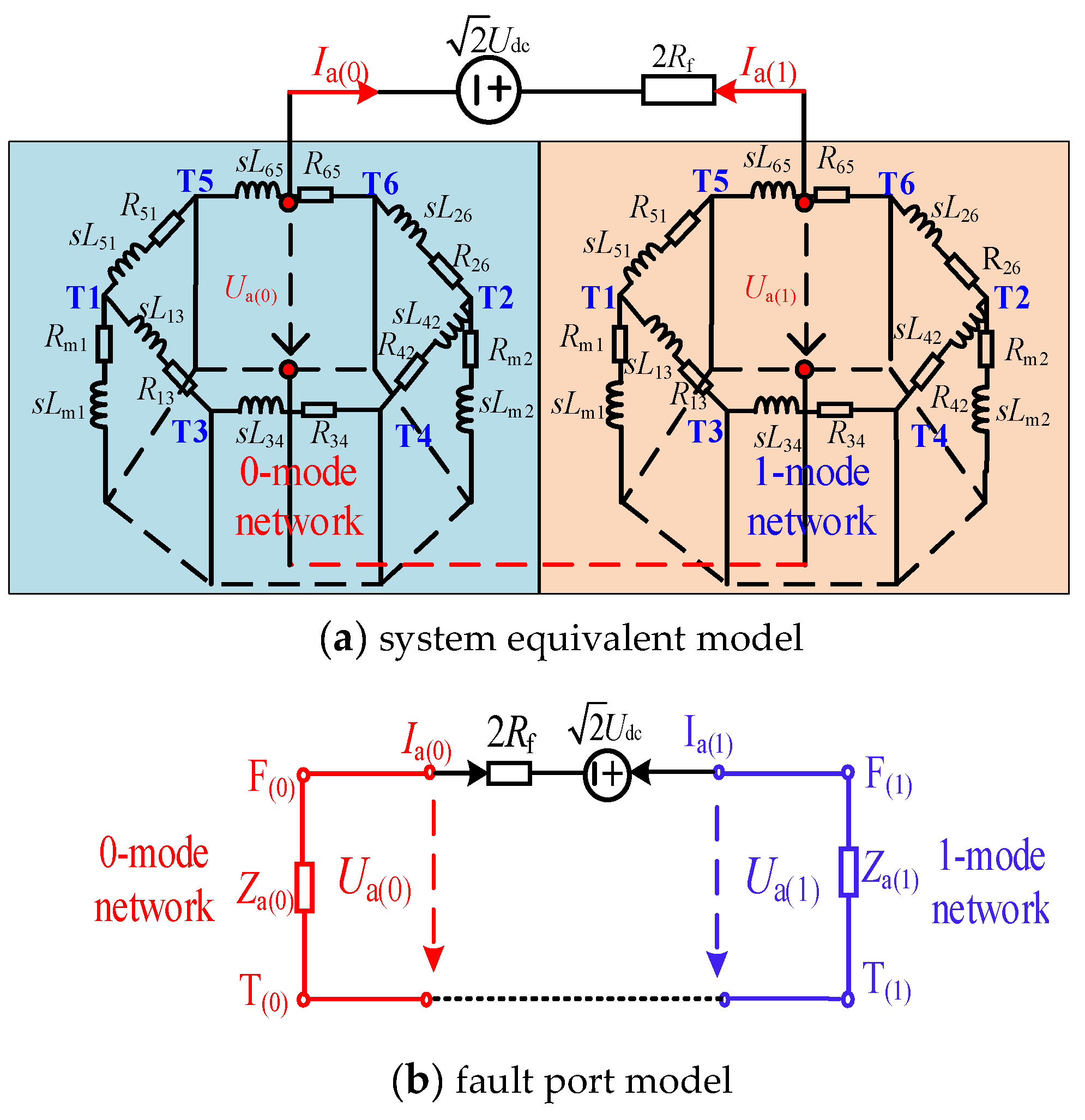
2.3. Equivalent Model During Fault Ride-Through Stage
2.4. Short-Circuit Calculation Method During Fault Ride-Through Stage
3. Results and Discussion
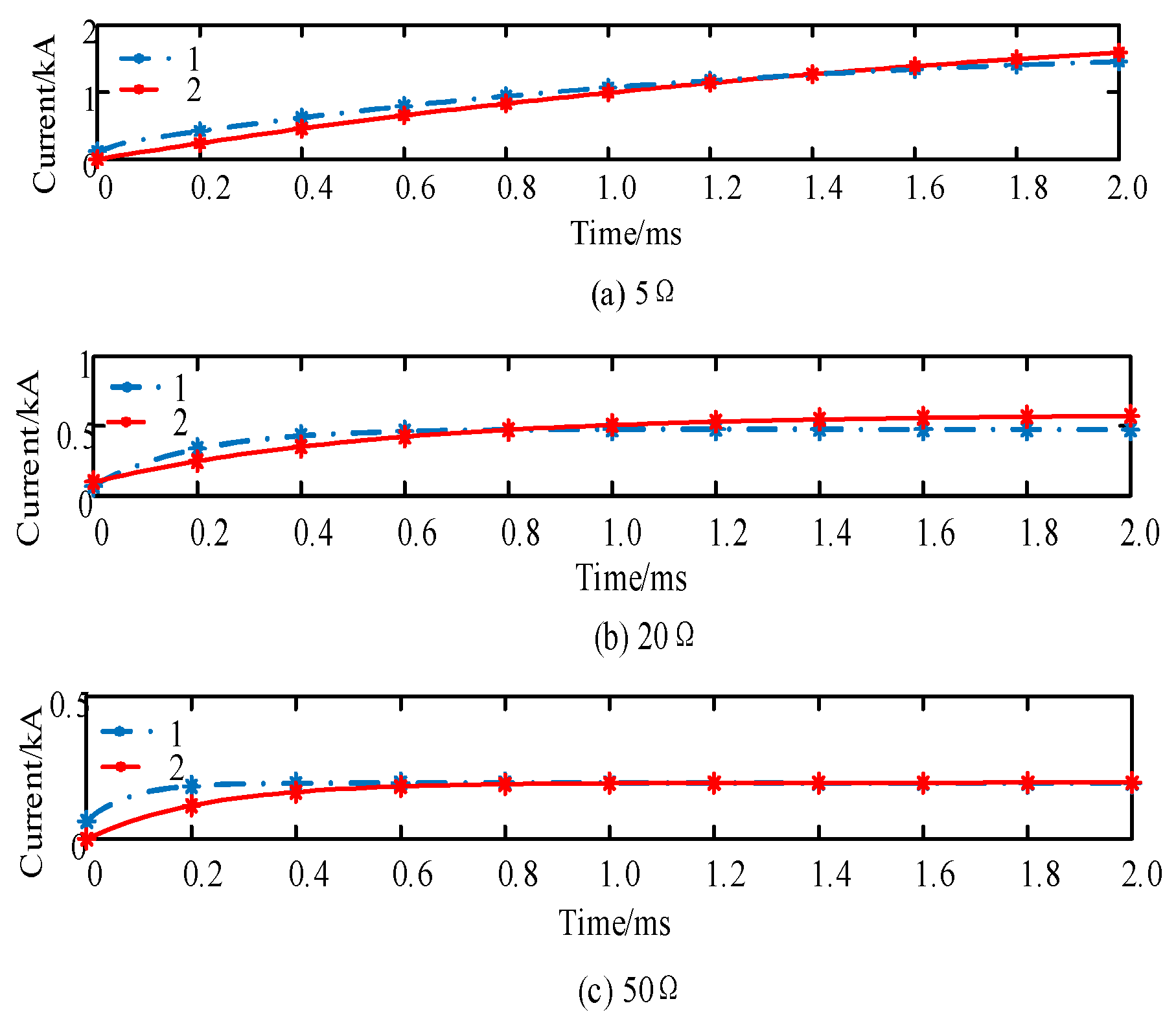
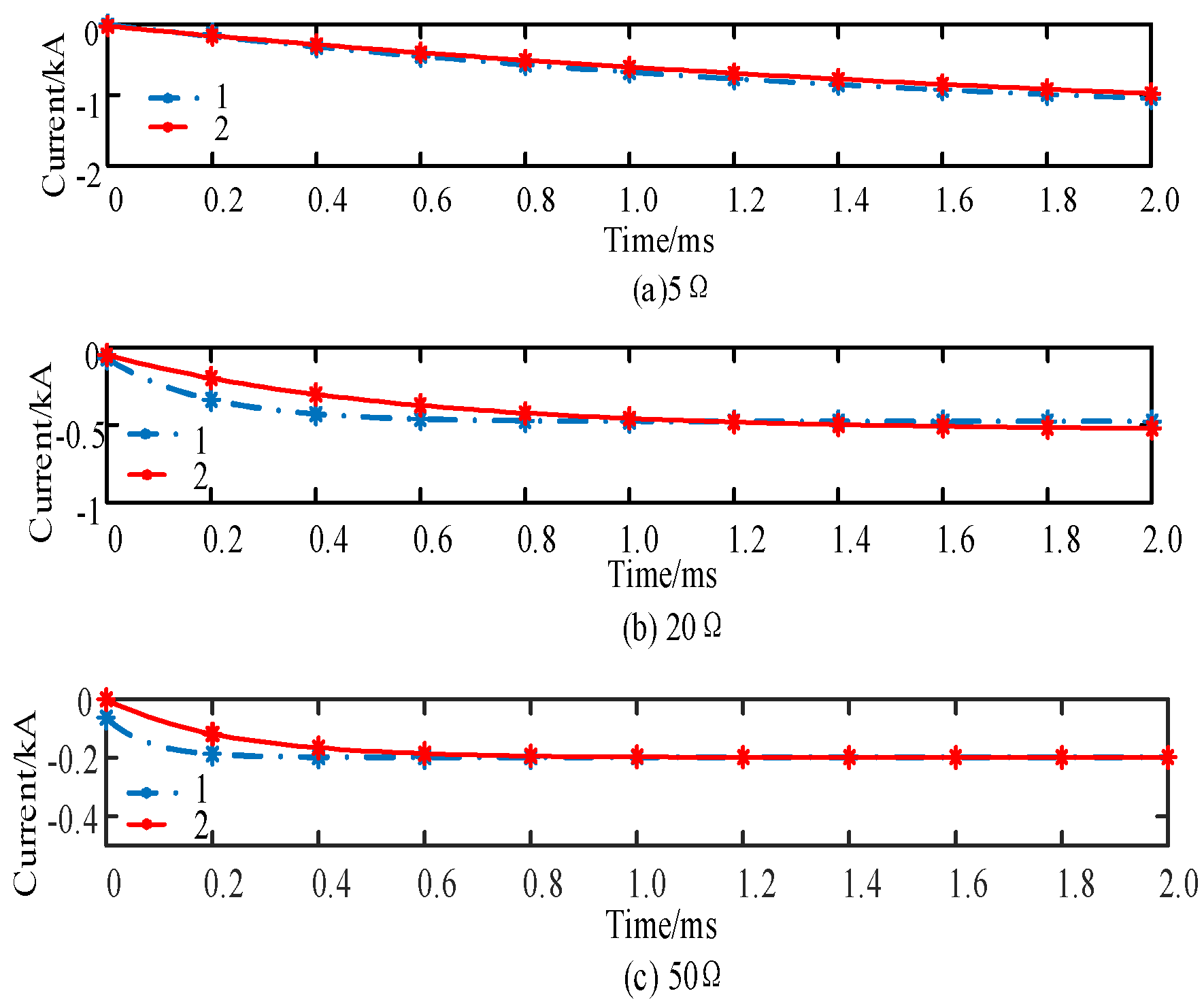
3.1. Capacitor Discharge Stage
3.2. Fault Ride-Through Stage
3.3. Comparative Analysis with Existing Methods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MMC | Modular multilevel converter |
| DCT | Direct circuit transformer |
| VSC | Voltage source converter |
| LCC | Line-commutated converter |
References
- He, J.; Liu, B.; Duan, S. A selective protection strategy for inverter-based power grid. High Volt. Eng. 2022, 48, 2357–2365. [Google Scholar]
- Zeng, R.; Zhao, Y.; Zhao, B.; Zhong, Q.; Tong, Y. A prospective look on research and application of DC power distribution technology. Proc. CSEE 2018, 38, 6791–6801. [Google Scholar]
- Zhou, F.; Kawaguchi, T.; Hashimoto, S. Multi-Terminal DC Transformer for Renewable Energy Cluster Grid Connection. Energies 2024, 17, 5152. [Google Scholar] [CrossRef]
- Lu, S.; Liu, H. Study on Investment Evaluation Index System of Pilot Project of Incremental Power Distribution Service Reform. Power Syst. Big Data 2022, 12, 77–84. [Google Scholar]
- Perera, C.; Salmon, J.; Kish, G.J. Multiport Converter with Independent Control of AC and DC Power Flows for Bipolar DC Distribution. IEEE Trans. Power Electron. 2021, 36, 3473–3485. [Google Scholar] [CrossRef]
- Kim, Y.H.; You, H.S.; Kim, S.J.; Choi, S.M.; Rho, D.S. An Implementation of Intelligent Fault Isolation Device for LVDC Distribution System Considering Slope Characteristics of Fault Current. Electronics 2025, 14, 171. [Google Scholar] [CrossRef]
- Javed, W.; Chen, D.; Farrag, M.E.; Xu, Y. System configuration, fault detection, location, isolation and restoration: A review on LVDC microgrid protections. Energies 2019, 12, 1001. [Google Scholar] [CrossRef]
- Lai, D.; Luo, W.; Huang, J. Adaptive Control of Hybrid Energy Storage Power for Multiple Microgrids Based on Edge Computing. Power Syst. Big Data 2023, 4, 28–35. [Google Scholar]
- Xu, J.; Zhao, X.; Jing, H.; Liang, J.; Zhao, C. DC Fault Current Clearance at the Source Side of HVDC Grid Using Hybrid MMC. IEEE Trans. Power Deliv. 2020, 35, 140–149. [Google Scholar] [CrossRef]
- Wang, C.; Tao, J.; Wang, Y.; Tan, K.; Xu, T. Research on topology and fault ride-through strategy of hybrid arm multiplexing MMC composed of HBSMs and FBSMs. Proc. CSEE 2022, 42, 8297–8309. [Google Scholar]
- Cwikowski, O.; Wickramasinghe, H.R.; Konstantinou, G.; Pou, J.; Barnes, M.; Shuttleworth, R. Modular Multilevel Converter DC Fault Protection. IEEE Trans. Power Deliv. 2018, 33, 291–300. [Google Scholar] [CrossRef]
- Li, H.; Dai, Z.; Shi, X.; Yang, M. Approximate Calculation Method of Short-Circuit Current of Multi-Terminal Hybrid DC Transmission System Considering Control Strategy. Trans. China Electrotech. Soc. 2024, 39, 2810–2824. [Google Scholar]
- Tang, L.; Dong, X. An approximate method for the calculation of transmission line fault current in MMC-HVDC grid. Proc. CSEE 2019, 39, 490–498. [Google Scholar]
- Xin, Y.; Luo, X.; Wang, T.; Wang, Y.; Wang, W. Simplified calculation method of fault current in different topological structures of DC grid considering the influence of transition resistance. Power Syst. Technol. 2023, 47, 804–817. [Google Scholar]
- Wang, Z.; Hao, L.; Wang, L.; He, J.; Chen, Z. Calculation method of nonmetallic short circuit fault current in DC side of MMC-HVDC system. Electr. Power Autom. Equip. 2024, 44, 187–194. [Google Scholar]
- Hao, L.; Li, W.; Wang, Z.; Gu, Y.; Wang, G. Practical calculation for bipolar short-circuit fault curren of transmission line in MMC-HVDC grid. Autom. Electr. Power Syst. 2020, 44, 68–76. [Google Scholar]
- Wang, Z.; Hao, L.; Wang, Z. Short-Circuit Current Calculation of Flexible Direct Current Transmission Lines Considering Line Distribution Parameters. Energies 2024, 17, 3800. [Google Scholar] [CrossRef]
- Liao, Y.; Jin, L.; You, J.; Xu, Z.; Liu, K.; Zhang, H.; Shen, Z.; Deng, F. A Novel Voltage Sensorless Estimation Method for Modular Multilevel Converters with a Model Predictive Control Strategy. Energies 2024, 17, 61. [Google Scholar] [CrossRef]
- Debnath, S.; Qin, J.; Bahrani, B.; Saeedifard, M.; Barbosa, P. Operation control and applications of the modular multilevel converter: A review. IEEE Trans. Power Electron. 2015, 30, 37–53. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Z.; Li, Z.; Babayomi, O. Predictive Control of Modular Multilevel Converters: Adaptive Hybrid Framework for Circulating Current and Capacitor Voltage Fluctuation Suppression. Energies 2023, 16, 5772. [Google Scholar] [CrossRef]
- Torwelle, P.; Bertinato, A.; Raison, B.; Le, T.; Petit, M. Fault current calculation in MTDC grids considering MMC blocking. Electr. Power Syst. Res. 2022, 207, 1–12. [Google Scholar] [CrossRef]
- Song, J.; Cheah-Mane, M.; Prieto-Araujo, E.; Amorós, J.; Gomis-Bellmunt, O. Grid Equivalent Representation of Power Systems With Penetration of Power Electronics. IEEE Trans. Power Deliv. 2023, 38, 2742–2756. [Google Scholar] [CrossRef]
- Deng, W.; Liu, Q.; Zhang, Y.; Liu, T.; Li, B. Short circuit current calculation method and grounding strategy of pole-to-ground fault in zhangbei flexible DC power grid. High Volt. Eng. 2022, 48, 4050–4059. [Google Scholar]
- Dai, Z.; Liu, X.; Liu, Z.; Li, Y.; Chen, X. Pilot Protection Scheme for Flexible DC Distribution Grids Based on Superimposed Current. High Volt. Eng. 2021, 47, 1684–1693. [Google Scholar]
- Ye, H.; Gao, S.; Li, G.; Liu, Y. Efficient Estimation and Characteristic Analysis of Short-Circuit Currents for MMC-MTDC Grids. IEEE Trans. Ind. Electron. 2020, 68, 258–269. [Google Scholar] [CrossRef]
- Liu, W.; Huang, S.; Xu, Y. Fault Analysis of Power System, 3rd ed.; China Electric Power Press: Beijing, China, 2010. [Google Scholar]
- Shi, X.; Wang, Z.; Liu, B.; Li, Y.; Tolbert, L.; Wang, F. DC impedance modelling of a MMC-HVDC system for DC voltage ripple prediction under a single-line-to-ground fault. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014. [Google Scholar]
- Chen, L.; Xu, F.; Wei, X.; Tang, G.; Cui, X. A Review on Large Capacity Controllable Switching Current Source Converter Research. Electr. Power. 2021, 54, 25–36. [Google Scholar]
- Ding, Y.; Mao, M. Comparison and analysis of CPT-and IRPT-based current decomposition in multi-scenario. Electr. Power Autom. Equip. 2023, 43, 166–173. [Google Scholar]
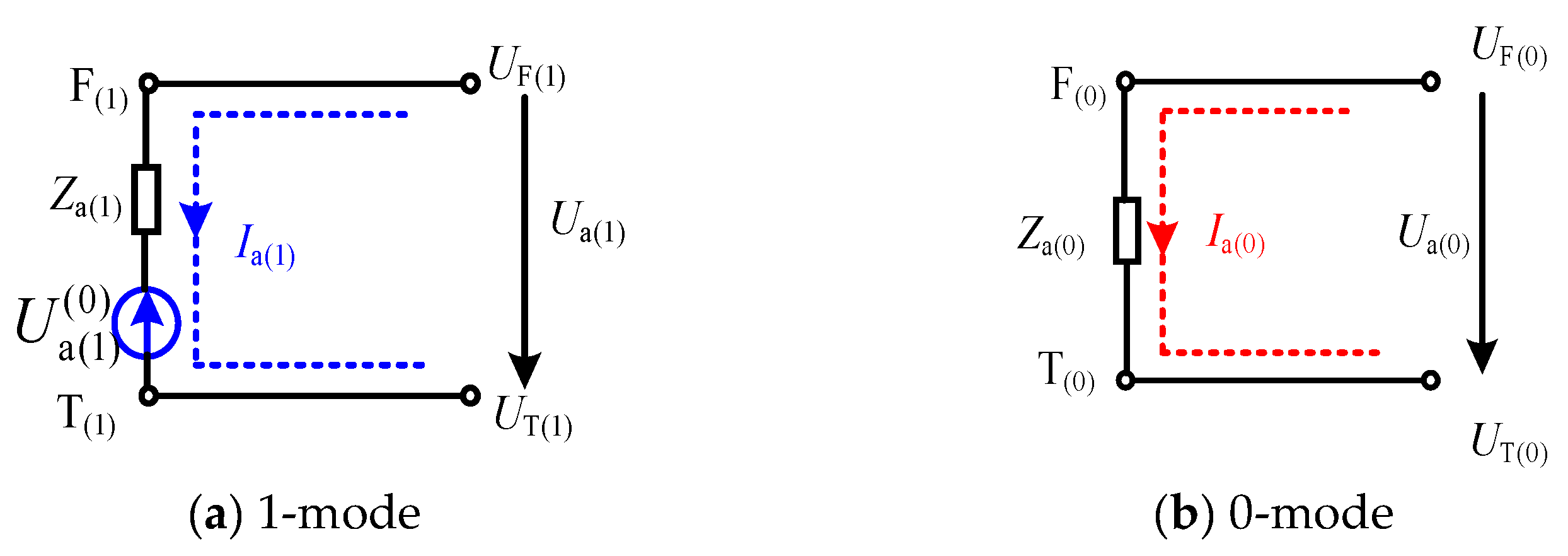



| Converter Station | System Parameters | Values |
|---|---|---|
| MMC converter station | Number of submodules on the bridge arm | 24 |
| Submodule capacitance/μF | 10,000 | |
| Bridge arm inductance/H | 0.01 | |
| Smoothing reactor/mH | 5 | |
| IGBT on-resistance/Ω | 0.01 | |
| VSC converter station | DC-side capacitance/μF | 4000 |
| Flat wave reactor/mH | 30 | |
| IGBT on-resistance/Ω | 0.005 | |
| DCT converter station | Low-voltage side capacitance/μF | 4000 |
| High-voltage side capacitance/F | 0.1 | |
| IGBT on-resistance/Ω | 0.01 |
| System Parameters | Values |
|---|---|
| DC voltage level/kV | ±10 |
| Current-limiting reactor/mH | 2 |
| Line inductance per unit length (mH/km) | 0.78 |
| Line resistance per unit length (Ω/km) | 0.083 |
| Line mutual inductance per unit length (mH/km) | 0.1 |
| Line 1, 2, 4, 5 length/km | 5 |
| Line 3, 6 length/km | 15 |
| Branch | Node 3–4 | Node 4–5 | Node 5–6 | Node 6–7 | Node 8–9 |
| error | 0.05% | −1.97% | 3.56% | −0.20% | 0.15% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Li, Q.; Li, H.; Zhou, X.; Dai, Z. Method for Network-Wide Characteristics in Multi-Terminal DC Distribution Networks During Asymmetric Short-Circuit Faults. Electronics 2025, 14, 1120. https://doi.org/10.3390/electronics14061120
Li X, Li Q, Li H, Zhou X, Dai Z. Method for Network-Wide Characteristics in Multi-Terminal DC Distribution Networks During Asymmetric Short-Circuit Faults. Electronics. 2025; 14(6):1120. https://doi.org/10.3390/electronics14061120
Chicago/Turabian StyleLi, Xinhao, Qianmin Li, Hanwei Li, Xinze Zhou, and Zhihui Dai. 2025. "Method for Network-Wide Characteristics in Multi-Terminal DC Distribution Networks During Asymmetric Short-Circuit Faults" Electronics 14, no. 6: 1120. https://doi.org/10.3390/electronics14061120
APA StyleLi, X., Li, Q., Li, H., Zhou, X., & Dai, Z. (2025). Method for Network-Wide Characteristics in Multi-Terminal DC Distribution Networks During Asymmetric Short-Circuit Faults. Electronics, 14(6), 1120. https://doi.org/10.3390/electronics14061120






