Integrated Waveform Design and Signal Processing Based on Composite Noise Nimble Modulated Signals
Abstract
1. Introduction
2. Scene Description
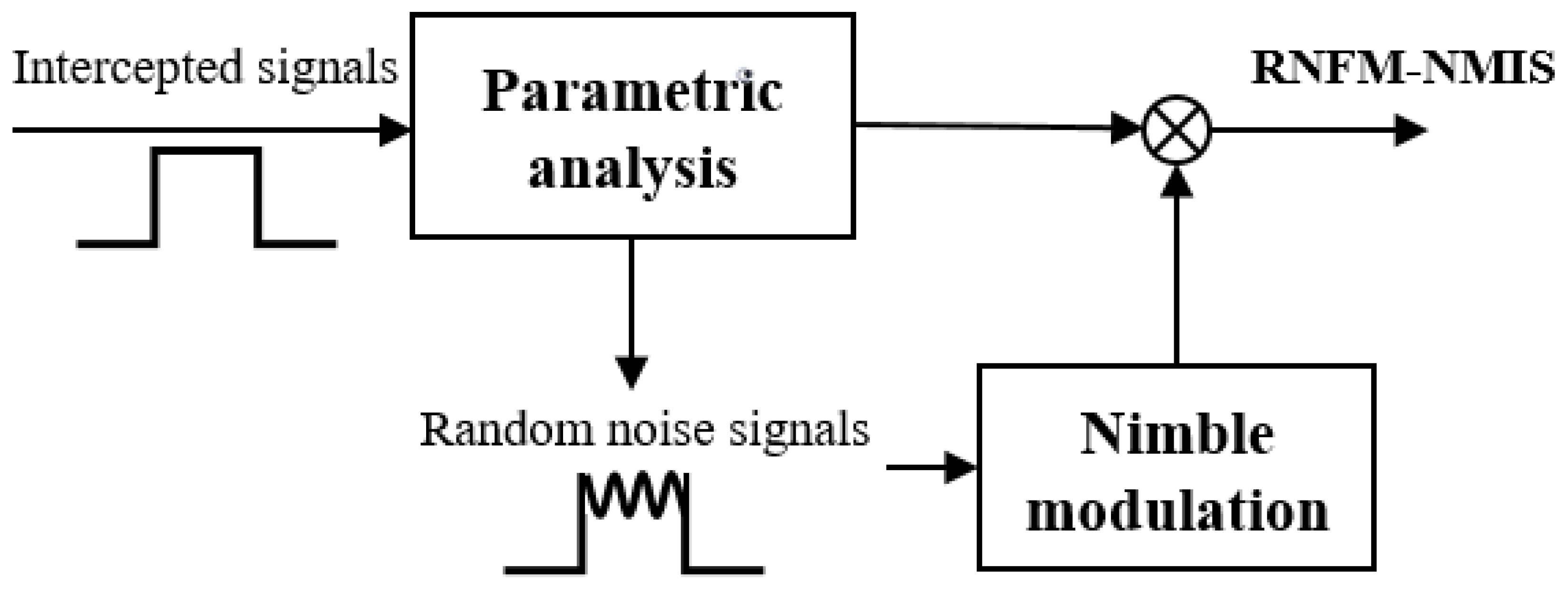
3. Design Scheme of RNFM-NMIS
3.1. Signal Model
3.2. Detection Performance
3.3. Interference Performance
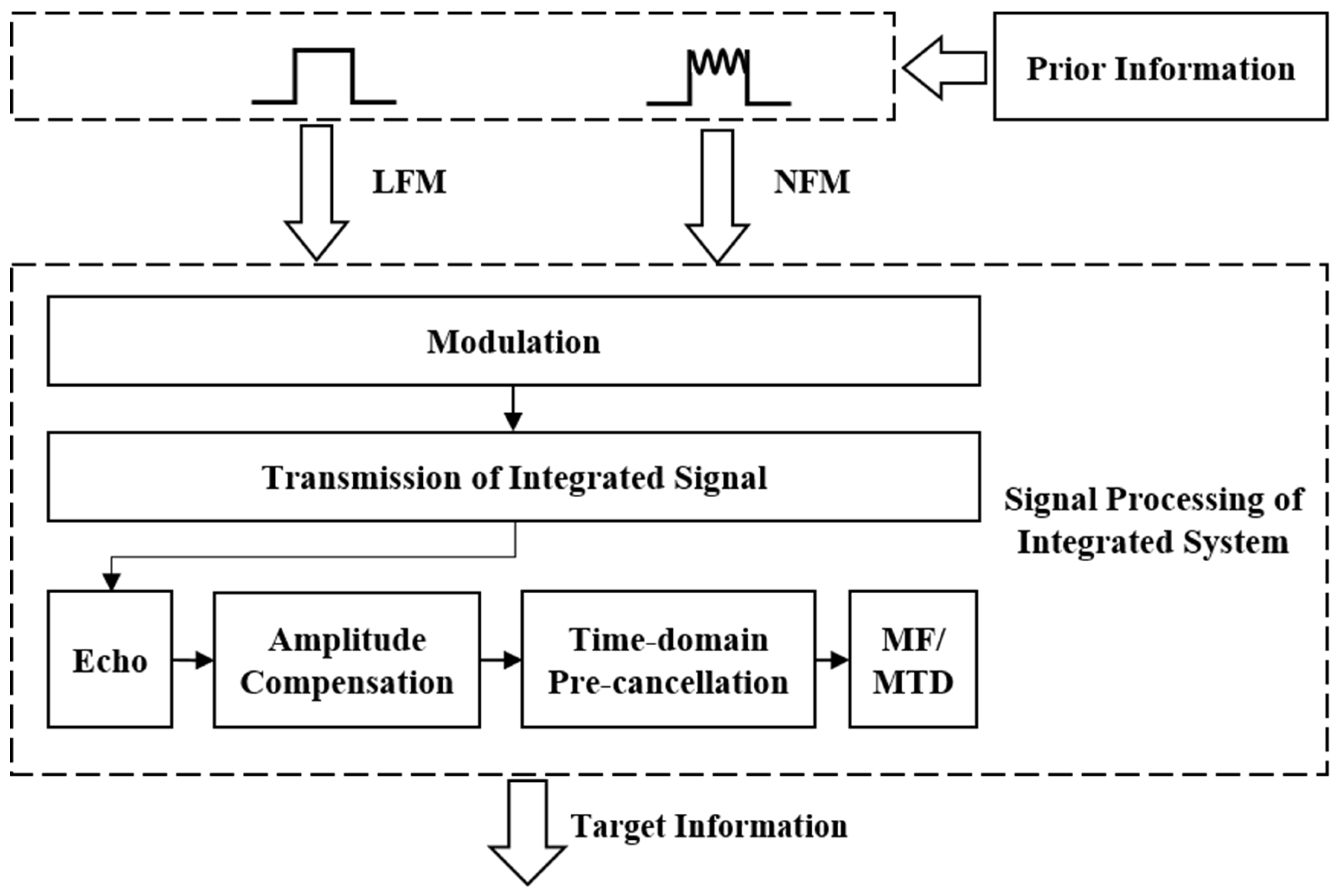
4. Direct-Wave Interference Suppression Based on Time-Domain Pre-Cancellation
4.1. Processing Algorithm Based on TDPC
4.2. Analysis of Computational Complexity
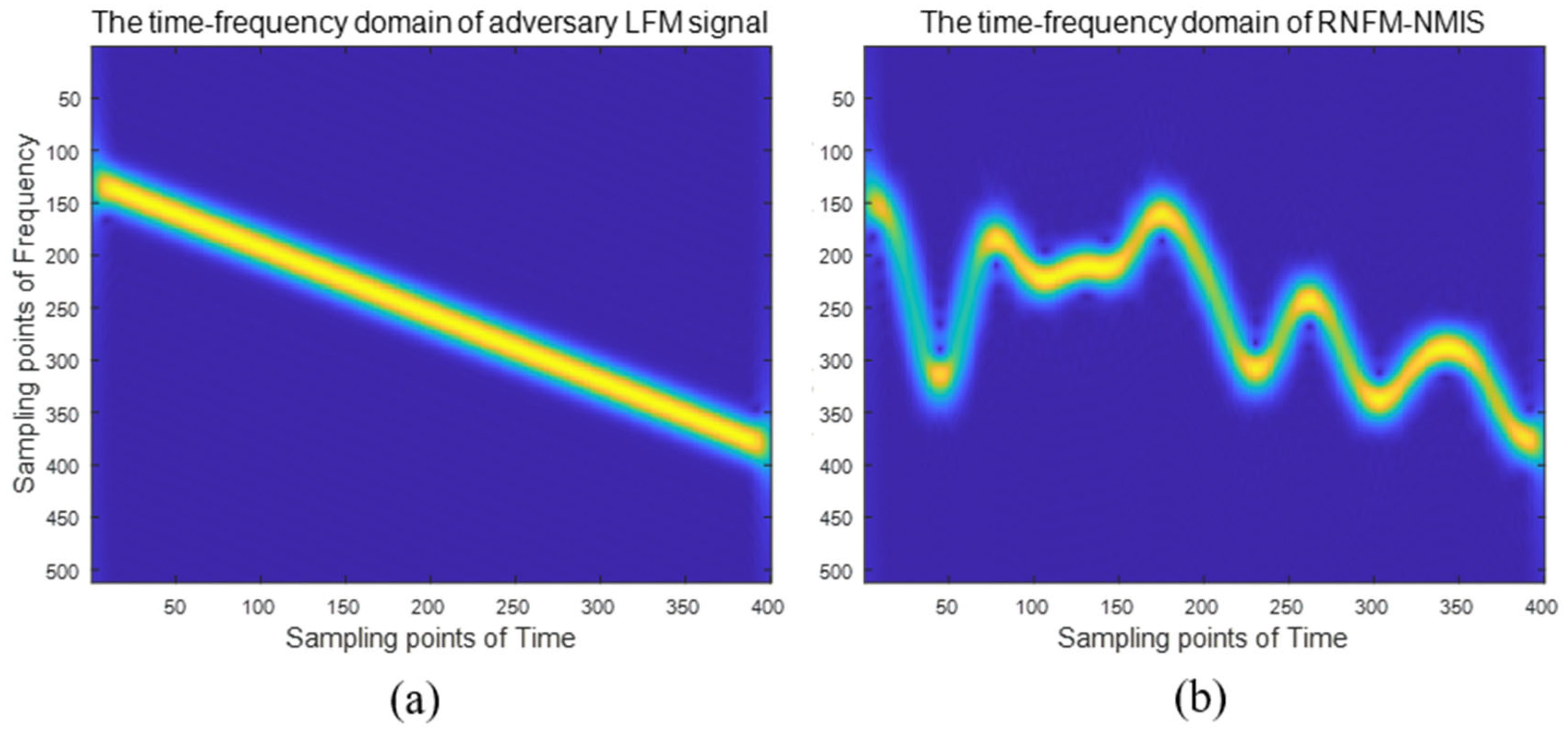
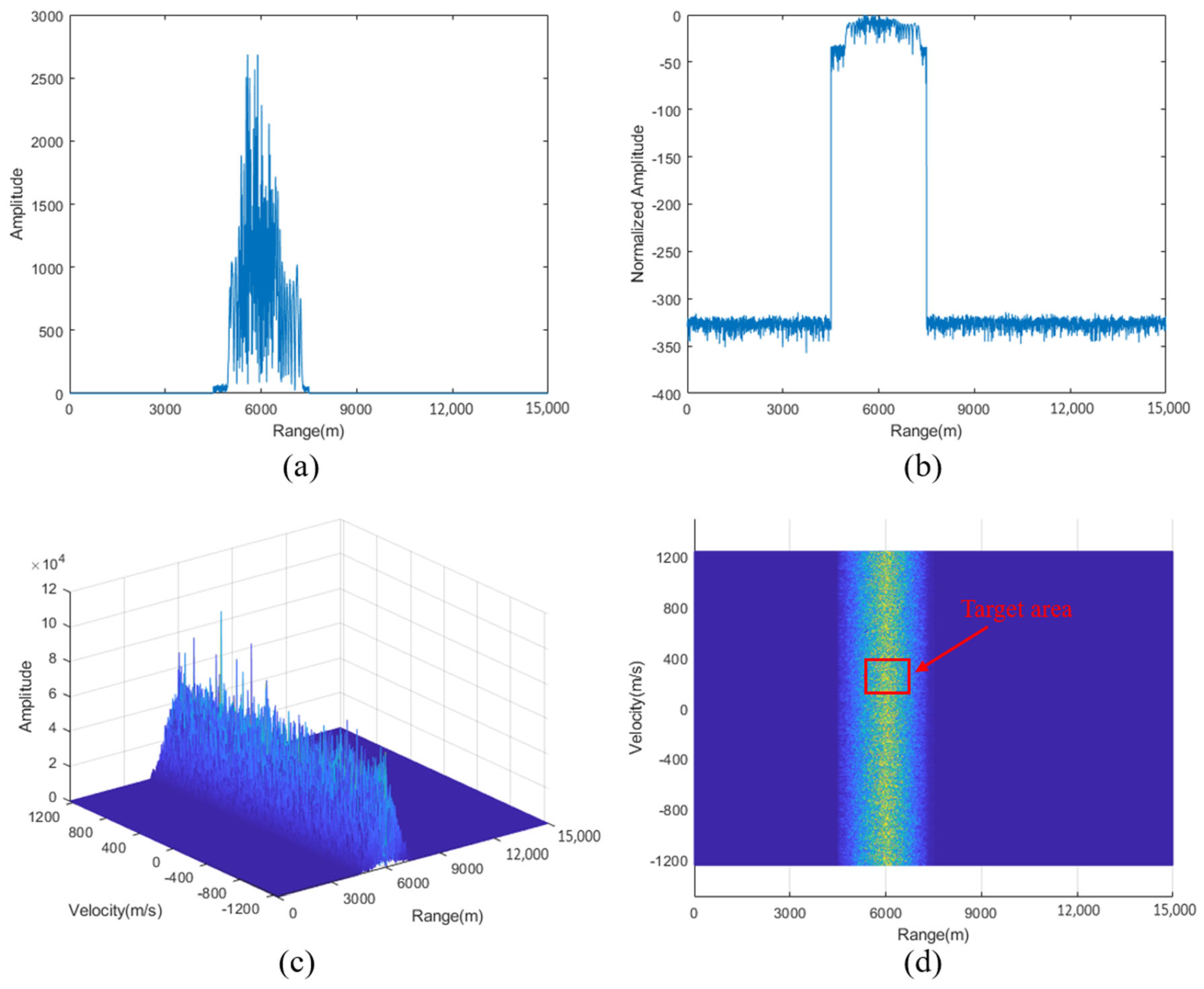
5. Practical Experiments Results on Signal Performance
6. Signal Processing Simulation Results
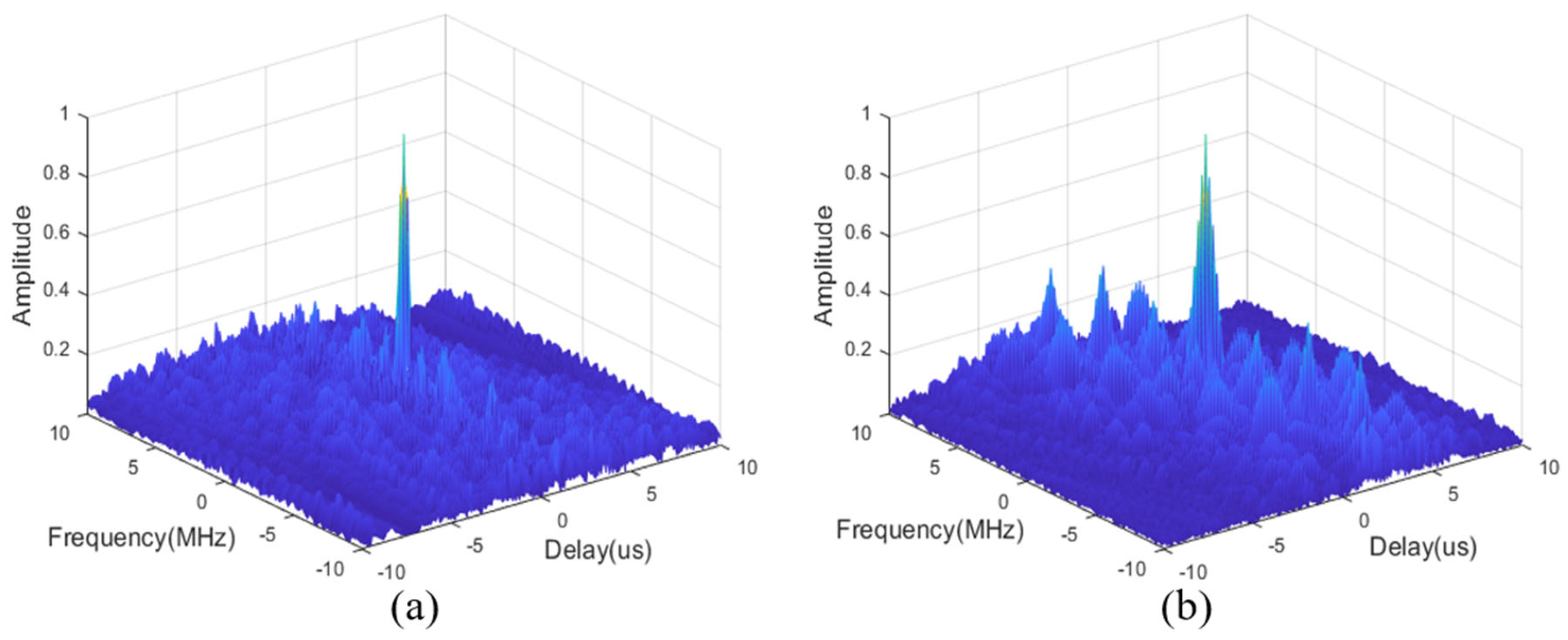
6.1. Comparison of Matched Filtering Results Under Single Target
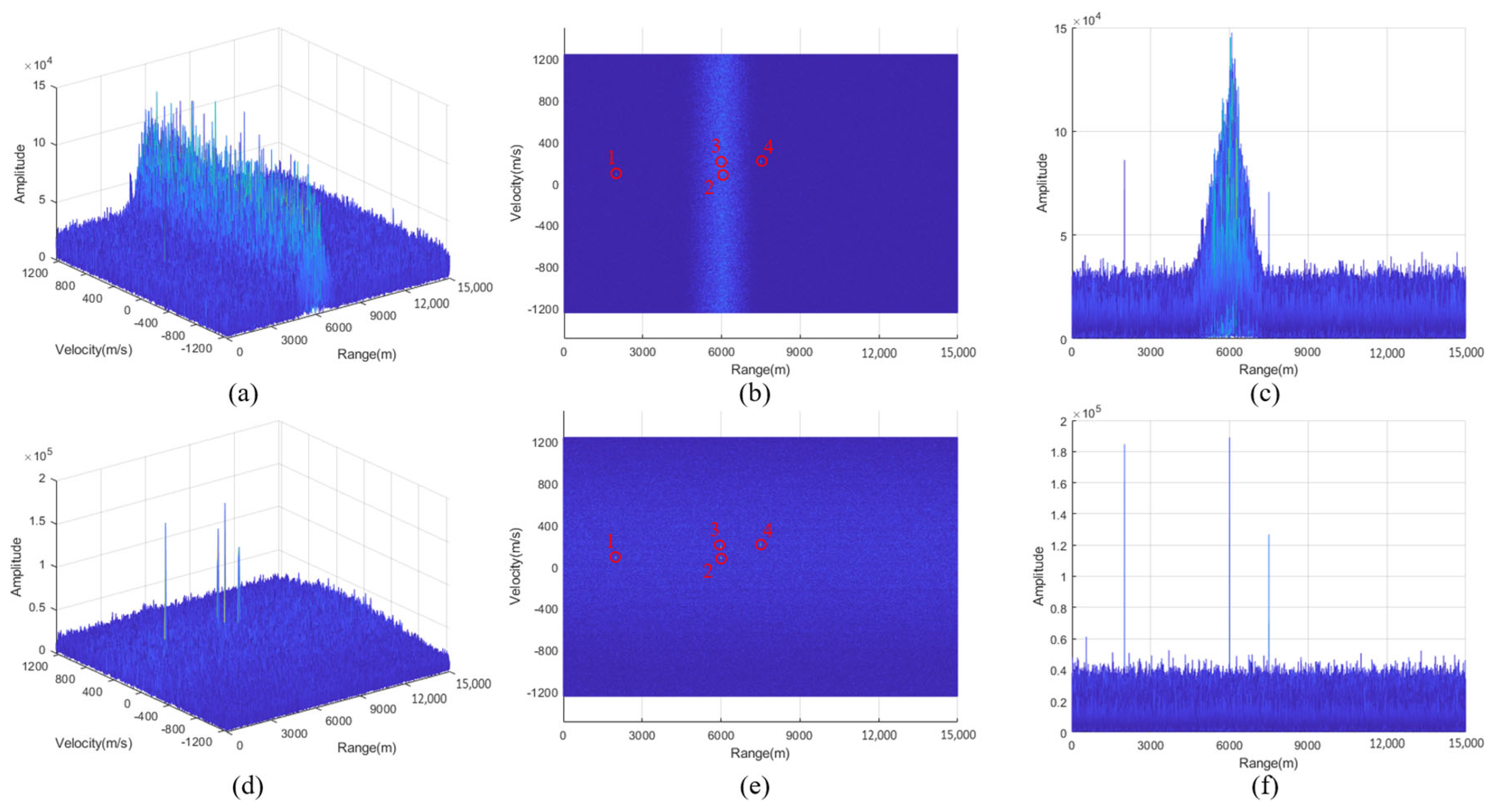
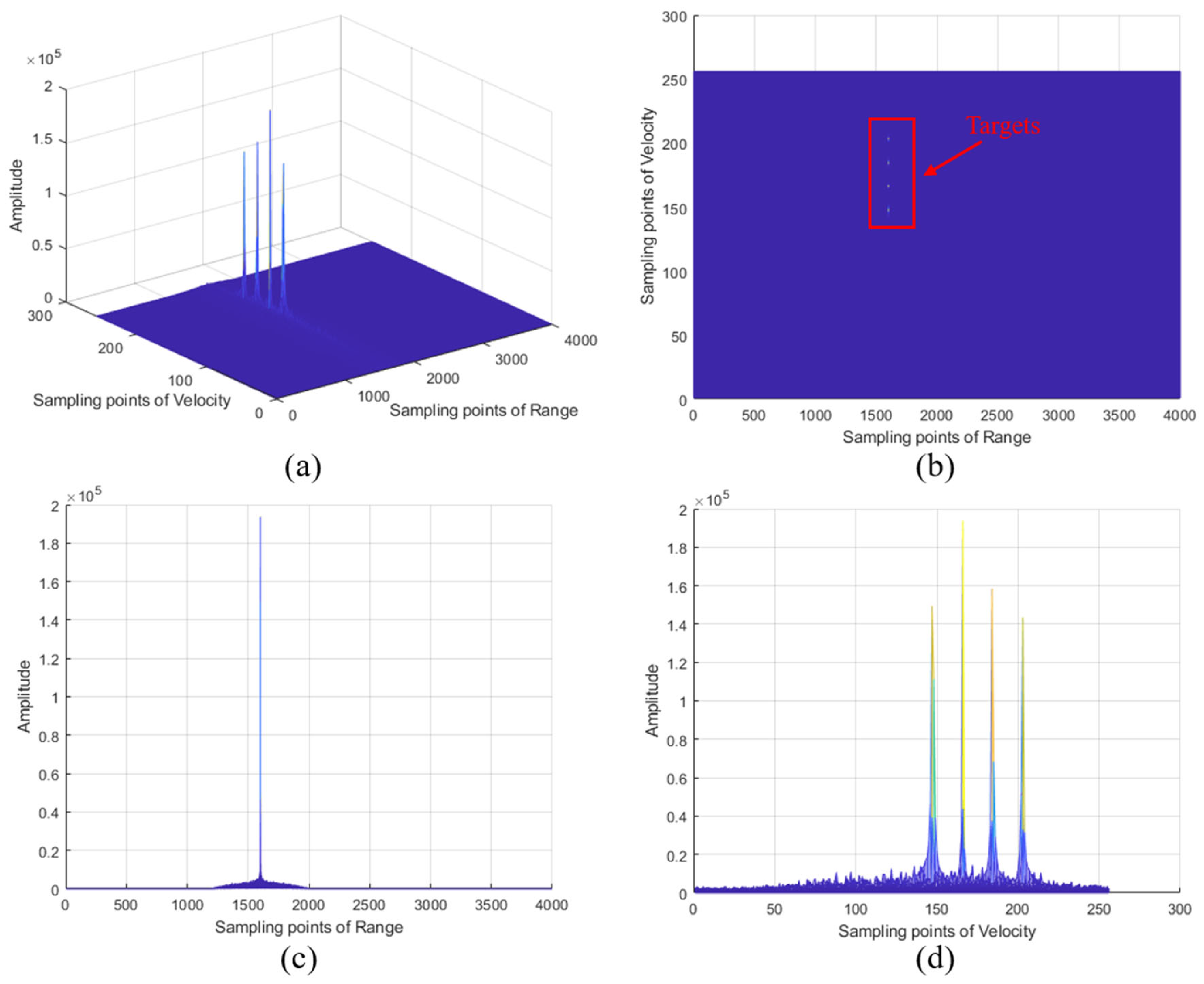
6.2. Multi-Target Detection Results in Complex Environments
6.3. Simulation of the Effect of Direct Wave Doppler Error on Algorithms
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, C.; Wang, L.; Jiang, R.; Hu, J.; Xu, S. Radar Jamming Decision-Making in Cognitive Electronic Warfare: A Review. IEEE Sens. J. 2023, 23, 11383–11403. [Google Scholar] [CrossRef]
- Moon, S.H.; Kim, K.I.; Choi, H.J.; Kim, K.T. Simulation of Ground Clutter Received Signals on Rough Surfaces in an Electronic Warfare Environment. J. Korean Inst. Electromagn. Eng. Sci. 2025, 36, 95–105. [Google Scholar] [CrossRef]
- Shen, Y.; Lv, Z.; Liu, M.; Liu, J. The Jamming Evaluation System of Intelligent Electromagnetic Spectrum Warfare. In Proceedings of the 2024 IEEE 12th International Conference on Information, Communication and Networks (ICICN), Guilin, China, 21–24 August 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 111–114. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, C.; Gai, W. Research on application and development trend of multi-domain cooperative combat for unmanned combat platform. In Proceedings of the 2021 2nd International Symposium on Computer Engineering and Intelligent Communications (ISCEIC), Nanjing, China, 6–8 August 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 297–301. [Google Scholar] [CrossRef]
- Fan, X. Intelligent Radio Spectrum Management and Dynamic Spectrum Allocation Algorithm. In Proceedings of the 2024 International Conference on Power, Electrical Engineering, Electronics and Control (PEEEC), Athens, Greece, 14–16 August 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 836–841. [Google Scholar] [CrossRef]
- Wei, Z.; Liu, F.; Ng, D.W.K.; Schober, R. Safeguarding UAV networks through integrated sensing, jamming, and communications. In Proceedings of the ICASSP 2022-2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 8737–8741. [Google Scholar] [CrossRef]
- Zhang, S.; Lu, X.; Tan, K.; Yan, H.; Yang, J.; Dai, Z.; Gu, H. Co-Frequency Interference Suppression of Integrated Detection and Jamming System Based on 2D Sparse Recovery. Remote Sens. 2024, 16, 2325. [Google Scholar] [CrossRef]
- Mokole, E.L.; Blunt, S.D. Some Current and Recent RF-Spectrum Research and Development, Applications, Management, and Interference Mitigation. In Proceedings of the 2023 IEEE Conference on Antenna Measurements and Applications (CAMA), Genoa, Italy, 15–17 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 417–422. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, Y.; Ouyang, Y. Integrated Detection of Respiration and Heartbeat with Communication Capabilities Using OFDM-LFM-MP Signals. IEEE Access 2025, 13, 4021–4033. [Google Scholar] [CrossRef]
- Uysal, F. Phase-coded FMCW automotive radar: System design and interference mitigation. IEEE Trans. Veh. Technol. 2019, 69, 270–281. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.; Shang, K. Design and performance simulation for the detection and jamming integrated signal waveform. J. Detect. Control 2020, 42, 39–43. [Google Scholar]
- Lu, J.; Zhang, Q.; Shi, W.; Zhang, L. Development and Prospect of Detection and Communication Integration. J. Signal Process. 2019, 35, 1484–1495. [Google Scholar] [CrossRef]
- Su, W.C.; Lai, Y.C.; Horng, T.S.; El Arif, R. Time-Division Multiplexing MIMO Radar System with Self-Injection-Locking for Image Hotspot-Based Monitoring of Multiple Human Vital Signs. IEEE Trans. Microw. Theory Tech. 2023, 72, 1943–1952. [Google Scholar] [CrossRef]
- Dong, B.; Jia, J.; Tao, L.; Li, G.; Li, Z.; Huang, C.; Shi, J.; Wang, H.; Tang, Z.; Zhang, J.; et al. Photonic-based w-band integrated sensing and communication system with flexible time-frequency division multiplexed waveforms for fiber-wireless network. J. Light. Technol. 2024, 42, 1281–1295. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, X.; Yang, J.; Cui, G. Cognitive Radar Subpulses Waveform Design via Online Greedy Search. IEEE Trans. Signal Process. 2025, 73, 1122–1137. [Google Scholar] [CrossRef]
- Song, Y.; Tian, B.; Wang, R.; Xu, S.; Chen, Z. Joint waveform design and resource allocation strategy for cognitive radar target situation awareness. IET Radar Sonar Navig. 2024, 18, 1364–1380. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, H. The design of integrated waveform based on MSK-LFM signal. In Proceedings of the 2020 15th IEEE International Conference on Signal Processing (ICSP), Beijing, China, 6–9 December 2020; Volume 1, pp. 565–569. [Google Scholar] [CrossRef]
- Li, C.; Wu, G. A shared waveform design and processing method for integrated radar detection and coherent jamming signal. In Proceedings of the 2022 IEEE 10th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 17–19 June 2022; IEEE: Piscataway, NJ, USA, 2022; Volume 10, pp. 373–380. [Google Scholar] [CrossRef]
- Li, Z.; Yang, Y. lfm interference suppression algorithm based on FrFT. In Proceedings of the 2020 IEEE 6th International Conference on Computer and Communications (ICCC), Chengdu, China, 11–14 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1161–1165. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, Y.; Yeo, T.S.; Cheng, Y.; Zhang, Y. Sparse reconstruction-Based joint signal processing for MIMO-OFDM-IM integrated radar and communication systems. Remote Sens. 2024, 16, 1773. [Google Scholar] [CrossRef]
- Fang, Y.; Pan, Y.; Ma, H.; Ma, D.; Guizani, M. A novel DCSK-based linear frequency modulation waveform design for joint radar and communication systems. IEEE Trans. Green Commun. Netw. 2024, 9, 354–366. [Google Scholar] [CrossRef]
- Jiang, X.; Wu, X.; Gu, Q.J.; Liu, X. On Amplitude Modulation in CW Doppler Radars for Remote Displacement Sensing Using ENVSIL Radar. IEEE Trans. Microw. Theory Tech. 2024; early access. [Google Scholar] [CrossRef]
- Chen, T.; Zhe, Z. Research on Smart Noise Frequency Modulation Jamming Technology Based on Convolution Modulation. In Proceedings of the 2024 9th International Conference on Electronic Technology and Information Science (ICETIS), Hangzhou, China, 17–19 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 195–199. [Google Scholar] [CrossRef]
- Zhang, S.; Lu, X.; Yu, W.; Wu, Y.; Yan, H.; Wu, M.; Gu, H. Direct Wave Suppression Technology Based on De-slope Filtering and Sparse Recovery of Integrated Detection and Jamming System. J. Signal Process. 2023, 39, 221–234. [Google Scholar] [CrossRef]
- Aldimashki, O.; Serbes, A. LFM signal parameter estimation in the fractional Fourier domains: Analytical models and a high-performance algorithm. Signal Process. 2024, 214, 109224. [Google Scholar] [CrossRef]
- A uniform-Laplace mixture distribution. J. Comput. Appl. Math. 2023, 429, 115236. [CrossRef]
- Jia, W.; Jiao, Z.; Zan, W.; Zhu, W. Probability density of the solution to nonlinear systems driven by Gaussian and Poisson white noises. Probabilistic Eng. Mech. 2024, 77, 103658. [Google Scholar] [CrossRef]
- Alpay, D.; De Martino, A.; Diki, K.; Struppa, D.C. Short-time Fourier transform and superoscillations. Appl. Comput. Harmon. Anal. 2024, 73, 101689. [Google Scholar] [CrossRef]
- Lyu, M.; Chen, H.; Yang, J.; Wu, X.; Zhou, M.; Ma, X. Sensing matrix optimization for random stepped-frequency signal based on two-dimensional ambiguity function. Chin. J. Electron. 2024, 33, 161–174. [Google Scholar] [CrossRef]








| Parameters | Values |
|---|---|
| LFM signal bandwidth | 20 MHz |
| Signal pulse width | 10 μs |
| Nimble modulation parameter | 0.2, 0.5, 1.0 |
| Type of noise | Gaussian distribution |
| Carrier frequency | 5 GHz |
| Pulse repetition interval | 50 μs |
| Sampling rate | 40 MHz |
| Transmit power | 10 dBm |
| Target category | Corner reflector |
| Target distance | 20 m |
| Parameters | Values |
|---|---|
| Adversary LFM signal bandwidth | 20 MHz |
| Adversary LFM signal pulse width | 10 μs |
| Our NFM signal bandwidth | 20 MHz |
| Our NFM signal pulse width | 10 μs |
| Carrier frequency | 600 MHz |
| Pulse repetition interval | 100 μs |
| Number of repetition cycles | 257 |
| Sampling rate | 80 MHz |
| Parameters | Values |
|---|---|
| Target distance | 6000 m |
| Target speed | 180 m/s |
| Time delay of direct wave | 40 μs |
| Doppler frequency of direct wave | 720 Hz |
| Signal-to-interference ratio (SIR) | −35 dB |
| Parameters | Values |
|---|---|
| Target distance and speed | (2000 m, 80 m/s), (6000 m, 80 m/s) |
| (6000 m, 180 m/s), (7500 m, 200 m/s) | |
| Time delay of direct wave | 40 μs |
| Doppler frequency of direct wave | 720 Hz |
| Signal-to-noise ratio (SNR) | −35 dB |
| Signal-to-interference ratio (SIR) | −35 dB |
| Parameters | Values |
|---|---|
| Target distance and speed | (6000 m, 180 m/s), (6000 m, 360 m/s) |
| (6000 m, 540 m/s), (7500 m, 720 m/s) | |
| Time delay of direct wave | 40 μs |
| Real Doppler frequency of direct wave | 720 Hz |
| Error coefficient | 0.3 |
| Signal-to-interference ratio (SIR) | −50 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, X.; Zhang, S.; Tan, K.; Lu, X.; Yang, J.; Dai, Z.; Gu, H. Integrated Waveform Design and Signal Processing Based on Composite Noise Nimble Modulated Signals. Electronics 2025, 14, 1227. https://doi.org/10.3390/electronics14061227
Cao X, Zhang S, Tan K, Lu X, Yang J, Dai Z, Gu H. Integrated Waveform Design and Signal Processing Based on Composite Noise Nimble Modulated Signals. Electronics. 2025; 14(6):1227. https://doi.org/10.3390/electronics14061227
Chicago/Turabian StyleCao, Xinquan, Shiyuan Zhang, Ke Tan, Xingyu Lu, Jianchao Yang, Zheng Dai, and Hong Gu. 2025. "Integrated Waveform Design and Signal Processing Based on Composite Noise Nimble Modulated Signals" Electronics 14, no. 6: 1227. https://doi.org/10.3390/electronics14061227
APA StyleCao, X., Zhang, S., Tan, K., Lu, X., Yang, J., Dai, Z., & Gu, H. (2025). Integrated Waveform Design and Signal Processing Based on Composite Noise Nimble Modulated Signals. Electronics, 14(6), 1227. https://doi.org/10.3390/electronics14061227







