An Innovative Digital Pulse Width Modulator and Its Field-Programmable Gate Array Implementation
Abstract
:1. Introduction
- A new DPWM (eDPWM) with zero phase delay or a programmable derivative action is proposed.
- The overall DPWM architecture complexity is simplified and relaxed. Indeed, in the architecture in [23], the derivative action is achieved by changing the values of a and b. This implies that the comparator slopes must be modified according to the values of a and b. Counting with programmable slopes overcomplicates the counter implementation. The new architecture eradicates the use of products between signals to achieve the derivative action and the DPWM counters always count with a constant slope (i.e., the ratio is constant). This greatly simplified the programmability of the derivative action and the overall architecture.
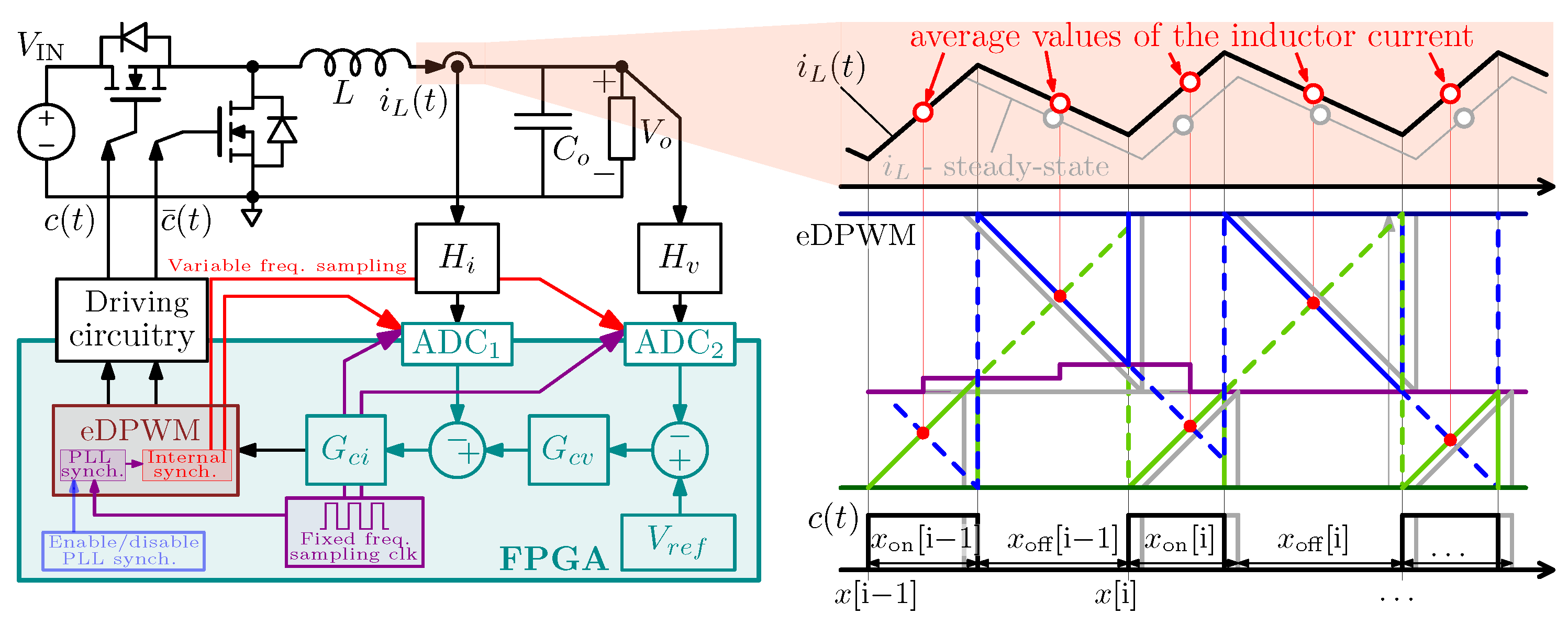
- The synchronism mechanism is greatly simplified. Indeed, the eDPWM intrinsically provides the instant corresponding to the middle of the ON and OFF phases. As required in countless digital controls for power electronic applications, such a signal triggers the ADC sampling to acquire the average value of piecewise linear signals. This trigger event is not intrinsically present in ADE-DPWM; adding it increases the system complexity, as shown in [24,25]. Conversely, in the eDPWM, the synchronism mechanism can be easily implemented using the aforementioned trigger signal without further increasing the architecture’s complexity.
- The DPWM architecture is optimized to use all available bits. Namely, since the comparator slopes are fixed and proportional to the ratio, and since they must always count in one direction (i.e., up-count or down-count), the resolution of the DPWM can be increased to make maximum use of all available bits, even doing better than the TTE-DPWM in which one bit is lost due to alternating up-count and down-count.
- Other original contributions in this article are the block diagram of ADE-DPWM modulators and other alternative implementations of eDPWMmodulators.
2. Enhanced DPWM: Main Concepts
2.1. Fixed-Frequency vs. Variable-Frequency DPWM Architectures
2.2. Challenges in ADE-DPWM Implementation
- Computational complexity: ADE-DPWM requires real-time multiplications and divisions, significantly increasing hardware resource utilization.
- Synchronization issues: Unlike fixed-frequency DPWM, ADE-DPWM lacks an intrinsic sampling synchronization mechanism, making accurate current measurement more challenging.
- Hardware limitations: ADE-DPWM is difficult to implement on FPGAs and is impossible to realize on microcontrollers due to excessive computational demands.
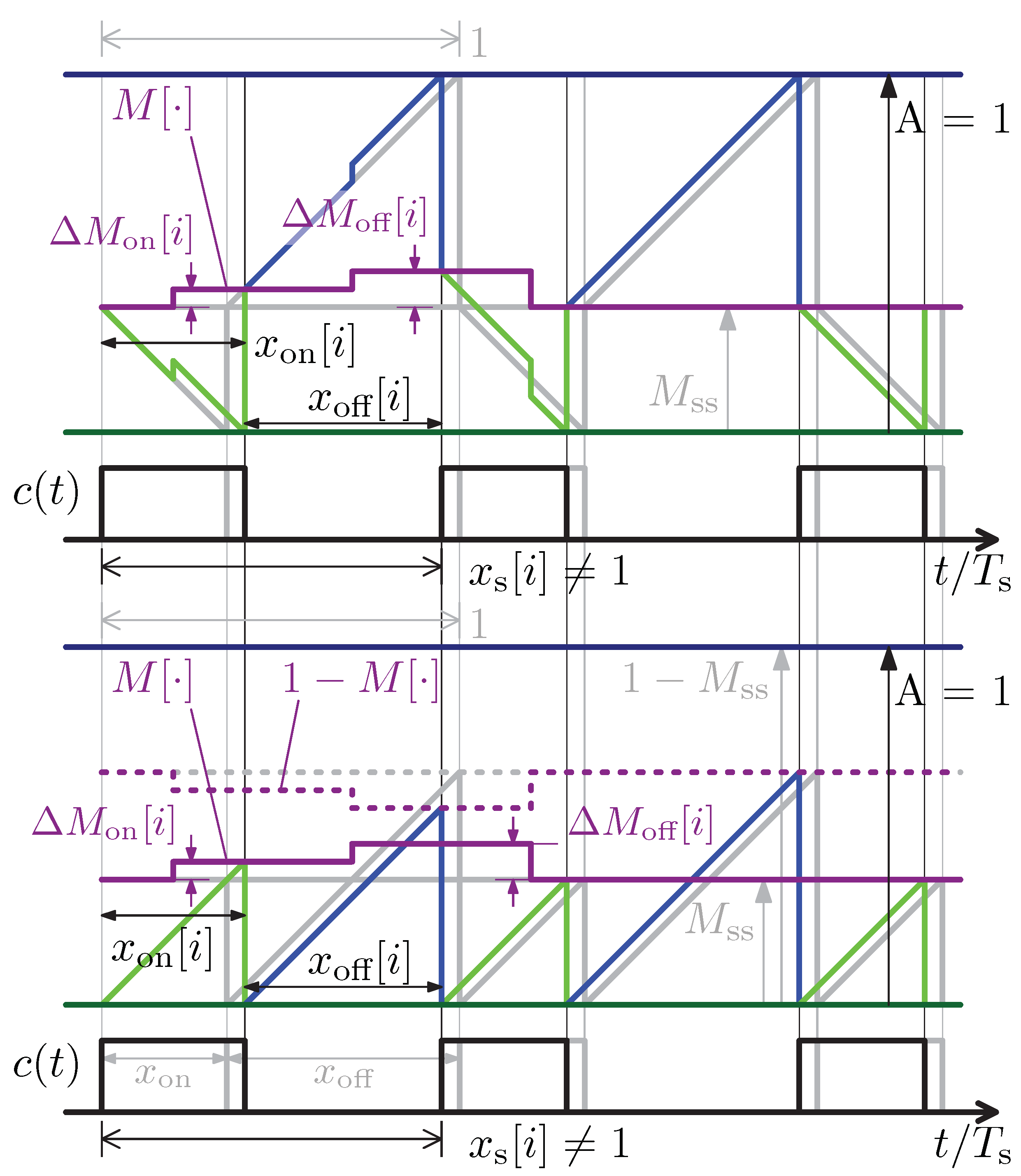
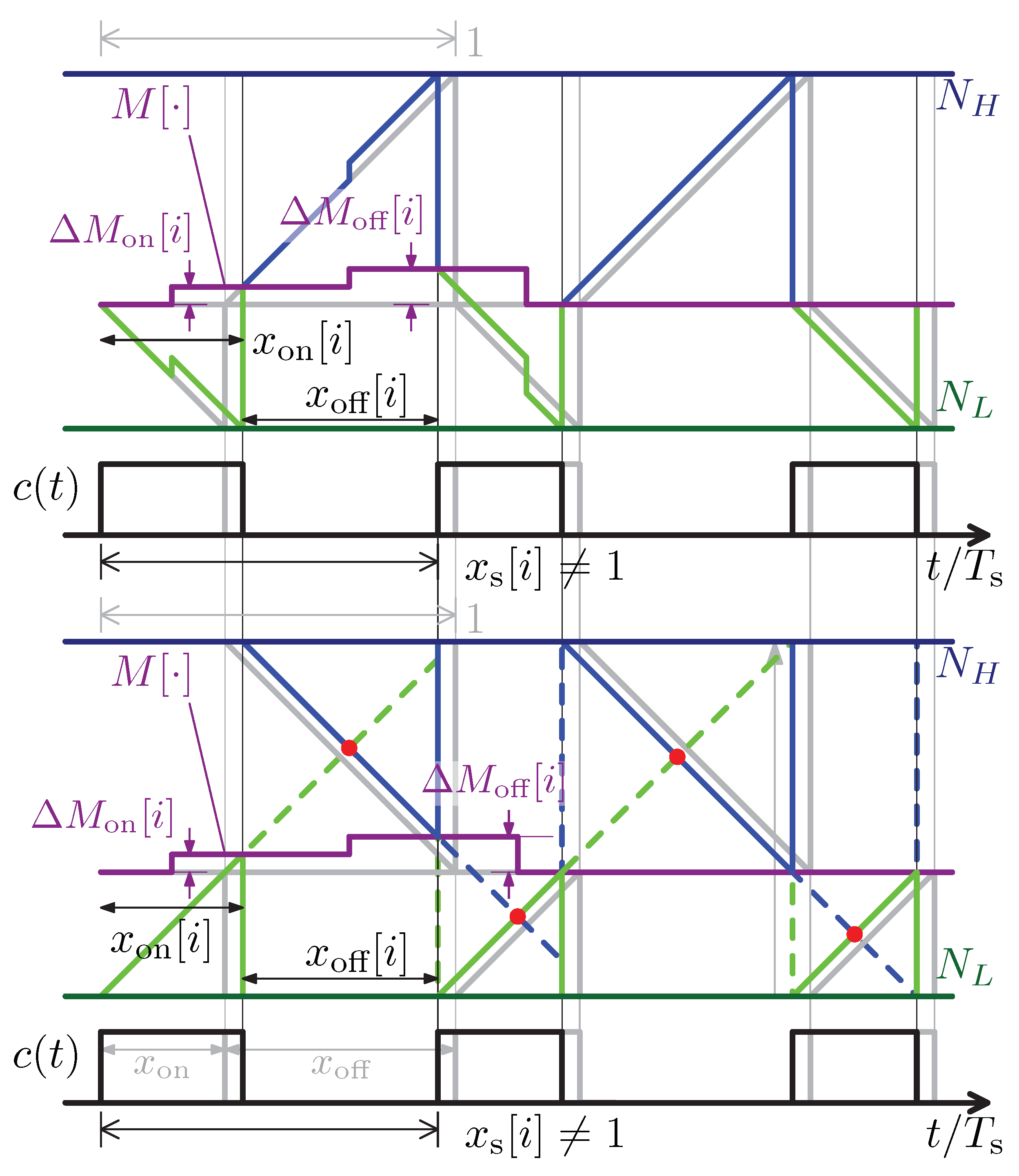
2.3. Proposed eDPWM Architecture
- The carrier counters always start from a constant value. In the ADE carrier-based structure, the starting point of the carrier must be updated at the beginning of each ON and OFF phases.
- Differently than ADE-DPWM, counting operations to implement the two carriers are uninterrupted. The counter always starts from zero, and the change in the modulating signal is not added to the counter. The only values that must be set are the compare values for the two carriers.
3. General eDPWM Organization
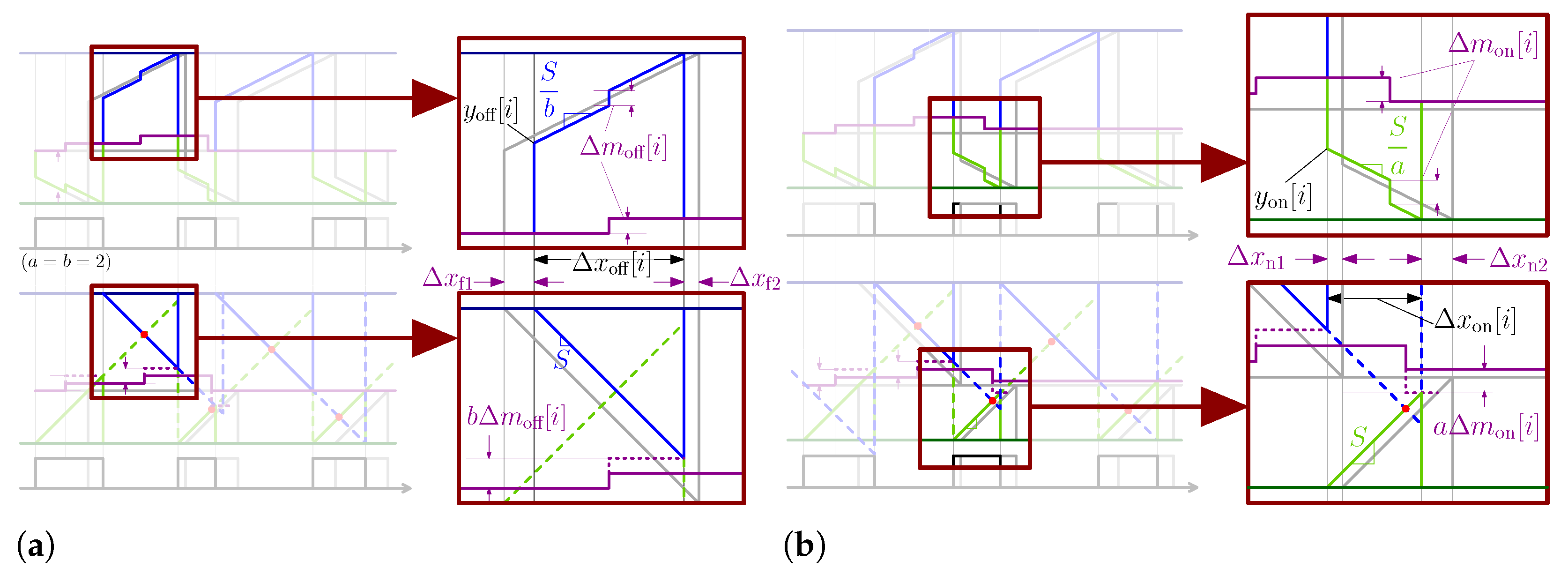
3.1. Intrinsic Programmable Derivative Actions
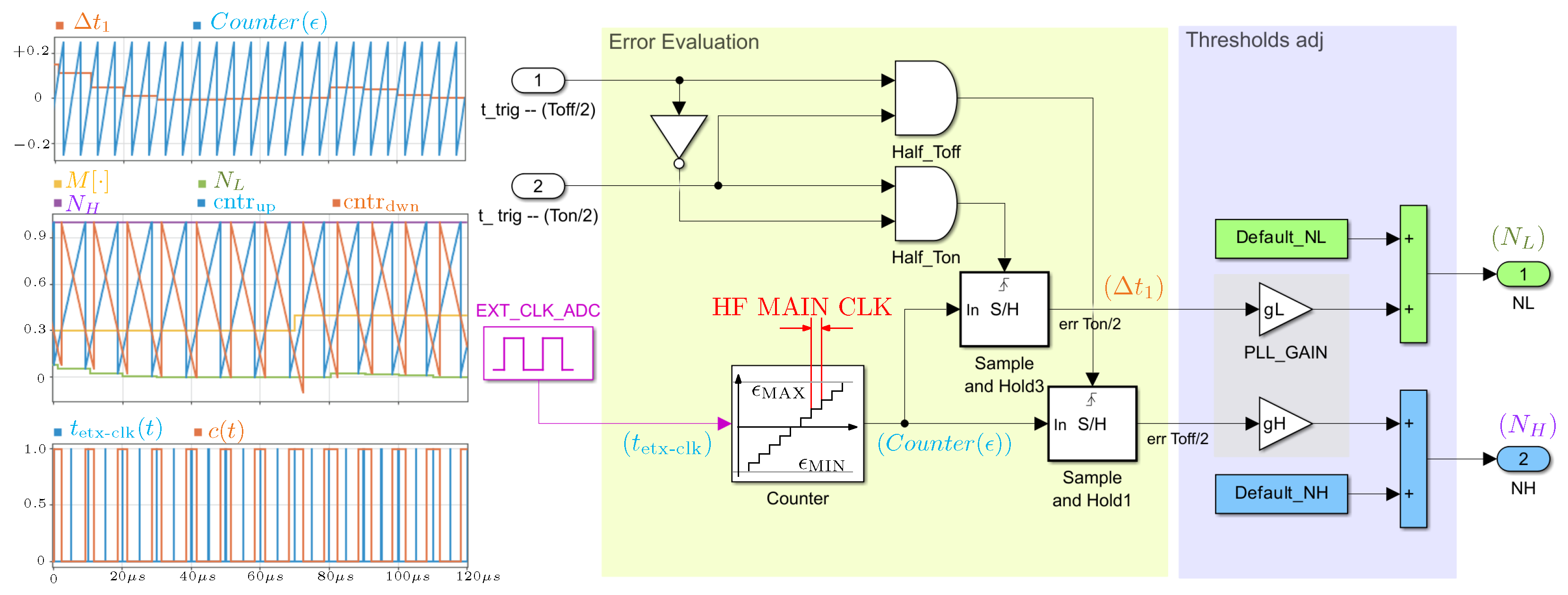
3.2. Synchronization Mechanism
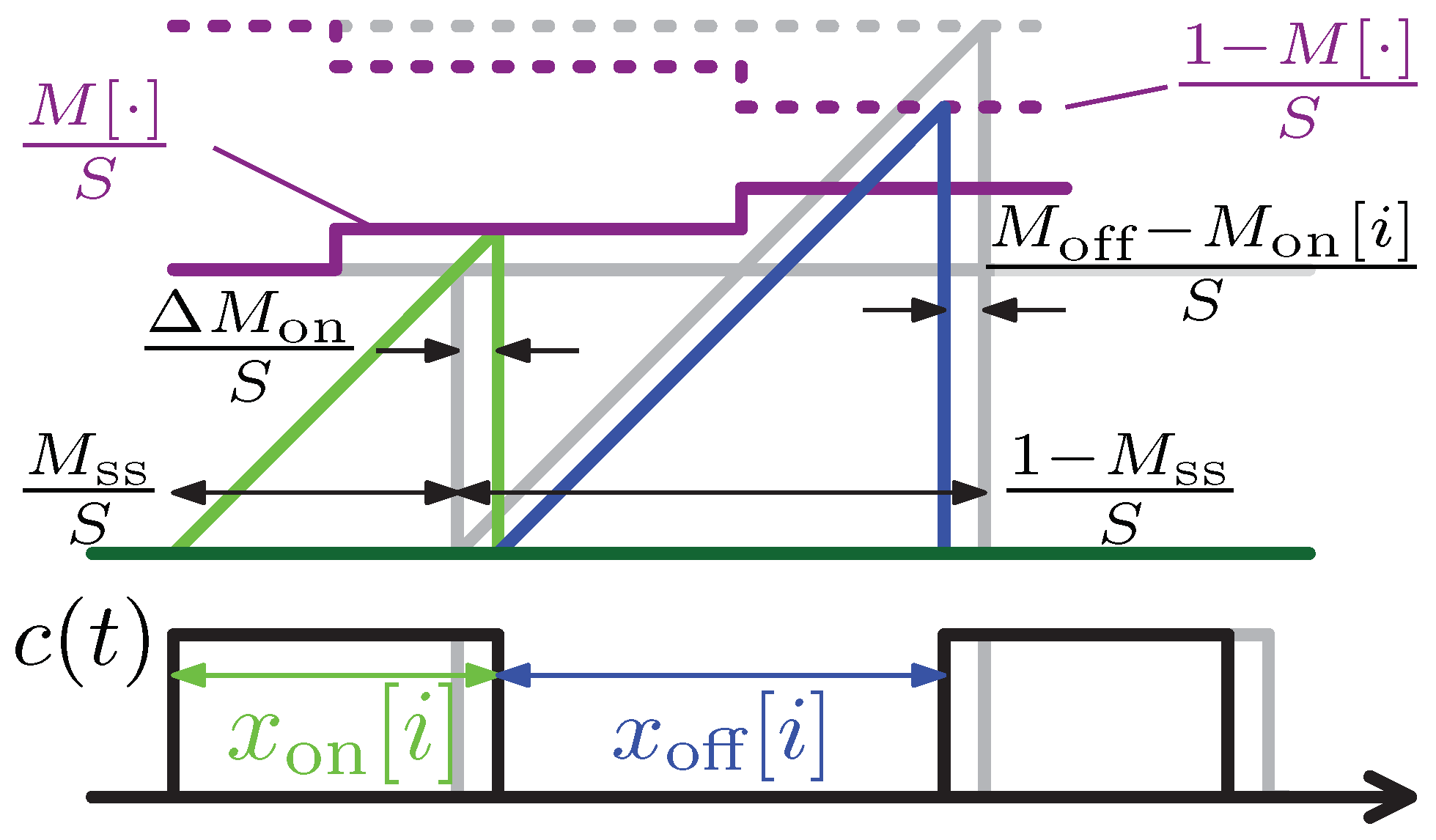
4. The Small Signal Model
4.1. Time Domain Operation
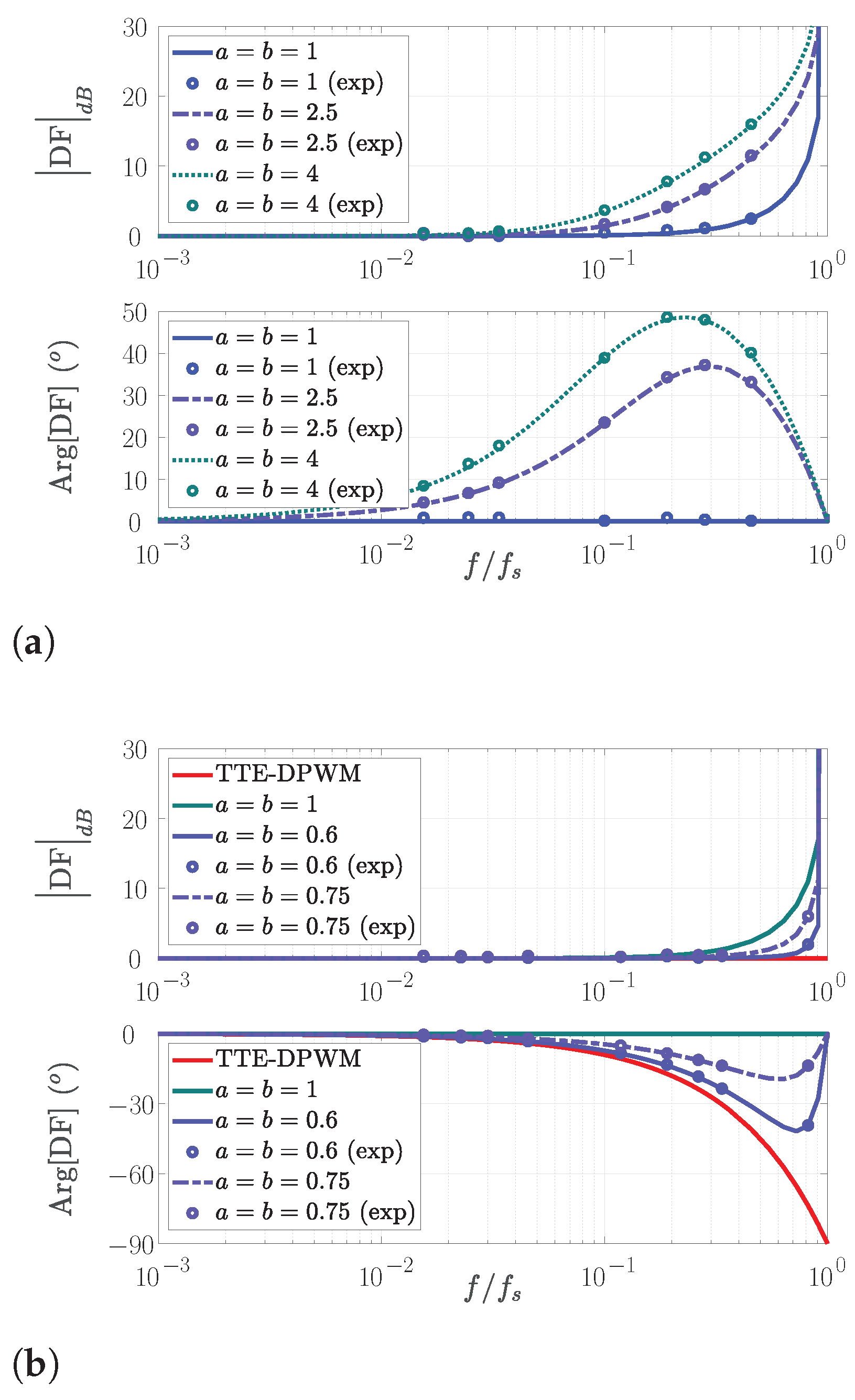
4.2. Frequency Domain Results
5. Experimental Validation
Discussion
6. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations and Main Definitions
| Symbol | Definition |
| DPWM | Digital Pulse Width Modulator; |
| eDPWM | Enhanced Digital Pulse Width Modulator; |
| ADE | Asymmetric Dual-Edge; |
| TTE | Trailing-Triangle Edge; |
| Modulation period; | |
| ON time of the pulse width modulation cycle; | |
| OFF time of the pulse width modulation cycle; | |
| Normalized ON phase duration (i.e., ); | |
| Normalized OFF phase duration (i.e., ); | |
| Normalized ON phase duration during the i-th cycle; | |
| Normalized OFF phase duration during the i-th cycle; | |
| Variation of the ON phase during the i-th cycle (i.e., ); | |
| Variation of the OFF phase during the i-th cycle (i.e., ); | |
| Modulating signal; | |
| Steady-state value of the modulating signal; | |
| Modulating signal variation during the ON phase; | |
| Modulating signal variation during the OFF phase; | |
| S | Carrier slope; |
| s | Complex independent variable of the transfer functions; |
| Output control signal; | |
| Small signal transfer function of the eDPWM V2.0; | |
| Steady-state switching frequency; | |
| Frequency of the input perturbation; | |
| High-frequency phase boost; | |
| PLL | Phase-Locked Loop; |
| Parameters to weight the derivative action; | |
| Upper and lower DPWM thresholds. |
References
- Li, W.; He, X. Review of Nonisolated High-Step-Up DC/DC Converters in Photovoltaic Grid-Connected Applications. IEEE Trans. Ind. Electron. 2011, 58, 1239–1250. [Google Scholar] [CrossRef]
- Forouzesh, M.; Siwakoti, Y.P.; Gorji, S.A.; Blaabjerg, F.; Lehman, B. Step-Up DC–DC Converters: A Comprehensive Review of Voltage-Boosting Techniques, Topologies, and Applications. IEEE Trans. Power Electron. 2017, 32, 9143–9178. [Google Scholar] [CrossRef]
- Mao, H.; Lee, C.; Boroyevich, D.; Hiti, S. Review of high-performance three-phase power-factor correction circuits. IEEE Trans. Ind. Electron. 1997, 44, 437–446. [Google Scholar] [CrossRef]
- de Castro, A.; Todorovich, E. High Resolution FPGA DPWM Based on Variable Clock Phase Shifting. IEEE Trans. Power Electron. 2010, 25, 1115–1119. [Google Scholar] [CrossRef]
- Le, H.; Dekka, A.; Ronanki, D.; Rodriguez, J. Predictive Current Control of a New Four-Level Voltage Source Inverter. In Proceedings of the 2022 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 14–17 December 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Buso, S.; Mattavelli, P. Digital Control in Power Electronics, 2nd ed.; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Sozański, K. Digital Signal Processing in Power Electronics Control Circuits, 2nd ed.; Springer: Cham, Switzerland, 2013. [Google Scholar]
- Buccella, C.; Cecati, C.; Latafat, H. Digital Control of Power Converters—A Survey. IEEE Trans. Ind. Inf. 2012, 8, 437–447. [Google Scholar] [CrossRef]
- Kelly, A.; Rinne, K. High Resolution DPWM in a DC-DC Converter Application Using Digital Sigma-Delta Techniques. In Proceedings of the 2005 IEEE 36th Power Electronics Specialists Conference, Recife, Brazil, 12–16 June 2005; pp. 1458–1463. [Google Scholar] [CrossRef]
- Huang, Y.; Cheung, C. Small signal modeling of the hysteretic modulator with a current ripple synthesizer. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 1616–1623. [Google Scholar] [CrossRef]
- Rodriguez, J.; Pontt, J.; Silva, C.A.; Correa, P.; Lezana, P.; Cortes, P.; Ammann, U. Predictive Current Control of a Voltage Source Inverter. IEEE Trans. Ind. Electron. 2007, 54, 495–503. [Google Scholar] [CrossRef]
- Singh, R.K.; Mishra, S. Synthetic-Ripple-Based Digital Hysteretic Modulator for Point-of-Load Converters. IEEE Trans. Ind. Electron. 2013, 60, 4996–5007. [Google Scholar] [CrossRef]
- Malesani, L.; Tenti, P. A novel hysteresis control method for current-controlled voltage-source PWM inverters with constant modulation frequency. IEEE Trans. Ind. Appl. 1990, 26, 88–92. [Google Scholar] [CrossRef]
- Nussbaumer, T.; Heldwein, M.L.; Gong, G.; Round, S.D.; Kolar, J.W. Comparison of Prediction Techniques to Compensate Time Delays Caused by Digital Control of a Three-Phase Buck-Type PWM Rectifier System. IEEE Trans. Ind. Electron. 2008, 55, 791–799. [Google Scholar] [CrossRef]
- Corradini, L.; Mattavelli, P.; Tedeschi, E.; Trevisan, D. High-Bandwidth Multisampled Digitally Controlled DC–DC Converters Using Ripple Compensation. IEEE Trans. Ind. Electron. 2008, 55, 1501–1508. [Google Scholar] [CrossRef]
- Petric, I.Z.; Mattavelli, P.; Buso, S. A Jitter Amplification Phenomenon in Multisampled Digital Control of Power Converters. IEEE Trans. Power Electron. 2021, 36, 8685–8695. [Google Scholar] [CrossRef]
- Corradini, L.; Mattavelli, P.; Saggini, S. Elimination of Sampling-Induced Dead Bands in Multiple-Sampled Pulsewidth Modulators for DC–DC Converters. IEEE Trans. Power Electron. 2009, 24, 2661–2665. [Google Scholar] [CrossRef]
- Petric, I.Z.; Mattavelli, P.; Buso, S. Investigation of Nonlinearities Introduced by Multi-sampled Pulsewidth Modulators. IEEE Trans. Power Electron. 2022, 37, 2538–2550. [Google Scholar] [CrossRef]
- Chen, J.; Prodic, A.; Erickson, R.; Maksimovic, D. Predictive digital current programmed control. IEEE Trans. Power Electron. 2003, 18, 411–419. [Google Scholar] [CrossRef]
- Mohamed, Y.A.R.I.; El-Saadany, E.F. Robust High Bandwidth Discrete-Time Predictive Current Control with Predictive Internal Model—A Unified Approach for Voltage-Source PWM Converters. IEEE Trans. Power Electron. 2008, 23, 126–136. [Google Scholar] [CrossRef]
- Mattavelli, P. An improved deadbeat control for UPS using disturbance observers. IEEE Trans. Ind. Electron. 2005, 52, 206–212. [Google Scholar] [CrossRef]
- Bonanno, G.; Corradini, L. Digital Predictive Current-Mode Control of Three-Level Flying Capacitor Buck Converters. IEEE Trans. Power Electron. 2021, 36, 4697–4710. [Google Scholar] [CrossRef]
- Bonanno, G.; Comacchio, A.; Mattavelli, P.; Corradin, M. Asymmetric Dual-Edge Digital Pulsewidth Modulator With an Intrinsic Derivative Action. IEEE Trans. Power Electron. 2023, 38, 304–315. [Google Scholar] [CrossRef]
- Bonanno, G.; Comacchio, A.; Mattavelli, P. Multisampling Digital Pulse-Width Modulator Based on Asymmetric Dual-Edge Carrier. IEEE Trans. Power Electron. 2024, 39, 5121–5134. [Google Scholar] [CrossRef]
- Comacchio, A.; Bonanno, G.; Hossein, A.; Mattavelli, P.; Corradin, M. A Digital Dual-Edge Modulator for Dynamic Performance Improvement of Multi-Loop Controlled VSI. IEEE Trans. Ind. Electron. 2022, 70, 4662–4671. [Google Scholar] [CrossRef]
- Cvetanovic, R.; Bonanno, G.; Comacchio, A.; Abedini, H.; Biadene, D.; Mattavelli, P. High Frequency Passivity Properties of Grid-Connected Admittance With Double-Sampling Asymmetric Dual-Edge Modulator. IEEE Open J. Power Electron. 2022, 3, 856–865. [Google Scholar] [CrossRef]
- da Silva Carvalho, S.; Halamíček, M.; Vukadinović, N.; Prodić, A. Digital PWM for Multi-Level Flying Capacitor Converters with Improved Output Resolution and Flying Capacitor Voltage Controller Stability. In Proceedings of the 2018 IEEE 19th Workshop on Control and Modeling for Power Electronics (COMPEL), Padova, Italy, 25–28 June 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Corradini, L.; Maksimović, D.; Mattavelli, P.; Zane, R. Digital Control of High-Frequency Switched-Mode Power Converters; Wiley: Hoboken, NJ, USA, 2015; pp. 1–342. [Google Scholar] [CrossRef]
- Ripamonti, G.; Saggini, S.; Corradini, L.; Rizzolatti, R.; Faccio, F.; Michelis, S.; Koukab, A.; Kayal, M. A Dual-Edge Pulsewidth Modulator for Fast Dynamic Response DC-DC Converters. IEEE Trans. Power Electron. 2019, 34, 28–32. [Google Scholar] [CrossRef]
- Huang, Y.; Cheung, C.; Jayaprakash, K.V.A. Small signal modeling of dual-edge PWM modulator with fixed clock frequency. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 1047–1053. [Google Scholar] [CrossRef]





| Architecture | Phase Delay | Comput. Complexity | Hardware Suitability |
|---|---|---|---|
| TTE | ≈ | Low | Simple for MCUs and FPGAs |
| ADE | zero † | High | Only FPGA |
| eDPWM | zero † | Low | Efficient on FPGA ★ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonanno, G. An Innovative Digital Pulse Width Modulator and Its Field-Programmable Gate Array Implementation. Electronics 2025, 14, 1522. https://doi.org/10.3390/electronics14081522
Bonanno G. An Innovative Digital Pulse Width Modulator and Its Field-Programmable Gate Array Implementation. Electronics. 2025; 14(8):1522. https://doi.org/10.3390/electronics14081522
Chicago/Turabian StyleBonanno, Giovanni. 2025. "An Innovative Digital Pulse Width Modulator and Its Field-Programmable Gate Array Implementation" Electronics 14, no. 8: 1522. https://doi.org/10.3390/electronics14081522
APA StyleBonanno, G. (2025). An Innovative Digital Pulse Width Modulator and Its Field-Programmable Gate Array Implementation. Electronics, 14(8), 1522. https://doi.org/10.3390/electronics14081522






