Wireless Charger for Pacemakers Controlled from Primary Current Without Communication with Secondary Side
Abstract
1. Introduction
2. State of the Art
2.1. Cardiac Pacemaker Technology
2.2. Wireless Charging in Pacemakers
2.3. Human Exposure Considerations
3. Power Stage Design
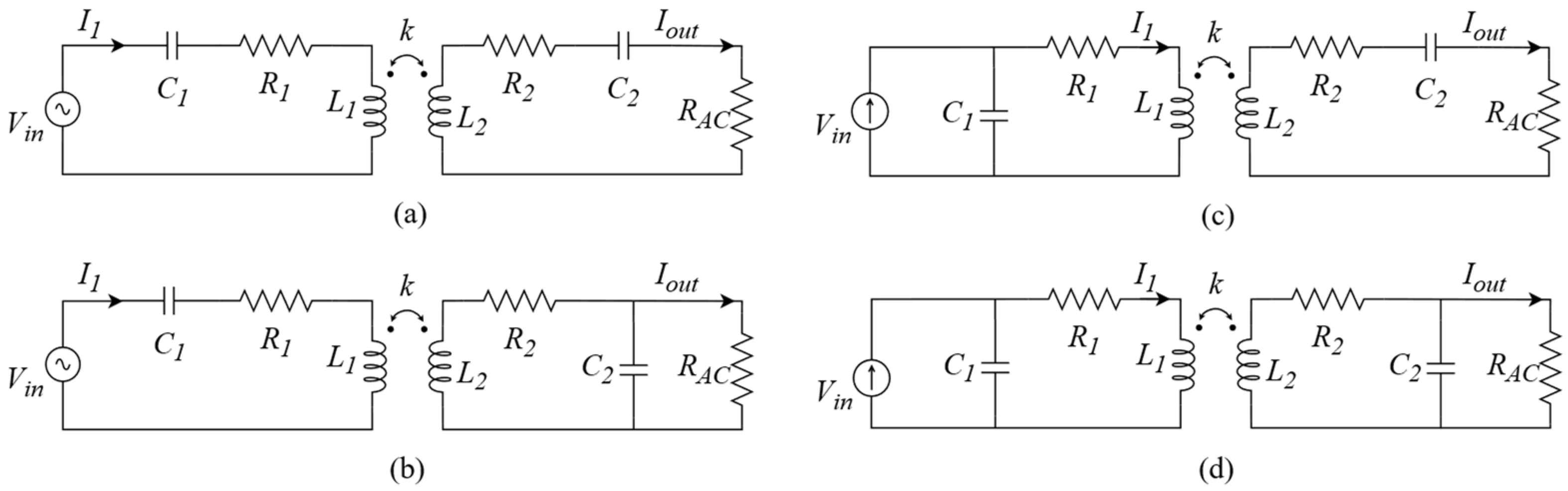
3.1. Topology Selection
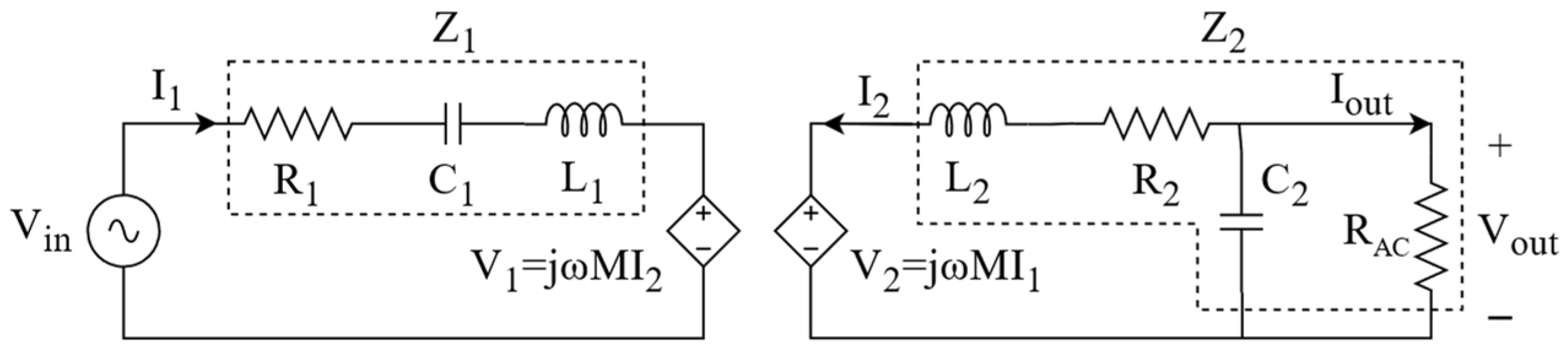
3.2. IPT System Modeling
3.3. Complete Power System
4. Design of the Control Stage
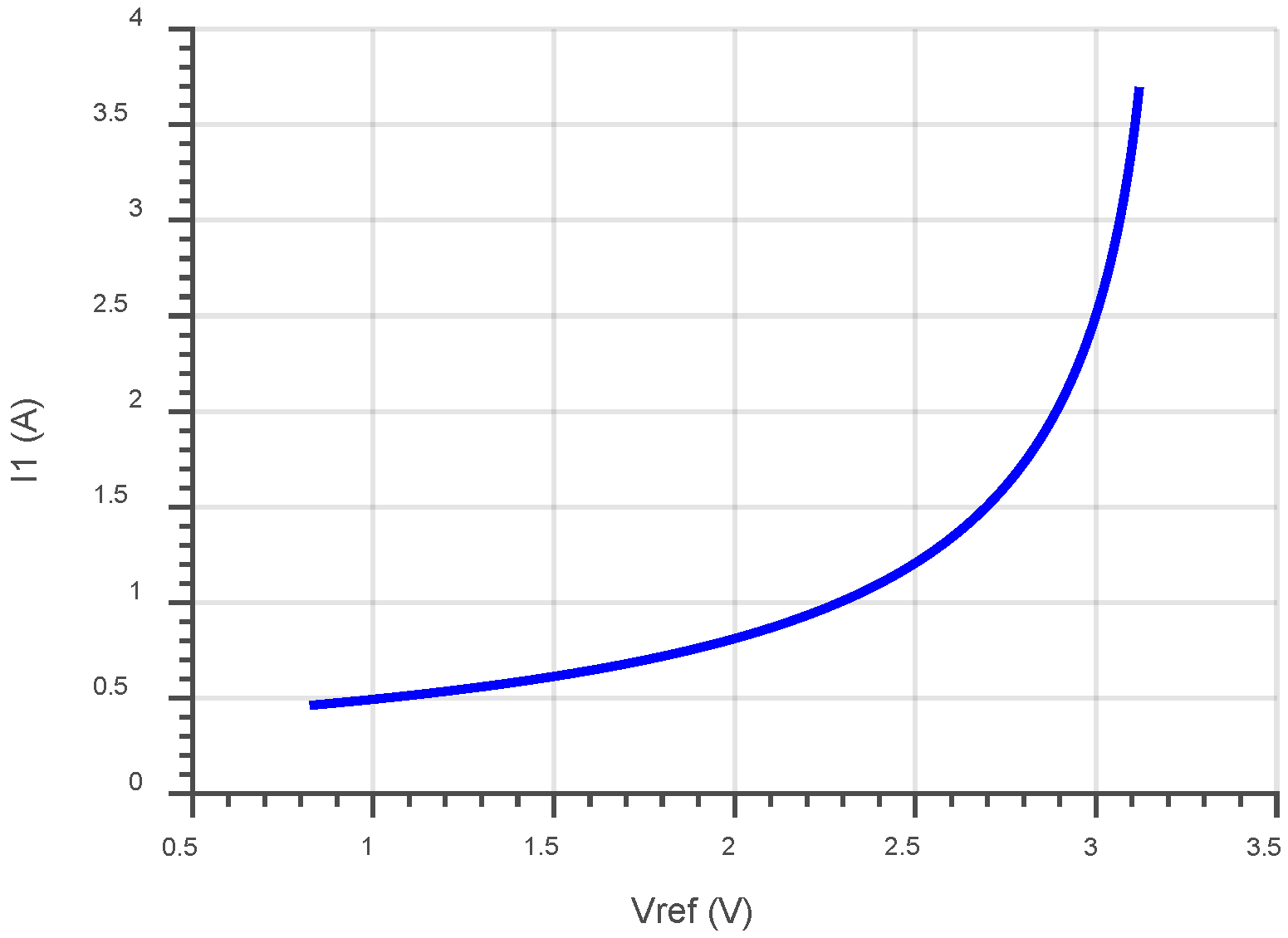
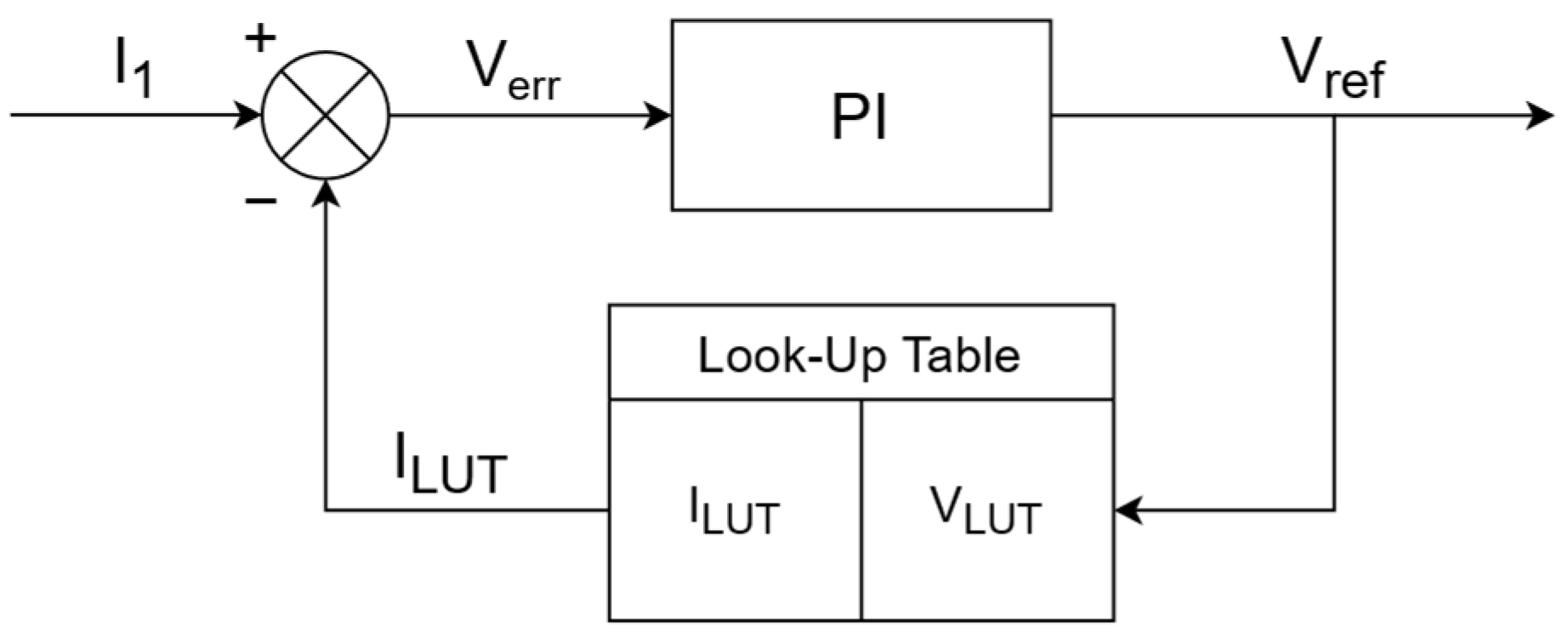
4.1. Control Strategy
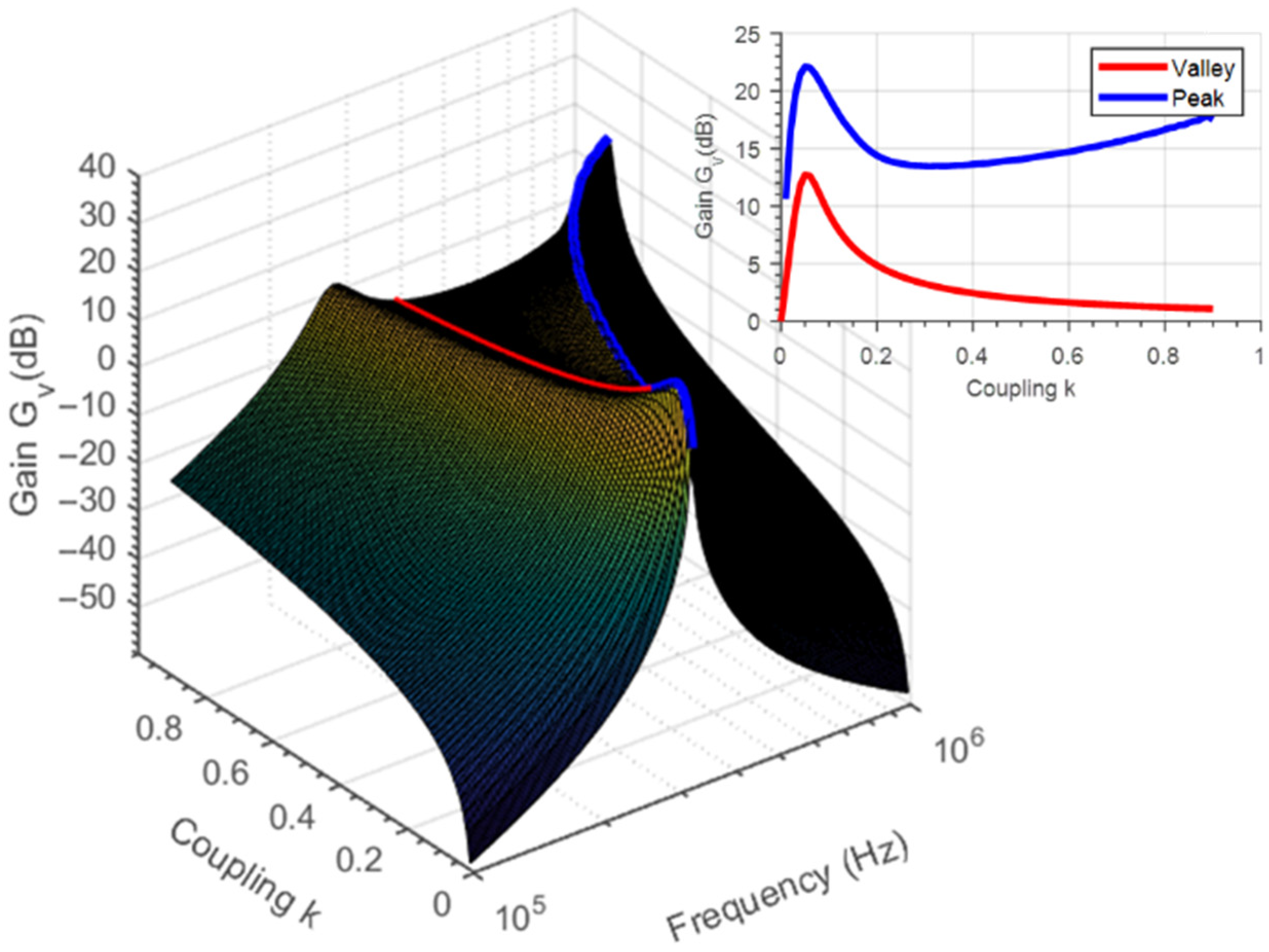
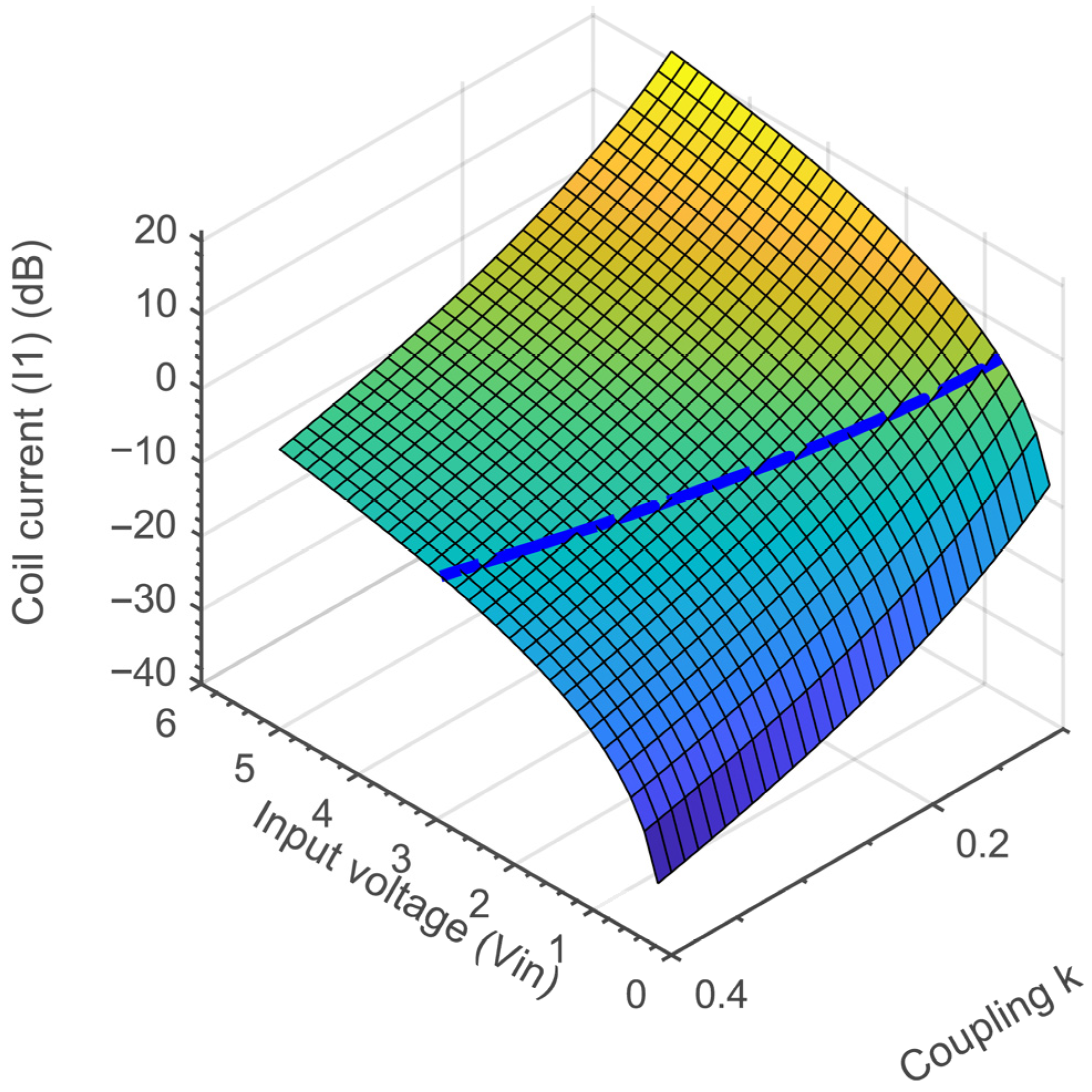
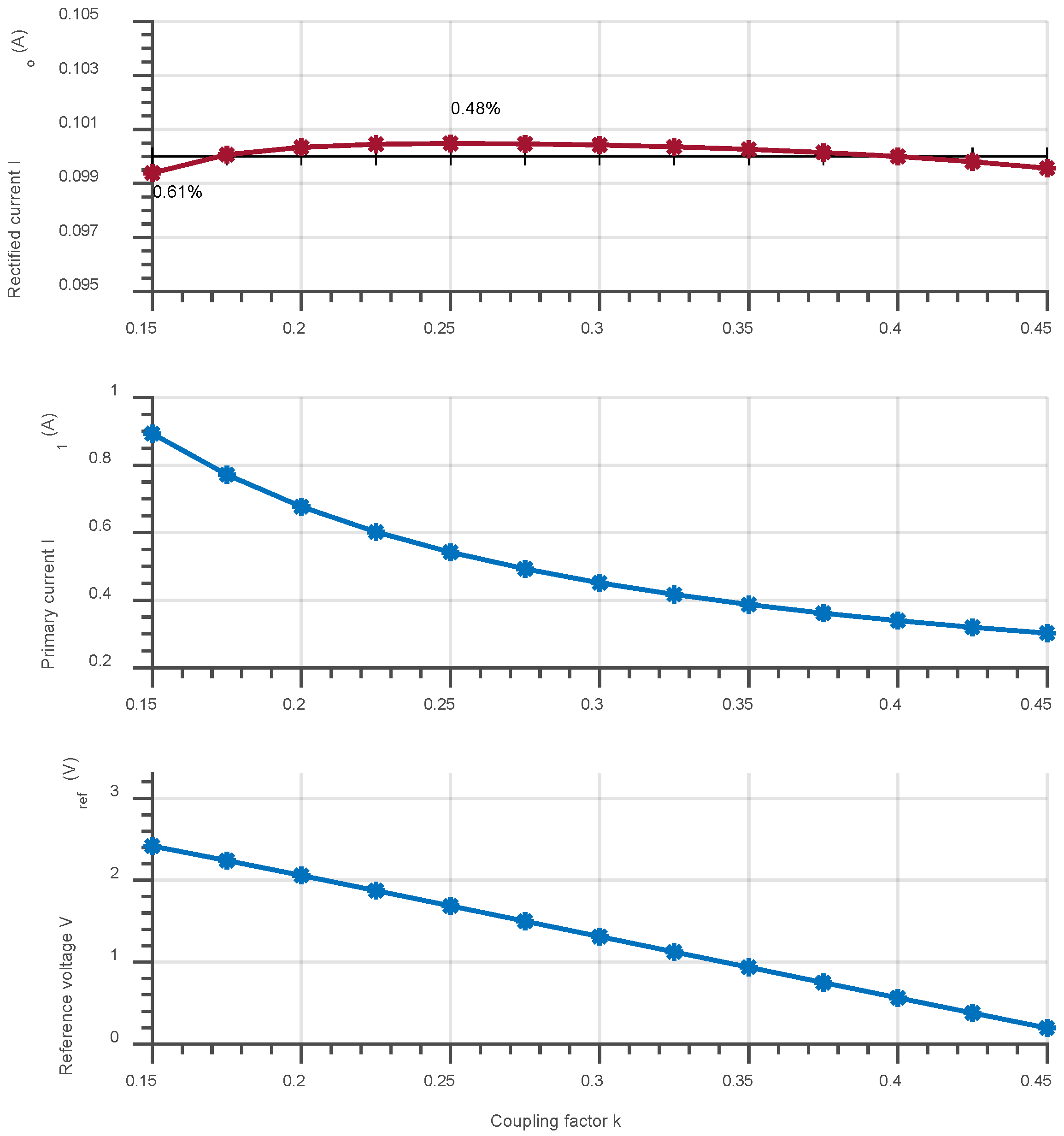
4.2. Simulation Results
5. Experimental Verification
5.1. WPT Charger Setup
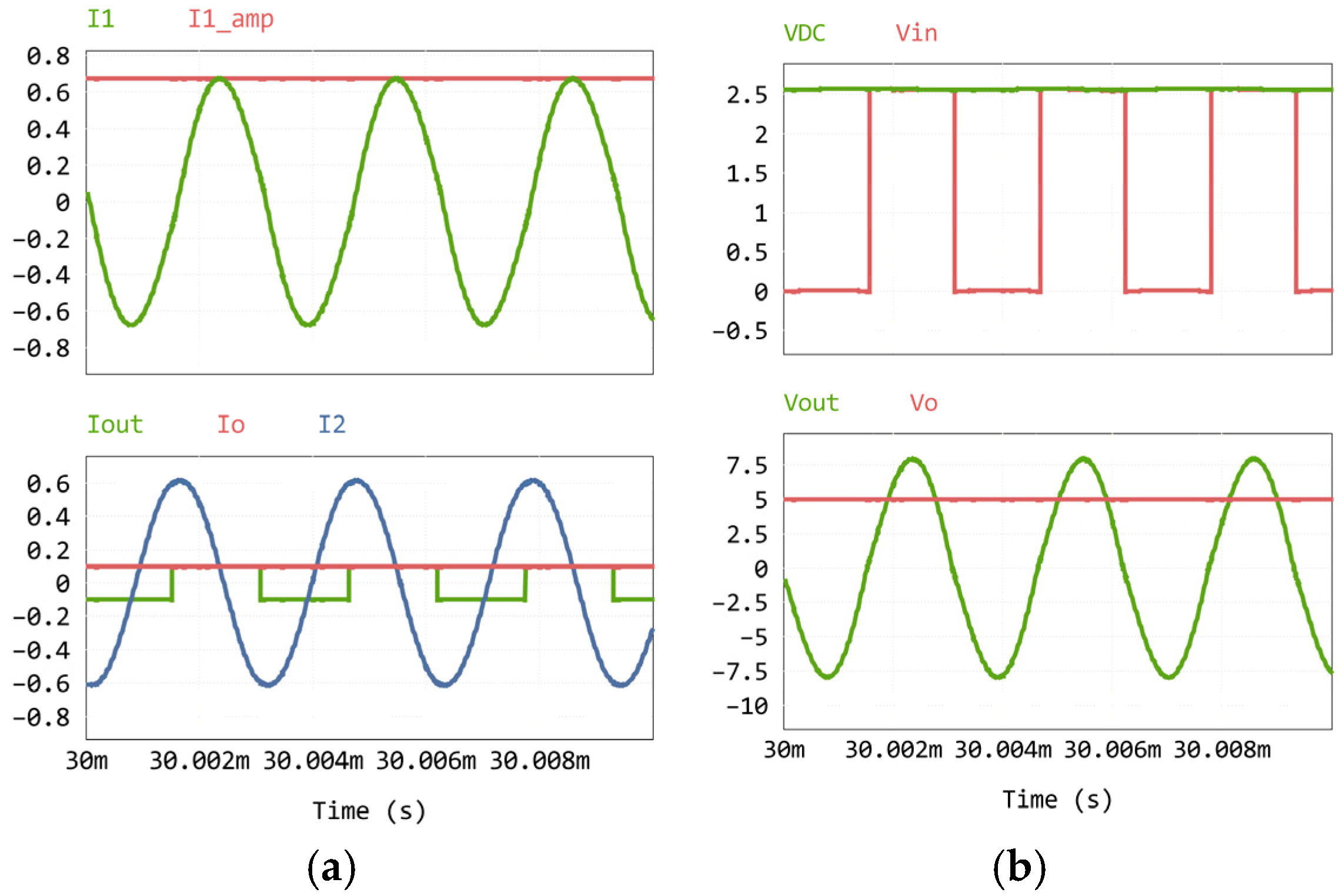
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AIMD | Active Implantable Medical Devices |
| IPT | Inductive Power Transfer |
| WPT | Wireless Power Transfer |
| MPE | Maximum Permissible Exposure |
| SAR | Specific Absorption Rate |
| SS | Series–Series |
| SP | Series–Parallel |
| PS | Parallel–Series |
| PP | Parallel–Parallel |
| FHA | First Harmonic Approximation |
| AC | Alternate Current |
| PWM | Pulse Width Modulation |
| LUT | Look-Up Table |
References
- Gururaj, S.; Applequist, A.; Bhattarai, S.; Appaji, A.M.; Kadambi, P. Self-Powered Cardiac Pacemaker: The Viability of a Piezoelectric Energy Harvester. In Proceedings of the 2020 International Conference on Communication Systems & Networks (COMSNETS), Bangalore, India, 7–11 January 2020; pp. 70–75. [Google Scholar] [CrossRef]
- Hueros, V.; Barrado, A.; Lázaro, A.; Fernández, C. A Review of Wireless Charging Systems for Cardiac Pacemakers. In Proceedings of the 2023 IEEE 17th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Tallinn, Estonia, 14–16 June 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Cruciani, S.; Campi, T.; Maradei, F.; Feliziani, M. Numerical simulation of Wireless Power Transfer system to recharge the battery of an implanted cardiac pacemaker. In Proceedings of the 2014 International Symposium on Electromagnetic Compatibility, Raleigh, NC, USA, 4–8 August 2014; pp. 44–47. [Google Scholar] [CrossRef]
- Liu, X.Q.; Li, Y.H.; Min, L.; Ping, H. The Design and Manufacture of the Wireless Power Transmission System in the Cardiac Pacemaker. Appl. Mech. Mater. 2014, 596, 100–103. [Google Scholar] [CrossRef]
- Ryu, H.; Park, H.-M.; Kim, M.-K.; Kim, B.; Myoung, H.S.; Kim, T.Y.; Yoon, H.-J.; Kwak, S.S.; Kim, J.; Hwang, T.H.; et al. Self-rechargeable cardiac pacemaker system with triboelectric nanogenerators. Nat. Commun. 2021, 12, 4374. [Google Scholar] [CrossRef] [PubMed]
- Rao, S.; Chiao, J.-C. Body Electric: Wireless Power Transfer for Implant Applications. IEEE Microw. Mag. 2015, 16, 54–64. [Google Scholar] [CrossRef]
- Zurbuchen, A.; Haeberlin, A.; Pfenniger, A.; Bereuter, L.; Schaerer, J.; Jutzi, F.; Huber, C.; Fuhrer, J.; Vogel, R. Towards Batteryless Cardiac Implantable Electronic Devices—The Swiss Way. IEEE Trans. Biomed. Circuits Syst. 2017, 11, 78–86. [Google Scholar] [CrossRef]
- Kok, C.L.; Fu, X.; Koh, Y.Y.; Teo, T.H. A Novel Portable Solar Powered Wireless Charging Device. Electronics 2024, 13, 403. [Google Scholar] [CrossRef]
- Zhang, W.; Mi, C.C. Compensation Topologies of High-Power Wireless Power Transfer Systems. IEEE Trans. Veh. Technol. 2016, 65, 4768–4778. [Google Scholar] [CrossRef]
- Zhang, W.; Wong, S.-C.; Tse, C.K.; Chen, Q. Analysis and Comparison of Secondary Series- and Parallel-Compensated Inductive Power Transfer Systems Operating for Optimal Efficiency and Load-Independent Voltage-Transfer Ratio. IEEE Trans. Power Electron. 2014, 29, 2979–2990. [Google Scholar] [CrossRef]
- Xiao, C.; Wei, K.; Cheng, D.; Liu, Y. Wireless Charging System Considering Eddy Current in Cardiac Pacemaker Shell: Theoretical Modeling, Experiments, and Safety Simulations. IEEE Trans. Ind. Electron. 2017, 64, 3978–3988. [Google Scholar] [CrossRef]
- Shevchenko, V.; Husev, O.; Strzelecki, R.; Pakhaliuk, B.; Poliakov, N.; Strzelecka, N. Compensation Topologies in IPT Systems: Standards, Requirements, Classification, Analysis, Comparison and Application. IEEE Access 2019, 7, 120559–120580. [Google Scholar] [CrossRef]
- Fernandez, C.; Garcia, O.; Prieto, R.; Cobos, J.A.; Uceda, J. Overview of different alternatives for the contact-less transmission of energy. In Proceedings of the IEEE 2002 28th Annual Conference of the Industrial Electronics Society, IECON 02, Sevilla, Spain, 5–8 November 2002; IEEE: Piscataway, NJ, USA, 2002; pp. 1318–1323. [Google Scholar] [CrossRef]
- Hueros, V.; Barrado, A.; Fernández, C.; Mattavelli, P. Coupling and Load Estimation with Current and Voltage Primary Sensing in Free Communication Wireless Power Charging. In Proceedings of the IECON 2023-49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 16–19 October 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Poole, J.E.; Gleva, M.J.; Mela, T.; Chung, M.K.; Uslan, D.Z.; Borge, R.; Gottipaty, V.; Shinn, T.; Dan, D.; Feldman, L.A.; et al. Complication Rates Associated with Pacemaker or Implantable Cardioverter-Defibrillator Generator Replacements and Upgrade Procedures. Circulation 2010, 122, 1553–1561. [Google Scholar] [CrossRef]
- Mallela, V.S.; Ilankumaran, V.; Rao, N.S. Technical Series Trends in Cardiac Pacemaker Batteries. Indian Pacing Electrophysiol. J. 2004, 4, 201. [Google Scholar]
- Vulfin, V.; Sayfan-Altman, S.; Ianconescu, R. Wireless power transfer for a pacemaker application. J. Med. Eng. Technol. 2017, 41, 325–332. [Google Scholar] [CrossRef] [PubMed]
- Campi, T.; Cruciani, S.; De Santis, V.; Feliziani, M. EMF Safety and Thermal Aspects in a Pacemaker Equipped with a Wireless Power Transfer System Working at Low Frequency. IEEE Trans. Microw. Theory Tech. 2016, 64, 375–382. [Google Scholar] [CrossRef]
- Cetin, S.; Demirci, Y.E. High-efficiency LC-S compensated wireless power transfer charging converter for implantable pacemakers. Int. J. Circuit Theory Appl. 2022, 50, 122–134. [Google Scholar] [CrossRef]
- Arana, J.I.; Bodegas, A.; Sainz, I. Longevidad de los marcapasos. Cuad. Estimul. Card. 2011, 11, 29–32. Available online: https://secardiologia.es/images/stories/secciones/estimulacion/cuadernos-estimulacion/11/longevidad-de-los-marcapasos.pdf (accessed on 1 March 2025).
- Xiong, Q. Wireless Charging Device for Artificial Cardiac Pacemaker. In Proceedings of the 4th International Conference on Information Technology and Management Innovation, Shenzhen, China, 12–13 September 2015; Atlantis Press: Dordrecht, The Netherlands, 2015. [Google Scholar] [CrossRef]
- van Schuylenbergh, K.; Puers, R. Inductive Powering: Basic Theory and Application to Biomedical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Campi, T.; Cruciani, S.; Palandrani, F.; De Santis, V.; Hirata, A.; Feliziani, M. Wireless Power Transfer Charging System for AIMDs and Pacemakers. IEEE Trans. Microw. Theory Tech. 2016, 64, 633–642. [Google Scholar] [CrossRef]
- Haerinia, M.; Shadid, R. Wireless Power Transfer Approaches for Medical Implants: A Review. Signals 2020, 1, 209–229. [Google Scholar] [CrossRef]
- Bocan, K.N.; Mickle, M.H.; Sejdić, E. Multi-Disciplinary Challenges in Tissue Modeling for Wireless Electromagnetic Powering: A Review. IEEE Sens. J. 2017, 17, 6498–6509. [Google Scholar] [CrossRef]
- Shadid, R.; Haerinia, M.; Roy, S.; Noghanian, S. Hybrid inductive power transfer and wireless antenna system for biomedical implanted devices. Prog. Electromagn. Res. C 2018, 88, 77–88. [Google Scholar] [CrossRef]
- Xiao, C.; Cheng, D.; Wei, K. An LCC-C Compensated Wireless Charging System for Implantable Cardiac Pacemakers: Theory, Experiment, and Safety Evaluation. IEEE Trans. Power Electron. 2018, 33, 4894–4905. [Google Scholar] [CrossRef]
- Patil, D.; McDonough, M.K.; Miller, J.M.; Fahimi, B.; Balsara, P.T. Wireless Power Transfer for Vehicular Applications: Overview and Challenges. IEEE Trans. Transp. Electrif. 2018, 4, 3–37. [Google Scholar] [CrossRef]
- Zhao, Q.; Niu, S.; Shao, Z.; Jian, L. Hull-Compatible Underwater IPT System with Enhanced Electromagnetic–Thermal Performance for USVs. Energies 2025, 18, 237. [Google Scholar] [CrossRef]
- Enssle, A.; Parspour, N. Power Loss Shifted Design of Inductive Energy Transfer Systems. IEEE Open J. Power Electron. 2020, 1, 113–123. [Google Scholar] [CrossRef]
- Niu, S.; Lyu, R.; Lyu, J.; Chau, K.T.; Liu, W.; Jian, L. Optimal Resonant Condition for Maximum Output Power in Tightly Coupled WPT Systems Considering Harmonics. IEEE Trans. Power Electron. 2025, 40, 152–156. [Google Scholar] [CrossRef]




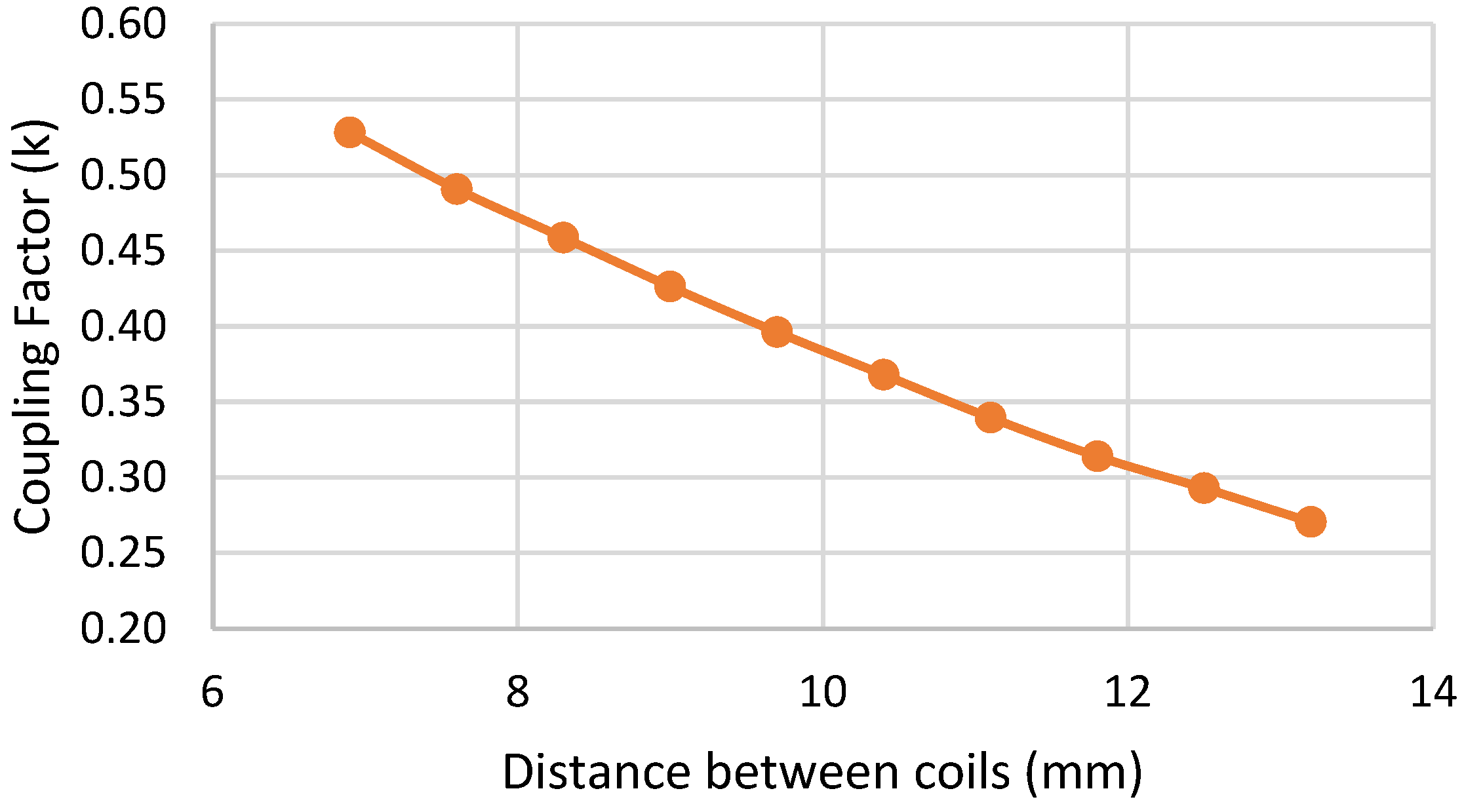

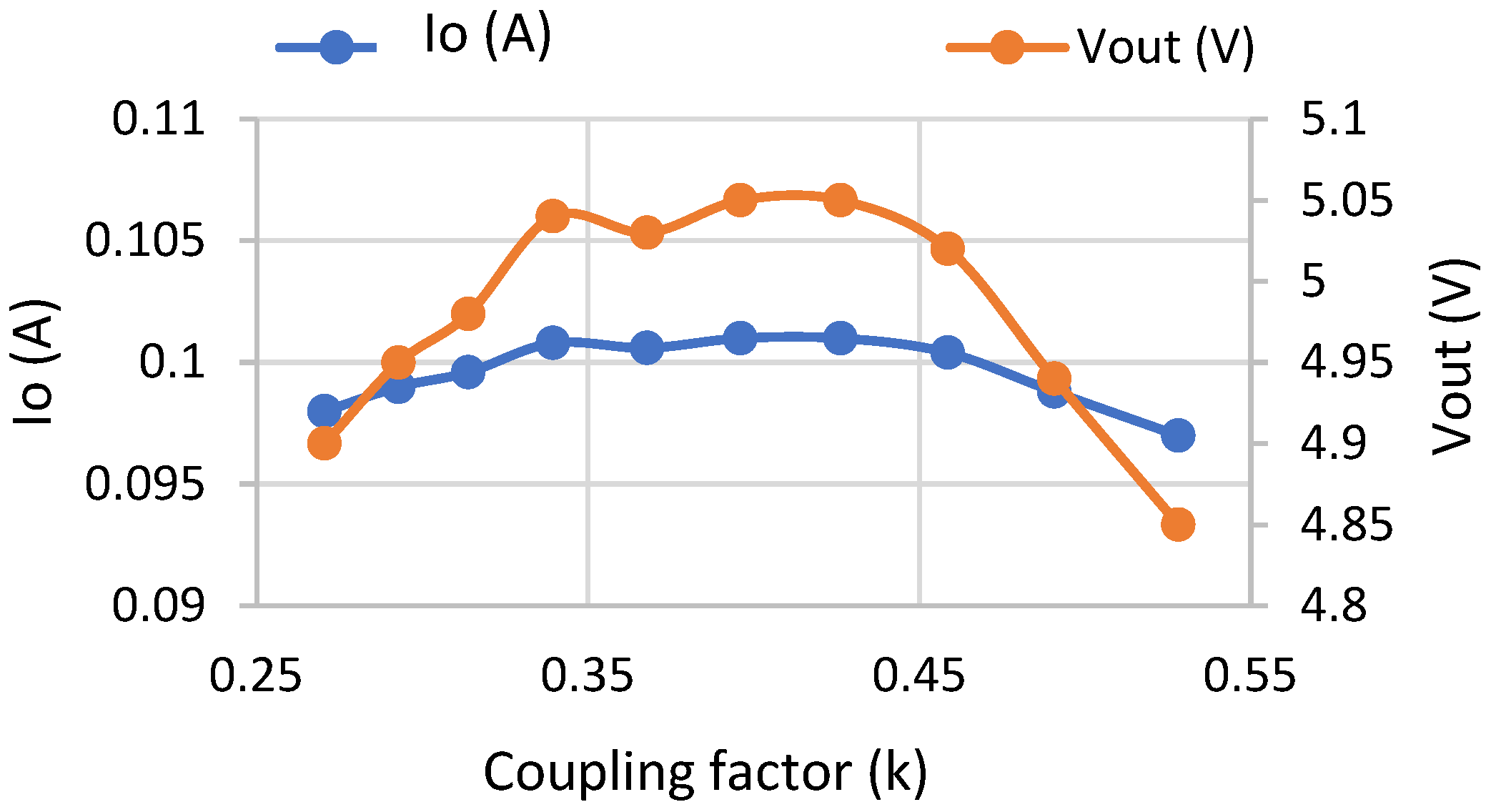

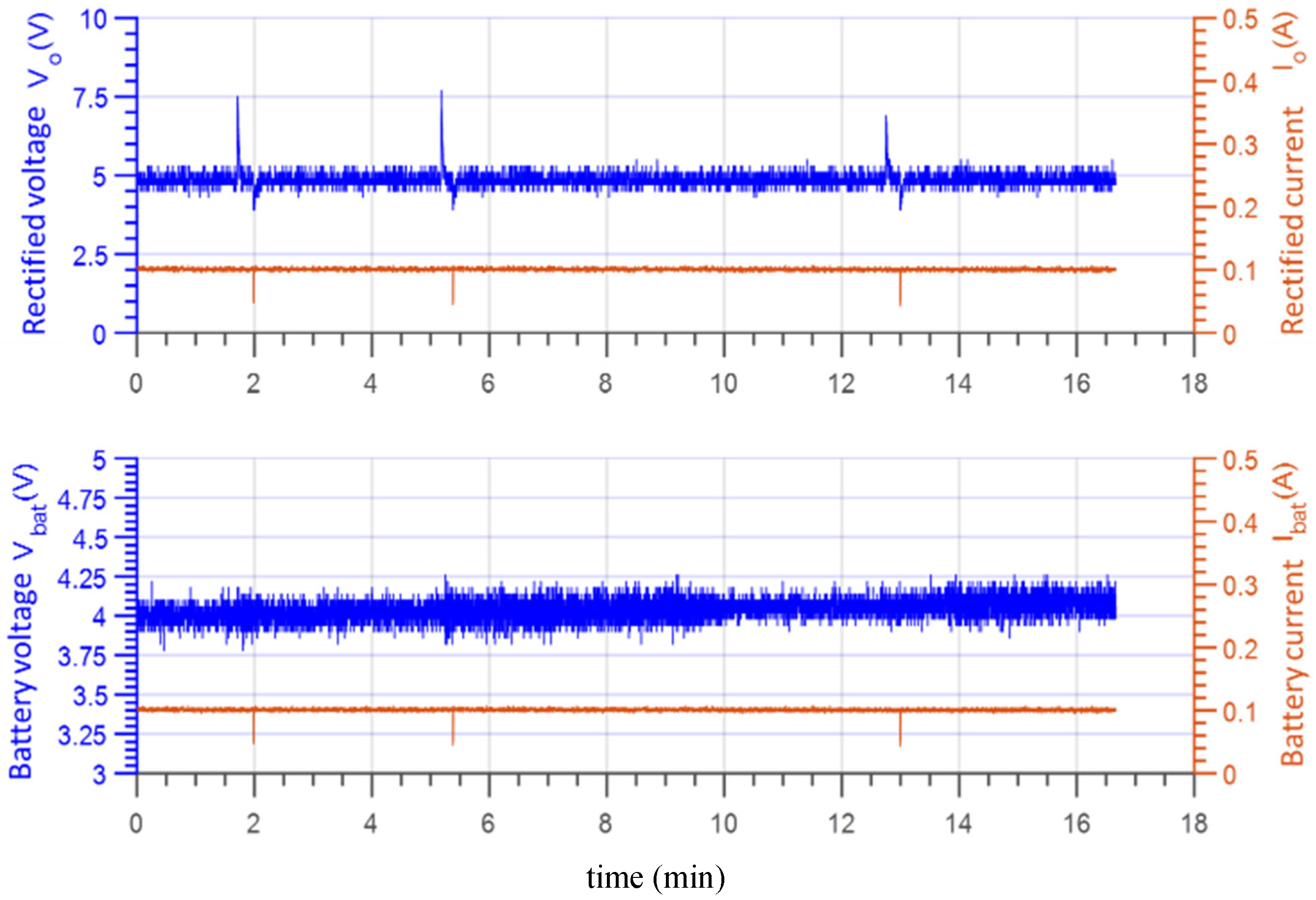
| M-Model | Series–Parallel |
|---|---|
| Parameters | Value | Unit |
|---|---|---|
| 500 | kHz | |
| 10 | µH | |
| 10 | µH | |
| 50 | mΩ | |
| 200 | mΩ | |
| 10 | nF | |
| 10 | nF | |
| 60 | Ω |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hueros, V.; Risquez, P.; Zumel, P.; Fernandez, C.; Barrado, A. Wireless Charger for Pacemakers Controlled from Primary Current Without Communication with Secondary Side. Electronics 2025, 14, 1563. https://doi.org/10.3390/electronics14081563
Hueros V, Risquez P, Zumel P, Fernandez C, Barrado A. Wireless Charger for Pacemakers Controlled from Primary Current Without Communication with Secondary Side. Electronics. 2025; 14(8):1563. https://doi.org/10.3390/electronics14081563
Chicago/Turabian StyleHueros, Victor, Pablo Risquez, Pablo Zumel, Cristina Fernandez, and Andrés Barrado. 2025. "Wireless Charger for Pacemakers Controlled from Primary Current Without Communication with Secondary Side" Electronics 14, no. 8: 1563. https://doi.org/10.3390/electronics14081563
APA StyleHueros, V., Risquez, P., Zumel, P., Fernandez, C., & Barrado, A. (2025). Wireless Charger for Pacemakers Controlled from Primary Current Without Communication with Secondary Side. Electronics, 14(8), 1563. https://doi.org/10.3390/electronics14081563






