An Integrated RF Sensor Design for Anchor-Free Collaborative Localization in GNSS-Denied Environments
Abstract
1. Introduction
1.1. Related Work
1.2. Motivation and Contributions
- In contrast to existing studies, we consider a more challenging but realistic unmanned vehicle system collaborative localization scenario in a GNSS-denied environment, where each unmanned vehicle is equipped with a multifunctional integrated RF sensor to achieve target position awareness through a hybrid AOA/TOA measurement approach.
- To achieve high-precision real-time positioning, we present a novel anchor-free positioning scheme that fully utilizes dual-channel sensor communication and detection capabilities. First, based on inter-node communication, the LLCR algorithm, implemented using an FPGA logic array, is proposed to facilitate the position estimation of neighboring asynchronous nodes within nanosecond-level latency. Then, this paper introduces a dual-channel unambiguous analogous synthetic aperture radar (ASAR) azimuth measurement method. Finally, we realize the relative position estimation of neighboring nodes by organically fusing and aligning the azimuth data with the distance data.
- To better validate the performance of the proposed positioning algorithm in real-world scenarios, we selected a highly integrated, low-power dual-channel RF transceiver and designed the sensor based on the principles of hardware reuse and software-based sensing, maximizing hardware resource utilization while integrating the positioning algorithm, achieving the unification of communication and sensing functions. Through an efficient exchange of information with neighboring nodes, the sensor enables precise positional awareness of asynchronous collaborative nodes in GNSS-denied environments. Subsequently, we complete the development of two generations of prototypes.
- Both anechoic chamber tests and outdoor field experiments with unmanned vehicles demonstrate that our sensors can achieve high-precision relative position estimation between collaborative nodes, maintaining a positioning error within 0.4 m in GNSS-denied environments, strengthening the robustness of the unmanned vehicle collaborative positioning system while reducing infrastructure costs and system complexity for sensor localization.
2. Design of the Collaborative Relative Positioning Algorithm
2.1. FPGA-Based LLCR Algorithm
2.1.1. System Model
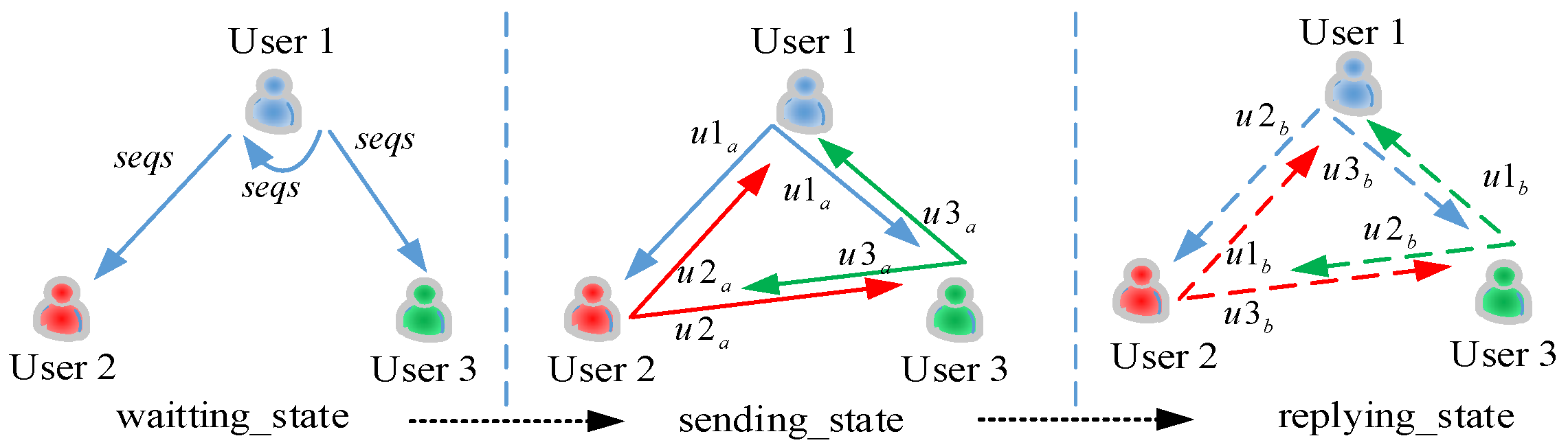
2.1.2. Measuring Demo with Three Nodes
2.1.3. Low-Latency Performance Modeling Analysis for Asynchronous Nodes
2.2. ASAR Azimuth Measurement Algorithm with No Ambiguity
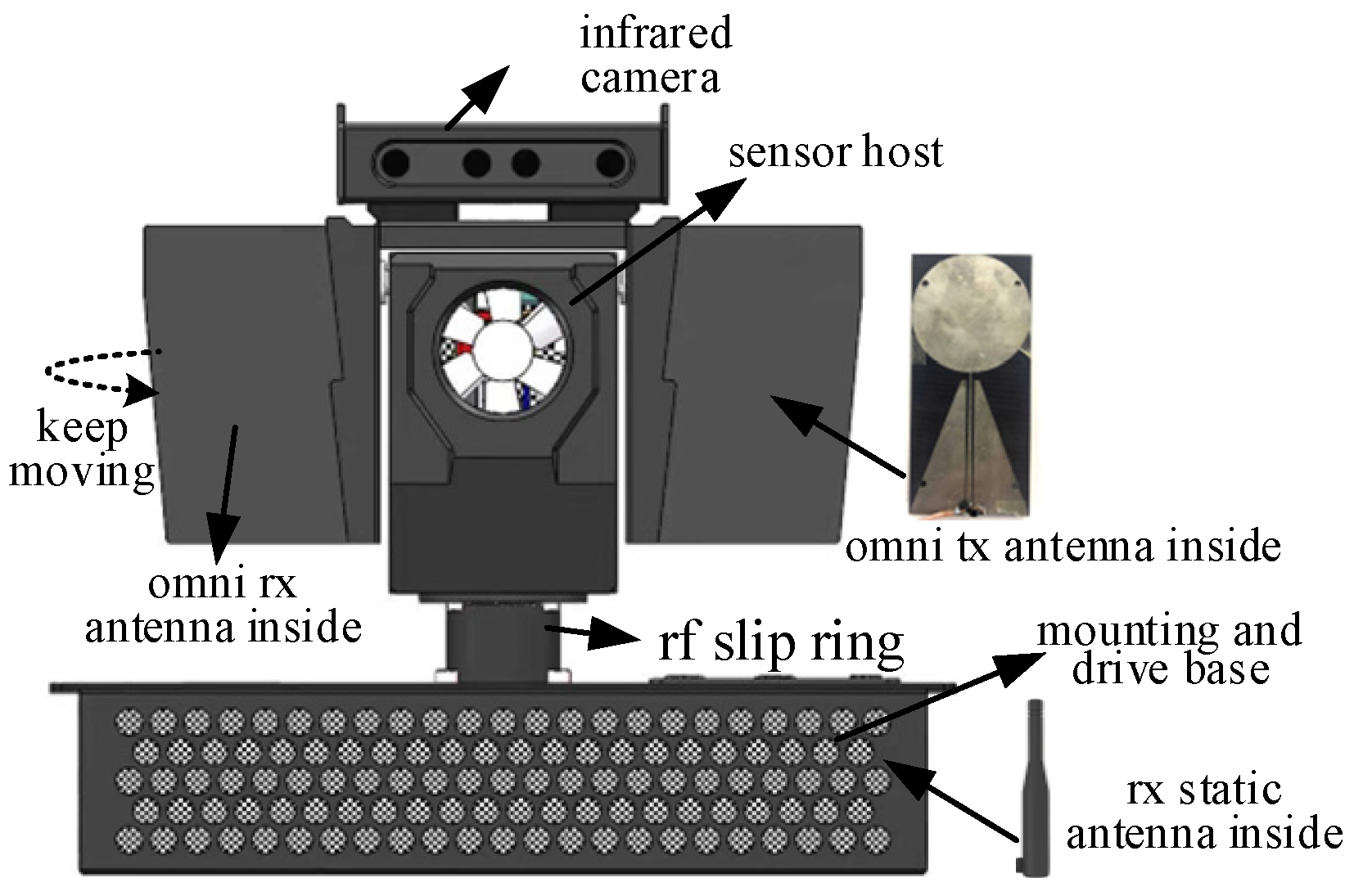
3. Design of the Sensor Hardware System
4. Experiments and Discussions
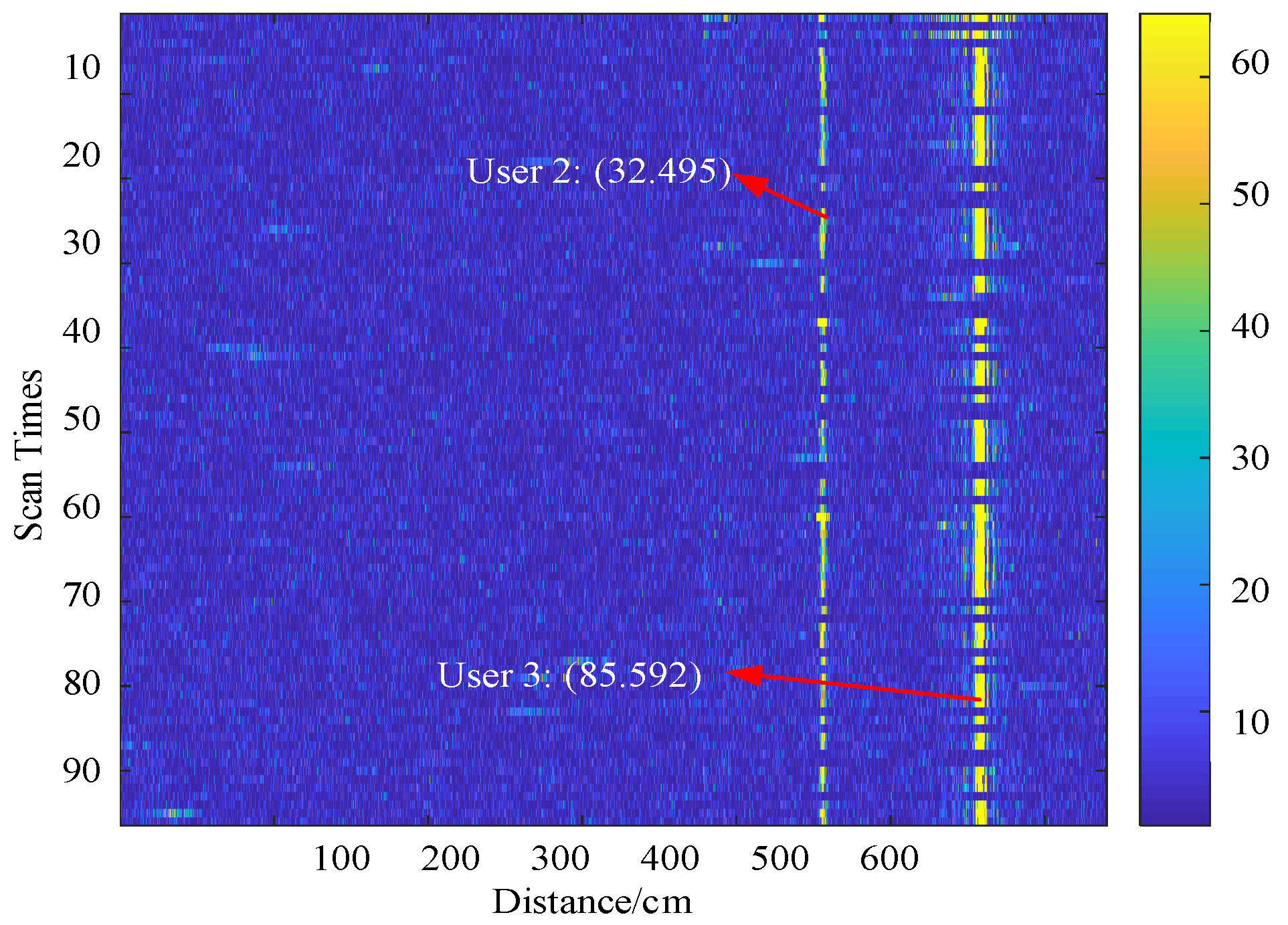
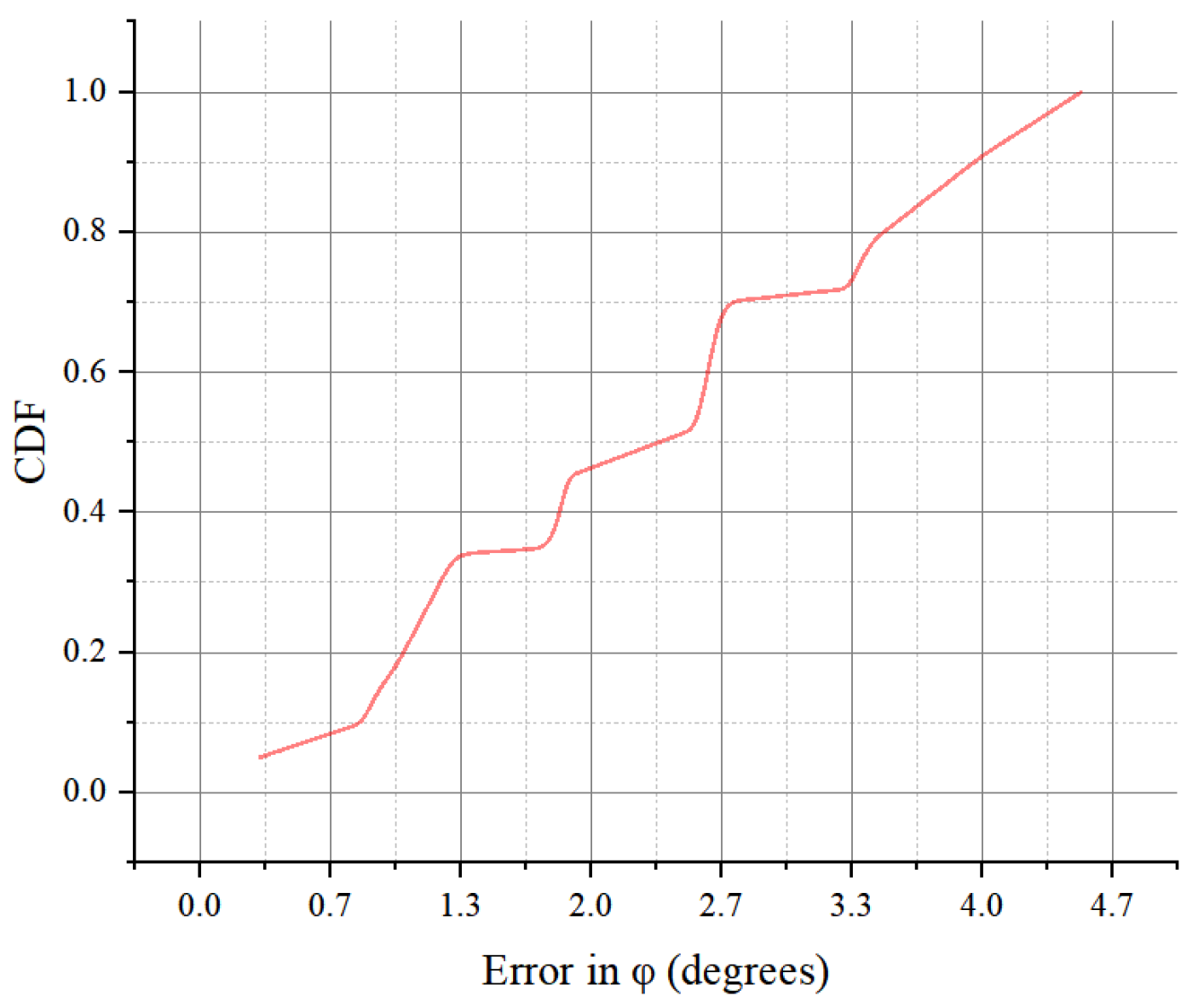
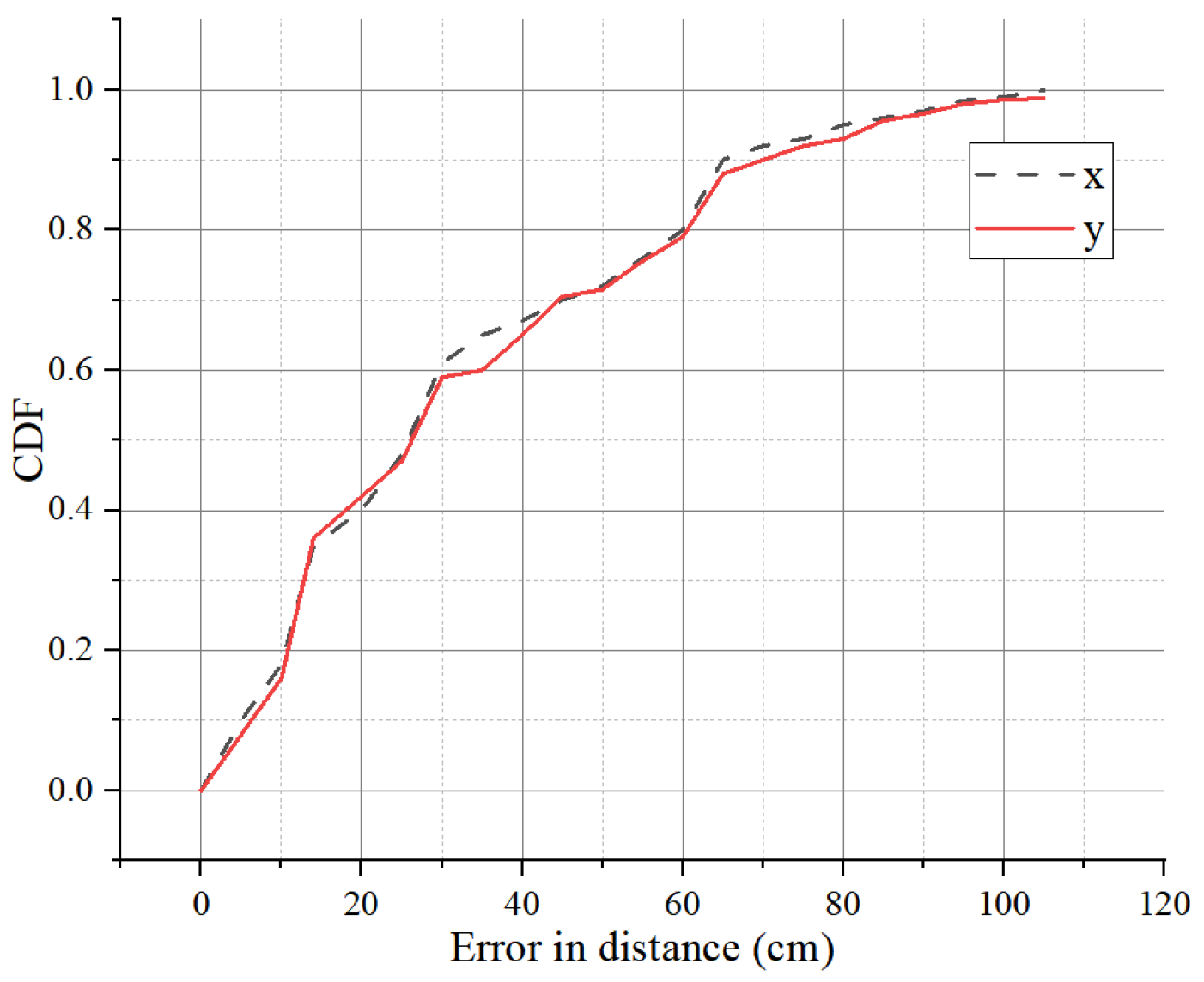
4.1. Microwave Anechoic Chamber Experiment
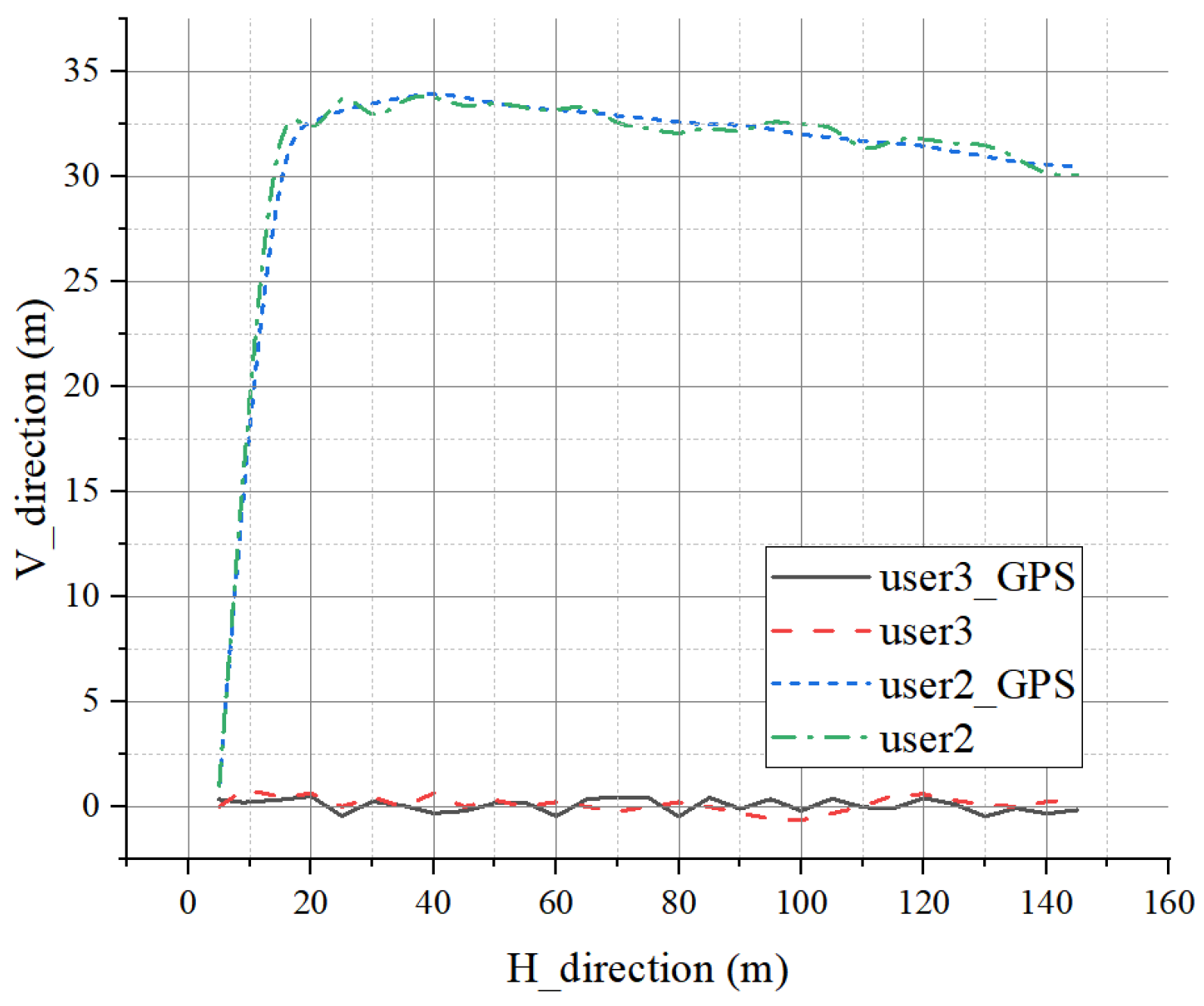
4.2. Field Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GNSS | Global navigation satellite system |
| RF | Radio frequency |
| FPGA | Field-programmable gate array |
| LLCR | Low-latency collaborative ranging |
| SoC | System-on-chip |
| AOA | Angle of arrival |
| RSS | Received signal strength |
| TOA | Time of arrival |
| TDOA | Time difference of arrival |
| RTT | Round-trip time |
| 3D | Three-dimensional |
| DTM | Digital terrain model |
| WSNs | Wireless sensor networks |
| SFO | Sunflower optimization algorithm |
| DV-Hop | Distance vector-hop |
| ASAR | Analogous synthetic aperture radar |
| 2D | Two-dimensional |
| IDs | Identifications |
| SNR | Signal-to-noise ratio |
| IP | Inter protocol |
| PS | Processing system |
| CFO | Carrier frequency offset |
| PL | Programmable logic |
| 4G | Fourth generation |
| MGC | Manual gain control |
| LoS | Line-of-sight |
| GPS | Global positioning system |
| NLOS | Non-line-of-sight |
| CDF | Cumulative distribution function |
References
- Win, M.Z.; Shen, Y.; Dai, W. A Theoretical Foundation of Network Localization and Navigation. Proc. IEEE 2018, 106, 1136–1165. [Google Scholar] [CrossRef]
- Dai, W.; Shen, Y.; Win, M.Z. Energy-Efficient Network Navigation Algorithms. IEEE J. Sel. Areas Commun. 2015, 33, 1418–1430. [Google Scholar] [CrossRef]
- Liu, Z.; Dai, W.; Win, M.Z. Mercury: An Infrastructure-Free System for Network Localization and Navigation. IEEE Trans. Mob. Comput. 2018, 17, 1119–1133. [Google Scholar] [CrossRef]
- Tian, X.; Song, Z.; Jing, B.; Zhang, Y.; Yu, T.; Wang, X. HiQuadLoc: A RSS Fingerprinting Based Indoor Localization System for Quadrotors. IEEE Trans. Mob. Comput. 2017, 16, 2545–2559. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, Y.; Lloret, J.; Kantarci, B.; Seah, W.K.G. A Localization Method Avoiding Flip Ambiguities for Micro-UAVs with Bounded Distance Measurement Errors. IEEE Trans. Mob. Comput. 2019, 18, 1718–1730. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Wang, J.; Shen, Y. Distributed 3D relative localization of UAVs. IEEE Trans. Veh. Technol. 2020, 69, 11756–11770. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Y.; Shen, Y. Cooperative Tracking by Multi-Agent Systems Using Signals of Opportunity. IEEE Trans. Commun. 2020, 68, 93–105. [Google Scholar] [CrossRef]
- Liu, J.; Hu, G. Relative Localization Estimation for Multiple Robots via the Rotating Ultra-Wideband Tag. IEEE Robot. Autom. Lett. 2023, 8, 4187–4194. [Google Scholar] [CrossRef]
- Cai, Y.; Shen, Y. An Integrated Localization and Control Framework for Multi-Agent Formation. IEEE Trans. Signal Process. 2019, 67, 1941–1956. [Google Scholar] [CrossRef]
- Li, X.; Ma, K.; Wang, J.; Shen, Y. An Integrated Design of Cooperative Localization and Motion Control. In Proceedings of the 2019 IEEE International Conference on Communications, Shanghai, China, 11–13 August 2019. [Google Scholar] [CrossRef]
- Li, X. Collaborative Localization with Received-Signal Strength in Wireless Sensor Networks. IEEE Trans. Veh. Technol. 2007, 56, 3807–3817. [Google Scholar] [CrossRef]
- Conti, A.; Guerra, M.; Dardari, D.; Decarli, N.; Win, M.Z. Network Experimentation for Cooperative Localization. IEEE J. Sel. Areas Commun. 2012, 30, 467–475. [Google Scholar] [CrossRef]
- Niculescu, D.; Nath, B. Ad Hoc Positioning System (APS) using AOA. In Proceedings of the Twenty-Second Annual Joint Conference of the IEEE Computer and Communications Societies, San Francisco, CA, USA, 30 March–3 April 2003. [Google Scholar] [CrossRef]
- Bartoletti, S.; Dai, W.; Conti, A.; Win, M.Z. A Mathematical Model for Wideband Ranging. IEEE J. Sel. Top. Signal Process. 2015, 9, 216–228. [Google Scholar] [CrossRef]
- Wennervirta, J.; Wigren, T. RTT Positioning Field Performance. IEEE Trans. Veh. Technol. 2010, 59, 3656–3661. [Google Scholar] [CrossRef]
- Tan, A.H. A New Distance Metric Based on Bias-Variance Tradeoff for Wireless Fingerprinting. IEEE Trans. Instrum. Meas. 2024, 73, 2532710. [Google Scholar] [CrossRef]
- Hayward, S.J.; van Lopik, K.; Hinde, C.; West, A.A. A Survey of Indoor Location Technologies, Techniques and Applications in Industry. Internet Things 2022, 20, 100608. [Google Scholar] [CrossRef]
- Zaarour, N.; Hakem, N.; Kandil, N. An Accurate Anchor-Free Contextual Received Signal Strength Approach Localization in a Wireless Sensor Network. Sensors 2024, 24, 1210. [Google Scholar] [CrossRef]
- Li, X.; Ban, B.; Yang, Y.; Jin, M. Localization of Networks on 3D Terrain Surfaces. IEEE Trans. Mob. Comput. 2022, 21, 1710–1722. [Google Scholar] [CrossRef]
- Rayavarapu, V.C.S.R.; Mahapatro, A. A Novel Range-Free Anchor-Free Localization in WSN Using Sun Flower Optimization Algorithm. In Proceedings of the 2021 Advanced Communication Technologies and Signal Processing (ACTS), Rourkela, India, 15–17 December 2021. [Google Scholar] [CrossRef]
- Aka, A.C.; Atta, A.F.; Keupondjo, S.G.A.; Oumtanaga, S. An Efficient Anchor-Free Localization Algorithm for all Cluster Topologies in a Wireless Sensor Network. Int. J. Comput. Commun. Control 2023, 18, 4961. [Google Scholar] [CrossRef]
- Shah, I.; Dohare, Y.; Yadav, D. A Modified Anchor Free Localization Technique for Wireless Sensor Network. EAI Endorsed Trans. Cloud Syst. 2020, 6, 166553. [Google Scholar] [CrossRef]
- He, W.; Cheng, R.; Mao, K.; Yan, K.; Wei, J.; Xu, Y. A Novel Anchorless Node Positioning Method for Wireless Sensor Network. J. Sens. 2022, 2022, 5385393. [Google Scholar] [CrossRef]
- IEEE 802.15.4a; IEEE Standard for Local and Metropolitan Area Networks—Part 15.4: Low-Rate Wireless Personal Area Networks (LR-WPANs)—Physical Layer (PHY) Specifications for Ultra Wideband (UWB). IEEE: New York, NY, USA, 2007. [CrossRef]
- Li, Y.; Zhang, Z.; Wu, L.; Dang, J.; Liu, P. 5G Communication Signal Based Localization with a Single Base Station. In Proceedings of the 2020 IEEE 92nd Vehicular Technology Conference, Victoria, BC, Canada, 4–7 October 2020. [Google Scholar] [CrossRef]
- Wang, W.; Yan, S.; Mao, L.; Guo, X. Robust Minimum Variance Beamforming with Sidelobe-Level Control Using the Alternating Direction Method of Multipliers. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3506–3519. [Google Scholar] [CrossRef]
- Zhao, C.; Chen, Z.; He, C.; Xie, F.; Chen, X. A Hybrid Beam-Forming and Direction-Finding Method for Wind Direction Sensing Based on HF Radar. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6622–6629. [Google Scholar] [CrossRef]
- Kim, J.S.; Lee, J.; Serpedin, E.; Qaraqe, K. Robust Clock Synchronization in Wireless Sensor Networks through Noise Density Estimation. IEEE Trans. Signal Process. 2011, 59, 3035–3047. [Google Scholar] [CrossRef]
- Mao, F.; Ma, H.; Jiao, Y.; Li, D.; Gao, Z. Analysis of the Research Status of Phase Interferometer Deblurring. In Proceedings of the 2021 IEEE International Conference on Artificial Intelligence and Industrial Design, Guangzhou, China, 28–30 May 2021. [Google Scholar] [CrossRef]
- Lu, L.; Li, Y.; Rizos, C. Virtual Baseline Method for Beidou Attitude Determination—An Improved Long-short Baseline Ambiguity Resolution Method. Adv. Space Res. 2013, 51, 1029–1034. [Google Scholar] [CrossRef]
- Li, Y.; Zou, X.; Liu, P.; Luo, B.; Pan, W.; Yan, L. Four-Element Array for GNSS Attitude Determination Using IRLS: An Improved Rounding of Long-Short Baseline Approach. IEEE Trans. Veh. Technol. 2020, 69, 4920–4934. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, D.; Li, X.; Zhou, L.; Yang, C.; Cui, Y.; Bai, L.; Chen, Y. An Integrated RF Sensor Design for Anchor-Free Collaborative Localization in GNSS-Denied Environments. Electronics 2025, 14, 1667. https://doi.org/10.3390/electronics14081667
Bai D, Li X, Zhou L, Yang C, Cui Y, Bai L, Chen Y. An Integrated RF Sensor Design for Anchor-Free Collaborative Localization in GNSS-Denied Environments. Electronics. 2025; 14(8):1667. https://doi.org/10.3390/electronics14081667
Chicago/Turabian StyleBai, Di, Xinran Li, Lingyun Zhou, Chunyong Yang, Yongqiang Cui, Liyun Bai, and Yunhao Chen. 2025. "An Integrated RF Sensor Design for Anchor-Free Collaborative Localization in GNSS-Denied Environments" Electronics 14, no. 8: 1667. https://doi.org/10.3390/electronics14081667
APA StyleBai, D., Li, X., Zhou, L., Yang, C., Cui, Y., Bai, L., & Chen, Y. (2025). An Integrated RF Sensor Design for Anchor-Free Collaborative Localization in GNSS-Denied Environments. Electronics, 14(8), 1667. https://doi.org/10.3390/electronics14081667




