Optimal Design of Resonant Network for 800 V Class 11.1 kW Wireless Power Transfer System with Double-Sided LCC Compensation Circuit
Abstract
:1. Introduction
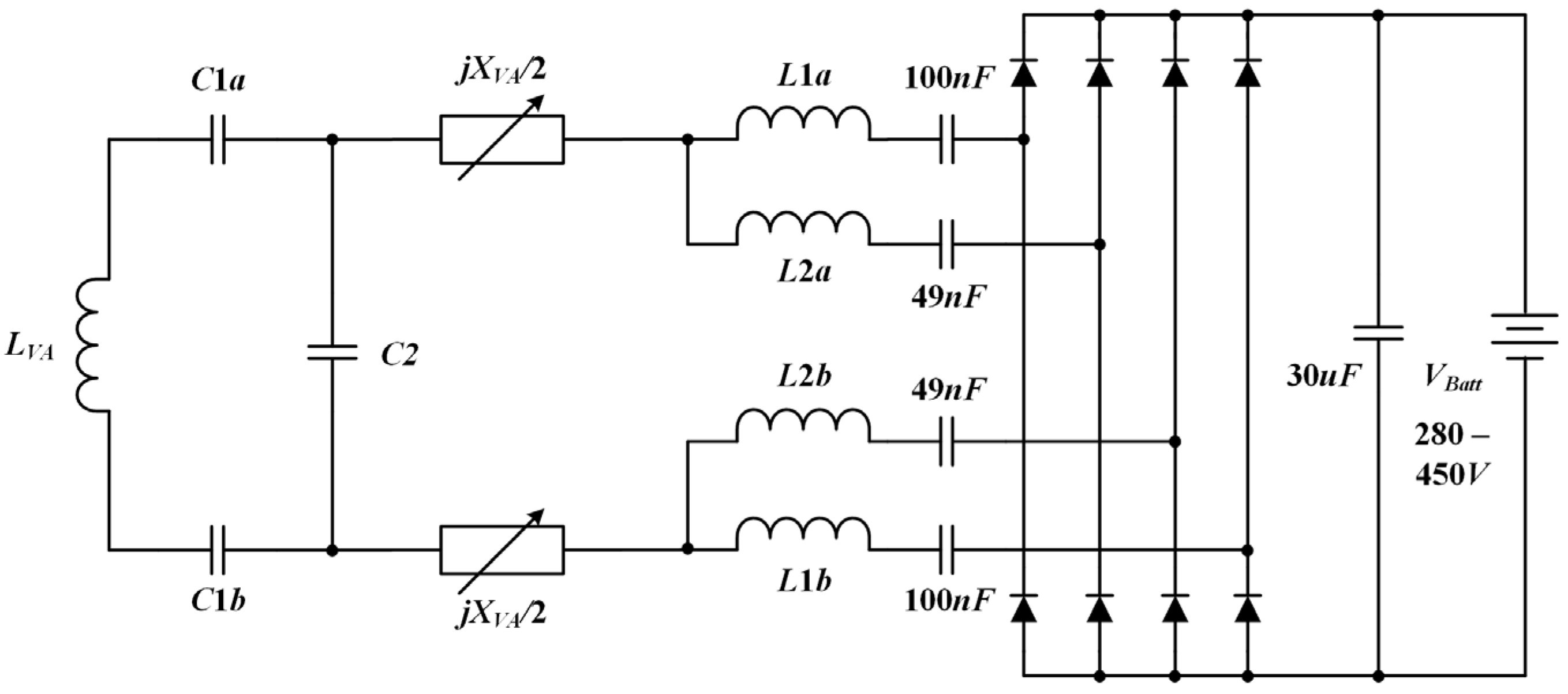
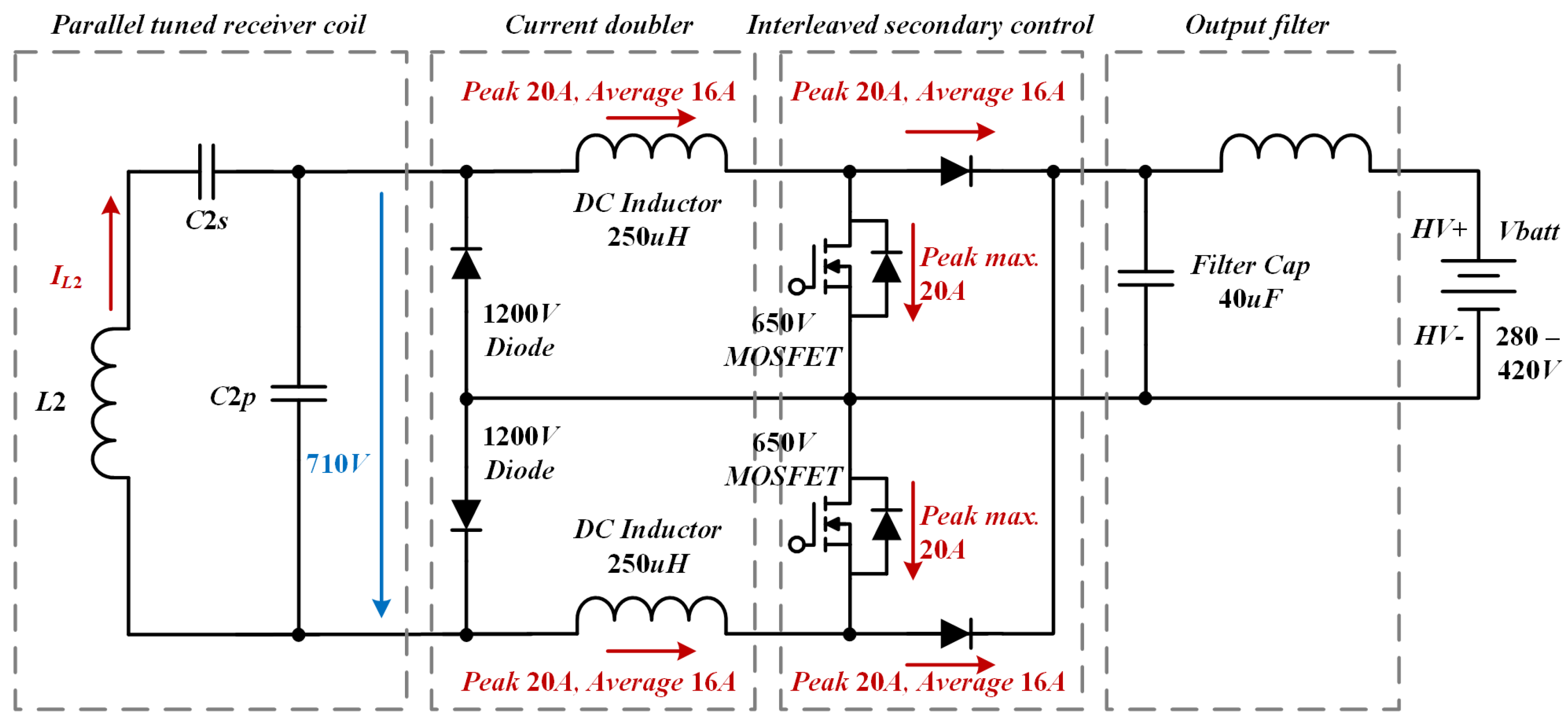
2. WPT for 400 V Class Battery Applications
- Output Voltage Limitations: The prescribed voltage ranges are insufficient to meet the requirements of 800 V battery packs.
- Excessive Component Stress: Even if the target charging voltage is achieved, the voltage and current stresses on the compensation circuit components (inductors and capacitors) become high, complicating practical implementation.
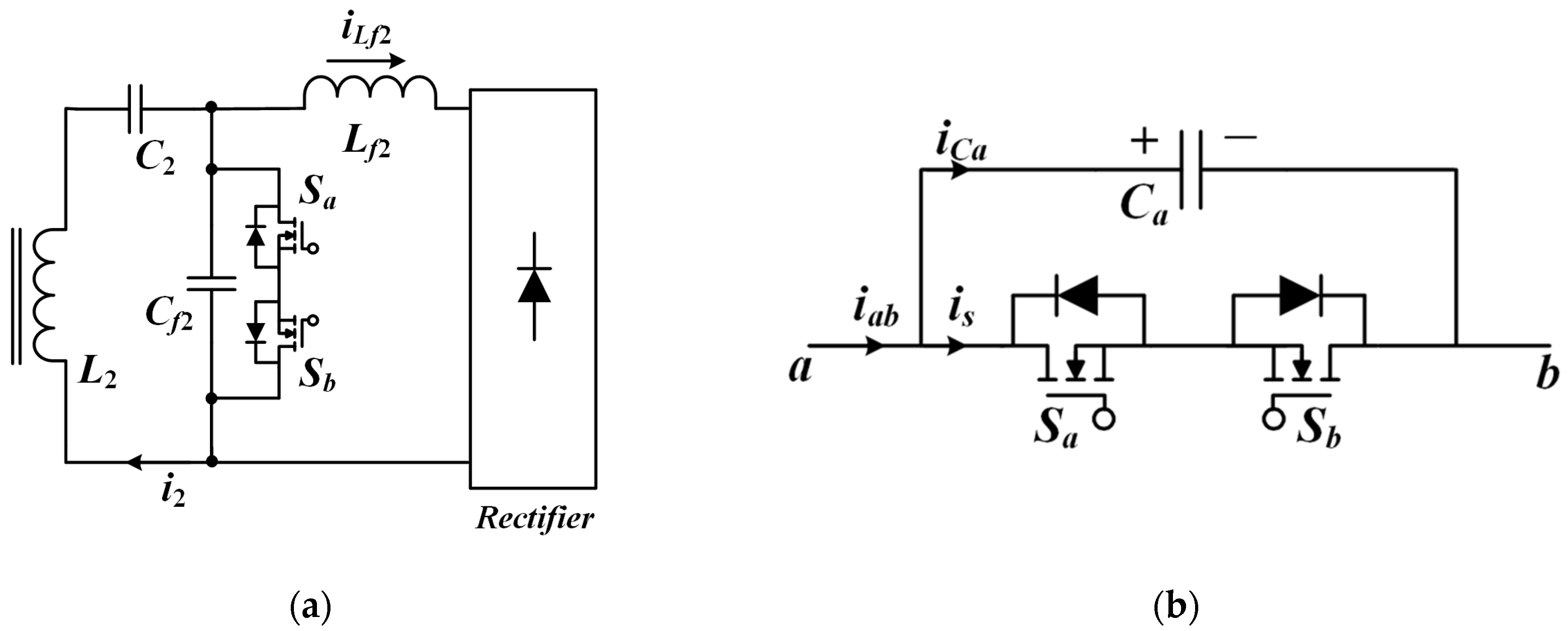
3. Double-Sided LCC Compensation WPT System
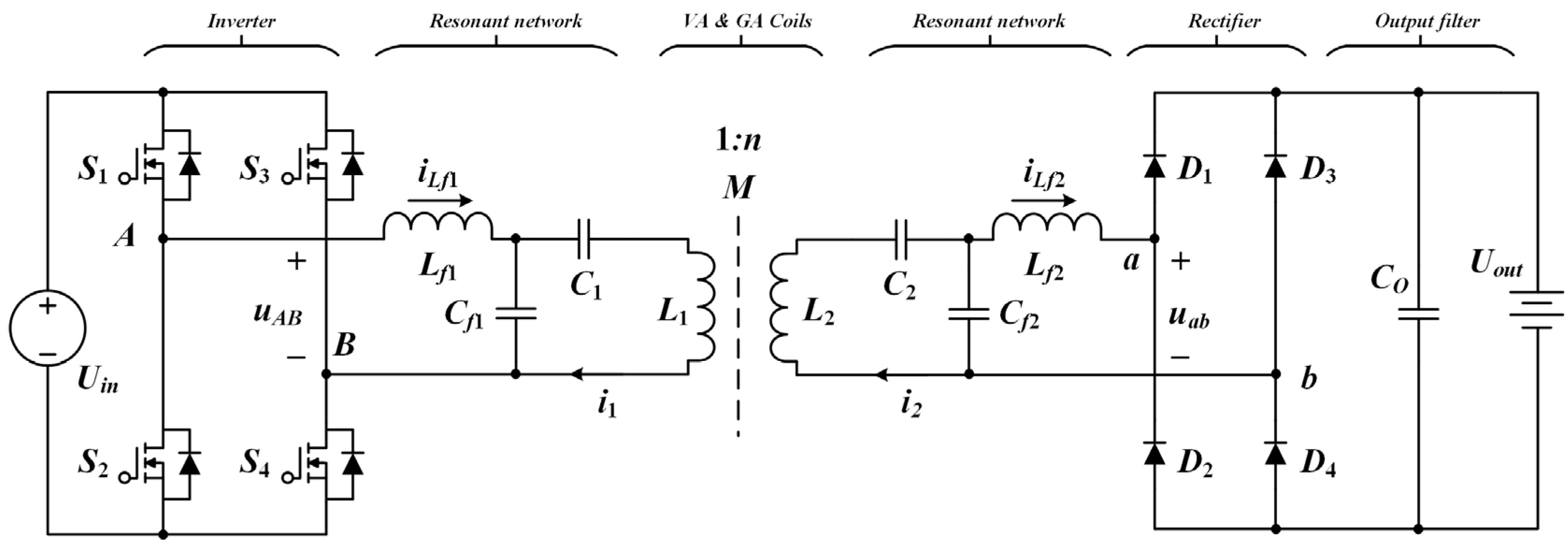
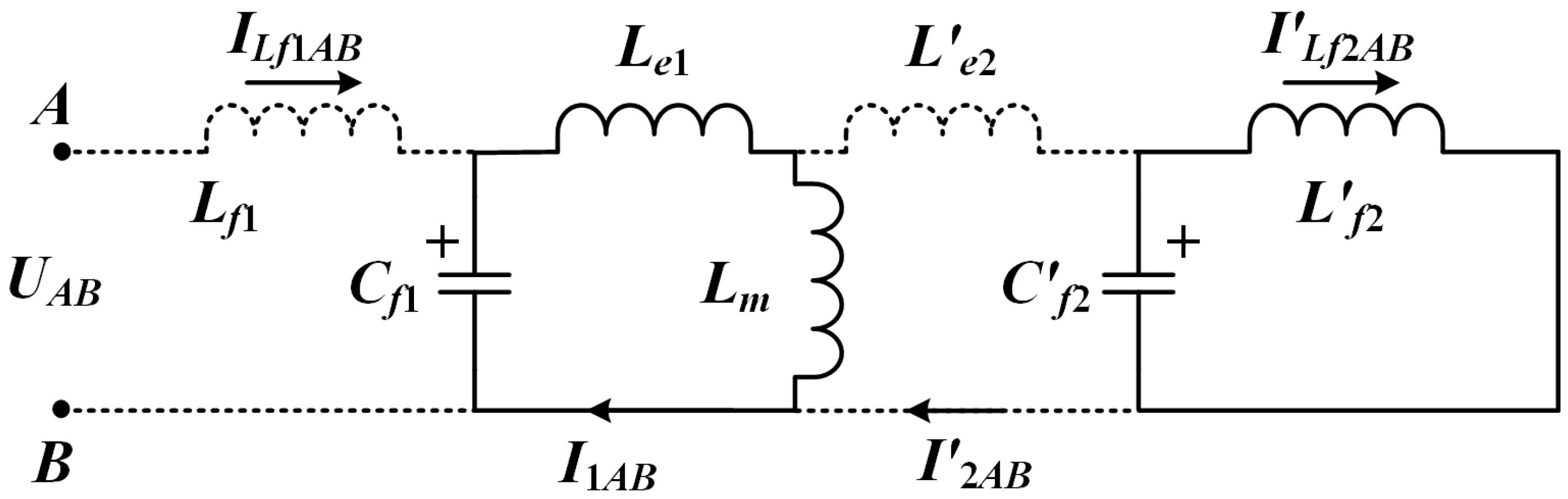
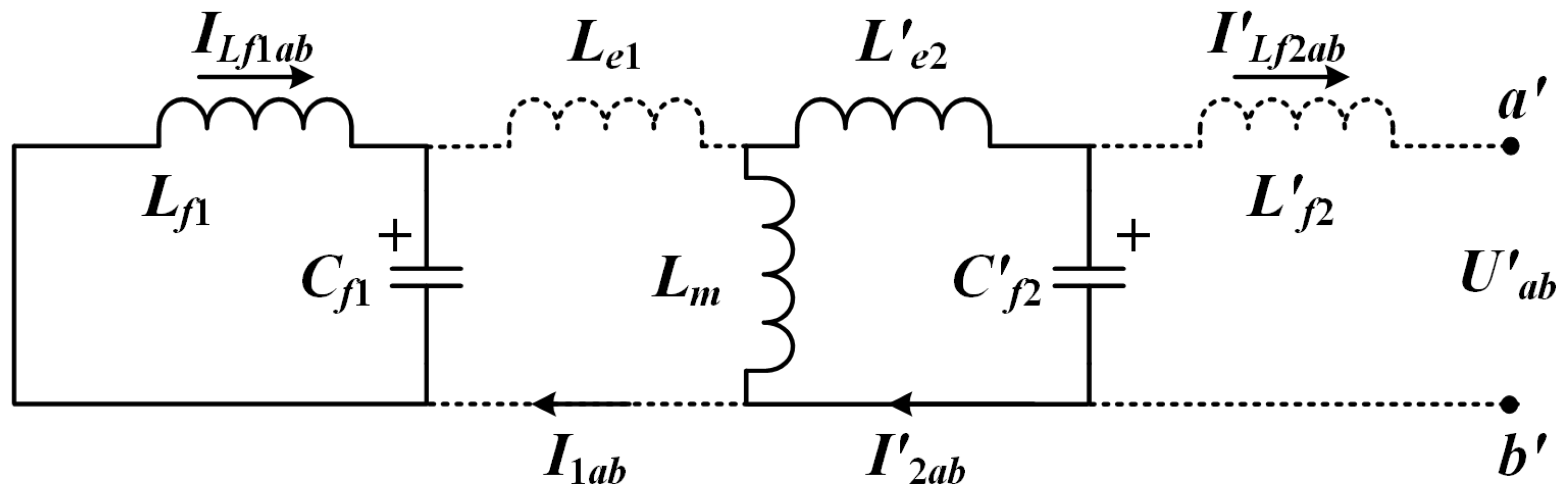
3.1. System Configuration and Modeling
3.2. Optimal Design of Resonant Network
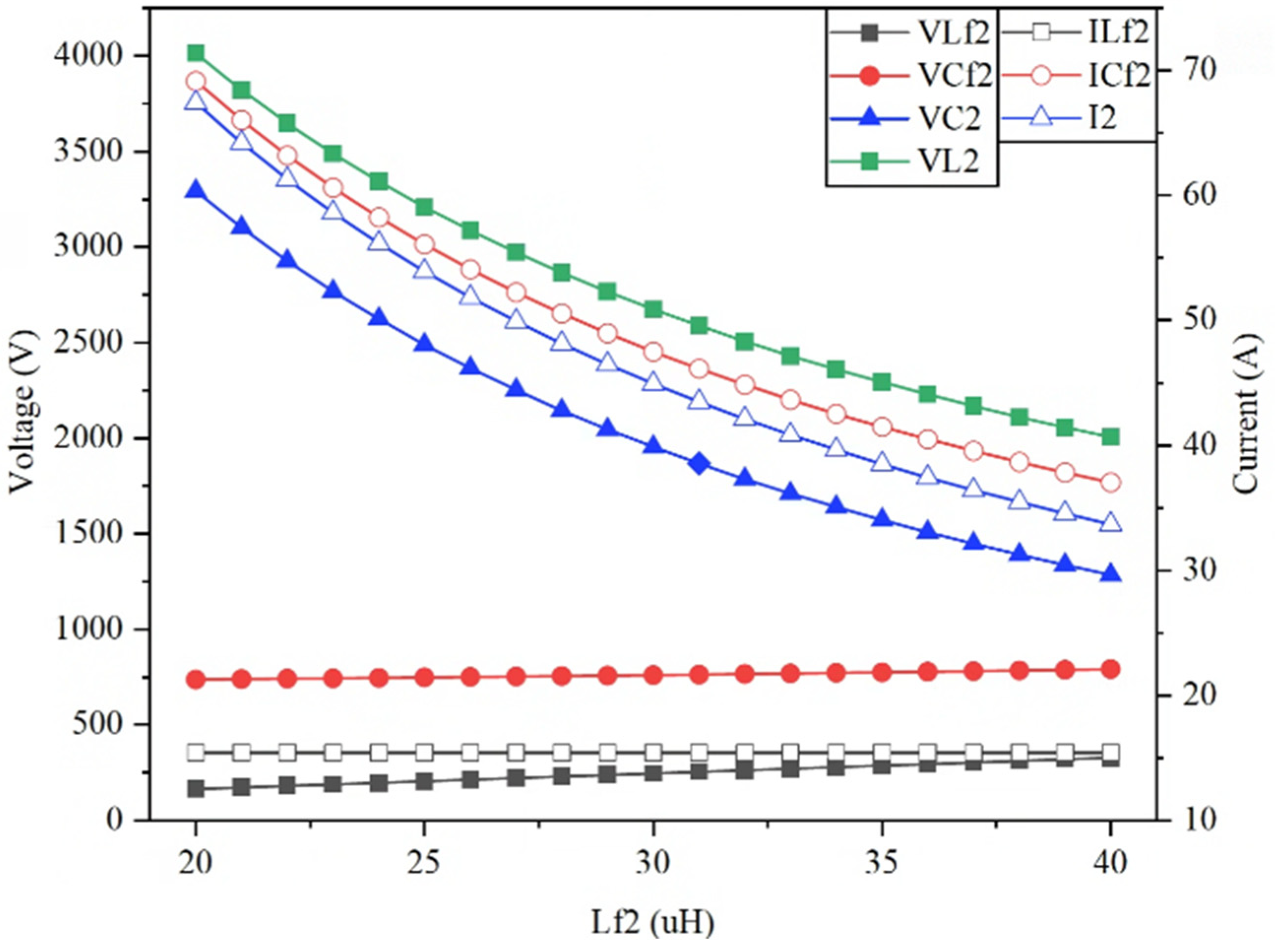
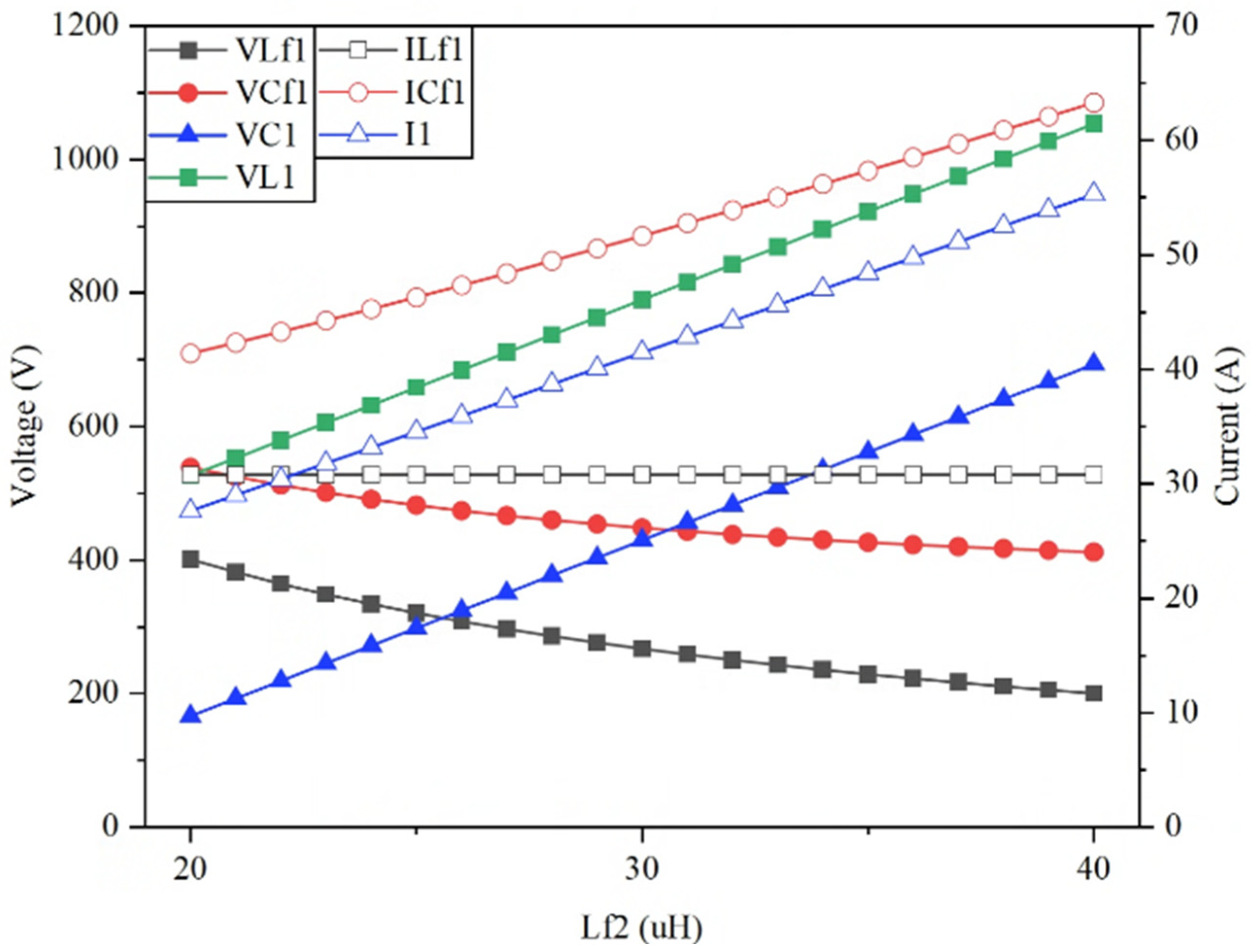
4. Simulation and Experiment Results
4.1. Simulation Results
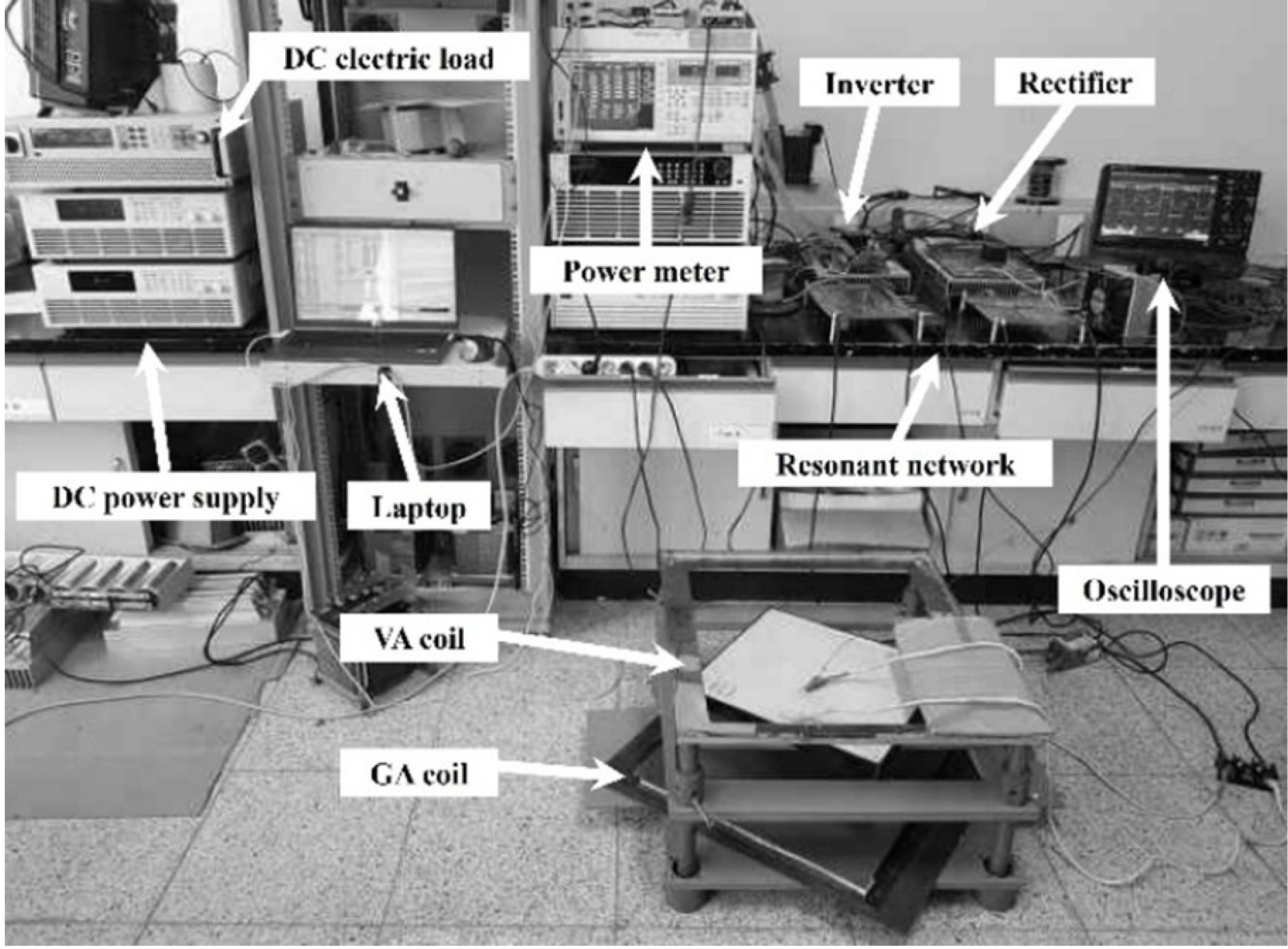
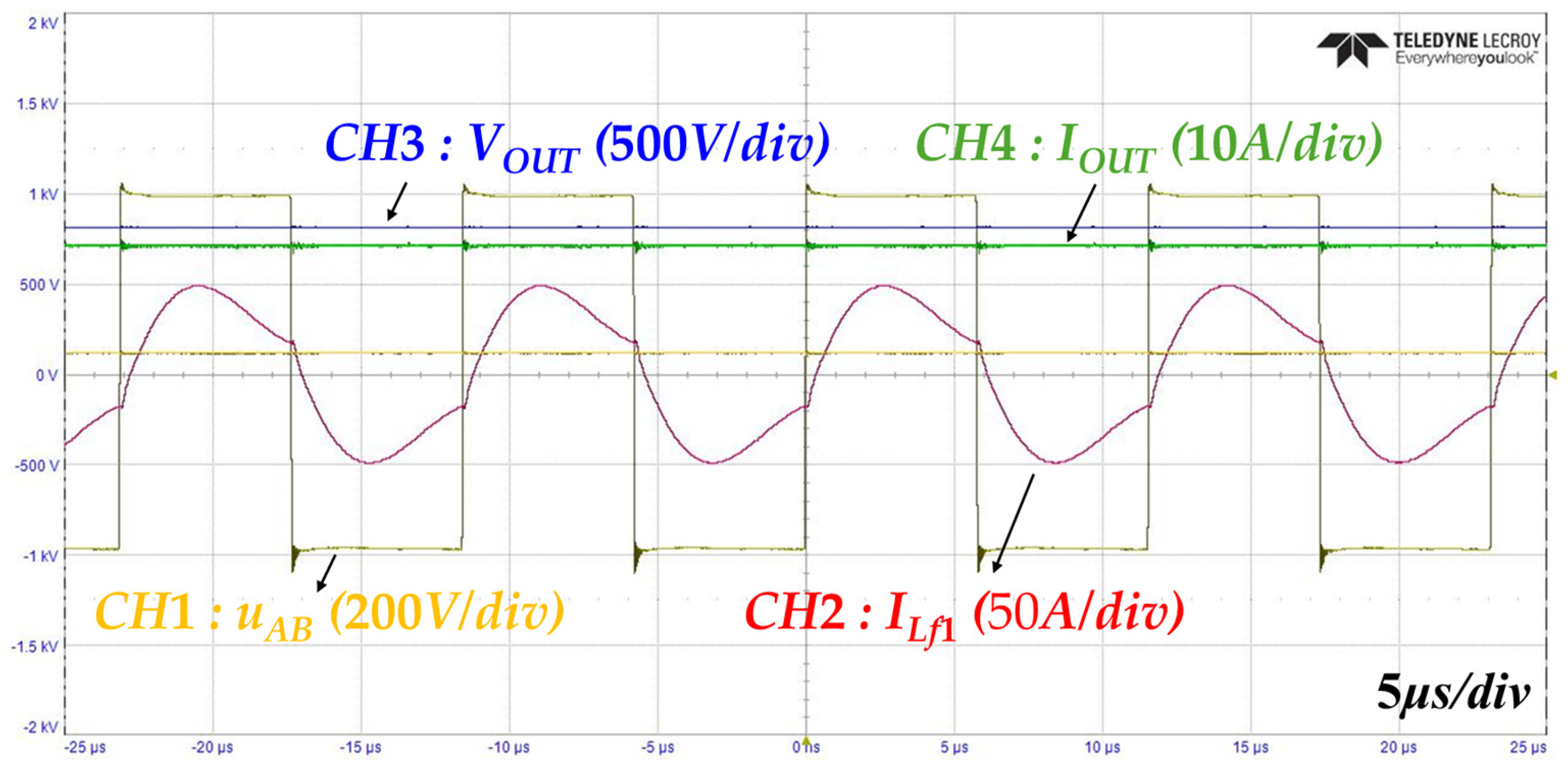
4.2. Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Okasili, I.; Elkhateb, A.; Littler, T. A Review of Wireless Power Transfer Systems for Electric Vehicle Battery Charging with a Focus on Inductive Coupling. Electronics 2022, 11, 1355. [Google Scholar] [CrossRef]
- Zhang, Z.; Pang, H.; Lee, C.H.T.; Xu, X.; Wei, X.; Wang, J. Comparative Analysis and Optimization of Dynamic Charging Coils for Roadway-Powered Electric Vehicles. IEEE Trans. Magn. 2017, 53, 9402106. [Google Scholar] [CrossRef]
- Fareq, M.; Fitra, M.; Irwanto, M.; Hasan, S.; Arinal, M. Low Wireless Power Transfer Using Inductive Coupling for Mobile Phone Charger. J. Phys. Conf. Ser. 2014, 495, 012019. [Google Scholar] [CrossRef]
- SAE Standard J2954; Wireless Power Transfer for Light-Duty Plug-In/Electric Vehicles and Alignment Methodology. SAE International: Warrendale, PA, USA, 2020.
- Wang, M.; Li, Y.; Zhang, W. Transitioning from 400 V to 800 V Battery Architectures for Enhanced Electric Vehicle Performance. IEEE Trans. Veh. Technol. 2020, 69, 1234–1242. [Google Scholar]
- Patel, S.; Kumar, D. Advantages of High-Voltage (800 V) Systems in Modern Electric Vehicles. In Proceedings of the IEEE International Conference on EV Technology, Online, 24–26 May 2021; pp. 45–50. [Google Scholar]
- Grazian, F.; Soeiro, T.B.; Bauer, P. Voltage/Current Doubler Converter for an Efficient Wireless Charging of Electric Vehicles with 400-V and 800-V Battery Voltages. IEEE Trans. Ind. Electron. 2023, 70, 7891–7903. [Google Scholar] [CrossRef]
- Vaddemani, G.P.R.; Karneddi, H.; Ronanki, D. A Single-Stage Reconfigurable Wireless Charger for 400-V and 800-V Electric Vehicle Battery Voltages. In Proceedings of the 2024 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 25–29 February 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1181–1186. [Google Scholar] [CrossRef]
- Allali, N. Enhancing Wireless Charging for Electric Vehicles: Active Load Impedance Matching and Its Impact on Efficiency, Cost and Size. Electronics 2024, 13, 2720. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, Y.; Zhu, C.; Sahoo, S.; Chen, Y.; Mai, R.; He, Z.; Blaabjerg, F. A Design Method to Minimize Detuning for Double-Sided LCC -Compensated IPT System Improving Efficiency Versus Air Gap Variation. IEEE Trans. Power Electron. 2024, 39, 1723–1737. [Google Scholar] [CrossRef]
- Gaona, D.E.; Jiang, C.; Long, T. Highly Efficient 11.1-kW Wireless Power Transfer Utilizing Nanocrystalline Ribbon Cores. IEEE Trans. Power Electron. 2021, 36, 9955–9969. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, C.Q.; Chen, C.; Wang, X.; Li, X.; Long, T. Design and Analysis of Inductive Power Transfer System Using Nanocrystalline Flake Ribbon Core. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 3334–3347. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, C.; Dou, R.; Liu, S.; Zhao, L.; Zhang, P.; Yang, Q. Ferrite Pads Gap Thermal-Magnetic Evaluation and Mitigation for 11.1 kW Wireless Power Transfer. IEEE Trans. Magn. 2023, 59, 8600806. [Google Scholar] [CrossRef]
- Mohamed, A.A.S.; Shaier, A.A.; Metwally, H.; Selem, S.I. Interoperability of the universal WPT3 transmitter with different receivers for electric vehicle inductive charger. eTransportation 2020, 6, 100084. [Google Scholar] [CrossRef]
- Herceg, D.; Rajs, V.; Despotović, Ž.; Popadić, B.; Šiljegović, M.; Kiraly, Z.; Vizvari, Z.; Wizner, K.; Felde, I.; Odry, P.; et al. Double-Layer Coils Design for 11 kW Wireless Power Transfer. Electronics 2024, 13, 547. [Google Scholar] [CrossRef]
- Niu, S.; Zhao, Q.; Niu, S.; Jian, L. A Comprehensive Investigation of Thermal Risks in Wireless EV Chargers Considering Spatial Misalignment From a Dynamic Perspective. IEEE J. Emerg. Sel. Top. Ind. Electron. 2024, 5, 1560–1571. [Google Scholar] [CrossRef]
- Rajamanickam, N.; Abraham, D.S.; Alroobaea, R.; Abdelfattah, W.M. Foreign Object Debris Detection on Wireless Electric Vehicle Charging Pad Using Machine Learning Approach. Processes 2024, 12, 1574. [Google Scholar] [CrossRef]
- Niu, S.; Zhang, C.; Shi, Y.; Niu, S.; Jian, L. Foreign object detection considering misalignment effect for wireless EV charging system. ISA Trans. 2022, 130, 655–666. [Google Scholar] [CrossRef]
- Woo, D.-G. Optimal Design and Control Strategy of Inductive Power Transfer Charging System for Electric Vehicles. Ph.D. Thesis, Sungkyunkwan University, Seoul, Republic of Korea, 2015. [Google Scholar]
- Ahmed, M.; Salama, M.M.A.; Mohamed, A.A.S. A Review of Inductive Power Transfer: Emphasis on Performance Parameters, Compensation Topologies, and Coil Design Aspects. IEEE Access 2023, 11, 10868–10886. [Google Scholar] [CrossRef]
- Ahire, D.; Gond, V.; Chopade, J. Compensation Topologies for Wireless Power Transmission System in Medical Implant Applications: A Review. Mater. Today Proc. 2022, 49, 2758–2764. [Google Scholar] [CrossRef]
- Liu, Y. Compensation Topologies in Wireless Power Transfer Converters. Ph.D. Thesis, Department of Electronic and Information Engineering, Hong Kong Polytechnic University, Hong Kong, China, 2021. Available online: https://theses.lib.polyu.edu.hk/handle/200/11518 (accessed on 18 April 2025).
- Fu, M.; Tang, Z.; Ma, C. Analysis and Optimized Design of Compensation Capacitors for a Megahertz WPT System Using Full-Bridge Rectifier. IEEE Trans. Ind. Inform. 2019, 15, 95–104. [Google Scholar] [CrossRef]
- Niu, S.; Lyu, R.; Lyu, J.; Chau, K.T.; Liu, W.; Jian, L. Optimal Resonant Condition for Maximum Output Power in Tightly Coupled WPT Systems Considering Harmonics. IEEE Trans. Power Electron. 2025, 40, 152–156. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Zhang, W.; Ma, L.; Lu, G.; Cheng, K.W.E. Switched-capacitor-based adaptive tuning for wireless power transfer systems. IEEE Trans. Power Electron. 2021, 36, 7321–7332. [Google Scholar]
- Zhu, H.; Zhao, C.; Deng, J.; Cheng, K.W.E. A variable capacitance technique using switched capacitors for resonant wireless charging. IEEE Trans. Ind. Electron. 2020, 67, 7433–7442. [Google Scholar]
- Wang, Y.; Zhao, S.; Zhang, H.; Zhu, C.; Mei, Y.; Jiao, N.; Lu, F. Compact Z-Impedance Compensation for Inductive Power Transfer and its Capacitance Tuning Method. IEEE Trans. Ind. Electron. 2023, 70, 3627–3640. [Google Scholar] [CrossRef]
- Lu, J.; Zhu, G.; Lin, D.; Wong, S.C.; Jiang, J. Load-independent voltage and current transfer characteristics of high-order resonant network in IPT system. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 422–436. [Google Scholar] [CrossRef]
- Vu, V.B.; Tran, D.H.; Choi, W.J. Implementation of the constant current and constant voltage charge of inductive power transfer systems with the double-sided LCC compensation topology for electric vehicle battery charge applications. IEEE Trans. Power Electron. 2018, 33, 7398–7410. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, W.; Ye, L.; Guo, J.; Liu, K.; Do, H.T. A Design Method to Implement ZVS for Electric Vehicle Wireless Charging System With Double-Side LCC Compensation. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3791–3801. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Vu, V.-B.; Gohil, G.; Fahimi, B. Coil-to-Coil Efficiency Optimization of Double-Sided LCC Topology for Electric Vehicle Inductive Chargers. IEEE Trans. Ind. Electron. 2022, 69, 11242–11252. [Google Scholar] [CrossRef]


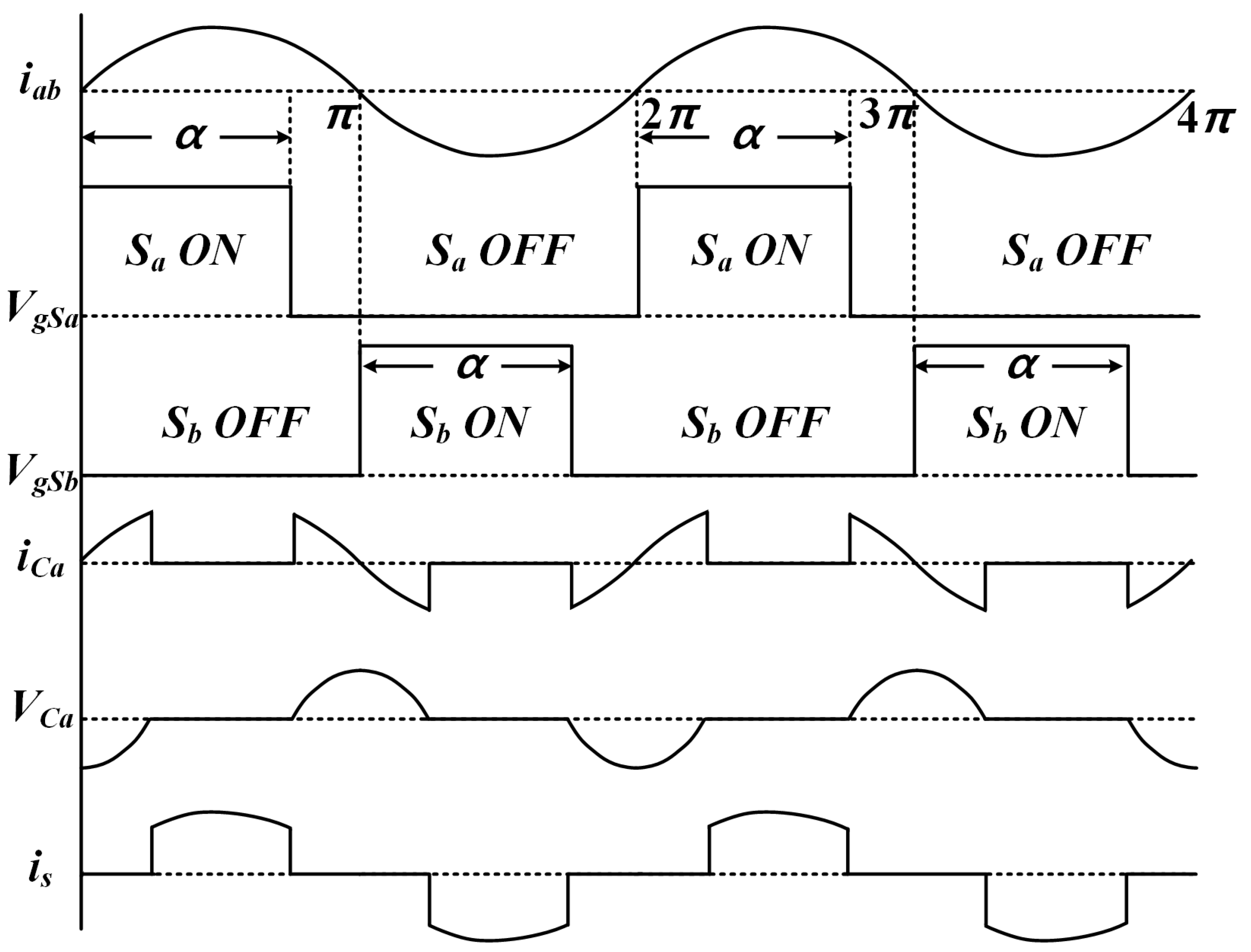
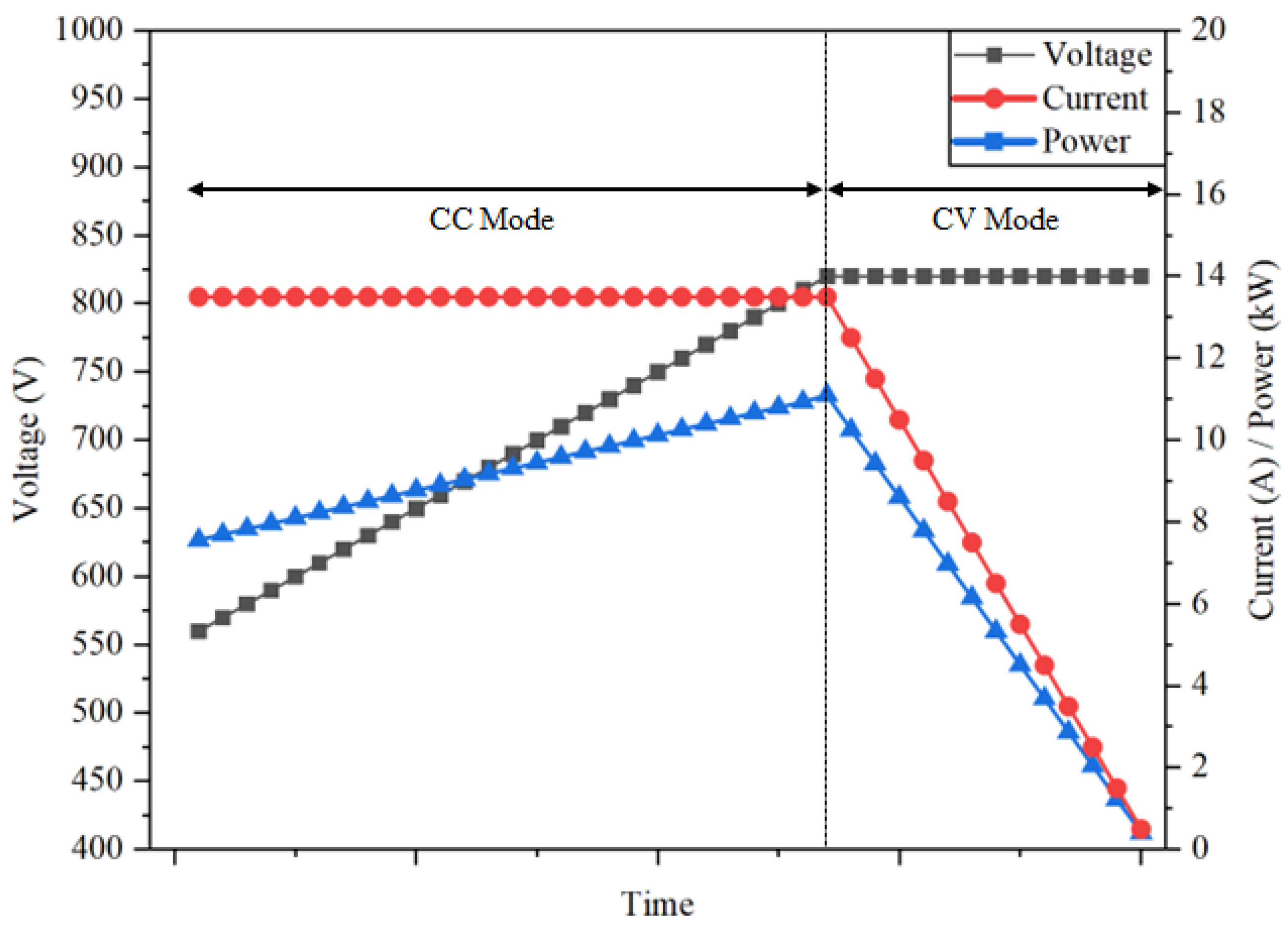
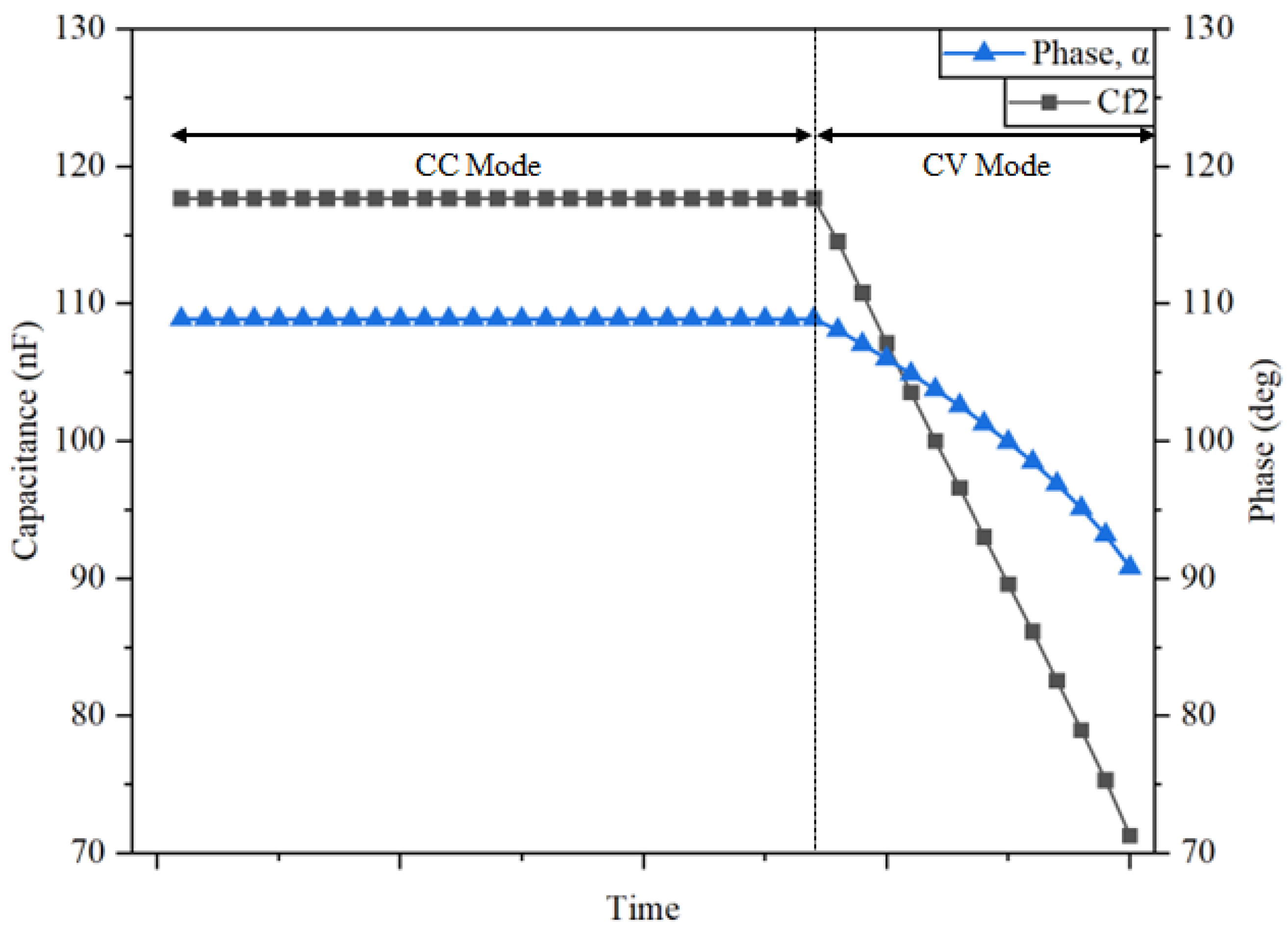
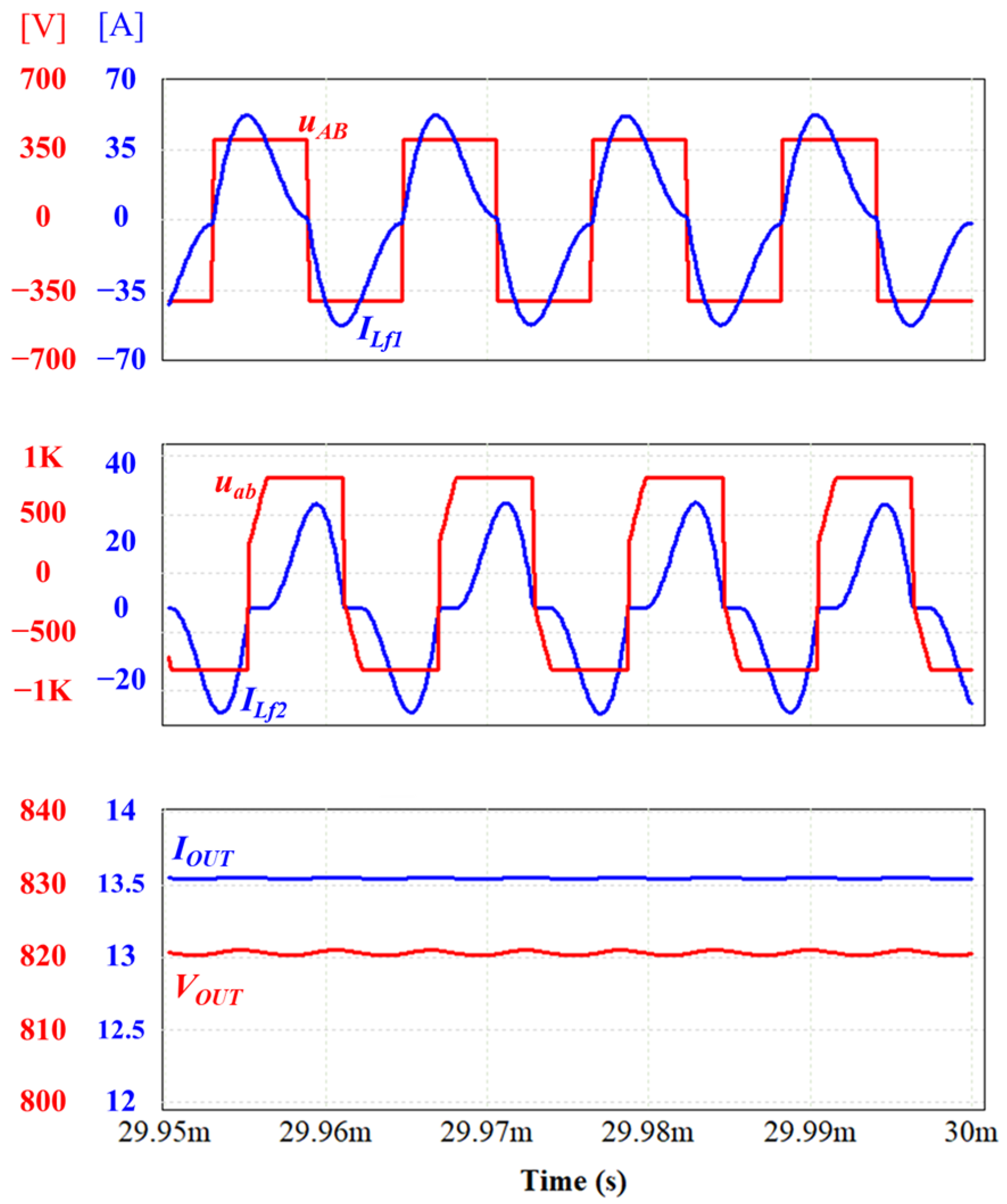
| Parameter | Value |
|---|---|
| C1a, C1b | 270 nF |
| C2 | 145 nF |
| jXVA/2 | 15 to 0 Ω |
| L1a, L1b | 54 μH |
| L2a, L2b | 54 μH |
| LVA_Min | 43.1 μH |
| LVA_Max | 44.0 μH |
| Parameter | Value |
|---|---|
| LMin | 44.4 μH |
| LMax | 48.2 μH |
| C2s/C2p | 165/146 nF |
| Parameter | Symbol | Value |
|---|---|---|
| Input voltage | Vin | 400 V |
| Input current | Iin | 27.75 A |
| Output voltage | Vout | 820 V |
| Output current | Iout | 13.5 A |
| Rated power | P | 11.1 kW |
| Switching frequency | fr | 85 kHz |
| GA-side coil | L1 | 35.67 μH |
| VA-side coil | L2 | 111.42 μH |
| Coil-to-coil distance | d | 150 mm |
| Coupling coefficient | k | 0.17 |
| Parameter | Value | |
|---|---|---|
| GA side | Lf1 | 16 μH |
| Cf1 | 216 nF | |
| C1 | 181 nF | |
| L1 | 36 μH | |
| VA side | Lf2 | 30 μH |
| Cf2 | 70 nF | |
| C2 | 43 nF | |
| L2 | 111 μH |
| Parameter | Calculate | Experiment | Error | |
|---|---|---|---|---|
| GA side | VLf1 | 302.74 V | 287.55 V | 5.02% |
| ILf1 | 27.59 A | 29.82 A | −8.08% | |
| VCf1 | 301.44 V | 287.55 V | 4.61% | |
| ICf1 | 58.21 A | 54.58 A | 6.23% | |
| VC1 | 428.38 V | 430.23 V | −0.43% | |
| IC1 | 41.57 A | 41.49 A | 0.19% | |
| VL1 | 906 V | 854.55 V | 5.68% | |
| VA side | VLf2 | 1705.27 V | 1854.07 V | −8.73% |
| ILf2 | 39.08 A | 40.36 A | −3.27% | |
| VCf2 | 761.82 V | 761.40 V | 0.06% | |
| ICf2 | 47.78 A | 47.52 A | 0.55% | |
| VC2 | 256.25 V | 246.92 V | 3.64% | |
| IC2 | 15.95 A | 15.41 A | 3.38% | |
| VL2 | 1089.53 V | 994.38 V | 8.73% |
| Ref. | System Structure | Operating Frequency | Target Battery | Power Level | Maximum Efficiency |
|---|---|---|---|---|---|
| [7] | S-S | 85 kHz | 400 V, 800 V | 7.2 kW | 97.5% |
| [8] | S-S | 85 kHz | 400 V, 800 V | 3.3 kW | - |
| [11] | S-S | 85 kHz | - | 11.1 kW | 95.5% |
| [13] | S-S | 85 kHz | - | 11.1 kW | - |
| [15] | LCC-S | 85 kHz | 400 V | 11.1 kW | 93% |
| [27] | Z-S | 85 kHz | 400 V | 3.47 kW | 96.8% |
| [10] | DS-LCC | 90 kHz | - | 1 kW | 92.63% |
| [28] | DS-LCC | 81.5 kHz, 90 kHz | 400 V | 3.3 kW | 92.6% |
| [29] | DS-LCC | 68 kHz, 79.1 kHz | 400 V | 6.6 kW | 96.1% |
| [30] | DS-LCC | 85 kHz | 400 V | 3.3 kW | 95.2% |
| [31] | DS-LCC | 85 kHz | - | 1 kW | 91.6% |
| This work | DS-LCC | 85 kHz | 800 V | 11.1 kW | 95% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, C.-M.; Kim, J.-S. Optimal Design of Resonant Network for 800 V Class 11.1 kW Wireless Power Transfer System with Double-Sided LCC Compensation Circuit. Electronics 2025, 14, 1701. https://doi.org/10.3390/electronics14091701
Kim C-M, Kim J-S. Optimal Design of Resonant Network for 800 V Class 11.1 kW Wireless Power Transfer System with Double-Sided LCC Compensation Circuit. Electronics. 2025; 14(9):1701. https://doi.org/10.3390/electronics14091701
Chicago/Turabian StyleKim, Chul-Min, and Jong-Soo Kim. 2025. "Optimal Design of Resonant Network for 800 V Class 11.1 kW Wireless Power Transfer System with Double-Sided LCC Compensation Circuit" Electronics 14, no. 9: 1701. https://doi.org/10.3390/electronics14091701
APA StyleKim, C.-M., & Kim, J.-S. (2025). Optimal Design of Resonant Network for 800 V Class 11.1 kW Wireless Power Transfer System with Double-Sided LCC Compensation Circuit. Electronics, 14(9), 1701. https://doi.org/10.3390/electronics14091701








