Mutual Knowledge Distillation-Based Communication Optimization Method for Cross-Organizational Federated Learning
Abstract
1. Introduction
- (1)
- We propose a new cross-organizational federated learning framework that allows multiple organizations to collaborate in training models without sharing sensitive data.
- (2)
- To optimize the federated learning process, we implement dynamic decision-making for local training rounds, eliminating the need for frequent model updates or transmissions. This approach reduces communication frequency, thereby lowering communication costs while preserving the effectiveness of model training.
- (3)
- Fed-MKD dynamically adjusts the distillation loss weights during local training, allowing each client to flexibly adjust the distillation strategy based on the current training progress and network conditions. This adaptive adjustment enhances the efficiency of the distillation process and ensures that model accuracy is maintained even when communication frequency is reduced.
2. Related Work
2.1. Joint Distillation
2.2. Distillation Compression
3. Preliminary
3.1. Problem Formulation
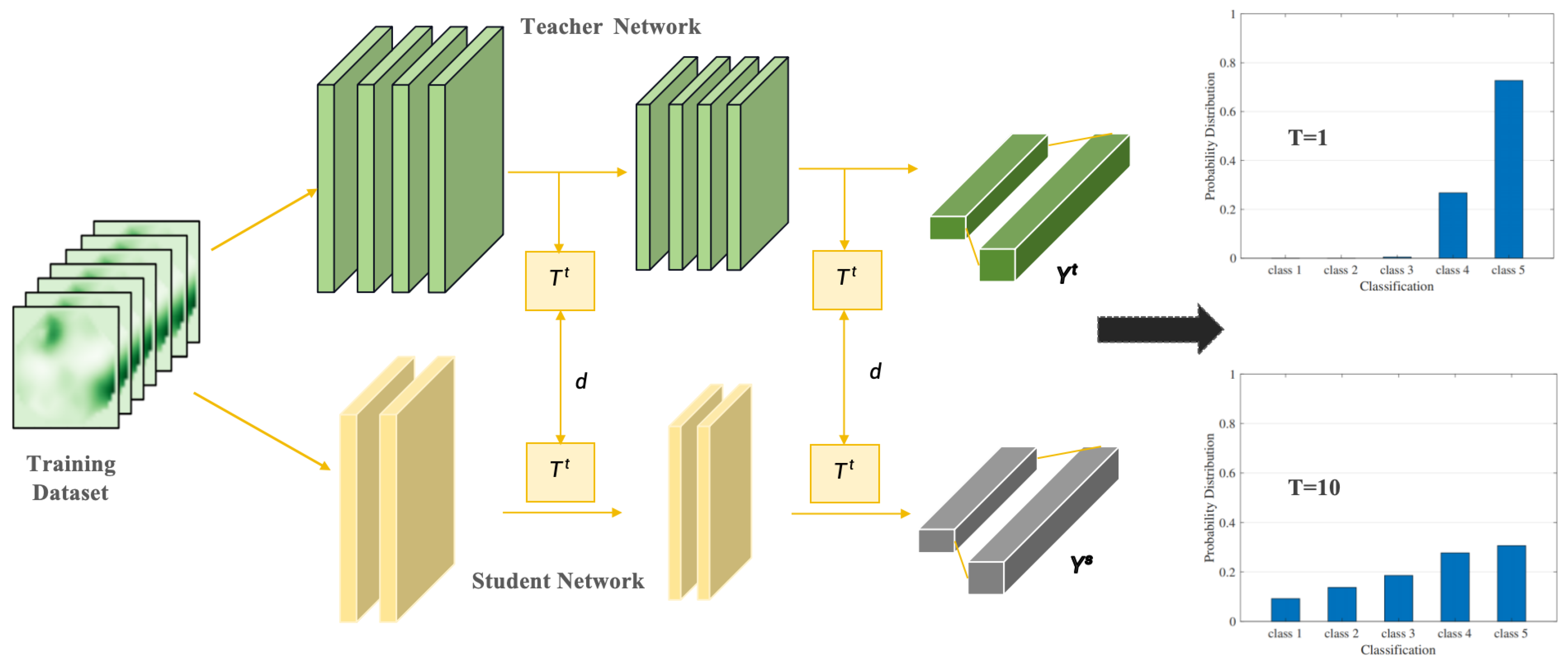
3.2. System Model Architecture
- Each DC trains two models using local data (the local training process includes mutual distillation between two models);
- DC pushes the updated student model parameters to PS;
- The PS aggregates the parameter updates from each DC;
- The PS generates the global student model using the aggregated results;
- DC pulls the updated global student model from the PS;
- DC updates the local student model using the global model.
4. Methodology
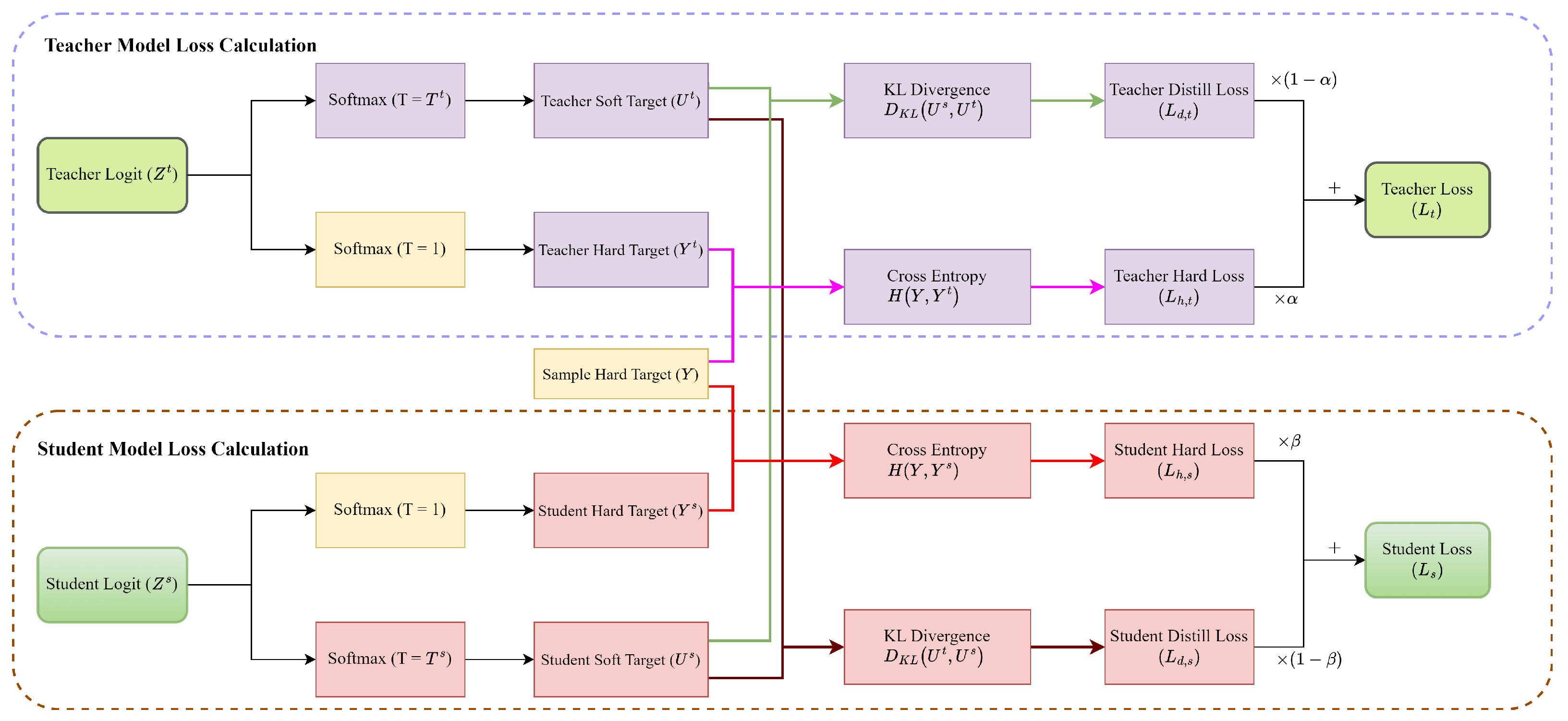
4.1. Mutual Knowledge Distillation Strategy
4.2. Implementation Process of Fed-MKD
4.2.1. Local Training Rounds Adjustment
4.2.2. Teacher Model Training with Adaptive Loss Weights
4.3. The Specific Algorithm Design
| Algorithm 1 Fed-MKD (Participating DC ) |
Require:
|
| Algorithm 2 Fed-MKD (Parameter Server) |
Require:
|
- (1)
- Teacher model forward pass: ;
- (2)
- Student model forward pass: ;
- (3)
- Mutual distillation loss calculation (KL divergence): ;
- (4)
- Student model backward propagation: ;
- (5)
- Dynamic weight update: .
5. Simulation Experiment and Results Analysis
5.1. Experimental Setup
5.1.1. Simulation Platform Setup
5.1.2. Dataset and Model Parameters
5.1.3. Comparative Schemes and Performance Metrics
- FedMD [14]: Locally trains only a larger teacher model to accelerate the learning process during training. This method serves as a baseline for comparing the effectiveness of training acceleration.
- FedGKT [13]: Locally trains only the student model, aiming to achieve performance comparable to the teacher model with fewer parameters.
- FedKD [15]: Employs the original mutual distillation framework for training.
- Fed-MKDFW: Utilizes fixed loss weights during training with Fed-MKD, designed to evaluate the advantages of Fed-MKD’s adaptive adjustment of distillation weights under non-IID data distribution scenarios.
5.2. Experimental Results and Analysis
5.2.1. Relationship Between Model Accuracy and Training Time
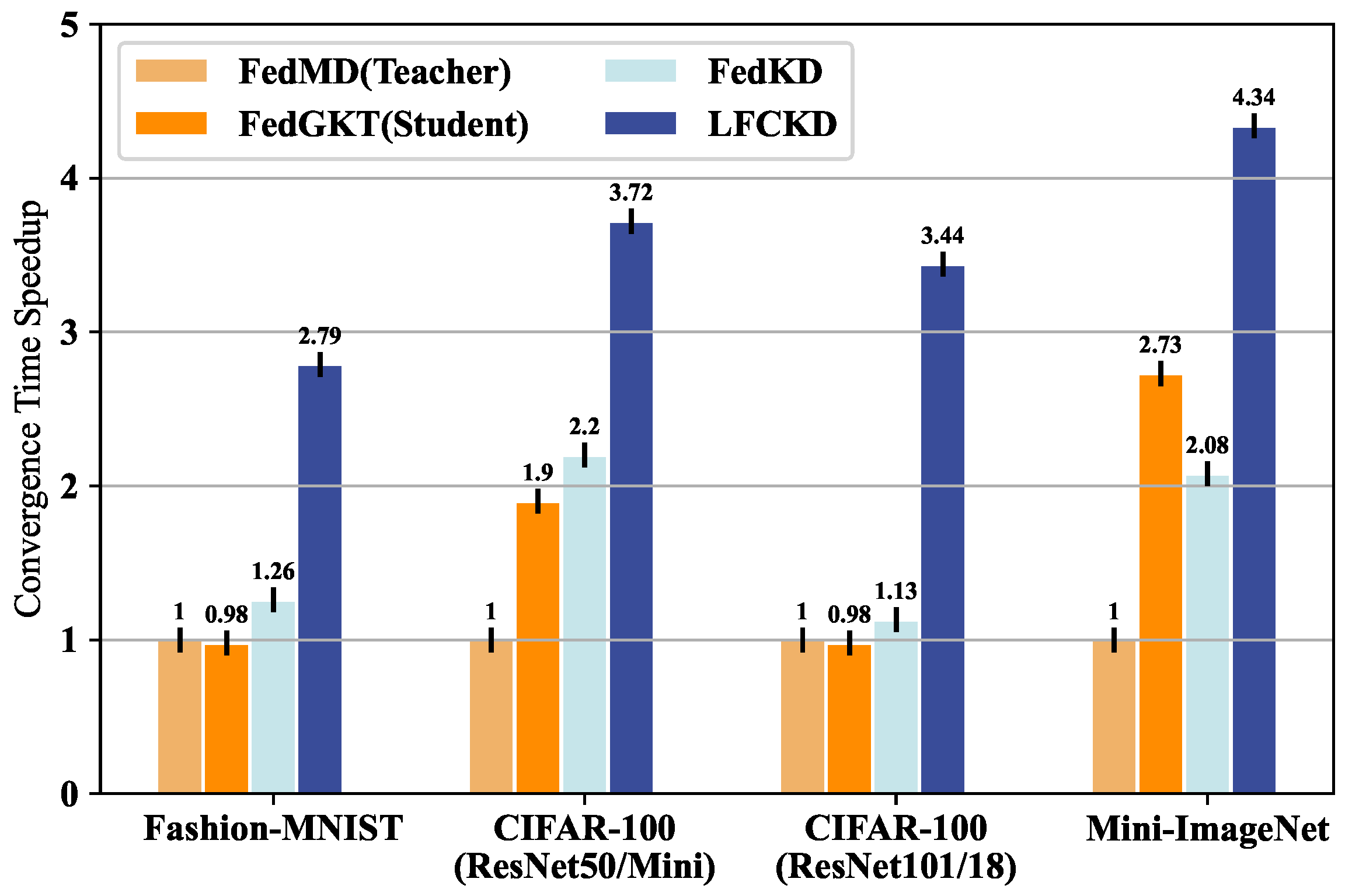
5.2.2. Model Top-1 Accuracy and Convergence Time Speedup Ratio
5.2.3. Total Compression Ratio
5.2.4. Global Model Accuracy Under the Non-IID Setting
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Devlin, J. BERT: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning transferable visual models from natural language supervision. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 8748–8763. [Google Scholar]
- Li, T.; Sahu, A.K.; Talwalkar, A.; Smith, V. Federated learning: Challenges, methods, and future directions. IEEE Signal Process. Mag. 2020, 37, 50–60. [Google Scholar] [CrossRef]
- Sattler, F.; Wiedemann, S.; Müller, K.-R.; Samek, W. Robust and communication-efficient federated learning from non-IID data. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 3400–3413. [Google Scholar] [CrossRef]
- Buyukates, B.; Ulukus, S. Timely communication in federated learning. In Proceedings of the IEEE INFOCOM 2021—IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Virtual, 10–13 May 2021; pp. 1–6. [Google Scholar]
- Shahid, O.; Pouriyeh, S.; Parizi, R.M.; Sheng, Q.Z.; Srivastava, G.; Zhao, L. Communication efficiency in federated learning: Achievements and challenges. arXiv 2021, arXiv:2107.10996. [Google Scholar]
- Zhao, Z.; Mao, Y.; Liu, Y.; Song, L.; Ouyang, Y.; Chen, X.; Ding, W. Towards efficient communications in federated learning: A contemporary survey. J. Frankl. Inst. 2023, 360, 8669–8703. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, M.; Wong, K.-K.; Poor, H.V.; Cui, S. Federated learning for 6G: Applications, challenges, and opportunities. Engineering 2022, 8, 33–41. [Google Scholar] [CrossRef]
- Panda, A.; Mahloujifar, S.; Bhagoji, A.N.; Chakraborty, S.; Mittal, P. Sparsefed: Mitigating model poisoning attacks in federated learning with sparsification. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Virtual, 28–30 March 2022; pp. 7587–7624. [Google Scholar]
- Peng, H.; Gurevin, D.; Huang, S.; Geng, T.; Jiang, W.; Khan, O.; Ding, C. Towards sparsification of graph neural networks. In Proceedings of the 2022 IEEE 40th International Conference on Computer Design (ICCD), Olympic Valley, CA, USA, 23–26 October 2022; pp. 272–279. [Google Scholar]
- Sui, D.; Chen, Y.; Zhao, J.; Jia, Y.; Xie, Y.; Sun, W. Feded: Federated learning via ensemble distillation for medical relation extraction. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), Online, 16–20 November 2020; pp. 2118–2128. [Google Scholar]
- Lin, T.; Kong, L.; Stich, S.U.; Jaggi, M. Ensemble distillation for robust model fusion in federated learning. Adv. Neural Inf. Process. Syst. 2020, 33, 2351–2363. [Google Scholar]
- He, C.; Annavaram, M.; Avestimehr, S. Group knowledge transfer: Federated learning of large CNNs at the edge. Adv. Neural Inf. Process. Syst. 2020, 33, 14068–14080. [Google Scholar]
- Li, D.; Wang, J. Fedmd: Heterogeneous federated learning via model distillation. arXiv 2019, arXiv:1910.03581. [Google Scholar]
- Wu, C.; Wu, F.; Lyu, L.; Huang, Y.; Xie, X. Communication-efficient federated learning via knowledge distillation. Nat. Commun. 2022, 13, 2032. [Google Scholar] [CrossRef]
- Zhang, L.; Shen, L.; Ding, L.; Tao, D.; Duan, L.-Y. Fine-tuning global model via data-free knowledge distillation for non-IID federated learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10174–10183. [Google Scholar]
- Lee, G.; Jeong, M.; Shin, Y.; Bae, S.; Yun, S.-Y. Preservation of the global knowledge by not-true distillation in federated learning. Adv. Neural Inf. Process. Syst. 2022, 35, 38461–38474. [Google Scholar]
- Zhang, X.; Zeng, Z.; Zhou, X.; Shen, Z. Low-dimensional federated knowledge graph embedding via knowledge distillation. arXiv 2024, arXiv:2408.05748. [Google Scholar]
- Liu, T.; Xia, J.; Ling, Z.; Fu, X.; Yu, S.; Chen, M. Efficient federated learning for AIoT applications using knowledge distillation. IEEE Internet Things J. 2022, 10, 7229–7243. [Google Scholar] [CrossRef]
- Malinovskiy, G.; Kovalev, D.; Gasanov, E.; Condat, L.; Richtarik, P. From local SGD to local fixed-point methods for federated learning. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 6692–6701. [Google Scholar]
- Ochiai, K.; Terada, M. Poster: End-to-End Privacy-Preserving Vertical Federated Learning using Private Cross-Organizational Data Collaboration. In Proceedings of the 2024 on ACM SIGSAC Conference on Computer and Communications Security, Salt Lake City, UT, USA, 14–18 October 2024; pp. 4955–4957. [Google Scholar]
- Fernandez, J.D.; Brennecke, M.; Barbereau, T.; Rieger, A.; Fridgen, G. Federated Learning: Organizational Opportunities, Challenges, and Adoption Strategies. arXiv 2023, arXiv:2308.02219. [Google Scholar]
- Che, L.; Wang, J.; Zhou, Y.; Ma, F. Multimodal federated learning: A survey. Sensors 2023, 23, 6986. [Google Scholar] [CrossRef]
- Dai, X.; Yan, X.; Zhou, K.; Yang, H.; Ng, K.W.; Cheng, J.; Fan, Y. Hyper-sphere quantization: Communication-efficient SGD for federated learning. arXiv 2019, arXiv:1911.04655. [Google Scholar]
- Qu, X.; Wang, J.; Xiao, J. Quantization and knowledge distillation for efficient federated learning on edge devices. In Proceedings of the 2020 IEEE 22nd International Conference on High Performance Computing and Communications; IEEE 18th International Conference on Smart City; IEEE 6th International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Virtual, 14–16 December 2020; pp. 967–972. [Google Scholar]
- Chen, Z.; Tian, P.; Liao, W.; Chen, X.; Xu, G.; Yu, W. Resource-aware knowledge distillation for federated learning. IEEE Trans. Emerg. Top. Comput. 2023, 11, 706–719. [Google Scholar] [CrossRef]
- Cui, J.; Tian, Z.; Zhong, Z.; Qi, X.; Yu, B.; Zhang, H. Decoupled kullback-leibler divergence loss. Adv. Neural Inf. Process. Syst. 2024, 37, 74461–74486. [Google Scholar]
- Huang, Y.; Shen, P.; Tai, Y.; Li, S.; Liu, X.; Li, J.; Huang, F.; Ji, R. Improving face recognition from hard samples via distribution distillation loss. In Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020, Proceedings, Part XXX 16; Springer: Berlin/Heidelberg, Germany, 2020; pp. 138–154. [Google Scholar]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-MNIST: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Moradi, R.; Berangi, R.; Minaei, B. Sparsemaps: Convolutional networks with sparse feature maps for tiny image classification. Expert Syst. Appl. 2019, 119, 142–154. [Google Scholar] [CrossRef]
- Vinyals, O.; Blundell, C.; Lillicrap, T.; Wierstra, D. Matching networks for one shot learning. Adv. Neural Inf. Process. Syst. 2016, 29. [Google Scholar]
- Cao, X. MLclf: The project machine learning CLassiFication for utilizing mini-ImageNet and tiny-ImageNet. 2022; Unpublished. [Google Scholar]
- Shafiq, M.; Gu, Z. Deep residual learning for image recognition: A survey. Appl. Sci. 2022, 12, 8972. [Google Scholar] [CrossRef]
- Li, C.; Li, G.; Varshney, P.K. Decentralized federated learning via mutual knowledge transfer. IEEE Internet Things J. 2021, 9, 1136–1147. [Google Scholar] [CrossRef]



| Notation | Definition |
|---|---|
| N | Number of DCs participating in the training process |
| w | Model parameters, , where d is the dimensionality of the parameters |
| The sample set (local dataset) independently owned and used for local model training by the i-th DC | |
| D | Entire dataset, encompassing all data utilized by the DCs, |
| The loss function computed under model parameters w for an input data x | |
| Objective function for global model optimization | |
| Loss function of the global model at the r-th round | |
| Local model parameters used by | |
| Global model parameters aggregated at the r-th round | |
| The teacher/student model parameters in | |
| Gradient at DCi | |
| The gradients of the teacher/student model in | |
| Learning rate of , controlling the step size of each gradient update | |
| R | Upper bound of the training frequency for the global model |
| Target threshold for the expected | |
| Communication time between and the PS during the r-th round of training | |
| Teacher/student model predictions | |
| Teacher/student model distillation loss | |
| Teacher/student model original loss | |
| Teacher/student model final loss combining distillation loss with original loss | |
| Teacher/student model hard decision (actual prediction result of the model) | |
| Teacher/student model soft decision (probability distribution output) | |
| Hyperparameters | |
| E | Number of global training rounds between all participating DCs |
| Dataset | Training System | Network Architecture | Communication Model Parameters | Top-1 Accuracy | Inference Speedup | Compression Ratio |
|---|---|---|---|---|---|---|
| Fashion-MNIST | FedMD (Teacher) | Custom CNN | 0.32 M | 91.42% | 1.00 | 1.00 |
| FedGKT (Student) | Custom CNN | 0.038 M | 89.81% (−1.61%) | 0.98× | 7.21× | |
| FedKD | - | 0.038 M | 90.41% (−1.28%) | 1.26× | 9.43× | |
| Fed-MKD | - | 0.038 M | 90.95% (−0.47%) | 2.79× | 28.45× | |
| CIFAR-100 | FedMD (Teacher) | ResNet50 | 24.47 M | 74.12% | 1.00 | 1.00 |
| FedGKT (Student) | ResNet-Mini | 5.37 M | 62.55% (−11.57%) | 1.90× | 2.72× | |
| FedKD | - | 5.37 M | 64.59% (−9.53%) | 2.20× | 2.45× | |
| Fed-MKD | - | 5.37 M | 69.48% (−4.64%) | 3.72× | 4.89× | |
| CIFAR-100 | FedMD (Teacher) | ResNet101 | 43.06 M | 76.15% | 1.00 | 1.00 |
| FedGKT (Student) | ResNet18 | 10.58 M | 71.19% (−4.96%) | 0.98× | 1.84× | |
| FedKD | - | 10.58 M | 72.68% (−3.47%) | 1.13× | 2.30× | |
| Fed-MKD | - | 10.58 M | 75.13% (−1.02%) | 3.44× | 9.16× | |
| Mini-ImageNet | FedMD (Teacher) | ResNet101 | 43.06 M | 69.34% | 1.00 | 1.00 |
| FedGKT (Student) | ResNet18 | 10.58 M | 64.89% (−4.45%) | 2.73× | 4.25× | |
| FedKD | - | 10.58 M | 66.73% (2.61%) | 2.08× | 3.47× | |
| Fed-MKD | - | 10.58 M | 67.96% (1.38%) | 4.34× | 8.68× |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Shen, H.; Law, E.K.L.; Lam, C.-T. Mutual Knowledge Distillation-Based Communication Optimization Method for Cross-Organizational Federated Learning. Electronics 2025, 14, 1784. https://doi.org/10.3390/electronics14091784
Liu S, Shen H, Law EKL, Lam C-T. Mutual Knowledge Distillation-Based Communication Optimization Method for Cross-Organizational Federated Learning. Electronics. 2025; 14(9):1784. https://doi.org/10.3390/electronics14091784
Chicago/Turabian StyleLiu, Su, Hong Shen, Eddie K. L. Law, and Chan-Tong Lam. 2025. "Mutual Knowledge Distillation-Based Communication Optimization Method for Cross-Organizational Federated Learning" Electronics 14, no. 9: 1784. https://doi.org/10.3390/electronics14091784
APA StyleLiu, S., Shen, H., Law, E. K. L., & Lam, C.-T. (2025). Mutual Knowledge Distillation-Based Communication Optimization Method for Cross-Organizational Federated Learning. Electronics, 14(9), 1784. https://doi.org/10.3390/electronics14091784







