Multiple-Particle Autofocusing Algorithm Using Axial Resolution and Morphological Analyses Based on Digital Holography
Abstract
:1. Introduction
2. Principles
3. Methodology
3.1. Axial Resolution
3.2. Constrained Intensity for Each Candidate Focused Particle
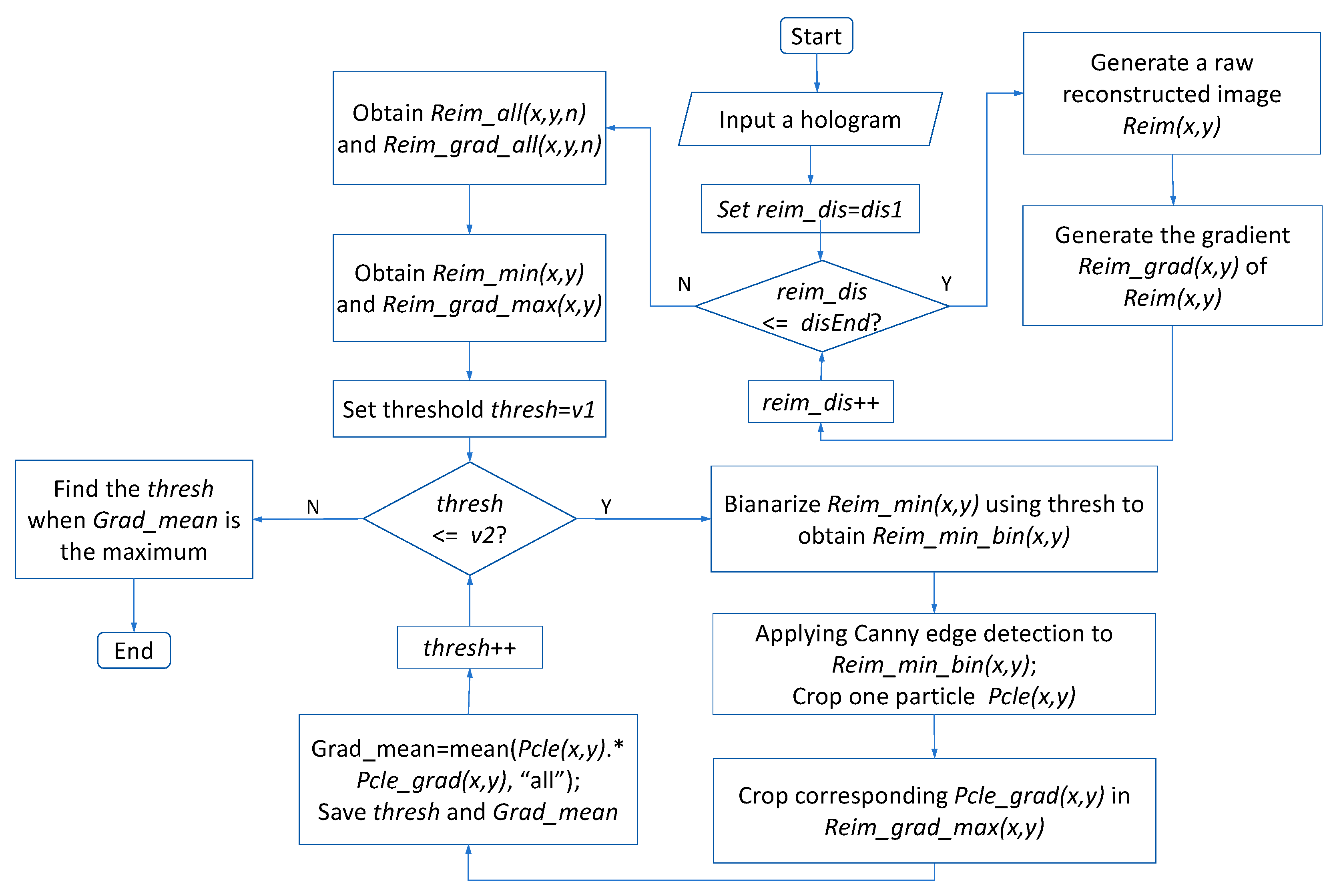
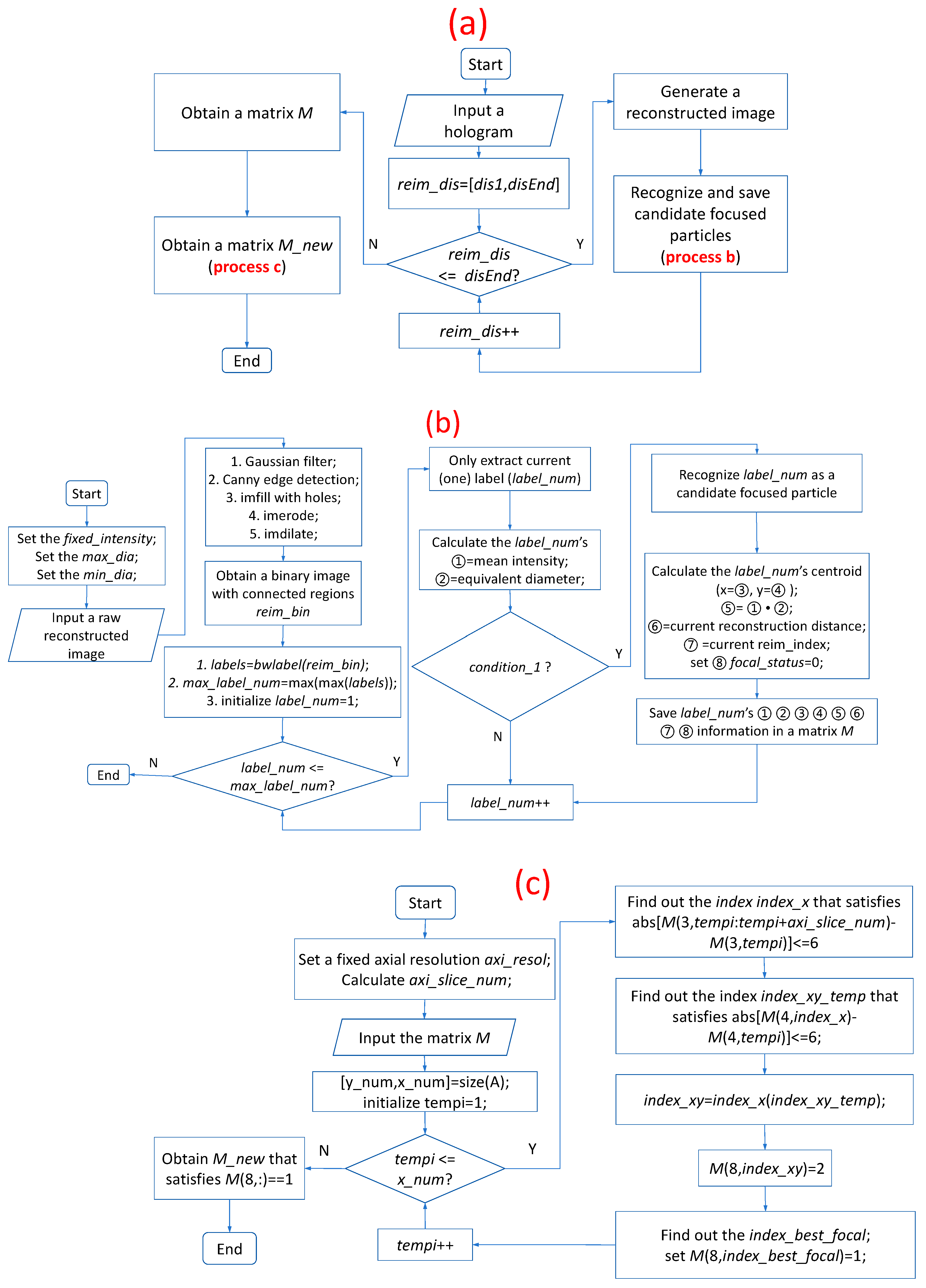
3.3. Description of Algorithm
4. Experimental Results and Analyses
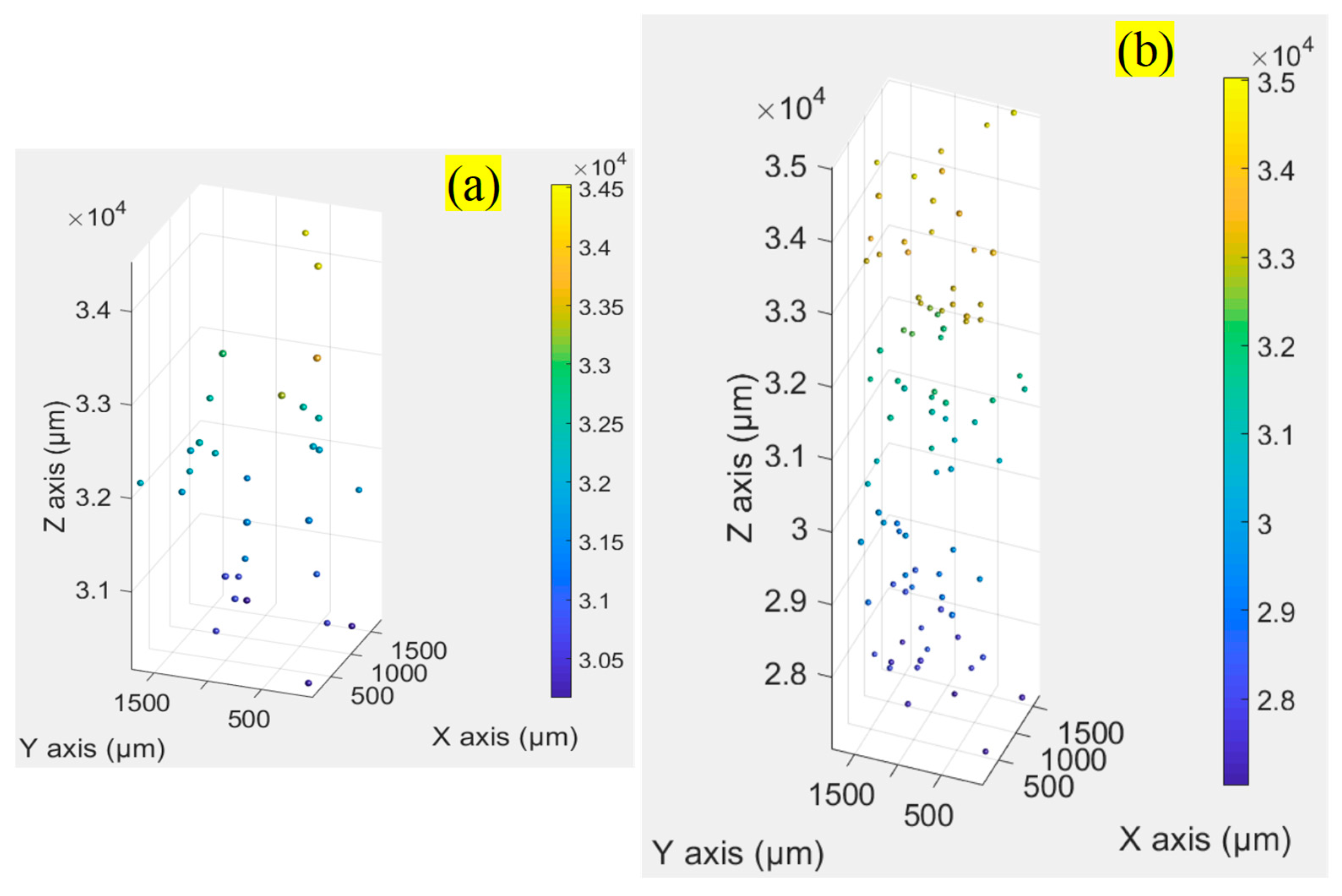
4.1. Particles in Two Layers
4.2. Particles in Cuvette
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Garcla-Sucerqula, J.; Xu, W.; Jericho, S.K.; Klages, P.; Jericho, M.H.; Kreuzer, H.J. Digital in-line holographic microscopy. Appl. Opt. 2006, 45, 836–850. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Yao, L.; Brunel, M.; Coëtmellec, S.; Li, R.; Lebrun, D.; Zhou, H.; Gréhan, G.; Cen, K. Characterizations of transparent particle holography in near-field using Debye series. Appl. Opt. 2016, 55, A60–A70. [Google Scholar] [CrossRef] [PubMed]
- Gao, P.; Yao, B.; Min, J.; Guo, R.; Ma, B.; Zheng, J.; Lei, M.; Yan, S.; Dan, D.; Ye, T. Autofocusing of digital holographic microscopy based on off-axis illuminations. Opt. Lett. 2012, 37, 3630–3632. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.; Gao, P.; Shao, X. Opposite-view digital holographic microscopy with autofocusing capability. Sci. Rep. 2017, 7, 4255. [Google Scholar] [CrossRef]
- Langehanenberg, P.; von Bally, G.; Kemper, B. Autofocusing in digital holographic microscopy. 3D Res. 2011, 2, 4. [Google Scholar] [CrossRef]
- Ilhan, H.A.; Doğar, M.; Özcan, M. Digital holographic microscopy and focusing methods based on image sharpness. J. Microsc. 2014, 255, 138–149. [Google Scholar] [CrossRef]
- Ren, Z.; Chen, N.; Lam, E.Y. Automatic focusing for multisectional objects in digital holography using the structure tensor. Opt. Lett. 2017, 42, 1720–1723. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Wu, Y.; Tamamitsu, M.; Ozcan, A. Edge sparsity criterion for robust holographic autofocusing. Opt. Lett. 2017, 42, 3824–3827. [Google Scholar] [CrossRef]
- Lyu, M.; Yuan, C.; Li, D.; Situ, G. Fast autofocusing in digital holography using the magnitude differential. Appl. Opt. 2017, 56, F152–F157. [Google Scholar] [CrossRef]
- Khanam, T.; Darakis, E.; Rajendran, A.; Kariwala, V.; Asundi, A.K.; Naughton, T.J. On-line digital holographic measurement of size and shape of microparticles for crystallization processes. Proc. SPIE 2008, 7155, 514–523. [Google Scholar]
- Darakis, E.; Khanam, T.; Rajendran, A.; Kariwala, V.; Naughton, T.J.; Asundi, A.K. Microparticle characterization using digital holography. Chem. Eng. Sci. 2010, 65, 1037–1044. [Google Scholar] [CrossRef]
- Kempkes, M.; Darakis, E.; Khanam, T.; Rajendran, A.; Kariwala, V.; Mazzotti, M.; Naughton, T.J.; Asundi, A.K. Three dimensional digital holographic profiling of micro-fibers. Opt. Express 2009, 17, 2938–2943. [Google Scholar] [CrossRef]
- Khanam, T.; Rajendran, A.; Kariwala, V.; Asundi, A.K. Measurement of two-dimensional crystal shape using digital holography. Cryst. Growth Des. 2013, 13, 3969–3975. [Google Scholar] [CrossRef]
- Tian, L.; Loomis, N.; Domínguez-Caballero, J.A.; Barbastathis, G. Quantitative measurement of size and three-dimensional position of fast-moving bubbles in air-water mixture flows using digital holography. Appl. Opt. 2010, 49, 1549–1554. [Google Scholar] [CrossRef] [PubMed]
- Lang, K.; Qiang, J.; Qiu, Y.; Wang, X. Autofocusing method for multifocal holograms based on connected domain analysis. Opt. Lasers Eng. 2025, 184, 108624. [Google Scholar] [CrossRef]
- Brady, D.J.; Choi, K.; Marks, D.L.; Horisaki, R.; Lim, S. Compressive holography. Opt. Express 2009, 17, 13040–13049. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, L.; Lee, J.W.; Huang, H.Y.H.; Triantafyllou, M.S.; Barbastathis, G. Scanning-free compressive holography for object localization with subpixel accuracy. Opt. Lett. 2012, 37, 3357–3359. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, L.; Hsieh, C.-H.; Barbastathis, G. Compressive holographic two-dimensional localization with 1/302 subpixel accuracy. Opt. Express 2014, 22, 9774–9782. [Google Scholar] [CrossRef]
- Chen, W.; Tian, L.; Rehman, S.; Zhang, Z.; Lee, H.P.; Barbastathis, G. Empirical concentration bounds for compressive holographic bubble imaging based on a Mie scattering model. Opt. Express 2015, 23, 4715–4725. [Google Scholar] [CrossRef]
- Li, W.-N.; Zhang, Z.; Su, P.; Ma, J.; Wang, X. Removal of defocused images using three- -dimensional nonlinear diffusion based on digital holography. J. Opt. 2020, 22, 051701. [Google Scholar] [CrossRef]
- Ren, Z.; Xu, Z.; Lam, E.Y. Learning-based nonparametric autofocusing for digital holography. Optica 2018, 5, 337–344. [Google Scholar] [CrossRef]
- Lee, S.J.; Yoon, G.Y.; Go, T. Deep learning-based accurate and rapid tracking of 3D positional information of microparticles using digital holographic microscopy. Exp. Fluids 2019, 60, 170. [Google Scholar] [CrossRef]
- Shao, S.; Mallery, K.; Hong, J. Machine learning holography for measuring 3D particle distribution. Chem. Eng. Sci. 2020, 225, 115830. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, J.; Jin, S.; Cao, L.; Jin, G. Dense-U-net: Dense encoder-decoder network for holographic imaging of 3D particle fields. Opt. Commun. 2021, 493, 126970. [Google Scholar] [CrossRef]
- Li, W.-N.; Su, P.; Ma, J.; Wang, X. Short U-net model with average pooling based on in-line digital holography for simultaneous restoration of multiple particles. Opt. Lasers Eng. 2021, 139, 106449. [Google Scholar] [CrossRef]
- Hao, Z.; Li, W.-N.; Hou, B.; Su, P.; Ma, J. Characterization method for particle extraction from raw-reconstructed images using U-net. Front. Phys. 2022, 9, 816158. [Google Scholar] [CrossRef]
- Ou, H.; Lin, W.; Li, W.-N.; Xie, X. Real-time particle concentration measurement from a hologram by deep learning. Phys. Scr. 2024, 99, 095512. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics, 4th ed.; W. H. Freeman: New York, NY, USA, 2017. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Meng, H.; Hussain, F. In-line recording and off-axis viewing technique for holographic particle velocimetry. Appl. Opt. 1995, 34, 1827–1840. [Google Scholar] [CrossRef]
- Li, H.; Ji, F.; Li, L.; Li, B.; Ma, F. In lab in-line digital holography for cloud particle measurement experiment. Proc. SPIE 2016, 10156, 1015618. [Google Scholar]



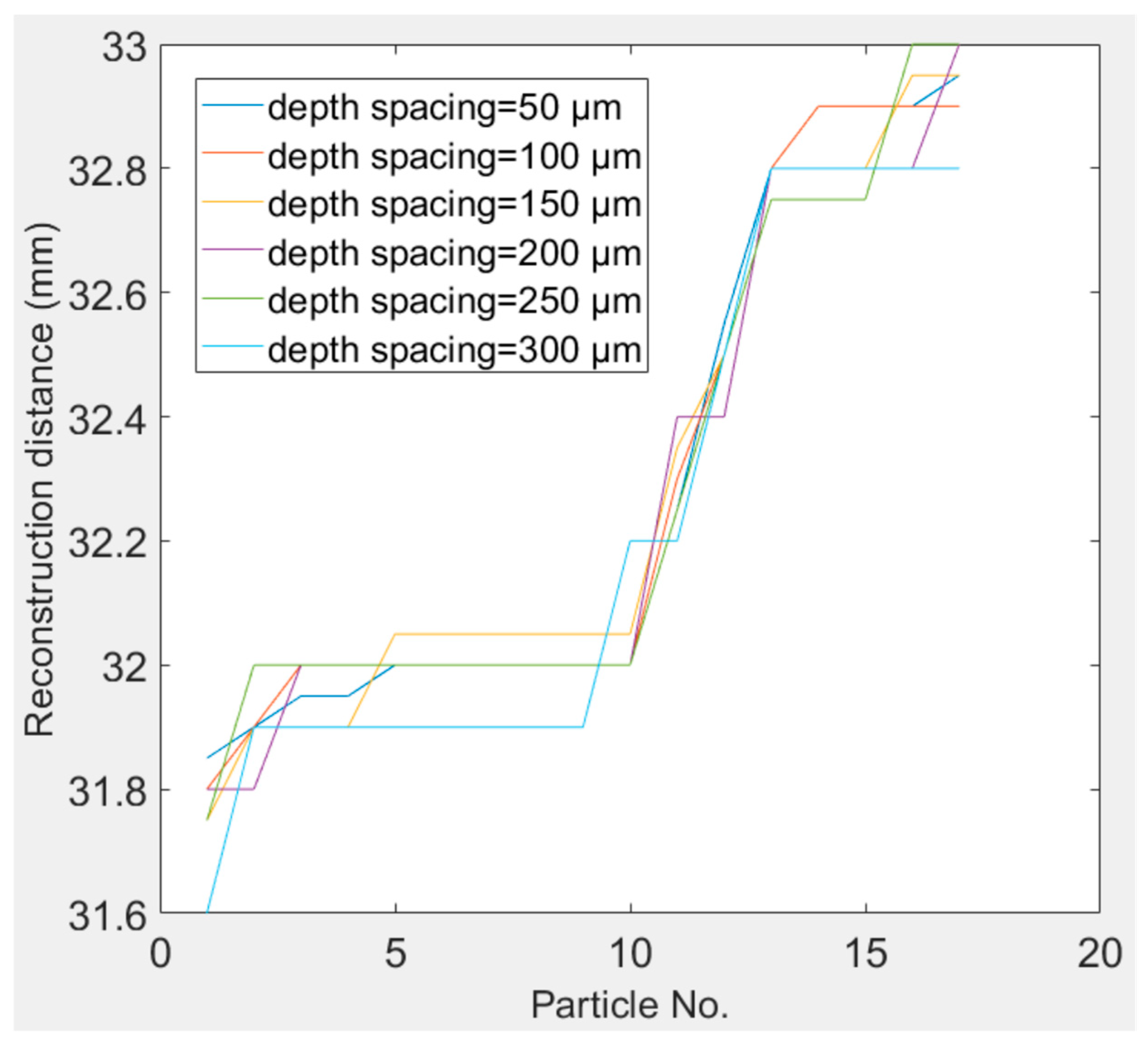

| Particle No. | Centroid [x, y] | Reim_Index | Reconstruction Distance (mm) |
|---|---|---|---|
| 1 | [1109, 628] | −43 | 31.85 |
| 2 | [1124, 51] | −42 | 31.90 |
| 3 | [513, 823] | −41 | 31.95 |
| 4 | [684, 590] | −41 | 31.95 |
| 5 | [551, 528] | −40 | 32.00 |
| 6 | [593, 537] | −40 | 32.00 |
| 7 | [609, 348] | −40 | 32.00 |
| 8 | [708, 725] | −40 | 32.00 |
| 9 | [934, 129] | −40 | 32.00 |
| 10 | [952, 555] | −40 | 32.00 |
| 11 | [215, 17] | −35 | 32.25 |
| 12 | [78, 419] | −29 | 32.55 |
| 13 | [197, 336] | −24 | 32.80 |
| 14 | [345, 515] | −22 | 32.90 |
| 15 | [1240, 572] | −22 | 32.90 |
| 16 | [1336, 512] | −22 | 32.90 |
| 17 | [122, 721] | −21 | 32.95 |
| Experiment No. | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Cuvette thickness (mm) | 3 | 3 | 3 | 10 |
| Distance from CMOS (mm) | 30 | 40 | 60 | 30 |
| Axial resolution (mm) | 2.5 | 2.5 | 2.5 | 2.5 |
| Hologram amount | 16 | 180 | 160 | 200 |
| Ground truth of particle amount | 480 | 5400 | 4800 | 20,000 |
| Particle amount recognized by proposed method | 498 | 5796 | 4841 | 18,851 |
| Deviation | 18 | 396 | 41 | 1149 |
| Relative error (%) | 3.75 | 7.33 | 0.85 | 5.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.-N.; Zhou, Y.; Chen, J.; Ou, H.; Xie, X. Multiple-Particle Autofocusing Algorithm Using Axial Resolution and Morphological Analyses Based on Digital Holography. Electronics 2025, 14, 1789. https://doi.org/10.3390/electronics14091789
Li W-N, Zhou Y, Chen J, Ou H, Xie X. Multiple-Particle Autofocusing Algorithm Using Axial Resolution and Morphological Analyses Based on Digital Holography. Electronics. 2025; 14(9):1789. https://doi.org/10.3390/electronics14091789
Chicago/Turabian StyleLi, Wei-Na, Yi Zhou, Jiatai Chen, Hongjie Ou, and Xiangsheng Xie. 2025. "Multiple-Particle Autofocusing Algorithm Using Axial Resolution and Morphological Analyses Based on Digital Holography" Electronics 14, no. 9: 1789. https://doi.org/10.3390/electronics14091789
APA StyleLi, W.-N., Zhou, Y., Chen, J., Ou, H., & Xie, X. (2025). Multiple-Particle Autofocusing Algorithm Using Axial Resolution and Morphological Analyses Based on Digital Holography. Electronics, 14(9), 1789. https://doi.org/10.3390/electronics14091789







