A Software Framework for Rapid Application-Specific Hybrid Photonic Network-on-Chip Synthesis †
Abstract
:1. Introduction
2. Related Work
2.1. Hybrid Photonic NoC Architectures
2.2. NoC Synthesis Approaches
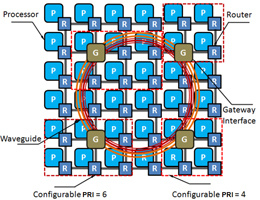
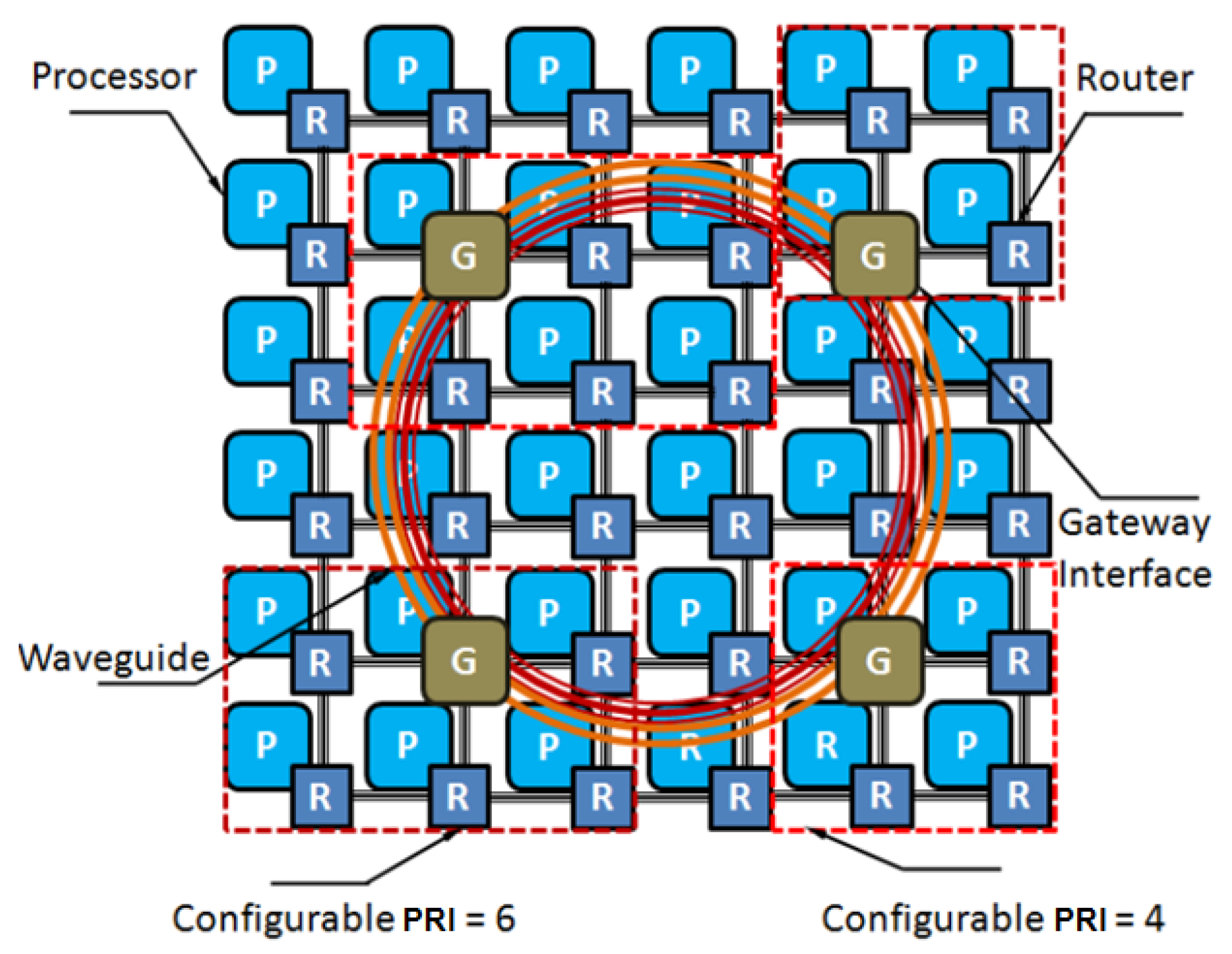
3. Hybrid Photonic NoC Architecture
3.1. PRI-Aware Routing
3.2. Photonic Ring Configuration
3.3. Flow Control Protocol
3.4. Serialization
4. Problem Formulation
- (1)
- A core graph G (V, E); with the set V of vertices {V1, V2, V¬3, …, VN} representing the N cores on which the given applications tasks have already been mapped, and the set of M edges {e1, e2, e3, …, eM} with weights that represent application-specific latency constraints between communicating cores,
- (2)
- A regular mesh-based CMP with T tiles such that T = (d2), where d is the dimension of the mesh, and each tile consists of a compute core and a NoC router,
- (3)
- The upper and lower bounds that define an acceptable value range for a set of parameters relevant to hybrid photonic NoC architectures, as defined in Table 1.
5. Synthesis Framework Overview
5.1. Core to Tile Mapping
5.2. NoC Synthesis
5.2.1. Particle Swarm Optimization (PSO)
5.2.2. Ant Colony Optimization (ACO)
5.2.3. Simulated Annealing (SA)
5.2.4. Genetic Algorithm (GA)
5.3. Cycle Accurate Simulation and Validation
6. Experiments
6.1. Experimental Setup
6.2. Results
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- ITRS Technology Working Groups. International Technology Roadmap for Semiconductors (ITRS). 2007. Available online: http://public.itrs.net (accessed on 2 December 2016).
- Benini, L.; De-Micheli, G. Networks on Chip: A new SoC paradigm. Computer 2002, 49, 70–71. [Google Scholar] [CrossRef]
- Goodman, J.; Leonberger, F.; Kung, S.-Y.; Athale, R. Optical interconnects for VLSI systems. Proc. IEEE 1984, 72, 850–866. [Google Scholar] [CrossRef]
- Chen, G.; Chen, H.; Haurylau, M.; Nelson, N.; Fauchet, P.M.; Friedman, E.G.; Albonesi, D. Predictions of CMOS compatible on-chip optical interconnect. In Proceedings of the 2005 International Workshop on System Level Interconnect pRediction, San Francisco, CA, USA, 2–3 April 2005; pp. 13–20.
- Le Beux, S.; Li, H.; O’Connor, I.; Cheshmi, K.; Liu, X.; Trajkovic, J.; Nicolescu, G. Chameleon: Channel efficient Optical Network-on-Chip. In Proceedings of the conference on Design, Automation & Test in Europe, Dresden, Germany, 24–28 March 2014; pp. 1–6.
- Le Beux, S.; Li, H.; Nicolescu, G.; Trajkovic, J.; O’Connor, I. Optical crossbars on chip, a comparative study based on worst-case losses. Concurr. Comput. Pract. Exp. 2014, 26, 2492–2503. [Google Scholar] [CrossRef]
- Vantrease, D.; Schreiber, R.; Monchiero, M.; McLaren, M.; Jouppi, N.; Fiorentino, M.; Davis, A.; Binkert, N.; Beausoleil, R.; Ahn, J. Corona: System implications of emerging nanophotonic technology. In Proceedings of the 35th Annual International Symposium on Computer Architecture, Beijing, China, 21–25 June 2008; pp. 153–164.
- Pan, Y.; Kumar, P.; Kim, J.; Memik, G.; Zhang, Y.; Choudhary, A. Firefly: Illuminating future network-on-chip with nanophotonics. In Proceedings of the 36th Annual International Symposium on Computer Architecture, San Diego, CA, USA, 3–5 December 2009; pp. 429–440.
- Shacham, A.; Bergman, K.; Carloni, L.P. The case for low-power photonic networks on chip. In Proceedings of the 44th Annual Design Automation Conference, San Diego, CA, USA, 4–8 June 2007; pp. 132–135.
- Bahirat, S.; Pasricha, S. METEOR: Hybrid Photonic Ring-Mesh Network-on-Chip for Multicore Architectures. ACM Trans. Embed. Comput. Syst. TECS. 2014, 13, 116:1–116:33. [Google Scholar] [CrossRef]
- Li, Z.; Fay, D.; Mickelson, A.; Shang, L.; Vachharajani, M.; Filipovic, D.; Park, W.; Sun, Y. Spectrum: A hybrid nanophotonic-electric on-chip network. In Proceedings of the 46th Annual Design Automation Conference, San Francisco, CA, USA, 26–31 July 2009; pp. 575–580.
- Joshi, A.; Batten, C.; Kwon, Y.; Beamer, S.; Shamim, I.; Asanovic, K.; Stojanovic, V. Silicon-Photonic clos networks for global on-chip communication. In Proceedings of the 2009 3rd ACM/IEEE International Symposium on Networks-on-Chip, San Diego, CA, USA, 10–13 May 2009; pp. 124–133.
- Morris, R.W.; Kodi, A.K. Power-efficient and high-performance multi-level hybrid nanophotonic interconnect for Multicores. In Proceedings of the 2010 Fourth ACM/IEEE International Symposium on Networks-on-Chip, Grenoble, France, 3–6 May 2010; pp. 207–214.
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Mazumder, P. Genetic Algorithms for VLSI Design, Layout and Test Automation; Prentice-Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Eberhart, R.; Kenned, J. A new optimizer using particle swarm theory. In Proceedings of the 6th International Symposium on Micromachine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43.
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. B 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Goldberg, D. Genetic Algorithms in Search, Optimization and Machine Learning; Kluwer Academic Publishers: Boston, MA, USA, 1989. [Google Scholar]
- Bahirat, S.; Pasricha, S. A particle swarm optimization approach for synthesizing application-specific hybrid photonic networks-on-chip. In Proceedings of the 17th International Conference on Parallel Architectures and Compilation Techniques, Toronto, ON, Canada, 25–29 October 2012; pp. 78–83.
- Collet, J.H.; Caignet, F.; Sellaye, F.; Litaize, D. Performance constraints for onchip optical interconnects. IEEE J. Sel. Top. Quantum Electron. 2003, 9, 425–432. [Google Scholar] [CrossRef]
- Tosik, G.; Gaffiot, F.; Lisik, Z.; O’Connor, I.; Tissafi-Drissi, F. Power dissipation in optical and metallic clock distribution networks in new VLSI technologies. Electron. Lett. 2004, 40, 198–200. [Google Scholar] [CrossRef]
- Kobrinsky, M.; Block, B.; Zheng, J.-F.; Barnett, B.; Mohammed, E.; Reshotko, M.; Robertson, F.; List, S.; Young, I.; Cadien, K. On-chip optical interconnects. Intel Technol. J. 2004, 2, 129–142. [Google Scholar]
- Bahirat, S.; Pasricha, S. HELIX: Design and synthesis of hybrid nanophotonic application-specific network-on-chip architectures. In Proceedings of the Fifteenth International Symposium on Quality Electronic Design, Santa Clara, CA, USA, 3–5 March 2014; pp. 91–98.
- Wang, J.; Zhu, M.; Peng, C.; Zhou, L.; Qian, Y.; Dou, W. Software-defined photonic network-on-chip. In Proceedings of the 2014 Third International Conference on E-Technologies and Networks for Development (ICeND), Beirut, Lebanon, 29 April–1 May 2014; pp. 127–130.
- Browning, M.; Li, C.; Gratz, P.; Palermo, S. LumiNOC: A low-latency, high-bandwidth per Watt, photonic Network-on-Chip. In Proceedings of the 2013 ACM/IEEE International Workshop on System Level Interconnect Prediction (SLIP), Austin, TX, USA, 2 June 2013; pp. 1–4.
- Ahmed, A.; Meyer, M.; Okuyama, Y.; Abdallah, A. Hybrid Photonic NoC Based on Non-Blocking Photonic Switch and Light-Weight Electronic Router. In Proceedings of the 2015 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Kowloon, Hong Kong, 9–12 October 2015; pp. 56–61.
- Pintus, P.; Gambini, F.; Faralli, S.; Pasquale, F.; Cerutti, I.; Andriolli, N. Ring Versus Bus: A Theoretical and Experimental Comparison of Photonic Integrated NoC. J. Lightwave Technol. 2015, 33, 4870–4877. [Google Scholar] [CrossRef]
- Li, Z.; Qouneh, M.; Joshi, M.; Zhang, W.; Fu, X.; Li, T. Aurora: A Cross-Layer Solution for Thermally Resilient Photonic Network-on-Chip. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2015, 23, 173–183. [Google Scholar]
- Murali, S.; Micheli, G.D. Bandwidth-Constrained Mapping of Cores onto NoC Architectures. In Proceedings of the Conference on Design, Automation and Test in Europe, Paris, France, 16–20 February 2004; Volume 2, pp. 896–901.
- Ascia, G.; Catania, V.; Palesi, M. Multi-objective mapping for mesh-based noc architectures. In Proceedings of the 2nd IEEE/ACM/IFIP International Conference on Hardware/Software Codesign and System Synthesis, Stockholm, Sweden, 8–10 September 2004; pp. 182–187.
- Hu, J.; Marculescu, R. Energy-aware mapping for tile-based noc architectures under performance constraints. In Proceedings of the 2003 Asia and South Pacific Design Automation Conference, Kitakyushu, Japan, 21–24 January 2003; pp. 233–239.
- Kapadia, N.; Pasricha, S. VISION: A framework for voltage island aware synthesis of interconnection networks-on-chip. In Proceedings of the 21st Edition of the Great Lakes Symposium on Great Lakes Symposium on VLSI, Lausanne, Switzerland, 2–4 May 2011; pp. 31–36.
- Murali, S.; Meloni, P.; Angiolini, F.; Atienza, D.; Carta, S.; Benini, L.; Micheli, G.D.; Raffo, L. Designing application-specific networks on chips with floorplan information. In Proceedings of the 2006 IEEE/ACM International Conference on Computer-Aided Design, San Jose, CA, USA, 5–9 November 2006; pp. 355–362.
- Kapadia, N.; Pasricha, S. A System-Level Cosynthesis Framework for Power Delivery and On-Chip Data Networks in Application-Specific 3-D ICs. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2016, 24, 3–16. [Google Scholar] [CrossRef]
- Srinivasan, K.; Chatha, K.S. A low complexity heuristic for design of custom network-on-chip architectures. In Proceedings of the Conference on Design, Automation and Test in Europe, Munich, Germany, 6–10 March 2006; pp. 130–135.
- Chan, J.; Parameswaran, S. NoCOUT: NoC topology generation with mixed packet-switched and point-to-point networks. In Proceedings of the 2008 Asia and South Pacific Design Automation Conference, Seoul, Korea, 21–24 January 2008; pp. 265–270.
- Kwon, S.; Pasricha, S.; Jeonghun, C. POSEIDON: A framework for application-specific network-on-chip synthesis for heterogeneous chip multiprocessors. In Proceedings of the 2011 12th International Symposium on Quality Electronic Design (ISQED), Santa Clara, CA, USA, 14–16 March 2011; pp. 1–7.
- Teo, C.; Foo, Y.; Chien, S.; Low, A.; Venkatesh, B.; You, A. Optimal placement of wavelength converters in WDM networks using particle swarm optimizer. In Proceedings of the 2004 IEEE International Conference on Communications, Paris, France, 20–24 June 2004; pp. 1669–1673.
- Payet, M.; Fresse, V.; Rousseau, F.; Remy, P. Dynamic data flow analysis for NoC based application synthesis. In Proceedings of the International Symposium on Rapid System Prototyping (RSP), Amsterdam, The Netherlands, 8–9 October 2015; pp. 61–67.
- Romanov, A.; Romanova, I. Use of irregular topologies for the synthesis of networks-on-chip. In Proceedings of the 2015 IEEE 35th International Conference on Electronics and Nanotechnology, Kiev, Ukraine, 21–24 April 2015; pp. 445–449.
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equations of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Černý, V. A thermodynamical approach to the travelling salesman problem: An efficient simulation algorithm. J. Optim. Theory Appl. 1985, 45, 41–51. [Google Scholar] [CrossRef]
- Lundy, M.; Mees, A. Convergence of an Annealing Algorithm. Math. Prog. 1986, 34, 111–124. [Google Scholar] [CrossRef]
- SystemC Initiative. Available online: http://www.systemc.org (accessed on 6 December 2015).
- Woo, S.C.; Ohara, M.; Torrie, E.; Singh, J.P.; Gupta, A. The SPLASH-2 programs: Characterization and methodological considerations. In Proceedings of the 22nd Annual International Symposium on Computer Architecture, Santa Margherita Ligure, Italy, 22–24 June 1995; pp. 24–36.
- Jin, H.; Frumkin, M.; Yan, J. The OpenMP Implementation of NAS Parallel Benchmarks and Its Performance; Technical Report NAS-99-011; NASA Ames Research Center: Mountain View, CA, USA, 1999. [Google Scholar]
- Bienia, C.; Kumar, S.; Singh, J.; Li, K. The PARSEC benchmark suite: characterization and architectural implications. In Proceedings of the 7th International Conference on Parallel Architectures and Compilation Techniques, New York, NY, USA, 25–29 October 2008; pp. 72–81.
- Barwicz, T.; Byun, H.; Gan, F.; Holzwarth, C.W.; Popovic, M.A.; Rakich, P.T.; Watts, M.R.; Ippen, E.P.; Kartner, F.X.; Smith, H.I.; et al. Silicon photonics for compact energy-efficient interconnects. J. Opt. Netw. 2007, 6, 63–73. [Google Scholar] [CrossRef]
- Hsieh, I.-W.; Chen, X.; Dadap, J.; Panoiu, N.; Osgood, R.; McNab, S.; Vlasov, Y. Ultrafast-pulse self-phase modulation and third-order dispersion in si photonic wire-waveguides. Opt. Express 2006, 14, 12380–12387. [Google Scholar] [CrossRef] [PubMed]
- Haurylau, M.; Chen, H.; Zhang, J.; Chen, G.; Nelson, N.; Albonesi, D.; Friedman, E.; Fauchet, P. On-chip optical interconnect roadmap: Challenges and critical directions. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 1699–1705. [Google Scholar] [CrossRef]
- Kahng, A.; Bin, L.; Li-Shiuan, P.; Samadi, K. ORION 2.0: A fast and accurate NoC power and area model for early-stage design space exploration. In Proceedings of the 2009 Design, Automation and Test in Europe Conference (DATE), Nice, France, 20–24 April 2009; pp. 423–428.














| Synthesis Parameters | Range Low | Range High |
|---|---|---|
| Photonic Uplinks | 4 | 32 |
| PRI | 1 | (num cores)/4 |
| WDM Density | 32 | 256 |
| Searialization Degree | 1 | 32 |
| Clock Frequency (GHz) | 1 | 6 |
| PRI data size threshold (Mth) | 4 | 1024 |
| Flit Width (bytes) | 4 | 256 |
| Waveguides | 2 | 256 |
| Component | Delay | DDE | SE | TTE |
|---|---|---|---|---|
| Modulator Driver | 9.5 ps | 20 fJ/bit | 5 fJ/bit | 16 fJ/bit/heater |
| Modulator | 3.1 ps | |||
| Waveguide | 15.4 ps/mm | - | - | - |
| Photo Detector | 0.22 ps | 20 fJ/bit | 20 fJ/bit | 16 fJ/bit/heater |
| Receiver | 4.0 ps |
| Synthesis Parameters | barns | lu | cholesky | fft | fmm | radiosity | radix |
|---|---|---|---|---|---|---|---|
| WDM | 68 | 122 | 44 | 83 | 135 | 132 | 143 |
| Uplinks | 4 | 4 | 4 | 4 | 4 | 8 | 12 |
| PRI | 15 | 12 | 10 | 10 | 12 | 12 | 12 |
| PRI Data Threshold | 96 | 4 | 120 | 48 | 7 | 54 | 96 |
| Clock Frequency | 5 | 4 | 5 | 4 | 4 | 2 | 2 |
| Source PRI Uplink | 9 | 7 | 8 | 9 | 8 | 9 | 9 |
| Dest PRI Uplinks | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| Flit Width | 43 | 256 | 28 | 85 | 256 | 128 | 128 |
| Serialization | 6 | 1 | 9 | 3 | 1 | 2 | 2 |
| Waveguides | 18 | 12 | 135 | 136 | 112 | 20 | 18 |
| Synthesis Parameters | barns | lu | cholesky | fft | fmm | radiosity | radix |
|---|---|---|---|---|---|---|---|
| WDM | 128 | 56 | 145 | 138 | 56 | 67 | 166 |
| Uplinks | 4 | 4 | 4 | 4 | 4 | 8 | 12 |
| PRI | 4 | 4 | 4 | 4 | 8 | 8 | 8 |
| PRI Data Threshold | 72 | 32 | 56 | 46 | 186 | 459 | 148 |
| Clock Frequency | 4 | 2 | 4 | 5 | 4 | 5 | 5 |
| Source PRI Uplink | 4 | 4 | 4 | 4 | 4 | 8 | 12 |
| Dest PRI Uplinks | 4 | 4 | 4 | 4 | 4 | 58 | 12 |
| Flit Width | 28 | 64 | 46 | 49 | 28 | 28 | 42 |
| Serialization | 12 | 4 | 3 | 8 | 12 | 18 | 10 |
| Waveguides | 48 | 32 | 58 | 108 | 128 | 128 | 256 |
| Synthesis Parameters | barns | lu | cholesky | fft | fmm | radiosity | radix |
|---|---|---|---|---|---|---|---|
| WDM | 102 | 79 | 58 | 128 | 93 | 141 | 63 |
| Uplinks | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| PRI | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| PRI Data Threshold | 176 | 16 | 60 | 96 | 280 | 459 | 168 |
| Clock Frequency | 4 | 2 | 4 | 5 | 6 | 5 | 4 |
| Source PRI Uplink | 4 | 4 | 4 | 4 | 5 | 5 | 4 |
| Dest PRI Uplinks | 5 | 5 | 4 | 4 | 5 | 5 | 4 |
| Flit Width | 23 | 64 | 85 | 43 | 26 | 15 | 37 |
| Serialization | 11 | 4 | 3 | 6 | 10 | 17 | 7 |
| Waveguides | 48 | 2 | 25 | 200 | 105 | 128 | 90 |
| Synthesis Parameters | barns | lu | cholesky | fft | fmm | radiosity | radix |
|---|---|---|---|---|---|---|---|
| WDM | 89 | 73 | 56 | 89 | 67 | 130 | 67 |
| Uplinks | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| PRI | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| PRI Data Threshold | 223 | 23 | 45 | 78 | 139 | 320 | 123 |
| Clock Frequency | 3 | 3 | 3 | 3 | 4 | 4 | 3 |
| Source PRI Uplink | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| Dest PRI Uplinks | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| Flit Width | 28 | 78 | 56 | 43 | 22 | 12 | 38 |
| Serialization | 11 | 12 | 13 | 11 | 11 | 12 | 11 |
| Waveguides | 35 | 25 | 45 | 178 | 99 | 111 | 89 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bahirat, S.; Pasricha, S. A Software Framework for Rapid Application-Specific Hybrid Photonic Network-on-Chip Synthesis. Electronics 2016, 5, 21. https://doi.org/10.3390/electronics5020021
Bahirat S, Pasricha S. A Software Framework for Rapid Application-Specific Hybrid Photonic Network-on-Chip Synthesis. Electronics. 2016; 5(2):21. https://doi.org/10.3390/electronics5020021
Chicago/Turabian StyleBahirat, Shirish, and Sudeep Pasricha. 2016. "A Software Framework for Rapid Application-Specific Hybrid Photonic Network-on-Chip Synthesis" Electronics 5, no. 2: 21. https://doi.org/10.3390/electronics5020021
APA StyleBahirat, S., & Pasricha, S. (2016). A Software Framework for Rapid Application-Specific Hybrid Photonic Network-on-Chip Synthesis. Electronics, 5(2), 21. https://doi.org/10.3390/electronics5020021